Abstract
Birthweight and gestational age are closely related and represent important indicators of a healthy pregnancy. Customary modeling for birthweight is conditional on gestational age. However, joint modeling directly addresses the relationship between gestational age and birthweight, and provides increased flexibility and interpretation as well as a strategy to avoid using gestational age as an intermediate variable. Previous proposals have utilized finite mixtures of bivariate regression models to incorporate well-established risk factors into analysis (e.g. sex and birth order of the baby, maternal age, race, and tobacco use) while examining the non-Gaussian shape of the joint birthweight and gestational age distribution. We build on this approach by demonstrating the inferential (prognostic) benefits of joint modeling (e.g. investigation of `age inappropriate' outcomes like small for gestational age) and hence re-emphasize the importance of capturing the non-Gaussian distributional shapes. We additionally extend current models through a latent specification which admits interval-censored gestational age. We work within a Bayesian framework which enables inference beyond customary parameter estimation and prediction as well as exact uncertainty assessment. The model is applied to a portion of the 2003–2006 North Carolina Detailed Birth Record data (n=336129) available through the Children's Environmental Health Initiative and is fitted using the Bayesian methodology and Markov chain Monte Carlo approaches.
Keywords: finite mixture model, hierarchical modeling, intermediate variable bias, interval censoring
1. Introduction
In this paper, on the merits of improved flexibility and interpretation (similarly argued by Tassone et al. [1]) we further investigate proposals in the spirit of Gage [2] and Ananth et al. [3] to use birthweight and gestational age as a joint outcome. In addition to illuminating the inferential (prognostic) uses and benefits of joint modeling, we clarify the advantages of bivariate covariance adjustment over, for example birthweight conditional on gestational age analyses, and extend the current proposals by providing a model that recognizes interval-censored gestational age (to the nearest completed week). Our approach is described and implemented in a Bayesian framework which enables inference beyond customary parameter estimation and prediction and exact assessment of uncertainty. It is demonstrated using the North Carolina Detailed Birth Record (NCDBR) database.
In Section 1.1, we briefly review the relevance and progress of birthweight and gestational age analyses, and position our work in this literature. Section 1.2 describes our motivating application data, the NCDBR. Section 2 reintroduces the finite mixture of bivariate regressions model specification for the joint variable birthweight and gestational age [2, 4, 5] and extends the model to allow for the common interval censored form of gestational age. In Section 3, the consequences of analyses using intermediate variables (e.g. birthweight conditional on gestational age analyses) are highlighted in contrast to joint analyses. Section 4 addresses model identifiability concerns. Finally, in Section 5 the inferential benefits of the bivariate model are demonstrated (e.g. in examination of disparities within the general population), as well as recovery of `conditional' results.
1.1. The birthweight and gestational age tradition
Low birthweight (LBW, <2500 g) and Preterm birth (PTB, <37 weeks gestational age) have long been associated with many adverse birth and developmental outcomes (e.g. [6, 7]). However, the joint role of birthweight and gestational age, while recognized, is not well understood. Often, Small for Gestational Age (SGA, smallest 10 per cent of birthweights for a gestational age) is used as a proxy for birthweight and gestational age's joint information. While LBW, PTB, and SGA are used prospectively as indicators of potential birth complications, their physiological importance is not so clear cut; as Grimes [8] relates, these classifications achieve relevant sensitivity to adverse birth outcomes (Type I error) at the cost of specificity (Type II error), often not corresponding to medical signs of abnormalities. For instance, Wilcox [9] notes that interventions aimed at reducing LBW have not yet met with success despite the widespread interpretation of LBW as a cause of adverse birth outcomes (e.g. [10]).
Work seeking to understand variables, such as LBW, PTB, and SGA, has thus far proved to be very productive, though it has perhaps not yet made its way into common practice. For instance, Wilcox [11] has brought attention to the varied relevance of LBW by sub-population (partially as a byproduct of arbitrary specification), and Platt et al. [12] and Hernández-Díaz et al. [13] have provided complementary constructive advice concerning once puzzling `birthweight paradoxes' (e.g. the `smokers' paradox) as they relate to `at risk' denominators and bias inducing statistical paradoxes, respectively. The former [12, 14–16] is particularly notable since it clarifies the difference between treating gestational age as a time axis versus a covariate (which does not capitalize on the temporal nature of gestational age). Namely, covariate strategies imply comparisons within gestational age week strata which is prognostic in nature whereas time axis strategies compare among the `at risk' population which is more traditionally `causal' in nature. Our emphasis, however, relates more to the latter [13] since it shows that the use of intermediate variables may introduce bias and thus provide an impetus for joint modeling.
One area of research frequently pursued is the exploration of LBW and PTB as adverse birth outcomes themselves, and some effort has been spent in carefully modeling these contexts (e.g. [9, 17–22]). The proposal to study birthweight and gestational age as a joint variable soon followed as the natural course of this tradition, and has appeared in several places, notably, [2] and [3]. Models for the joint birthweight and gestational age variable have subsequently been incorporated as sub-models in analyses of further adverse birth outcomes (e.g. fetal death), as in [4, 5]. These models introduce a logistic regression conditional birthweight and gestational age to model a trivariate outcome. As gestational age is again used as a covariate rather than as a time axis these models are prognostic in nature as indicated by the discussion from Platt et al. [12].
This work pursues the original proposal to study birthweight and gestational age jointly and re-emphasizes that they are intimately related and thus natural candidates for a joint outcome. Further, jointly modeling birthweight and gestational age provides a means to bypass the potential difficulties associated with conditional modeling while at the same time facilitating understanding and interpretation of these important indicators of pregnancy health.
1.2. Data application: NCDBR
Through a negotiated data sharing agreement with the NC state center for health statistics, the Children's Environmental Health Initiative (CEHI) at Duke University has access to the NCDBR. These data include birth certificate information about all NC births from 1990 to 2007 (n=1862405 births). We limit our study to birth records from 2004 to 2006, (n=371924). We further restrict our data set to women who self-declare as non-Hispanic white (NHW), non-Hispanic black (NHB), and Hispanic (H) mothers, aged 15–44, who report no alcohol use during pregnancy. We only consider singleton births with no congenital anomalies, birthweight greater than 399 g, and gestational age from 24 to 42 weeks. Finally, we proceed with a complete case analysis using the variables' birthweight, gestational age, reported smoking, infant sex, reported marital status, maternal race, maternal age (15–19, 20–24, 30–34, 35–39, 40–44, and the referent 25–29), maternal education (middle-school or less, some high school, some college, at least college, and the referent high school), and first birth infant. Thus our final data set has n=336129 observations. The population characteristics of this data set is given in the table in the final column labeled `Overall'. This research was conducted according to a human subjects research protocol approved by the University's institutional review board.
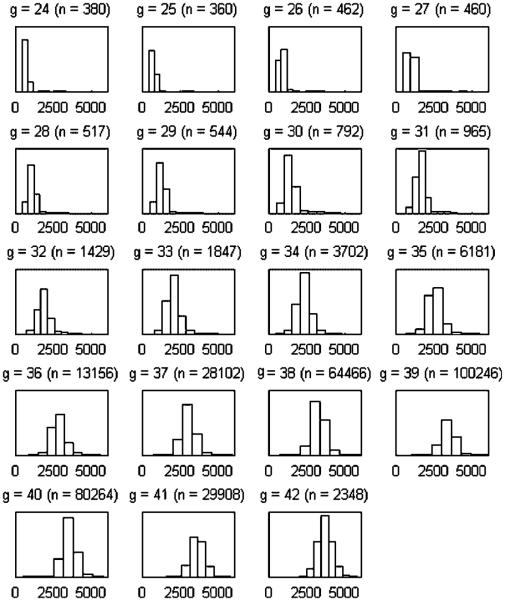
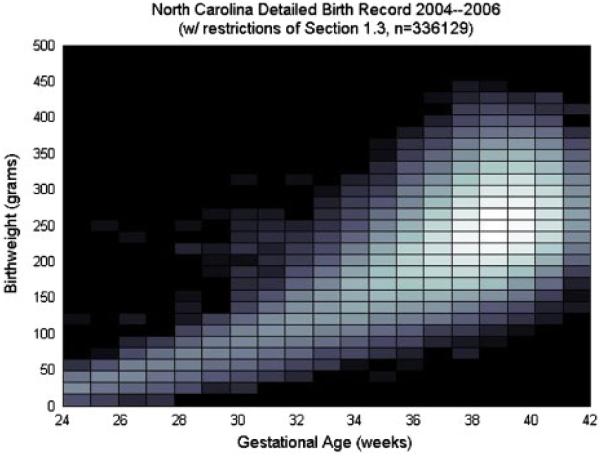
Birthweight is reported in pounds and ounces and converted to grams for the analysis. Gestational age is reported as a clinical estimate of the number of weeks' gestation completed. Gestational age is thus a (censored) integer valued response. Figure 1 displays the histograms of the birthweights for each gestational age from 24 to 42, a conditional description. Figure 2 displays the same data in `bivariate' form. Both figures reveal the strong dependence between the birthweight and gestational age with the latter revealing that a simple bivariate Gaussian specification may not suffice.
Figure 1.
Histograms of birthweight by gestational age (g, 24–42) for the data subset described in Section 1.2.
Figure 2.
A log-scale heatmap version of a bivariate histogram of birthweight and gestational ages for the data subset described in Section 1.2.
2. Joint birthweight and gestational age model
2.1. Likelihood specification
The unique shape of the joint birthweight and gestational age distribution (see Figure 2) can be flexibly modeled using finite-mixture models [23, 24] as discussed in [2, 4, 5]. We use the s-component mixture model specified by normal distributions
| (1) |
i.e. each component is specified as a marginal times conditional form which allows, within component, the quite natural interpretation of birthweight conditional on the gestational age. In (1), for individual i, bi, and gi are the (continuous) variables' birthweight and gestational age, respectively, and is the vector of risk factors with coefficients βk and intercept μk. The mixing weights (which sum to 1) are πk, and the variances are given by the σ2's. As shown in Section 5.1, we found justification for allowing coefficient parameters to differ by component.
The `centering' (see [25]) of gi in (1) results in the equivalent bivariate regression mixture model specification
with
where
Model (1) provides the framework to treat birthweight and gestational age as a (continuous) joint variable. The bivariate regression structure incorporates covariates into the component means (though not in the mixing proportions as proposed in the univariate case in [26]). The mixture portion of the model provides a flexible structure to model the resulting residuals for bi and gi given , i.e. .
The mixture structure for the residuals provides aggregated bivariate structure for birthweight and gestational age. The local-scale structure within each component is modeled by ρk which depends on β*k, σb|g,k, and σg,k. Both covariate coefficients and resulting birthweight and gestational age residuals are component dependent due to the component-varying parameters. The covariance structure Sk also varies by component. Finally, conditional models may be recovered from our joint specification; e.g. the conditional distribution bi|gi can be derived from (1) and is , where qk(gi)=πkfk(gi).
2.2. Additional specification
In contrast to Gage et al. [2, 4, 5] who use direct maximum likelihood (ML) estimation, we employ the data augmented form for finite mixture models and introduce latent indicators vi~MN(π1,⋯,πs), , denoting the component to which (gi,bi)′ belongs. The resulting model is marginally equivalent to the original specification:
| (2) |
Under this specification, ML estimation of model parameters proceeds through the Expectation-Maximization (EM) algorithm, whereas full Bayesian posterior inference proceeds by specifying priors and utilizing Markov chain Monte Carlo (MCMC) methodology. The details can be found in [23] and [24]. Whereas Gage [2] uses a bootstrapping approach to estimate parameter uncertainty, we pursue full Bayesian inference via a Gibbs sampling algorithm to directly provide parameter estimates and the associated uncertainty [27, 28]. To complete our specification, we employ the following conjugate and assumed mutually independent prior distributions for the model parameters:
| (3) |
where μk has been incorporated into βk. This specification avoids the use of Inverse-Wishart prior specifications for the covariance matrix of birthweight and gestational age.
2.3. Censored continuous gestational age
Within the proposed framework we can readily deal with the often ignored issue of interval censorship of gestational age. Gestational age is reported in many ways, though all are typically interval censored. A standard reporting measure of gestational age is as Last Menstrual Period (LMP), which is reported as days since LMP. On the other hand, our gestational age data is reported as an integer representing the clinical estimate of the number of completed weeks of gestation (no uniform definition exists and the meaning of `clinically estimated gestational age' varies by state). We imagine gi to be the true gestational age (a continuous variable) which we are unable to observe. We assume that the observed is an interval-censored version of gi. For the NCDBR data, we observe the number of complete weeks hence . Defining , we assign ui∈[0,1) to take the role of an unknown parameter. If is interpreted differently we would modify this specification accordingly. For instance, if we had LMP gestational age we could introduce a Berkson measurement error model, centering true gi around the observed gestational age in days.
Upon specification of a prior, ui may be seamlessly incorporated into the posterior sampling scheme. The simple prior we use is ui~U[0,1). However, it may be argued that, given , the distribution for gi is likely to put more mass on days later in the week, i.e. the probability of birth increases on a daily basis, particularly for preterm and early term gestational ages. Thus, a more general beta prior for ui is an alternate choice. Using ui~Beta(ai,ri) specifies a non-conjugate prior for this model, requiring a Metropolis-Hastings or Importance sampling step in the model fitting. The truncated conjugate prior may also be considered.
Recognizing the censored nature of reported gestational age measurements allows us to: (1) treat gestational age as a continuous parameter; (2) acknowledge the uncertainty associated with censorship of gestational age; and (3) allow the data to inform us about the actual effect of the censorship (ui).
Clinically estimated gestational age and LMP measurements are known to have error, indeed, with certain sub-populations possibly having more or less accurate reporting of the gestational age than others. The model presented here assumes that the reported clinical estimate of gestational age is accurate. For our data, clinical estimates of gestational age for many sub-populations are considered to be relatively reliable post 2000, whereas for the remaining sub-populations this may not be so. The nature, effect, and size of such bias in our model is unclear. However, this consideration, in part, influenced our data restriction to the years 2004–2006. Alternative measures of gestational age such as ultrasound are more precise, but LMP and (many) clinical estimations of gestational age remain much more prevalent. As such, models that can account for measurement error are still needed.
3. Bivariate modeling vs conditional modeling
A wide range of literature cautions against the `fallacy of controlling for an intermediate outcome' [13, 29–37]. The apparent alternative to exclude intermediate variables from analyses does not seem reasonable in the birthweight and gestational age context. For example, in the context of a `birthweight conditional on gestational age' analysis, ignoring gestational age entails a large loss of information, as evidenced by Wilcox and Skjaerven [17]. Unfortunately, as is now understood, adjusting for an intermediate variable can result in the other observed covariate effects being wrongly boosted, attenuated, or even reversed. This happens for two reasons: (1) indirect effects of covariates which were mediated through gestational age are no longer attributed to the covariates (see, e.g. the reduced effect of smoking in [3]) and (2) spurious associations are artificially induced by back-door criteria violations caused by conditioning on an intermediate variable (e.g. Berkson's and Simpson's paradox). These issues were noted by Gage [2] and the above citations connect this rightful concern to the additional literature.
Using the data subset described in Section 1.3, we demonstrate the extent of change brought about by these issues in regression coefficients using ordinary least squares. Table I shows the coefficients resulting from birthweight regressions with and without gestational age as a covariate. Nearly all coefficients change between regressions, some (e.g. smoking and NHB mother) are attenuated, whereas others (e.g. Infant sex and H mother) are boosted; some coefficients even have sign changes. The direction and extent of difference suggests that the behavior of lost mediated effect is due to controlling for gestational age. However, the difference may instead be due to the interference of spurious relationships artificially induced by back-door criteria violations. Because the relative contributions of back-door effect and lost mediated effect cannot be separated, intermediate variables should be used as covariates if coefficients are to retain their meaningful interpretation. Ignoring an intermediate variable (e.g. gestational age) is not necessary, however, if one employs joint modeling techniques. The modeled bivariate relationship of birthweight and gestational age replaces the use of either as an intermediate variable in a conditional model.
Table I.
Birthweight (standard) regressions with/without gestational age included; 95 per cent confidence intervals are also included.
| Covariate | Birthweight regression coefficients | |||
|---|---|---|---|---|
| Intercept | −3578.8 | (−3606.9,−3550.7) | 3385.5 | (3379.7,3391.4) |
| Reported maternal smoking | −187.8 | (−192.5,−183.0) | −227.2 | (−233.4,−221.0) |
| Male infant | 126.2 | (123.4,129.0) | 114.1 | (110.3,117.8) |
| Mother reported not married | −36.2 | (−39.8,−32.5) | −39.6 | (−44.4,−34.7) |
| Non-Hispanic black mother | −176.5 | (−180.3,−172.7) | −233.7 | (−238.7,−228.6) |
| Hispanic mother | −70.2 | (−75.1,−65.2) | −24.3 | (−30.8,−17.9) |
| Mother complete MS | −30.1 | (−36.9,−23.3) | −25.9 | (−34.7,−17.0) |
| Mother complete some HS | −30.2 | (−34.9,−25.5) | −39.2 | (−45.3,−33.0) |
| Mother complete some college | 26.5 | (22.3,30.6) | 27.3 | (21.8,32.7) |
| Mother complete college | 28.5 | (23.9,33.0) | 65.4 | (59.4,71.3) |
| Maternal age 15–19 | −35.4 | (−41.2,−29.5) | −26.9 | (−34.5,−19.2) |
| Maternal age 20–24 | −27.0 | (−31.0,−22.9) | −14.0 | (−19.4,−8.7) |
| Maternal age 30–34 | 18.1 | (13.9,22.2) | 0.8 | (−4.6,6.3) |
| Maternal age 35–40 | 21.9 | (16.5,27.2) | −15.3 | (−22.3,−8.3) |
| Maternal age 41–45 | −0.4 | (−11.2,10.3) | −58.7 | (−72.8,−44.6) |
| First birth infant | −120.1 | (−123.3,−116.9) | −93.9 | (−98.1,−89.7) |
| Gestational age | 180.2 | (179.5,180.9) | ||
4. Identifiability
4.1. Alternative non-identified parameterization
Correlation between MCMC posterior draws of parameters can render attempted posterior sampling useless (see, e.g. [25, 38]). The `centering' of g in our model curbs such unattractive circumstances. If we do not `center' in (1), and replace with only gi, we have that . It follows that μb,k,β*,k and βb,k will tend to drift as only the sums they are involved in are identified.
4.2. More identifiability and number of components
Model (1) is invariant under re-ordering of the labels k, i.e. k! differently parameterizations result in identical models. This well-known conundrum for mixture models known as `label switching' is discussed in [39]. Often, order constraints on parameters (e.g. θi<θj for i<j) are utilized to identify components. This was our initial approach; however, under usual specifications of our model, the constraints never came into play: While label-switching is common in univariate normal mixture models, we observed no such label-switching in our mixing. This appears to be the result of the mixing relative to the `high-dimensional' nature of the proposed mixture model. In essence, for label switching to occur, components parameters (e.g. two `intercept' parameters, one `slope' parameter, two variance parameters) must be exchanged with their counterparts in another component.
When `many' (i.e. s=4 or more) components are specified, the posterior becomes multimodal (within the symmetric multimodality induced by label switching) and mixing across the posterior modes becomes poor. With s=4 components, the observed parallel posterior chains (with different initial value specifications) did not meet and instead each exhibited intermittent periods of apparent stability punctuated by sporadic—often slightly less favorable (as judged by log-likelihood)—re-configurations (rarely returning to the original configuration). The re-configurations amounted to slight changes in the component location and almost no detectable difference in the covariate coefficients. Thus, the mixing issue appears to be primarily one of location of the residual components. Nevertheless, the posterior chains showed several different plausible models, none of which appeared preeminent, and across which mixing was poor (indeed, we did not uncover label switching which would indicate good mixing). It is possible that a Metropolis step within the Gibbs sampler we employed could improve mixing, but we have not experimented with this. This same circumstance of `numerous adequate models' no doubt exists under ML estimation, but is more easily uncovered through Bayesian analysis since in ML estimation only a single model is returned once the maximization algorithm has `converged' (i.e. stopped making meaningful changes to the likelihood) to some mode.
Model selection involving competing unconverged chains (models) is a difficult issue. One pragmatic (though somewhat ad hoc) approach might use an EM algorithm to find the best initial values (as judged by largest likelihood), and then proceed with full Bayesian inference using the stable part of the chain. Various competing `models' may then be pragmatically chosen using minimum posterior predictive loss in cross-validation [40], or naive Bayesian information criterion (BIC). Although it is not theoretically appropriate to use BIC in the finite mixture model setting (even for converged chains), it has seen some application and success [23], and hence we pursue this criterion. For both three-component (s=3) and two-component (s=2) models, we did not observe the mixing issues described above. Indeed, proper identification of a two component (s=2) model is shown in [41]. Thus, we assumed that these models (chains) had converged and compared them using the BIC criterion which for our data set strongly suggested the superiority of three-component (s=3) models to two-component (s=2) models. Our choice to avoid comparison to any four component (s=4) models was driven by the mixing issues described above, and is thus an artifact of the operational fitting of the model rather than a judgement of clinical significance or a model choice criterion.
5. Model demonstration
This section demonstrates our three component (s=3) model using the subset of data described in Section 1.2. A wide range of alternative prior and initial value specifications produced only slightly varied results in the three-component (s=3) case, and thus we restrict our demonstration to specifications of Table II. Burn in was set at 5000; results of this section were generated from the subsequent 100 000 MCMC draws provided by the Gibbs sampler directly available under our specification. The mixing of individual chains did not show lack of convergence.
Table II.
Initial values and prior specifications for the results of a three-component (s=3) model, used throughout in Section 5.
| Comp. 1 | Comp. 2 | Comp. 3 | ||||
|---|---|---|---|---|---|---|
| Initial values |
||||||
| π | 0.34 | 0.33 | 0.33 | |||
| μ b | 3000 | 2500 | 1500 | |||
| μ g | 40 | 37 | 33 | |||
|
|
250 000 | 250 000 | 250 000 | |||
|
|
2 | 2 | 2 | |||
| β |
|
|
|
|||
| Prior hyperparameter values |
||||||
| p | 1 | 1 | 1 | |||
| μ b | 3000 | 2500 | 1500 | |||
| μ g | 40 | 37 | 33 | |||
| β 0 | μb, μg, | μb, μg, | μb, μg, | |||
| Σ 0 | 1000/ | 1000/ | 1000/ | |||
| a | 1 | 1 | 1 | |||
| r | 1 | 1 | 1 | |||
Where useful, we illustrate inference under our model through a series of `prototypical' individuals, A–H. A–H represent the possible configurations of NHB/NHW, reported smoking, and reported marital status, for a 25- to 30-year-old mother at the high school education level with a male infant. The covariate configurations of A–H are given in Table III.
Table III.
Individuals A–H provide eight risk factor sets for mothers used for demonstration in Section 5 and Tables VII–X; all mothers are 25–30 years old and at the high school education level with a male infant.
| Individual | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|
| Mother reported not married | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| Non-Hispanic black mother | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| Reported maternal smoking | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
5.1. Bivariate regression
One benefit of using a bivariate regression model is that a single model produces coefficient estimates of the relationship between birthweight and gestational to covariates (and each other) simultaneously. Further, the mixture model framework provides s=3 regressions (not just one), with each component supporting a separate regression. This allows for improved flexibility in the variety of shapes that may be captured by the model as well as the potential to uncover the differential strength of covariate effects across components as shown in Table IV. The ability to explicitly model and detect how relationships differ by component sub-populations may be contrasted with Table I.
Table IV.
Birthweight and gestational age regression coefficients with 95 per cent credible intervals for each mixture model component.
| Covariate | Component k=1 | Component k=2 | Component k=3 | ||||
|---|---|---|---|---|---|---|---|
| BW | Reported maternal smoking | −205.0 | (−211.6,−198.4) | −227.8 | (−241.3,−214.6) | −85.1 | (−116.3,−53.9) |
| Male infant | 137.2 | (133.2,141.2) | 80.7 | (72.4,88.9) | 52.6 | (29.7,75.7) | |
| Mother reported not married | −26.4 | (−31.5,−21.2) | −40.3 | (−51.0,−29.7) | −83.6 | (−109.8,−57.3) | |
| Non-Hispanic black mother | −188.4 | (−193.7,−183.0) | −231.0 | (−241.8,−220.0) | −318.0 | (−344.9,−291.2) | |
| Hispanic mother | −49.1 | (−56.1,−42.1) | 44.0 | (29.6,58.5) | 111.3 | (76.5,145.9) | |
| Mother complete MS | −26.3 | (−35.8,−16.9) | −8.8 | (−27.7,10.1) | 23.5 | (−18.5,65.1) | |
| Mother complete some HS | −35.9 | (−42.5,−29.4) | −24.9 | (−38.0,−11.7) | 10.8 | (−20.6,42.0) | |
| Mother complete some college | 20.1 | (14.4,25.8) | 47.2 | (35.4,59.2) | 49.6 | (20.4,78.7) | |
| Mother complete college | 27.8 | (21.5,34.2) | 125.9 | (112.9,139.0) | 201.5 | (169.6,233.1) | |
| Maternal age 15–19 | −51.1 | (−59.1,−43.0) | 8.5 | (−7.5,24.4) | 43.8 | (8.0,79.3) | |
| Maternal age 20–24 | −29.6 | (−35.3,−24.0) | 12.2 | (0.7,23.7) | 71.0 | (42.3,100.0) | |
| Maternal age 30–34 | 18.6 | (12.8,24.5) | 7.6 | (−4.6,19.9) | 17.1 | (−12.9,46.9) | |
| Maternal age 35–40 | 25.2 | (17.7,32.8) | −41.6 | (−57.1,−25.9) | −15.2 | (−50.2,19.4) | |
| Maternal age 41–45 | 2.3 | (−12.6,17.1) | −88.4 | (−116.5,−60.1) | −35.4 | (−83.2,12.8) | |
| First birth infant | −55.1 | (−59.6,−50.6) | −116.9 | (−126.3,−107.6) | −162.0 | (−186.5,−137.7) | |
| Residuals gestational age | 104.7 | (102.0,107.5) | 146.7 | (143.0,150.4) | 146.2 | (143.1,149.2) | |
| GA | Reported maternal smoking | −0.06 | (−0.08,−0.04) | −0.36 | (−0.41,−0.31) | −0.30 | (−0.50,−0.11) |
| Male infant | −0.01 | (−0.02,−0.00) | −0.12 | (−0.16,−0.09) | −0.09 | (−0.22,0.05) | |
| Mother reported not married | 0.07 | (0.06,0.08) | −0.07 | (−0.11,−0.03) | −0.47 | (−0.63,−0.31) | |
| Non−Hispanic black mother | −0.03 | (−0.05,−0.02) | −0.43 | (−0.47,−0.39) | −1.75 | (−1.91,−1.59) | |
| Hispanic mother | 0.19 | (0.17,0.21) | 0.42 | (0.37,0.47) | 0.52 | (0.30,0.73) | |
| Mother complete MS | 0.08 | (0.06,0.11) | −0.07 | (−0.14,0.01) | −0.04 | (−0.33,0.24) | |
| Mother complete some HS | 0.01 | (−0.00,0.03) | −0.11 | (−0.16,−0.06) | −0.04 | (−0.23,0.16) | |
| Mother complete some college | −0.04 | (−0.05,−0.02) | 0.07 | (0.03,0.12) | 0.20 | (0.02,0.38) | |
| Mother complete college | 0.05 | (0.04,0.07) | 0.39 | (0.34,0.44) | 0.94 | (0.74,1.13) | |
| Maternal age 15–19 | −0.01 | (−0.03,0.01) | 0.09 | (0.03,0.15) | 0.08 | (−0.15,0.31) | |
| Maternal age 20–24 | 0.02 | (0.01,0.03) | 0.11 | (0.06,0.15) | 0.39 | (0.21,0.57) | |
| Maternal age 30–34 | −0.04 | (−0.06,−0.03) | −0.04 | (−0.09,0.00) | 0.12 | (−0.06,0.31) | |
| Maternal age 35–40 | −0.09 | (−0.11,−0.07) | −0.21 | (−0.26,−0.15) | −0.02 | (−0.24,0.20) | |
| Maternal age 41–45 | −0.10 | (−0.13,−0.06) | −0.39 | (−0.51,−0.28) | −0.22 | (−0.59,0.14) | |
| First birth infant | 0.40 | (0.39,0.42) | −0.19 | (−0.23,−0.16) | −0.60 | (−0.75,−0.46) | |
5.2. Mixture sub-populations
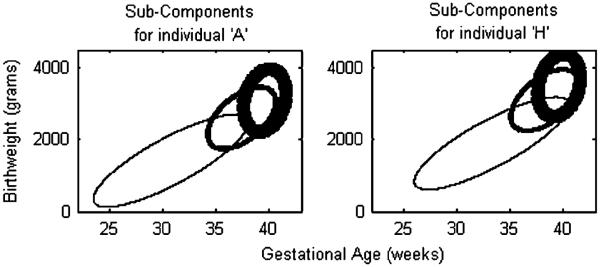
As was the emphasis in [2], a benefit of the mixture model approach is that the components provide a natural classification mechanism. In finite mixtures of regressions, this classification is an augmentation of the covariate set because the mixture feature of the model is defined on the residuals. After covariance adjustment, the leftover structure defines the components and the corresponding memberships. The location and shape parameters for the three components are given in Table V. The component configuration (distributional location) is governed by the covariates (which creates flexibility in modeling), as in Figure 3 which shows a general lowering in birthweight and lengthening of gestational age towards shorter ages for individual A relative to individual H.
Table V.
Location and shape parameter estimates with 95 per cent credible intervals for each mixture model component.
| Component k=1 | Component k=2 | Component k=3 | |||||
|---|---|---|---|---|---|---|---|
| pk | 0.716 | (0.708, 0.724) | 0.249 | (0.241, 0.257) | 0.035 | (0.034, 0.036) | |
|
|
175073 | (173 808, 176 345) | 127073 | (123 911, 130 318) | 131820 | (124 370, 139 481) | |
|
|
0.96 | (0.95, 0.97) | 2.48 | (2.42, 2.54) | 13.23 | (12.78, 13.67) | |
| μ b,k | 3514 | (3507, 3521) | 3103 | (3088, 3118) | 1899 | (1864, 1934) | |
| μ b,k | 39.59 | (39.58, 39.61) | 38.26 | (38.20, 38.32) | 33.29 | (33.07, 33.51) | |
| ρ k | 0.238 | (0.232, 0.2425) | 0.544 | (0.533, 0.555) | 0.826 | (0.816, 0.835) | |
Figure 3.
A posterior point estimate of the component configuration for individual A. The ellipses correspond to contours containing ≈86.5 per cent of mass associated with the component. The thickness conveys the relative proportions in the mixture distribution (see Table V).
Under our latent indicator specification (Section 2.2), the components are formed by repeatedly stochastically assigning every individual observation i membership in one of the components. Specifically, for each posterior iteration t, every individual i is randomly assigned to a component according to probabilities of component membership (under the current iteration of the model: θ(t)) determined by the residual resulting from bi,gi, and ; the memberships then inform the components for the next iteration, and θ(t) in general. The posterior distribution of vi,k expresses the propensity for individual i to join component k, and allows us to learn about the propensities of individual i, or perhaps the propensities of a collection of individuals. We can also learn about the overall composition of covariates across components, as in Table VI.
Table VI.
The compositional makeup of each mixture model component as observed in posterior sampling.
| Component composition | Component 1 | Component 2 | Component 3 | Overall |
|---|---|---|---|---|
| Subcomponent size | 240679.77 (2 401 180, 241 120) | 83702.95 (83 301, 84 277) | 11746.28 (11 600, 11 905) | 336 129 |
| Reported maternal smoking (per cent) | 11.6 (11.6, 11.7) | 12.0 (11.8, 12.2) | 14.3 (13.9, 14.7) | 11.8 |
| Male infant (per cent) | 51.0 (50.9, 51.1) | 51.1 (50.9, 51.4) | 53.1 (52.4, 53.8) | 51.1 |
| Mother reported not married (per cent) | 38.1 (38.0, 38.2) | 38.8 (38.5, 39.1) | 44.5 (44.0, 45.2) | 38.5 |
| Non-Hispanic black mother (per cent) | 23.3 (23.2, 23.3) | 23.9 (23.7, 24.1) | 30.8 (30.3, 31.3) | 23.7 |
| Hispanic mother (per cent) | 16.4 (16.3, 16.5) | 16.5 (16.3, 16.8) | 15.0 (14.6, 15.6) | 16.4 |
| Mother completed MS (per cent) | 7.2 (7.1, 7.2) | 7.3 (7.2, 7.5) | 6.8 (6.5, 7.2) | 7.2 |
| Mother completed some HS (per cent) | 15.9 (15.8, 16.0) | 16.3 (16.1, 16.6) | 18.0 (17.5, 18.4) | 16.1 |
| Mother completed some college (per cent) | 22.1 (22.0, 22.2) | 22.1 (21.8, 22.3) | 22.3 (21.8, 22.9) | 22.1 |
| Mother completed college (per cent) | 26.1 (26.0, 26.2) | 25.6 (25.4, 25.8) | 23.0 (22.4, 23.4) | 25.9 |
| Maternal age 15–19 (per cent) | 11.4 (11.4, 11.5) | 11.7 (11.5, 12.0) | 13.2 (12.8, 13.5) | 11.6 |
| Maternal age 20–24 (per cent) | 27.1 (27.0, 27.2) | 27.4 (27.1, 27.6) | 26.8 (26.4, 27.5) | 27.1 |
| Maternal age 30–44 (per cent) | 22.1 (22.0, 22.2) | 21.8 (21.6, 22.2) | 21.8 (21.3, 22.3) | 22.0 |
| Maternal age 35–39 (per cent) | 10.1 (10.0, 10.2) | 10.0 (9.8, 10.2) | 10.9 (10.6, 11.2) | 10.1 |
| Maternal age 40–44 (per cent) | 1.9 (1.8, 1.9) | 1.9 (1.8, 2.0) | 2.4 (2.2, 2.6) | 1.9 |
| First birth infant (per cent) | 40.8 (40.7, 40.8) | 41.3 (41.0, 41.5) | 45.0 (44.3, 45.8) | 41.0 |
Final column labeled `Overall' shows the characteristics of the original population.
Table VI was generated from 1000 random assignments of every individual i to a component according to their posterior distribution vi,k. In each one of the 1000 complete assignments, covariate distribution was calculated, and from these 1000 samples, the mean and 95 per cent credible intervals for the covariate distribution were determined. Table VI shows that the distribution of the covariates is relatively uniform among components. Thus, there seems to be no combination of the specified covariates that strongly interact to inform component membership; membership is driven by a factor that has not been identified. Despite the inability to predict component membership from the specified covariates, component 3 is associated with elevated vulnerability to adverse birth outcomes and, hence, is the natural sub-population to focus on for exploration of risk.
To the extent that covariates are balanced between the three components there would seem to be no benefit in incorporating covariates to influence the mixing proportions since the covariates do not provide further information beyond the overall proportions. However, Gage et al. [26] found that covariates did affect the mixing proportions in a univariate mixture model for birthweight.
5.3. Prediction
Bivariate predictions can be made from the model, as well as predictions from the induced distributions of gi|bi,zi and bi|gi,zi. Bivariate predictions are given by:
| (4) |
Tables IV and V give some indication of bivariate predictions, but they provide estimates and credible intervals for parameters, rather than predictions; calculating equation (4) at each posterior iteration t provides the correct estimates and uncertainties.
Predictions of birthweight given gestational age (or vice versa) may be conditional on any continuous value, e.g. birthweight conditional on the `true' gestational age, and not only integer (censored) gestational age, as given by:
| (5) |
| (6) |
where
In equations (5) and (6) above μ has been incorporated into β for compactness which has generated the byproduct . The conditional prediction (distribution) of gestational age given birthweight while not a standard consideration may have uses, e.g. in imputation of missing values and detection of mismeasured gestational ages.
A related conditional prediction is the small for gestational age cutpoint SGA(gi), which is found through area prediction in the conditional model of birthweight given gestational age:
| (7) |
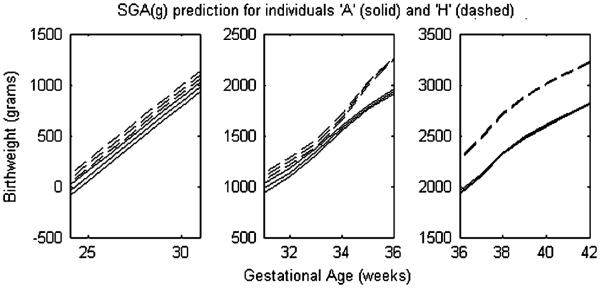
In Tables VII–IX conditional predictions of birthweight given gestational age, gestational age given birthweight, and the SGA cutpoint are given for individuals A–H (see Table III). Prediction and interval curves are available for the three conditional predictions described above, but are only demonstrated for the SGA cutpoint in Figure 4 which contrasts SGA for individuals A and H. The differences in predictions seen in Tables VII–IX are due to the different covariate configurations of individual A–H which result in different joint birthweight gestational age distributions (as in Figure 3).
Table VII.
Conditional expectation of birthweight given gestational age along with 95 per cent credible interval for individuals A–H at gestational ages 34, 37, 39, and 40 weeks.
| A | B | C | D | |
|
| ||||
| 34 | 2039.2 (2018.3, 2059.7) | 2.0547 (2.0308, 2.0779) | 2103.8 (2076.6, 2130.3) | 2113.3 (2085.9, 2140.1) |
| 37 | 2579.5 (2564.9, 2594.2) | 2.6160 (2.6005, 2.6316) | 2743.8 (2729.8, 2757.7) | 2780.0 (2767.2, 2792.9) |
| 39 | 3008.7 (3001.0, 3016.5) | 3.0415 (3.0333, 3.0498) | 3183.5 (3176.3, 3190.6) | 3216.3 (3209.6, 3223.2) |
| 40 | 3130.9 (3122.8, 3139.1) | 3.1632 (3.1545, 3.1719) | 3309.8 (3302.3, 3317.4) | 3341.5 (3334.4, 3348.6) |
| E | F | G | H | |
| 34 | 2126.6 (2103.6, 2149.0) | 2131.9 (2106.8, 2156.2) | 2142.0 (2111.9, 2171.6) | 2146.5 (2119.5, 2173.2) |
| 37 | 2752.5 (2740.7, 2764.3) | 2788.9 (2777.1, 2800.9) | 2914.3 (2901.7, 2926.7) | 2950.3 (2940.1, 2960.6) |
| 39 | 3197.5 (3191.4, 3203.5) | 3230.5 (3224.2, 3236.8) | 3371.4 (3365.2, 3377.6) | 3404.6 (3399.3, 3410.0) |
| 40 | 3324.6 (3318.2, 3330.8) | 3356.4 (3349.9, 3363.0) | 3501.9 (3495.4, 3508.3) | 3533.2 (3527.8, 3538.6) |
Table IX.
SGA cutpoint predictions and 95 per cent credible interval for individuals A–H at gestational ages 34, 37, 39, and 40.
| A | B | C | D | |
|
| ||||
| 34 | 1579.9 (1557.9, 1601.2) | 1594.9 (1570.2, 1619.0) | 1642.5 (1613.8, 1670.4) | 1651.8 (1622.7, 1679.9) |
| 37 | 2112.1 (2096.8, 2127.2) | 2146.6 (2130.6, 2162.5) | 2276.2 (2261.6, 2290.7) | 2310.5 (2297.1, 2323.8) |
| 39 | 2483.1 (2475.2, 2491.1) | 2516.0 (2507.6, 2524.5) | 2660.6 (2653.1, 2668.0) | 2693.4 (2686.3, 2700.5) |
| 40 | 2599.3 (2590.9, 2607.7) | 2632.1 (2623.1, 2641.0) | 2780.4 (2772.6, 2788.1) | 2812.7 (2805.3, 2820.0) |
| E | F | G | H | |
| 34 | 1666.0 (1641.8, 1689.7) | 1670.9 (1644.3, 1696.7) | 1679.5 (1647.4, 1711.0) | 1683.8 (1654.6, 1712.7) |
| 37 | 2285.8 (2273.2, 2298.1) | 2320.3 (2307.7, 2332.8) | 2446.8 (2433.8, 2459.9) | 2480.8 (2469.9, 2491.7) |
| 39 | 2674.3 (2667.9, 2680.6) | 2707.2 (2700.6, 2713.8) | 2850.6 (2844.1, 2857.1) | 2883.6 (2878.0, 2889.3) |
| 40 | 2794.6 (2788.0, 2801.1) | 2827.0 (2820.2, 2833.8) | 2974.2 (2967.5, 2980.8) | 3006.1 (3000.4, 3011.8) |
Figure 4.
Conditional predictions of the small for gestational age cutpoint SGA(g) (the 10th percentile cutpoint of birthweight at gestational age g) for individuals A and H. The single gestational age axis is separated into three plots so that the 95 per cent credible intervals may be examined. The predictions were generated from the conditional distributions implied by the joint distributions represented in Figure 3. Table IX provides the related results for other individuals.
5.4. Bivariate distribution
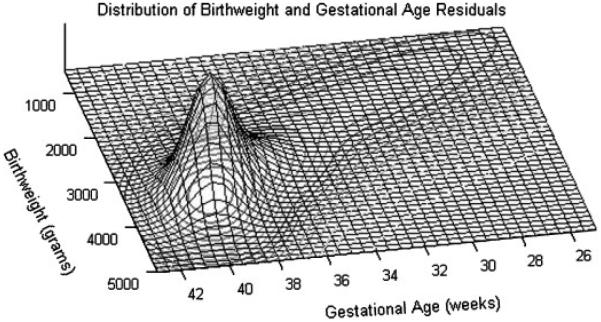
Our model provides a bivariate distribution to capture the empirical joint distribution of birthweight and gestational age (e.g. recall Figures 1 and 2). Such a parametric model allows us to incorporate covariates and provide a joint surface from which to proceed with inference, e.g. see Figure 5. We are not limited to the previously discussed conditional inferences, as we can address joint inference associated with the joint distribution.
Figure 5.
Point estimate of the surface of the mixture distribution for birthweight and gestational age for the referent individual H. The orientation of this plot is a nonstandard ≈180° rotational form. As a result, birthweight increases from top to bottom and gestational age decreases from left to right. Posterior 95 per cent credible intervals of the surface tightly fit this curve, and so were not included in this image.
Table X provides estimates of the probability of both LBW and PTB for individuals A–H, using
| (8) |
Table X.
Probability estimates and 95 per cent credible intervals for LBW and PTB, AI(35) (less than 2000 g for 35 and 36 weeks gestational age), and AI(37+) (less than 2500 g for greater or equal to 37 weeks gestational age) for individuals A–H at gestational ages 34, 37, 39, and 40 weeks.
| A | B | C | D | |
|
| ||||
| LBW+PTB (per cent) | 9.55 (9.27, 9.83) | 8.97 (8.69, 9.27) | 6.49 (6.29, 6.69) | 6.01 (5.83, 6.19) |
| AI(35) (per cent) | 0.88 (0.83, 0.93) | 0.78 (0.73, 0.84) | 0.44 (0.41, 0.47) | 0.39 (0.37, 0.42) |
| AI(37+) (per cent) | 1.52 (1.45, 1.60) | 1.34 (1.27, 1.41) | 0.64 (0.60, 0.68) | 0.55 (0.52, 0.59) |
| E | F | G | H | |
| LBW+PTB (per cent) | 6.90 (6.73, 7.07) | 6.44 (6.27, 6.61) | 4.61 (4.49, 4.74) | 4.26 (4.15, 4.36) |
| AI(35) (per cent) | 0.42 (0.39, 0.45) | 0.37 (0.35, 0.40) | 0.21 (0.20, 0.23) | 0.20 (0.18, 0.21) |
| AI(37+) (per cent) | 0.59 (0.56, 0.62) | 0.51 (0.48, 0.53) | 0.23 (0.21, 0.24) | 0.20 (0.18, 0.21) |
Again for individuals A–H, Table X provides probability estimates for two age inappropriate (AI(gi)) birthweight classifications: AI(35) (less than 2000 g for 35 and 36 weeks gestational age) and AI(37+) (less than 2500 g for greater or equal to 37 weeks gestational age). These probability estimates are provided using an expression similar to (8).
6. Discussion and future work
Our demonstration has highlighted the gradient of differences between individuals A–H with respect to the joint variable birthweight and gestational age. Specifically, we have quantified a gradient of impacts associated with the characteristics of individual A through the referent individual H. For example, we demonstrate in Figure 3 how the overall joint distribution is less favorable for A than H. As indicated in Table IV, race is the primary variable associated with distribution location difference (of up to approximately −320 g and approximately −1.75 weeks gestation), with the strongest differences appearing in the tail of the joint distribution. Smoking is also a major driver accounting for location difference (of up to approximately −230 g and approximately −0.35 weeks gestation) and tends to affect birthweight in the main mass and gestational age in the tail of the distribution. Marital status contributes additional difference (of up to approximately −80 g and approximately −0.5 weeks gestation) for unmarried women, primarily in the tail. Further detail of the varying impacts of individual covariates across the joint distribution is given in Table IV and may be contrasted with Table I. Again, as discussed in Section 3, our joint variable framework provides these coefficient estimates (Table IV), free of the problem of treating birthweight or gestational age as intermediate variables.
Because of the gradient of distributional differences from individuals A through H, there is a resulting gradient of differences SGA and expected birthweight conditional on gestational age, with the curves separating by as much as approximately 400 g in places. An analogous gradient occurs in the percentage of PTB and LBW infants (with up to an approximately twofold prevalence increase), and the percentage of age inappropriate births for gestational ages 35 and 37+ (with up to approximately fivefold and approximately eightfold prevalence increases, respectively).
Our model provides a joint distribution of birthweight and gestational age conditional on covariates, and hence readily accommodates inference concerning disparities in birthweight and/or gestational age in a richer way than previously considered. Further work may provide even more opportunities. Certainly thorough attention to mis-measurement in gestational age and further exploration of the role of covariates in the model's mixing proportions are warranted. Given the longitudinal nature of birth record data, a dynamic perspective could also be considered to investigate whether and how the joint distribution is changing over time. A spatial component could be brought into the modeling to accommodate birth records that have been geocoded and hence learn about the possible spatial structure underlying the data.
Table VIII.
Conditional expectation of gestational age given birthweight along with 95 per cent credible interval for individuals A–H at birthweights 1500, 2500, 3500, and 4000 g.
| A | B | C | D | |
|
| ||||
| 1500 | 32.41 (32.21, 32.62) | 32.26 (32.03, 32.48) | 31.77 (31.54, 31.99) | 31.78 (31.55, 32.00) |
| 2500 | 38.26 (38.22, 38.29) | 38.17 (38.13, 38.21) | 37.95 (37.91, 37.99) | 37.88 (37.84, 37.92) |
| 3500 | 39.76 (39.73, 39.78) | 39.67 (39.65, 39.69) | 39.66 (39.64, 39.68) | 39.58 (39.56, 39.60) |
| 4000 | 40.06 (40.04, 40.08) | 39.98 (39.96, 40.01) | 40.00 (39.98, 40.02) | 39.92 (39.90, 39.94) |
| E | F | G | H | |
| 1500 | 31.41 (31.22, 31.60) | 31.41 (31.20, 31.61) | 31.41 31.19 31.63 | 31.47 (31.28, 31.67) |
| 2500 | 37.90 (37.87, 37.94) | 37.83 (37.79, 37.87) | 37.60 37.56 37.65 | 37.54 (37.50, 37.58) |
| 3500 | 39.67 (39.66, 39.69) | 39.59 (39.57, 39.61) | 39.56 39.55 39.58 | 39.49 (39.47, 39.50) |
| 4000 | 40.01 (39.99, 40.03) | 39.93 (39.91, 39.95) | 39.95 39.93 39.96 | 39.87 (39.86, 39.89) |
Acknowledgements
This work was supported in part by the Southern Center on Environmentally Driven Disparities in Birth Outcomes (SCEDDBO), a subcenter of the Children's Environmental Health Initiative (CEHI) at Duke University (http://www.nicholas.duke.edu/cehi/projects/projects.htm) through EPA award RD-83329301. The authors thank Geeta K. Swamy and Betsy Enstrom for valuable discussions, and the very helpful reviewers for pointing out several key papers and generally improving the subject-matter and technical presentation.
Contract/grant sponsor: Southern Center on Environmentally Driven Disparities in Birth Outcomes (SCEDDBO); contract/grant number: RD-83329301
References
- 1.Tassone EC, Miranda ML, Gelfand AE. Disaggregated spatial modeling for areal unit categorical data. Journal of the Royal Statistical Society: Series C. 2010;59:175–190. doi: 10.1111/j.1467-9876.2009.00682.x. DOI: 10.1111/j.1467-9876.2009.00682.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gage TB. Classification of births by birth weight and gestational age: an application of multivariate mixture models. Annals of Human Biology. 2003;30:589–604. doi: 10.1080/03014460310001592678. DOI: 10.1080/030144603103590605. [DOI] [PubMed] [Google Scholar]
- 3.Ananth CV, Platt RW. Reexamining the effects of gestational age, fetal growth, and maternal smoking on neonatal mortality. BMC Pregnancy Childbirth. 2004;4 doi: 10.1186/1471-2393-4-22. DOI: 10.1186/1471-2393-4-22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Fang F, Stratton H, Gage TB. Multiple mortality optima due to heterogeneity in the birth cohort: a continuous model of birth weight by gestational age specific infant mortality. American Journal of Human Biology. 2007;19:475–486. doi: 10.1002/ajhb.20607. DOI: 10.1002/ajhb.20607. [DOI] [PubMed] [Google Scholar]
- 5.Gage TB, Fang FHS. Modeling the pediatric paradox: birth weight by gestational age. Biodemography and Social Biology. 2008;54:95–112. doi: 10.1080/19485565.2008.9989134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ylppö A. Das wachstum der frühgeborenen yon der geburt bis zum schulalter. Z Kinderheilkd. 1919;24:111–178. [Google Scholar]
- 7.Karn MN, Penrose LS. Birthweight and gestation time in relation to maternal age, parity and infant survival. Annals of Eugenics. 1951;16:147–160. [PubMed] [Google Scholar]
- 8.Grimes DA. Discussion: impaired growth and risk of fetal death: is the tenth percentile the appropriate standard? American Journal of Obstetrics and Gynecology. 1998;178:658–669. doi: 10.1016/s0002-9378(98)70475-2. DOI: 10.1016/S0002-9378(98)70475-2. [DOI] [PubMed] [Google Scholar]
- 9.Wilcox AJ. On the importance—and the unimportance—of birthweight. International Journal of Epidemiology. 2001;30:1233–1241. doi: 10.1093/ije/30.6.1233. DOI: 10.1093/ije/30.6.1233. [DOI] [PubMed] [Google Scholar]
- 10.Paneth NS. The problem of low birth weight. The Future of Children. 1995;5:19–34. [PubMed] [Google Scholar]
- 11.Wilcox AJ, Russell I. Why small black infants have a lower mortality rate than small white infants: the case for population-specific standards for birth weight. The Journal of Pediatrics. 1990;116:7–10. doi: 10.1016/s0022-3476(05)81638-5. DOI: 10.1016/S0022-3476(05)81638-5. [DOI] [PubMed] [Google Scholar]
- 12.Platt RW, Joseph KS, Ananth CV, Gordines J, Abrahamowicz M, Kramer MS. A proportional hazards model with time-dependent covariates and time-varying effects for analysis of fetal and infant death. American Journal of Epidemiology. 2003;160:199–206. doi: 10.1093/aje/kwh201. DOI: 10.1093/aje/kwh201. [DOI] [PubMed] [Google Scholar]
- 13.Hernández-Díaz S, Schisterman EF, Hernán MA. The birth weight `paradox' uncovered? American Journal of Epidemiology. 2006;164:1115–1120. doi: 10.1093/aje/kwj275. DOI: 10.1093/aje/kwj275. [DOI] [PubMed] [Google Scholar]
- 14.Joseph KS, Liu S, Demissie K, Wen SW, Platt RW, Ananth CV, Dzakpasu S, Sauve R, Allen AC, Kramer MS. A parsimonious explanation for intersecting perinatal mortality curves: understanding the effect of plurality and of parity. BMC Pregnancy and Childbirth. 2004;7 doi: 10.1186/1471-2393-3-3. DOI: 10.1186/1471-2393-3-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Joseph KS, Demissie K, Platt RW, Ananth CV, McCarthy BJ, Kramer MS. A parsimonious explanation for intersecting perinatal mortality curves: understanding the effects of race and maternal smoking. BMC Pregnancy and Childbirth. 2004;7 doi: 10.1186/1471-2393-4-7. DOI: 10.1093/aje/kwf077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Joseph KS. Theory of obstetrics: an epidemiological framework for justifying medically indicated early delivery. BMC Pregnancy and Childbirth. 2007;7 doi: 10.1186/1471-2393-7-4. DOI: 10.1186/1471-2393-7-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wilcox AJ, Skjaerven R. Birth weight and perinatal mortality: the effect of gestational age. American Journal of Public Health. 1992;82:378–382. doi: 10.2105/ajph.82.3.378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Oja H, Koiranen M, Rantakallio P. Fitting mixture models to birth weight data: a case study. Biometrics. 1991;47:883–897. DOI: 10.2307/2532646. [PubMed] [Google Scholar]
- 19.Gage TB, Therriault G. Variability of birth-weight distributions by sex and ethnicity: an analysis using mixture models. Human Biology. 1998;70:517–534. [PubMed] [Google Scholar]
- 20.Gage TB. Variability of gestational age distributions by sex and ethnicity: an analysis using mixture models. American Journal of Human Biology. 2000;12:181–191. doi: 10.1002/(SICI)1520-6300(200003/04)12:2<181::AID-AJHB3>3.0.CO;2-0. [DOI] [PubMed] [Google Scholar]
- 21.Gage TB. Birth-weight-specific infant and neonatal mortality: effects of heterogeneity in the birth cohort. Human Biology. 2002;74:165–184. doi: 10.1353/hub.2002.0020. [DOI] [PubMed] [Google Scholar]
- 22.Gage TB, Bauer MJ, Heffner N, Stratton H. Pediatric paradox: heterogeneity in the birth cohort. Human Biology. 2004;76:327–342. doi: 10.1353/hub.2004.0045. [DOI] [PubMed] [Google Scholar]
- 23.McLachlan G, Peel D. Finite Mixture Models. Wiley; New York: 2000. [Google Scholar]
- 24.Dey D, Rao C. Handbook of Statistics 25: Bayesian Thinking, Modeling and Computation. Chapter 16. Elsevier; New York: 2005. Bayesian modeling and inference on mixtures of distributions. [Google Scholar]
- 25.Gelfand AE, Sahu SK. Identifiability, improper priors, and Gibbs sampling for generalized linear models. Journal of the American Statistical Association. 1999;94:247–253. [Google Scholar]
- 26.Gage TB, Fang F, ONeill EHS. Maternal age and infant mortality: a test of the Wilcox-Rrussell hypothesis. American Journal of Epidemiology. 2008;169:294–303. doi: 10.1093/aje/kwn308. DOI: 10.1093/aje/kwn308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Gelfand AE, Smith AFM. Sampling-based approaches to calculating marginal densities. Journal of the American Statistical Association. 1990;85:398–409. [Google Scholar]
- 28.Diebolt J, Robert CP. Estimation of finite mixture distributions through Bayesian sampling. Journal of the Royal Statistical Society: Series B. 1994;56:363–375. [Google Scholar]
- 29.Gelman A. Statistical modeling, causal inference, and social science. 2008 Jul 18; Available from: http://www.stat.columbia.edu/~cook/movabletype/archives/2006/04/amusing_example.html.
- 30.Delbaere I, Vansteelandt S, De Bacquer D, Verstraelen H, Gerris J, De Sutter P, Temmerman M. Should we adjust for gestational age when analyzing birth weights? the use of z-scores revisited. Human Reproduction. 2007;22:2080–2083. doi: 10.1093/humrep/dem151. DOI: 10.1093/humrep/dem151. [DOI] [PubMed] [Google Scholar]
- 31.Rosenbaum P. The consquences of adjustment for a concomitant variable that has been affected by the treatment. Journal of the Royal Statistical Society: Series B. 1984;147:656–666. [Google Scholar]
- 32.Pearl J. Causal diagrams for empirical research. Biometrika. 1995;82:669–710. DOI: 10.1093/biomet/82.4.669. [Google Scholar]
- 33.Greenland S, Pearl J, Robins JM. Causal diagrams for epidemiological research. Epidemiology. 1999;10:37–48. DOI: 10.1097/00001648-199901000-00008. [PubMed] [Google Scholar]
- 34.Pearl J. Causality: Models, Reasoning, and Inference. Cambridge University Press; New York: 2000. [Google Scholar]
- 35.Robins J, Greenland S, Hu FC. Estimation of the causal effect of a time-varying exposure on the marginal mean of a repeated binary outcome. Journal of the American Statistical Association. 1999;94:687–700. [Google Scholar]
- 36.Robins JM, Hernán MA, Brumback B. Marginal structural models and causal inference in epidemiology. Epidemiology. 2000;11:550–560. doi: 10.1097/00001648-200009000-00011. DOI: 10.2307/3703997. [DOI] [PubMed] [Google Scholar]
- 37.Rubin DB. Direct and indirect causal effects via potential outcomes. Scandinavian Journal of Statistics. 2004;31:161–170. DOI: 10.1111/j.1467-9469.2004.02-123.x. [Google Scholar]
- 38.Gelfand AE, Sahu SK, Carlin BP. Efficient parameterizations for normal linear mixed models. Biometrika. 1995;82:479–488. [Google Scholar]
- 39.Jasra A, Holmes CC, Stephens DA. Markov chain monte carlo methods and the label switching problem in bayesian mixture modeling. Statistical Science. 2005;20:50–67. DOI: 10.1214/088342305000000016. [Google Scholar]
- 40.Gelfand AE, Ghosh SK. Model choice: a minimum posterior predictive loss approach. Biometrika. 1998;85:1–11. DOI: 10.1093/biomet/85.1.1. [Google Scholar]
- 41.Frimpong EY, Gage TB, Stratton H. American Statistical Association Joint Statistical Meetings Proceedings. Washington, DC: 2008. Identifiability of bivariate mixtures: an application to infant mortality models. [Google Scholar]