Interactions between demography, genetics, and landscape connectivity increase extinction probability for a small population of large carnivores in a major metropolitan area

Abstract

The extinction vortex is a theoretical model describing the process by which extinction risk is elevated in small, isolated populations owing to interactions between environmental, demographic, and genetic factors. However, empirical demonstrations of these interactions have been elusive. We modelled the dynamics of a small mountain lion population isolated by anthropogenic barriers in greater Los Angeles, California, to evaluate the influence of demographic, genetic, and landscape factors on extinction probability. The population exhibited strong survival and reproduction, and the model predicted stable median population growth and a 15% probability of extinction over 50 years in the absence of inbreeding depression. However, our model also predicted the population will lose 40–57% of its heterozygosity in 50 years. When we reduced demographic parameters proportional to reductions documented in another wild population of mountain lions that experienced inbreeding depression, extinction probability rose to 99.7%. Simulating greater landscape connectivity by increasing immigration to greater than or equal to one migrant per generation appears sufficient to largely maintain genetic diversity and reduce extinction probability. We provide empirical support for the central tenet of the extinction vortex as interactions between genetics and demography greatly increased extinction probability relative to the risk from demographic and environmental stochasticity alone. Our modelling approach realistically integrates demographic and genetic data to provide a comprehensive assessment of factors threatening small populations.

1. Introduction

Understanding factors that influence extinction in wild populations is a fundamental challenge for population ecology and conservation biology [1–3]. Habitat fragmentation can result in small, isolated wildlife populations within which extinction risk may be elevated by interactions between environmental, demographic, and genetic factors, often referred to as the extinction vortex or small-population paradigm [4–5]. Stochasticity in demography from sampling variance within small populations (demographic stochasticity) causes variation in realized vital rates, even in a constant environment, which can greatly increase extinction risk. Small, isolated populations also lose genetic diversity over time, principally through inbreeding and genetic drift, which may further increase extinction risk if demographic performance becomes compromised by inbreeding depression [4,6,7].

The importance of inbreeding depression in influencing extinction of small populations is theoretically robust, but empirical support remains scant as few studies have documented the causes of extinction in nature [3,5,8]. Theory also predicts that when populations become small enough for inbreeding depression to occur, demographic and environmental stochasticity are likely to cause extinction before inbreeding will play an important role [5,9,10]. These conflicting predictions have led to a considerable debate regarding the relative influence of demographic and genetic factors on the viability of small populations [6,10–12]. There is now substantial evidence that inbreeding depression can strongly influence demographic performance of individuals and populations [8,13–15]. Fagan & Holmes [1] retrospectively characterized the decline to extinction of 10 wild vertebrate populations providing key insight into the extinction process; however, they could not demonstrate the importance of inbreeding depression and associated demographic consequences directly because they lacked genetic data. Thus, the relative influences of demographic and genetic factors on the extinction of wild populations remain poorly understood and controversial [3,8,16,17]. Modelling dynamics of small populations with empirical demographic and genetic data may be effective to elucidate the mechanisms of the extinction vortex for wild populations [18].

Large carnivores, and specifically mountain lions (Puma concolor), are excellent study species with which to investigate interactions between demography and genetics, and their influence on extinction risk in fragmented landscapes. Large carnivores occupy large home ranges and exist at low density, making them sensitive to habitat fragmentation and anthropogenic barriers to connectivity [19]. Recently, there have been examples of small populations of felid and canid top predators in North America being pushed to the brink of extinction by negative consequences of low genetic diversity [14,15]. For mountain lions, a relatively small number of males often dominate breeding opportunities in wild populations, which can further reduce the effective population size [14,20]. Recent work showed that major freeways and development represent substantial barriers to movement of mountain lions between areas of formerly connected habitat and documented strong genetic structuring, high rates of inbreeding, and low genetic diversity in isolated populations in southern California [20,21].

Another population of mountain lions, Florida panthers (Puma concolor coryi), declined rapidly in the twentieth century owing to overhunting and habitat loss until a small, isolated population of 20–30 animals persisted in south Florida [14]. This population exhibited low genetic diversity and poor demographic performance resulting from inbreeding depression [14]. Detailed research on the near-extinction and subsequent genetic restoration of panthers provided quantitative predictions for (i) levels of genetic diversity at which inbreeding depression may occur in mountain lion populations and (ii) demographic consequences of inbreeding depression for this species [14,22,23]. Mountain lion populations isolated by habitat fragmentation and major freeways in the greater Los Angeles area have the lowest levels of genetic diversity documented for this species aside from Florida panthers [20,21], causing concern regarding inbreeding depression.

We developed an individual-based population model with empirical data from a 13 year (2002–2015) study during which we quantified survival, reproduction, movements, and multilocus genotypes of individual mountain lions (n = 45) within and adjacent to an isolated population in the Santa Monica Mountains (SMMs) west of Los Angeles [20] (figure 1). We constructed a starting population of individuals that reflected the age, sex, and genetic structure of the 2015 population and projected the model forward to estimate stochastic population growth, extinction probability, and measures of genetic diversity over the next 50 years. We used genotypes of mountain lions captured or otherwise sampled in areas adjacent to the SMMs to simulate individual-level immigration events and additional gene flow into the SMMs. We used the model to address the following questions. (i) Is the population currently demographically vigorous? (ii) What is the probability of extinction due purely to stochastic demography? (iii) At what rate will genetic diversity decline under a range of immigration scenarios reflecting potential future variation in landscape connectivity? (iv) If the model predicts rapid declines in genetic diversity, how would reductions in vital rates proportional to those documented in Florida panthers experiencing inbreeding depression influence population growth and extinction probability of SMM mountain lions?

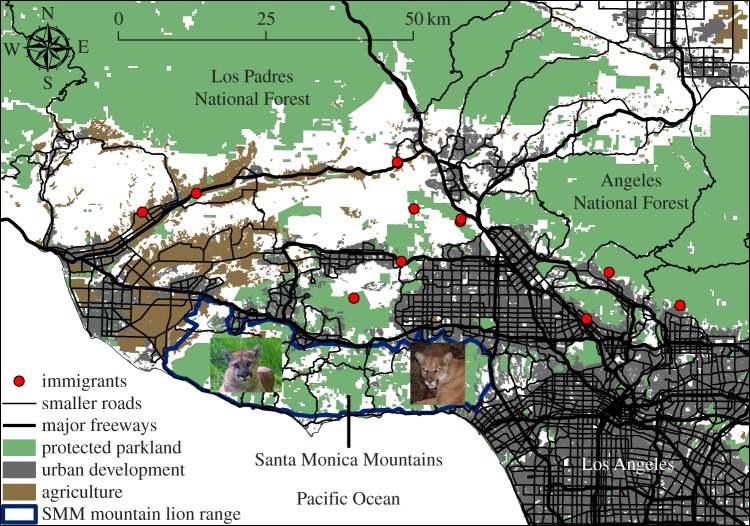
Figure 1.

Santa Monica Mountains (SMMs) and adjacent areas in the greater Los Angeles metropolitan area, California. The blue polygon is the composite home range for mountain lions tracked from 2002 to 2015 within the SMMs. Red circles are locations of mountain lions captured or otherwise sampled in adjacent areas used to simulate immigration in our model.

2. Material and methods

(a). Capture and monitoring

We captured mountain lions using Aldrich foot-snares or cable restraints, baited cage-traps, or by treeing them with trained hounds. We deployed global positioning system (GPS) collars (Followit AB, Simplex and Tellus models, Stockholm, Sweden; North Star Science and Technology LLC, Globalstar Tracker model, King George, VA; or Vectronic Aerospace, GPS Plus model, Berlin, Germany) on adults. We also captured three- to five-week-old kittens at natal dens by hand and implanted very high-frequency (VHF) transmitters (Telonics, IMP/200/L, Mesa, AZ) in their peritoneal cavities (details in [24]). We monitored the survival of GPS-collared adult and subadult mountain lions daily via remote download and VHF instrumented kittens greater than or equal to three times per week using ground telemetry. When we detected mortality, we hiked into the locations to retrieve carcasses and attempted to determine cause of death. Additionally, all carcasses were necropsied by experienced veterinarians to confirm our field diagnoses and to gain additional information. We monitored reproduction of all collared females, using GPS telemetry to locate natal dens and capture, count, sex, and mark kittens [24].

(b). DNA genotyping

We genotyped all captured mountain lions at 54 microsatellite loci using laboratory methods and markers described previously [20]. We also genotyped mountain lions from samples obtained in areas adjacent to the SMMs (figure 1).

(c). Estimating demographic parameters

We separated mountain lions tracked within the SMMs into three age classes for parameter estimation: kittens, subadults, and adults. Kittens were dependent offspring with their mothers. Subadults were independent animals prior to reproduction, whereas adults were resident, reproducing animals. Kittens in the SMMs became independent from their mothers at a mean of 408 days (range = 348–515, n = 12). Thus, we considered mountain lions of both sexes to be kittens from 0 to 14 months. We considered females to be subadults from 14 to 25 months (age of youngest known-age female documented breeding). We considered males to be subadults from 14 to 42 months (age of the youngest known-age male documented breeding). We estimated sex and age-class-specific survival rates using the Kaplan–Meier estimator generalized for staggered entry [25] and the Greenwood method for estimating variance implemented in R v. 3.1.3 (R Development Core Team 2015) with the ‘survival’ package. We pooled sexes for kitten survival estimates owing to relatively small sample sizes (n = 16). We allowed females in the model to breed in the first month after reaching adulthood. Females raising kittens within the model were not eligible to breed again until they either lost the entire litter to mortality or the kittens became independent, whichever came first. Females in the model bred in the first month following loss or independence of kittens as all females we tracked in the SMMs bred within 25 days (mean = 17 days, range 11–25, n = 4) of losing kittens to mortality or independence. Mean litter size was 2.88 in the SMMs (range 2–4, n = 8 litters). We estimated the probability of a female having two (0.375), three (0.375), or four (0.250) kittens in a litter based on the proportion of these litter sizes documented in our study.

(d). Model overview

We developed an individual-based population model for mountain lions that incorporated demographic and environmental stochasticity, as well as a simple form of density-dependence (figure 2). Individual-based population models differ from classical models in that population-level processes are explicitly modelled as the outcome of the variable performance of individuals, which are tracked through time and allowed to differ in important ways [26,27]. We began the model with a starting population that reflected the sex, age, and genetic structure of the current (2015) population and projected the model forward to estimate the demographic and genetic structure of future populations (figure 2). Specifically, both adult males (including the sole known breeder) and three of the (presumed) four to six adult females residing in the SMMs during 2015 were included in the starting population. Two additional females that had been captured in the SMMs and subsequently died were included as adults. Eight additional mountain lions born in the SMMs during 2012–2015 were included as kittens and subadults (two males and two females of both age classes). Thus, the starting population comprised 15 SMM mountain lions (nine females, six males) with empirical genotypes at 54 loci. Offspring produced in the model were assigned genotypes derived through simple Mendelian genetics (i.e. one allele randomly inherited from each parent at each loci).

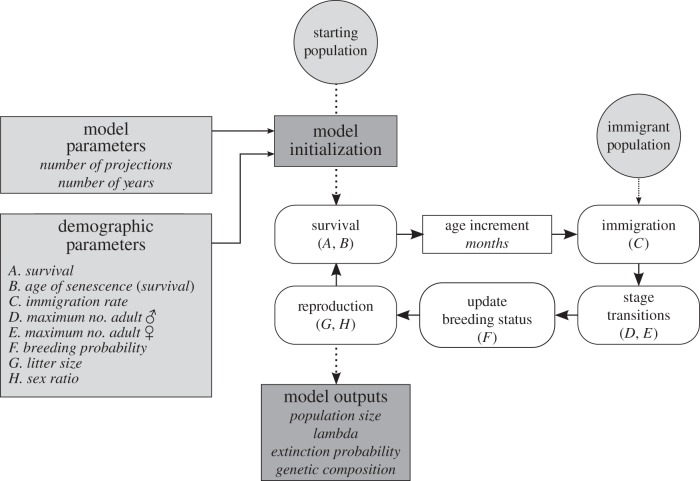
Figure 2.

Flow diagram shows demographic parameters, population model loop (in white boxes) and model outputs. Demographic parameters are labelled with letters (A–H) to indicate which parameters are relevant to each portion of the main population model loop.

We ran simulations consisting of 5000 population projections of 50 years, unless noted otherwise. The population dynamics simulated by the model was a reflection of individual-based demographic processes specified by empirical probability distributions estimated with data collected from wild mountain lions in the SMMs. Population size was updated at each monthly time step by subtracting individuals lost through mortality and adding individuals gained through reproduction or immigration (figure 2). We imposed mortality (survival senescence) on all mountain lions of both sexes in the model that reached 15 years of age as mountain lions have rarely been documented living beyond that age in the wild [28]. We incorporated density-dependence by imposing a maximum number of adult males (n = 2) and females (n = 6) that could exist in the population at any given time. When all of the adult slots of a given sex were occupied, we eliminated individuals of that sex that would have otherwise transitioned from subadults to adults. This process simulated density-dependent population regulation through death or dispersal. This density-dependence provided an important limitation on population growth, which otherwise would have resulted in population sizes larger than the SMMs could realistically support given the limited space and barriers to movement [20]. Although the upper limits for adult males and females were fixed, the number of adults varied stochastically during model projections owing to variation in survival and reproduction. The sex-specific maximum values reflected our understanding of the size and space limitations of the population based on intensive monitoring with telemetry, genetic analysis, and remote cameras for more than 13 years. See additional details of the modelling procedures in electronic supplementary material, appendix A.

(e). Submodel structure

(i). Survival

We generated environmentally stochastic monthly survival probabilities by transforming estimated Kaplan–Meier survival rates and their standard deviations into beta shape parameters, using the betaval function in the R package ‘popbio’ [29]. At each monthly time step, we drew a random survival value from this beta distribution which was used as the environmentally stochastic survival probability for all individuals of the same sex and age class during that time step. We then assessed demographically stochastic survival of each individual, using a Bernoulli trial with the monthly survival probability as the threshold between survival and mortality.

(ii). Immigration

We assigned a fixed annual immigration rate prior to starting a simulation. This annual rate was transformed into a monthly probability and was assessed stochastically, using Bernoulli trials during each monthly time step. For our main analysis, we restricted immigration to subadult males. In addition to being more likely to disperse, males are also more likely to undertake longer and riskier dispersal events [30,31]. Indeed, the single immigration event documented into the SMM population during our study was a radio-collared subadult male that crossed the 101 freeway [20]. Although we expect most immigrants into the SMMs will be males, we also ran simulations where both subadult males and females immigrated with equal probability to investigate the influence of female immigration. We assigned genotypes to immigrants from mountain lions captured or otherwise genotyped in adjacent areas north and east of the SMMs (n = 18). The model sampled immigrant genotypes without replacement from the 18 genotypes available. If all genotypes were used during a given population projection, the pool of potential immigrants was reset and once again populated with all 18 available genotypes from north and east of the SMMs. Each immigrant was randomly assigned an age from 14 to 42 months (for males) or 14–25 months (for females). Once in the SMM population, these immigrants were subjected to the same demographic procedures as other subadults in the model.

(iii). Age class adjustment

We allowed some flexibility in the age that subadults of both sexes transitioned to adults. For females, we incorporated stochasticity into the age of first reproduction (and therefore in their transition to adulthood) by sampling each individual's age of transition from a uniform distribution between 25 and 33 months. Males transitioned to adulthood at 42 months if there was room for an additional adult male in the population based on our density-dependent limit. However, if there were no adult males present in the population, then subadult males greater than or equal to 36 months of age were eligible to transition to adulthood and begin breeding. We implemented this flexibility because breeding for male mountain lions in wild populations is probably delayed beyond the age of sexual maturity. Thus, when no adult males were present, we assumed younger males would begin breeding sooner.

(iv). Breeding status

We designated reproductive males and females in the starting population and, thereafter, the model randomly selected breeding animals from subadults eligible to transition to adults when openings became available. Males reaching breeding status remained reproductive for the remainder of their lives. Breeding females were eligible to become pregnant throughout the remainder of their lives whenever they did not have dependent offspring. New offspring were produced three months after pregnancy to simulate the gestation period for mountain lions.

(v). Reproduction

Females produced offspring at any time of the year consistent with mountain lion reproductive ecology and our documentation of litters throughout the year in the SMMs. When one breeding male was present in a simulated population, he mated with all adult females. When two males were present, they each mated with half the adult females. When an odd number of females were present, one was designated as a ‘floater’ that could mate with either male randomly. Litter size varied stochastically by generating a random, uniform value between 0 and 1 for each reproductive female and comparing the value to a cumulative probability distribution for litter sizes of 2, 3, and 4 based on the proportion of these litter sizes documented during our study. We determined the sex of each offspring using a Bernoulli trial with a probability of 0.5.

We documented either one or two adult males in the population at any one time throughout the 13 year field study. Thus, the number of breeding males may have fluctuated between one and two males at different times during the study. However, we never confirmed that two males were ever breeding simultaneously in the population with genetic data. In fact, parentage analysis indicated that only two males were responsible for all known reproduction from 2002 to 2015 with sequential breeding periods that did not overlap. To account for this uncertainty we modelled the two possible scenarios separately: (i) a situation where less than or equal to two adult males could be present but only a single male bred at any one time, and (ii) a situation where less than or equal to two adult males were present and both bred with half of the females present. We present both sets of results because both were plausible and had consequences for the rate at which genetic diversity eroded in our simulations.

(f). Model outputs

(i). Demography and extinction

We estimated λ at time t as N_t/N_t−1, where N_t = total population size at time t. We estimated λ_s (stochastic lambda) across time periods of interest with the formula

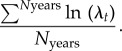We report median λ_s from the distribution of values across all 50 year projections for simulations of interest. We estimated credible intervals for λ_s using the highest posterior density (HPD) derived using the R package ‘coda’ (v. 0.17–1). We estimated probability of extinction as the proportion of projections that went extinct during a given simulation and derived estimates of variability by conducting a non-parametric bootstrapping procedure implemented in the R package ‘boot’ (v. 1.3–17). We ran 1000 bootstraps of 5000 population projections to estimate uncertainty regarding extinction probability, which we present with 95% HPD intervals. We estimated the effective population size based on a census of the breeding animals in simulated populations using the formula: N_e = (4 × N_BF × N_BM)/(N_BF + N_BM). Where N_e is effective population size, N_BF is number of breeding females, and N_BM is number of breeding males.

(ii). Genetic parameters

We estimated measures of genetic diversity for starting populations and simulated populations 1–50 years in the future using mean values from genotypes of individuals across all projections in a given simulation. We estimated expected (H_e) and observed (H_o) heterozygosity, individual inbreeding coefficient (F_is), the mean number of alleles per loci (N_A), and the proportion of polymorphic loci using the R package ‘adegenet’ v. 2.0.0 [32].

(g). Elasticity analysis

We investigated sensitivity and proportional sensitivity (elasticity) of λ_s estimated by our model to small (5%) increases in vital rates [29]. We conducted these analyses with the density-independent model to investigate which demographic parameters had the greatest influence on λ_s in the absence of density-dependent limitations. We calculated sensitivity values (S) for 5% increases in each demographic parameter following Morris & Doak [29]

Where ‘adjusted’ refers to demographic rates increased by 5% and the resulting value of λ_s, and ‘original’ refers to the original demographic rates and resulting value of λ_s prior to these increases. We then calculated elasticity values (E) for each demographic parameter following Morris & Doak [29]

(h). Simulating inbreeding depression

We simulated inbreeding depression by running population projections with input parameters reduced to reflect proportional changes in age and sex-specific survival rates consistent with differences documented between Florida panthers experiencing inbreeding depression and outbred panthers following the genetic restoration programme [14,22,23]. These adjusted input parameters are provided in electronic supplementary material, table S3.

3. Results

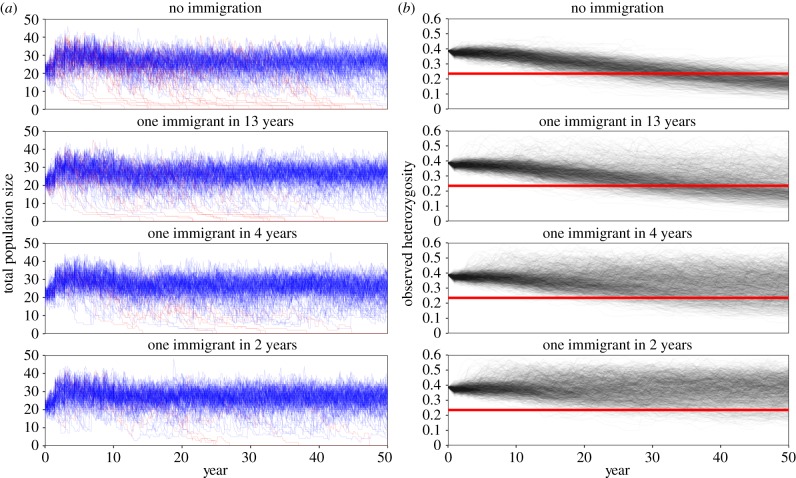
Demographic parameters estimated from SMM mountain lions used to construct the model are summarized in electronic supplementary material, table S1. Density-independent λ_s over 25 years was 1.19 [1.13, 1.23] and was most sensitive to changes in adult female survival (electronic supplementary material, table S2). Probability of extinction from the density-independent model was 0.009. More realistic, density-dependent simulations predicted stable median population growth (λ_s = 1.01) over the next 50 years, regardless of the level of immigration (table 1 and figure 3a). However, there was a 15–22% probability of extinction owing to demographic stochasticity with no or low immigration into this small population (table 1). Moderately higher levels of immigration (one every 2–4 years) reduced probability of extinction due purely to demographic factors to 2–8% (table 1 and figure 3a).

Table 1.

Demographic results predicted by individual-based population model for Santa Monica Mountain lions, Southern California. Values are mean (unless otherwise noted) estimates at year 50 based on 5000 population projections.

	no immigration		one immigrant per 13 years		one immigrant per 4 years		one immigrant per 2 years
	estimate	95% HPDa	estimate	95% HPDa	estimate	95% HPDa	estimate	95% HPDa
one male breeding
λb	1.01	(0.91, 1.02)	1.01	(0.92, 1.02)	1.01	(0.95, 1.02)	1.01	(0.99, 1.02)
extinction prob.	0.211	(0.200, 0.222)	0.156	(0.145, 0.165)	0.078	(0.07, 0.09)	0.024	(0.020, 0.029)
extinction time	30.79	(12.83, 49.20)	30.37	(12.08, 49.17)	32.44	(12.58, 49.67)	31.87	(11.50, 48.67)
adults (n)	5.20	(0, 8)	5.60	(0, 8)	6.23	(0, 8)	6.68	(0, 8)
NE	2.91	(0, 3.43)	2.94	(0, 3.43)	3.00	(0, 3.43)	3.09	(0, 3.43)
two males breeding
λb	1.01	(0.91, 1.02)	1.01	(0.93, 1.02)	1.01	(0.96, 1.02)	1.01	(0.99, 1.02)
extinction prob.	0.220	(0.208, 0.231)	0.150	(0.140, 0.160)	0.066	(0.058, 0.072)	0.030	(0.025, 0.035)
extinction time	30.79	(12.08, 47.33)	30.37	(12.08, 49.17)	30.48	(12.08, 48.42)	33.55	(12.67, 49.75)
adults (n)	5.16	(0, 8)	5.66	(0, 8)	6.30	(0, 8)	6.69	(4, 8)
NE	3.95	(0, 6)	4.060	(0, 6)	4.21	(0, 6)	4.45	(0, 6)

^a95% highest posterior density credible intervals.

^bMedian stochastic population growth rate.

Figure 3.

Results from individual-based population model for mountain lions projected 50 years showing predictions for population size and genetic diversity. Darker and lighter colours in the plots reflect highest and lowest probability of predicted values, respectively. (a) Population projections showing generally stable population size and growth, regardless of immigration and a 3–22% probability of extinction. Persistent projections shown in blue, projections going extinct shown in red. (b) Predicted values of observed heterozygosity (H_o) declined rapidly with no or low (one every 13 years) immigration, whereas H_o was largely maintained with moderate increases in immigration (one every 2–4 years). Red bands indicate the level of H_o documented in Florida panthers experiencing inbreeding depression (from Johnson et al. [14]), calculated as proportional loss of heterozygosity relative to outbred pumas (additional details in Discussion).

With little or no immigration, which reflects our understanding of the current level of isolation of this population [20], heterozygosity decreased precipitously (table 2; figures 3b and 4). However, when we simulated increased connectivity, heterozygosity declined much more slowly and was largely (73–94%) maintained (table 2; figures 3b and 4). Other measures of genetic diversity such as per cent polymorphism, inbreeding coefficient (F_is), and the number of alleles per loci (N_A) responded to variation in male immigration similarly (table 2). Allowing both males and females to immigrate yielded similar results, although loss of heterozygosity was slightly greater and extinction risk was slightly higher than when only males immigrated (electronic supplementary material, tables S3–S4). When we simulated inbreeding depression by reducing age-class-specific survival rates proportional to reductions documented between inbred and outbred Florida panthers (electronic supplementary material, table S5), the population declined dramatically (λ_s = 0.88 [0.76, 0.98]) with an estimated probability of extinction of 99.7% in 50 years and an estimated median extinction time of 14.5 years (4.25, 30.25; electronic supplementary material, table S6).

Table 2.

Genetic results predicted by individual-based population model for Santa Monica Mountain mountain lions, Southern California. Values are mean estimates at year 50 based on 5000 population projections.

	starting population		no immigration		one migrant per 13 years		one migrant per 4 years		one migrant per 2 years
	estimate	s.e.	estimate	s.e.	estimate	s.e.	estimate	s.e.	estimate	s.e.
one male breeding
He	0.352	0.032	0.143	0.027	0.189	0.027	0.248	0.028	0.297	0.029
Ho	0.388	0.040	0.165	0.032	0.217	0.033	0.283	0.034	0.337	0.034
NA	2.220	0.123	1.431	0.074	1.624	0.082	1.882	0.093	2.098	0.100
Fis	0.127	0.022	0.191	0.022	0.184	0.019	0.172	0.020	0.127	0.021
polymorphic (%)	0.778	—	0.400	—	0.527	—	0.674	—	0.776	—
two males breeding
He	0.352	0.032	0.156	0.027	0.206	0.028	0.276	0.028	0.328	0.029
Ho	0.388	0.040	0.178	0.032	0.234	0.033	0.311	0.034	0.366	0.034
NA	2.220	0.123	1.468	0.077	1.669	0.085	1.960	0.096	2.190	0.104
Fis	0.127	0.022	0.186	0.018	0.179	0.019	0.168	0.020	0.159	0.021
polymorphic (%)	0.778	—	0.429	—	0.556	—	0.715	—	0.814	—

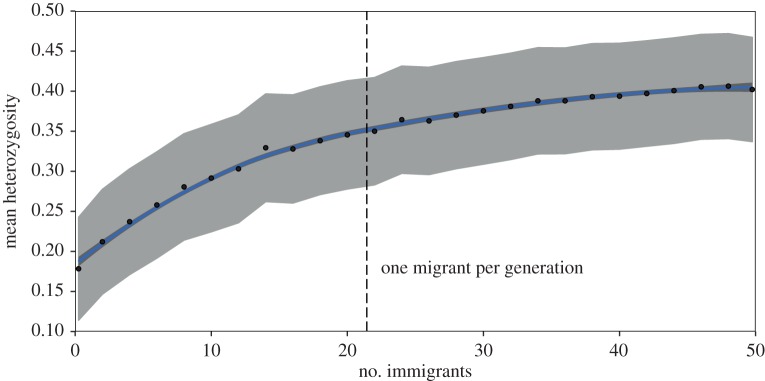
Figure 4.

Relationship between genetic diversity and immigration predicted by individual-based model for mountain lions projected forward 50 years. Blue trend line depicts mean (with 95% confidence interval in grey) relationship between immigration and observed heterozygosity derived by simulating a range of immigration (0–50 immigrants over 50 years) reflecting variation in connectivity and gene flow for mountain lions between the Santa Monica Mountains and surrounding areas. (Online version in colour.)

4. Discussion

The SMM mountain lion population is currently demographically vigorous with no indication of inbreeding depression as evidenced by estimated survival and reproductive rates that were mostly similar or slightly higher than other unhunted mountain lion populations across North America [22,23,28,33]. The lone exception was subadult survival, which was lower than other populations, likely because dispersal of subadults was frustrated and many were killed by adult males [20]. The population has strong growth potential as the density-independent model predicted a rapidly increasing population and an extremely low (less than 1%) probability of extinction over the next 25 years. In the absence of inbreeding depression, and with no or low immigration, the density-dependent model predicted a stable median growth rate and a 15–22% probability of extinction over the next 50 years owing to demographic stochasticity (figure 2a). However, without additional gene flow, the predicted erosion of genetic diversity within 50 years warrants concern regarding inbreeding depression and the potential for rapid extinction.

In the context of population viability analysis (PVA), 5–10% reduction in mean heterozygosity has been suggested to be the maximum acceptable loss over 100–200 years to avoid inbreeding depression in wild populations [34,35]. Our model predicted much greater reduction in heterozygosity (40–57%) over only 50 years. Predicted observed heterozygosity in 50 years with no or low immigration were similar to values reported for inbred Florida panthers prior to genetic introgression [14], although these values may not be directly comparable owing to the use of different microsatellite loci between studies. To account for differences in the panel of loci, we compared the proportion of heterozygosity retained in inbred panthers and SMM mountain lions relative to values quantified for outbred populations using the same loci. In the years prior to genetic introgression, inbred Florida panthers exhibited 54–58% of the observed heterozygosity of outbred pumas from Texas released into south Florida during the genetic restoration programme [14]. For comparison, mountain lions in our model at year 50, with no or low immigration, exhibited 39–56% of the observed heterozygosity documented in mountain lions sampled east and north of the SMMs in southern California [20]. Thus, our results suggest mountain lions in the SMMs will lose as much or more genetic diversity within 50 years, relative to outbred populations, than was lost by the panther population that nearly went extinct from consequences of inbreeding depression. Not surprisingly for a population of five to eight adults, the model predicted rapid extinction of SMM mountain lions when we simulated inbreeding depression. More optimistically, our simulations predicted that modest increases in immigration would allow mountain lions in the SMMs to retain 67–87% of the heterozygosity exhibited by outbred mountain lions in southern California.

Our model predictions were consistent with empirical genetic data collected within this population to date as genetic diversity declined and inbreeding increased from 2004 to 2010 [20]. In 2010, the single immigrant documented entering the population arrived, and there was a brief (2 years) increase in genetic diversity and reduction in inbreeding [20]. However, the positive influence of this rare immigration event was short-lived as the immigrant male began to breed with his daughters and genetic diversity began to decline again [20]. Thus, the low level of immigration occurring under the current landscape conditions appears to be insufficient to reduce inbreeding and maintain genetic diversity for the long-term. In addition to concern over the absolute loss of heterozygosity predicted by our model, the rapid rate of this loss may further exacerbate extinction probability. Populations experiencing slower erosion of genetic diversity may be more likely to maintain evolutionary potential and responsiveness to environmental change [36,37].

The SMM mountain lion population has persisted at a very small population size for at least several decades and is predicted to exhibit generally stable population growth in the absence of inbreeding depression. Importantly, our model predicts a much lower probability of extinction (2–22%) due purely to demographic and environmental stochasticity compared with the probability of extinction following inbreeding depression (100%). Thus, our results support the central tenet of the extinction vortex that demography and genetics interact to elevate extinction risk in small, isolated populations [4,6], and do not support previous contentions that demographic stochasticity and deterministic factors generally cause extinction before inbreeding depression can negatively influence viability [5,10,11]. Our results also provide insight into the one migrant per generation (OMPG) rule, which suggests that OMPG is sufficient to minimize the loss of polymorphism and heterozygosity [38]. Simulating OMPG (generation time = 28–36 months) resulted in the population retaining 76–97% of its observed heterozygosity and 86–105% of its polymorphism over 50 years (table 2 and figure 3).

Large carnivores persisting within a metropolitan area as large as Los Angeles is extremely rare and our model elucidated interactions between inbreeding and demography that substantially elevated extinction probability. However, the interactions themselves are not rare and are likely to become more common in wild populations as activities of the growing human population increasingly isolate populations of wildlife in small patches of otherwise highly suitable habitat. Indeed, wolves (Canis lupus) on Isle Royale appear to be on the brink of extinction following increased isolation associated with decreased frequency of sufficient winter lake-ice formation to allow immigration of wolves from mainland populations, which has been linked to global climate change [15]. Florida panthers nearly went extinct from consequences of inbreeding depression after being isolated from other mountain lion populations due to overhunting and habitat loss in eastern North America. Following restoration of genetic variability through an intentional introgression programme, demographic performance of panthers improved and the population rapidly expanded numerically [14]. Inbreeding depression may be less important in influencing extinction than deterministic factors when populations continue to decline rapidly, because the rate of decline is faster than the effects of inbreeding depression [16]. For example, high mortality in endemic bird populations from introduced predators on islands is a situation where inbreeding depression is predicted to be less likely to influence viability than deterministic factors [39]. However, inbreeding depression can strongly influence extinction in cases where the deterministic decline has been slowed or halted and small populations persist in isolated patches of suitable habitat, as with Florida panthers and SMM mountain lions.

Despite wide recognition of the value of explicitly incorporating interactions between demographic, genetic, and landscape processes into PVA, and using measures of genetic diversity to improve estimates of extinction probability, these goals have remained elusive [40]. This limitation has persisted despite the increasing availability of detailed genetic data accompanying demographic studies of wildlife populations of conservation concern. Our results provide managers with an opportunity to develop proactive conservation strategies that could prevent inbreeding depression and extinction. A highway crossing structure to facilitate immigration into the SMMs could increase gene flow sufficiently to minimize the loss of genetic diversity, as well as reduce extinction probability due purely to demographic stochasticity. Mountain lions readily use highway crossing structures [41] and are known to traverse areas immediately adjacent to the SMMs [20]. If a crossing structure is implemented, mountain lions entering the SMMs via the structure should be monitored with remote cameras in conjunction with continued demographic and genetic monitoring of the population to test the predictions of our model. Alternatively, translocation of mountain lions into the SMMs from other areas could be considered in the future to facilitate genetic restoration or recolonization. However, a crossing structure might eliminate the need for translocation and, importantly, would also benefit other species for whom these freeways represent significant barriers [42]. Furthermore, although genetic rescue through translocation can be an effective short-term solution, previous work has highlighted the importance of addressing environmental factors that threaten small populations in a comprehensive manner to achieve long-term genetic restoration and viability [43,44].

Maintaining healthy populations of native top predators within greater Los Angeles, the second largest metropolitan area in the USA, would provide a model for successful large carnivore conservation within highly fragmented, urban landscapes. This would have broad implications given the rapid rate of global urbanization and importance of carnivores as critical elements of healthy ecosystems [19]. We show that demography and genetics can be modelled synergistically within PVA to provide a comprehensive assessment of factors threatening small populations with extinction. This framework can be applied globally to other small populations for which detailed demographic and genetic data are available to increase understanding of these processes and improve wildlife conservation in fragmented landscapes.

Ethics

Animal capture and handling protocols were approved by the National Park Service Institutional Animal Care and Use Committee.

Data accessibility

Data analysed in this paper are accessible through Dryad: http://dx.doi.org/10.5061/dryad.82pm0 [45].

Authors' contributions

Designed the study: J.F.B., P.J.M., J.A.S., S.P.D.R. Collected data: J.A.S., L.E.K.S., J.P.P., H.B.E., S.P.D.R. Analysed data: J.F.B., P.J.M. Wrote manuscript: J.F.B. Revised manuscript: J.F.B., P.J.M., J.A.S., L.E.K.S., J.P.P., H.B.E., S.P.D.R.

Competing interests

We declare we have no competing interests.

Funding

The research was suported by the La Kretz Center for California Conservation at UCLA, California State Parks, the Santa Monica Mountains Fund, Santa Monica Mountains Conservancy/Mountains Recreation and Conservation Authority and the Calabasas Landfill.