Skip to main content
PMC home page
Toxicological Sciences logoLink to Toxicological Sciences
. 2016 Jun 2;153(1):18–27. doi: 10.1093/toxsci/kfw100

Generalized Concentration Addition Modeling Predicts Mixture Effects of Environmental PPARγ Agonists

James Watt 1, Thomas F Webster 1, Jennifer J Schlezinger 1,1
PMCID: PMC5013877  PMID: 27255385

Abstract

The vast array of potential environmental toxicant combinations necessitates the development of efficient strategies for predicting toxic effects of mixtures. Current practices emphasize the use of concentration addition to predict joint effects of endocrine disrupting chemicals in coexposures. Generalized concentration addition (GCA) is one such method for predicting joint effects of coexposures to chemicals and has the advantage of allowing for mixture components to have differences in efficacy (ie, dose-response curve maxima). Peroxisome proliferator–activated receptor gamma (PPARγ) is a nuclear receptor that plays a central role in regulating lipid homeostasis, insulin sensitivity, and bone quality and is the target of an increasing number of environmental toxicants. Here, we tested the applicability of GCA in predicting mixture effects of therapeutic (rosiglitazone and nonthiazolidinedione partial agonist) and environmental PPARγ ligands (phthalate compounds identified using EPA’s ToxCast database). Transcriptional activation of human PPARγ1 by individual compounds and mixtures was assessed using a peroxisome proliferator response element-driven luciferase reporter. Using individual dose-response parameters and GCA, we generated predictions of PPARγ activation by the mixtures, and we compared these predictions with the empirical data. At high concentrations, GCA provided a better estimation of the experimental response compared with 3 alternative models: toxic equivalency factor, effect summation and independent action. These alternatives provided reasonable fits to the data at low concentrations in this system. These experiments support the implementation of GCA in mixtures analysis with endocrine disrupting compounds and establish PPARγ as an important target for further studies of chemical mixtures.

Keywords: mixtures, PPARγ, modeling, phthalates

Exposure to environmental chemicals is rarely on a single-chemical basis, requiring risk assessments needing to address chemical mixtures. Because testing all mixture combinations is experimentally impossible, risk assessors and toxicologists use models that predict mixture effects from minimal data that may vary chemical-to-chemical, such as dose-response curves characterizing a compound’s potency (eg, EC50) and efficacy (maximum response) when acting on a specific biological target.

Current chemical mixtures analysis for endocrine disrupting compounds emphasize concentration addition (also called dose addition) (US EPA, 2000), whereby individual component concentrations producing a given mixture effect are scaled by their proportion in the mixture and summed (Rajapakse et al., 2001). This method is generally preferred for chemicals that act by similar mechanisms over models such as independent action (IA) or effect summation (ES). For example, concentration addition may be applicable in cases of mixtures with components that act via the same molecular pathway, such as mixtures of dioxin-like polychlorinated biphenyls (PCBs) that act through the aryl hydrocarbon receptor (AhR), a ligand-activated transcription factor with one ligand-binding site.

Toxic equivalency factor (TEF) is a special case of concentration addition whereby the relative potency of a mixture component is used to generate an equivalent dose of a well-characterized reference compound (Safe, 1998). In cases where the dose-response curves of all the components differ only in potency (same shape and maximal effect), TEFs are generated by comparing the potency of each component to a reference compound, eg, 2,3,7,8-TCDD for the dioxin-like compounds (Safe, 1998). Toxic Equivalents use TEFs to calculate an equivalent total dioxin dose. The effect of the mixture is then calculated from the dose-response curve of the dioxin. This model has the advantage of easy interpretation and implementation where reference chemical data are available, but crucially relies on the assumption that the dose-response curves of component chemicals differ only in potency; the assumptions for use of TEFs are violated when compounds differ in efficacy.

Howard and Webster (2009) introduced generalized concentration addition (GCA) to allow for differences in efficacy among mixture components. This model uses inverse mathematical functions allowing for some components to have submaximal efficacy. They demonstrated the utility of this model toward a mixture of AhR agonists with different efficacies (Howard et al., 2010). GCA accurately fit the experimental data of a full and a partial AhR agonist mixture, whereas TEF did not predict the competitive effect of a partial agonist at high concentrations in a mixture.

Current research has identified peroxisome proliferator–activated receptor gamma (PPARγ) as an important target molecule in endocrine disruption and developmental biology. PPARγ is a nuclear receptor that acts as a metabolic sensor and forms an obligate, permissive heterodimer with the retinoid X receptor alpha (RXRα) (Tontonoz et al., 1994). As the list of environmental toxicants that activate PPARγ grows in number and structural variety (Fang et al., 2015; Hurst and Waxman, 2003; Li et al., 2012; Riu et al., 2011; Springer et al., 2012), there is increasing concern over the influence of environmental chemical exposure on PPARγ-regulated endpoints, namely, lipid homeostasis (Feige et al., 2006), obesity (Janesick and Blumberg, 2011; Chamorro-García et al., 2013), and bone homeostasis (Baker et al., 2015; Lecka-Czernik et al., 1999; Watt and Schlezinger, 2015; Yanik et al., 2011). The extent of exposures and toxicological importance of PPARγ ligands further support the need for the development of flexible models to predict mixture effects.

Here, we tested the applicability of GCA in modeling mixture effects of full and partial PPARγ agonists and compared GCA’s performance against the TEF, IA, and ES models. IA and ES are arguably inappropriate here: IA is intended to be applied when compounds act by different modes of action, while ES is generally considered inappropriate by mixtures toxicologists (Silva et al., 2002). However, investigators do not always know the mechanism of action, and it is not always clear how similar mechanisms need to be for CA to apply (Webster, 2013). It is therefore useful to see how these different models compare with GCA.

Using human PPARγ1 and RXRα and a peroxisome proliferator response element–dependent luciferase reporter, we generated dose-responses for individual ligands. We predicted mixture effects using the different additivity models, and compared these predictions with experimental mixture results. We establish GCA as a model for predicting mixture effects of synthetic PPARγ agonists and show it to be a reasonable additive model of PPARγ activation by mixtures, including therapeutic drugs and phthalates that we identified as PPARγ agonists from the ToxCast data set.

MATERIALS AND METHODS

Chemical Suppliers

Rosiglitazone was obtained from Cayman Chemicals (Ann Arbor, Michigan). Nonthiazolidinedione partial agonist (nTZDpa) was from Tocris Biochemicals (Bristol, UK). Di-(2-ethylhexyl) phthalate (DEHP), mono-(2-ethylhexyl) phthalate (MEHP), mono-butyl phthalate (MBP), butyl-benzyl phthalate (BBP), and mono-benzyl phthalate (MBzP) were obtained from Sigma (St Louis, Missouri).

Reporter Assay

Cos7 cells were plated in 96-well plates and transiently transfected with human PPARG1 (provided by V.K. Chatterjee, University of Cambridge, Cambridge, UK) and human RXRΑ (plasmid 8882; Addgene, Cambridge, Massachusetts) (Tontonoz et al., 1994) expression vectors, with peroxisome proliferator response element 3x-TK-Luc (plasmid 1015; Addgene) (Kim et al., 1998) and cytomegalovirus-enhanced green fluorescent protein reporter using Lipofectamine 2000 (Invitrogen, Carlsbad, California). After overnight incubation at 37 °C, the media was replaced and cells received no treatment (medium only), Vh (dimethyl sulfoxide 0.1%), or PPARγ ligands at a range of concentrations either alone or in combination (rosiglitazone 1 × 10 − 10 M – 1 × 10 − 6 M; nTZDpa 1 × 10 − 9 M – 5 × 10 − 6 M; DEHP 1 × 10 − 7 M – 2 × 10 − 4 M; MEHP 1 × 10 − 7 M – 1 × 10 − 4 M; BBP 1 × 10 − 7 M – 5 × 10 − 4 M; MBP 1 × 10 − 7 M – 5 × 10 − 4 M; MBzP 1 × 10 − 7 M – 5 × 10 − 4 M). Concentrations of individual chemicals were chosen using pilot studies designed to identify the highest, nontoxic dose. After 24 hours of treatment, cells were lysed with GloLysis buffer and mixed with BrightGlo Luciferase buffer (Promega Inc, Madison, Wisconsin). Luminescence and fluorescence were determined using a Synergy2 plate reader (Biotek Inc, Winooski, Vermont). Luminescence of each well was normalized to green fluorescent protein-fluorescence, and the resulting values were normalized to medium-only wells to obtain fold change in PPARγ activation.

ToxCast PPARγ Agonist Identification

ToxCast assay and chemical data were downloaded from EPA’s ToxCast portal at (http://www2.epa.gov/chemical-research/toxicity-forecaster-toxcasttm-data) in May of 2015 (US EPA, 2014). Chemicals were selected for inclusion that showed dose-response data fit with a monotonic Hill function in the Attagene PPRE_cis_up assay and the Attagene PPARγ_trans_up assays. To limit the selection to chemicals that did not also activate RXRα, these candidates were limited to those that fit RXRα-specific assays Odyssey Thera NURR1_NURR1RXRa_1440, Attagene RXRa_TRANS_up, and Odyssey Thera NURR1_NURR1RXRa_0480 with a constant (ie no response) model. Of the resulting 88 chemicals from this screening process, we identified 5 phthalates for testing, 2 parent phthalate compounds (DEHP and BBP) and 3 phthalate metabolites (MEHP, MBP, and MBzP).

Experimental Fits

GCA requires specification of mathematical dose-response functions that are invertible yielding real numbers for all effect levels of interest. As in our previous work (Howard et al., 2010), we chose the function based on a biologically based model for binding of a ligand to a receptor at a single binding site followed by activation, where the degree of activation can depend on the ligand; the compounds we are investigating bind PPARγ, not RXRα. This model yields Hill functions with a Hill coefficient of 1. Individual chemical dose-response data were therefore fit to the following equation:

f([A])= min + (max−min)([A])/(KA+ [A]), (1)

where KAis the macroscopic equilibrium constant for agonist A (EC50, equal to the dose producing a 50% maximal effect), min and max are the curve minimum and maximum effect levels, respectively, and [A] is the dose of ligand A. For mixtures experiments, data points were adjusted by subtracting the response value of Vh-only–treated wells, allowing the curves to be fit with a 2-parameter Hill function: f([A]) = αA([A])/(KA + [A])f, where αA is the maximum effect level.

Toxic Equivalency Factor

TEF is a special case of concentration addition (and GCA) requiring parallel dose-response curves, including the same efficacy. When efficacies differ, TEFs will not in principle work. However, relative potencies may still be computed and may provide approximate answers in some cases (Howard et al., 2010) although results will depend on the choice of reference compound and its efficacy. For a reference compound, we used rosiglitazone, the compound with the highest potency and efficacy, and traditionally used as a positive control for PPARγ activity. The relative potency (γi) is determined by γi = KA/Ki, where A is the reference compound rosiglitazone. The total effect of the mixture, estimated for n components, is

ETEF=fAA+∑i=1nγi[Xi]=αA(A+∑i=1nγi[Xi])KA+ (A+∑i=1nγi[Xi]) (2)

Generalized Concentration Addition

GCA relaxes the requirement of equal dose-response maxima. The general GCA equation for n components is

1= ∑i=1n[Xi]fi-1(E)  (3)

where fi−1(E) is the mathematical inverse of the individual chemical dose-response function and E is the mixture effect level. The inverse of the 2-parameter Hill function above is fi−1(E)=EKi/(α1−E), a function that yields real numbers for positive values of αi, Ki and E. Substituting this equation into (3) allows for easy calculation of the effect level at a given mixture of n components with efficacies αi and EC50s given by Ki:

EGCA=fmixture[X1],…,[Xn]=∑i=1nαi[Xi]Ki1+ ∑i=1n[Xi]Ki (4)

Although (3) is the general definition of GCA, the form of (4) also depends on the specific dose-response function being modeled and may not apply more generally.

Effect Summation and Independent Action

ES and IA are response-additive models that sum the individual responses, rather than the doses, of the mixture components. For ES

EES=fmixtureX1,…Xi=∑i=1nfi(Xi) (5)

IA is generally used for compounds that act by different mechanisms. IA assumes that compounds have the same maximal effect of one:

EIA=fmixtureX1,…Xi=1-∏i=1n1-fi(Xi)

When efficacies differ, the standard formula needs to be modified, and the best procedure is not clear. Following Payne et al (2001), we scaled the response of individual components to the maximum efficacy, αmax, then scaled the overall results to the same maximum:

EIA=fmixtureX1,…Xi=αmax1-∏i=1n1-fi(Xi)αmax (6)

The estimated maximum efficacy here was for MBzP, 7% larger than that of rosiglitazone (Figure 3B). Scaling components by their own maximums (αi) produces predictions that are larger and closer to those provided by the TEF model (data not shown).

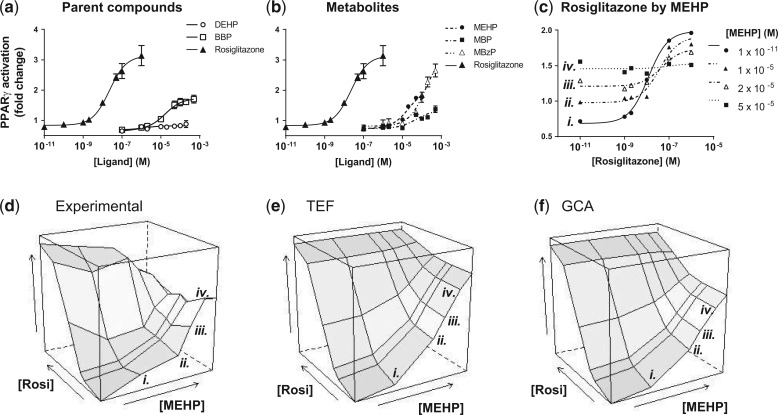
FIG. 3.

FIG. 3.

Open in a new tab

Phthalate esters activate PPARγ with varying efficacies. Cos-7 cells were transfected with a peroxisome proliferator response element–dependent 3× luciferase reporter as described in Materials and Methods and dosed with Vh (dimethyl sulfoxide) or the indicated concentrations of agonists. Green fluorescent protein normalized luminescence was normalized to that of untreated culture wells. Positive control data (rosiglitazone) is included for comparison. N = 4 separate transfections. A. Dose-response curves of parent phthalates DEHP and BBP. B. Dose-response curves of metabolite phthalate compounds MEHP, MBP, and MBzP. C. Rosiglitazone dose-response curves with increasing concentrations of MEHP. Error bars omitted for clarity. All curves were fit with a 3-parameter Hill equation (with Hill coefficient constrained at 1). Dose-response parameters for phthalate components are listed in Table 1. D. Experimental dose-response surface of rosiglitazone/MEHP mixture. E. TEF-predicted surface. F. GCA-predicted surface. Interior values predicted using parameters derived from A (rosiglitazone EC50: 2.3 × 10 − 8 M) and Table 1. Rosiglitazone dose-response curves by increasing MEHP are labeled i.–iv. to facilitate comparison to C.

Statistics and Software

Individual dose-response curves were fit and relevant parameters were estimated using Prism (version 6; GraphPad). Combination dose-response surfaces were generated in R using the wireframe() function. The R code for generating the additive model predictions is available at the Boston University Superfund Research Program website (www.busrp.org). Model extrapolations were performed in Mathematica (version 9.0.1.0; Wolfram Alpha). Differences in experimental distributions and model predicted distributions were tested using the nonparametric Wilcoxon rank-sum and Komolgorov-Smirnov tests.

RESULTS

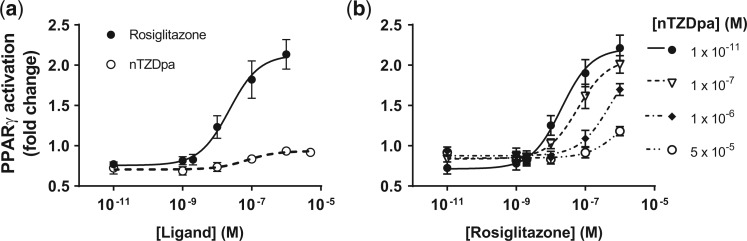
We began by establishing the dose-responses of 2 synthetic PPARγ ligands, rosiglitazone (full agonist) and nTZDpa (partial agonist). Cos-7 cells were transfected with expression vectors for human RXRα and PPARγ1 and a luciferase reporter gene under transcriptional control of a direct repeat 1 peroxixome proliferator response element; cells were treated with each chemical separately and in combination. As shown in Figure 1A, the individual dose-response data were well fit by Hill functions with a Hill coefficient of 1 (the “S” shape of the data in the figure is partly due to plotting concentration on the log scale). nTZDpa and rosiglitazone stimulate PPARγ activation with similar potencies (EC50s of 2.2 × 10 − 8 M and 7.1 × 10 − 8 M, respectively), which were comparable with established estimates (4.3 × 10 − 8 M for rosiglitazone [Lehmann et al., 1995], 5.7 × 10 − 8 M for nTZDpa [Berger et al., 2003]). nTZDpa is a significantly less efficacious PPARγ ligand, with a response maximum of only approximately 17% of rosiglitazone (Figure 1A). A PPARγ-dominant negative construct suppresses luciferase gene expression stimulated by rosiglitazone in this system (Pillai et al., 2014), indicating that the increased luminescence as a function of concentration is due specifically to PPARγ binding and activation by the agonists.

FIG. 1.

FIG. 1.

Open in a new tab

The maximal response to rosiglitazone is decreased by high concentrations of nTZDpa. A, Individual (marginal) dose-response curves of rosiglitazone (full agonist) and nTZDpa (partial agonist). Cos-7 cells were transfected with peroxisome proliferator response element dependent 3× luciferase reporter as described in Materials and Methods and dosed with Vh (dimethyl sulfoxide) or the indicated concentrations of agonist. Green fluorescent protein-normalized luminescence was normalized to that of untreated culture wells. EC50 rosiglitazone: 2.2 × 10 − 8 M; EC50 nTZDpa: 7.1 × 10 − 8 M. N = 4 separate transfections. B. Dose-response curves of rosiglitazone in combination with increasing partial agonist concentration (error bars: SEM) (N = 4).

We hypothesized that mixtures of rosiglitazone and nTZDpa would show a reduction in overall PPARγ activation at effect levels above the efficacy of nTZDpa, owing to the behavior of a partial agonist to act in the manner of a competitive antagonist in a mixture. Figure 1B demonstrates that at high effect levels, the response to rosiglitazone is antagonized and the overall activation of PPARγ by the mixture decreases: note that the 1 × 10 − 11 nTZDpa curve (solid line, black circles) closely approximates the rosiglitazone curve in Figure 1a, but increasing concentrations of nTZDpa reduce the curve closer to that of nTZDpa in Figure 1a. These data support the conclusion that nTZDpa is outcompeting rosiglitazone for PPARγ binding and that a higher proportion of partial agonist-bound receptors is attenuating the overall effect.

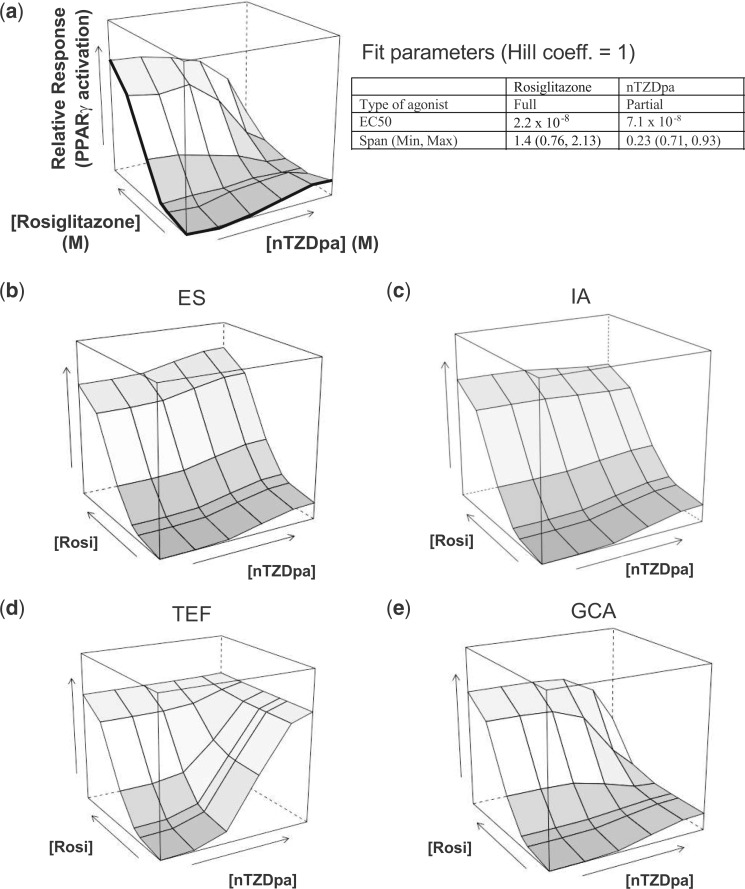
To compare the empirical dose response data with those predicted by different additive models, 3-dimensional response surfaces of PPARγ activation by the rosiglitazone/nTZDpa combinations were plotted (Figure 2). Marginal (ie, individual) dose-response curves lie along the front edges of the box (in bold) and combination effects comprise the interior surface. The antagonistic effect of nTZDpa is evident in the dose-response surface, with the surface dropping downward at high concentrations of nTZDpa and rosiglitazone (Figure 2A). Using individual-chemical fit parameters (listed in the embedded table in Figure 2), we generated predicted response surfaces under different additive models (ES, TEF, IA, and GCA).

FIG. 2.

FIG. 2.

Open in a new tab

Generalized concentration addition (GCA) provides an accurate prediction of full and partial PPARγ agonist mixture effects. A. Experimental joint dose-response surface of rosiglitazone and nTZDpa dose combinations. Vertical axis: fold change in PPARγ activation over untreated cultures (linear). Marginal curves correspond to individual dose-response curves shown in Figure 1. B. Effect summation (ES), (C) independent Action (IA), (D) toxic equivalency factor (TEF), and (E) GCA model fits based on parameters (with Hill coefficient constrained at 1.0) listed in embedded table and formulations listed in Materials and Methods.

The ES model, generated from equation 5, sums the individual effect levels of each combination of rosiglitazone and nTZDpa. At low concentration combinations, the ES surface approximates the empirical surface (Figure 2B). However, at high concentration combinations, the modeled surface implies supramaximal activation, as the effect of nTZDpa is added to the effect of rosiglitazone.

IA (equation 6) assumes the observed individual effects result from independent mechanisms of action. Like ES, at low concentration, the model approximates the empirical surface (Figure 2C). Higher concentration combinations begin to show the characteristic competitive antagonism effect of the full and partial ligand mixture, but the model fails to fully capture the reduction in overall effect.

TEF, defined in equation 2, assumes that the efficacies of rosiglitazone and nTZDpa are equal, and that nTZDpa is a diluted form of the more potent rosiglitazone. The modeled response surface generated by TEF shows no antagonistic effect of nTZDpa at high concentrations (Figure 2D).

Because GCA was formulated to allow for differences in efficacy among mixture components (Howard and Webster, 2009), we hypothesized that the surface generated by GCA would most accurately resemble the empirical surface. The GCA-modeled surface (equation 4) captures the attenuating effect of high concentrations of nTZDpa (Figure 2E). The nonparametric Wilcoxon rank-sum and Komologorov-Smirnov tests indicate that the distribution of GCA-modeled estimates is not significantly different from empirical results (P > .05), whereas the TEF and ES distributions do differ significantly from the experimental data (P > .01 for both comparisons). Generation of modeled distributions using the upper and lower bounds of the experimental standard errors resulted in minimal changes to the modeled estimates (Supplementary Figure S1). From these results, we concluded that GCA is a viable model for predicting combination effects of 2 PPARγ-specific agonists that have different efficacies.

Next, we tested the applicability of GCA in modeling PPARγ activation stimulated by mixtures of environmental ligands. From EPA’s ToxCast data set, we identified potential PPARγ agonists, including 5 phthalate compounds: DEHP, BBP, MEHP, MBP, and MBzP. Individually, all but DEHP activated PPARγ in our assay. Table 1 lists the efficacy (as maximum-minimum) and potency (EC50) derived from the dose-response curve of each parent (Figure 3A) and metabolite (Figure 3B) compound. Although the potencies were mostly within the same order of magnitude (with MBzP being slightly less potent than the other phthalates), the efficacies varied roughly 4-fold between the least (MBP) and most efficacious (MBzP).

TABLE 1.

Modeled Parameters for Phthalate Compounds From Dose-Response Fits Using 3-Parameter Hill equation (With Hill Coefficient of 1) (Figs. 3A and B)

DEHP MEHP BBP MBP MBzP
EC50 (M) (95% CI) N.D. 2.2 × 10−5 1.7 × 10−5 5.1 × 10−5 1.6 × 10−4
(9.8 × 10−6, 4.7 × 10−5) (7.9 × 10−6, 3.6 × 10−5) (1.5 × 10−5, 1.7 × 10−4) (8.3 × 10−5, 3.0 × 10−4)
Span (max-min) (95% CI) N.D. 1.3 (1.0–1.6) 1.0 (0.89–1.2) 0.61 (0.42–0.79) 2.5 (1.9–3.1)
Efficacy relative to rosiglitazone maximum (2.3-fold change (95% CI, 2.0–2.6)) N.D. 0.56 0.43 0.26 1.1
R2 N.D. 0.87 0.88 0.71 0.90
Open in a new tab

Abbreviation: CI, confidence interval; N.D., not detected.

Because of the minimal efficacy and poor statistical fit, DEHP was considered to be inactive for the purpose of the mixture experiments. 95% CI associated with fit estimate. Span: difference in estimated curve maximum and curve minimum (equation 1).

We began by testing an array of rosiglitazone (full agonist) and MEHP (partial agonist) combinations. Similar to rosiglitazone and nTZDpa mixtures, MEHP increases PPARγ activation at low effect levels (Figure 3C, left side), but antagonizes the PPARγ activation stimulated by rosiglitazone at higher effect levels, reducing the mixture activation of PPARγ to the response maximum of MEHP (Figure 3C, right side). The predictions of GCA fit the observed data somewhat better than the TEF model at high concentration combinations where a small amount of antagonism by MEHP becomes evident (Figs. 3–F). The difference between the 2 models is not as stark as that for the rosiglitazone/nTZDpa mixture (Figure 2). The reason is that the estimated efficacy for MEHP is 80% that of rosiglitazone, far closer in maximal effect compared to nTZDpa.

Next, we tested a complex mixture of phthalates. We hypothesized that, given the different efficacies among the phthalates, GCA would again provide the most accurate fit, whereas the response-additive models and TEF would overestimate the mixture effect. To test this hypothesis, we constructed 2 mixtures of multiple phthalates. Because of the logistical complication of testing mixtures with >2 components, we used ray designs in which each component is in constant proportion to one another across mixture dilutions. We excluded DEHP from the rays because of its lack of activity in the PPARγ activation assay. The starting solution for the first ray (A) consisted of BBP, MEHP, MBP, and MBzP at concentrations just below their respective EC10 values, as determined by their individual dose-responses (Table 2). The starting solution for the second ray (B) combined the 4 phthalates at concentrations that produced the same effect level as 10% of rosiglitazone’s maximum effect (Table 2). Each mixture was diluted by factors of 2, 5, 10, 20, 50, and 100, and the dilution series were applied in the PPARγ activation assay. Using the individual dose-response parameters listed in Table 1, mixture responses also were predicted using the ES, TEF, GCA, and IA models.

Table 2.

Phthalate Components of Mixture Rays

MEHP BBP MBP MBzP Stock Mixture Concentration (Total)
Ray A Concentration (M) in stock mixture 2.2 × 10−6 1.7 × 10−6 4.3 × 10−6 1.6 × 10−5 2.4 × 10−5 M
Effect level % max 9.3 9.2 7.7 9.5
Ray B Concentration (M) in stock mixture 3.8 × 10−6 3.7 × 10−6 1.5 × 10−5 1.6 × 10−5 3.9 × 10−5 M
Effect level % max 15 18 23 9.4
Open in a new tab

DEHP excluded from rays (see footnote in Table 1).

Ray A: phthalates mixed at initial concentrations below the calculated EC10 from individual dose-response curves. Ray B: phthalates mixed at initial concentrations producing the equivalent effect as rosiglitazone’s EC10 from control dose-response curve (Figs. 3A and B).

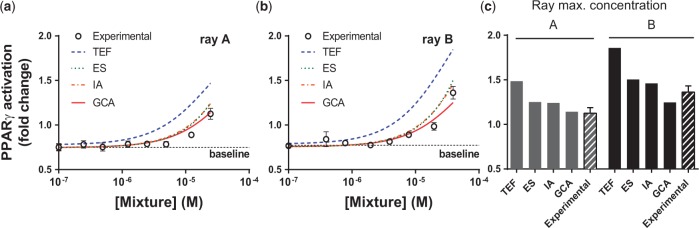
The starting concentrations of mixtures A and B produced effect levels that were 7% and 30% higher, respectively, than the predicted individual effect of the most efficacious component (MBzP) at the concentration at which it was added to each mixture (1.6 × 10 − 5 M; Table 2). By the second and fourth dilutions of ray A and B, respectively, the activation of PPARγ by the mixture was indistinguishable from baseline (Figs. 4A and b). At low concentrations, all 4 models—GCA, TEF, ES, and IA—adequately fit the empirical data. At higher concentrations, the TEF predictions strongly diverge from the observed data, whereas GCA may provide a slightly better fit than ES and IA. Figure 4C provides a closer comparison of the starting mixture concentrations and the modeled values.

FIG. 4.

FIG. 4.

Open in a new tab

Comparison of experimentally determined PPARγ activation with model predictions. A. Phthalates combined at starting concentrations below individual EC10’s. B. Phthalates combined at starting concentrations producing effect levels equal to 10% of rosiglitazone’s maximal effect. C. Comparison of rays and models at highest concentrations. Ray design specifications listed in Table 2. Experimental data N = 4 separate transfections, mean ± SEM. Baseline: Experimental curve fit estimated minimum (experimental curve fit omitted for clarity).

To examine the behavior of these models at high concentrations, we used the same fitting parameters to extrapolate models to high concentration levels for ray A. As shown in Figure 5, the models diverge with increasing mixture concentration. At high mixture concentration, the ES model vastly exceeds the other models. Both the TEF and IA models overestimate effects compared with GCA; this occurs in part because only GCA takes into account the antagonistic effect of partial agonists.

FIG. 5.

FIG. 5.

Open in a new tab

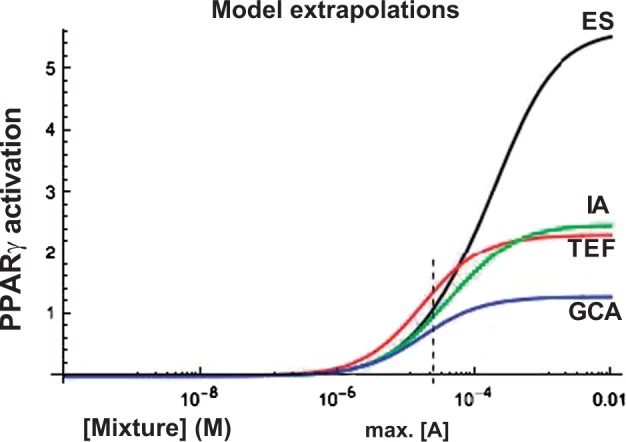
Extrapolations of modeled dose-responses to high concentrations for ray A. Vertical line: maximum mixture concentration tested (Figure 4A).

DISCUSSION

Current methods for estimating risk from chemical exposure predominately focus on single chemical exposure instead of the more realistic scenario of coexposure to multiple chemicals. At the same time, several agencies are recognizing the need to focus research on low dose exposures to endocrine disrupting chemicals that act via inappropriate activation of nuclear receptors (Carlin et al., 2013; Reif et al., 2010; World Health Organization, 2013). One such nuclear receptor is PPARγ, which plays a central role in toxic mechanisms related to lipid homeostasis, bone quality, and other endpoints (Ahmadian et al., 2013). Given its status as a target of endocrine disruption by a variety of environmental agonists, PPARγ is an important model for which to study chemical co-exposures and develop ways to predict toxicity of chemical mixtures. Here, we established the utility of GCA (Howard and Webster, 2009) in modeling joint effects of chemical coexposures that activate PPARγ.

The experimental design used to generate experimental mixture data and test the additive models was similar to that of Howard et al. (2010), who used GCA to model mixture effects of AhR agonists. In that study, they showed experimentally that the partial AhR agonist (galangin) could decrease the overall mixture effect when combined with a full AhR agonist (PCB126). This effect of galangin resembled that of a competitive antagonist. The difference is that a partial agonist increases the mixture effect at levels below its efficacy, but decreases the mixture effect at levels above its efficacy.

We began by testing the utility of GCA in predicting the activation of PPARγ by a mixture containing a full (rosiglitazone) and partial (nTZDpa) agonist. At high combined concentrations, the activation of PPARγ was reduced by nTZDpa, and this was predicted by GCA (Figure 2D). Because of overt toxicity and the comparable potencies between rosiglitazone and nTZDpa, nTZDpa could not be added to a level that fully reduced the activity of the mixture to that of the maximum effect of nTZDpa. However, GCA was able to model the decrease in mixture effect, whereas the TEF model, in assuming equal efficacy between the 2 components (and using rosiglitazone as the reference compound), inflated the effect of high concentrations of nTZDpa (Figure 2C). ES and IA proved inadequate as well (Figure 2A). These results indicate that GCA is a viable model in the case of a mixture of 2 chemicals designed specifically as PPARγ ligands.

Phthalates comprise a group of chemicals designed for use in consumer products and manufacturing but also show biological activity. Manufactured at high volume for use as plasticizing agents and flame retardants, phthalates can act on numerous targets, especially in the male reproductive system (Dalgaard et al., 2001; Howdeshell et al., 2008; Parks et al., 2000). Specific phthalate esters (MEHP, MBzP, MBP, and BBP) have also been shown to activate peroxisome proliferator (Hurst and Waxman, 2003; Pereira-Fernandes et al., 2013). Exposure to phthalates is widespread and detected in human biomonitoring data, including National Health and Nutrition Examination Survey (Buser et al., 2014; Hatch et al., 2010). Parent phthalate compounds such as DEHP and BBP undergo biotransformation to multiple metabolites following absorption, making phthalate mixtures biologically relevant (Langer et al., 2014; Zota et al., 2014). Typically, phthalate metabolites are more biologically active than the parent compounds with regard to activation of PPARs (Cornu et al., 1992; Hurst and Waxman, 2003).

To identify phthalates that activate PPARγ, we used EPA’s ToxCast database (US EPA, 2014). Because our assay uses a transfected luciferase reporter construct under the transcriptional control of a peroxisome proliferator response element, we selected compounds that activated an equivalent model assay in ToxCast. To increase the specificity for identifying PPARγ ligands, we included chemicals that also activated a PPARγ ligand binding domain fused with a Gal-4 reporter, and excluded chemicals that showed any activity in assays for PPARγ’s permissive heterodimer partner, RXRα. Contrary to the ToxCast screen, DEHP did not activate PPARγ transcriptional activity in our assay. We speculate that this is due to differences in the source of the cell line (human liver in ToxCast, African Green monkey for Cos-7 cells in our assay) although others have shown that DEHP does not activate human PPARγ in vitro (Hurst and Waxman, 2003).

In a binary mixture, MEHP reduced the activation of PPARγ by rosiglitazone at higher concentrations of both compounds, which was predicted by GCA (Figs. 3C and F). GCA also accurately predicted the activation of PPARγ by a more complex phthalate mixture. However, ES, IA, and TEF all approximated GCA and fit the observed data at low concentrations of both rays. In contrast to our results, Silva et al. (2002) demonstrated that ES and IA do not sufficiently predict mixture effects of estrogen receptor full agonists at low concentrations; this is caused by the nonlinear shape of the dose-response curves for these compounds at low doses. Our dose-response data are nearly linear at low concentrations (equation 1). As a result, the predictions of ES and IA approximate those of GCA. One would not expect the dramatic “Something from Nothing” effect that can occur with mixtures that have linear dose-response curves (Silva et al., 2002).

When we extrapolate these models to higher concentration levels of the phthalate mixture (where the dose-response curve departs from linearity), we see considerable divergence among the models (Figure 5). We also see this pattern in the ES prediction of the mixture of rosiglitazone and nTZDpa (Figure 2A), where ES overestimates the effect of the mixture at high concentrations.

GCA requires that the user specify a dose-response function that can be inverted, yielding real numbers for effect levels of interest. Based on the biological mechanism of PPARγ, where ligands bind the receptor at a single site, we used a Hill function with a Hill coefficient of 1 (Howard et al., 2010; Howard and Webster, 2009). This function meets the invertibility requirement. Some scenarios may warrant fitting dose-response data with different dose-response functions. For example, ligands for receptors that homodimerize (e.g., estrogen receptor) would be expected to be nonlinear at low dose. We would not expect such data to be adequately fit by a Hill function with a Hill coefficient of 1; on the other hand, use of a Hill function of 2 would violate the invertibility requirement needed for applying GCA to partial agonists. We are currently working on appropriate biologically based models for these types of systems. GCA may not be applicable to all mixtures of full and partial agonists. Accordingly, careful consideration should be placed on properly specifying the individual dose-response functions.

As an alternative to GCA, Scholze et al. (2014) introduced the Toxic Unit Extrapolation model for predicting the joint effect of a mixture that includes partial agonists, and applied it to ligands of the estrogen receptor. However, toxic unit extrapolation does not account for the antagonistic effect of partial agonists at high doses; this effect may in principle occur even when there are 2 binding sites as in a homodimer. We attempted to limit our biological mechanism exclusively to PPARγ-specific binding via our selection of candidate compounds. Future work will address whether concentration additive models are appropriate for cases involving agonist mixtures that activate separate components of permissive heterodimers, or whether it is better fit by an IA model.

Although TEF overestimates the mixture response, the model does have the advantage of easy interpretability and use, as each component is treated as a dilution of a well-characterized reference compound (for PPARγ, we used rosiglitazone). For regulatory purposes, TEF would provide conservative estimates that may be of use to risk assessors, where applicable. On the other hand, the model prediction is dependent on the choice of reference compound and its efficacy; the model overestimation will increase with increasing efficacy of the reference compound. Given the variety of sources, structures, and pharmacodynamics (Tan et al., 2012) of PPARγ agonists, the choice of a “correct” reference compound for PPARγ agonism is not clear.

Realistic exposures to environmental endocrine disrupting compounds tend to be at low concentrations, where GCA, TEF, IA, and ES produced similar results for PPARγ ligands. However, GCA produced estimates quite different from the other models when the mixture concentration was extrapolated to high doses. For PPARγ ligands, GCA may be particularly useful in determining effects of interactions between environmental exposures and therapeutic treatments. PPARγ already serves as a relevant model for this type of mixture, given its well-established role as a target for insulin-sensitizing drugs. For example, Cmax estimates of rosiglitazone in human blood during therapeutic use range from 200 nM to 1.2 μM (Avandia, Rx List website), concentrations that fall within the drug’s maximal efficacy for PPARγ activation. When co-exposure to low efficacy environmental PPARγ ligands occurs, the efficacy of the administered therapeutic may be reduced. Given the breadth of PPARγ’s biologic influence and the increasing number of identified ligands in the indoor and outdoor environment, future studies should characterize mixture effects on relevant endpoints under control of PPARγ activation, such as insulin sensitivity and lipid accumulation, to better inform the biology behind predictive models.

SUPPLEMENTARY DATA

Supplementary data are available online at http://toxsci.oxfordjournals.org/.

FUNDING

This work was supported by the National Institute of Environmental Health Sciences Superfund Research Program (P42ES007381).

Supplementary Material

Supplementary Data
supp_153_1_18__index.html (801B, html)

REFERENCES

  1. Ahmadian M., Suh J. M., Hah N., Liddle C., Atkins A. R., Downes M., Evans R. M. (2013). PPARγ signaling and metabolism: the good, the bad and the future. Nat. Med 19, 557–566. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Avandia (Rosiglitazone maleate) Drug Information. RxList website. Available at: http://www.rxlist.com/avandia-drug/clinical-pharmacology.htm. Accessed February 11, 2016.
  3. Baker A. H., Watt J., Huang C. K., Gerstenfeld L. C., Schlezinger J. J. (2015). Tributyltin engages multiple nuclear receptor pathways and suppresses osteogenesis in bone marrow multipotent stromal cells. Chem. Res. Toxicol 28, 1156–1166. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Berger J. P., Petro A. E., Macnaul K. L., Kelly L. J., Zhang B. B., Richards K., Elbrecht A., Johnson B. A., Zhou G., Doebber T. W., et al. (2003). Distinct Properties and Advantages of a Novel Peroxisome Proliferator-Activated Protein Selective Modulator. Mol. Endocrinol 17, 662–676. [DOI] [PubMed] [Google Scholar]
  5. Buser M. C., Murray H. E., Scinicariello F. (2014). Age and sex differences in childhood and adulthood obesity association with phthalates: analyses of NHANES 2007-2010. Int. J. Hyg. Environ. Health 217, 687–694. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Carlin D. J., Rider C. V., Woychik R., Birnbaum L. S. (2013). Unraveling the Health Effects of Environmental Mixtures: An NIEHS Priority. Environ. Health Perspect 121, A6–A8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Chamorro-García R., Sahu M., Abbey R. J., Laude J., Pham N., Blumberg B. (2013). Transgenerational inheritance of increased fat depot size, stem cell reprogramming, and hepatic steatosis elicited by prenatal exposure to the obesogen tributyltin in mice. Environ. Health Perspect 121, 359–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Cornu M. C., Lhuguenot J. C., Brady A. M., Moore R., Elcombe C. R. (1992). Identification of the proximate peroxisome proliferator(s) derived from di (2-ethylhexyl) adipate and species differences in response. Biochem. Pharmacol 43, 2129–2134. [DOI] [PubMed] [Google Scholar]
  9. Dalgaard M., Nellemann C., Lam H. R., Sørensen I. K., Ladefoged O. (2001). The acute effects of mono(2-ethylhexyl)phthalate (MEHP) on testes of prepubertal Wistar rats. Toxicol. Lett 122, 69–79. [DOI] [PubMed] [Google Scholar]
  10. Fang M., Webster T. F., Ferguson P. L., Stapleton H. M. (2015). Characterizing the peroxisome proliferator-activated receptor (PPARγ) ligand binding potential of several major flame retardants, their metabolites, and chemical mixtures in house dust. Environ. Health Perspect 123, 166–172. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Feige J. N., Gelman L., Michalik L., Desvergne B., Wahli W. (2006). From molecular action to physiological outputs: peroxisome proliferator-activated receptors are nuclear receptors at the crossroads of key cellular functions. Prog. Lipid Res 45, 120–159. [DOI] [PubMed] [Google Scholar]
  12. Hatch E. E., Nelson J. W., Stahlhut R. W., Webster T. F. (2010). Association of endocrine disruptors and obesity: perspectives from epidemiological studies. Int. J. Androl 33, 324–332. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Howard G. J., Webster T. F. (2009). Generalized concentration addition: a method for examining mixtures containing partial agonists. J. Theor. Biol 259, 469–477. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Howard G. J., Schlezinger J. J., Hahn M. E., Webster T. F. (2010). Generalized concentration addition predicts joint effects of aryl hydrocarbon receptor agonists with partial agonists and competitive antagonists. Environ. Health Perspect 118, 666–672. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Howdeshell K. L., Wilson V. S., Furr J., Lambright C. R., Rider C. V., Blystone C. R., Hotchkiss A. K., Gray L. E., Jr. (2008). A mixture of five phthalate esters inhibits fetal testicular testosterone production in the sprague-dawley rat in a cumulative, dose-additive manner. Toxicol. Sci 105, 153–165. [DOI] [PubMed] [Google Scholar]
  16. Hurst C. H., Waxman D. J. (2003). Activation of PPARα and PPARγ by environmental phthalate monoesters. Toxicol. Sci 74, 297–308. [DOI] [PubMed] [Google Scholar]
  17. Janesick A., Blumberg B. (2011). Minireview: PPARγ as the target of obesogens. J Steroid Biochem. Mol. Biol. 127, 4–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Kim J. B., Wright H. M., Wright M., Spiegelman B. M. (1998). ADD1/SREBP1 activates PPARγ through the production of endogenous ligand. Proc. Natl. Acad. Sci. U.S.A. 95, 4333–4337. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Langer S., Bekö G., Weschler C. J., Brive L. M., Toftum J., Callesen M., Clausen G. (2014). Phthalate metabolites in urine samples from Danish children and correlations with phthalates in dust samples from their homes and daycare centers. Int. J. Hyg. Environ. Health 217, 78–87. [DOI] [PubMed] [Google Scholar]
  20. Lecka-Czernik B., Gubrij I., Moerman E. J., Kajkenova O., Lipschitz D. A., Manolagas S. C., Jilka R. L. (1999). Inhibition of Osf2/Cbfa1 expression and terminal osteoblast differentiation by PPARγ2. J. Cell Biochem. 74, 357–371. [PubMed] [Google Scholar]
  21. Lehmann J. M., Moore L. B., Smith-Oliver T. A., Wilkison W. O., Willson T. M., Kliewer S. A. (1995). An antidiabetic thiazolidinedione is a high affinity ligand for peroxisome proliferator-activated receptor γ (PPARγ). J. Biol. Chem. 270, 12953–12956. [DOI] [PubMed] [Google Scholar]
  22. Li X., Pham H. T., Janesick A. S., Blumberg B. (2012). Triflumizole is an obesogen in mice that acts through peroxisome proliferator activated receptor gamma (PPARγ). Environ. Health Perspect 120, 1720–1726. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Parks L. G., Ostby J. S., Lambright C. R., Abbott B. D., Klinefelter G. R., Barlow N. J., Gray L. E., Jr. (2000). The plasticizer diethylhexyl phthalate induces malformations by decreasing fetal testosterone synthesis during sexual differentiation in the male rat. Toxicol. Sci. 58, 339–349. [DOI] [PubMed] [Google Scholar]
  24. Payne J., Scholze M., Kortenkamp A. (2001). Mixtures of four organochlorines enhance human breast cancer cell proliferation. Environ. Health Perspect. 109, 391–397. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Pereira-Fernandes A., Demaegdt H., Vandermeiren K., Hectors T. L., Jorens P. G., Blust R., Vanparys C. (2013). Evaluation of a screening system for obesogenic compounds: screening of endocrine disrupting compounds and evaluation of the PPAR dependency of the effect. PLoS One 8, e77481.. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Pillai H. K., Fang M., Beglov D., Kozakov D., Vajda S., Stapleton H. M., Webster T. F., Schlezinger J. J. (2014). Ligand binding and activation of PPARγ by Firemaster® 550: effects on adipogenesis and osteogenesis in vitro. Environ. Health Perspect. 122, 1225–1232. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Rajapakse N., Ong D., Kortenkamp A. (2001). Defining the impact of weakly estrogenic chemicals on the action of steroidal estrogens. Toxicol. Sci. 60, 296–304. [DOI] [PubMed] [Google Scholar]
  28. Reif D. M., Martin M. T., Tan S. W., Houck K. A., Judson R. S., Richard A. M., Knudsen T. B., Dix D. J., Kavlock R. J. (2010). Endocrine profiling and prioritization of environmental chemicals using ToxCast data. Environ. Health Perspect. 118, 1714–1720. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Riu A., Grimaldi M., le Maire A., Bey G., Phillips K., Boulahtouf A., Perdu E., Zalko D., Bourguet W., Balaguer P. (2011). Peroxisome proliferator-activated receptor γ is a target for halogenated analogs of bisphenol A. Environ. Health Perspect. 119, 1227–1232. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Safe S. H. (1998). Hazard and risk assessment of chemical mixtures using the toxic equivalency factor approach. Environ. Health Perspect. 106(Suppl 4), 1051–1058. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Scholze M., Silva E., Kortenkamp A. (2014). Extending the applicability of the dose addition model to the assessment of chemical mixtures of partial agonists by using a novel toxic unit extrapolation method. PLoS One 9, e88808.. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Silva E., Rajapakse N., Kortenkamp A. (2002). Something from “nothing”–eight weak estrogenic chemicals combined at concentrations below NOECs produce significant mixture effects. Environ. Sci. Technol. 36, 1751–1756. [DOI] [PubMed] [Google Scholar]
  33. Springer C., Dere E., Hall S. J., McDonnell E. V., Roberts S. C., Butt C. M., Stapleton H. M., Watkins D. J., McClean M. D., Webster T. F., et al. (2012). Rodent thyroid, liver, and fetal testis toxicity of the monoester metabolite of bis-(2-ethylhexyl) tetrabromophthalate (tbph), a novel brominated flame retardant present in indoor dust. Environ. Health Perspect. 120, 1711–1719. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Tan Y., Muise E. S., Dai H., Raubertas R., Wong K. K., Thompson G. M., Wood H. B., Meinke P. T., Lum P. Y., Thompson J. R., and., et al. (2012). Novel transcriptome profiling analyses demonstrate that selective peroxisome proliferator-activated receptor γ (PPARγ) modulators display attenuated and selective gene regulatory activity in comparison with PPARγ full agonists. Mol. Pharmacol. 82, 68–79. [DOI] [PubMed] [Google Scholar]
  35. Tontonoz P., Hu E., Graves R. A., Budavari A. I., Spiegelman B. M. (1994). mPPAR gamma 2: tissue-specific regulator of an adipocyte enhancer. Genes Dev. 8, 1224–1234. [DOI] [PubMed] [Google Scholar]
  36. US EPA (2000). Supplemental Guidance for Conducting Health Risk Assessment of Chemical Mixtures. Published August 2000.
  37. US EPA (2014). ToxCast & Tox21 Summary Files from invitrodb_v1. Retrieved from http://www2.epa.gov/chemical-research/toxicity-forecaster-toxcasttm-data. Accessed December 19, 2015.
  38. Watt J., Schlezinger J. J. (2015). Structurally-diverse, PPAR-activating environmental toxicants induce adipogenesis and suppress osteogenesis in bone marrow mesenchymal stromal cells. Toxicology 331, 66–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Webster T. F. (2013). Mixtures of endocrine disruptors: How similar must mechanisms be for concentration addition to apply? Toxicology 313, 129–133. [DOI] [PubMed] [Google Scholar]
  40. World Health Organization (WHO) (2013). State of the science of endocrine disrupting chemicals – 2012. Available at http://www.who.int/ceh/publications/endocrine/en/. Accessed December 19, 2015.
  41. Yanik S. C., Baker A. H., Mann K. K., Schlezinger J. J. (2011). Organotins are potent activators of PPARγ and adipocyte differentiation in bone marrow multipotent mesenchymal stromal cells. Toxicol. Sci 122, 476–488. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Zota A. R., Calafat A. M., Woodruff T. J. (2014). Temporal trends in phthalate exposures: findings from the National Health and Nutrition Examination Survey, 2001-2010. Environ Health Perspect 122, 235–241. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
supp_153_1_18__index.html (801B, html)
supp_kfw100_toxsci-16-0097-File002.docx (131.8KB, docx)

Articles from Toxicological Sciences are provided here courtesy of Oxford University Press

RESOURCES