Pathway-based approach using hierarchical components of collapsed rare variants

Abstract

Motivation: To address ‘missing heritability’ issue, many statistical methods for pathway-based analyses using rare variants have been proposed to analyze pathways individually. However, neglecting correlations between multiple pathways can result in misleading solutions, and pathway-based analyses of large-scale genetic datasets require massive computational burden. We propose a Pathway-based approach using HierArchical components of collapsed RAre variants Of High-throughput sequencing data (PHARAOH) for the analysis of rare variants by constructing a single hierarchical model that consists of collapsed gene-level summaries and pathways and analyzes entire pathways simultaneously by imposing ridge-type penalties on both gene and pathway coefficient estimates; hence our method considers the correlation of pathways without constraint by a multiple testing problem.

Results: Through simulation studies, the proposed method was shown to have higher statistical power than the existing pathway-based methods. In addition, our method was applied to the large-scale whole-exome sequencing data with levels of a liver enzyme using two well-known pathway databases Biocarta and KEGG. This application demonstrated that our method not only identified associated pathways but also successfully detected biologically plausible pathways for a phenotype of interest. These findings were successfully replicated by an independent large-scale exome chip study.

Availability and Implementation: An implementation of PHARAOH is available at http://statgen.snu.ac.kr/software/pharaoh/.

Contact:tspark@stats.snu.ac.kr

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Over the past decade, rapid advances in DNA sequencing technology have enabled extensive investigations into human genetic architecture, especially for the identification of genetic variants associated with complex traits. In particular, genome-wide association studies (GWAS) have identified more than 14 000 single nucleotide variants (SNVs) associated with over 1400 traits, including Mendelian heritable diseases, common diseases and numerous cancers (Bertram et al., 2008; Hindorff et al., 2014; McCarthy et al., 2008; Seng and Seng, 2008). However, even while the number of detectable genetic variants increases, the proportion of the variance of complex traits explained by common variants has been generally very small (Maher, 2008; Manolio et al., 2009). This so-called ‘missing heritability’ problem has continually confounded the precise role of such identified common genetic variants (Manolio et al., 2009). Moreover, one potential approach to the missing heritability issue, the analysis of rare variants, is generally not feasible by GWAS (Li and Leal, 2008; Wu et al., 2011).

To deal with the sparseness of rare variants, early approaches simply aggregated multiple rare variants of a gene by the existence of minor alleles or by summation of minor alleles (Li and Leal, 2008; Price et al., 2010). In contrast, more recent methods seek to consider biological information, such as linkage disequilibrium, and the biological effects of genetic variants, to enhance biological interpretation (Hu et al., 2013; Wu et al., 2011). These approaches have been useful for identifying statistically significant genes associated with several complex traits, including high-density lipoprotein levels, obesity, schizophrenia and multiple cancer types (Ahituv et al., 2007; Brunham et al., 2006; Cohen et al., 2004; Slatter et al., 2008; Walsh et al., 2008).

Most approaches for identifying rare variants focus mainly on individual gene analysis. However, it has now been recognized that a majority of biological behaviors manifest from a complex interaction of biological pathways (Costanzo et al., 2010; Hirschhorn, 2009). In this respect, using pathway or gene-set information to analyze next generation sequencing data has several advantages in addressing the multiple testing problems and improving biological interpretation. First, it is possible to dramatically reduce the number of tests, because tens of millions of SNVs or tens of thousands of genes are grouped into hundreds of pathways. By grouping such large numbers of SNVs into pathways, pathway-based analysis is much less restricted by multiple testing problems, even compared to gene-based analyses. Second, interpreting statistically significant pathways can be easier than interpreting individual SNVs or genes. By analyzing pathway information that associates with biological processes, components or structures, the underlying bases for biological traits can be characterized more intuitively than by examining individual genes (Khatri et al., 2012; O'Dushlaine et al., 2009). Moreover, many successful discoveries of pathways that underlie complex traits have proven the utility of pathway-based analysis (Askland et al., 2009; International Multiple Sclerosis Genetics Consortium, 2013; Lesnick et al., 2007). However, these methods are mainly designed for the analysis of common variants and are not suitable for analysis of rare variants including the most recent pathway-level analyses using genetic information such as linkage disequilibrium or gene-environmental interaction (Lamparter et al., 2016; Qian et al., 2016).

Recent pathway-based methods for the analysis of rare variants have extended gene-based analysis methods for rare variants by aggregating P values from each gene-based test, or extending existing powerful gene-based tests to pathways (Wu and Zhi, 2013; Yan et al., 2014; Zhao et al., 2014). For example, the Weighted Kolmogorov–Smirnov (WKS) method, the Direct Region-Based (DRB) method (Wu and Zhi, 2013) and Smoothed Functional Principal Component Analysis (SFPCA) (Zhao et al., 2014) are approaches that extend pathway-based analyses of GWAS data to pathway-based analyses of high-throughput sequencing data. The WKS method, a modification of Gene Set Enrichment Analysis (GSEA) (Wang et al., 2007), uses the results of single-variant analysis. Moreover, DRB methods have extended existing gene-based methods, including the Burden type (Li and Leal, 2008), C-alpha type (Neale et al., 2011; Wu et al., 2011) and Optimal type (Lee et al., 2012), to pathway analysis for rare variants.

However, there are several limitations to using current pathway approaches to identify rare variants. First, a substantial number of genes are shared by pathways, potentially leading to high correlations between pathways. Thus, neglecting these correlations can result in misleading solutions. For example, high correlations between pathways can yield highly correlated results or confound the interpretation of significant pathways (Alexa et al., 2006; Jiang and Gentleman, 2007; Skarman et al., 2012). Second, the multiple testing problem is another challenge for current pathway-based analyses. Although the number of pathway-based tests is far less than that of variant-level or gene-based tests, the required P value threshold by Bonferroni correction is quite small, leading to low statistical power. In addition, methods using permutation tests suffer from a heavy computational burden to obtain more precise P values, when the P value threshold is very small.

In this report, we propose a novel statistical approach for the analysis of rare variants using pathways, named Pathway-based approach using HierArchical components of collapsed RAre variants Of High-throughput sequencing data (PHARAOH). Our method has several unique distinctive features. First, PHARAOH can examine associations between a phenotype and entire pathways with a single model, using collapsed rare variants derived from gene information. Using this model, PHARAOH can evaluate effects of pathways to the phenotype, in addition to effects of genes to the phenotype via the pathway. Thus, PHARAOH provides an expansive view of biological processes underlying the trait of interest by examining entire pathways. Second, PHARAOH can account for potential correlations between pathways by imposing a ridge penalty on the effects of pathways on a phenotype. PHARAOH also adds another ridge penalty on the weights of genes to their corresponding pathways, allowing consideration of potential correlations between genes. In this regard, PHARAOH is a doubly ridge-regularized method (Hwang, 2009). Although there is a number of alternative penalization approach such as LASSO (Tibshirani, 1996) or Elastic-Net (Zou and Hastie, 2005), we choose ridge method as our first try from its computational efficiency.

Through simulation studies, the proposed method was shown to have higher statistical power than the existing pathway-based methods. In addition, using large-scale, whole-exome sequencing data from a Korean population study of liver enzyme levels, PHARAOH was compared to several existing pathway-based analyses of genetic variants, using two well-known pathway databases Biocarta (http://cgap.nci.nih.gov/Pathways/BioCarta_Pathways) and KEGG (Kanehisa et al., 2004). These comparisons demonstrated that PHARAOH not only identified associated pathways, with no need for multiple comparisons, but also successfully detected biologically plausible pathways for a phenotype of interest. Furthermore, we developed the PHARAOH software to provide a graphical display of pathway-based analysis results, thus allowing for easy and detailed interpretations. The software is provided in both R and C/C ++, and is freely available at the website (http://statgen.snu.ac.kr/software/pharaoh/) which provides a detailed and complete instruction including dataset preparation, parameter selection and result interpretation.

2 Materials and methods

2.1 PHARAOH method

Let us assume that y_j is the j^th observation of a specific phenotype independently following an exponential family distribution (j = 1,…,N). The density function or probability distribution for y_j can be expressed as Equation (1),

$$p(y_j;{\gamma }_j,\delta )=\exp \left((y_j{\gamma }_j-\xi ({\gamma }_j))/\zeta (\delta )+\nu (y_j,\delta )\right)$$ (1)

for some known functions ξ(·), ζ(·) and ν(·). If the dispersion parameter δ is known, (1) belongs to the exponential family with canonical parameter γ_j. In (1), y_j is independently distributed with a mean of µ_j. The dispersion parameter is assumed to be constant over all observations (McCullagh and Nelder, 1989, p. 30).

Let g_ij be the genotype of the i^th genetic variant of the j^th individual, which is defined as 0, 1 or 2 by the number of minor alleles. Since our approach is needed to collapse multiple rare variants into gene-based summaries with appropriate weights, we define x_jkt as the collapsed genotype of the t^th gene in the k^th pathway from the equation x_jkt $={\Sigma }_{i\in G_t}{\omega }_i$g_ij (k= 1,…,K; t = 1,…,T_k, where K is the number of pathways and T_k is the number of genes in k^th pathway), and G_t is the set of genetic variants indices in the t^th gene and ω_i is the predefined weight for the i^th variant. For the pre-defined weight, the PHARAOH software supports both user-defined weight or previously proposed weighting approaches, such as inverse minor allele frequency (MAF) (${\omega }_i=1/\sqrt{\mathrm{M}\mathrm{A}{F}_i\left(1\hspace{0.5em}-\hspace{0.5em}MA{F}_i\right)}$, where MAF_i is the MAF of i^th variant), or beta-transformed MAF (ω_i=Beta(MAF_i;1,25)), as suggested by Wu et al. (2011). In our study, the beta-transformed MAF was used as a default weight.

We next define each pathway as a weighted composite or component of a set of genes. Let w_kt denote a weight assigned to x_jkt, leading to the k^th pathway. Let β₀ denote the intercept and β_k denote the coefficient connecting the k^th pathway to the phenotype y_j. Let η_j and g(·) denote a linear predictor and a link function, respectively. We can then specify the relationship between a linear predictor and a link function as Equation (2),

$${\eta }_j={\beta }_0+{\displaystyle \sum _{k=1}^K\left[{\displaystyle \sum _{t=1}^{T_k}{x}_{jkt}{w}_{kt}}\right]{\beta }_k}={\beta }_0+{\displaystyle \sum _{k=1}^K{f}_{jk}{\beta }_k}={\displaystyle \sum _{k=0}^K{f}_{jk}{\beta }_k}=g({\mu }_j)$$ (2)

where $f_{jk}={\Sigma }_{t=1}^{T_k}{x}_{jkt}{w}_{kt}$ indicates the j^th observation’s score of the k^th pathway when k > 0, and is equal to one when k = 0. If γ_j= η_j, and we have a canonical link; for instance, the identity, logit, log, inverse and squared inverse functions are the canonical links for the normal, binomial, Poisson, gamma and inverse Gaussian distributions, respectively.

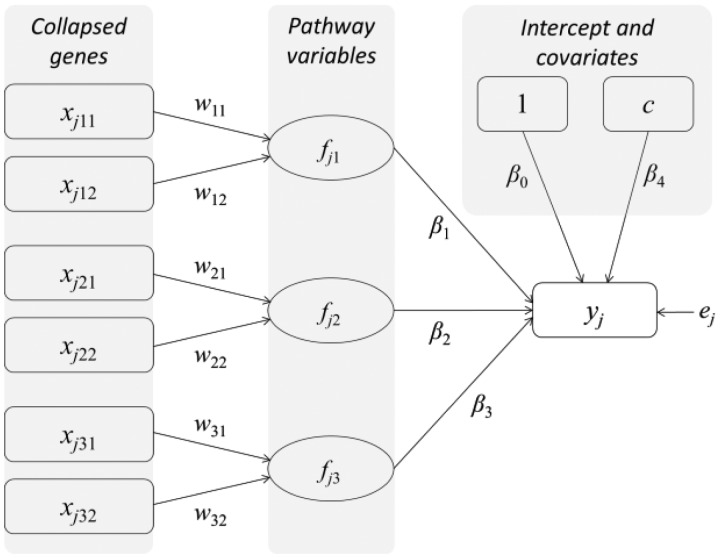
To explain our proposed model, we provide an example in Figure 1. This exemplary model assumes that a phenotype is normally distributed and involves three pathways (K = 3), each of which consists of two genes (T_k = 2). Each pathway is then constructed by adding weights to its genes, featured by straight lines; the pathway, in turn, influences a phenotype, signified by single-headed arrows. When the phenotype is continuous (or normally distributed), this model can be viewed as a special type of structural equation model known as extended redundancy analysis (Desarbo et al., 2013; Hwang et al., 2013; Takane and Hwang, 2005), in which all latent variables are equivalent to components of observed variables (e.g. genes), and serve as exogenous variables that affect a single endogenous and an observed variable (e.g. a phenotype). Nonetheless, the proposed method is built on the framework of generalized linear models (GLM) (McCullagh and Nelder, 1989; Nelder and Wedderburn, 1972), to accommodate phenotype data arising from a variety of exponential-family distributions. Furthermore, as shown below, the proposed method aims to address the issue of multicollinearity in parameter estimation, which is likely to be present among both genes and pathways.

Fig. 1.

A schematic diagram of the proposed model

To estimate parameters, we seek to maximize a penalized log-likelihood function taking the general form of:

$${\phi }_1={\displaystyle \sum _{j=1}^N\log p(y_j;{\gamma }_j},\delta )-\frac{1}{2}{\lambda }_G{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{t=1}^{T_k}{w}_{kt}^2}-\frac{1}{2}{\lambda }_P{\displaystyle \sum _{k=0}^K{\beta }_k^2}}.$$ (3)

with respect to w_kt and β_k, subject to the conventional scaling constraint ${\Sigma }_{i=1}^N{f}_{jk}^2=N$ (Takane and Hwang, 2005), where λ_G and λ_P are ridge parameters for gene and pathway, respectively. This optimization function can be viewed as the L₂-norm penalized log-likelihood (Le Cessie and van Houwelingen, 1992; Lee and Silvapulle, 1988), where the L₂-norm or ridge penalty (Hoerl and Kennard, 1970) is imposed on both weights and coefficients. The two ridge penalties are added to address potential multicollinearity in both genes and pathways, which can adversely affect the estimation of weights and coefficients.

Let w_k= ${\left[w_{k1},\dots ,w_{k{T}_k}\right]}^{\text{'}}$, β = [β₀, β₁, …, β_K]' and F = [f₁, …, f_N]', where f_i= [1, f_j1, …, f_jK]. Maximizing Equation (3) via iteratively reweighted least squares (Green, 1984) is equivalent to minimizing the following penalized least-squares function:

$$\begin{array}{c}{\phi }_2={\displaystyle \sum _{j=1}^N{v}_j{(z_j-{\displaystyle \sum _{k=0}^K{f}_{jk}}{\beta }_k)}^2}+{\lambda }_G{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{t=1}^{T_k}{w}_{kt}^2}+{\lambda }_P{\displaystyle \sum _{k=0}^K{\beta }_k^2}}\\ ={\displaystyle \sum _{j=1}^N{v}_j{(z_j-f_j\mathbf{\beta })}^2}+{\lambda }_G{\displaystyle \sum _{k=1}^K(w_k\text{'}{w}_k)}+{\lambda }_P(\mathbf{\beta }\text{'}\mathbf{\beta })\\ =(z-F\mathbf{\beta })\text{'}V(z-F\mathbf{\beta })+{\lambda }_G{\displaystyle \sum _{k=1}^K(w_k\text{'}{w}_k)}+{\lambda }_P(\mathbf{\beta }\text{'}\mathbf{\beta }),\end{array}$$ (4)

with respect to w_t and β, subject to diag(F'F)= NI, where V is an N by N diagonal matrix with elements ν_j= (∂μ_j/∂η_j)^2/τ_j, where τ_j is the variance function evaluated at µ_j, and z is an N by 1 vector of the so-called adjusted response variable with elements z_j= η_j+ (y_j − μ_j)_/ν_j (McCullagh and Nelder, 1989, Chapter 2).

To minimize Equation (4), we use an iterative algorithm similar to the alternating regularized least-squares algorithm (Hwang, 2009). However, we still should determine the values of λ_G and λ_P before applying the parameter estimation procedure. We may use k-fold cross-validation (CV) to decide the values of λ_G and λ_P. In our results, we used the same penalty parameter for both gene and pathway (i.e. λ_G = λ_P) for computational efficiency.

For the given ridge estimates of parameters, the asymptotic approximation to the variances of these parameter estimates cannot be used directly for obtaining their confidence intervals, because their biases should be taken in account (Le Cessie and van Houwelingen, 1992). Instead, resampling methods can be used to test the statistical significance of the estimated effects of all pathways on the phenotype, as well as the estimated weights assigned to genes. Although other resampling methods (e.g. bootstrap or jackknife) can also be used for examining the statistical significance of the estimates, in the proposed method, we utilize a permutation test to obtain P values. By permuting the given phenotype, our method first generates null distributions of both pathway and gene coefficients in empirical manner. Then we can get empirical P values of both pathway and gene from each empirical null distribution.

2.2 Simulation study

To perform simulation, we used well-established simulation data that was generated under pathway model, Genetic Analysis Workshop (GAW) 17 dataset for the simulation (Almasy et al., 2011). In brief, the GAW17 dataset is a simulated dataset consisting of 697 individuals from 1000 Genomes Project and 24 487 SNVs, along with 200 replicates of four simulated traits (Q1, Q2, Q4 and AFFECTED). Among those traits, only Q1 was simulated to be affected by an age factor and 39 SNVs residing in nine genes from the vascular endothelial growth factor (VEGF) pathway defined by Ingenuity Pathway Analysis (http://www.ingenuity.com). Other traits were generated without using pathway information and thus not considered further in our simulation studies. Since Q1 reflects combinatorial effect of multiple genes in a pathway, VEGF, we examined the power of the proposed method by the proportion of identifying the pathway. First, 21 028 SNVs in 3179 genes from 697 unrelated samples were selected as rare variants by MAF filtering, i.e. less than 5%. Subsequently, all of the rare variants were collapsed into genes. Here, MAFs for all rare variants were computed directly from the data. The names of all the genes were annotated using the HUGO Gene Nomenclature Committee database. Here, each rare variant was assigned to a gene if its location was in the gene or within 10 kilobases 5′ or 3′ to the transcribed region. For pathway-gene mapping, we extracted 217 pathways from Biocarta and 186 pathways from KEGG (Kanehisa et al., 2004), and mapped the genes to the pathways.

2.3 Whole exome sequencing dataset for pathway discovery

We applied PHARAOH to perform a pathway analysis of whole-exome sequencing (WES) data from a Korean population study, via our membership in the Type 2 Diabetes Genetic Exploration by Next-generation sequencing in multi-Ethnic Samples (T2D-GENES) Consortium. Specifically, the genomes of 1087 individuals, selected from the Korean Association REsource (KARE) study (Cho et al., 2009), were sequenced using the Illumina HiSeq2000 platform (Illumina, Inc., San Diego, CA, USA). The levels of aspartate aminotransferase (AST), a liver enzyme, were measured in the morning, before the first meal of the day. Prior to the analysis, 1046 samples were chosen after excluding participants taking medications likely to influence liver enzyme levels. For 1046 participants, 399 729 variants, mapped to the UCSC hg19 genomic coordination, were retained after a quality control process. Here, the quality control process was an exclusion of variants with genotype call rates < 95% or Hardy–Weinberg Equilibrium (HWE) test P < 10⁻⁵. Using 120 807 rare variants with MAF < 5%, rare variant collapsing and pathway-gene mapping were then performed, as in the simulation study. MAFs for all rare variants were computed directly from the data. The final datasets consisted of 1190 genes, with 55 978 rare variants for Biocarta, and 4913 genes, with 216 531 rare variants for KEGG, respectively. Note that the numbers of genes and variants per pathway included those shared with other pathways.

2.4 Exome chip dataset for replication of discoveries

To further confirm our discovered pathways in an independent cohort, we conducted a replication study using an independent Korean cohort from the Health Examinee shared control study, a part of the KoGES population based cohort, initiated in 2001 (Kim et al., 2011). Among these, 3445 samples were used for the replication study. Samples were genotyped using the HumanExome BeadChip v1.1 (Illumina, Inc., San Diego, CA, USA), which contains approximately 240 000 variants. All samples passed quality control tests using the following exclusion criteria: a genotype call rate <99%, excessive heterozygosity and sex inconsistency. The exclusion criterion for variants was as follows: HWE test P < 10⁻⁶, genotype call rates <95% and monomorphic variants. After quality control, 60 628 variants remained for further analysis. For all participants from the cohort, AST was measured identically to the KARE study. Rare variant collapsing and pathway-gene mapping were then performed, as in the discovery study. MAFs for all rare variants were computed directly from the data. Consequently, 517 genes mapped to 210 pathways, and 2391 genes mapped to 186 pathways, were then used in the replication study for Biocarta and KEGG, respectively.

3 Results

3.1 Comparison of methods using simulation dataset

For the purpose of power comparison, PHARAOH and existing pathway-based methods, including aforementioned WKS (WKS-Variant and WKS-MinP) and DRB (Direct-Burden and Direct-SKAT-o) (Wu and Zhi, 2013), were applied to the GAW17 simulation dataset. We did not include the SFPCA method because it was proposed for binary traits (Zhao et al., 2014). First, the performance of methods was carried out by comparing empirical power which is a proportion of VEGF pathway (true causal pathway in the simulation) P < 0.05 from 200 replicates of Q1. For PHARAOH, the tuning parameters, λ_G and λ_P, were chosen based on five-fold CV using 11 different starting points of ridge parameter ranging from 10⁻² to 10⁸ on a logarithmic base 10 scale, and it was fixed to 4000 across simulation study. An analysis time of PHARAOH was 15 min. As shown in Figure 2, PHARAOH showed 0.87 of empirical power to detect VEGF pathway, while those of WKS were only 0.105 and 0.055, respectively. We excluded the results from DRB since it showed substantial inflation of P values (Supplementary Fig. S1). Notably, PHARAOH also identified the focal adhesion pathway in 77% of replicates, since the pathway is a subsequent pathway of VEGF pathway and the pathway contains five of significantly simulated genes (FLT1, FLT4, KDR, VEGFA and VEGFC). Second, we generated and tested another 5000 replicates of Q1 by permuting the first original replicate, to assess type I error. As shown in Table 1, all of the methods controlled their type I errors, despite of slight conservative trend of PHARAOH.

Fig. 2.

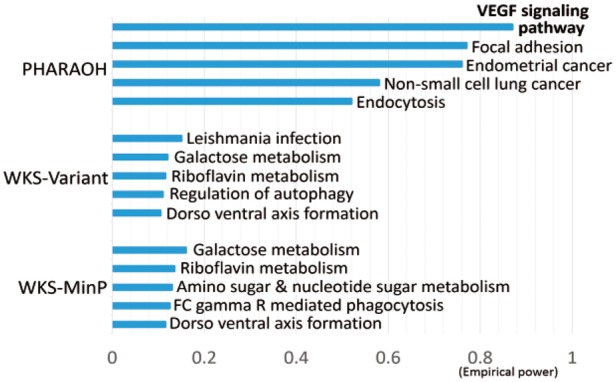
Empirical powers of simulation dataset using KEGG pathway database. Empirical power indicates the times of identification among 200 replicates. (A) Empirical power of top five pathways from PHARAOH. (B) Empirical power of top five pathways from WKS-Variant. (C) Empirical power of top five pathways from WKS-MinP

Table 1.

Type 1 errors of PHARAOH, WKS and DRB

Method	α = 0.05	α = 0.01
PHARAOH	0.040 (±0.019)	0.0083 (±0.008)
WKS-Variant	0.056 (±0.028)	0.0156 (±0.017)
WKS-MinP	0.049 (±0.025)	0.0101 (±0.010)
Direct-Burden	0.051 (±0.044)	0.0103 (±0.017)
Direct-SKAT-o	0.049 (±0.043)	0.0105 (±0.017)

Finally, we also performed literature search to investigate empirical powers of other methods to detect VEGF pathway in GAW17 dataset. For the methods using both common rare variants, one comparison study that compared four extensions of gene-based methods to pathway-based, using both rare and common variants, showed that the highest empirical power among them was 0.65 (Uh et al., 2011). In contrast, another comparison demonstrated up to 0.93 of empirical power (Ngwa et al., 2011). However, since they considered all of nine causal genes are belong to VEGF pathway, their assumption contains much more causal genes compared to our KEGG mapping, as shown above. With reflection of this difference, a subsequent analysis using PHARAOH with modified VEGF pathway contains all of significant genes showed 0.935 of empirical power even without the presence of common variants (data not shown). Among the methods using only rare variants of GAW17, only one method could handle joint effects of multiple rare variants (Hu et al., 2011). Its maximum empirical power for VEGF pathway was only 0.182, which demonstrates superior performance of PHARAOH.

3.2 Discovery study using whole exome sequencing dataset

PHARAOH and the existing methods were applied to a large Korean population WES dataset (n = 1046) to examine possible associations between pathways and AST liver enzyme levels in participants’ serum. AST can be used for determining liver function abnormalities, in addition to other liver enzymes such as alanine aminotransferase (ALT) (Huang et al., 2006). As WKS and our method require phenotype permutation, we generated 1000 and 10 000 permuted replicates of phenotypes for PHARAOH and WKS, respectively. Following association tests conducted by Cho et al. (2009), age, sex and area were included as covariates in the pathway analyses. The chosen λ values for AST were 5500 for Biocarta and 9500 for KEGG. The total computing times were 67, 113 and 22 min for PHARAOH, WKS and DRB methods, respectively. Quantile–quantile plots of the results showed no explicit inflation or deflation of P values (Fig. 3).

Fig. 3.

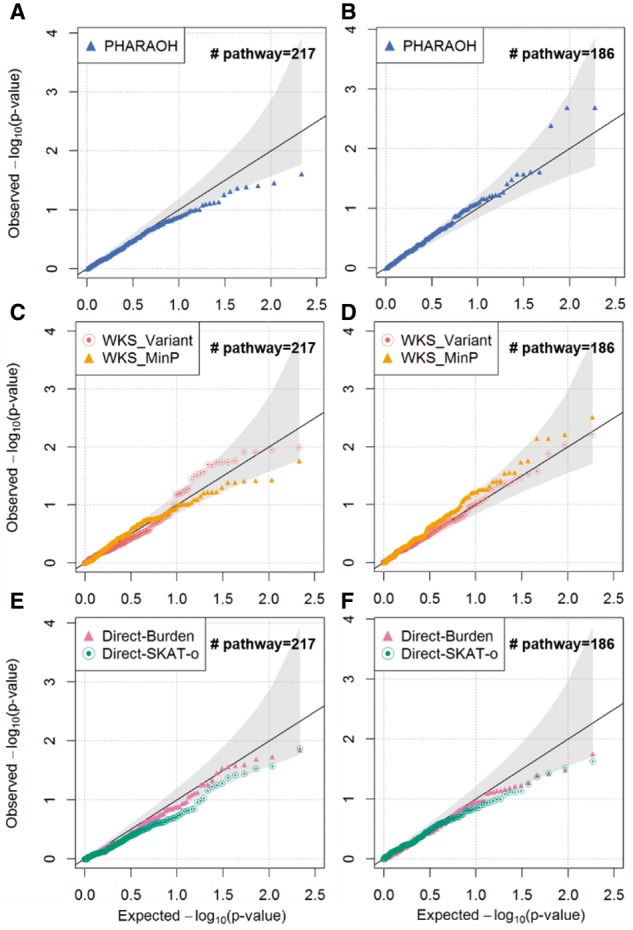
Quantile–quantile (QQ) plots for levels of the liver enzyme AST, with adjustment for covariates. The QQ-plots are provided for PHARAOH, WKS and DRB, with 95% confidence interval. (A) QQ-plot of PHARAOH using Biocarta. (B) QQ-plot of PHARAOH using KEGG. (C) QQ-plot of WKS using Biocarta. (D) QQ-plot of WKS using KEGG. (E) QQ-plot of DRB using Biocarta. (F) QQ-plot of DRB using KEGG

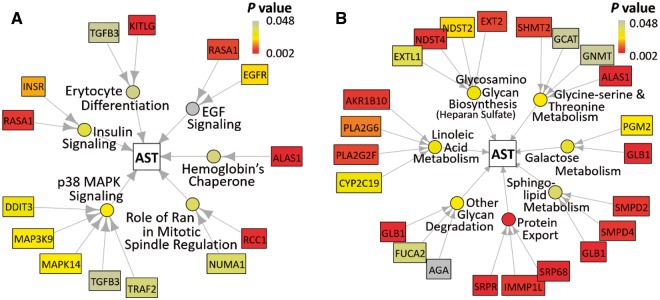
The discovery study using WES dataset using PHARAOH identified six pathways for Biocarta, and seven pathways for KEGG, at a 5% significance level (Table 2). Significant pathways and their significant genes for Biocarta and KEGG are depicted in Figure 4A and B, respectively. However, none of the existing methods identified statistically significant pathways after Bonferroni correction at the 5% significance level, as shown in Table 2. The Bonferroni-corrected P value thresholds were 2.3 × 10⁻⁴ (# pathways = 217) for Biocarta and 2.69 × 10⁻⁴ (# pathways = 186) for KEGG.

Table 2.

Pathways identified by PHARAOH in the discovery study

Pathway DB	Pathway	# of mapped SNVsa	# of mapped genesb	P values
				PHARAOH	WKS-Variant	WKS-MinP	Direct-Burden	Direct-SKAT-o
Bio-carta	p38 MAPK signaling pathway	1321	47	0.024	0.259	0.735	0.175	0.316
	Insulin signaling pathway	806	26	0.034	0.679	0.854	0.734	0.411
	Role of Ran in mitotic spindle regulation	441	18	0.038	0.379	0.264	0.847	1
	Hemoglobin's Chaperone	350	12	0.040	0.176	0.857	0.099	0.17
	Erythrocyte differentiation pathway	354	21	0.042	0.723	0.068	0.222	0.38
	EGF signaling pathway	1173	43	0.048	0.546	0.657	0.528	0.76
KEGG	Protein export	575	28	0.004	0.04	0.738	0.808	0.479
	Glycine, serine and threonine metabolism	1312	39	0.024	0.127	0.467	0.893	0.589
	Other glycan degradation	879	22	0.024	0.978	0.829	0.126	0.166
	Glycosaminoglycan biosynthesis (heparan sulfate)	966	35	0.026	0.773	0.101	0.709	0.387
	Linoleic acid metabolism	1180	35	0.026	0.752	0.462	0.648	0.559
	Galactose metabolism	1649	43	0.032	0.677	0.033	0.207	0.164
	Sphingolipid metabolism	1347	50	0.038	0.829	0.917	0.195	0.195

Pathway names with bold text and underlined text indicate the replicated pathways in the independent dataset and another independent study (Sookoian and Pirola, 2012), respectively.

^aThe number of mapped genetic variants to the pathway.

^bThe actual number of genes included in the pathway.

Fig. 4.

Visualizations generated by PHARAOH in the discovery study of AST levels. Outermost rectangles indicate statistically significant genes within significant pathways, circles represent statistically significant pathways, and center square indicate the phenotype of interest. (A) Result using the Biocarta pathway database and (B) result using the KEGG database

The pathways identified by PHARAOH from the discovery study are reported to have strong biological relevance to the liver. The pathways linoleic acid metabolism, galactose metabolism, erythrocyte differentiation and alpha-hemoglobin stabilizing protein all relate to liver function. One previous study showed that dietary conjugated linoleic acid alleviated non-alcoholic fatty liver disease by reducing levels of hepatic injury markers in Zucker (fa/fa) rats (Nagao et al., 2005). Conjugated linoleic acid supplementation also lowered levels of serum ALT and alkaline phosphatase in Zucker (fa/fa) rats (Noto et al., 2006). Galactose, a mono saccharide sugar metabolized primarily in the liver, and galactose elimination capacity, have been widely used for estimating quantitative liver function (Lindskov, 1982). Two other pathways, erythrocyte differentiation and alpha-hemoglobin stabilizing protein, were found to be related to red blood cells (Table 2). Erythrocyte differentiation pathway and Hemoglobin’s Chaperone pathway describe the process of preventing precipitation of hemoglobin alpha-subunits by alpha-hemoglobin-stabilizing protein. The liver is a major hematopoietic organ during fetal life (Cardier and Barbera-Guillem, 1997).

We next compared the list of identified pathways from PHARAOH with previous pathway-based analyses of AST and ALT results from Sookoian and Pirola (2012) (Hereinafter SP). Despite the use of different pathway databases, we found that the sphingolipid metabolic process was significant in both results (P= 0.038 from PHARAOH and q value= 0.018, where the q value is the false discovery rate-adjusted P value (Benjamini and Hochberg, 1995)). Notably, PHARAOH also successfully identified the sphingolipid pathway, well known to relate to liver diseases (Alexaki et al., 2014; Pralhada Rao et al., 2013), thus further supporting our approach. Moreover, our detection of the glycine-serine and threonine metabolism pathways of KEGG concurs with SP that identified three of four significant genes in those pathways (SHMT2, GCAT and ALAS1). Moreover, the ALAS1 gene was also statistically significant in the Hemoglobin’s Chaperone pathway of Biocarta (P = 0.002) and the glycine serine and threonine metabolism pathways (P= 0.002) of KEGG.

3.3 Replication study using exome chip dataset

In the replication study with an independent Korean population dataset using exome array (n = 3445), the chosen λ values were 245 for Biocarta and 8000 for KEGG. An execution time was 37 min for Biocarta and 38 min for KEGG. The replication study identified eight pathways from Biocarta and nine pathways from KEGG (Table 3). Despite the limited number of rare variants included on the exome array used in our replication study, we were able to successfully replicate the Erythrocyte Differentiation pathway of Biocarta, and the KEGG pathways glycine-serine and threonine metabolism and glycosaminoglycan biosynthesis. In addition, the insulin signaling pathway was also replicated, despite the differences between pathway databases. Among the replicated pathways, we were able to discover a number of associations between the identified pathways and liver function. The insulin signaling pathway manifests selective insulin resistance in diabetic mice (Li et al., 2010). Additionally, a study of the AST values of a high protein diet suggested that hepatic utilization of glycine-serine and threonine in the liver varied between fed and starved rats, thus also reflecting the role of the glycine-serine and threonine pathways in the liver (Remesy et al., 1983).

Table 3.

Significant pathways from PHARAOH in the replication study

DB	Pathway	PHARAOH
Biocarta	HIV-I Nef: negative effector of Fas and TNF	0.006
	Feeder pathways for glycolysis	0.016
	Human cytomegalovirus and map kinase pathways	0.018
	Lck/Fyn tyrosine kinases in initiation of TCR Activation	0.022
	Erythrocyte differentiation pathway	0.026
	NFkB activation by Nontypeable Hemophilus influenza	0.048
	Growth hormone signaling pathway	0.049
	Influence of Ras and Rho proteins on G1 to S Transition	0.049
KEGG	Glycine, serine and threonine metabolism	0.01
	Metabolism of xenobiotics by cytochrome P450	0.018
	Insulin signaling pathway	0.028
	Glycosaminoglycan biosynthesis (keratan sulfate)	0.032
	Phenylalanine metabolism	0.036
	Tryptophan metabolism	0.044

Pathway names with bold text and underlined text indicate the replicated pathways in the independent dataset using the same pathway database, an independent dataset and a different pathway database (SP), respectively.

4 Discussion

In this study, we developed a novel statistical method for pathway-based analysis of large-scale genetic data. Using GAW17 simulation dataset, we have demonstrated substantial empirical power using PHARAOH, compared to several methods for pathway analysis, with an appropriate control of type I error. While other methods require common variants to achieve large empirical power, our method could achieve higher power without common variants. In addition, by applying PHARAOH to large-scale WES and exome chip data, we identified several pathways biologically associated with levels of AST or overall liver function, in accord with previous findings (Alexaki et al., 2014; Cardier and Barbera-Guillem, 1997; Li et al., 2010; Lindskov, 1982; Nagao et al., 2005; Noto et al., 2006; Pralhada Rao et al., 2013; Remesy et al., 1983; Sookoian and Pirola, 2012). Generally, it is not straightforward to replicate findings of rare variant analysis (Liu and Leal, 2010), because the composition of rare variants can differ in independent datasets. Nonetheless, we successfully replicated four pathways using an independent dataset, representing potential candidates for biological validation.

Compared to other existing pathway-based tests, our method has several advantages. First, the proposed method is not restricted by the multiple testing problem, because PHARAOH fits only a single model that considers all pathways of interest, testing the statistical significance of all parameter estimates at once. Although the number of tests in a pathway-based analysis is much smaller than that of variant-level or gene-based analysis, its cutoff value of Bonferroni corrected P value at a 5% significance level was 2.3 × 10⁻⁴ for 217 pathways in Biocarta, making it highly untenable to reject the null hypothesis. Because it is free from the multiple testing problem, PHARAOH requires substantially smaller numbers of permutations than other existing permutation-based methods. In practice, PHARAOH requires at most 1000 permutations at a 5% significance level, whereas other existing permutation-based methods require much larger numbers of permutations (e.g. 10 000 or more) (Kim et al., 2011; Weng et al., 2011).

Second, PHARAOH can accommodate potentially high correlations between pathways, which cannot be efficiently controlled by other existing methods using a series of single pathway analyses. As shown by several studies of pathway-based or gene set-based methods (Alexa et al., 2006; Jiang and Gentleman, 2007; Skarman et al., 2012), it is necessary to consider correlations between pathways, because such correlations influence the combined effects of pathways on the phenotype. Whereas other existing methods adopt an additional step to adjust for the effect caused by overlap between pathways, our method seeks to control for correlations between genes in a specific pathway, as well as correlations between pathways, by imposing ridge-type penalties on both gene and pathway coefficient estimates. In addition, the proposed method provides P values not only for pathway coefficient estimates, but also for gene estimates per pathway.

Although we identified and addressed a number of issues in this report, several challenges are still remained. Unlike other methods, our proposed approach analyzes all pathways simultaneously in very short time (e.g. several hours). However, the permutation scheme used to obtain P values increases the time required for an entire analysis. Thus, it would be desirable to extend the proposed method without heavy permutation, to achieve faster and more accurate computation.

An optimal choice of weight would increase the performance of PHARAOH. The current default weight is the beta-transformed MAF in the collapsing of multiple rare variants of specific genes, as suggested by Wu et al. (2011) for rare variant analysis. However, recent studies suggest that other weighting approaches, based on the number of informative family members or the predicted functional effects of variants, can reduce false positive rates and increase statistical power (De et al., 2013; Hu et al., 2013; Shugart et al., 2012; Sifrim et al., 2013). The application of such weighting variants represents one possible extension of our future work.

Cross validation for PHARAOH can often be time-consuming because it considers large combinations of candidate values for the two penalty parameters for gene and pathway. To reduce computational burden, we applied cross validation to select only a single value for the parameters, constraining them to be equal. This may lead to less optimal values for the parameters. According to our limited experience, if cross validation is applied to decide the two parameters freely without the equality constraint on the parameters, the penalty parameter for gene tends to remain the same as the common penalty parameter obtained under the equality constraint. This may suggest that if we can derive the penalty value for pathway as a function of that for gene in some way (e.g. λ_G=cλ_P, where c is a constant), using cross validation with this constraint could be more computationally efficient. However, a careful investigation into the feasibility of this approach is warranted.

Although there exist other penalization approaches such as LASSO (Tibshirani, 1996) or Elastic-Net (Zou and Hastie, 2005), we choose a ridge method due to its computational efficiency. Hence, our future work can be an extension of the proposed approach to the model using different penalizations. Moreover, PHARAOH can be flexible by allowing pathways and genes to have their own penalty parameters. We strongly believe that our novel method will enhance the success of pathway-based analysis using genetic datasets, thus addressing, at least in part, the problem of missing heritability.