Gene-set association tests for next-generation sequencing data

Abstract

Motivation: Recently, many methods have been developed for conducting rare-variant association studies for sequencing data. These methods have primarily been based on gene-level associations but have not been proven to be as effective as expected. Gene-set-level tests have shown great advantages over gene-level tests in terms of power and robustness, because complex diseases are often caused by multiple genes that comprise of biological gene sets.

Results: Here, we propose several novel gene-set tests that employ rapid and efficient dimensionality reduction. The performance of these tests was investigated using extensive simulations and application to 1058 whole-exome sequences from a Korean population. We identified some known pathways and novel pathways whose rare or common variants are associated with elevated liver enzymes and replicated the results in an independent cohort.

Availability and Implementation: Source R code for our algorithm is freely available at http://statgen.snu.ac.kr/software/QTest.

Contact: tspark@stats.snu.ac.kr

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Genome-wide association studies (GWAS) have focused on the associations between complex diseases and common genetic variants, and have successfully reported an extensive list of single nucleotide polymorphisms (SNPs) associated with complex diseases. However, it has been shown that the associated common variants could explain only a small fraction of the heritability of many common diseases (Bansal et al., 2010). This suggests that other genetic mechanisms such as gene–gene interactions, gene-set-level actions of common variants, or the action of multiple rare variants, could contribute to disease susceptibility. Among these mechanisms, rare variants have become the focus of intense investigation following the development of next-generation sequencing (NGS) technology (Adzhubei et al., 2010; Manolio et al., 2009).

In recent years, many statistical tests have been proposed for detecting the signals of rare variants (Lee et al., 2012; Li and Leal, 2008; Lin and Tang, 2011; Madsen and Browning, 2009; Morris and Zeggini, 2010; Price et al., 2010; Wu et al., 2011). However, current approaches are in the early stages of development, and significant improvements are required, in terms of increasing statistical power and considering the biological context of diseases. Ladouceur et al. (2012) demonstrated that assessing the association between rare variants and complex diseases is still a challenging task and that no single method yields consistently high power, even using large sample sizes.

Complex diseases often result from the combined action of multiple risk factors in a gene or across genes that comprise a gene set or a pathway. Gene-set analysis (GSA) has been widely used for analyses of microarray data (Peng et al., 2010; Subramanian et al., 2005; Wang et al., 2007) and GWAS data (Chai et al., 2009; Goeman et al., 2004), and has played an important role in uncovering the mechanisms of complex diseases. GSA has been shown to possess great advantages over single-gene tests. GSA incorporates related SNPs or genes into a single statistic, and thus requires a small number of tests and yields high power to detect association signals. Even if individual genes of a set have weak or moderate association signals, GSA can combine those into a single strong signal. Incorporation of verified biological knowledge in GSA facilitates interpretation of the underlying genetic background of identified gene sets and reduces false positive results. However, current rare-variant studies have focused mainly on gene-level associations, and GSA of rare variants are scant, as very few pathway-based methods [e.g. smoothed functional principal component analysis (SFPCA; Zhao et al., 2014), for binary traits] have been proposed.

The previously introduced GSA methods can be classified into two types of analysis strategies. The first type of GSA is a one-step method that regards a gene set as a large ‘super-gene’. This approach has limited application to high-throughput NGS data in that, as the number of variants within a gene set increases, the power of the analysis decreases. The second type is a two-step method that consists of a gene-level association test followed by a test for association of a gene set with a trait. The two-step method has been widely used in traditional GSA. However, direct application of the traditional two-step GSA used in GWAS to NGS data is not appropriate because the gene-level summarization in the traditional two-step GSA does not collapse or consider rare variants. Although gene-level summarization can be replaced by P-values for currently available rare variant association tests, a gene-set-level test that combines P-values for multiple genes might be underpowered, due to high degrees of freedom. Combining P-values with the assumption of independence could also yield false positive results, if correlations among variants or genes are not taken into account (Price et al., 2010). Therefore, the development of a new GSA is warranted to test gene-set associations by considering the characteristics of rare variants, to increase statistical power by reducing dimensionality, and to account for all possible correlations among variants or genes.

In this article, we propose a powerful gene-set test as well as a single-gene test for use with NGS data. For quantitative traits in particular, we first derive powerful gene-level tests as quadratic forms (QTest) using an eigenvalue decomposition of regression coefficients and applying a dimensionality reduction method. This eigenvalue decomposition step allows our tests to account for correlated variants. Based on the QTest, we then develop the proposed gene-set-level quadratic test (GS.QTest) using an efficient method for reducing degrees of freedom. The proposed tests possess four advantages: (1) QTests provide higher statistical power than existing gene-level tests; (2) GS.QTests are flexible in that they can easily incorporate other existing gene-level tests for rare variants, such as the sequence kernel association test (SKAT); (3) the proposed QTests and GS.QTests cover a broad range of scenarios for joint action of rare variants and common variants; and (4) the tests do not require heavy computational effort because they employ parametric or pre-calculated empirical distributions.

Through extensive simulations, we investigated the performance of the proposed methods by comparing them with other gene-level and gene-set-level association methods. For example, available gene-level association methods include collapsing methods such as GRANVIL (Morris and Zeggini, 2010), weighted sum statistic (MB; Madsen and Browning, 2009) and variable threshold (VT; Price et al., 2010). For the collapsing of rare variants, GRANVIL counts the rare variants; MB aggregates weighted sum based on minor allele frequency (MAF); VT uses the partial sum based on optimal MAF threshold. For bidirectional approaches, we included SKAT (Wu et al., 2011), SKAT-O (Lee et al., 2012), the likelihood ratio test (LRT), and estimated regression coefficients (EREC; Lin and Tang, 2011) in simulation studies. SKAT uses score-based variance component model and SKAT-O is an optimal test combining a burden-type test and SKAT. EREC estimates the regression coefficients and uses these as weights. These bidirectional approaches are useful when deleterious and protective variants are simultaneously present. For the gene-set-level association methods, we included the traditional gene-set-level association methods, GLOSSI (Chai et al., 2009) and GlobalTest (Goeman et al., 2004). GLOSSI combines variant-level P-values based on the chi-square statistic, while GlobalTest uses score tests in the framework of generalized linear models.

Finally, we applied the proposed methods to exome sequencing data of 1058 Korean samples (Cho et al., 2009) and some liver enzyme traits and identified some known and novel pathways including the beta-alanine metabolism pathway, lysine degradation pathway which are known to be related to liver cancer. To further validate the potential association of the pathways with elevated liver enzymes, we conducted a replication study in an independent cohort comprising 897 samples; some pathways were successfully replicated (P-value < 0.05).

2 Methods

2.1 Generation of simulated sequencing data

To generate simulation data, we used the software SimRare (Li et al., 2012), which generates sequencing data based on demographic and evolutionary scenarios for the real population. One thousand replicates for the sequence and trait data for 3000 samples were generated for this simulation study. For each individual, we generated a quantitative trait value by adding the effect of multiple causal rare variants and an error term that followed a standard normal distribution. To simulate a gene-level test, we varied the gene size, which is the number of rare variants (10, 20) within a gene, the proportion of causal variants (10, 20, 30, 50 and 70%) and the effect size (β) of causal variants (0.75, 1.0, 1.25 and 1.5).

To check the type 1 error, two million replicates of traits from the null distribution were generated. The type 1 error was defined as the proportion of P-values less than various specified significance levels (10⁻³, 10⁻⁴, 10⁻⁵ and 2.5 × 10⁻⁶) among two million P-values. The type 1 errors were calculated for various gene sizes (10, 20 and 50) given the sample size 3000, minimum minor allele count (MAC) 1 and maximum MAF 0.01.

To investigate the performance of the proposed tests for each gene set, another simulation for gene-set analysis was conducted. Based on simulated sequencing data, we assembled a gene set that included 12 genes. In the scenario set for gene-set analysis, trait values were generated under 135 different scenarios by varying the number of causal genes (2, 3 and 4), proportion of causal variants (10, 20, 30, 50 and 70%), effect size (0.75, 1.0 and 1.25) and size of causal gene (10, 30 and 50 variants).

The gene-level power was defined as the proportion of P-values less than 2.5 × 10⁻⁶ among P-values from the simulation under the corresponding scenarios. This cut-off was based on a 5% significance level with Bonferroni correction, under the assumption that 20 000 genes are being tested simultaneously (Lee et al., 2012). Similarly, the gene-set-level power was defined as the proportion of P-values less than 2.5 × 10⁻⁵ among P-values under the assumption that 2000 gene-sets are being tested simultaneously.

2.2 Gene-level association methods based on quadratic tests

As a gene-level association test for rare variants, we introduced a method for combining regression coefficients from a multiple regression framework. Regression coefficients for rare variants can be combined using three different methods according to the relationships among the rare variants. The followings are plausible scenarios for multiple rare variants:

1. All variants within a region have a common effect, either deleterious or protective, or

2. Some variants are deleterious and others are protective.

QTest₁: If there are m rare variants within a region, we can regress a trait, y, on rare variants (S_k’s) and covariates. We can first assume that rare variants within a region have common effects, producing either deleterious or protective signals. Given this assumption, the collapsing method, which aggregates effects in only one direction, provides powerful performance. We derived the QTest₁, the inverse variance weighting method for a pooled effect size (β_pooled). A chi-square statistic based on pooled effect size is computed as follows:

$$\begin{array}{l}y={\beta }_0+{\displaystyle \sum _{k=1}^m{\beta }_k{S}_k}+\gamma Z+\epsilon ,\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}where\hspace{0.17em}\hspace{0.17em}}\epsilon \sim N(0,1)\\ \widehat{\mathbf{\beta }}={\left({\widehat{\beta }}_k\right)}_{m\times 1},\mathbf{\alpha }={\left({\alpha }_k\right)}_{m\times 1},\text{where\hspace{0.17em}\hspace{0.17em}}{\alpha }_k=\frac{1/\mathrm{var}({\widehat{\beta }}_k)}{{\displaystyle {\sum }_{k=1}^m\left(1/\mathrm{var}({\widehat{\beta }}_k)\right)}}\text{,}\\ V=\mathrm{var}(\widehat{\mathbf{\beta }}),W=\left(\begin{array}{ccc}{w}_1& 0& 0\\ 0& \ddots & 0\\ 0& 0& w_m\end{array}\right)\text{where\hspace{0.17em}}{w}_k\text{\hspace{0.17em}is\hspace{0.17em}a\hspace{0.17em}weight\hspace{0.17em}for\hspace{0.17em}}k\text{th\hspace{0.17em}variant}\\ {\widehat{\beta }}_{Pooled}={\mathbf{\alpha }}^{T}W\widehat{\mathbf{\beta }}={\displaystyle {\sum }_{k=1}^m{\alpha }_k{w}_k{\widehat{\beta }}_k}\sim N(0,{\mathbf{\alpha }}^{T}WVW\mathbf{\alpha })\\ Q_1={({\mathbf{\alpha }}^{T}WVW\mathbf{\alpha })}^{-1}{\widehat{\beta }}_{Pooled}^2\sim {\chi }_1^2\end{array}$$

QTest₂: We can also assume that some rare variants are deleterious and other rare variants are protective. In this case, the QTest₁ shows very poor performance because deleterious and protective signals are offset when combined. To combine association signals with different directions without loss of power, we propose the QTest₂.

$$\begin{array}{l}\widehat{\mathbf{\beta }}={\left({\widehat{\beta }}_k\right)}_{m\times 1,}\text{for\hspace{0.17em}\hspace{0.17em}}k=1,\dots ,m,\\ V=\mathrm{var}(\widehat{\mathbf{\beta }})=U\Lambda U^{\text{T}}\text{\hspace{0.17em}\hspace{0.17em}where\hspace{0.17em}}\Lambda =diag({\lambda }_k)\\ \text{where\hspace{0.17em}}U\text{\hspace{0.17em}consists\hspace{0.17em}of\hspace{0.17em}eigenvalue\hspace{0.17em}vectors\hspace{0.17em}of\hspace{0.17em}}V,\\ \text{and\hspace{0.17em}}\Lambda \text{\hspace{0.17em}is\hspace{0.17em}the\hspace{0.17em}diagonal\hspace{0.17em}matrix\hspace{0.17em}whose\hspace{0.17em}diagonal\hspace{0.17em}elements\hspace{0.17em}are\hspace{0.17em}eigenvalues\hspace{0.17em}of\hspace{0.17em}}V\\ Q_{\text{2}}^{Wald}={\widehat{\mathbf{\beta }}}^{\text{T}}{V}^{-1}\widehat{\mathbf{\beta }}={\widehat{\mathbf{\beta }}}^{\text{T}}U{\Lambda }^{-1}{U}^{\text{T}}\widehat{\mathbf{\beta }}\sim {\chi }_m^2\\ p_j=2\left(1-\Phi \left(u_j^{\text{T}}\widehat{\mathbf{\beta }}/\sqrt{{\lambda }_j}\right)\right)\text{\hspace{0.17em}\hspace{0.17em}where\hspace{0.17em}\hspace{0.17em}}{u}_j=j^{th}\text{\hspace{0.17em}column\hspace{0.17em}\hspace{0.17em}of\hspace{0.17em}\hspace{0.17em}}U\\ Q_2={\displaystyle {\sum }_{j=1}^m{G}_{a,1}^{-1}(1-p_j)}\sim G_{ma,1}=\frac{1}{2}{\chi }_{2ma}^2\end{array}$$

G denotes gamma distribution.

QTest₃: Although the QTest₂ can handle effect sizes that differ in direction, it does not provide better performance than the QTest₁ when multiple rare variants have an aggregated effect in the same direction. In order to account for the etiology of rare variants, we should consider all possible cases. Our newly proposed optimal quadratic test (QTest₃) statistic is a weighted average of the QTest₁ and the QTest₂. The QTest₃ can operate under assumptions (i) and (ii). The steps for the QTest₃ are as follows:

The empirical distribution of 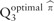was calculated by generating a pair of random variables from a chi-square distribution with one degree of freedom, and computing their maximum value of weighted averages over the eleven values of π. In our simulation studies and real data analyses, 10⁹ pairs of random variables were generated, and the empirical distribution of was summarized in a cumulative distribution table. Then, the QTest₃ used this pre-calculated cumulative distribution table for every gene-level test.

2.3 Gene-set-level analysis for rare and common variants

In order to maximize the genetic variation caused by moderate association, gene-set analysis (GSA) can use prior biological knowledge based on pathway information. We propose two types of gene set tests, the GS_Q.QTest and the GS_B.QTest. The proposed GS_Q.QTest for rare variants requires the following two steps:

• Step 1. Compute gene-level P-values for rare and common variants using QTests.

• Step 2. Combine gene-level chi-square statistics within a pre-defined gene set.

In Step 1, any possible rare variants association test can be used to obtain the gene-level P-values, allowing great flexibility. In Step 2, given a gene set (GS), a gene-set level statistic can be computed based on an inverse gamma transformation (Zhao et al., 2014):

$$\begin{array}{l}{Q}_{GS}={\displaystyle \sum _{t\in GS}2G_{a,1}^{-1}(1-p_t)\sim }{\chi }^2\left(2ma\right)\\ p_t=\text{p\hspace{0.17em}value\hspace{0.17em}for\hspace{0.17em}\hspace{0.17em}}t\text{th\hspace{0.17em}\hspace{0.17em}gene,\hspace{0.17em}\hspace{0.17em}}m=\text{size\hspace{0.17em}of\hspace{0.17em}}GS\end{array}$$

We also proposed another type of gene-set test, the GS_B.QTest. The proposed GS_B.QTest requires the following two steps:

• Step 1. Collapse multiple rare variants in each gene within a GS.

• Step 2. Using the collapsed variants and common variants, conduct QTests.

In Step 1, the collapsing method is applied only to rare variants. In Step 2, we can use any possible association test, such as the SKAT or the SKAT-O.

3 Results

3.1 Simulation study for gene-level tests

The proposed gene-level test includes three versions that can be applied to various scenarios for rare variants within a gene. The first version (QTest₁) is a burden-type test and the second version (QTest₂) is a non-burden-type test. The third version (QTest₃) is an optimal QTest that combines QTest₁ and QTest₂ such that it maintains high power regardless of the direction of effects and proportion of causal variants.

The simulation results of type 1 errors of QTests are summarized in Table 1 for several gene sizes and several significance levels. Table 1 shows that the proposed QTests well-preserve the type 1 errors under the null distribution.

Table 1.

Type 1 error of proposed gene-level QTests

α	Gene size 10			Gene size 50
	QTest1	QTest2	QTest3	QTest1	QTest2	QTest3
1.0E-03	1.03E-03	1.02E-03	1.06E-03	9.75E-04	1.01E-03	1.05E-03
1.0E-04	9.40E-05	1.06E-04	1.07E-04	1.00E-04	9.39E-04	1.02E-04
1.0E-05	9.00E-05	8.50E-06	8.50E-06	9.95E-06	1.10E-05	9.95E-06
2.5E-06	3.00E-06	1.50E-06	2.50E-06	2.50E-06	2.00E-06	2.50E-06

We compared the performance of the proposed QTests to existing methods, such as SKAT, SKAT-O, VT, LRT, MB, GRANVIL and EREC under various scenarios. MB, VT and EREC were implemented by SCORE-Seq (Lin and Tang, 2011). All methods were conducted using the default parameter values. MAF threshold value was fixed as 0.01 for rare variant analysis. We generated trait values by varying the causal gene size, the proportion of causal variants, and the effect size of the causal variants. The relationships between power and effect size are displayed in Figure 1. In general, as the effect size increased, the power increased. Figure 1a shows the result when the proportion of causal variants is low (10 or 20%), and Figure 1b shows the result when the proportion of causal variants is high (50 or 70%). In Figure 1a, QTest₂, QTest₃, LRT, SKAT and EREC performed much better than burden tests, and QTest₂ had the highest power when the effect size was larger than 0.75. As shown in Figure 1b, the optimal tests, such as QTest₃ and SKAT-O, perform better than other methods, especially when the effect size is 0.75.

Fig. 1.

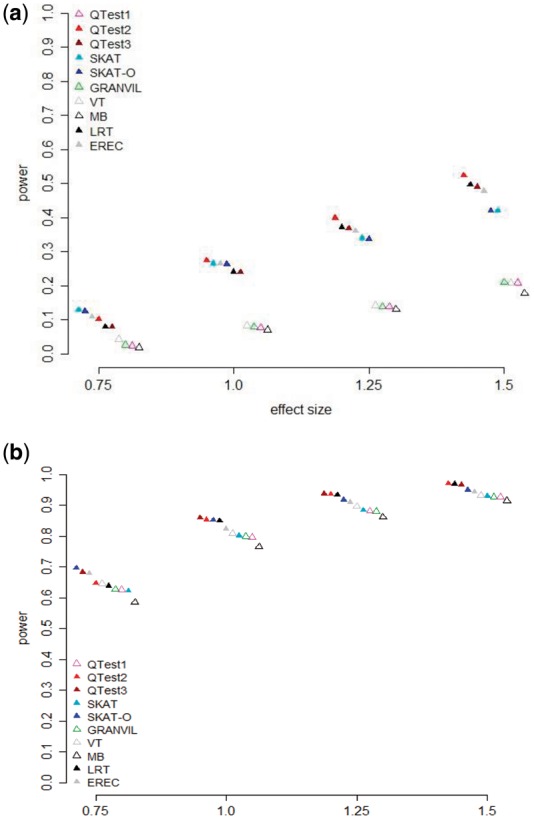
Comparison of the power of gene-level tests for varying effect sizes; (a) for a low proportion of causal variants; (b) for a high proportion of causal variants

For application to other scenarios, we varied the proportion of protective variants among causal variants within a gene, given a proportion of causal variants 0.5 and effect size 1.0. We also varied the proportions of common variants among causal variants, given a proportion of causal variants 0.5, proportion of common variants 0.5, and effect size 1.0, to observe the joint effect of common and rare variants. In these scenarios, QTest₂, QTest₃, SKAT, SKAT-O and LRT are robust enough to include protective causal variants or common variants. QTest₂, QTest₃ and LRT had the largest power among all methods (see Supplementary Figs. S1 and S2). With the existence of non-causal common variants, the burden tests QTest₁ and GRANVIL showed poor performance, but other burden tests, MB and VT, showed very good performance, because they focus on rare variants by weighting or thresholding. EREC showed much lower power than QTest₂, QTest₃, SKAT and SKAT-O, when the proportion of protective variants among causal variants was large; for the cases when the regression coefficients are negative, the weight used in EREC tends to decrease the signal. EREC also showed poor performance when there were non-causal common variants together with causal rare variants (see Supplementary Fig. S2).

For the simulation study of one-directional effects, we varied the effect size of causal variants with the assumption that all variants were deleterious causal variants. The burden tests QTest₁ and GRANVIL showed greater power than other tests. The non-burden tests QTest₂, SKAT, and LRT showed poor performance, especially when the effect size was not large (see Supplementary Fig. S3).To illustrate a computational burden for QTests, a specific computational time for one simulation setting is summarized in Supplementary Table S1. QTests showed a similar computing time to that of SKAT, and QTest₃ was found to be computationally much more efficient than SKAT-O, when implemented in R.

3.2 Simulation study for gene-set-level tests

We developed two types of proposed gene-set-level tests: the GS_Q.QTest and the GS_B.QTest. The GS_Q.QTest calculates gene-level P-values by applying the QTest to multiple variants within a gene and then combines the P-values using an efficient dimensionality reduction method. The GS_B.QTest employs a burden-type summarization at the gene level and applies the QTest to the collapsed gene-level variants within a set.

Other rare-variants association methods, such as SKAT and GRANVIL, can easily be incorporated into the proposed gene-set methods. When SKAT was used instead of the QTest in the proposed two gene-set-level tests, the proposed gene set tests are denoted as GS_Q.SKAT and GS_B.SKAT, respectively.

In simulation studies, the following gene-set methods were compared: two traditional gene set analysis methods (GLOSSI, GlobalTest), two QTest-based gene set analysis methods (GS_Q.QTest, GS_B.QTest) and two SKAT-based gene set analysis methods (GS_Q.SKAT, GS_B.SKAT). GLOSSI and GlobalTest are one-step gene set tests that regard all variants from the same gene set as one super-gene. The one-step SKAT method, which employs a similar method, was not included in the Figures because the one-step SKAT method produced a very similar pattern to the GlobalTest (data not shown). Under our simulation setting, GS_Q.SKAT was consistently more powerful than the one-step SKAT. In general, considering gene-level summarization makes the gene-set analysis more powerful; however, a few exceptions exist. If causal variants are concentrated in a very few genes, the gene-level summarization may produce a loss of power. Figure 2 shows the relationship between the effect size of causal variants and the power of the gene-set test. Figure 2a shows the result when the proportion of causal variants is low (10 or 20%), whereas Figure 2b shows the result when the proportion of causal variants is high (50 or 70%). As shown in Figure 2a, for a low proportion of causal variants, the GS_Q.SKAT method performs best when the effect size is 0.75, whereas the GS_Q.QTest₂ performs best when the effect size is larger than 0.75. In this setting, GS_B-type tests show poorer performance than GS_Q-type tests because collapsing a high proportion of non-causal variants within a gene decreases the power of the analysis. For a high proportion of causal variants, performance of GS_B-type tests is similar to or better than GS_Q-type tests when the effect size is 0.75 whereas the power of the GS_Q.QTest₂ and the GS_Q.QTest₃ exceeds the power of the other tests when effect size is larger than 0.75 (Fig. 2b).

Fig. 2.

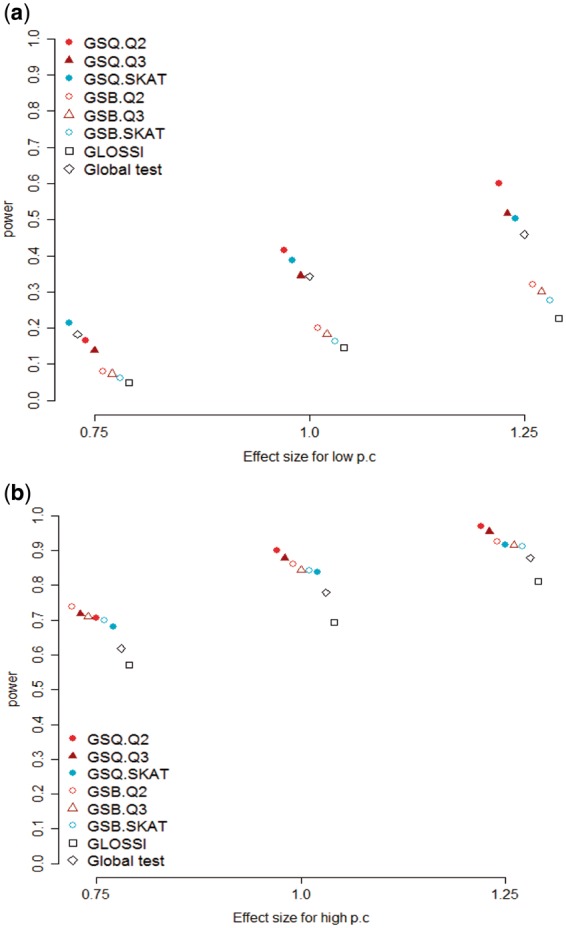
Comparison of the power of gene-set-level tests for varying effect sizes; (a) for a low proportion of causal variants; (b) for a high proportion of causal variants

3.3 Application for Korean liver enzymes and exome data

We applied the proposed tests to examine possible associations between liver enzymes and whole-exome sequencing data collected in the Korean Association REsource (KARE; Cho et al., 2009) study. After excluding samples from individuals who were taking medication likely to influence liver enzymes, 1058 samples were used for the proposed tests. For the analysis, 22 654 rare variants and 11 895 common variants of 8322 corresponding genes were included, after excluding low-quality variants and selecting functional variants. In tests for pathways, we used 0.05 or 0.5 as cut-off for maximum MAF and 2 for minimum MAC. We used 1320 canonical pathways from the MSigDB database v.4.0 (Subramanian et al., 2005). The association was declared to be significant if the P-value was less than a threshold applying Bonferroni correction over the total number of tests.

For the single rare variants with a MAC > 5, we performed a linear regression in PLINK, and the minimum P-values for the three liver enzymes traits [alanine aminotransferase (ALT), aspartate aminotransferase (AST), and gamma glutamyltransferase (GGT)] were 5.18E-06, 5.23E-06 and 1.25E-05 (q-value = 0.31, 0.29, 0.43), respectively. Thus, no rare variant was found to be significantly associated with the three traits, after Bonferroni correction. For the genes with gene size >1, the results of the gene-level test based on rare variants showed that no gene was statistically significant if the Bonferroni correction was applied (See Supplementary Table S2).

In the gene-set level test for rare variants, we discovered that NODAL signaling pathway (P = 3.4E-05; GS.QTest₃) significantly associated with AST after Bonferroni correction, and in the gene-set level tests for common and rare variants, we discovered two KEGG pathways significantly associated with GGT after Bonferroni correction; beta-alanine metabolism (P = 4.5E-06; GS.QTest₂) and lysine degradation (P = 4.7E-06; GS.QTest₂). Table 2 provides the P-values from the proposed gene-set-level tests and those from the permutation tests by generating 10¹⁰ permuted samples. The P-values from our approach coincide well with those from the permutation tests for gene-set-level tests.

Table 2.

Gene sets found to be highly associated with liver enzymes in KARE (P < 1E-03)

Phenotype	Gene-set	KARE results
		Maximum MAF	minimum MAC	P-value
				GS. QTest1	GS. QTest2	GS. QTest3	GS. SKAT	GS. SKATO
ALT	PID_AURORA_A_PATHWAY	0.05	2	5.0E-04 (4.2E-04)*	1.2E-01 (1.5E-01)	1.2E-03 (1.2E-03)	1.8E-01 (1.9E-01)	5.9E-03 (6.2E-03)
	BIOCARTA_RELA_PATHWAY	0.05	2	8.4E-04 (8.7E-04)	2.2E-02 (2.7E-02)	2.0E-03 (2.3E-03)	2.4E-01 (2.2E-01)	8.2E-02 (8.1E-02)
	KEGG_FOLATE_BIOSYNTHESIS	all	2	4.6E-02 (4.5E-02)	7.7E-04 (7.9E-04)	2.7E-03 (2.8E-03)	6.9E-01 (6.8E-01)	7.0E-01 (6.8E-01)
AST	REACTOME_SIGNALING_BY_NODAL	0.05	2	9.9E-01 (9.9E-01)	4.2E-05 (4.1E-05)	3.4E-05 (3.4E-05)	1.1E-03 (9.8E-04)	2.3E-03 (2.2E-02)
	REACTOME_GRB2_SOS_PROVIDES_LINKAGE_TO_MAPK_SIGNALING_FOR_INTERGRINS	0.05	2	4.7E-04 (4.5E-04)	4.3E-02 (4.3E-02)	1.1E-03 (1.0E-03)	1.3E-01 (1.4E-01).	1.1E-02 (1.3E-02)
	REACTOME_CHEMOKINE_RECEPTORS_BIND_CHEMOKINES	0.05	2	7.5E-01 (7.5E-01)	7.5E-04 (7.8E-04)	1.2E-03 (1.3E-03)	9.3E-03 (9.5E-03)	1.9E-02 (1.8E-02)
	PID_RETINOIC_ACID_PATHWAY	all	2	9.7E-01 (9.6E-01)	9.6E-04 (9.3E-04)	1.2E-03 (1.0E-03)	4.1E-02 (4.3E-01)	8.3E-02 (8.3E-02)
GGT	PID_ARF6_PATHWAY	0.05	2	4.3E-04 (4.2E-04)	6.9E-02 (6.9E-02)	1.1E-04 (9.9E-05)	1.5E-01 (1.7E-01)	2.4E-03 (2.4E-03)
	KEGG_BETA_ALANINE_METABOLISM	all	2	2.1E-01 (1.9E-01)	4.7E-06 (5.1E-06)	1.1E-05 (1.3E-05)	7.8E-02 (7.8E-02)	8.6E-02 (8.6E-02)
	KEGG_LYSINE_DEGRADATION	all	2	4.0E-02 (4.5E-02)	4.5E-06 (4.7E-06)	1.9E-05 (2.0E-05)	3.0E-03 (2.8E-03)	2.0E-03 (2.0E-03)
	KEGG_BUTANOATE_METABOLISM	all	2	1.6E-01 (1.6E-01)	6.8E-05 (6.6E-05)	2.1E-04 (2.0E-04)	3.8E-02 (3.7E-02)	6.5E-02 (6.3E-02)
	REACTOME_ETHANOL_OXIDATION	all	2	5.0E-04 (5.3E-04)	6.1E-05 (6.1E-05)	2.5E-04 (2.6E-04)	1.7E-07 (1.6E-07)	2.9E-07 (3.1E-07)
	KEGG_VALINE_LEUCINE_AND_ISOLEUCINE_DEGRADATION	all	2	2.4E-01 (2.7E-01)	8.5E-05 (8.3E-05)	1.0E-03 (1.1E-03)	8.8E-02 (8.6E-02)	1.6E-01 (1.6E-01)
	REACTOME_IL_6_SIGNALING	all	2	2.4E-04 (2.3E-04)	1.8E-03 (1.8E-03)	5.6E-04 (5.9E-04)	4.1E-03 (4.5E-03)	1.8E-03 (1.9E-03)

*Permutation P-values are given in parentheses.

The results show similar patterns to those of simulation results. For example, the significances of Aurora pathway and ARF6 pathway were identified by the GS.QTest₁, since most genes within these pathways showed effects in the same direction (Supplementary Fig. S4). On the other hand, NODAL signaling pathway was significant by the GS.QTest₂ and the GS.QTest₃, because the genes within this pathway have effects with different directions (Supplementary Fig. S4). The parameter values used in simulation studies such as MAF, effect size and proportion of causal variants were similar to those in these pathways.

These results were applied to the replication study for further validation. Replication analyses for the pathway results were conducted in an independent study population including 897 Korean individuals, a portion of the Cardiovascular Disease Association Study (CAVAS) cohort (Kim et al., 2016a, b). NODAL signaling pathway was not replicated and some pathways including two KEGG pathways were successfully replicated (P < 0.05) (Table 3).

Table 3.

Results of the replication study conducted in CAVAS

Phenotype	Gene-set	Replication results
		Maximum MAF	Minimum MAC	P-value
				GS.QTest1	GS. QTest2	GS. QTest3	GS. SKAT	GS. SKATO
GGT	KEGG_BETA_ALANINE_METABOLISM	all	1	3.6E-08	2.8E-01	8.3E-05	1.5E-01	5.9E-02
	KEGG_LYSINE_DEGRADATION	all	1	1.2E-06	5.6E-01	6.9E-05	1.4E-01	1.1E-01

We also deconstructed the nature of the signals, which provides the list of key genes involved in the two replicated pathways along with the number of variants in each gene and the gene-level P-value (Supplementary Table S3). The gene-level P-values from the permutation tests were also computed using the 10¹⁰ permuted samples. The P-values of our gene-set-level tests coincide well with those from the permutation tests. The deconstruction of the two replicated pathways shows that ALDH2 [MIM 100650] is a key gene. The strong effect of ALDH2 and the weak effects of other genes together yielded a strong signal for the two gene sets. In the discovery study, ALDH2 consists of only one common variant, rs671, with a strong statistical significance (MAF = 0.15, single variant P-value = 9.58E-08) which has been reported to be associated with GGT (Kamatani et al., 2010). In the replication study, ALDH2 consists of rs671 and two non-significant rare variants.

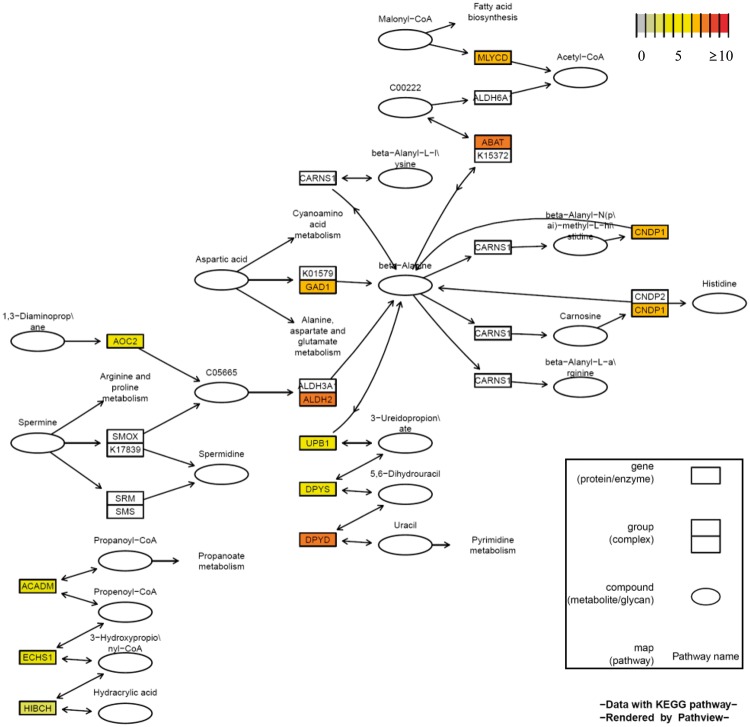
The two pathways identified here were known to relate to liver functions. Lysine is an essential amino acid that stimulates the biosynthesis of cholesterol in the liver (Schmeisser et al., 1983). Beta-alanine is involved in liver function, and has a protective effect in the presence of toxins (Choi et al., 2009; Lee and Kim, 2007). Graphical representation of genes in the pathway, including information on genetic variants, may help to understand the biological mechanisms underlying the function of the pathways and the accumulated genetic effect of the pathway. For example, Figure 3 shows the genes involved in the pathways and their relationships.

Fig. 3.

Beta-alanine metabolism pathway found to be associated with liver enzymes

Each gene is colored according to the number of variants used in the association analysis. Red indicates enrichment of variants (≥10) whereas white indicates that no variant of the gene was used in the association analysis. Because we performed the association analysis using only functional variants, such as non-synonymous, loss-of-function and splice-site variants, the number of rare functional variants accumulated for each gene can be interpreted as the functional genetic effect on the gene. Several complexes and genes directly related to beta-alanine were shown to be enriched with variants. This indicates that the accumulated functional genetic effects of variants in the beta-alanine metabolic pathway may disrupt the function of the pathway.

Table 2 shows the association results accompanied by their suggestive statistical significance (P ≤ 1E-03). Most of the pathways revealed by the test were also biologically plausible in the context of liver function. The overexpression of Aurora-A, which frequently occurs in hepatocellular carcinoma (HCC), causes p53-dependent pre-mitotic arrest during liver regeneration (Li et al., 2009). RelA pathway is associated with the prevention of hepatic apoptosis in mice (Rosenfeld et al., 2000). Folate can affect a decrease of serum ALT level in hypertensive patients (Qin et al., 2012). The NODAL signaling pathway, combined with NANOG, plays a critical role in HCC metastasis (Sun et al., 2013). ARF6 plays an essential role in hepatic cord formation during liver development in mice (Suzuki et al., 2006). Butanoate metabolism is one of the pathways which displayed significant differences during liver development in HCC patients (Diana et al., 2012). Ethanol oxidation was found to occur via hepatic enzymes or liver microsomes (Lieber et al., 1987). IL-6 was upregulated in human HCC and it plays an important role in a tumor development (Ji et al., 2010). Valine, leucine and isoleucine are found to mediate activation of important hepatic metabolic signaling pathways and play a critical role in development of liver disease (Lake et al., 2015).

4 Discussion and conclusions

Many methods focusing on gene-level associations have recently been developed to assess the association between rare variants and complex diseases. However, those methods have some limitations in terms of power because the number of samples of rare variants available is not as large as the number of common variants. Even for large sample sizes, no methods for single-gene analysis have consistently high power across the various rare variant scenarios. In this article, we propose gene-set tests as well as single-gene tests for NGS data, including rare and common variants.

Recent rare-variant association methods usually focus on gene-level analysis. However, the interplay of rare variants affecting complex diseases arises not only at the gene level, but also at the gene-set or pathway level. If multiple mutations in the same functional class can influence a disease or trait, then a gene-set, as well as a gene, can be a key functional class. Here, the quadratic tests for multiple variants within a gene are first defined, and then an efficient method for gene-set-level associations is introduced. The performance of the proposed gene-set tests is demonstrated by comparison with other gene-set-level association methods in various simulation scenarios. This demonstration shows that one-step tests are limited in their applications to gene-set-level analysis, compared to two-step tests. When a gene set contains a large number of variants, one-step tests using SKAT or GlobalTest often lose power because of the many non-causal variants present in a given gene set. Based on our simulation studies, the GS_B.QTest performs best among other gene-set methods in cases containing a large proportion of causal variants with small effects. In many cases, the GS_Q.QTest outperforms other methods.

Our simulation raised some issues that need to be considered for optimization of the performance of rare-variants association methods. In the gene-level analysis, the first issue is that the power of the association tests depends on the proportion and effect sizes of the causal rare variants in a region. In some cases, a small proportion of the causal rare variants affect the disease traits, and in other cases, a large proportion of the causal variants affect them. Non-burden tests, such as the QTest₂ and the SKAT, can sensitively detect signals in the former cases. Burden tests, such as the QTest₁ and the GRANVIL, performed well in the latter cases, especially when the effect size is small or moderate (e.g. 0.5 or 0.75). However, in our simulation studies, the optimal tests, such as the SKAT-O and the QTest₃, yielded higher power than the burden tests except when all the variants were causal and one-directional. In the former case, optimal tests also yielded higher power because they take advantage of the properties of both burden and non-burden tests, and usually maintain consistently high power. In our simulation studies, when the effect of the causal variant was large (e.g. 1.25 or 1.5), the proposed QTest₂ and QTest₃ were found to detect signals sensitively, regardless of the proportion of causal variants.

The second issue is the direction of the causal variant effects. The burden tests assume that rare variants in a given region have effects in the same direction. However, this is not always the case. When deleterious and protective alleles are combined, the burden tests may lose power because they do not consider opposing effects. On the contrary, the non-burden tests, which do consider effects that operate in different directions, may lose power when the causal variants have signals of the same direction. The QTest₃, which combines the burden and non-burden tests, tends to yield fairly consistent power.

The third issue is the existence of common variants within a region. Most association tests for sequencing data focus only on rare variants and give greater weight to rarer variants as a function of MAF. For this reason, the common causal variants in sequencing data would not be focused in these tests. However, it may be better to consider the case when both rare and common variants exist together within a region. QTests can analyze both rare and common variants, because rare and common variants can be included simultaneously as explanatory variables in a multiple regression. QTests are also robust to inclusion of non-causal common variants.

Through extensive simulation studies, we investigated these issues in detail. Our simulation studies for gene-level and gene-set-level analyses show that the proposed QTests maintain consistent performance and high power, regardless of the above issues. The GS_Q.QTests do not lose power, even when faced with a small proportion of causal variants or small effect size, and are robust to inclusion of protective variants with negative effect as well as common variants. In cases with a high proportion of causal variants, the GS_B.QTests increase the power of the gene-set association analysis, but suffer from power loss in the presence of non-causal variants.

To account for heterogeneity between genes, GS_B.QTests can use a function of gene units or of biological importance as a weight. In the case of GS_Q.QTests, the development of a new approach using the weighted sum of gamma random variables is desirable in a future study that considers heterogeneity.

The current versions of the proposed tests can assess only quantitative traits. If the trait in question is binary, then the association statistic (e.g. P-value, chi-square statistic) for each rare variant appears not to be stable, in the sense that they can have a very large standard error. However, by collapsing rare variants within a sub-region first or by providing a penalty parameter to better estimate the regression coefficients, the proposed QTests could be extended to analysis of binary traits.

Funding

This work was supported by the National Research Foundation of Korea (NRF) grant (2012R1A3A2026438), the Bio-Synergy Research Project (2013M3A9C4078158) of the Ministry of Science, ICT and Future Planning through the NRF and an intramural grant from the Korea National Institute of Health (2014-NI73001-00), the Republic of Korea. Sequencing data from the T2D-GENES Consortium was supported by NIH/NIDDK U01’s DK085501, DK085524, DK085526, DK085545 and DK085584. The exome chip data was supported by the Korean Genome Analysis Project (4845-301), the Korean Genome and Epidemiology Study (4851-302) and the Korea Biobank Project (4851-307) of the Korea Center for Disease Control and Prevention, Republic of Korea.