GTRAC: fast retrieval from compressed collections of genomic variants

Abstract

Motivation: The dramatic decrease in the cost of sequencing has resulted in the generation of huge amounts of genomic data, as evidenced by projects such as the UK10K and the Million Veteran Project, with the number of sequenced genomes ranging in the order of 10 K to 1 M. Due to the large redundancies among genomic sequences of individuals from the same species, most of the medical research deals with the variants in the sequences as compared with a reference sequence, rather than with the complete genomic sequences. Consequently, millions of genomes represented as variants are stored in databases. These databases are constantly updated and queried to extract information such as the common variants among individuals or groups of individuals. Previous algorithms for compression of this type of databases lack efficient random access capabilities, rendering querying the database for particular variants and/or individuals extremely inefficient, to the point where compression is often relinquished altogether.

Results: We present a new algorithm for this task, called GTRAC, that achieves significant compression ratios while allowing fast random access over the compressed database. For example, GTRAC is able to compress a Homo sapiens dataset containing 1092 samples in 1.1 GB (compression ratio of 160), while allowing for decompression of specific samples in less than a second and decompression of specific variants in 17 ms. GTRAC uses and adapts techniques from information theory, such as a specialized Lempel-Ziv compressor, and tailored succinct data structures.

Availability and Implementation: The GTRAC algorithm is available for download at: https://github.com/kedartatwawadi/GTRAC

Contact: kedart@stanford.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Genome sequencing technology is becoming extremely cost-effective. As an example, Illumina is offering whole human genome sequencing for a few thousand USD (Illumina Inc., 2015). The affordability and accessibility of this data is making personalized genomic medical research a reality. Furthermore, it is allowing the creation of massive sequencing projects like the UK10K project (The UK10K Consortium, 2013), the Personal Genomes Project (Ball et al., 2012) and the Million Veteran Project (U.S. Department of Veteran Affairs, 2008), with the number of sequenced genomes planned of the order of a few thousands to one million. Efficient storage and access of this data is essential for its analysis, toward new medical and biological insights.

Due to the inherent redundancies present in the genomes of individuals of the same species, most of the medical and genetic research deals with the variants (differences) present in the genomes as compared with a reference sequence, rather than with the complete assembled genomes. Currently, these variants are stored in VCF files (Danecek et al., 2011), which contain the information of the called variants together with significant amount of metadata related to the process of calling these variants. The variants of a set of samples (e.g. individuals) are either stored as a collection of VCF files (one per sample), or as a single VCF file that contains the information pertaining to each of the samples.

The metadata is primarily used for filtering the variants, and thus once the variants are filtered, the genotype information associated with each sample generally becomes the main information for downstream analyses. This information is constantly queried to extract information regarding, for example, common variants among individuals or groups of individuals, or all variants from a certain group of individuals. Thus, efficient access and retrieval of variant information is of utmost importance. Moreover, although currently storing the genotype information of a collection of samples does not raise a great concern in terms of storage, their size is expected to exponentially grow in the future as the massive sequencing projects advance (U.S. Department of Veteran Affairs, 2008; The UK10K Consortium, 2013). Therefore, an efficient representation of this information will be necessary.

With this in mind, in this paper we consider the problem of representing the genotype information of a collection of samples in an efficient manner, such that fast querying of the data is still possible. In other words, we look at compressing this information while allowing for random access in the compressed domain.

To date only one algorithm has (partially) addressed this problem, namely, the TGC Compressor (Deorowicz et al., 2013). The TGC algorithm retains only the genotype information contained in the VCF files (Referred to as VCFmin in Deorowicz et al., 2013), and employs a specialized variant of the LZ77 algorithm (Ziv and Lempel, 1977) for the compression. Although the TGC compressor achieves very high compression ratios, it does not allow for efficient querying in the compressed domain. Thus, querying of a snippet of a single sample requires the decompression of the complete compressed archive, which requires significant time and memory. This restricts the usage of the previously proposed compressed representation to long-term archival purposes.

In this work, we propose GTRAC (GenoType Random Access Compressor), an algorithm that achieves compression rates comparable to the state-of-the-art compressors, while allowing for ultra fast querying on the compressed domain. Specifically, the proposed algorithm allows for fast retrieval of all individuals/samples that possess certain variants, and the retrieval of all variants from a group of individuals/samples (see Fig. 1). Thus GTRAC will allow researchers to work efficiently with a highly compressed database containing the genotype information of a collection of samples.

Fig. 1.

GTRAC allows for fast access of information of a specific variant or the genotype of a sample/group of samples over the compressed VCF file

In the next section, we detail the proposed algorithm GTRAC. In particular, we discuss the compression and the local decompression methods employed by our algorithm. We then report on experimental results obtained when applying the algorithm over two large datasets, and discuss the implications.

2 Methods

As stated above, we aim to efficiently represent the genotype pertaining to a set of samples. Specifically, we consider N m-ploid samples (e.g. for Homo sapiens, m = 2, as the human genome is diploid).

The proposed algorithm GTRAC first expresses the genotype information in the following format:

1. A variant dictionary (denoted as ${\mathcal{V}}_{\mathcal{D}}$), which corresponds to an indexed dictionary of all the variants present in the samples. We denote by V the total number of variants (i.e., the length of the dictionary).

2. A set of $m·N$ binary vectors of length V, one for each haplotype. Specifically, each binary vector represents the absence/presence of the indexed variants in the corresponding haplotype. Thus, a value 1 at location k corresponds to the presence of the kth variant (of the indexed variant dictionary) in the haplotype, while a 0 represents its absence.

We represent the set of binary vectors as a binary matrix, denoted as $\mathcal{H}$, of dimension $(mN)\times V$. In this representation, each row corresponds to individual haplotypes, and each column corresponds to a specific variant from the variant dictionary (see Fig. 2). We refer to the overall representation as the $(\mathcal{H},{\mathcal{V}}_{\mathcal{D}})$ format.

Fig. 2.

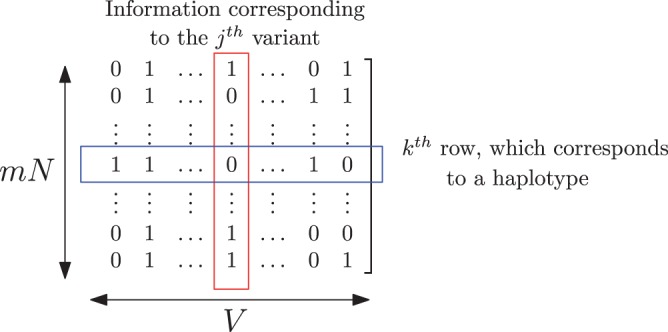
Example of a binary matrix $\mathcal{H}$ representing the presence/absence of variants in the haplotypes. Note that in this representation, columns represent variant information across samples and rows represent haplotypes of a given sample

Note that we can convert the variants contained in a set of VCF files into the $(\mathcal{H},{\mathcal{V}}_{\mathcal{D}})$ format using a similar methodology as the one proposed in (Deorowicz et al., 2013).

For a large number of samples N, the variant dictionary ${\mathcal{V}}_{\mathcal{D}}$ represents a very small fraction of the total representation (about 5–10% in both the uncompressed and the compressed domain, see Supplementary Materials for details). Thus, we focus our compression efforts on the binary matrix $\mathcal{H}$. Our goal is to achieve high compression ratios while allowing for efficient row-wise extraction, which corresponds to single haplotype variant sequence extraction, and efficient column-wise extraction, which corresponds to a specific variant information extraction across all the haplotypes. Note that these also imply efficient extraction of the genotypes of a set of samples (by extracting the corresponding m haplotypes).

We refer the reader to the Supplementary Materials for details on the compression of the variant dictionary ${\mathcal{V}}_{\mathcal{D}}$. Next we focus on the compression and local decompression methods used by GTRAC to represent the binary matrix $\mathcal{H}$.

2.1 Compression details

To compress the binary matrix $\mathcal{H}$, we first convert it into a symbol matrix, where a symbol is defined as the concatenation of K bits (i.e. K/8 bytes). This operation is performed per haplotype (row-wise), yielding a symbol matrix ${\mathcal{H}}_K$ of size $(mN)\times (V/K)$ (see e.g. Fig. 3). Choosing K to be a multiple of 8 has significant benefits in terms of the decompression speed and memory handling, since working with bytes is more efficient.

Fig. 3.

A simple example of the parsing process. The $3\times 20matrix\mathcal{H}$ is first converted to the $3\times 10$ symbol matrix ${\mathcal{H}}_2$ ($K=2$). Then the parsing is performed sequentially at each row (starting on the first row), from left to right

The compression of ${\mathcal{H}}_K$ is composed of mainly two steps: (i) a parsing of each row in the matrix ${\mathcal{H}}_K$, such that each row can be described as a concatenation of phrases (sub-strings), which are represented as tuples; and (ii) an efficient encoding of these tuples. The parsing and the encoding are done in a way that supports local decompression of rows and columns of ${\mathcal{H}}_K$. Next we describe each of these steps in more detail.

2.1.1 Parsing of the rows of ${\mathcal{H}}_K$

We parse the rows of the matrix (i.e. each haplotype) sequentially from left to right. At every position p we look for the longest match in any of the previously processed rows starting from the same position p. The parsing results in a phrase represented as a tuple of the form (s, C, e), where s is the index of the row where the match was found, C is the mismatching symbol, and e represents the phrase ending position in the current row. We refer to the row of ${\mathcal{H}}_K$ with row-id s as the source of the phrase. Note that each tuple defines the sub-string of row s starting at position p, of length $l=e-p+1$. If no match is found, we represent the phrase by the mismatching symbol (C) at position p, and continue the parsing at position p + 1. To differentiate between the two types of phrases, we also store a phrase-type identifier bit t, where t = 0 if a match was found, and t = 1 otherwise. Thus, the overall phrase representation is of the form $(0,s,C,e)$, or $(1,C)$. Note that each row will be composed of phrases which when concatenated yield the original row.

Restricting the starting positions for the parsing makes sense due to aligned redundancy in the rows (as we are dealing with genomic data). Moreover, reducing the possibilities for the start positions also makes the representation of the phrases more compressible. We impose an additional constraint in the parsing: a matching must end at a phrase-ending position corresponding to some phrase in the previously parsed rows. These restrictions are similar to the ones in the LZ-End parsing algorithm (Kreft and Navarro, 2010) and, as we will see later, enable us to efficiently decompress any sub-sequence of the rows.

Figure 3 shows an example of the parsing process. Note that the first row is always represented with phrases of the type $(1,C)$. The reason is that no matches can be found to previously processed rows, as there are none.

2.1.2 Phrase parameter encoding

We first introduce the ‘succinct bitvectors’ (Navarro and Providel, 2012), which are a key component in the encoding of the phrase parameters. The succint bitvector is a compressed data structure representing a binary sequence, which allows for efficient random access of every bit of the binary sequence. Specifically, given a binary sequence, the succint bitvector data structure can achieve a compression rate of $H+\mathrm{ϵ}$, where H denotes the entropy of the sequence and ϵ represents a small overhead. The succinct bitvector representation also provides an efficient way of addressing rank & select queries over the binary sequence, where a rank query returns the number of 1fm before a given position in the binary sequence, and a select query returns the position of the kth 1 in the binary sequence, for a given k (see (Navarro and Providel, 2012) for details). As we will later see, these are the properties which we use for local decompression of the compressed rows and columns. We will discuss the use of the rank & select queries when introducing the decompression details of GTRAC.

We next look at the encoding procedure of the phrase parameters obtained from the parsing.

1. Phrase-type identifier t: We first form binary sequences (one per row) by concatenating the phrase-type identifier bits corresponding to every phrase. Thus, we have mN binary sequences, each representing the phrase-type identifiers corresponding to the rows of ${\mathcal{H}}_K$. Each of these binary sequences are encoded as succinct bitvectors, thus providing random access to every phrase-type identifier bit t.

2. Source row-id s: We encode the source row-id s as a variable-byte encoding using succinct bitvectors. In the variable-byte encoding, the parameter s is stored using bytes optimal for its size. For example, for $s\in (0,255)$, we use 1 byte, for $s\in (256,65535)$, we use 2 bytes, and so on. We then encode the value of s in its standard binary representation. The succinct bitvectors are used to mark the number of bytes used by the s variable-byte representation. The reason to use variable-byte-encoding with succinct bitvector representation, as opposed to using entropy encoders (arithmetic encoding, huffman encoding, etc.), is to achieve random access of the s parameter.

3. Mismatching Symbol C: We store the C parameter of every phrase using variable-byte and succinct bitvector encoding. The encoding is very similar to the s parameter encoding mentioned earlier. Again, the aim here is to achieve random access over the C parameter along with compression.

4. Phrase-end position e: We represent the phrase-end position parameters e as binary sequences, with a single bit for every symbol of the rows. Thus, we have mN binary sequences of size V/K, each corresponding to a row of ${\mathcal{H}}_K$. The bit 1 marks the phrase-ending position in the binary sequences. That is, if the kth binary sequence has a bit 1 at position p, then it implies that e = p for some phrase of the kth row (see Fig. 4). These binary sequences are encoded as succinct bitvectors. We denote these bitvectors as phraseEnd.

Fig. 4.

A simple example of rank and select usage corresponding to the phraseEnd vectors of example of Figure 3

Recall that the parsing of the first row yields all phrases of the type $(1,C)$. Thus, we store the first row in an uncompressed form. We denote it as the refVect, since in some sense it acts as the reference vector while parsing other rows. Although this has very small benefits in terms of memory usage, it has significant benefits in terms of decompression speeds.

Also note that the overall compression complexity of GTRAC is similar to that of TGC. More details about implementation of the parsing and the encoding stages can be found in the Supplementary Materials.

We next describe the row-wise and column-wise local decompression methods employed by the proposed algorithm GTRAC.

2.2 Decompression details

GTRAC offers local decompression that is time and memory efficient. In particular, the proposed algorithm provides two different types of local decompression capabilities on the compressed symbol matrix ${\mathcal{H}}_K$:

1. Efficient row-wise extraction, i.e. local decompression of a single row (or a sub-sequence of it) from the compressed symbol matrix ${\mathcal{H}}_K$. Note that this corresponds to extracting variants pertaining to a specific haplotype from the compressed domain.

2. Efficient column-wise extraction, i.e. local decompression of a single column of the compressed symbol matrix ${\mathcal{H}}_K$. This corresponds to extraction of the information (presence/absence) of a specific set of variants across all the haplotypes of the compressed samples.

GTRAC is able to achieve efficient local decompression by using a specialized variant of the LZ-End algorithm (Kreft and Navarro, 2010). Note that compressing with general LZ77 based methods (e.g. 7 z and gzip), although very fast, does not provide random access capabilities. In other words, to achieve the decompression of a specific row of the compressed symbol matrix ${\mathcal{H}}_K$, it is necessary to decompress all the previous rows. In the worst case, this effectively corresponds to decompressing the whole file, which makes local decompression time as well as memory inefficient. Note that this is also the case for the previously proposed algorithm TGC (Deorowicz et al., 2013), which is based on LZ77.

Before describing the row-wise and column-wise extraction methods employed by GTRAC in more detail, we define a few operators that will be used for the descriptions and the decompression algorithm pseudo-codes. Some of these operators relate to the parameters of the phrases used to represent each row of the symbol matrix ${\mathcal{H}}_K$. We also describe the use of the rank and select queries related to the succinct data structures used for compression.

1. $phraseType[vid][pid],source[vid][pid],C[vid][pid]$: Returns the phrase parameters t, s and C, respectively, of the phrase with index pid corresponding to the row vid of the symbol matrix ${\mathcal{H}}_K$.

2. $phraseEnd[vid][pos]$: phraseEnd corresponds to the succinct bitvector encoding of the phrase parameter t, where $phraseEnd[vid][pos]=1$ denotes the ending of some phrase of the row $vid$ at position $pos$.

3. $ran{k}_1[vid][pos]$: Returns the number of 1’s before the position pos in $phraseEnd[vid]$. Thus, it represents the number of completed phrases before the location $pos$ in the row $vid$.

4. $selec{t}_1[vid][k]$: Returns the position of the k^th 1 in phraseEnd[vid]. Thus, it returns the phrase-ending position of the k^th phrase of the row $vid$.

5. $refVect[pos]$: Returns the symbol at position $pos$ in the first row, which we have encoded in its uncompressed form.

The simple example in Figure 4 should clarify the use of these operators.

2.2.1 Row-wise extraction

The basic idea of the row-wise extraction is as follows: recall that during the encoding process, we find the longest sub-sequence match with the previously parsed rows, with the restriction that the $match$ must end at a phrase-ending position corresponding to some phrase in the previously parsed rows. We also add the mismatching symbol $C$ at the end of this $match$, such that the concatenation of both forms the sub-string that constitutes our new phrase. Now, while decoding this phrase, due to the phrase-ending restriction, we can pop out the symbol $C$ (which is stored explicitly) and then recursively extract the remaining symbols of the phrase from the $source$ row (represented by parameter $s$ of the phrase). In a sense, we are reconstructing the phrase one symbol at a time by recursively popping out the last symbol of the phrase from the corresponding $source$ rows. This allows us to decompress any given sub-sequence of length $\ell \text{in}\mathcal{O}(\ell )$ time and approximately $\mathcal{O}(\ell )$ memory. Note that to achieve this efficient decompression, our algorithm needs constant time random access to the encoded phrase parameters $Cands$. This is possible because of the variable-byte and succinct bitvector based encoding of these parameters. The pseudo-code for the sub-sequence extraction algorithm is given in Figure 5.

Fig. 5.

The recursive algorithm for sub-string extraction from the compressed symbol matrix ${\mathcal{H}}_K$. The input parameters $(vid,start,len)$ correspond to the row-id, the start position, and the length, respectively, of the sub-string we want to extract

The decompression approach described earlier is based on the LZ-End algorithm presented in (Kreft and Navarro, 2010). Though similar to LZ-End, it has several important differences. In particular, the LZ-End algorithm needs the index of the phrase at which the match ends. However, this information is redundant to us, as we have a restriction of position aligned matches, and thus we are able to save a significant amount of memory in effect. Also, as we keep the first row uncompressed, whenever the source is the first row ($s=1$), we can just extract the whole phrase from the uncompressed row. This speeds up the decompression significantly for larger sub-sequences.

Another advantage of the sub-sequence extraction algorithm is that it can be very easily parallelized. Thus, if the sub-sequence to be extracted is long, we can extract smaller sub-sequences in parallel and then merge them together.

2.2.2 Column-wise extraction

Let $cid$ be the column-id which we want to extract from the compressed symbol matrix ${\mathcal{H}}_K$. The column-wise extraction (i.e. single-variant extraction) proceeds as follows: we sequentially extract the symbol corresponding to the position $cid$ from the rows, starting from the first row. For the first row (i.e. the $refVect$), as it is encoded in its uncompressed form, we can always output the symbol at position $cid$. For other rows, if $cid$ corresponds to a phrase-ending position, then we can just output the corresponding mismatching symbol $C$ (which has been stored explicitly). If $cid$ does not correspond to a phrase-ending, then as we have the restriction of position aligned matches, we can output the previously extracted symbol of the corresponding $source$ row at position $cid$. The pseudo-code for the sub-sequence extraction algorithm is given in Figure 6.

Fig. 6.

The Recursive Algorithm for extraction of a specific variant with column-id $cid$, from all the rows

In brief, the algorithm uses the fact that whenever we are finding a match for a phrase, we impose a restriction of position aligned matches, and in case of a mismatch, the mismatched symbol is stored explicitly.

3 Results

We first describe the machine specifications and the datasets used for our experiments. We then provide the experimental results.

3.1 Datasets and machine specifications

We use two large datasets for the experiments. The first one is the publicly available database of Phase 1 of the 1000 Genome Project (Consortium et al., 2012), which contains data for 1092 H.sapiens samples. The variants are stored in the VCF format, with one file for each chromosome. These files contain information about the variants and their presence or absence in every sample (individual). The genomes contained in the 1000 GP dataset are phased. Thus, effectively, the dataset corresponds to 2184 haplotypes. The other dataset which we use is the 1001 Genomes Project (The 1001 Genomes Consortium, 2008) dataset for Arabidopsis thaliana. This collection contains 775 haploid sequences each consisting of 7 chromosomes. We refer the reader to the Supplementary Materials for details on how to access these datasets.

Recall that our compression algorithm is concerned with the compression of the genotypes. However, note that these VCF files contain other information apart from the genotypes (e.g. quality values of the variants). Thus GTRAC first converts the information contained in the VCF files into the binary matrix and the variant dictionary representation [i.e. the ($\mathcal{H},{\mathcal{V}}_{\mathcal{D}}$) format].

For our experiments we used a machine with Intel core-i7 processor with 12 GB of RAM. The operating system was Ubuntu 14.04 LTS. Note that, as our decompression algorithm is parallelizable, we expect better performance with a CPU with higher number of cores.

3.2 Experimental results

We show the performance of GTRAC on the aforementioned datasets, and compare it with the state-of-the-art compressor TGC, as well as the generic compressor 7 z. For comparison, we also state the size of the data when expressed in the ($\mathcal{H},{\mathcal{V}}_{\mathcal{D}}$) format. The processing was done one chromosome at a time, mainly for making the compression possible on machines with small RAM sizes, and also to improve the compression ratios of the generic compressors.

During the compression, we experimented with different symbol-sizes $K$ for forming the symbol matrix ${\mathcal{H}}_K$. The results discussed here are for $K=8$ (symbol-size of 1 byte). In the Supplementary Materials we discuss the effect of the parameter $K$ on the compression and the decompression.

Table 1 shows the results for the H.sapiens dataset. The archival memory required by GTRAC for compression of the whole variant dataset is 1.1 GB, which is <2.5 times that of the state-of-the-art compressor TGC. The overhead is expected as our algorithm is designed to achieve efficient random access capabilities, at the expense of a compromise in compression. Overall, GTRAC achieves a compression ratio of 160 as compared with the VCF file (compared by retaining only the genotype information) and a compression ratio of 10.5 as compared with the $(\mathcal{H},{\mathcal{V}}_{\mathcal{D}})$ representation. If we compare the decompression times for extracting a single haplotype (row-wise extraction), then GTRAC significantly outperforms the TGC and the generic compression algorithms. Our algorithm achieves decompression times of less than a second for all the chromosomes, which is about an order of magnitude faster than the TGC compressor and the 7 z compressor. The difference is even more significant if we consider local decompression of a sub-sequence of a haplotype. For sub-sequences of length 1000, we achieve an average decompression time of 40 ms, which corresponds to a performance boost of more than two orders of magnitude. The single variant extraction (column-wise extraction) for GTRAC takes 17 ms, which is more than two orders of magnitude faster (a few hundred times faster) than the TGC and 7 z compressors. Observe that the single variant extraction times are similar for all the chromosomes, as it only depends upon the number of samples in the dataset.

Table 1.

Comparison of the proposed algorithm GTRAC with the current state-of-the-art compressor TGC and the universal compressor 7 z, on the 1000 GP H.sapiens dataset

Experiments on H.Sapiens dataset
Data	VCFa	$\mathcal{H},{\mathcal{V}}_{\mathcal{D}}$	TGC compressor		7 z		GTRAC
	size	size	size	d-time	size	d-time	size	r-time	c-time
Chr. 1	13 249	890.6	32.3	6.4	55.9	6.9	78	0.91	0.017
Chr. 2	14 569	979.7	34.2	7.2	60.6	9.1	84	0.83	0.018
Chr. 3	12 173	818.1	28.3	5.6	48.3	8.2	70	0.64	0.017
Chr. 4	12 056	810.1	28.6	6.2	47.8	7.4	70	0.61	0.017
Chr. 5	11 145	748.9	26.0	5.6	45.5	6.8	64	0.62	0.017
Chr. 6	10 680	717.4	25.9	5.4	44.4	6.7	63	0.62	0.017
Chr. 7	9761	655.2	24.6	5.1	41.4	6.4	59	0.56	0.017
Chr. 8	9619	645.7	22.3	4.6	38.3	5.6	55	0.52	0.017
Chr. 9	7280	488.4	18.4	3.5	31.7	4.7	45	0.35	0.016
Chr. 10	8295	556.5	20.4	3.9	35.5	6.2	50	0.45	0.017
Chr. 11	8351	560.1	20.2	3.8	33.1	5.5	49	0.44	0.016
Chr. 12	8054	540.3	19.9	3.6	34.4	5.5	48	0.38	0.016
Chr. 13	6049	405.5	14.8	2.7	25.3	4.8	36	0.34	0.016
Chr. 14	5545	371.5	13.7	2.6	23.2	4.9	34	0.34	0.016
Chr. 15	4982	333.6	13.0	2.4	21.1	3.5	31	0.34	0.016
Chr. 16	5333	357.0	14.0	2.4	22.6	3.7	33	0.30	0.016
Chr. 17	4613	308.6	12.8	2.1	21.4	3.3	31	0.28	0.015
Chr. 18	4797	321.0	19.9	2.2	20.7	3.3	30	0.28	0.015
Chr. 19	3597	240.5	10	1.9	18.2	3.1	26	0.26	0.015
Chr. 20	3767	252.0	9.7	1.8	15.8	2.9	24	0.25	0.016
Chr. 21	2286	153.0	6.3	1.2	10.4	2.4	15	0.17	0.015
Chr. 22	2179	145.7	6.5	1.2	10.6	1.9	16	0.17	0.015
Total	168 380	11 300	422		706		1011

All sizes are in MB and times in seconds. The ‘size’ refers to the archival size after applying the compression algorithms on the VCF file converted into the binary matrix and the variant dictionary (denoted as $\mathcal{H},{\mathcal{V}}_{\mathcal{D}}$) format. The ‘r-time’ refers to the average time to decompress a complete single genome, while ‘c-time’ refers to average time to decompress specific variant information. As TGC and 7 z don’t support local decompression, the ‘d-time’ corresponds to both of these quantities. Best results are highlighted in bold.

^aFor fair comparison, the VCF file mentioned corresponds to only the genotype information (i.e., VCF file without the metadata).

The results for the A.thaliana dataset are shown in Table 2. Recall that the A.thaliana dataset consisted of 775 haploid sequences containing 7 chromosomes. As can be observed, the results follow a similar trend as those obtained with the H.sapiens dataset. Overall, GTRAC achieves a compression ratio of 90 as compared with the VCF file (compared by retaining only the genotype information) and a compression ratio of 7.5 as compared with the $(\mathcal{H},{\mathcal{V}}_{\mathcal{D}})$ representation. The single haplotype extraction times for GTRAC are about an order of magnitude faster than the TGC, 7 z compressors. The single-variant extraction performance is much more impressive, with GTRAC performing up to three orders of magnitude (500–1000 times) faster than the TGC and 7 z compressors.

Table 2.

Evaluations of the universal compressor 7 z, the TGC compressor and the proposed algorithm GTRAC on the 1001 GP A.thaliana dataset containing 775 samples

Experiments on A.thaliana dataset
Data	VCFa	$\mathcal{H},{\mathcal{V}}_{\mathcal{D}}$	TGC compressor		7 z		GTRAC
	size	size	size	d-time	size	d-time	size	r-time	c-time
Chr. 1	4945	406	26	4.5	35	3.6	55	0.81	0.006
Chr. 2	3629	304	19	5.9	25	2.7	41	0.65	0.006
Chr. 3	4295	361	23	7.0	30	3.3	48	0.72	0.006
Chr. 4	3386	281	18	6.1	24	2.6	38	0.61	0.006
Chr. 5	4324	358	23	8.5	30	3.5	48	0.74	0.006
Chr. C	0.09	0.01	0.01	0.03	0.004	0.04	0.2	0.02	0.003
Chr. M	176	13	0.2	0.14	0.3	0.18	0.8	0.01	0.004
Total	20 756	1723	110		144		231

All sizes are in MB and times in seconds. The ‘size’, ’d-time’, ‘c-time’ and ‘r-time’ notations are the same as in Table 1. Best results are highlighted in bold.

^aFor fair comparison, the VCF file mentioned corresponds to only the genotype information (i.e., VCF file without the metadata).

Table 3 summarizes the performance of GTRAC for the 1000 GP H.sapiens dataset (similar results for the A.thaliana dataset are presented in Table 4). Note that, although GTRAC requires less than 2.5 times archival memory as compared with the TGC compressor, the total amount of ∼1.1 GB required is still very low for a dataset of 1092 genome sequences, and is still very convenient to handle on machines with relatively small memory and computing power. Along with achieving sub-second single genome extraction, GTRAC also achieves fast variant extraction (17 ms) across all genomes. This feature was not present in TGC, which required decompression of the entire dataset. In addition, along with achieving fast random access, our algorithm results in a much smaller memory footprint during the random access, as is evident from the results. This is important as it implies that very large variant datasets can be handled efficiently even on machines with limited computation. Also, we note that as the dataset size increases, local decompression times and memory requirement for the TGC and 7 z algorithms will increase linearly with the size of the dataset, while local decompression time for GTRAC will remain essentially constant.

Table 3.

Comparison of the TGC compressor and the proposed algorithm GTRAC for the 1000 GP H.Sapiens dataset

Summary of H.Sapiens experiments
	TGC compressor	GTRAC
Total archive memory	422 MB	1.1 GB
Per genome decompression time	7 s	1 s
Per genome decompression memory	1 GB	90 MB
Per variant decompression time	7 s	17 ms
Per variant decompression memory	1 GB	90 MB

Best results are highlighted in bold.

Table 4.

Comparison of the TGC compressor and the proposed algorithm GTRAC for the 1001 GP A.thaliana dataset

Summary of A.thaliana experiments
	TGC compressor	GTRAC
Total archive memory	110 MB	231 MB
Per genome decompression time	6 s	1 s
Per genome decompression memory	400 MB	60 MB
Per variant decompression time	6 s	6 ms
per variant decompression memory	400 MB	60 MB

Best results are highlighted in bold.

4 Discussion

We examined the possibility of achieving good compression of the genotype of a collection of samples, along with fast and memory efficient local decompression results. Our algorithm GTRAC achieves good row-wise and column-wise random access (i.e. single haplotype variant sequence extraction, and specific variant information extraction across all the haplotypes, respectively) over the compressed symbol matrix ${\mathcal{H}}_K$. Such row-based and column-based fast random access can be used as atomic blocks to construct more complex and generic queries on the compressed domain. Also, although we have presented GTRAC as an algorithm to compress the genotype of a collection of samples, it can in fact be easily adapted to efficiently compress other types of genomic datasets which have positional cross-correlation between different samples.

The good local decompression performance of the proposed algorithm can be attributed to the LZ-End style parsing together with the position-aligned correlation present in the sequences. Factors that may influence the compression performance include reordering the samples, which could result in better parsing and encoding, and using multiple reference vectors (we use only the first row of the symbol matrix ${\mathcal{H}}_K$ as a reference). Storing multiple reference vectors in an uncompressed form involves a tradeoff between the compression ratio and the decompression speed. It would be interesting to explore this tradeoff, which would involve optimization for determining which specific reference vectors to choose as references.

Our algorithm allows local decompression of variants corresponding to a specific haplotype in the dataset. A somewhat related functionality would be addition/removal of specific haplotypes to/from the dataset. Currently, changing the archival content can be done by re-compressing the compressed dataset. However, dynamic addition, removal or editing of the existing dataset would be an immensely useful feature, and a step towards a dynamic compressed representation. Storing additional information in the compressed domain, such as the quality of each genotype, could also improve the functionality and utility of the proposed algorithm GTRAC.

5 Conclusion

We have presented GTRAC, an algorithm for representing the genotype of a collection of samples in an efficient manner while allowing for local decompression (random access). In particular, the proposed algorithm supports extraction of the genotype of a given sample within the dataset, as well as the information pertaining to a given variant (i.e. which samples contain a specific variant).

As an example of the performance, GTRAC is capable of compressing the genotype of 1092 H.sapiens diploid samples in 1.1 GB, while achieving local decompression of a sample in less than a second, and local decompression of the information pertaining to a specific variant in 17 ms. This is the first algorithm in the literature that can achieve high compression ratios of this information while allowing for local decompression that does not require the decompression of the whole compressed archive.