L₁ regularization facilitates detection of cell type-specific parameters in dynamical systems

Abstract

Motivation: A major goal of drug development is to selectively target certain cell types. Cellular decisions influenced by drugs are often dependent on the dynamic processing of information. Selective responses can be achieved by differences between the involved cell types at levels of receptor, signaling, gene regulation or further downstream. Therefore, a systematic approach to detect and quantify cell type-specific parameters in dynamical systems becomes necessary.

Results: Here, we demonstrate that a combination of nonlinear modeling with L₁ regularization is capable of detecting cell type-specific parameters. To adapt the least-squares numerical optimization routine to L₁ regularization, sub-gradient strategies as well as truncation of proposed optimization steps were implemented. Likelihood-ratio tests were used to determine the optimal regularization strength resulting in a sparse solution in terms of a minimal number of cell type-specific parameters that is in agreement with the data. By applying our implementation to a realistic dynamical benchmark model of the DREAM6 challenge we were able to recover parameter differences with an accuracy of 78%. Within the subset of detected differences, 91% were in agreement with their true value. Furthermore, we found that the results could be improved using the profile likelihood. In conclusion, the approach constitutes a general method to infer an overarching model with a minimum number of individual parameters for the particular models.

Availability and Implementation: A MATLAB implementation is provided within the freely available, open-source modeling environment Data2Dynamics. Source code for all examples is provided online at http://www.data2dynamics.org/.

Contact: bernhard.steiert@fdm.uni-freiburg.de

1 Introduction

The progress in the development of experimental assays like the establishment of high-throughput measurement techniques raised new demands on statistical methodology. Many scientific questions in the field of Bioinformatics and Systems Biology nowadays require large models with hundreds or even thousands of parameters or variables. Therefore, a major issue in many applications is feature selection, i.e. determination of informative parameters or variables, which are required to explain experimental observations, for identification of differential expression and/or for making reliable predictions.

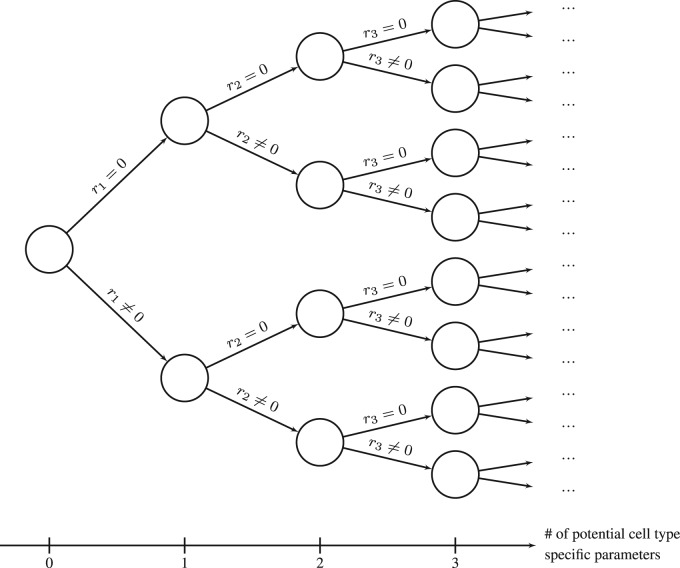
Selecting parameters of interest is one of the most important tasks during modeling as it heavily influences predictions. In many cases, feature selection is equivalent to model discrimination (Box and Hill, 1967) since a set of features corresponds to a specific model with a corresponding set of parameters. In multiple linear regression, as an example, feature selection corresponds to choosing appropriate prediction variables used to fit an experimentally observed response variable. The traditional approach for choosing a suitable level of detail and the respective optimal set of features is iteratively testing many models (Thompson, 1978), i.e. different subsets of features by forward- or backward selection or combinations thereof (Efroymson, 1960; Hocking and Leslie, 1967). However, if the number of potential predictors is large, the number of possible combinations increases dramatically as shown in Figure 1, rendering such iterative procedures as infeasible.

Fig. 1.

Naïve approach to select cell type-specific parameters. Each parameter p_i for two cell types could be either cell type-independent or -specific. Then, the log fold-change $r_i={\log }_{10}(p_{i,\text{ct2}}/p_{i,\text{ct1}})$ is either $=0$, or $\ne 0$, respectively. Hence, the number of model candidates (circles) grows exponentially with the number of potential cell type-specific parameters (x-axis)

Regularization techniques have been suggested as an alternative approach for selecting features and fitting parameters in a single step. The idea is to estimate the parameters by optimizing an appropriate objective function, e.g. by maximizing the likelihood. If then, in addition, the impact of individual features is penalized, the optimal solution becomes sparse and the level of sparsity can be controlled by the strength of penalization. It has been shown that such penalties are equivalent to utilization of prior knowledge supplemental to the information provided by the data.

The additional information provided by penalties reduces the variance of the estimated parameters but at the same time introduces a bias. This effect has been termed as shrinkage. If the regularizing penalties are chosen appropriately, e.g. if the L₀- or L₁-norms are applied, a second effect occurs which can be utilized for selection. Because the L₀- and L₁-norms penalize parameters unequal to zero, only parameters remain in the model, which are mandatory for explaining the data. Since the penalized likelihood is discontinuous for L₀ regularization, L₁ penalties are usually preferred.

The concept of using the L₁-norm for data analysis and for calibrating a model has been applied in several fields like for deconvolution of wavelets (Taylor et al., 1979), reconstruction of sparse spike trains of Fourier components (Levy and Fullagar, 1981), recovering acoustic impedance of seismograms (Oldenburg et al., 1983) as well as for compressed sensing (Candes and Wakin, 2008; Cheng, 2015) and clinical prediction models (Hothorn and Bühlmann, 2006). Additionally, it has been used to establish statistical methods which are robust against violations of distributional assumptions about measurement errors (Barrodale and Roberts, 1973; Claerbout and Muir, 1973). Moreover, L₁ penalties have been utilized to incorporate Laplacian priors (Kabán, 2007). Despite this variety of applications, the usability for feature selection and a comprehensive statistical interpretation was not established until introduction of the LASSO (least absolute shrinkage and selection operator). This prominent approach for linear models was published in Tibshirani (1996) when the first affordable high-throughput techniques were available and the necessity of new approaches for analyzing high-throughput data became inevitable.

The standard LASSO has been generalized and adapted specifically in several directions. Feature selection via LASSO was discussed for the regression case in more detail in Tibshirani (1996), for Cox-regression in Tibshirani (1997), and for clustering e.g. in Witten and Tibshirani (2010). The elastic net has been introduced as a combination of L₁ and L₂ regularization (Zou and Hastie, 2005). The so-called group-LASSO has been established to select between predefined groups of features (Ming Yuan, 2006), the fused LASSO has been introduced to account for additional constraints of pairs of parameters (Tibshirani et al., 2005), and the generalized LASSO has been developed to regularize arbitrary prespecified parameter linear combinations (Tibshirani and Taylor, 2011).

Mechanistic ordinary differential equation (ODE) models are applied in Systems Biology for describing and understanding cellular signal transduction pathways, gene regulatory networks, and metabolism. For such ODE models, the selection issue occurs when several cell types are considered. Since each cell type has different concentrations of intracellular compounds and diverse structures, each parameter of a reaction network could potentially be different. We suggest L₁ regularization in this setting to predict parameter differences between cell types. In contrast to the usual context of L₁ regularization, cell type-specific parameters instead of variables are selected. All components of mechanistic models have counterparts in the biological pathway of interest. Therefore, the models are large and the effect of the parameters on the dynamics is typically strongly nonlinear. For estimating parameters in such ODE models, only a small subset of optimization routines in combination with appropriate strategies for calculating derivatives of the objective function, dealing with non-identifiability, handling of local minima etc. are applicable (Raue et al., 2013). We therefore augment an existing and well-tested implementation for parameter estimation for such systems (Raue et al., 2015) to perform selection of cell type-specific parameters based on L₁ regularization. For this purpose, trust-region optimization (Coleman and Li, 1996) was combined with a suitable strategy as presented in Schmidt et al. (2009) to enable efficient optimization in the presence of L₁ penalties in nonlinear models.

Since shrinkage, i.e. decreasing the variance by introducing a bias is not intended for mechanistic models, we only use L₁ regularization for selection, i.e. determining the cell type-specific parameters, and then use the resulting parsimonious model to estimate the unbiased magnitude of all parameters in a second step. An appropriate strategy for choosing the optimal regularization strength in this setting is presented. The applicability is demonstrated using a benchmark model from the DREAM (Dialogue for Reverse Engineering Assessment and Methods) parameter estimation challenge (Meyer et al., 2014). The presented approach constitutes a suitable methodology to infer cell type-specific parameters. In addition, these could be used to predict cell type-specific sensitivities for drugs, which is a prominent challenge in cancer research.

2 Problem statement

Given a model $\mathcal{M}$ describing the kinetics of c reaction network components x_q with $q\in [1,\dots ,c]$ by a system of ODEs

$$\dot{x}(t)=f(x(t),u(t,p_u),p_x)$$ (1)

with a solution vector x(t) representing concentrations of molecular compounds, for external inputs u(t). States x are mapped to experimental data y using an observation function g, yielding

$$y(t)=g(x(t),p_y)+\mathrm{ϵ}(\sigma (p_{\sigma },x(t))).$$ (2)

The measurement error $\mathrm{ϵ}\sim \mathcal{N}(0,{\sigma }^2)$ is assumed to be normally distributed according to an error model $\sigma (p_{\sigma },x(t))$, although the presented approach is not limited to this assumption. Initial concentrations p₀, as well as parameters p_x of the ODE, p_u of the input, p_y of the observation function, $p_{\sigma }$ of the error model, are subsumed in the parameter vector

$$p=[p_0,p_x,p_u,p_y,p_{\sigma }].$$ (3)

The expressions (Equations 1–3) fully specify $\mathcal{M}$. To ensure positive values and improve numerical stability, all parameters are log-transformed.

Given data from two cell types can be described by a common ODE structure (Equation 1). Then, in general, the parameters p are specific for each cell type (ct), i.e. $p_{\text{ct1}}\ne p_{\text{ct2}}$. However, some of the components of $p_{\text{ct1}}$ and $p_{\text{ct2}}$ may be independent from the cell type. Discovering which of the components in $p_{\text{ct1}}$ and $p_{\text{ct2}}$ are most likely to be cell type-specific is the main topic of this manuscript. A naïve approach is to simply test all possibilities for cell type-specific parameters. However, as depicted in Figure 1, the number of model candidates grows exponentially with the number of parameters, rendering such an approach as infeasible.

2.1 Unbiased parameter estimation

To estimate parameters p for n data points $y_j$, given the corresponding observation function observation $g(x(t_j),p_y)$, which is dependent on the ODE solution, the negative 2-fold log-likelihood

$$-2\log \mathcal{L}(p)={\displaystyle \sum _{j=1}^n\frac{{(y_j-g(x(t_j),p_y))}^2}{{\sigma }_j^2}}=:{\chi }^2$$ (4)

is optimized, resulting in the maximum likelihood estimate

$$\widehat{p}=\text{arg}\min \left[{\chi }^2(p)\right].$$ (5)

In general, the ODE system cannot be solved analytically. Therefore, numerical methods as implemented in the Data2Dynamics modeling environment (Raue et al., 2015) are used for calculating ODE solutions and performing maximum likelihood estimation. In addition, we employ multi-start deterministic local optimization as an established approach to ensure that $\widehat{p}$ is in fact the global optimum, as presented in Raue et al. (2013).

2.2 Regularization

Regularization constitutes a prominent method to incorporate prior knowledge, for parameter selection, or to improve numerics of parameter estimation. Here, we use L_k regularization by a penalty to assess the fold-change ${\tilde{r}}_i$ of parameters between cell type 1 and cell type 2, i.e. $p_{i,\text{ct2}}={\tilde{r}}_i·p_{i,\text{ct1}}$. Therefore, the penalized likelihood

$${\chi }_{L_k}^2(p,r)={\chi }^2(p)+\lambda {\left({\displaystyle {\sum }_i|\log {\tilde{r}}_i{|}^k}\right)}^{1/k}$$ (6)

is implemented consisting of the likelihood (Equation 4) and a L_k regularization term weighted by λ. In the following, we substitute $r_i:=\log {\tilde{r}}_i$. The regularization term corresponds to a prior in a Bayesian framework: e.g. for k = 1 the L₁ prior is a Laplacian function, and for k = 2 the L₂ prior is a Gaussian function. Using the definition

$$\left|\right|r|{|}_k:={\left({{\displaystyle {\sum }_i\left|r_i\right|}}^k\right)}^{1/k}$$ (7)

of a L_k-norm, we derive properties of L_k for ranges of $k\in {ℝ}^{+}$, similar to Vidaurre et al. (2013). L₀ is the apparent choice for parameter selection due to its direct penalization of the number of $r_i\ne 0$. However, L₀ is not recommended because the associated optimization problem is known to be NP-hard, i.e. the exact solution cannot be obtained within polynomial computation time. In general, for k < 1, the L_k metric is non-convex which severely hampers numerical methods for parameter estimation. On the positive side, $k\le 1$, for example L₀ and L₁, induces sparsity with the results usually being similar. In contrast, the L_k metric for k > 1 does not lead to sparse results. L₂, which is the metric used for the well-known least squares, can be handled efficiently but does not produce sparse results without introducing heuristics. In that sense, the L₁ metric is unique because it is the only one that combines both features, convexity and sparsity. Therefore, L₁ is the natural choice for parameter selection and is used in the following.

Figure 2 demonstrates how sparsity is induced by the L₁-norm. In the upper row, the data contribution (${\chi }^2$) is depicted by the solid black line, representing a hypothetical model. The L₁ contribution is shown by the dashed blue line. With increasing λ from panels left to right, the influence of the L₁ term is increased. The lower row shows the penalized likelihood (Equation 6) for k = 1, i.e. the sum of the two lines in the corresponding upper panel. For $\lambda =0.5$, the minimum is shifted towards zero (middle panel) in contrast to the unregularized minimum (left panel) but still different from zero. In contrast, the minimum is exactly at zero for λ = 2 (right panel).

Fig. 2.

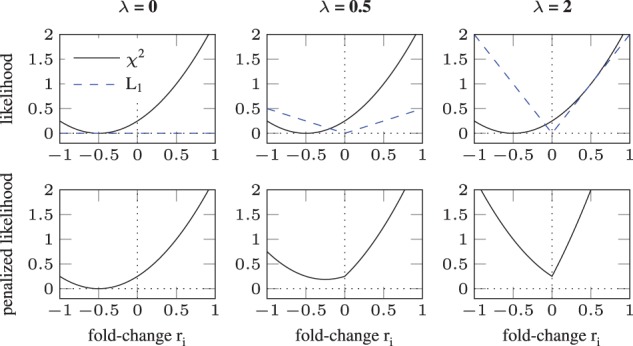
Sparsity and bias introduced by L₁ regularization. Regularization weight λ is increased from panels left to right. In the upper row, the contributions from the data (${\chi }^2$—black line) and a L₁ regularization term (dashed blue line) are shown. Their sum is plotted in the lower row. For $\lambda =0.5$, a bias is introduced shifting the minimum towards zero (middle column). When λ is increased to 2, the minimum is exactly at zero, i.e. sparsity is induced (right column)

2.3 Regularized parameter estimation

Optimization in context of partially observed nonlinear coupled ODEs is challenging. However, methods have been developed to efficiently compute solutions of this problem (Raue et al., 2013). To augment the existing implementations with L₁ regularization, i.e. to minimize the penalized likelihood

$${\chi }_{L_1}^2(p,r,\lambda )={\chi }^2(p)+\lambda {\displaystyle {\sum }_i\left|r_i\right|}$$ (8)

the adaptations described in the following were implemented. Efficient optimization routines like Gauss-Newton or Levenberg-Marquardt exploit the quadratic form in Equation (4). For example, the implementation of a trust-region method lsqnonlin in MATLAB requires residuals

$${\text{res}}_j=\frac{y_j-g(x(t_j),p_y)}{{\sigma }_j}$$ (9)

for data points y_j as input and implicitly calculates the value of the objective function by summation over squares of all residuals. To enable optimization of the penalized likelihood (Equation 8),

$${\text{res}}_i=\sqrt{\frac{\left|r_i\right|}{1/\lambda }}$$ (10)

is appended to the residuals vector for each fold-change r_i. The associated sensitivities

$${\text{sres}}_{ij}:=\frac{\partial {\text{res}}_j}{\partial p_i}$$ (11)

to the regularization residuals ${\text{res}}_i$ are calculated as

$${\text{sres}}_{ii}=\frac{\text{sgn}(r_i)}{\frac{2}{\lambda }\sqrt{\frac{\left|r_i\right|}{1/\lambda }}}.$$ (12)

The gradient components

$${\nabla }_{r_i}{\chi }_{L_1}^2=2{\text{res}}_i·{\text{sres}}_{ii}=\pm \lambda$$ (13)

coincide with the slope $\pm \lambda$ induced by the L₁ term. For r_i = 0, Equation (12) is not defined. In this case, the convergence criterion

$$(\widehat{p},\widehat{r})=\underset{(p,r)}{\arg \max }{\chi }_{L_1}^2(p,r,\lambda )$$ (14)

$$\iff \{\begin{array}{cc}{\nabla }_{p_i}{\chi }^2=0,& \forall i\\ {\nabla }_{r_i}{\chi }^2+\lambda \text{\hspace{0.17em}sign}({\widehat{r}}_i)=0,& \text{for\hspace{0.17em}}\left|{\widehat{r}}_i\right|>0\\ \left|{\nabla }_{r_i}{\chi }^2\right|\le \lambda ,& \text{for\hspace{0.17em}\hspace{0.17em}}{\widehat{r}}_i=0\end{array}$$ (15)

is implemented for r_i = 0 by setting

$$\{\begin{array}{cc}{\text{sres}}_{ii}=0,& \text{for\hspace{0.17em}}|{\nabla }_i{\chi }^2(r_i)|>\lambda \\ {\text{sres}}_{ij}=0\forall j,& \text{for\hspace{0.17em}}|{\nabla }_i{\chi }^2(r_i)|\le \lambda .\end{array}$$ (16)

The rationale behind Equation (15) is that in addition to the classical optimization criterion of vanishing gradient, the L₁ gradient either compensates the data gradient, or the L₁ contribution dominates the data gradient and constrains the estimate to its center ${\widehat{r}}_i=0$. During optimization, this parameter-wise convergence criterion is checked for each candidate r_i at every optimization step. If the latter criterion is fulfilled, the derivative of each residual ${\text{res}}_j$ with respect to r_i is set to zero, i.e. ${\text{sres}}_{ij}=0\hspace{0.17em}\forall j$. Thereby, r_i is fixed to zero for the next iteration step. If at a certain optimization step, the convergence criterion is violated, only the ith L₁ contribution to the gradient is set to zero. This in turn enables r_i that were zero to be released during optimization if there is enough evidence in the data. Both options are formulated in Equation (16).

The L₁ metric has a discontinuous derivative at zero. Therefore, the optimization routine encounters sudden jumps of the derivatives as the sign of r_i changes. For n parameters, there exist $2^n$ combinations of signs. These hyper-quadrants are called orthants. For an efficient optimization, proposed optimization steps from one orthant to another have to be avoided. There are several methods that cope with this problem. They have in common that they split a proposed optimization step into two: first a step towards zero, then potentially a step away from zero. Their major difference is the strategy how zero-values are achieved. To mimic most of the original behavior of trust-region based methods, we implemented the truncation, i.e. scaling, of an optimization step such that the orthant is maintained. Both convergence and truncation are depicted in Figure 3.

Fig. 3.

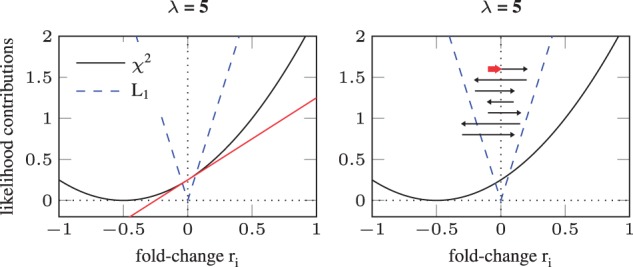
Convergence criterion and truncation for an optimum of ${\chi }_{L_1}^2$ at zero. Left panel: the implementation considers a L₁ regularized parameter r_i = 0 to be converged if the gradient from the data (${\chi }^2$—black line) is smaller than the slope of the L₁ term (dashed blue line). For r_i = 0, the algorithm compares the red line, which is the slope of the black line at this point, to the blue dashed line. In this example, the slope of the L₁ term is larger than that of the ${\chi }^2$ term, hence the minimum is at zero and the corresponding entries in the sensitivity matrix are set to zero. Right panel: The black arrows from top to bottom give a cartoonish representation of optimization steps. To avoid jumping back and forth, i.e. numerical instability by changing the sign of r_i due to discontinuously changing slope of L₁, optimization steps are truncated to the boundary of the orthant as indicated by the red arrow

2.4 Regularization strength λ

To choose the optimal value ${\lambda }^{*}$ of the regularization strength, λ is scanned from low to high values and the unregularized likelihood is re-optimized until the mismatch between model and data is too large to accept the associated simplification. Thus, likelihood-ratio statistics are employed to discover admissible values. For L₁ based parameter selection, cross validation has been suggested as an alternative approach to choose the final value for the regularization weight λ. However, for nonlinear models, leaving data out could produce non-identifiabilities and the effect on the prediction error can be ambiguous. Therefore, we decided to use an information theory based test criterion. The most prominent methods are the likelihood ratio test (LRT; Wilks, 1938), the Akaike information criterion (AIC; Akaike, 1974) and the Bayesian information criterion (BIC; Schwarz, 1978). In certain settings these are equivalent: AIC resembles LRT for fixed $\alpha =15.6\%$ and one degree of freedom. Further, AIC is known to select systematically too large models and is thus not a consistent model selection criterion, especially for many data points. BIC considers the number of data points and is a consistent model selection criterion. Moreover, BIC is equivalent to LRT with an adjusted α level. Therefore, we only use the LRT in the following without loss of generality.

For certain values of λ, each r_i is estimated either to zero or non-zero by optimizing Equation (8). Then, using Equation (4) the unbiased maximum likelihood estimate is calculated, under the constraint that fold-changes with ${\widehat{r}}_i=0$ are fixed to zero. The value of the objective function for this constrained but unbiased solution is denoted as ${\chi }_{\lambda }^2$. The LRT statistic

$$D(\lambda )={\chi }_{\lambda }^{\text{2}}-{\chi }_{\text{λ=0}}^{\text{2}}$$ (17)

quantifies the discrepancy to the full model with solely cell type-specific parameters. The cut-off for determining the parsimonious model, i.e. the model with a minimal number of differences for a given α level which allows fitting the data, is given by the ${\chi }_{m_{\lambda },\alpha }^2$ distribution with degrees of freedom $m_{\lambda }=\#r_i-\#{({\widehat{r}}_i=0)}_{\lambda }$. Thus, the parsimonious model is given by

$${\lambda }^{*}=\max \lambda \text{s.t.}D(\lambda )<{\chi }_{m_{\lambda },\alpha }^2$$ (18)

We use the significance level $\alpha =0.05$ in the following.

2.5 Profile likelihood

The profile likelihood (PL) constitutes a method to calculate confidence intervals (CI) of parameters or predictions, see Raue et al. (2009) and Kreutz et al. (2012) for an overview. It only requires weak assumptions and therefore performs well even for strongly nonlinear problems where asymptotic methods based on the Fisher Information matrix fail. The basic idea is to fix a certain model quantity of interest, e.g. a parameter, and re-optimize all remaining parameters. This re-optimization procedure is iterated for different fixed values of the quantity of interest. By comparing the increase in ${\chi }^2$ with respect to the maximum likelihood the CI is calculated.

Here, we use the PL to check the parameter differences discovered by our L₁ based implementation. Thus, the unregularized PL of a fold-change parameter r_i that has been proposed using L₁ regularization is calculated. If selection was successful, the PL should not be compatible with zero. This interpretation is equivalent to a likelihood ratio test between the null model r_i = 0 and the alternative model $r_i\ne 0$. Note that we did not use the PL in the first place, as the combinatorial issue shown in Figure 1 is not solved by this approach.

In addition, the PL can be used to investigate the uniqueness of the solution. In a non-unique setting there are multiple alternatives to select parameter differences. For instance, a selected cell type-specific parameter could be exchanged with another parameter that was not selected as different. For testing uniqueness, the PL for each r_i with estimate ${\widehat{r}}_i=0$ is calculated. This is equivalent to testing a model with one additional free parameter (r_i) in comparison to the parsimonious model (${\widehat{r}}_i\equiv 0$). If inside the CI of r_i, another parameter that was originally different to zero is then compatible with zero, one cannot decide, based on the given data, which one is different. To resolve such an ambiguity, either additional experimental data needs to be collected, or the biologically more reasonable solution could be chosen.

3 Approach

The approach presented in this manuscript extends the available methodology as implemented in the Data2Dynamics modeling environment (Raue et al., 2015) by L₁ regularization. Data2Dynamics is a state-of-the-art software package that has been used in a variety of applications (Bachmann et al., 2011; Becker et al., 2010; Beer et al., 2014) to perform parameter estimation, uncertainty analysis, and experimental design of partially observed nonlinear ODE systems. In the following, we summarize the L₁ specific enhancements in addition to the established modeling routine as implemented in our approach for discovering cell type-specific parameters.

Given an overarching model that is able to describe two cell types with two independent parameter vectors $p_{\text{ct1}}$ and $p_{\text{ct2}}$ for cell types 1 and 2, respectively. Fold-changes r_i are calculated to express the parameters of cell type 2 relative to cell type 1, i.e. $p_{i,\text{ct2}}={\tilde{r}}_i·p_{i,\text{ct1}}$. Equation (8) is used to L₁ penalize deviations of the fold-change parameter vector r to zero. In contrast to many other LASSO-like techniques, our method consists of two consecutive steps:

(i) Determination of cell type-specific parameters using the regularized ${\chi }_{L_1}^2$

(ii) Determination of the parsimonious model and parameter estimates using the unregularized ${\chi }^2$

In the first step, λ is scanned and the cell type-specific parameters are determined for each value of λ. Then, in the second step, for choosing the optimal ${\lambda }^{*}$ the unregularized Equation (4) is optimized, under the constraint that parameters with ${\widehat{r}}_i=0$ are shared between both cell types. The full model with all parameters specific for each cell type is compared by the likelihood ratio test to each of the models that were selected using L₁ regularization. Thereby, the parsimonious model is defined as the minimal unbiased model that cannot be rejected by the likelihood ratio test.

To cope with diverging terms in the Hessian matrix, we implemented a heuristic that tests each L₁ parameter r_i against zero in the order of their magnitude of deviation from zero. If the likelihood did not increase by more than one, the correction was accepted. Potential alternatives to such a strategy are provided in the discussion.

Additionally, the PL can be utilized to further reduce the number of cell type-specific parameters, which we illustrate exemplarily. Further, we show investigation of uniqueness using the PL. However, since the calculation of profiles for each parameter and λ can take up to several hours for each of the N = 500 runs, these steps were not included for performance assessment of L₁ regularization. When applied in practice, usually only a single experimental setup is analyzed. Then, results can be further improved by calculation of the PL pointing out even smaller and/or biologically more plausible solutions.

4 Application

4.1 Model description

In the following, we use model M1 from the DREAM6 (Dialogue for Reverse Engineering Assessment and Methods) challenge as benchmark for our approach (Steiert et al., 2012). The model represents a gene-regulatory network and was chosen because it enables testing many observation setups and parameter differences. It was used in 2011 to evaluate the performance of experimental design strategies to optimize parameters and predictions. The model incorporates transcription and translation of six genes. Therefore, the dynamic variables represent six mRNAs, as well as the six associated proteins with known initial concentrations. Genes can positively and/or negatively regulate each other. Taken together, the model consists of 29 kinetic parameters. 13 are associated with synthesis and degradation of molecules: 1 protein degradation rate which is shared among all proteins; 6 ribosomal strengths determining the synthesis rate of mRNAs; 6 protein synthesis strengths which define how strongly mRNA presence induces protein production. The remaining 16 parameters define the interaction of genes by Hill kinetics, thus 8 K_D values and 8 Hill coefficients are assumed.

DREAM6 M1 was simulated with gold-standard parameters that were made publicly available after completion of the challenge. We used this gold-standard as cell type 1. When complete data is provided, i.e. all observables measured at all possible experimental conditions, all parameters are identifiable, except for one Hill coefficient which is only restricted to lower values. Thus, we conclude that determining parameter differences between cell types is possible in principle. Next, we assumed one third of all parameters to be cell type-specific. We therefore randomly simulated fold-changes $r\in \{1/10,1/5,1/2,2,5,10\}$ for non-Hill parameters. For Hill coefficients, fold changes $r\in \{1/4,1/2,2,4\}$ were assumed such that Hill coefficients are within the interval $[1,4]$ for both cell types. This range is motivated biologically as thereby the number of binding sites on a molecule is considered. Taken together, the number of possible models is 2²⁹, i.e. more than 10⁸.

We chose the following two observation types from the original DREAM6 challenge setup: (i) mRNA measurements for all mRNAs with 21 data points each, and (ii) protein measurements for two selected proteins, each with 41 data points. The observation function is the identity, i.e. the molecular compounds are observed directly without scaling or offset parameters. The error model contains an absolute term as well as a relative term with fixed weighting. In addition to wild type data, there is the option of performing three possible perturbations for each of the six nodes:

(i) knock-out $\text{(mRNA}\_{\text{syn}}_i=\text{Prot}\_{\text{syn}}_i=0)$

(ii) knock-down $\text{(mRNA}\_{\text{deg}}_i\to 5·\text{mRNA}\_{\text{deg}}_i)$

(iii) over-expression $\text{(mRNA}\_{\text{syn}}_i\to 2·\text{mRNA}\_{\text{syn}}_i)$

In total, this results in 18 possible experimental conditions. Wild type data, i.e. mRNA and protein data for all observables, was included for parameter estimation to have a reference for perturbations. Within the challenge, an identifiable setting has been achieved using 9 additional data sets out of 331 possibilities. To allow variability in the number of experiments, we randomly (50%) selected for each of the 18 conditions whether it was observed or not. To mimic the partial observation, which was one task of the DREAM6 challenge, we chose randomly whether mRNA (one-third) or proteins (two-third) were observed for a given condition. Given the latter, two out of six proteins were randomly selected. We chose the same experimental conditions and observables for both cell types.

After implementing the fold-changes between cell types, as well as perturbations and observations, we used a L₁ regularization for all fold-change parameters and scanned along λ for parameter selection. To choose the optimal regularization strength ${\lambda }^{*}$ we used the unregularized ${\chi }^2$. Thus, we could select the parsimonious model and ensure unbiased estimates of the fold-change parameters.

4.2 Performance assessment

The procedure of selecting fold-changes and observations was repeated N = 500 times, representing 500 different cell type comparison studies. Afterwards, the presented algorithm for L₁ regularized parameter selection was applied in an unsupervised manner for each data setting. The performance is summarized in Figure 4. For each run, a receiver operating characteristic (ROC) curve is calculated by scanning λ from 10⁻⁴ to 10⁶. The black line depicts the arithmetic mean ROC curve and the shading the standard deviation over all N = 500 repetitions. For each of these, the blue dot shows the parsimonious model selected by the likelihood-ratio test. Usually, for a given ROC curve the selection criterion is chosen to maximize both sensitivity and specificity simultaneously, which is the point on the ROC curve closest to the upper left corner. Because the blue dots appear centered around this ‘kink’, we consider the LRT based selection criterion appropriate. On average, the implementation results in an around 74% true positive rate (TPR) and an around 20% false positive rate (FPR) for the given setting. The overall accuracy (ACC) is around 78%. Despite this imperfect accuracy and related classification errors, 91% out of the inferred differences, and 93% out of the true positives were estimated closest to their true fold-change. Within the subset of parameters that were modified and afterwards detected as different, 99.5% had the correct sign. Thus, we conclude that the strategy to calculate unbiased estimates for selected fold-changes is robust against misclassification.

Fig. 4.

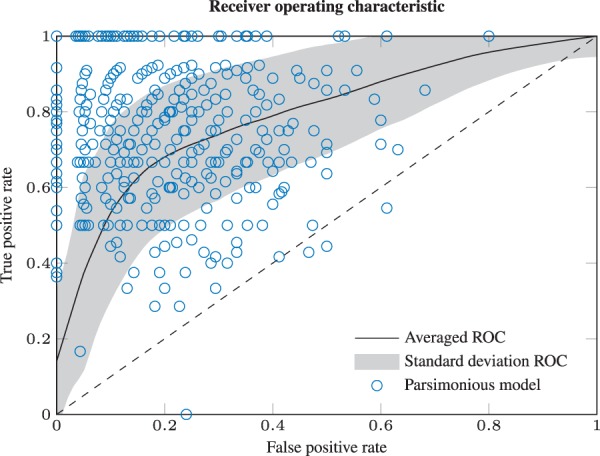
Averaged ROC curve. For each of the N = 500 runs, the ROC curve is calculated in dependence of λ. The black line depicts the arithmetic mean ROC curve and the shading the standard deviation. Blue circles denote the selected model for each repetition. Because the dots appear on average near the maximum of sensitivity and specificity (upper left corner), we consider the LRT based selection criterion as appropriate. The points $(0,0)$ and $(1,1)$ are the limiting cases of no and all, respectively, parameters cell type-specific

We further evaluated the performance of our L₁ fold-change detection routine for different parameter types. The results are summarized in Table 1. The protein degradation rate is shared among all proteins. It is detected in 100% as different when there was a difference simulated. On the other hand, this parameter also had the highest FPR with approximately 46%. A possible explanation is given by the fact that our method is data driven and hence differences are more likely to be detected in points of the network with more data available. This is the case for the protein degradation rate because it influences all proteins in the network. The individual mRNA and protein synthesis strengths have a FPR around 20% and a TPR of approximately 80%. In contrast, Hill regulation parameters (K_D and Hill coefficient) are detected less frequently as different. This is due to identifiability issues as K_D values and Hill coefficients are only identifiable if the corresponding regulator is in the concentration range around K_D, which is often only given for a small subset of perturbations.

Table 1.

Performance of algorithm for DREAM6 M1

Parameter class	$N_{\text{test}}$	$N_{\text{mod}}$	FPR	TPR	ACC
Protein degradation rate	500	181	0.4577	1.0000	0.7080
mRNA synthesis strength	3000	1032	0.2393	0.7965	0.7730
Protein synthesis strength	3000	986	0.1927	0.7982	0.8043
KD value	4000	1365	0.1624	0.6989	0.7903
Hill coefficient	4000	1311	0.1852	0.6461	0.7595
All	14 500	4875	0.2006	0.7366	0.7783

On average, one-third of the parameters that could potentially be cell type-specific ($N_{\text{test}}$) were drawn to actually be cell type-specific ($N_{\text{mod}}$). Overall, parameter differences are inferred with 78% ACC. The model contains a shared degradation rate for all proteins, which is often diagnosed as different. Protein production and ribosomal strengths are on average for FPR and TPR. K_D and Hill coefficients are difficult to detect because the concentration range around K_D has to be covered to see an effect on the dynamics. 500 repetitions were computed. Each run, i.e. L₁ regularized scan and subsequent unregularized scan to identify the parsimonious model, took 28.8 min on average on an Intel Xeon E5-1620 3.60 GHz desktop computer.

4.3 Supervised examination

In the following, we select one representative setup out of the N = 500 given by a minimal deviation of its ROC curve to the average ROC curve for supervised examination. The regularization path is plotted in the left panel of Figure 5. With increasing λ, fold-change parameters are shrinked towards zero, and at some point eventually estimated equal to zero. Thus, the number of cell type-specific parameters decreases for larger λ. The dependency of the likelihood ratio D(λ), i.e. the decrease of the unregularized ${\chi }_{\lambda }^2$ compared with the full model with only cell type-specific parameters, is shown by the blue line in the right panel of Figure 5. The statistical threshold ${\chi }_{m_{\lambda },0.05}^2$ is depicted by the dashed red line. The regularization strength λ* at which both lines cross marks the parsimonious model that has minimal complexity but cannot be statistically rejected.

Fig. 5.

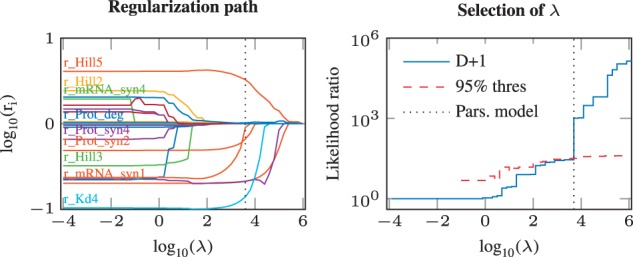
Left: Regularization path of a representative setup. On the x-axis, the regularization weight λ is depicted. As λ is increased, the number of fold-change parameters unequal to zero is reduced and the estimates are shrinked towards zero. The labels are not exhaustive. As expected for nonlinear models, the individual paths are not necessarily monotonous. The vertical dashed line depicts the parsimonious model. Right: Selection of λ. The likelihood-ratio test statistic D is calculated for each value of λ (blue solid line). The value where D crosses the statistical threshold ${\chi }_{m_{\lambda },0.05}^2$ (dashed red line) marks the parsimonious model (dotted black line). To allow plotting in log-space, one is added to all quantities

We checked by calculating the PL of the unregularized fold-change parameters whether parameters predicted as cell type-specific are indeed not compatible with zero (Fig. 6). False positive fold change parameters are shown in panels A, D and F. When the PL (black line) crosses zero (black vertical dashed line) below the statistical threshold (red horizontal dashed line), the parameter is a candidate for supervised removal. Here, this procedure enables the detection of three additional parameters that could be independent from cell type. Interestingly, all these were false positives. In comparison to the automatically inferred parameter differences, the result of the supervised examination increased the ACC from 79 to 86%. We elaborate more detailed on the origins and consequences of this observation in the discussion.

Fig. 6.

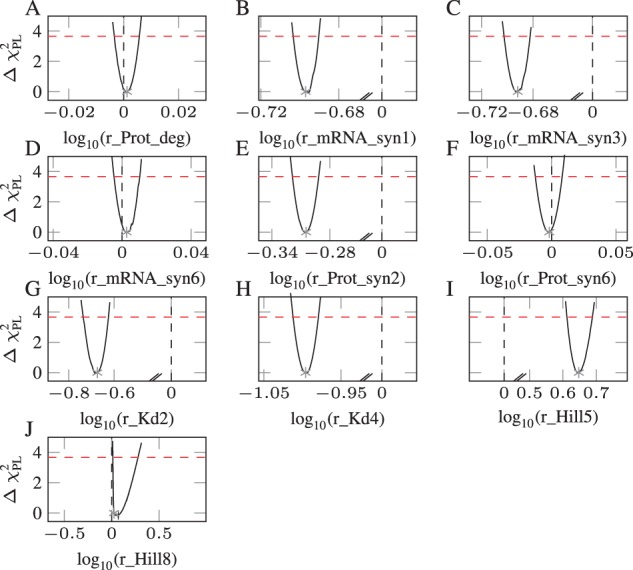
Determining fold-changes that are compatible with zero (dashed black vertical line) using the PL. The parameters in panels B, C, E, G, H, I and J are significantly different from zero, whereas the parameters in panels A, D and F are compatible with zero. These latter ones are actually false positives that could be transformed into true negatives by this supervised examination. Two small diagonal lines depict a discontinuous x-axis

Further, we checked uniqueness of the solution as shown in Figure 7. The unregularized PL of fold-change parameters r_i that were estimated to zero (gray asterisk) is calculated (upper row, black line). Inside the 95%-CI, which is defined by the x-interval for which the PL (black line) is below the statistical threshold (red horizontal dashed line), the value of the remaining fold-change parameters r_i is observed (lower row). Then, two scenarios may occur:

Fig. 7.

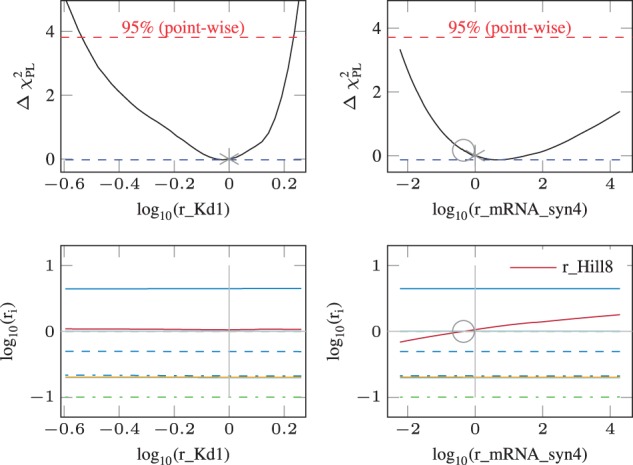
Uniqueness and exchangeability. The results of the supervised examination example are shown. We used the PL to check whether (r_i = 0 and $r_j\ne 0$) gives equivalent results as ($r_i\ne 0$ and r_j = 0) for $i\ne j$. In the upper row, the PL of a fold-change parameter that was estimated to zero is shown. The optimum (asterisk) may not be exactly at the minimum because the model has one additional degree of freedom over the parsimonious model. On the lower row, the respective values of the other $\left\{r_i\right\}$ are shown. When along the profiled parameter (x-axis), a parameter that was originally non-zero (y-axis) is compatible with zero, it is marked with a circle. On the left hand side, the fold-change parameter $r\_\text{Kd}1$, which is a true negative, cannot be exchanged with any other parameter. However, on the right hand side, a false negative fold-change $r\_\text{mRNA}\_\text{syn}4$ could be exchanged with the false positive Hill coefficient $r\_\text{Hill}8$. Thus although the solution is incorrect in classifying these two parameters, the PL pinpoints the alternative of the correct solution. Given the available data, both cases cannot be distinguished and experimental design would be necessary to decide which one of the parameters is cell type-specific

1. none of the r_i is estimated to zero

2. one or more r_i is estimated to zero

For the PL and CI shown in the upper left panel, the re-optimized parameters r_i in the lower panel are not compatible with zero. This corresponds to the first scenario. In contrast, as depicted in the right panels, another fold-change parameter r_i (here: $r\_\text{Hill}8$) may be compatible with zero (circle) if the parameter shown on the x-axis ($r\_\text{mRNA}\_\text{syn}4$) is allowed to deviate from zero. This corresponds to the second scenario. Therefore, based on the data, it is not possible to decide which of these two parameters is in fact cell type-specific and which one is independent from cell type. Interestingly, the underlying truth ($r\_\text{Hill}8=0$ and $r\_\text{mRNA}\_\text{syn}4\ne 0$) is contrary to the originally selected difference ($r\_\text{Hill}8\ne 0$ and $r\_\text{mRNA}\_\text{syn}4=0$). Thus, although the PL cannot provide which solution is correct it enables to generate alternative hypotheses that are in statistical agreement with the data. Using these hypotheses, experiments could be designed as described in Steiert et al. (2012) to eventually obtain an unique solution.

Due to the presented benefits and additional insights, we advise a supervised examination of the results in a real world application to maximize the performance of the method.

5 Discussion

In this manuscript, we used L₁ regularization to predict cell type-specific parameters in systems of coupled partially observed ODEs. When compared with the classical LASSO, which was designed for linear models, many pitfalls emerge for parameter estimation in nonlinear ODE systems. Therefore, we augmented an available implementation by L₁ peculiarities and thereby focused on optimization routines that can efficiently handle nonlinearity. Conversely, the popular LARS algorithm (Efron et al., 2004) sequentially adds predictors to the model, which is not likely to produce a globally optimal solution in the nonlinear setting. Further, pathwise coordinate optimization (Friedman et al., 2007) exploits that a linear model can be efficiently evaluated, while solving the ODE system is the major bottleneck in our application. Although we cannot completely exclude that the presented methodology may be improved in terms of numerical performance by concepts presented in the vast amount of literature on extending LASSO, we could implement a robust and numerically stable algorithm. In our example, cell type-specific parameters were reliably predicted for 500 different data setups.

Because model predictions nonlinearly depend on parameters, the regularization paths depicting the dependency of the cell specific parameters on the regularization strength are not linear between knots. Therefore the regularization paths have to be calculated by discretely scanning λ instead of calculating the paths for whole intervals as it is feasible for linear systems.

Local optima are of major concern in partially observed nonlinear ODE systems. An established method to discover local optima is to perform multi-start deterministic optimization and compare the results. For different λ, other local optima could become globally optimal or even new, additional optima could emerge for a specific range of λ. To circumvent such issues, the multi-start optimization could be applied for each value of λ. However, comprehensively sampling the parameter space by such a strategy is usually computationally infeasible for most realistic models. Therefore, the approach we applied is finding the global optimum for each cell type individually and then gradually increasing λ using the previous fit as initial guess.

Identified differences between cell types may not be unique, i.e. a difference could be exchanged with a parameter that is cell type-independent without significantly changing the fit. Only subgroups of such coupled parameters are necessary to be different. However, this ambiguity is not a shortcoming of the L₁ regularization but rather a manifestation of lacking informative data to uniquely determine cell type-specific parameters.

Most nonlinear optimization algorithms efficiently handle least squares problems but have shortcomings for L₁ regularized optimization. A key challenge that we faced was that numerics became problematic for parameters in the vicinity of zero. For Gauss-Newton steps, the Hessian

$$H_{ij}\approx {\text{sres}}_{ii}·{\text{sres}}_{jj}=\frac{\text{sgn}(r_i)}{\frac{2}{\lambda }\sqrt{\frac{\left|r_i\right|}{1/\lambda }}}·\frac{\text{sgn}(r_j)}{\frac{2}{\lambda }\sqrt{\frac{\left|r_j\right|}{1/\lambda }}}.$$ (19)

is approximated by the first-order derivatives ${\text{sres}}_{ii}$. In this case, r_i appears in the denominator. Therefore, as r_i approaches zero, the Hessian

$$\underset{r_i\to 0}{\lim }{H}_{ij}=\underset{r_j\to 0}{\lim }{H}_{ij}=\pm \infty$$ (20)

diverges. For large entries in the Hessian, the optimizer decreases the step size and therefore may get stuck when approaching zero. Thereby, the FPR is increased since parameters compatible with zero shrink but may not be able to actually reach zero. We conclude that the FPR could be further improved if such numerical issues were completely solved. To overcome these limitations, norms with k > 1 could be employed. Although in the proximity of zero L₁ dominates the Hessian, an additional L₂ term like in the elastic net could provide enough directional information to come closer to zero. We postpone this analysis to future research.

Another remaining open question is to which extent cross-validation strategies are applicable in the Systems Biology setting. A basic assumption for cross-validation is that the drawn subsets contain qualitatively the same information than the original, full data set. This assumption, however, is violated for pathway models and manifests in a strong dependency of parameter identifiability on resampled data and the experimental setup. The latter originates from the complex grouping structure of measurements given by common treatment conditions, jointly observed dynamic states, as well as by available sampling times.

We chose a benchmark model from the DREAM6 parameter estimation challenge to demonstrate applicability of our implementation because it provides a variety of predefined realistic experimental setups. For assessing the performance, cell type dependencies of parameters were introduced and then recovered in an unsupervised manner. When compared with typical pathway models, the DREAM6 setting exhibits two major simplifications. First, the components of the reaction network are directly observed, i.e. there are no scaling parameters. Second, the initial concentrations were assumed as known. However, we do not expect issues if both simplifications are relaxed because the unregularized parameter estimation implementation is well-tested for such cases.

In partially observed nonlinear ODE systems, it has been shown that non-identifiability is of major concern. A non-identifiable parameter can be associated with a flat PL, i.e. the effect on observed quantities by changing one parameter can be compensated by others. If the range of a fold-change parameter is compatible with zero, the L₁ regularization will force the estimate to zero. Hence, the presence of non-identifiabilities may decrease the TPR. One example for such a behavior are Hill kinetics, i.e. Hill coefficients and K_D values, which also appeared as most difficult to detect. We conclude that identifiability is limiting the TPR in this setting. Since the subset of available data sets was randomly drawn from the predefined set of experiments, it is not expected that all subsets contain comprehensive information for estimating all parameters. Therefore, identifiability issues naturally occur and appear as false negatives in the parameter selection step. In general, the magnitude of both, correct and incorrect predictions depends on the amount and quality of data, as well as on the size of the underlying differences.

It has to be stated that cell type differences are detected only if there is evidence in the data. Therefore, unobserved components and specific, incomplete measurement conditions increase the chance of missing biologically relevant cell-specific characteristics. However, we could show that the unbiased estimates of true positive fold-changes are robust to misclassification of others. Nevertheless, the final model should always be checked for biological completeness and plausibility.

In summary, we demonstrated the usage of L₁ regularization in combination with nonlinear models based on ODE systems. Theoretical considerations were given and the approach was tested for random designs of a DREAM benchmark model. The ability to improve the results using the PL was demonstrated. Concludingly, the presented methodology is shown to facilitate detection of relevant differences between dynamical models of cell types, which is an important step towards discovering drug targets specifically affecting cells of interest.

Funding

This work was supported by the German Ministry of Education and Research through the grants LungSys II (Grant No. 0316042G), SBEpo (Grant No. 0316182B), e:BIO3 (Grant No. 031L0080) and LiSyM (Grant No. 031L0048).

Conflict of Interest: none declared.