The impact of phylogenetic dating method on interpreting trait evolution: a case study of Cretaceous–Palaeogene eutherian body-size evolution

Abstract

The fossil record of the earliest Cenozoic contains the first large-bodied placental mammals. Several evolutionary models have been invoked to explain the transition from small to large body sizes, but methods for determining evolutionary mode of trait change depend on input from tree topology and divergence dates. Different dating methods may therefore affect inference of evolutionary model. Here, we fit models of body mass evolution onto dated phylogenies of Cretaceous and Palaeogene mammals, comparing the effect of dating method on interpretation of evolutionary model. Among traditional palaeontological dating approaches, an Ornstein–Uhlenbeck model with high alpha parameters is recovered as best-fitting when minimum-age dating is used, while branch-sharing methods are highly sensitive to topology. Release or release–radiate models are preferred when Bayesian fossilized birth–death method is used, but when using stochastic cal3 dating of trees, a model of increased evolutionary rate without a release in constraint at the Cretaceous–Palaeogene boundary has highest support. These results demonstrate unambiguously that choice of dating method is critical for interpretation of continuous trait evolution, and that care must therefore be taken to consider these effects in macroevolutionary studies.

1. Background

Ancestral trait reconstruction and the fitting of models of trait evolution to phylogenies is commonplace in evolutionary biology [1]. To understand how clades developed key traits or responded to environmental changes, such approaches are extremely useful. However, as most methods for reconstructing trait evolution require a dated phylogeny [2,3], conclusions may be heavily influenced by variations in tree topology, taxonomic sample or reconstructed divergence dates.

Mammalian body mass has received much attention in macroevolutionary studies, particularly across the Cretaceous–Palaeogene (K-Pg) boundary [4–7]. The fossil record suggests that mean body mass of eutherians [7,8] and overall rate of morphological evolution [9] increased over the K-Pg boundary. However, body mass reconstructions onto different eutherian phylogenies have found either stasis [5] or a reduction in rate of body-size evolution combined with a release of constraints [6] at 66 Ma.

Several methods exist for dating divergences in fossil-based phylogenies. Fossil ages provide minimum estimates for dating clades including that taxon, but some analyses have directly used fossil ages as divergence dates [10], a potentially problematic approach [11]. Alternative ‘branch-sharing’ methods divide ancestral branch lengths proportionally to the amount of morphological change [12] or equally [13] among descendant branches. Finally, the rate-calibrated cal3 approach [14], which under some conditions better approximates true dates in simulations [15], and Bayesian approaches (e.g. [16]) use parametric models of diversification and sampling to derive divergence dates. If dating methods systematically result in different patterns of divergence, this would be expected to impact inference of models of continuous trait evolution due to differences in phylogenetic variance–covariance structure across the tree. We assess the impact of different methods for estimating divergence dates on support for a range of evolutionary models of placental body-size evolution.

2. Material and methods

(a). Mass estimation

Body masses were estimated using dental, cranial and postcranial proxies for 177 eutherian genera (electronic supplementary material, figure S1, File S1) sampled in a recent phylogenetic analysis of K-Pg taxa [17], sampling 76% of known Cretaceous and 66% of Paleocene eutherian families, densely sampling eutherian diversity around the K-Pg boundary. Standard deviation on body size was assumed to be 0.15, following previously published estimates [18].

(b). Dating

Four methods were used to date six previously published sets of phylogenies derived from different topological constraints [17]. The first method used fossil occurrences as minimum clade ages. Second, the ‘equal’ branch-sharing method [13] was applied. This approach uses minimum-age dating, but, where zero-length branches exist, ‘shares’ the duration of the ancestral branch with the daughter branches, preventing simultaneous occurrence of nested branching events. Third, trees dated using ‘cal3’—a stochastic method incorporating estimates of sampling, speciation and extinction rate [14]—were used. Fourth, a fossilized birth–death (FBD) model was used to date the phylogeny in MrBayes v. 3.2.6 [19] in which the topology was fixed, but allowing free resolution of polytomies. Branch rates were drawn from a gamma distribution, with tip ages calibrated based on fossil occurrences (electronic supplementary material, Files S2–S4).

Taxon first occurrences were taken from the literature and www.paleobiodb.org (accessed 3 November 2015) and divided into stage and North American Land Mammal Age time bins. Tip-dates were assigned randomly and uniformly within the earliest bin in which that taxon occurred for minimum-age and branch-sharing dating; for the FBD, the same uniform distributions formed tip date priors. Models were fitted to a sample of 50 resolved, dated trees from each pattern of constraint and dating method; these were the 50 trees with the highest posterior probability in the FBD, and a random sample of trees for other methods.

(c). Modelling evolution

We used the fitContinuous_paleo function [6] to fit seven macroevolutionary models to comparative datasets spanning all dating approaches. Akaike weights [20] were used to assess relative support, in each case comparing between Brownian motion (BM), Ornstein–Uhlenbeck (OU), white noise, and trend models, as well as three models incorporating changes in parameters at a fixed point in time—here, 66 Ma. These three models are the ‘rate-shift’, which assumes BM before and after the shift point, with rates free to vary before and after, ‘release’, which assumes an OU model before the shift point, and BM with an identical rate parameter after, and ‘release–radiate’ model, which is the ‘release’ model with rates free to vary before and after the shift point [6].

3. Results

The minimum-age method produced multiple zero-length branches, and dating using cal3 resulted in multiple short, non-zero-length branches concentrated near the K-Pg boundary. The FBD approach resulted in trees with considerably older divergence dates, with long branches at the tips. Branch-sharing spread internal nodes more evenly through time than other methods (figure 1; electronic supplementary material, table S1).

Figure 1.

Exemplar dated phylogenies from each of four dating methods. In each case, the topology is derived from the discretized dataset of Halliday et al. [17] under the ‘full’ constraint. (a) Minimum-age dating contains multiple polytomies due to taxa that are both early and deeply nested. (b) ‘Equal’ branch-sharing causes internal nodes to be much earlier, and divides the long temporal gap between the ancestors of the early Cretaceous stem-eutherians and the crown group evenly. (c) Dating using cal3 results in ages intermediate between (a) and (b), including several very short (but non-zero) branches near the diversification of major clades. (d) FBD dating gives relatively long terminal branches, with most diversification occurring earlier in the tree.

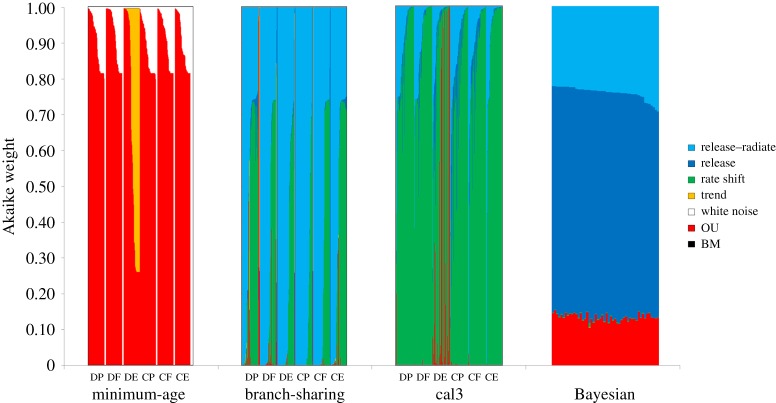
Support for each evolutionary model was strongly influenced by the dating method (figure 2; electronic supplementary material, File S5). OU models received greatest support under minimum-age dating, while the best-fitting models for topologies dated using the ‘equal’ method depended on the topology, and included rate-shift, release–radiate and OU. Similarly, FBD dating resulted in greatest support for a release model, but also release–radiate and OU models. The most strongly supported model for cal3-dated trees was a 10-fold increase in rate at the K-Pg boundary (electronic supplementary material, table S2).

Figure 2.

Akaike weights for models of body mass evolution reconstructed on trees dated using minimum-age, branch-sharing, cal3 and Bayesian methods. Each barplot shows the Akaike weights for models reconstructed on all trees, divided into sets based on their constraints (see Halliday et al. [17] for details of those constraints). When using minimum-age dating, OU models best fit the data; under branch-sharing methods, release–radiate models have greatest support, with rate-shift models also fitting the data well. Under cal3 dating, rate-shift models have greatest support, while the best-fitted models under FBD dating are trend models.

4. Discussion

Different evolutionary models affect our understanding of the effect of the end-Cretaceous mass extinction on eutherian evolution. Models without a shift component like the OU model here best supported by the data when dating trees with minimum-age approaches imply no change in body-size evolution at the K-Pg boundary. Similar results have previously been interpreted to show little effect of the mass extinction on mammal evolution [5,21]. The rate-shift and release–radiate models preferred by cal3, FBD, or branch-sharing dating methods imply a change in tempo, and perhaps mode, in body-size evolution, and thus a significant effect of the extinction on subsequent mammal evolution.

These patterns may not hold for other datasets, and simulations would establish which dating method produces trees that better fit real evolutionary scenarios. Some discussion of the merits of each is possible in this specific example.

Some authors have noted a tendency to erroneously recover strong support for OU models in simulated data where the true model is unbounded BM [22]. However, these effects are strongest in small trees and are indicated by low alpha parameters, neither of which occurs here. The OU models preferred by minimum-age dating in this study have high alpha values, indicating a strong pull towards the optimum—here, the root state, reconstructed as approximately the size of the tree shrew Tupaia—and, as a result, low variance. For highly nested early Paleocene taxa such as Periptychus in the dataset, the placental diversification is reconstructed as the simultaneous emergence of several lineages across the majority of the diversity of Placentalia; most lineages include taxa of approximately this size. Moreover, the sampling of extant taxa is limited to small afrotheres, xenarthrans, euarchontans (including Tupaia) and eulipotyphlans, most of which are small in size, and which might appear as an ultimate optimum size. Testing with an expanded sample of extant taxa might alter this observed pattern.

Preference between evolutionary models for ‘equal’ dated trees is strongly influenced by topology, resulting in well supported but contradictory models. The problem of early but highly nested taxa manifests itself differently here, as the duration of an ancestral branch must be shared among more zero-length descendant branches than if phylogenetic position and stratigraphy were better correlated. This branch-sharing results in older divergence dates for large clades, affecting the timescales over which character evolution is reconstructed. Differences in topology, especially for key early taxa, have a relatively strong impact on choice of different models under branch-sharing dating compared with other dating methods. To some extent, the models best-fitting the data when using FBD dating also varied, but most often the model with greatest support was one of a change in mode of evolution, with or without a shift in rates.

The rate-shift models that had greatest support when using cal3-dated trees reconstruct a large increase in evolutionary rate at the K-Pg boundary, contrary to the findings of Slater [6] of a reduction in rate but a shift in mode. This difference is perhaps a result of the focus in this dataset on Palaeogene taxa. With a large number of taxa that are close in time to one another and passing through multiple time bins, the estimated sampling and speciation rates are high, leading to a concentration of short branches around the K-Pg boundary. With shorter branches, similar changes in body mass must occur over shorter timescales, resulting in increased rates around the end-Cretaceous mass extinction. As our sampling of the Cretaceous and Paleocene fossil record is relatively even and far more complete than previous studies, it allows the reconstruction of hypothesized rate changes during this interval, but the caveat must be introduced that as the dataset still substantially undersamples the Oligocene and Neogene, and if a change in mode did occur at the end-Cretaceous mass extinction, it is conceivable that the Palaeogene represents only the initial phase of the new evolutionary model. Increased sampling of later Cenozoic taxa might help place any observed transitions in greater context, and would help to identify any later transitions.

The dates reconstructed by the different dating methods vary considerably and imply very divergent evolutionary histories for mammals based on the same observed pattern. The assumptions about the quality of the fossil record and the nature of speciation that underlie each choice of dating method colour our subsequent interpretation of trait evolution. Describing the history of mammal evolution in the context of a release in constraint or a shift in rates (or both) at the end-Cretaceous mass extinction tells very different stories. The former suggests some form of ecological interaction between mammals and some clade that became extinct at 66 Ma, the latter alone some intrinsic key adaptation that allowed larger body sizes. Interpreting a single-optimum OU model for the whole of eutherian evolution requires alternative explanations for increased body size in the Early Palaeogene. The results of this study strongly demonstrate the importance of being explicit with one's assumptions when dating phylogenies, and the need for continued effort in the development of robust methods for dating trees of fossil organisms.

Data accessibility

All data from this study are deposited in Dryad at the following address: http://dx.doi.org/10.5061/dryad.7tp7f [23].

Authors' contributions

T.J.D.H. collected the data and conducted the analyses. T.J.D.H. and A.G. conceived the study, wrote the manuscript, approved the publication and agree to be accountable for the work herein.

Competing interests

We have no competing interests.

Funding

Funding was provided by Leverhulme grant no. 2014-364 to A.G. and T.J.D.H.