Global storm time depletion of the outer electron belt

Abstract

The outer radiation belt consists of relativistic (>0.5 MeV) electrons trapped on closed trajectories around Earth where the magnetic field is nearly dipolar. During increased geomagnetic activity, electron intensities in the belt can vary by orders of magnitude at different spatial and temporal scales. The main phase of geomagnetic storms often produces deep depletions of electron intensities over broad regions of the outer belt. Previous studies identified three possible processes that can contribute to the main‐phase depletions: adiabatic inflation of electron drift orbits caused by the ring current growth, electron loss into the atmosphere, and electron escape through the magnetopause boundary. In this paper we investigate the relative importance of the adiabatic effect and magnetopause loss to the rapid depletion of the outer belt observed at the Van Allen Probes spacecraft during the main phase of 17 March 2013 storm. The intensities of >1 MeV electrons were depleted by more than an order of magnitude over the entire radial extent of the belt in less than 6 h after the sudden storm commencement. For the analysis we used three‐dimensional test particle simulations of global evolution of the outer belt in the Tsyganenko‐Sitnov (TS07D) magnetic field model with an inductive electric field. Comparison of the simulation results with electron measurements from the Magnetic Electron Ion Spectrometer experiment shows that magnetopause loss accounts for most of the observed depletion at L>5, while at lower L shells the depletion is adiabatic. Both magnetopause loss and the adiabatic effect are controlled by the change in global configuration of the magnetic field due to storm time development of the ring current; a simulation of electron evolution without a ring current produces a much weaker depletion.

Key Points

• Main‐phase depletions are caused by magnetopause losses

• Losses are enabled by a diamagnetic effect due to storm time ring current

• Both the third and the second invariants are violated in the loss process

1. Introduction

The outer radiation belt is populated by relativistic ($\gtrsim 0.5$ MeV) electrons trapped on closed trajectories around Earth where the planetary magnetic field is nearly dipolar. During geomagnetic storms electron intensities in the belt can vary by orders of magnitude on time scales from minutes to days. Storm main phase produces depletions of intensities by often more than an order of magnitude that can extend over broad regions of the belt. The intensities generally increase during storm recovery phase. Poststorm intensity levels, however, have no apparent relation to their values prior to the storm: storms can dramatically increase, decrease, or produce no substantial change in electron intensities in the belt [Reeves et al., 2003]. This inconsistency in the response of relativistic electron intensities to geomagnetic storms is one of the long‐standing mysteries of radiation belt physics.

It has long been recognized that both permanent loss processes and fully adiabatic variations of electron intensities can contribute to radiation belt depletions during storm main phase (see review by Millan and Thorne [2007]). Electrons can be permanently lost from the belt either by means of precipitation into the atmosphere or escape through the magnetopause boundary [e.g., Dungey, 1963; Roederer, 1968]. Adiabatic depletions of electron intensities (henceforth “the adiabatic effect”) can be caused by a slow inflation of electron drift orbits in response to the diamagnetic effect produced by the storm time ring current system [e.g., Dessler and Karplus, 1960, 1961; McIlwain, 1966]. For radiation belt intensities to grow in the recovery phase, permanent losses must be replenished by transport of new electrons into the outer belt and their acceleration to relativistic energies. On the other hand, a decrease of intensities associated with the adiabatic effect is fully reversible; the intensities grow back by the same amount after the ring current decay, without any additional transport or acceleration processes. Quantifying the contribution of the adiabatic effect to main‐phase depletion events is, therefore, essential to understanding the relationship between the prestorm and poststorm intensities of the outer belt.

A variety of plasma waves can resonantly interact with the gyromotion of relativistic electrons leading to electron scattering into the drift and bounce loss cones and subsequent precipitation into the atmosphere (see review by Thorne [2010]). Potentially relevant wave modes include electromagnetic ion cyclotron, whistler chorus, and magnetosonic waves which draw their energy from energetic plasma populations produced during the storm main phase. Consequently, wave occurrence and the expected atmospheric loss rates are higher during storms [e.g., Li et al., 2011; Keika et al., 2013; Ma et al., 2013]. Similarly, a number of main‐phase processes such as nonadiabatic drift orbit expansion due to rapidly growing ring current [Ukhorskiy et al., 2006a] and enhanced outward radial transport due to sharp gradients at the boundary and intensified ULF wave activity [e.g., Shprits et al., 2006; Ukhorskiy et al., 2009] can increase electron loss through the magnetopause.

The relative contributions of the adiabatic effect and electron loss into the atmosphere and through the magnetopause to the main‐phase depletion of radiation belt intensities have been a subject of ongoing debate. From the analysis of the 3 November 1993 magnetic storm (min D s t=−120 nT), Li et al. [1997] concluded that the adiabatic effect alone cannot account for the observed depletion of electron intensities at L>4 and that the presence of either atmospheric precipitation or magnetopause loss is required. Green et al. [2004] used >2 MeV electron measurements at geosynchronous orbit in a superposed epoch analysis of the main‐phase depletions in 52 moderate storms (min D s t>−60 nT). The study concluded that the nonadiabatic portion of the observed depletions is caused by atmospheric precipitation rather than magnetopause loss. Ohtani et al. [2009] conducted a statistical analysis of >2 MeV electron measurements at geosynchronous orbit from 1998 to 2005. They found that irrespective of storm activity, the day‐night asymmetry of the magnetic field is enhanced during the majority of depletion events, leaving electrons on open drift paths intersecting the magnetopause. This study suggests that radiation belt depletions are mainly controlled by magnetopause loss. Yuan and Zong [2013] arrived to a similar conclusion with the superposed epoch analysis of electron intensities measured by Solar Anomalous and Magnetospheric Particle Explorer during 110 coronal mass ejection (CME)‐driven geomagnetic storms.

The analysis of a large geomagnetic storm (min D s t=−427 nT) of 20 November 2003 [Bortnik et al., 2006] suggested that the outer belt depletion at L>5 is attributed to magnetopause loss, while at lower L shells, the depletion is caused by atmospheric precipitation. Ukhorskiy et al. [2006a] conducted two‐dimensional test particle simulations of the evolution of the outer belt intensity during a more moderate (min D s t=−160 nT) storm of 7 September 2002. Despite the difference in magnitude of the storm compared to [Bortnik et al., 2006], it was also found that magnetopause loss was active above L=5. All electrons at L>5 were lost from the belt in less than 2.5 h after the storm onset. The losses were primarily attributed to a nonadiabatic drift orbit expansion caused by the diamagnetic effect of the storm time ring current.

Turner et al. [2012] used multiple equatorial and low‐altitude spacecraft to analyze the evolution of the outer belt intensity during the main phase of a moderate storm (min D s t=−50 nT). The study provides strong observational evidence that the deep depletion of intensities observed down to L=4 were caused by electron loss through the magnetopause. Recently, Turner et al. [2014] considered a radiation belt depletion during a larger storm (min D s t=−135 nT) on 30 September 2012, with the use of multiple equatorial spacecraft. This study concludes that the depletion of electron intensities observed at L ^*>4 is consistent with magnetopause loss, while an additional loss mechanism is required to explain the depletion observed at L ^*<4. Hudson et al. [2014] conducted a global test particle simulation of the 8 October 2012 storm (min D s t=−106 nT) with the use of the coupled Lyon‐Fedder‐Mobarry Rice Convection Model magnetospheric model, which showed strong magnetopause loss down to about L=7. It was concluded that the observed depletion of electron intensities down to L=3 involves additional loss mechanisms not accounted for by the model.

In this paper we analyze the main phase of the 17 March 2013 magnetic storm that produced a deep depletion of electron intensities across the entire radial extent of the outer belt. We conduct global simulations of storm time evolution of radiation belt intensities and then compare the simulation results with electron intensities observed by the Magnetic Electron Ion Spectrometer (MagEIS) experiment [Blake et al., 2013] of the Van Allen Probes mission [Mauk et al., 2012].

Our model computes three‐dimensional motion of relativistic electrons and is therefore not constrained by unphysical limitations of previous two‐dimensional simulations of the equatorially mirroring particles [e.g., Ukhorskiy et al., 2006a]. In two‐dimensional models, radiation belt electrons in steady state drift along B = const contours of the equatorial plane. If the drift contour intersects the magnetopause, the electrons are lost from the belt. In three dimensions, electrons bouncing at the magnetic equator on the nightside can exhibit drift orbit bifurcations on the dayside, where the magnetic field is compressed, and then traverse across the dayside magnetosphere off the equatorial plane along the magnetopause boundary without ever crossing it [e.g., Ukhorskiy et al., 2011]. On the other hand, electron orbits in the bifurcation region are not stable. Bifurcations violate the second adiabatic invariant of the electron drift‐bounce motion, leading to fast radial transport across the bifurcation region [Ukhorskiy et al., 2014] and can therefore provide a mechanism for electron escape from the region of stable outer belt orbits to the magnetopause.

The goal of this paper is to investigate the role of the adiabatic effect and magnetopause loss in the observed rapid depletion of relativistic electron intensities. To simulate electron motion, we used the (TS07D) magnetic field model [Tsyganenko and Sitnov, 2007] with an inductive electric field [Ukhorskiy et al., 2014]. The TS07D model was selected for this analysis for the following two reasons. First, the model provides a realistic specification of storm time currents that determine the distribution of magnetic field across the inner magnetosphere [Sitnov et al., 2008, 2010] and accurate location of the magnetopause boundary [Shue et al., 1998], which are important for quantifying both the adiabatic effect and magnetopause loss. Second, the state of the TS07D model is defined by a set of solar wind and geomagnetic input parameters. Individual input parameters can be adjusted independently, which can be used to analyze how the depletion of radiation belt intensities depends on various solar wind and geomagnetic conditions.

One possible interpretation of the discrepancy among previous results is that there is little correlation between the magnitude of the storm time ring current system (measured by min D s t) and the balance between atmospheric and magnetopause losses. Since the SYM‐H index (1 min analog of D s t) and its time derivative are among the main input parameters of TS07D, we can directly address the role of the storm time ring current in radiation belt depletions by adjusting model input parameters throughout storm main phase.

The following section gives an overview of the radiation belt depletion event during the main phase of 17 March 2013 storm. In section 3, we discuss the details of our test particle model. In sections 4 and 5, followed by conclusions, we present simulation results and discuss the comparison with observations.

2. The 17 March 2003 Depletion Event

The Van Allen Probes Mission comprises two spacecraft (A and B) on nearly identical low inclination (10°) orbits with perigee of ∼600 km, apogee of 5.8R _E, and orbital period of approximately 9 h [Mauk et al., 2012]. Figure 1 shows variability of radiation belt intensities observed by Van Allen Probes over March 2013 when the spacecraft apogees were in the postmidnight sector. Figures 1c and 1d show the observation at Probe A of the omnidirectional intensity of 1.25 MeV electrons measured by the MagEIS instrument [Blake et al., 2013] and the intensity of 5.6 MeV electrons measured by Relativistic Electron‐Proton Telescope (REPT) [Baker et al., 2013]. Figures 1a and 1b display the time series of the solar wind dynamic pressure P _dyn and the D s t index.

Figure 1.

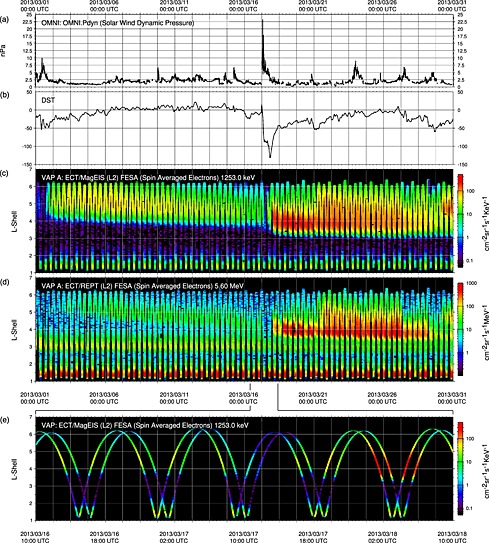
Relativistic electron intensities observed by Van Allen Probes during March 2013. The figure shows (a) solar wind dynamic pressure at ACE, (b) SYM‐H index, (c) omnidirectional intensity of 1.25 MeV electrons on MagEIS Probe A, (d) omnidirectional intensity of 5.6 MeV electrons on REPT A, and (e) omnidirectional intensity of 1.25 MeV electrons measured by MagEIS on Probes A and B during a 48 h interval on 17–18 March centered at the electron depletion event during storm main phase.

The storm of 17 March began with a sudden commencement at approximately 06:00 UT with a rapid increase of P _dyn from about 1 nPa to over 20 nPa, triggered by the arrival of an interplanetary shock at the front end of a coronal mass ejection, followed by the southward turning of the interplanetary magnetic field (IMF) (not shown). The main phase continued until approximately 18:00 UT when the IMF turned northward, starting the recovery phase. During the main phase, the D s t index dropped down to approximately −120 nT.

The storm main phase depleted the intensities of $\gtrsim$ 1–6 MeV electrons by more than an order of magnitude over the entire radial extent of the outer belt. The intensities of lower energy electrons (not shown) increased due to direct injections of particles from the magnetotail to deep inside the outer belt. Figure 1e shows the intensity of 1.25 MeV electrons measured by MagEIS on Probes A and B over a 48 h interval centered at the depletion event. As can be seen from the figure, the depletion of electron intensity occurred in less than 6 h after the storm sudden commencement. The intensities recovered to their prestorm values by the end of the main phase, exceeding the prestorm values by more than an order of magnitude in less than 7 h after beginning of the recovery phase (for more details see Figure S1 in the supporting information). Quantifying the processes that produced the depletion of radiation belt intensities in the beginning of the storm is necessary for understanding whether their rapid growth in the recovery phase was caused by the adiabatic effect or transport and acceleration of a fresh electron population.

3. Test Particle Model

To simulate the global evolution of radiation belt intensities during storm main phase, we used a test particle approach. First, dynamics of a large number of test particles were computed in the magnetic and electric fields precalculated for the entire simulation interval. Then, the computed phase space trajectories were used to trace the electron phase space density in time from the simulation start. The initial distribution of the electron phase space density was derived from the MagEIS measurements.

Test particle trajectories were computed in storm time magnetic and inductive electric fields. The potential electric field due to global magnetospheric convection [e.g., Weimer, 2001] does not significantly affect relativistic electron motion [e.g., Ukhorskiy et al., 2006a] and therefore was neglected. The fields were calculated with the use of an empirical model, TS07D, which provides an accurate specification of the magnetic field in the inner magnetosphere during storms [Sitnov et al., 2008, 2010].

The TS07D model employs a flexible basis function representation of storm time equatorial currents free of any a priori assumptions of current location or morphology typical for earlier versions of the model. To reconstruct a global distribution of the geomagnetic field at a given moment of time, the model uses a large database of in situ measurements of the magnetic field from historic and current spacecraft missions that provide comprehensive coverage of the inner magnetosphere and the magnetotail at various solar wind and geomagnetic conditions. At a given moment of time, the model coefficients are computed from a subset of the whole database (nearest neighbors) selected to represent similar solar wind and geomagnetic conditions. The nearest neighbors are defined based on three global input parameters 〈v B _S〉, 〈S Y M‐H〉, and D〈S Y M‐H〉/D t, derived from the time series of the solar wind electric field and the SYM‐H index using 6 h cosine and sine masked averaging in the spirit of principle component analysis of nonlinear time series [Broomhead and King, 1986]. The averaging includes 3 h of the input time series prior to the current state and extends by 3 h into the future. The first two input parameters have the physical meaning of time‐averaged quantities, while the third parameters corresponds to the average time derivative centered on the current state (for more details, see Sitnov et al. [2008, 2010]).

In addition to average solar wind and geomagnetic input parameters, the model state is defined by the instantaneous value of the solar wind dynamic pressure, P _dyn, that scales all model current systems. Time dependence in the model comes through the input parameters. Variation of the input parameters changes the distribution of magnetic field coherently over the entire model domain. The model therefore does not account for any effects of plasma waves and is therefore only applicable on time scales longer than the transit time of 1–3 min, i.e., the time it takes for a magnetosonic wave to propagate from the magnetopause though the inner magnetosphere [Ukhorskiy et al., 2006a, 2006b; Ukhorskiy and Sitnov, 2008; Ukhorskiy et al., 2014].

The magnetic field was specified on a Cartesian grid in GSM coordinates with dx=dy=dz=0.2R _E. To simplify the analysis of simulation results, the dipole tilt angle was set to zero. For zero tilt angle, the GSM and the SM coordinates are equivalent, and the magnetic equator is a plane given by z=0.

The inductive electric field induced by variations in the global state of the model was calculated from the time derivative of the magnetic field vector potential: A=α∇β. The values of Euler potentials α and β were calculated numerically by tracing magnetic field lines from the grid points to Earth's surface, where the potential values were determined from the analytical expressions for a dipolar magnetic field [Ukhorskiy et al., 2014]. This approach for determining inductive electric field from empirical magnetic field models has been used in a number of past studies including a computation of the electric field during storm main phase [Ukhorskiy et al., 2006a] and analysis of the electric fields induced by ULF fluctuations in the solar wind dynamic pressure [Ukhorskiy et al., 2006a, 2006b; Ukhorskiy and Sitnov, 2008; Ukhorskiy et al., 2014] (for a comparison of the solar wind pressure‐induced electric fields computed from the TS07D and a global MHD model [Claudepierre et al., 2010] see Figure S2 in the supporting information).

The electron motion was calculated in the guiding center approximation based on our Hamiltonian formulation [Ukhorskiy et al., 2011, 2014]. Five‐dimensional phase space of the guiding center motion is specified by (r,γ,α), where r is the particle location, γ is the relativistic factor, and α is the pitch angle. In this paper we focus on the evolution of 1.25 MeV electrons, i.e., the lowest MagEIS energy channel that shows the depletion of electron intensities unattenuated by direct injections. To avoid introducing an unphysical bias into the electron distribution function, test particles must initially be evenly distributed over the phase space domain around 1.25 MeV. The energy range of test particles must be sufficiently broad to capture adiabatic effects, i.e., it must include sufficiently low/high energy particles that can be accelerated/decelerated to 1.25 MeV in the course of the storm main phase. The following procedure was used to initialize test particles.

First, in a static magnetic field corresponding to t=0 of the simulation process, we computed a set of stable (i.e., nonbifurcating) drift‐bounce trajectories using the initial conditions along the midnight meridian of the equatorial plane (y=z=0), distributed between x=−7.6 and x=−3.0. At each initial location, the trajectories were computed for equatorial pitch angles between α _eq=10° and α _eq=90° at increments of 5°. The solar wind dynamic pressure before the storm was only P _dyn=1.35 nPa. The earthward boundary of the drift orbit bifurcation region at such low value of the dynamic pressure was as far as x=−6.9, i.e., at x>−6.9, drift‐bounce orbits were stable at all pitch angles. At x=−7.6 the orbits were stable only for α _eq<30°. The data points of all stable drift‐bounce trajectories with common value of α _eq were then combined into 17 different sets.

Second, we introduced a 21×40 polar grid in the equatorial plane, (L,ϕ), between L=3 and L=7.2 and chose 100 values of initial particle energy distributed evenly between γ=2.5 (0.77 MeV) and γ=6 (2.8 MeV). For each energy value, we used the points of stable drift‐bounce trajectories calculated in the previous step to randomly select one point per grid cell of the equatorial polar grid from each of the 17 sets corresponding to different equatorial pitch angle values. This gave us 21 × 40 × 17 × 100 = 1,428,000 initial conditions evenly distributed in L, the azimuthal drift angle ϕ, the bounce phase, equatorial pitch angle (at the midnight meridian), and energy.

The initial distribution of electron phase space density was computed from the radial profiles and pitch angle distributions of electron intensities measured by MagEIS on the inbound pass of Probe A prior to the storm (02:24–06:00 UT). Figure 2 shows the radial profiles of γ=2–6 electron intensities at nearly 90° pitch angle (Figure 2a) along with the derived distribution of their phase space density, f(L,γ) (Figure 2b). We used sinn α fits to approximate the pitch angle distributions. According to the MagEIS measurements (not shown), n varied monotonically between n=1 at L=3.5 and n=0 at L=6. It was assumed that for quiet conditions prior to the storm, the phase space density was independent of the azimuthal drift angle. Since the spacecraft apogee on 17 March 2013 was close to midnight, the L values of the MagEIS measurements approximately correspond to the midnight meridian: L _M=L(x<0,y=0). We also assumed that being at low latitude, MagEIS captures equatorial pitch angle distributions. Therefore, the phase space density of the outer electron belt prior to the storm was approximated as

$$f(L_M,\gamma )\stackrel{n\left(L_M\right)}{\sin }{\alpha }_{\text{eq}}.$$ (1)

Figure 2.

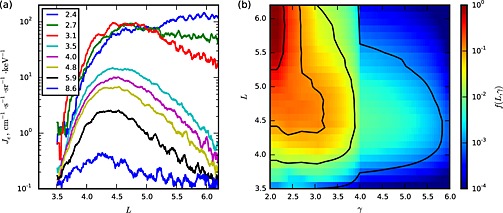
(a) Radial profiles of intensities and the (b) phase space density of γ = 2–4 relativistic electrons with near‐perpendicular pitch angles measured by MagEIS on Probe A during its inbound pass prior to the storm (17 March 2013, 02:24–06:00 UT) used to initialize the phase space density in the test particle simulations.

The initial distribution (1) was used to assign weights to the test particles based on their initial location in phase space. We set up a regular grid in the guiding center phase space on the hyperplane corresponding to the magnetic equator z = 0: {X ^k}≡{L ⁱ, ${\varphi }^j,{\alpha }_{\text{eq}}^l$, γ ^m}. Test particles initially located in a kth cell of the grid (i.e., {X _i(t = 0)|X _i∈[X ^k,X ^k+δ X)}) were assigned weights equal to the ratio of the number of “physical” particles in this grid cell, computed with the use of the phase space density value in the cell center, to the number N _i of test particles in this cell:

$$w_i=\frac{1}{N_i}f(〈L_M〉,{\gamma }^m)\stackrel{n(〈L_M〉)}{\sin }{\alpha }_{\text{eq}}^l·\delta \mathrm{\Gamma }\left({\mathbf{X}}^k\right),$$ (2)

where 〈L _M〉 is the average value of the test particle location in L _M and δ Γ(X ^k) is the volume of the phase space grid cell. The value of the phase space density in a kth grid cell at time t > 0 of the simulation process is then computed by dividing the sum of the weights of all N _k test particles currently located in that cell by the cell volume:

$$f(t,{\mathbf{X}}^k)=\frac{1}{\delta \mathrm{\Gamma }\left({\mathbf{X}}^k\right)}\sum _{j=1}^{N_k}{w}_j;\text{where}\left\{{\mathbf{X}}_j\right(t\left)\right|{\mathbf{X}}_j\in [{\mathbf{X}}^k,{\mathbf{X}}^k+\delta \mathbf{X})\}.$$ (3)

The value of the phase space density in a given cell can be changed in two ways: by changing the number of test particles in the cell, e.g., by particle escape through the magnetopause boundary, and by particle transport that changes the average value of test particle weights in the cell, e.g., an interchange of equal number of particles between two cells with lower and higher values of the phase space density (Figure 3). By tracking the evolution of the number of particles and their average weights, one can determine what processes control the evolution of electron intensities in the belt. A decrease of the number of particles with fixed values of the initial energy and pitch angle everywhere in the computation domain indicates permanent loss of particles from this region of phase space either through the magnetopause boundary or by precipitation into the atmosphere. On the other hand, a change in the average weights of test particles at given values of energy and pitch angle, without a substantial variation in their number, implies that the phase space density is changed by particle redistribution over the phase space.

Figure 3.

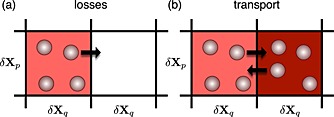
Illustration of two limits of the processes contributing to variation in the phase space density in a grid cell of test particle simulations: (a) variation of the number of particles, N _k without changing the average weight; and (b) variation of the average weight, 〈w〉_k without changing the number of particles.

To determine whether the dynamics underlying the permanent loss of particles, as well as redistribution over phase space, are produced by fully adiabatic effects or transport across their drift shells, it is necessary to quantify radial transport rates. During elevated levels of the solar wind dynamic pressure, a large portion of the outer belt orbits undergo drift orbit bifurcations. Since the bifurcations violate the second adiabatic invariant, the third invariant and L ^*, commonly used to quantify radial transport, are not defined in the bifurcation region. To measure radial transport we use the generalized $\overline{L}$ variable computed from the time‐dependent drift‐bounce orbits,

$$\overline{\mathrm{\Phi }}=\underset{0}{\overset{2\pi }{\int }}\alpha \mathrm{d}\beta =-\frac{2\pi B_0{R}_E^2}{\overline{L}}$$ (4)

It was previously shown [Ukhorskiy et al., 2014] that $\overline{L}$ provides a good measure of radial transport, i.e., (a) for stable orbits in a static field $\overline{L}=L^{*}$; (b) for time‐varying adiabatic variations in the field (Φ = const), $\overline{L}=L^{*}$; and (c) for nonadiabatic transport (Φ ≠ const); $\overline{L}$ is approximately the average of L ^* over a particle drift orbit.

4. Global Simulations of Storm Time Depletion

The results of our test particle simulation of the first 6 h of the storm are shown in Figure 4 (also see Movie S1 in the supporting information). Figures 4a and 4b display the time series of the solar wind dynamic pressure P _dyn and the SYM‐H index used as the inputs of the TS07D model. Note that in order to avoid unrealistically large inductive electric fields due to coherent compressions of the quasi‐static magnetic field model at sharp increases of P _dyn, the input time series were parsed with a 10 min cadence. Consequently, having the Nyquist period of 20 min, the model does not resolve any fluctuations in the magnetospheric fields that could exhibit resonance with the drift motion of ∼1–2 MeV electrons in the bulk of the outer belt (the drift period T _D<20 min for L>3.3).

Figure 4.

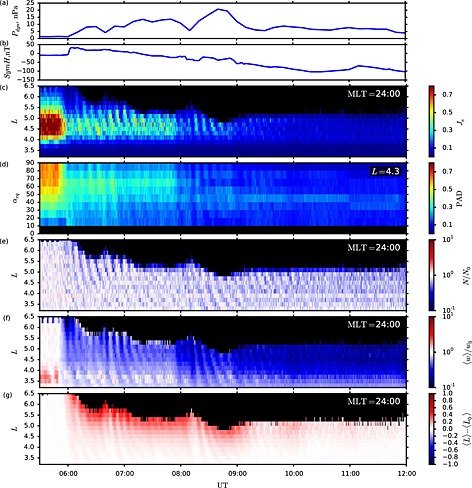
Test particle simulation of electron intensities during first 6 h of 17 March 2013 storm. The figure shows (a) 10 min averaged solar wind dynamic pressure, P _dyn; the (b) SYM‐H index; (c) the simulated intensity of 1.25–1.50 MeV electrons with near‐perpendicular pitch angles of 80–90° along the midnight meridian at the magnetic equator; (d) the pitch angle distribution of 1.25–1.5 MeV electron intensity at L = 4.3, (e) the normalized number of particles with initial energies of 1.25–1.50 MeV and initial pitch angles of 80–90°; (f) the normalized average weight of particles with current values of energy of 1.25–1.50 MeV and pitch angles of 80–90°; and (g) the average change in their $\overline{L}$ location along the midnight meridian at the magnetic equator. More details can be seen in Movie S1 in the supporting information.

Figure 4c shows evolution of the intensity of 1.25–1.50 MeV electrons with near‐perpendicular pitch angles of 80–90°, along the midnight meridian at the magnetic equator computed at 30 s cadence. The midnight projection approximately corresponds to the radial profiles of electron intensity captured at Van Allen Probes whose apogees were close to midnight. Figure 4d displays the pitch angle distribution of electron intensity at L=4.3, near the maximum of its radial distribution. The model shows strong depletion of electron intensity starting after the storm sudden commencement and continuing through the entire simulation interval. The periodic temporal modulations of the intensity seen until approximately 10:00 UT are attributed to the drift echoes associated with changes in the solar wind P _dyn. The drift echoes exhibit T∼1/L temporal dispersion in accordance with the L dependence of the electron azimuthal drift period (at a given energy). The depletion is first observed at nearly perpendicular pitch angles and then expands toward smaller pitch angle values. About 3 h into the storm main phase, the electron intensities are depleted by an order of magnitude or more at all pitch angles over the entire radial extent of the outer belt.

Figures 4e–4g illustrate the processes controlling the depletion of radiation belt intensities. Figure 4e shows evolution of the number of particles that comprised the radial profile of the near‐equatorial electron intensity at the simulation start. It displays the number of particles, N, currently in the grid cells along the midnight meridian of the equatorial plane whose initial energies were in the range of 1.25–1.50 MeV, and the initial pitch angles were in the range of 80–90°. The number of particles found in each grid cell is normalized to the number of particles, N ₀, initialized in this cell at the simulation start. The figure shows strong electron losses that start at the outer edge of the electron belt after the storm sudden commencement and expand inward to below L=5 over the next 3 h following the increase in P _dyn and the ring current enhancement (decrease in SYM‐H). According to the model, all permanent losses were caused by particle escape through the magnetopause boundary. By the end of the simulation, no particles remain in the belt above L=5.3.

Figure 4f shows average weight, 〈w〉, of test particles in the grid cells along the midnight meridian of the equatorial plane that constitute the radial profiles of the electron intensity shown in Figure 4c. The average weight in each grid cell is normalized by the initial value, w ₀, assigned to the particles in this grid cell at the simulation start. A decrease in 〈w〉/w ₀ starts at the storm sudden commencement and deepens with subsequent development of the ring current (decrease in SYM‐H). By the end of the simulation, 〈w〉/w ₀ is decreased by a factor of 10 or more over the entire range of the remaining outer belt. Since, according to Figure 4e, there is little or no particle loss below L=5, the depletion of the electron intensity in the remaining portion of the belt is attributed to redistribution of particles in the phase space.

Figure 4g displays the difference in the average values of $\overline{L}$ of test particles in the grid cells along the midnight meridian of the equatorial plane that constitute the radial profiles of the electron intensity shown in Figure 4c and the average values of ${\overline{L}}_0$ these particles had at the simulation start. As can be seen from the figure, by the end of the simulation the difference $〈\overline{L}〉-〈{\overline{L}}_0〉$ is approximately zero over the entire radial extent of the remaining outer belt. Recall that $\overline{L}$, like L ^*, is a measure of the third invariant. We therefore conclude that the depletion of the electron intensity observed at L<5 is primarily attributed to the adiabatic effect rather than particle transport across drift shells.

Figure 5 shows the comparison of the simulation results with the MagEIS measurements. The radial profile of 1.25–1.50 MeV electron intensity measured on Probe A prior to the storm, which was used to initialize electron phase space density in the simulations, is shown in cyan. The intensity distribution measured by MagEIS on the outbound pass of Probe A during storm main phase (11:07–14:40 UT) is shown with yellow. The intensity was depleted by more than an order of magnitude compared to its prestorm value. The radial distribution of electron intensity computed at the end of our test particle simulations is shown with blue. From the close agreement between the observed and the simulated profiles of the electron intensity, it follows that our test particle model provides a realistic description of global evolution of radiation belt intensities during storm main phase and that the observed deep depletion of electron intensities is caused primarily by a combination of magnetopause loss at L > 5 and the adiabatic effect at L < 5.

Figure 5.

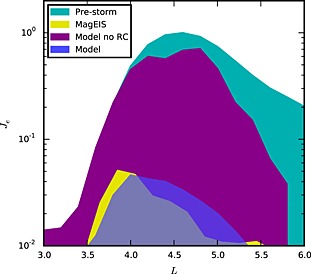
The comparison of radial profiles of 1.25–1.50 MeV electron intensities at near‐equatorial pitch angles from test particle simulations with the MagEIS measurements. The figure shows electron measurements along the inbound pass of Probe A (02:24–06:00 UT) prior to the storm (cyan color) and the outbound pass (11:07–14:40 UT) during storm main phase (yellow color); the results of a full test particle simulation (blue color) and a simulation without the ring current (purple color).

The strongest magnetopause losses and adiabatic depletions in the model were associated with increases in the solar wind dynamic pressure P _dyn at storm sudden commencement and around 08:10 UT. Magnetopause compressions lead to earthward expansion of the drift orbit bifurcation region; an increase in P _dyn from 2 to 9 nPa moves the boundary between the stable and bifurcating orbits on the nightside from above the geosynchronous orbit to 5.5 R _E [Ukhorskiy and Sitnov, 2012]. Electrons transformed from stable to bifurcating orbits can be quickly lost through the magnetopause due to rapid radial transport associated with violations of the second invariant at bifurcations [Ukhorskiy et al., 2014]. Magnetopause compressions also affect the global distribution of magnetic field across the outer belt and therefore can produce adiabatic changes of electron intensities.

To understand how the intensification of the storm time current system contributes to the depletion of electron intensities, we conducted the following experiment. We recalculated the magnetospheric fields varying only P _dyn and keeping all other inputs in TS07D fixed at their quiet time prestorm values. The obtained fields still capture the effects of the magnetopause compressions but do not account for field line stretching due to the diamagnetic effect caused by storm time ring current. We then ran our test particle model using the same initial conditions for the electron phase space density as in the previous simulation. The results are summarized in Figure 6 in the form similar to Figure 4 (more details can be seen in Movie S2 in the supporting information).

Figure 6.

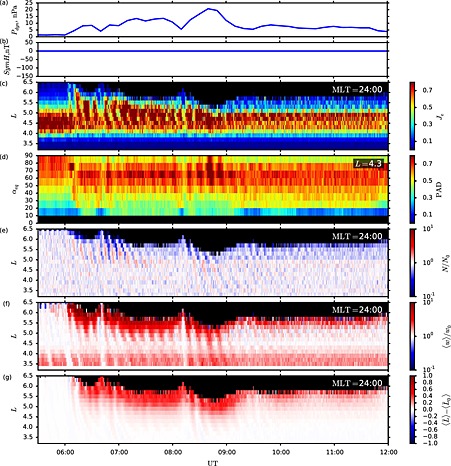
(a–g) Test particle simulations without the ring current (same format as Figure 4). More details can be seen in Movie S2 in the supporting information.

The comparison of corresponding panels in Figures 4 and 6 reveals that the storm time ring current dramatically affects evolution of electron intensities in response to increases in the solar wind dynamic pressure. From Figures 4c and 4d and Figures 6c and 6d it can be seen that the depletion of intensities of 1.25–1.50 MeV electrons with near‐perpendicular pitch angles is much less pronounced without the ring current. There is no evident depletion of electron intensities at pitch angles of 60° and less. The difference in the response of the near‐equatorial electrons is elucidated by Figures 6e and 6f. According to Figures 4e and 6e, magnetopause loss is much weaker without the ring current. At the end of the simulation interval without a ring current, the outer edge of the belt was at L=5.8 and only 20% of the initial particle population was lost through the magnetopause, whereas in the simulation with the ring current the outer edge was at L=5.3 and as much as 55% of the initial particle population was lost. As can be seen from Figure 6f, increases of the solar wind dynamic pressure without a ring current cause adiabatic enhancement of the electron intensity as opposed to strong adiabatic depletions due to the ring current enhancement in Figure 4f.

The radial profile of 1.25–1.50 MeV electron intensity at the end of the simulation without a ring current is shown in Figure 5 with purple color. As can be seen from the comparison with observations at MagEIS (yellow color), the model without a ring current underestimates the depletion of electron intensity by more than a factor of 10. Consequently, we conclude that the diamagnetic effect due to the ring current system is a key factor in the observed deep depletion of radiation belt intensities during storm main phase.

5. Transport During Magnetopause Loss

According to the results discussed in the previous section, electrons that remain in the outer belt at L<5 at the end of the simulation interval behave mostly adiabatically. It is also important to determine whether the magnetopause loss that depletes the belt above L=5 involved radial transport of electrons across their drift shells. Indeed, a number of previous studies [e.g., Kim et al., 2008; Turner et al., 2014] evaluated the extent of magnetopause loss based on the instantaneous location of the boundary between closed electron orbits and open orbits intersecting the magnetopause. If, however, the loss processes involve strong radial transport, estimates based on the location of open‐closed boundary can substantially underestimate both the extent and the rates of the magnetopause loss.

Two processes in the TS07D model can lead to radial transport of electrons in the outer belt: large‐scale inductive electric fields and drift orbit bifurcations. Variations of the solar wind dynamic pressure along with intensification of the ring current system produce global reconfigurations of the magnetic field across the inner magnetosphere. The time‐varying magnetic field induces an inductive electric field which can drive radial transport by means of the E × B drift in the direction perpendicular to the electron gradient and curvature drift motion. Figure 7 shows instantaneous radial profiles (yellow symbols) of the azimuthal electric field component (responsible for drift in the radial direction) at different times of the simulation interval. Average values are shown with red symbols. According to the figure the average absolute value of the azimuthal electric field component at L>5 was above 0.2 mV/m, whereas its instantaneous values periodically exceeded 1 mV/m. Considering that an instantaneous value of the inductive electric field in the model is calculated from the change in magnetic field over a 10 min period (time cadence of the model), these large‐scale inductive electric fields can provide a viable mechanism of radial transport at L>5. This point can be illustrated with a simple estimate of radial transport of equatorially mirroring particles in a dipole magnetic field. The radial component of E × B drift in this case is given by

$$u_r(R_E/\min )=c\frac{E_{\varphi }{L}^3}{B_0}\frac{60}{R_E}\simeq 3·10^{-4}{E}_{\varphi }\left(\text{mV/m}\right)L^3,$$ (5)

Figure 7.

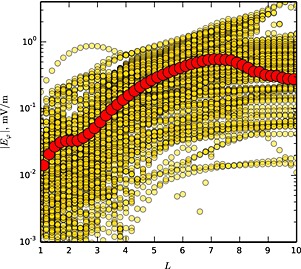
The amplitude of the azimuthal component of the inductive electric field along the y=z=0 axis of the TS07D model. Yellow symbols show instantaneous values, and red symbols show the average values computed over the entire simulation period.

where c is the speed of light and B ₀ is the magnetic field intensity on Earth's surface at the equator. Taking the average value of E _ϕ=0.2mV/m at L=5 and integrating over 10 min, we obtain a change in the radial position of Δ L≃7.5·10⁻², which corresponds to a relative change in radial position of 1.5% over 10 min.

As was previously discussed, transition of electrons with large pitch angles from the region of stable closed orbits to the magnetopause boundary generally involves drift orbit bifurcations. Bifurcations break the second adiabatic invariant associated with the electron bounce motion, leading to their scattering in the radial direction. The rates of the bifurcation‐driven transport can exceed the rates of radial transport due to ULF waves by an order of magnitude [Ukhorskiy et al., 2014]. The total radial distance meandered by electrons across their drift shells depends on the number of bifurcations they underwent during the transition from the stable region to the magnetopause.

To quantify radial transport in the simulations, we use the cumulative distance traveled by particles in the $\overline{L}$ space:

$$\mathrm{\Delta }\overline{L}\left(T\right)=\sqrt{\sum _{t=1}^{N_t}{({\overline{L}}_t-{\overline{L}}_{t-1})}^2},T=N_t\mathrm{\delta t},$$ (6)

where δ t is the time step of test particle simulations. Figure 8 shows the transport of ∼2·10³ particles that were lost from the belt in approximately 1.5 h after the simulation start. Black lines show trajectories of individual particles, and the red symbols show their average. Figure 8a shows the solar wind dynamic pressure, P _dyn. As can be seen from the correlation of P _dyn and the average transport curve, two increases in P _dyn at storm sudden commencement, around T=0.5h and around T=1.2h, lead to increases in radial transport rates. The points of drift orbit bifurcations are marked with yellow symbols. We calculated that the jumps in $\overline{L}$ at orbit bifurcations account for approximately 60% of the cumulative transport. The remaining 40% can then be attributed to large‐scale inductive electric fields.

Figure 8.

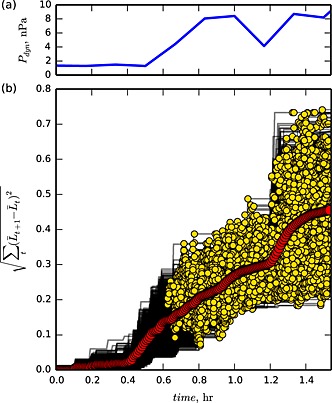
Radial transport of ∼2·10³ particles. Time is measured in hours from the simulation start. All particles are lost through the magnetopause in 1.5 h. (a) The solar wind dynamic pressure, P _dyn. (b) $\mathrm{\Delta }\overline{L}\left(T\right)$ along individual particle trajectories (black lines). The points of drift orbit bifurcations are marked with yellow symbols. Evolution of $〈\mathrm{\Delta }\overline{L}\left(T\right)〉$ computed by averaging transport over all trajectories is shown in red.

Between the time of the storm sudden commencement and particle loss through the magnetopause, the average transport rate was $\mathrm{\Delta }\overline{L}\simeq 0.$ h⁻¹. To put this result in a context, we compared it with the radial diffusion rates ($D_{\text{LL}}^E$) derived by Brautigam and Albert [2000] (see Figure 4 of their paper). We found that the average transport rates of radiation belt electrons prior to magnetopause loss in our model exceeded the fastest radial diffusion rates at highly disturbed geomagnetic conditions (K p=6).

6. Conclusions

In this study we analyzed a strong depletion of radiation belt intensities during the 17 March 2013 geomagnetic storm. During the main phase of the storm, the intensities of the preexisting ∼1–6 MeV electron population were depleted by more than an order of magnitude over the entire radial extent of the outer belt. The analysis was based on global three‐dimensional test particle simulations of global evolution of the outer electron belt based on the TS07D storm time magnetic field model with the inductive electric field. Simulation results were then compared with relativistic electron measurements by the MagEIS instrument of the Van Allen Probes Mission. The following are our conclusions:

1. The observed depletion was produced by a combination of the permanent loss of relativistic electrons through the magnetopause boundary at L>5 and the adiabatic effect at L<5. As much as 55% of the prestorm electron population was lost from the belt through the magnetopause in less than 6 h after the storm sudden commencement. No particles remained in the outer belt above L=5.3. The adiabatic effect was attributed to development of the storm time ring current. Simulation without a ring current exhibited an inverse effect: adiabatic heating of particles at L<5 produced by strong magnetopause compressions at increases in the solar wind dynamic pressure. Good agreement of the simulation results and MagEIS measurements suggests that atmospheric precipitation (not observed on the model) did not substantially contribute to the decrease of radiation belt intensities during storm main phase.

2. Magnetopause loss during storm main phase is controlled by only a couple of global processes. At storm sudden commencement, the solar wind dynamic pressure, P _dyn, increased from about 1 nPa to over 20 nPa. Large variations in P _dyn continued over approximately 3 h into the main phase. Magnetopause compressions lead to earthward expansion of the drift orbit bifurcation region. Consequently, electrons previously on a stably trapped orbits in the bulk of the radiation belt become unstable, bifurcations coupled with rapid radial transport lead to their loss through the magnetopause boundary. Another key factor in the magnetopause loss is the buildup of the storm time ring current. Its diamagnetic effect leads to strong stretching of the magnetic field on the nightside, pushing electron drift orbits outward and increasing the loss. Stretched magnetic configurations also inhibit inward transport of radiation belt electrons. Consequently, radial transport during magnetopause compressions is predominantly outward, leading to the magnetopause loss and depletion of radiation belt intensities.

3. Magnetopause loss involves strong radial transport of radiation belt electrons across their drift shells. It was found that average transport rates exceeded the earlier calculations of rates of radial diffusion during highly disturbed geomagnetic conditions (K p=6). Our model includes two sources of radial transport: drift orbit bifurcations and effect of large‐scale inductive electric fields induced by global variations of the magnetic field. It was found that drift orbit bifurcations accounted for approximately 60% of the transport, while the remaining 40% were attributed to the inductive electric fields.

It is important to note that global evolution of the magnetic and electric fields in the TS07D model which determines storm time dynamics of the outer radiation belt is mainly controlled by two parameters: the solar wind dynamic pressure P _dyn and the SYM‐H index. It can therefore be expected that the conclusions of this paper, based on the simulation of one storm on 17 March 2013, will remain relevant to other CME‐driven storms with similar time history of P _dyn and SYM‐H. We can expect that the main phases of all similar storms would produce strong depletions of radiation belt intensities attributed to permanent electron loss from a large portion of the outer L shells, dominated by electron escape through the magnetopause boundary, and the adiabatic effect at the lower L shells.

The fact that the main‐phase depletion of electron intensities at L>5 are irreversible has an important implication: no correlation should be expected between the prestorm and after‐storm intensities in this portion of the outer radiation belt. Consequently, the state of the outer belt after the storm recovery is largely determined by the injections of “seed” electrons during storm main phase and the balance among their acceleration and loss mechanisms in the recovery phase.

Supporting information

Figures S1 and S2

Movie S1

Movie S2

Ukhorskiy, A. Y. , Sitnov M. I., Millan R. M., Kress B. T., Fennell J. F., Claudepierre S. G., and Barnes R. J. (2015), Global storm time depletion of the outer electron belt. J. Geophys. Res. Space Physics, 120, 2543–2556, doi: 10.1002/2014JA020645.