Folded isometric deformations and banana-shaped seedpod

Abstract

Thin vegetal shells have recently been a significant source of inspiration for the design of smart materials and soft actuators. Herein is presented a novel analytical family of isometric deformations with a family of θ-folds crossing a family of parallel z-folds; it contains the isometric deformations of a banana-shaped surface inspired by a seedpod, which converts a vertical closing into either an horizontal closing or an opening depending on the location of the fold. Similarly to the seedpod, optimum shapes for opening ease are the most elongated ones.

1. Introduction

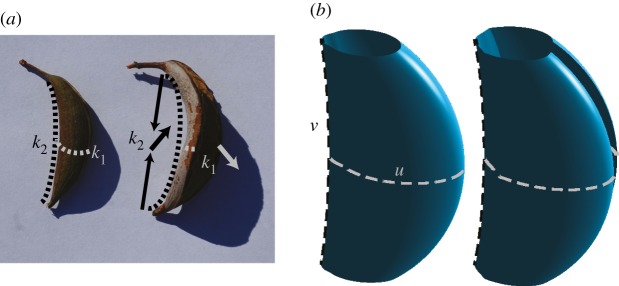
Thin vegetal shells and rods have recently been a significant source of inspiration for the design of smart materials and soft actuators: pinecone for a bending actuator [1], orchid seedpod [2] and the seed of Erodium for a twisting actuator [3]. Recent progress in chemistry and in the synthesis of fibrous material has reproduced this behaviour in biomimetic devices [4]. Theoretical progress involving differential geometry has procured a deeper insight into the design principles of these structures [3,5,6]. In parallel, the description of folds on plates has significantly been improved in the last 20 years: an energy for straight folds has been rigorously derived and validated [7,8] and some examples of curved folds have been treated [9]; current focus is rather on more complicated Miura-Ori structures [10–15]. Folds on shells have comparatively received much less attention, two topics having been well-studied: the rigidity induced by folds on shells [16] and the ridge bounding a dimple on a sphere for which a rigorous energy has been derived [17,18]. Once again classical differential geometry could be of great use for the understanding of folded shells. Herein is described another kind of folded smart shell inspired by the banana-shaped seedpod of Accacia caven from southern Chile. While dessicating, the longitudinal curvature at the saddle point of the banana-shaped seedpod increases while its meridional curvature decreases which triggers the opening of the shell and enables seed-dispersal (figure 1a,b). It is a classical result that the most energetically economical modes of deformation for thin shells are the isometric ones, when they are possible [19]. The local scenario is compatible with isometry as the product of the principal curvatures (Gaussian curvature) at the saddle point could be kept constant if both curvatures vary inversely. Proving this local scenario can be extended for the whole surface is in general a complex problem of PDE [20]. Another possible approach is to construct an analytical solution.

Figure 1.

(a) (Left) A sealed and turgid seedpod of Acaccia caven. (Right) An open and desiccated seedpod. k₁, k₂ stand for the meridional and the longitudinal curvatures at the saddle point. During desiccation the shortening of some external fibres at the back could increase k₂ and by consequence as the product k₁ k₂ is conserved for an isometry k₁ should decrease; it would thus actuate the opening of the seedpod. (b) A folded Goursat surface behaving similarly to the seedpod. (R₁=0.58, α₁=α₂=0.7752, b=0.5, c=10, d=30, ϵ=sign(u_jun,2−u), v₀=0.94). (Left) Rest state h=0. (Right) Deformed state h=0.05. u (grey dashed line) and v (black dashed line) are the two coordinates lines of the system presented in §3a crossing at the saddle point. (Online version in colour.)

While looking for such a solution, we ended up with a new family of W^1,2 isometric deformations generalizing the classical Goursat family [21,22] (i.e. isometric deformations conserving both z-contour lines and θ-contour lines in conjugate coordinates) by naturally adding folds: the simple yet original idea of this article is that any of these θ-planes or z-planes can be used as a permanent mirror-symmetry plane, thus creating a wide family of isometric deformations with non-moving θ-folds and z-folds. Our family of surfaces includes banana-shaped surfaces which behave similarly to the seedpod around the saddle point (an increase in longitudinal curvature induces meridional opening) while further away the fold antagonistically tends to close the shell. Depending on the fold location, either the opening component or the closing component will dominate. Two examples are provided in this article: a $C^{\mathrm{\infty }}$ family of shells for which an increase of the longitudinal curvature at the saddle point does not trigger the opening but triggers the closing of the aperture instead, and a biomimetic family of folded shells for which an increase of the longitudinal curvature at the saddle point does indeed trigger the opening. Shape optimization in the latter family, easily carried out thanks to the analytic formulation, shed a new light on the elongated seedpod design which minimizes the cost both in energy and in longitudinal deformation for the opening.

2. Folded Goursat surfaces and pure bending energy

(a). Geometry of Goursat surfaces

In 1891, Goursat discovered the widest family of surfaces which can be isometrically deformed while preserving two orthogonal systems of parallel planes (§4 of [21], rewritten more clearly in [22]); 10 years later, Raffy [23] even proved that this family could not be enlarged requiring only one system of parallel planes to be preserved. At the time, the family was coined: ‘Surfaces deforming such as contour lines remain contour lines’ [22]. Let $u_{min}<u_{max}$, $v_{min}<v_{max}$, $I=[u_{min},u_{max}]$, $J=[v_{min},v_{max}]$, h>0, U₁, U₂, U₃ three real functions on I and V ₁, V ₂ two real functions on J. The Goursat family can be written as

$$\begin{array}{rl}\mathrm{\forall }\hspace{0.17em}h& \ge 0,\hspace{0.17em}\mathrm{\forall }\hspace{0.17em}u\in I,\hspace{0.17em}\mathrm{\forall }\hspace{0.17em}v\in (J\cap {(V_2^{\mathrm{\prime }2}-h{V}_1^{\mathrm{\prime }2})}^{-1}(]0,+\mathrm{\infty }[))\\ \mathrm{and}S(u,v,h)& =V_1(v)f(u,h)e_r+{\int }_{t=0}^{t=u}{U}_3(t)\mathrm{\Gamma }(t,h)\hspace{0.17em}\mathrm{d}t+({\int }_0^v\sqrt{V_2^{\mathrm{\prime }2}-h{V}_1^{\mathrm{\prime }2}}\hspace{0.17em}\mathrm{d}v)e_z\end{array}\},$$ 2.1

where f, θ, e_r, e_θ, e_z and Γ read:¹

$$\begin{array}{rl}\mathrm{\forall }\hspace{0.17em}h\ge 0,\hspace{0.17em}\mathrm{\forall }\hspace{0.17em}u\in I,f(u,h)& =\sqrt{U_1{(u)}^2+U_2{(u)}^2+h}\\ \theta (u,h)& ={\int }_0^u\frac{\sqrt{{(U_1{U}_2^{\prime }-U_2{U}_1^{\prime })}^2+h(U_1^{\mathrm{\prime }2}+U_2^{\mathrm{\prime }2})}}{f^2}\mathrm{d}u\\ e_r(u,h)& =(\cos (\theta (u,h)),\sin (\theta (u,h)),0)\\ e_{\theta }(u,h)& =(-\sin (\theta (u,h)),\cos (\theta (u,h)),0)\\ e_z& =(0,0,1)\\ \mathrm{\Gamma }(u,h)& =\frac{\mathrm{\partial }(\hspace{0.17em}f{e}_r)}{\mathrm{\partial }u}(u,h)=f_u(u,h)e_r(u,h)+{\theta }_u(u,h)f(u,h)e_{\theta }(u,h),\end{array}$$ 2.2

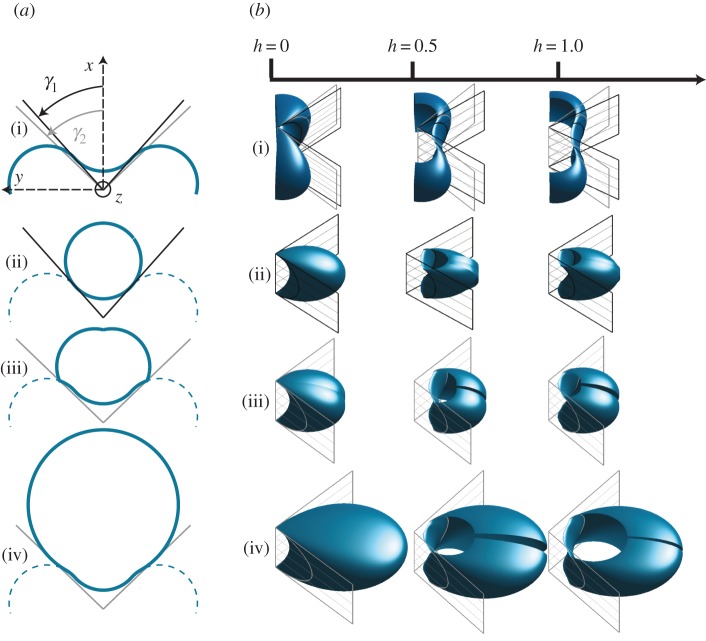
where u, v are the coordinates (figure 1b) and h is the parameter of deformation. An example of Goursat surface is represented in figure 2b(i). The set where v can be chosen is smaller than J and depends on h because if h is superior to $h_{max}=V_2^{\prime }{(v)}^2/V_1^{\prime }{(v)}^2$, V ′₂(v)²−hV ′₁(v)² is negative and thus the surface becomes partly imaginary.

Figure 2.

(a) Each panel (i–iv) represents the z=0-trace, or intersection between the horizontal plane z=0 and a surface of the family at rest state (h=0). Some of the parameters are shared by all the surfaces: R₁=1, α₁=0.7752 and b=1. In each case, we choose $u_{max}=u_{\mathrm{cl},0}$ to close the contour. The trace of the Goursat surface (ϵ=1) is represented by a full-blue line in (i) and by a dashed-blue line in (iii–iv). The black (resp. grey)straight line forming an angle γ₁ (resp. γ₂) with the x-axis correspond to the trace of the black (resp. grey) mirror-plane in the plane z=0: (i) α₁=α₂ and ϵ=1, it is a Goursat surface without fold; (ii) α₁=α₂, γ₁=θ^ϵ(u_fo,1,0)=θ^ϵ(u_jun,1,0), there is no fold as the mirror-plane is tangent to the surface; (iii) α₁=α₂, γ₂=θ^ϵ(u_fo,1,0)> θ^ϵ(u_jun,1,0), there is two folds (located at the intersection between the grey straight lines and the blue contour) as the mirror-plane is not tangent to the surface; (iv) α₁>α₂, γ₂=θ^ϵ(u_fo,1,0)=θ^ϵ(u_jun,2,0), there is no fold as the mirror-plane is tangent to the surface. (b) Family of isometric deformations corresponding to the traces in (a) with c=10 and d=10. The deformation increases from left to right (h=0, 0.5, 1). The black (resp. grey) plane corresponds to the mirror-plane containing the z-axis and making an angle γ₁ (resp. γ₂) with the x-axis. The curves in black (resp. grey) are the intersections of the banana-shaped surface with the mirror-planes. (i) The surface opens with increasing h. (ii) The presence of the fold counteracts the opening at the saddle point. The surface closes on itself while increasing its longitudinal deformation. (iii) As the fold is further away along the surface, the opening dominates the closing effect of the fold. (iv) As the fold is further away along the surface, the opening dominates the closing effect of the fold. (Online version in colour.)

For h>0, for u∈I and for $v\in (\hspace{0.17em}J\cap {(V_2^{\mathrm{\prime }2}-h{V}_1^{\mathrm{\prime }2})}^{-1}(]0,+\mathrm{\infty }[))$, the first fundamental form reads

$$\begin{array}{rl}E& =S_u^2={(V_1+U_3)}^2(U_1^{\mathrm{\prime }2}+U_2^{\mathrm{\prime }2}),\\ F& =S_u\cdot S_v=(V_1+U_3)V_1^{\prime }(U_1{U}_1^{\prime }+U_2{U}_2^{\prime })\\ \mathrm{and}G& =S_v^2=V_1^{\mathrm{\prime }\mathrm{\prime }2}(U_1^2+U_2^2)+V_2^{\mathrm{\prime }2}\end{array}\}$$ 2.3

It is easy to check that the first fundamental form does not depend on the parameter h, which implies that the deformation is an isometry (2.3).

The second fundamental form reads

$$\begin{array}{rl}L& =\frac{\det (S_{uu},S_u,S_v)}{\sqrt{EG-F^2}}=\frac{{(V_1+U3)}^2\sqrt{V_2^{\mathrm{\prime }2}-h{V}_1^{\mathrm{\prime }2}}\delta }{\sqrt{EG-F^2}},\\ M& =\frac{\det (S_{uv},S_u,S_v)}{\sqrt{EG-F^2}}=0\\ \mathrm{and}N& =\frac{\det (S_{vv},S_u,S_v)}{\sqrt{EG-F^2}}=f^2{\theta }_u\frac{(V_1+U_3)V_2^{\prime }(V_1^{″}{V}_2^{\prime }-V_1^{\prime }{V}_2^{″})}{\sqrt{V_2^{\mathrm{\prime }2}-h{V}_1^{\mathrm{\prime }2}}(\sqrt{EG-F^2})}\end{array}\},$$ 2.4

where $\delta =(f_{uu}-f{\theta }_u^2)f{\theta }_u-f_u(2f_u{\theta }_u+f{\theta }_{uu})$.

The third coefficient N of the second fundamental form diverges, where $V_2^{\mathrm{\prime }2}-h{V}_1^{\mathrm{\prime }2}=0$ as well as the pure bending energy given by

$$E_b={\int }_u{\int }_{v}B({({\kappa }_1-{\kappa }_{1,0})}^2+2\nu ({\kappa }_1-{\kappa }_{1,0})({\kappa }_2-{\kappa }_{2,0})+{({\kappa }_2-{\kappa }_{2,0})}^2)\sqrt{EG-F^2}\hspace{0.17em}\mathrm{d}u\hspace{0.17em}\mathrm{d}v,$$ 2.5

where κ₁, κ₂ stand for the principal curvatures² at the deformed state (h>0) and κ_1,0, κ_2,0 stand for the curvatures at the rest state, h=0.

The expression of the square of the element of surface can be simplified as

$$EG-F^2={(V_1+U_3)}^2(V_1^{\mathrm{\prime }2}{(U_1^{\prime }{U}_2-U_2^{\prime }{U}_1)}^2+V_2^{\mathrm{\prime }2}(U_1^{\mathrm{\prime }2}+U_2^{\mathrm{\prime }2})).$$ 2.7

(b). Folded Goursat surface, isometric W^1,2 deformations

The Goursat family of isometric deformations conserves two systems of planes mutually parallel: one defined by a constant u (θ-planes) and the other by a constant v (z-plane); the simple yet original idea of this article is that any of these planes can be used as a plane for a mirror-symmetry, thus providing the widest-known family of analytical isometric deformations with folds. An admissible fold for an isometric deformation is a non-moving line joining two surfaces both deforming with an isometry.

Mathematically, the presence of a vertical fold or θ-fold (mirror-plane defined by u=cst) can be encoded by incorporating a piece-wise constant function ϵ:I→{−1,1} into the formula for θ.

$$\mathrm{\forall }\hspace{0.17em}h\ge 0,\hspace{0.17em}\mathrm{\forall }\hspace{0.17em}u\in I,{\theta }^{ϵ}(u,h)={\int }_0^uϵ\frac{\sqrt{{(U_1{U}_2^{\prime }-U_2{U}_1^{\prime })}^2+h(U_1^{\mathrm{\prime }2}+U_2^{\mathrm{\prime }2})}}{f^2}\mathrm{d}u.$$ 2.8

Let N be the number of points (u_fo,i)_{i∈{1,…,N}} ³ where τ=ϵsign(U₁U′₂−U₂U′₁) switches its sign on the interval I. θϵ_u can be rewritten

$${\theta }_u^{ϵ}=ϵ\frac{\sqrt{{(U_1{U}_2^{\prime }-U_2{U}_1^{\prime })}^2}}{U_1^2+U_2^2}=\tau \frac{U_1{U}_2^{\prime }-U_2{U}_1^{\prime }}{U_1^2+U_2^2}=\tau {\left(\arctan \left(\frac{U_2}{U_1}\right)\right)}^{\prime }.$$ 2.9

The integration gives, for u∈[u_fo,i,u_fo,i+1]

$${\theta }^{ϵ}(u,0)=\sum _{j=1}^i\tau \left(\frac{u_{fo,j}+u_{fo,j-1}}{2}\right){\left[\arctan \left(\frac{U_2}{U_1}\right)\right]}_{u_{fo,j-1}}^{u_{fo,j}}+\tau (u){\left[\arctan \left(\frac{U_2}{U_1}\right)\right]}_{u_{fo,i}}^u.$$ 2.10

For a general ϵ, the jump in slope of θ^ϵ at each u_fo,i will correspond to a fold on the shell for any h≥0. For a given v∈J, Ω_i(v,h), the dihedral angle of the fold situated along the line u=u_fo,i is fully prescribed by the mirror-symmetry. The dot product between ${\mathcal{N}}^{-}$, the normal to the surface calculated in $(u_{fo,i}^{-},v)$ on one side of the fold, and ${\mathcal{N}}^{+}$, the normal in $(u_{fo,i}^{+},v)$ on the other side, yields

$$\cos ({\mathrm{\Omega }}_i(v,h))={(V_1+U_3)}^2\frac{(f^2{\theta }_u^{ϵ,+}{\theta }_u^{ϵ,-}(V_2^{\mathrm{\prime }2}-h{V}_1^{\mathrm{\prime }2})+f_u^2(V_2^{\mathrm{\prime }2}-h{V}_1^{\mathrm{\prime }2})+f^4{\theta }_u^{ϵ,+}{\theta }_u^{ϵ,-}{V}_1^{\mathrm{\prime }2})}{EG-F^2}.$$ 2.11

There is not a fold at the rest state (h=0) if and only if $ϵ=\mathrm{sign}(U_1{U}_2^{\mathrm{\prime }}-U_2{U}_1^{\mathrm{\prime }})$. In this latter case, the expression for θ^ϵ is simpler

$$\begin{array}{rl}{\theta }^{ϵ}(\cdot ,0)& =\arctan \left(\frac{U_2}{U_1}\right)\\ \mathrm{and}(\cos ({\theta }^{ϵ}(\cdot ,0)),\sin ({\theta }^{ϵ}(\cdot ,0)))& =\frac{(U_1,U_2)}{\sqrt{U_1^2+U_2^2}}\end{array}\}$$ 2.12

as well as for the expression of the rest state surface (h=0)

$$\mathrm{\forall }\hspace{0.17em}u\in I,\hspace{0.17em}\mathrm{\forall }\hspace{0.17em}v\in J,S(u,v,0)=V_1(v)(U_1(u),U_2(u),0)+{\int }_0^u{U}_3(U_1^{\prime },U_2^{\prime },0)+(0,0,V_2(v)).$$ 2.13

The undeformed surface S(⋅,⋅,0) is a $C^{\mathrm{\infty }}$ surface.

Horizontal folds or z-fold are introduced by incorporating a piece-wise constant function η:J→{−1,1} into the formula for the z-coordinate of the surface.

$$\begin{array}{rl}\mathrm{\forall }\hspace{0.17em}h& \ge 0,\hspace{0.17em}\mathrm{\forall }\hspace{0.17em}v\in (J\cap {(V_2^{\mathrm{\prime }2}-h{V}_1^{\mathrm{\prime }2})}^{-1}(]0,+\mathrm{\infty }[)),\\ \mathrm{and}{z}^{\eta }(v,h)& ={\int }_0^v\eta \sqrt{V_2^{\mathrm{\prime }2}-h{V}_1^{\mathrm{\prime }2}}\hspace{0.17em}\mathrm{d}v\end{array}\}$$ 2.14

Let M be the number of points (v_fo,i)_{i∈{1,…, M}} where η switches its sign on the interval J. For a given u∈I, Λ_i(u,h), the dihedral angle of the ith z-fold situated along the line v=v_fo,i is fully prescribed by the mirror-symmetry. The dot product between ${\mathcal{N}}^{-}$ the normal to the surface calculated in $(u,v_{fo,i}^{-})$ on one side of the fold and ${\mathcal{N}}^{+}$ the normal in $(u,v_{fo,i}^{+})$ on the other side gives $\cos ({\mathrm{\Lambda }}_i(u,h))$

$$\cos ({\mathrm{\Lambda }}_i(u,h))={(V_1+U_3)}^2\frac{(-f^2{({\theta }_u^{ϵ})}^2(V_2^{\mathrm{\prime }2}-h{V}_1^{\mathrm{\prime }2})-f_u^2(V_2^{\mathrm{\prime }2}-h{V}_1^{\mathrm{\prime }2})+f^4{({\theta }_u^{ϵ})}^2{V}_1^{\mathrm{\prime }2})}{EG-F^2}.$$ 2.15

θ-folds and z-folds are two families of folds laying in two orthogonal families of planes; they do not affect the bending energy as the mirror-symmetries simultaneously change the sign of both the fundamental forms and the principal curvatures

$$\begin{array}{rl}(L^{ϵ},M^{ϵ},N^{ϵ})& =ϵ\eta (L,0,N)\\ \mathrm{and}(k_1^{ϵ},k_2^{ϵ})& =ϵ\eta (k_1,k_2)\end{array}\}$$ 2.16

For straight and curved folds on developable surfaces, the dihedral angles, (Ω_i) and (Λ_i), serve to express the energy associated with the fold [9,24]; no such general expression of the energy is known for shells.

3. Isometric deformations of a banana-shaped family of surfaces

(a). A family of banana-shaped surfaces

Let us choose the following parameters: R₁>0, α₁∈ [0,π/2], α₂∈ [0,α₁],α₂≠π/2, b>0, c>0, d>0. We introduce the two circles ${\mathcal{C}}_1$, ${\mathcal{C}}_{1,r}$ of identical radius R₁, centred respectively at

$$\begin{array}{rl}(x_1,\hspace{0.17em}{y}_1)& =R_1(\frac{1}{\cos ({\alpha }_1)},0)\\ \mathrm{and}(x_{1,r},\hspace{0.17em}{y}_{1,r})& =R_1(\frac{1}{\cos ({\alpha }_1)}-2\cos ({\alpha }_1),2\sin ({\alpha }_1))\end{array}\}$$ 3.1

and the circle ${\mathcal{C}}_2$ of radius $R_2=(2\sin ({\alpha }_1)/\sin ({\alpha }_2)-1)R_1$ centred at

$$(x_2,y_2)=(x_{1,r}+(R_1+R_2)\cos ({\alpha }_2),0).$$ 3.2

By construction, ${\mathcal{C}}_1$ is tangent to ${\mathcal{C}}_{1,r}$, and ${\mathcal{C}}_{1,r}$ is tangent to ${\mathcal{C}}_2$; a C¹ curve (U₁,U₂) can be constituted by joining arcs of these three circles at the two tangent intersections (figure 2a). We note: u_jun,1⁴ =R₁α₁,u_jun,2=u_jun,1+ R₁(α₁−α₂),u_cl,0⁵ =u_jun,2+R₂(π−α₂). U₁ and U₂ are piece-wise functions on [0,u_cl,0] defined by

$$\begin{array}{rl}& \mathrm{\forall }\hspace{0.17em}u\in [0,u_{\mathrm{jun},1}],\\ & (U_1(u),U_2(u))=(x_1+R_1\cos (\pi -\frac{u}{R_1}),\hspace{0.17em}b{R}_1\sin (\pi -\frac{u}{R_1})),\\ & \mathrm{\forall }\hspace{0.17em}u\in [u_{\mathrm{jun},1},u_{\mathrm{jun},2}],\\ & (U_1(u),U_2(u))=(x_{1,r}+R_1\cos \left(\frac{u-u_{\mathrm{jun},1}}{R_1}\right),\hspace{0.17em}b(y_{1,r}+R_1\sin \left(\frac{u-u_{\mathrm{jun},1}}{R_1}\right)))\\ \mathrm{and}& \mathrm{\forall }\hspace{0.17em}u\in [u_{\mathrm{jun},2},u_{\mathrm{cl},0}],\\ & (U_1(u),U_2(u))=(x_2+R_2\cos (\pi -{\alpha }_2-\frac{u-u_{\mathrm{jun},2}}{R_2}),\hspace{0.17em}b{R}_2\sin (\pi -{\alpha }_2-\frac{u-u_{\mathrm{jun},2}}{R_2}))\end{array}\}$$ 3.3

b is an additional parameter tuning the ellipticity of the shape. In the case, α₁=α₂, the curve (U₁,U₂) coincides with the circle ${\mathcal{C}}_1$.

The additional function U₃ is chosen null on [0,u_cl,0], η=1 and V ₁, V ₂ are defined by

$$\mathrm{\forall }\hspace{0.17em}v\in [-\frac{\pi }{2},\frac{\pi }{2}],(V_1(v),V_2(v))=(c\cos (v),d\sin (v)).$$ 3.4

If either ϵ=sign(u_jun,1−u) or ϵ=sign(u_jun,2−u), the folded Goursat surface has no apparent fold at the undeformed state; if additionally α₁=α₂, the rest state surface is $C^{\mathrm{\infty }}$. The curve (U₁,U₂) is complemented by its y=0 mirror-symmetry (U₁,−U₂).

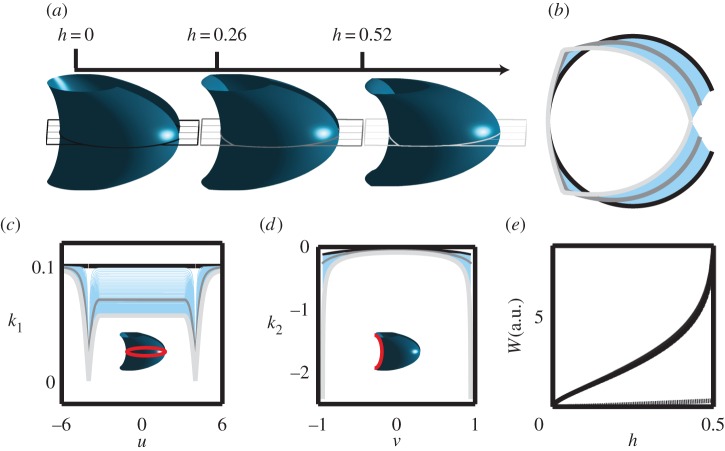
The behaviour of the surfaces under bending depends on the presence of the folds and their location: the Goursat isometric family of deformations (ϵ=1) opens while increasing the longitudinal curvature at the saddle point (figure 2b (i)); the presence of the fold tends to counteract this effect and to close the shell (figure 2b (ii)). However, provided the fold is far enough from the junction point (i.e. u_fo,1 sufficiently bigger than u_jun,1), the opening dominates the closure for small enough deformations and biomimetic thin shells can be devised (figure 2b (iii,iv)). The upper and lower extremities of the surface progressively become imaginary when the parameter h increases and thus progressively disappear on figure 2b.

(b). Design of a $C^{\mathrm{\infty }}$ thin shell transferring a vertical closing movement into an horizontal closing movement

The family of isometries derived herein is an interesting tool to design self-sealing thin shells. For instance, given v₀∈[0,π/2] the size of the aperture u_c which seals the shell at a prescribed vertical deformation

$$\lambda =\frac{z_c}{z_0}$$

can be worked out by simply looking for the solutions (u_cl,hλ,h_λ) of (3.5) (figure 3a,b).

$$\begin{array}{rl}0& =\theta (u_{\mathrm{cl},h_{\lambda }},h_{\lambda })\\ \mathrm{and}\lambda & =\frac{{\int }_0^{v_0}\sqrt{d^2\cos {(v)}^2-h_{\lambda }{c}^2\sin {(v)}^2}\hspace{0.17em}\mathrm{d}v}{c\sin (v_0)}\end{array}\}$$ 3.5

The quantitative behaviour of the curvatures at the saddle point can also be observed: the meridional curvature decreases in absolute value (figure 3c) while the longitudinal curvature increases. When reaching

$$h_{max}=\frac{d^2}{c^2\tan (v_0^2)},$$

both the longitudinal curvature k₂ (figure 3d) and the bending energy (2.5) diverge (figure 3e).

Figure 3.

(a) Isometric deformations of a banana-shaped surface (R₁=1, α₁=α₂= 0.7752, b=1, c=10, d=10, v₀=0.94, ϵ=sign(u_jun,1−u), h∈{0, 0.26, h_max=0.52}). The width of the aperture has been calculated to close the shell at the maximal deformation corresponding to the initial surface. (b) Horizontal section of the surface: the family of isometries behaves similarly at the saddle point as the seedpod but not globally. Owing to the fold, the decrease in meridional curvature triggers a closing rather than an opening of the shell. The black, dark-grey and light-grey contours correspond to the intersecting planes in the (a) panel. (c) Meridional curvature k₁ in the horizontal plane of symmetry: the meridional curvature decreases in absolute value with the deformations. (d) Longitudinal curvature k₂ in the vertical plane of symmetry: the longitudinal curvature increases in absolute value with the deformations. It diverges at the lower and upper boundary when reaching the maximal deformation. (e) Pure bending energy. The bending energy diverges at $h_{max}$. (Online version in colour.)

(c). Design optimization of the biomimetic thin shell family transferring a vertical closing movement into an horizontal opening movement

Constraint optimization on the parameters can be carried out, the cost function being either the energy or the vertical deformation, and the utility function being the opening area ΔS defined by

$$\mathrm{\Delta }S(R_1,{\alpha }_1,{\alpha }_2,b,c,d,v_0,h)={\int }_{v=-v_0}^{v=+v_0}y(u_{\mathrm{cl},0},v,h)z^{\prime }(v)\hspace{0.17em}\mathrm{d}v,$$ 3.6

with R₁>0, α₁∈ [0,π/2], α₂∈ [0,α₁],α₂≠π/2, b>0, c>0, d>0, v₀>0, h>0.⁶

As the rest state surface is closed, the inner volume, Vol, is well-defined. Changing R₁, b, c, d corresponds to applying an affine transformation on the rest state surface which modifies Vol according to

$$\mathit{\text{Vol}}(R_1,{\alpha }_1,{\alpha }_2,b,c,d,v_0)=R_1^{2}b{c}^{2}d\hspace{0.17em}\mathit{\text{Vol}}(1,{\alpha }_1,{\alpha }_2,1,1,1,v_0).$$ 3.7

For this reason, the constant Vol is a convenient hard constraint in the minimization: modifying a parameter can easily be compensated by inversely changing another one. For the constant Vol minimization, it is convenient to normalize the opening: $\overline{\mathrm{\Delta }S}=S/{\mathit{\text{Vol}}}^{2/3}$.

Another possible hard constraint for the minimization is λ, the vertical deformation, defined by

$$\lambda (R_1,{\alpha }_1,{\alpha }_2,b,c,d,v_0,h)=\frac{z(v_0,h)}{z(v_0,0)}.$$ 3.8

For $h_{max}=d^2/(c^2\tan (v_0^2))\hspace{0.17em}{\lambda }_{max}$, the maximal deformation after which the upper part of the surface becomes imaginary, simplifies into

$$\begin{array}{rl}\lambda (R_1,{\alpha }_1,{\alpha }_2,b,c,d,v_0,h_{max})& =\frac{{\int }_{v=0}^{v=v_0}\sqrt{d^2\cos {(v)}^2-(d^2/(c^2\tan (v_0^2)))c^2\sin {(v)}^2}\hspace{0.17em}\mathrm{d}v}{d\sin (v_0)}\\ \mathrm{and}\lambda (R_1,{\alpha }_1,{\alpha }_2,b,c,d,v_0,h_{max})& =\frac{{\int }_{v=0}^{v=v_0}\sqrt{\cos {(v)}^2-(\sin {(v)}^2/\tan (v_0^2))}\hspace{0.17em}\mathrm{d}v}{\sin (v_0)}\end{array}\}$$ 3.9

${\lambda }_{max}$ is thus independent of both d and c but depends only of v₀.

The influence of some of the parameters have been studied around an initial shape determined by the parameter (R_1,0, α_1,0, α_2,0, b₀, c₀, d₀, v₀):

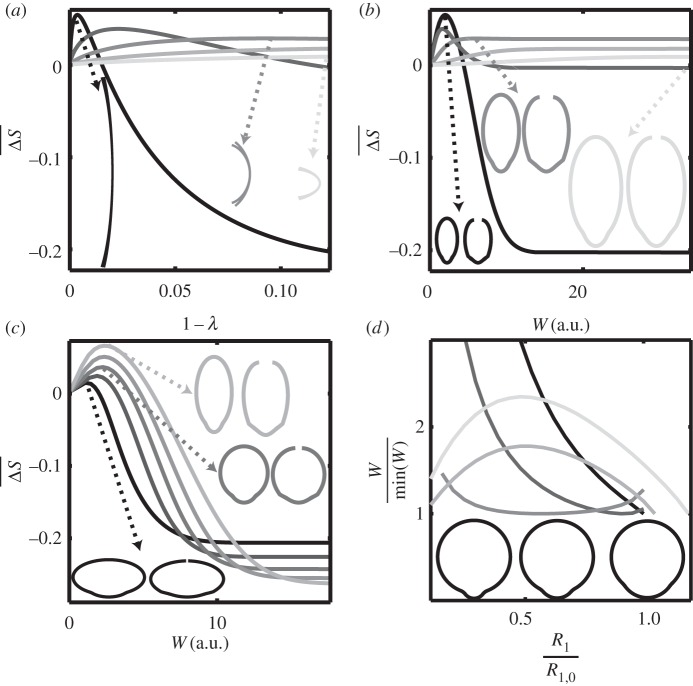
• — The influence of the y=0 trace (or x−z contour) on opening efficiency has been assessed. The parameter d was made to vary while maintaining Vol constant by adjusting $R_1=R_{1,0}\sqrt{d_0/d}$. If increasing d does not affect ${\lambda }_{max}$, it increases $h_{max}$ and thus the maximal x−y deformation. Provided d is sufficiently large, the movement first consists in an opening dominated by the saddle point ($\overline{\mathrm{\Delta }S}>0$, figure 4a), and then in a closure dominated by the fold ($\overline{\mathrm{\Delta }S}<0$, figure 4a); for smaller d, the shell opens, but the top of the shell becomes imaginary before reaching the closing phase. Increasing d increases the opening amplitude (maximum of $\overline{\mathrm{\Delta }S}$ on figure 4a) and decreases the vertical deformation necessary to trigger this maximum; increasing d also decreases the energetic cost of the maximal opening (figure 4b). The elongated shapes are the most efficient to trigger an opening according to both criteria of vertical deformation efficiency and energetic cost.

• — The influence of the z=0 trace (or x−y contour) on opening efficiency has been assessed: the ellipticity b was modified while maintaining Vol constant by adjusting $R_1=R_{1,0}\sqrt{b_0/b}$. Decreasing b increases the amplitude of the maximal opening and decreases the energetic cost of it (figure 4c). The most efficient shapes are obtained for ellipsis elongated in the x direction (b small). A second minimization was carried out with two hard constraints: constant opening and constant initial volume. The influence of the even repartition of the curvature along the x−y closed profile on the energetic cost was investigated. Practically, R₁ was modified while both Vol and ΔS were maintained constant by only adjusting α₁, α₂. For each R₁, α₁ and α₂ were obtained by solving the two following equations with the Matlab function ‘fsolve’

  $$\begin{array}{rl}\mathit{\text{Vol}}(1,{\alpha }_1,{\alpha }_2,1,1,1,v_0)& ={\left(\frac{R_{1,0}}{R_1}\right)}^2\mathit{\text{Vol}}(1,{\alpha }_{1,0},{\alpha }_{2,0},1,1,d,v_0)\\ \mathrm{and}\mathrm{\Delta }S(R_1,{\alpha }_1,{\alpha }_2,b,c,d,v_0,h)& =\mathrm{\Delta }S(R_{1,0},{\alpha }_{1,0},{\alpha }_{2,0},b,c,d,v_0,h).\end{array}\}$$ 3.10

Figure 4.

(a,b) Influence of x−z shape, the rest state volume Vol being identical. R₁∈{0.71,0.96,1.23,1.48,1.73}, α₁=0.54, α₂=0.37, b=0.5, c=10, $d=10/R_1^2$ (the darkness of the grey of the line in the plot increases with d). $v_0=0.94,0<h<d^2/(c^2\tan (v_0^2))$. (a) Normalized opening $\overline{\mathrm{\Delta }S}$ versus vertical deformation 1−λ. The arrows point to the corresponding rest state contour (x(0,.,0),z(0,.,0)) and deformed contour (x(0,.,h),z(0,.,h)) at maximal opening. (b) Normalized opening $\overline{\mathrm{\Delta }S}$ versus energetical cost W. The arrows point to the corresponding rest state contour (x(0,.,0),y(0,.,0)) and deformed contour (x(0,.,h),y(0,.,h)) at maximal opening (the scale is 0.3 smaller than that for the x−z curve on (a)). (c,d) Influence of x−y shape: (c) at constant Vol, normalized opening $\overline{\mathrm{\Delta }S}$ versus energetic cost W. R₁∈{0.71,0.96,1.23,1.48,1.73}, α₁=0.54, α₂=0.37, $b=1/R_1^2$ (the darkness of the grey of the line in the plot increases with b), $c=10,\hspace{0.17em}d=50,v_0=0.94,0<h<d^2/(c^2\tan (v_0^2))$. The arrows point to the corresponding rest state contour (x(0,.,0),y(0,.,0)) and deformed contour (x(0,.,h),y(0,.,h)). (d) Energetic cost normalized by its minimum versus R₁ for constant $\overline{\mathrm{\Delta }S}$ and constant rest state volume Vol. R_1,0∈{0.71,0.96,1.23,1.48,1.73}, 0.1<R₁/R_1,0<1.1, α_1,0=0.54, α_2,0=0.37, b=1, c=10, $d=10/R_{1,0}^2$, v₀=0.94, $0<h<d^2/(c^2\tan (v_0^2))$. The three contours represented at the bottom are the rest state contours (x(0,.,0),y(0,.,0)), while R₁ is varying.

The location of the minimum for the energetic cost strongly depends on the x−z shape (figure 4d): for d high enough (i.e d≫1), the optimum is located at the highest R₁ which corresponds to the most homogeneous repartition of curvature (see the z=0 trace rest state profile at the bottom of figure 4d); for d≈1, the minimum shifts to lower R₁ which means more even distribution of curvature; for smaller d there are two optima, one with the least homogeneous distribution of curvature (R₁ minimal) and one with the most homogeneous distribution of curvature (R₁ maximal).

4. Conclusion

Isometric families of deformations were traditionally one of the few ways to provide analytical examples for the deformation of thin shells. The geometers and mechanicians of the late nineteenth century and early twentieth century have intensely looked for such solutions. In 1890, Bianchi proved that surfaces in conjugate systems of coordinates admit one integrable mode of deformation [25]. Constructing a conjugate system of coordinate for a surface involves finding solutions of Moutard equations verifying additional conditions: Goursat [21] & Tzizeica [26] families are two fully integrable examples, though they were obtained by methods different to Bianchi’s method. While the subsequent research improved the integration of Moutard equations [27,28], it did not lead to any new simple family of analytical isometric deformations [29]. Some of these results were proposed by Eisenhart as exercises without the references of the authors [30]. This work is nowadays rather forgotten and not even mentioned in modern textbooks. In this context, this article provides a new one-parameter family of W^1,2 surfaces extending the classical $C^{\mathrm{\infty }}$ family of Goursat by naturally adding two families of mutually crossing curved folds. This theoretical family of surfaces is illustrated by two examples of banana-shaped surfaces: a shell transforming a vertical closure into an horizontal sealing, similar to the carnivorous plant Aldrovanda [31] which has recently inspired architects for smart shutters [32,33], and a biomimetic shell triggering an horizontal opening by a vertical closure. In order to actually trigger these modes of deformation in experiments, the fold area has to be elastically softer than the remaining part of the shell: this effect has been studied numerically by varying both the fold thickness and the fold width [32].

Even if folded Goursat surfaces only describe restricted modes of deformation, their analytical formulation could help both experimentalists to conceive set-ups estimating fold energy on shells other than spheres and cylinders, and theoreticians to calibrate and to check the accuracy of their simulations of folded shells. Analytical isometric deformations of maps similar to Miura-Ori patterns but with non-zero Gaussian curvature are also included in our family corresponding to periodic patterns of z-folds crossed by patterns of θ-folds.

Vegetal thin shells, e.g. pollen grains and seedpods, are a biomimetic source of inspiration for packaging designers. Analytical families of deformations are obtained much more rapidly than simulations; as such they constitute a valuable guide for designers enabling them to explore the potentialities of different shapes and to design precisely the apertures. As illustrated herein, parametric optimization for opening or closing shells can be easily carried out thanks to the pure bending energy; the actual energy necessary to trigger a given deformation is slightly lowered by some stretching which nevertheless corresponds to very mild geometrical distortions [5,6].

Competing interests

I have no competing interests.

Funding statement

E.C. has been funded by CNRS and by the Fondecyt postdoctoral fellowship 3120105.