Wrinkling of a stiff thin film bonded to a pre-strained, compliant substrate with finite thickness

Abstract

A stiff thin film bonded to a pre-strained, compliant substrate wrinkles into a sinusoidal form upon release of the pre-strain. Many analytical models developed for the critical pre-strain for wrinkling assume that the substrate is semi-infinite. This critical pre-strain is actually much smaller than that for a substrate with finite thickness (Ma Y et al. 2016 Adv. Funct. Mater. (doi:10.1002/adfm.201600713)). An analytical solution of the critical pre-strain for a system of a stiff film bonded to a pre-strained, finite-thickness, compliant substrate is obtained, and it agrees well with the finite-element analysis. The finite-thickness effect is significant when the substrate tensile stiffness cannot overwhelm the film tensile stiffness.

1. Introduction

A stiff film bonded to a pre-strained, compliant substrate wrinkles upon releasing the pre-strain [1,2]. Such a system has many important applications in stretchable inorganic electronics [3–8], micro/nano pattern formation [9–11], high-precision micro/nano measurement techniques [12], tuneable metamaterials [13], nanocomposites [14], stretchable transistors [15] and biomimetic materials [16]. Analytical models have been developed for wrinkling of a stiff thin film on a pre-strained compliant substrate [17–21]. The results identify the critical pre-strain for wrinkling, below which the film remains flat. However, all of these studies assume that the substrate is semi-infinite such that its tensile stiffness overwhelms that of the film. Consequently, the substrate recovers the initial length after the pre-strain is released and its bottom remains flat.¹

The critical pre-strain for wrinkling obtained for a semi-infinite substrate, however, is smaller than the numerical and experimental results for a substrate with finite thickness [22], even for substrates that are more than 1000 times thicker than the film. This is because the substrate elastic modulus E_s is often more than five orders of magnitude smaller than the film elastic modulus E_f [1,2], such that the substrate tensile stiffness E_sH cannot overwhelm the film tensile stiffness E_fh, where H and h are the substrate and film thicknesses, respectively (figure 1a). Consequently,

• (1) the substrate cannot shrink back to its initial length after release of the pre-strain; and

• (2) the film/substrate system may bend after the pre-strain is released (figure 1b).

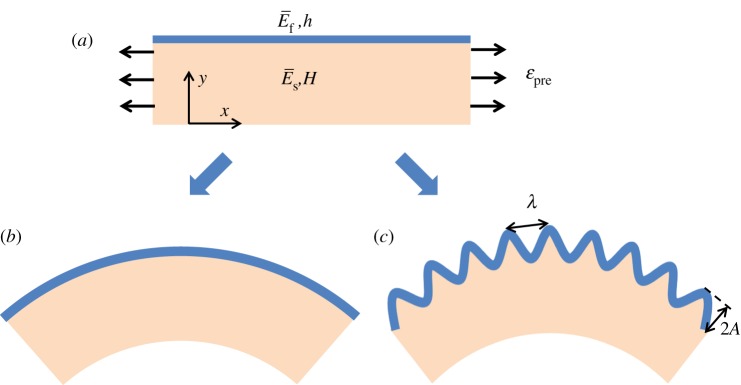
Figure 1.

Schematic illustrations. (a) A stiff thin film bonded to a pre-strained, compliant substrate with finite thickness; (b) bending of the film/substrate system upon release of the small pre-strain; and (c) wrinkling of the stiff thin film, along with bending of the film/substrate system, upon release of large pre-strain. (Online version in colour.)

The recent study by Ma et al. [22] accounted for (1), while this paper aims to establish an analytic model for both (1) and (2). The resulting critical pre-strain will be useful for many applications such as the strain-limiting design of materials [22] and tuneable optical design of the intensity for diffraction peaks [23].

2. Analytical model

A stiff thin film is bonded onto a pre-strained (ε_pre), compliant substrate (figure 1a). For small pre-strain, the stiff film does not wrinkle upon release of the pre-strain; instead, the film and substrate bend (figure 1b). Let ε denote the membrane strain in the film. The strain in the substrate is ε_s(y)=ε_pre+ε−κ(H−y), where κ is the curvature of the substrate, and the co-ordinate y is shown in figure 1a. The potential energy is

$$U_{\mathrm{bend}}=\frac{1}{2}{\overline{E}}_{\mathrm{f}}h{\epsilon }^2+\frac{1}{2}{\overline{E}}_{\mathrm{s}}{\int }_0^H{[{\epsilon }_{\mathrm{pre}}+\epsilon -\kappa (H-y)]}^2\mathrm{d}y,$$ 2.1

where ${\overline{E}}_{\mathrm{f}}=E_{\mathrm{f}}/(1-v_{\mathrm{f}}^2)$ and ${\overline{E}}_{\mathrm{s}}=E_{\mathrm{s}}/(1-v_{\mathrm{s}}^2)$ are the plane-strain moduli of the stiff thin film and compliant substrate, respectively, and v_f and v_s are the Poisson’s ratios.

Minimization of the potential energy ∂U_bend/∂ε=0 and ∂U_bend/∂κ=0 gives $\epsilon =-{\overline{E}}_{\mathrm{s}}H{\epsilon }_{\mathrm{pre}}/(4{\overline{E}}_{\mathrm{f}}h+{\overline{E}}_{\mathrm{s}}H)$ and $\kappa =-6{\overline{E}}_{\mathrm{f}}h{\epsilon }_{\mathrm{pre}}/[H(4{\overline{E}}_{\mathrm{f}}h+{\overline{E}}_{\mathrm{s}}H)]$. Equation (2.1) then becomes

$$U_{\mathrm{bend}}=\frac{{\overline{E}}_{\mathrm{f}}h{\overline{E}}_{\mathrm{s}}H{\epsilon }_{\mathrm{pre}}^2}{2(4{\overline{E}}_{\mathrm{f}}h+{\overline{E}}_{\mathrm{s}}H)}.$$ 2.2

Once the pre-strain exceeds the critical pre-strain (to be determined), the stiff film wrinkles on the top surface of the substrate (figure 1c) and the film/substrate bends. In addition to the membrane strain ε, the film is also subjected to wrinkling with amplitude A and period λ to be determined. The strain energy in the film is [24]

$$U_{\mathrm{film}}=\frac{1}{2}{\overline{E}}_{\mathrm{f}}h{\epsilon }^2-\frac{1}{4}{\overline{E}}_{\mathrm{f}}h|\epsilon |k^2{A}^2+\frac{1}{32}{\overline{E}}_{\mathrm{f}}h{k}^4{A}^4+\frac{1}{48}{\overline{E}}_{\mathrm{f}}{h}^3{k}^4{A}^2,$$ 2.3

which degenerates to the first term on the right-hand side of equation (2.1) when the amplitude A=0; here k=2π/λ. The strain energy in the substrate is

$$U_{\mathrm{substrate}}=\frac{1}{2}{\overline{E}}_{\mathrm{s}}{\int }_0^H{[{\epsilon }_{\mathrm{pre}}+\epsilon -\kappa (H-y)]}^2\mathrm{d}y+\frac{{\overline{E}}_{\mathrm{s}}}{4}k{A}^{2}g(kH),$$ 2.4

which degenerates to the last term in equation (2.1) when the amplitude A=0. The last term in the above equation is the strain energy in the substrate due to wrinkling [24], and the function g is

$$g(x)=\frac{\cosh (2x)+1+2x^2}{2\sinh (2x)-4x},$$ 2.5

for an incompressible substrate (v_s=0.5), and g approaches 1/2 for a semi-infinite substrate. The potential energy is the sum of U_film and U_substrate,

$$\begin{array}{rl}{U}_{\mathrm{bend}+\mathrm{wrinkle}}=& \frac{1}{2}{\overline{E}}_{\mathrm{f}}h{\epsilon }^2+\frac{1}{2}{\overline{E}}_{\mathrm{s}}{\int }_0^H{[{\epsilon }_{\mathrm{pre}}+\epsilon -\kappa (H-y)]}^2\mathrm{d}y\\ & +\frac{1}{4}{\overline{E}}_{\mathrm{f}}h(\hspace{0.17em}f-|\epsilon |)k^2{A}^2+\frac{1}{32}{\overline{E}}_{\mathrm{f}}h{k}^4{A}^4,\end{array}$$ 2.6

where

$$f=\frac{k^2{h}^2}{12}+\frac{{\overline{E}}_{\mathrm{s}}g(kH)}{kh{\overline{E}}_{\mathrm{f}}}.$$ 2.7

Minimization of the potential energy with respect to k and A, ∂U_bend+wrinkle/∂k=0 and ∂U_bend+wrinkle/∂A=0, gives

$$6\frac{g(kH)-g^{\prime }(kH)kH}{{(kH)}^3}=\frac{{\overline{E}}_{\mathrm{f}}{h}^3}{{\overline{E}}_{\mathrm{s}}{H}^3}$$ 2.8

and

$$k^2{A}^2=4(|\epsilon |-f),$$ 2.9

where g′(x)=dg(x)/dx. Equation (2.8) suggests that the normalized period, $\mathrm{\lambda }/[{({\overline{E}}_{\mathrm{f}}/{\overline{E}}_{\mathrm{s}})}^{1/3}h]$, or equivalently $kh/{({\overline{E}}_{\mathrm{s}}/{\overline{E}}_{\mathrm{f}})}^{1/3}$, depends only on the film/substrate bending stiffness ratio ${\overline{E}}_{\mathrm{f}}{h}^3/{\overline{E}}_{\mathrm{s}}{H}^3$, as shown in figure 2. The period becomes independent of the substrate thickness H when the bending stiffness ratio ${\overline{E}}_{\mathrm{f}}{h}^3/{\overline{E}}_{\mathrm{s}}{H}^3$ is less than 0.01, which is consistent with Huang et al. [24].

Figure 2.

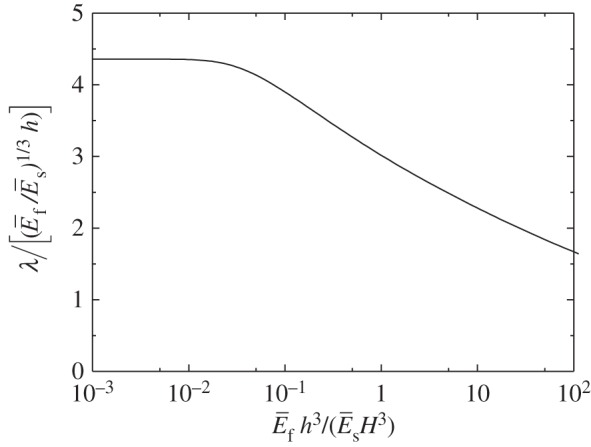
The normalized wrinkle period $\mathrm{\lambda }/[{({\overline{E}}_{\mathrm{f}}/{\overline{E}}_{\mathrm{s}})}^{1/3}h]$ versus the film-to-substrate bending stiffness ratio $[{\overline{E}}_{\mathrm{f}}{h}^3/({\overline{E}}_{\mathrm{s}}{H}^3)]$.

Minimization of the potential energy with respect to ε and κ, ∂U_bend+wrinkle/∂ε=0 and ∂U_bend+wrinkle/∂κ=0, gives $\epsilon =4{\overline{E}}_{\mathrm{f}}hf/({\overline{E}}_{\mathrm{s}}H)-{\epsilon }_{\mathrm{pre}}$, and $\kappa =6{\overline{E}}_{\mathrm{f}}hf/({\overline{E}}_{\mathrm{s}}{H}^2)$, where f is obtained from equation (2.7). The potential energy then becomes

$$U_{\mathrm{bend}+\mathrm{wrinkle}}={\overline{E}}_{\mathrm{f}}hf\left[{\epsilon }_{\mathrm{pre}}-\frac{1}{2}\left(\frac{4{\overline{E}}_{\mathrm{f}}h}{{\overline{E}}_{\mathrm{s}}H}+1\right)f\right].$$ 2.10

Comparison of the potential energy in equations (2.2) and (2.10) suggests that wrinkling occurs when U_bend>U_bend+wrinkle, which gives

$${\epsilon }_{\mathrm{pre}}>\left(\frac{4{\overline{E}}_{\mathrm{f}}h}{{\overline{E}}_{\mathrm{s}}H}+1\right)f=\left(\frac{4{\overline{E}}_{\mathrm{f}}h}{{\overline{E}}_{\mathrm{s}}H}+1\right)\left[\frac{k^2{h}^2}{12}+\frac{{\overline{E}}_{\mathrm{s}}g(kH)}{kh{\overline{E}}_{\mathrm{f}}}\right],$$ 2.11

where k, f and g are obtained from equations (2.5), (2.7) and (2.8), respectively. It should be pointed out that equation (2.11) also ensures that the right-hand side of equation (2.9) is positive such that there is a solution for the amplitude A.

3. Discussion

When the bending stiffness of the substrate overwhelms that of the film, i.e. ${\overline{E}}_{\mathrm{f}}{h}^3/({\overline{E}}_{\mathrm{s}}{H}^3)<\sim 0.01$, equation (2.11) can be further simplified as

$${\epsilon }_{\mathrm{pre}}>{\epsilon }_{\mathrm{pre}}^{\mathrm{c}}=\frac{1}{4}\left(\frac{4{\overline{E}}_{\mathrm{f}}h}{{\overline{E}}_{\mathrm{s}}H}+1\right){\left(\frac{3{\overline{E}}_{\mathrm{s}}}{{\overline{E}}_{\mathrm{f}}}\right)}^{2/3}.$$ 3.1

For $H\to \mathrm{\infty }$, the above equation degenerates to that for a semi-infinite substrate [1,2]. The critical pre-strain ε^c_pre in equation (3.1) is larger than $\frac{1}{4}(({\overline{E}}_{\mathrm{f}}h/{\overline{E}}_{\mathrm{s}}H)+1){(3{\overline{E}}_{\mathrm{s}}/{\overline{E}}_{\mathrm{f}})}^{2/3}$ [22], which neglects the effect of film/substrate bending. Figure 3 shows the critical pre-strain ε^c_pre versus the thickness ratio H/h for a polyimide film (E_f=2.5 GPa, v_f=0.34) on a polydimethylsiloxane substrate (E_s=1 MPa, v_s=0.5). The results obtained from finite-element analysis agree well with the critical pre-strain in equation (3.1).

Figure 3.

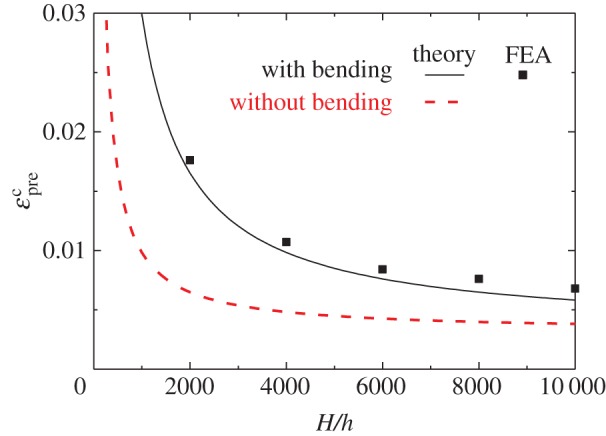
The critical pre-strain ε^c_pre versus the substrate-to-film thickness ratio (H/h) for a polyimide film on a PDMS substrate. FEA, finite-element analysis; PDMS, polydimethylsiloxane. (Online version in colour.)

Competing interests

We declare we have no competing interests.

Funding

Y.M. and X.F. acknowledge support from the National Basic Research Program of China (grant no. 2015CB351900) and the National Natural Science Foundation of China (grant nos. 11402135, 11320101001). Y.X. gratefully acknowledges support from the Ryan Fellowship and the Northwestern University International Institute for Nanotechnology. Y. H. acknowledges support from NSF (DMR-1121262, CMMI-1300846 and CMMI-1400169) and the NIH (grant no. R01EB019337).