Conserved size and periodicity of pyramidal patches in layer 2 of medial/caudal entorhinal cortex

ABSTRACT

To understand the structural basis of grid cell activity, we compare medial entorhinal cortex architecture in layer 2 across five mammalian species (Etruscan shrews, mice, rats, Egyptian fruit bats, and humans), bridging ∼100 million years of evolutionary diversity. Principal neurons in layer 2 are divided into two distinct cell types, pyramidal and stellate, based on morphology, immunoreactivity, and functional properties. We confirm the existence of patches of calbindin‐positive pyramidal cells across these species, arranged periodically according to analyses techniques like spatial autocorrelation, grid scores, and modifiable areal unit analysis. In rodents, which show sustained theta oscillations in entorhinal cortex, cholinergic innervation targeted calbindin patches. In bats and humans, which only show intermittent entorhinal theta activity, cholinergic innervation avoided calbindin patches. The organization of calbindin‐negative and calbindin‐positive cells showed marked differences in entorhinal subregions of the human brain. Layer 2 of the rodent medial and the human caudal entorhinal cortex were structurally similar in that in both species patches of calbindin‐positive pyramidal cells were superimposed on scattered stellate cells. The number of calbindin‐positive neurons in a patch increased from ∼80 in Etruscan shrews to ∼800 in humans, only an ∼10‐fold over a 20,000‐fold difference in brain size. The relatively constant size of calbindin patches differs from cortical modules such as barrels, which scale with brain size. Thus, selective pressure appears to conserve the distribution of stellate and pyramidal cells, periodic arrangement of calbindin patches, and relatively constant neuron number in calbindin patches in medial/caudal entorhinal cortex. J. Comp. Neurol. 524:783–806, 2016. © 2015 The Authors. The Journal of Comparative Neurology Published by Wiley Periodicals, Inc.

The entorhinal cortex is uniquely positioned as a gateway between the neocortex and the hippocampus, and the discovery of grid cells and their remarkable discharge pattern (Hafting et al., 2005) established it as a key structure for spatial representation in mammals. In rats, grid cells are most abundant in layer 2 of the medial entorhinal cortex (Boccara et al., 2010). However, grid cells were not only recorded in rats but also in the entorhinal cortex of a range of mammalian species including mice (Fyhn et al., 2008), bats (Yartsev et al., 2011), monkeys (Killian et al., 2012), and humans (Doeller et al., 2010; Jacobs et al., 2013; reviewed in Las and Ulanovsky, 2014). To understand the structural basis of cellular activity in the entorhinal cortex, we thus compare the organization in layer 2 of five mammalian species (Etruscan shrews, mice, rats, Egyptian fruit bats, and humans), which come from four mammalian orders covering almost 100 million years of divergent evolutionary history and span an ∼20,000 fold range of brain sizes.

The simplest areal partitioning scheme of the human entorhinal region consists of two subdivisions, a lateral and a medial entorhinal area (Brodmann, 1909). These areas have been identified even in the smallest mammals (Rose, 1927a), and hence we follow this scheme. Studies in the human entorhinal cortex have suggested a multitude of parcellation schemes with up to 23 subfields (Rose, 1927b; Sgonina, 1938; Braak, 1972; Krimer et al., 1997; Hanke and Yilmazer‐Hanke, 1997); however, a subdivision into eight fields adapted from studies on macaque monkeys (Amaral et al., 1987) is now most commonly used (Beall and Lewis, 1992; Insausti et al., 1995; Insausti and Amaral, 2011). It is likely that the medial entorhinal cortex of rodents corresponds to the dorsocaudal part of the entorhinal cortex in primates because both are close to the parasubiculum and presubiculum (Bakst and Amaral, 1984) or mediocaudal on the basis of their projections to the dentate gyrus (Insausti, 1993). Consequently, the rodent lateral entorhinal cortex may correspond to the ventrorostral primate entorhinal cortex.

Anatomical modules in the supragranular layers of the cerebral cortex have been described in a wide range of species and cortical areas (Manger et al., 1998; Ding and Rockland, 2001; Ichinohe et al., 2003; Ichinohe, 2012). Such modules are characterized by their complex and variable anatomical structure (Rockland and Ichinohe, 2004; Rockland, 2010) and their relation to various neurotransmitter systems (Gaspar et al., 1990; Akil and Lewis, 1994; van Kleef et al., 2012). In the entorhinal cortex, this complexity is exemplified even within a single cortical region containing different types of modules (Beall and Lewis, 1992). Recent studies in rodents identified functional modules of grid cells with different spacing between their firing fields along the dorsoventral axis of entorhinal cortex (Barry et al., 2007; Brun et al., 2008; Stensola et al. 2012) and also provided evidence for anatomical modularity of entorhinal circuits (Burgalossi et al., 2011; Ray et al., 2014; Heys et al., 2014). However, relating functional and anatomical modularity has been difficult in the entorhinal cortex in particular (Burgalossi and Brecht, 2014) and throughout cortex in general (Horton and Adams, 2005; da Costa and Martin, 2010).

The human temporal lobe shows a distinct surface structure comprising myelinated fibers and cellular islands in the entorhinal cortex and presubiculum (Klingler, 1948). Islands can be visualized by Nissl staining, histochemistry, or immunoreactivity (Braak, 1972; Solodkin and van Hoesen, 1996; Mikkonen et al, 1997; van Hoesen et al, 2000). In primates, most cellular islands consist mainly of stellate cells (Braak et al., 1976), which stain positively for neurofilament protein and cytochrome oxidase, and are surrounded by parvalbumin‐positive neuropil (Beall and Lewis, 1992; Hevner and Wong‐Riley, 1992).

Another set of modules, formed by a class of small pyramidal cells located in between and deep to the islands, is stained by an antibody against calbindin (Beall and Lewis, 1992; Suzuki and Porteros, 2002). Calbindin‐positive cells in superficial cortical layers show pyramidal morphology (Hayes and Lewis, 1992) and are typically not γ‐aminobutyric acid (GABA)ergic (Kubota et al., 1994; Kitamura et al., 2014). In the rodent entorhinal cortex, ∼88% of calbindin‐positive cells are glutamatergic (Peterson et al., 1996) and form discrete cell clusters (Fujimaru and Kosaka, 1996; Ray et al., 2014).

In layer 2 of the medial entorhinal cortex, stellate cells have markedly different electrophysiological properties from pyramidal cells (Alonso and Llinás, 1989; Alonso and Klink, 1993). Reelin‐positive cells project to the dentate gyrus and show electrophysiological parameters of stellate cells (Varga et al., 2010), whereas calbindin‐positive cells project to CA1 (Kitamura et al., 2014) and have electrophysiological properties described previously for pyramidal cells (Klink and Alonso, 1997). Calbindin‐positive pyramidal cells show strong theta modulation and are arranged in a hexagonal grid of patches that receives cholinergic innervation (Ray et al., 2014). Grid cells occur in discrete spatial patterns (Barry et al., 2007; Stensola et al., 2012; Heys et al., 2014). Thus, based on clustering, rhythmicity, cholinergic modulation (Ray et al., 2014), and spatial discharge properties (Tang et al., 2014), we proposed that calbindin‐positive pyramidal cells play an important role in generating grid cell activity. Another line of work implicated the same neuron clusters as key regulators of temporal association memory (Kitamura et al., 2014).

Here we compare the laminar structure, the spatial arrangement of patches in the tangential plane, the cholinergic innervations, and the patch size and numbers of calbindin‐positive pyramidal cells in medial/caudal entorhinal cortex across five mammalian species.

MATERIALS AND METHODS

All experimental procedures were performed according to German and Israeli guidelines on animal welfare.

Animals

Male and female young adult Wistar rats (n = 22), C57BL/6JOlaHsd inbred mice (n = 16), Etruscan shrews (n = 13), and Egyptian fruit bats (n = 10) were used in the study. All experimental procedures were performed according to the German guidelines on animal welfare under the supervision of local ethics committees.

Human brain tissue

Brain autopsies (n = 6) were performed following written consent for pathological examination according to the law of the city of Berlin, Germany. Brain tissues were obtained from males and females varying within the age of 56 and 67 years and having postmortem processing intervals between 24 and 96 hours. Brain tissue was then fixed in 4% formaldehyde, derived from paraformaldehyde, in 0.1 M phosphate buffer (PFA) for 1 to 4 days. Following routine diagnostic neuropathological examination, parts of the medial entorhinal cortex were obtained by separating the entorhinal cortex from the remaining hemisphere by a cut parallel to the surface of the medial entorhinal cortex and were thereafter used for sectioning and conventional as well as immunohistochemical stainings. This procedure was approved by the Charité ethics commission (EA1/320/13).

Tissue preparation

Etruscan shrews, mice, and rats were anesthetized by isoflurane, and then euthanized by an intraperitoneal injection of 20% urethane; bats were euthanized by an overdose of pentobarbital. Animals were then perfused transcardially with first 0.9% phosphate‐buffered saline solution, followed by PFA. After perfusion, brains were removed from the skull and postfixed in PFA overnight. Brains were then transferred to 10% sucrose solution for one night and subsequently immersed in 30% sucrose solution for at least one night for cryoprotection. The brains were embedded in Jung Tissue Freezing Medium (Leica Microsystems Nussloch, Germany), and subsequently mounted on the freezing microtome (Leica 2035 Biocut) to obtain coronal, sagittal, or tangential sections parallel to the pia. We used 20‐µm‐thick sections for tangential sections of shrew cortex, 30‐µm‐thick sections for coronal sections of shrew cortex and tangential sections of mouse cortex, 60‐µm‐thick sections for human cortex, and 40‐µm‐thick sections in all other cases.

Tangential sections of the medial entorhinal cortex were obtained by separating the entorhinal cortex from the remaining hemisphere by a cut parallel to the surface of the medial entorhinal cortex. For subsequent sectioning the surface of the entorhinal cortex was attached to the block face of the microtome, which means the most superficial sections were cut last. We found this reliably generates sections parallel to the surface of the entorhinal cortex.

Histochemistry

Acetylcholinesterase activity

Acetylcholinesterase (AChE) was stained following the method of Ichinohe et al. (2008) and Tsuji (1998). After washing in a mixture containing 1 ml of 0.1 M citrate buffer (pH 6.2) and 9 ml 0.9% saline (CS), sections were incubated with CS containing 3 mM CuSO₄, 0.5 mM K₃Fe(CN)₆, and 1.8 mM acetylthiocholine iodide for 30 minutes. After rinsing in 0.1 M phosphate buffer (PB), sections were intensified in PB containing 0.05% 3,3′‐diaminobenzidine (DAB) and 0.03% nickel ammonium sulfate.

Myelin

For myelin staining we used the gold–chloride protocol (Schmued, 1990). Briefly, free‐floating cryostat sections were incubated for 2–4 hours in a 0.1% solution of gold chloride in 0.02 M phosphate buffer, pH 7.4, and 0.9% sodium chloride. After staining, sections were rinsed for 5 minutes in 0.9% sodium chloride, fixed for 5 minutes in a 2.5% solution of sodium thiosulfate, and rinsed again for 30 minutes before mounting with Mowiol.

Cytochrome oxidase

Cytochrome oxidase activity was visualized according to the protocol of Wong‐Riley (1979).

Synaptic zinc

After perfusion with 0.1% sodium sulfide in 0.1 M PB, brain sections were rinsed with 0.1 M PB, followed by 0.01 M PB. For the visualization of synaptic zinc, sections were developed as described by Danscher and Stoltenberg (2006). In brief, sections were exposed to a solution containing gum arabic, citrate buffer, hydroquinone, and silver lactate for 60–120 minutes, in the dark at room temperature. Development of reaction products was checked under a microscope and terminated by rinsing the sections in 0.01 M PB and, subsequently in 0.1 M PB.

NADPH diaphorase

NADPH diaphorase activity was visualized according to the protocol of Paxinos et al. (2009). Sections were washed in 0.1 M PB and then incubated in 0.1 M PB containing 1.35 mM ß‐NADPH (N1630, Sigma, St. Louis, MO), 305 µM nitroblue tetrazolium (Sigma, N6876), 1 mM MgCl₂, and 0.5% Triton X‐100. The incubation was done at 37 °C for 30 minutes and terminated by washing in PB.

Immunohistochemistry

Tangential, horizontal, and sagittal sections were immunostained with the antibodies listed in Table 1. For multiple antibody labeling, antibodies raised in different host species were combined. In each series of sections the primary antibody was omitted in one section to control for secondary antibody specificity. This always led to complete absence of staining. In one human brain, we compared antigen retrieval to no pretreatment in adjacent tissue slabs. We used the antigen retrieval method indicated by Evers and Uylings (1997) for anti‐calbindin antibodies. However, we did not detect a qualitative improvement in staining, possibly due to the short fixation time of the human brain tissue we used. Overall we found staining quality to be more variable in human brain tissue than in perfusion‐fixed animals, possibly due to the long and variable postmortem interval. For immunofluorescence, the sections were preincubated in a blocking solution containing 0.1 M phosphate‐buffered saline (PBS), 2% bovine serum albumin (BSA), and 0.5% Triton X‐100 (PBS‐X) for 1 hour. Following this, the primary antibody was diluted as described in Table 1 with PBS‐X and 1% BSA and incubated overnight at 4 °C. Subsequently, secondary antibodies conjugated to different fluorophores (Invitrogen, Carlsbad, CA; 488 nm, 546 nm excitation wavelength) and reactive to different species were diluted (1:500) with PBS‐X to incubate the sections for 2 hours, in the dark, at room temperature. After the staining procedure, sections were mounted on gelatin‐coated glass slides and coverslipped with Fluoromount (0100‐01, Southern Biotech, Birmingham AL) mounting medium.

Table 1.

Antibodies

Name	Immunogen	Supplier	Cat. no., RRID	Species	Dilution	Specificity
SMI‐32	Nonphosphorylated epitope of neurofilament H isolated from homogenized hypothalami from Fischer 344 rats	Chemicon (now part of Millipore, Billerica, MA)	NE1023, RRID:AB_2043449	Mouse monoclonal	1:1,000	Sternberger and Sternberger, 1983
NeuN	N‐terminus of recombinant protein corresponding to mouse NeuN	Chemicon	MAB377, RRID:AB_2298772	Mouse monoclonal	1:1,000	Lind et al., 2005
Calbindin D‐28k	Calbindin D‐28k purified from chicken gut	Swant (Bellinzona, Switzerland)	300, RRID: AB_10000347	Mouse monoclonal	1:5,000	Celio et al., 1990
Calbindin D‐28k	Calbindin D‐28k purified from recombinant rat calbindin D‐28k	Swant	CB38, RRID: AB_10000340	Rabbit polyclonal	1:5,000	Airaksinen et al., 1997

SMI‐32

The SMI‐32 mouse monoclonal IgG1 antibody was prepared against the nonphosphorylated epitope of neurofilament H isolated from homogenized hypothalami from Fischer 344 rats. SMI‐32 has been shown to visualize two bands (200 and 180 kDa), which merge into a single neurofilament H line on two‐dimensional blots and is expressed in neuronal cell bodies, dendrites, and some thick axons in both the central and the peripheral nervous systems (Sternberger and Sternberger, 1983). SMI‐32 immunreactivity has previously been shown to label stellate cells, multipolar neurons, and modified pyramidal neurons in layer 2 of human entorhinal cortex (Beall and Lewis, 1992). These studies demonstrate that this antibody generally produces strong labeling in medium‐sized to large pyramidal neurons located in layers 3 and 5 as well as demarcating the six cortical layers of the ferret visual cortex (Homman‐Ludiye et al., 2010).

Calbindin

The mouse monoclonal anti‐calbindin antibody was raised using hybridization of mouse myeloma cells with spleen cells from mice immunized with the calbindin D‐28k that was purified from the chicken gut (Celio et al., 1990). This monoclonal antibody is not known to cross‐react with other known calcium binding‐proteins and specifically stains the 45Ca‐binding spot of calbindin D‐28k (MW 28,000, IEP 4.8) of different mammals in a two‐dimensional gel (manufacturer's technical information). The rabbit polyclonal anti‐calbindin antiserum was raised against recombinant rat calbindin D‐28k (Airaksinen et al., 1997). It cross‐reacts with calbindin D‐28k from many mammalian species. In immunoblots it recognizes a single band of approximately 27–28 kDa (manufacturer's technical information).

NeuN

One series of coronal sections was stained for neuronal nuclei with mouse anti‐neuronal nuclei I (NeuN) antibody. This purified monoclonal (Clone A60) antibody (cat. no. MAB377, Chemicon, Temecula, CA), which we used at a dilution of 1:1,000, was raised against purified cell nuclei from mouse brain. A previous lot of this antibody recognized two to three bands in the 46–48 kDa range and possibly another band at approximately 66 kDa (manufacturer's technical information). Staining of sections through the cerebral cortex produced a pattern of neuronal nuclei as expected from previous descriptions (Lind et al., 2005).

Cell counts and patch sizes

In the analysis for determining cell numbers and patch sizes, patches in consecutive sections were matched by overlaying them in Adobe Photoshop, and only the ones that could be reliably followed in all the sections under consideration were taken up for further analysis. Image stacks were first converted into .tiff files for different channels and focal planes using ImageJ. These files were then merged back together into a single file using the Neurolucida image stack module. In these patches all cells positive for calbindin were counted manually. In the rat brains, cells positive for NeuN were also counted.

Quantification of patch sizes was done with the Neurolucida software by using the mean of maximum and minimum Feret diameter, defined as the maximum and minimum diameter of the patch, respectively. To correct for overestimation of neurons due to potential double counting in adjacent sections, we estimated the number of cells in a section assuming uniform cell density and uniform spherical cell shape in the section and applied a correction factor of s/(s+d) where s is the section thickness and d is the diameter of a cell, to correct for the cells that would be counted again in an adjacent section (Abercrombie, 1946).

Analysis of spatial periodicity

To determine the spatial periodicity of calbindin‐positive patches, we calculated spatial autocorrelations and spatial Fourier spectrograms. The spatial autocorrelogram was based on Pearson's product moment correlation coefficient (as in Sargolini et al., 2006):

$$r({\tau }_x,{\tau }_y)=\frac{\mathrm{n}{{\displaystyle \sum }}^{}f\left(x,y\right)f\left(x-{\tau }_x,y-{\tau }_y\right)-{{\displaystyle \sum }}^{}f(x,y){{\displaystyle \sum }}^{}f\left(x-{\tau }_x,y-{\tau }_y\right)}{\sqrt{n{{\displaystyle \sum }}^{}f{(x,y)}^2-{({{\displaystyle \sum }}^{}f(x,y))}^2}\sqrt{n{{\displaystyle \sum }}^{}f{(x-{\tau }_x,y-{\tau }_y)}^2-{({{\displaystyle \sum }}^{}f(x-{\tau }_x,y-{\tau }_y))}^2}}$$

where, $r({\tau }_x , {\tau }_y)$ is the autocorrelation between pixels or bins with spatial offset τ _x and τ _y. f is the image without smoothing, and n is the number of overlapping pixels. Autocorrelations were not estimated for lags of τ _x and τ _y, where n < 20. Grid scores were calculated as previously described (Sargolini et al., 2006) by taking a circular sample of the spatial autocorrelation map, centered on, but excluding the central peak. Autocorrelograms were obtained by calculating the Pearson correlation coefficient of this circle with its rotation by every degree for up to 180 degrees. On‐peak rotations were defined as the Pearson correlation values for rotations of 60 degrees and 120 degrees and off‐peak rotations as the Pearson correlation coefficient values for rotations of 30 degrees, 90 degrees, and 150 degrees. Gridness was defined as the minimum difference between the on‐peak rotations and off‐peak rotations. To determine the grid scores, gridness was evaluated for multiple circular samples surrounding the center of the spatial autocorrelation map with circle radii increasing in unitary steps from a minimum of 10 pixels more than the width of the radius of the central peak to the shortest edge of the spatial autocorrelation map. The grid score was defined as the best score from these successive samples (Langston et al., 2010). The radius of the central peak was defined as the distance from the central peak to its nearest local minima in the spatial autocorrelogram.

Grid scores reflect both the hexagonality in a spatial field and the regularity of the hexagon. To disentangle the effect of regularity of the hexagon from this index, and consider only hexagonality, we transformed the elliptically distorted hexagon into a regular hexagon (Barry et al., 2012) and computed the grid scores. A linear affine transformation was applied to the elliptically distorted hexagon, to stretch it along its minor axis, until it lay on a circle, with the diameter equal to the major axis of the elliptical hexagon. The grid scores were computed on this transformed regular hexagon.

To assess whether the grid pattern was rectangular, as opposed to hexagonal, analogous 90‐degree grid scores (hereafter called cartesian scores) were evaluated analogous to grid scores but with on peak rotation at 90 degrees, and off‐peak rotations at 45 degrees and 135 degrees. No elliptical modifications were made to this score, and to ensure compatibility, comparisons were always made between cartesian scores and unmodified grid scores.

Furthermore, to determine the generality of the spatial structure, we performed a modifiable areal unit problem (MAUP) analysis (Gehlke and Biehl, 1934; Openshaw, 1983) to determine the spatial characteristics of the grid in an unbiased manner. The two critical issues when performing a spatial analysis are 1) scaling and 2) zoning. The scaling issue refers to how looking at a problem over different scales can lead to different results. This issue is present because we boil down spatial features to a single number, namely, the grid score. To counteract this problem, we analyzed a subset of the data at multiple scales, i.e., systematically choosing different window sizes. We utilized two scales for each of the three species with large entorhinal cortices (rat, bat, human), which were obtained by dividing the entire medial/caudal entorhinal cortex into square grids with the smallest side being divided into three and six parts, respectively, for the two scales. The zoning issue refers to selection of the boundaries of the window, which can lead to a selection bias in the analysis. To cope with this issue, we performed a sliding window analysis with 50% overlap in successive samples, and calculated the spatial autocorrelation, grid scores, and cartesian scores for each sample. To ensure comparability, grid scores without elliptical modifications were used for comparison with cartesian scores.

We performed a shuffling procedure on the block pattern of the original image. The blocks representing the patches were shuffled in original space, and no overlap or abutting of the patches was allowed during the shuffling. This resulted in the original number of patches being randomly distributed in the same area without overlapping. We evaluated the 95th percentile of the grid scores from the shuffled data. However, because shuffled images often led to spatial autocorrelations without clear peaks, it was not always possible to obtain elliptically modified grid scores to compare with our data. This, however, means that the grid scores and cartesian scores attained from the spatial autocorrelation analysis are only indicative of the particular geometry exhibited and not proof of it. However, to counteract the issue of whether a particular pattern, regardless of its particular geometry, was only a chance occurrence, we performed a spatial Fourier analysis, which can be performed independent of this issue.

The spatial Fourier spectrogram was calculated by implementing a two‐dimensional discrete Fourier transform and determining its power (Krupic et al., 2012):

$$F\left(x,\hspace{0.17em}y\right)\hspace{0.17em}=\hspace{0.17em}\frac{1}{\sqrt{MN}}{\displaystyle \sum }_{n=0}^{N-1} {\displaystyle \sum }_{m=0}^{M-1}f\left(m,n\right)e^{-2\pi i\left(\frac{mx }{M}+\frac{ny}{N}\right)}$$

$$P\left(x,y\right)\hspace{0.17em}=\hspace{0.17em}\sqrt{F_r{}^2(x,y)+F_i{}^2(x,y)}$$

where F is the spatial Fourier transform of f, which is a binary image representing the sample with regions of interest (patches) marked as white blocks, with the remaining area as black and zero padded to 2,048 × 2,048. M and N are the width and height of the image before zero‐padding. Normalization by $\sqrt{MN}$ enables comparison of Fourier power in differently sized samples. P is the power of the Fourier transform, with F _r and F _i being the real and imaginary parts of the Fourier transform. To determine the probability that the spatial structure of the patches present in the selected area was not a chance effect, we employed a shuffling procedure. This shuffling was performed on all samples on a sample‐by‐sample basis until the 99th^h percentile of the maximum power Fourier component converged to a constant. This indicated that the spatial structure present in the sample analyzed, regardless of the particular geometry of the structure, was highly unlikely to arise out of chance.

Light and fluorescence microscopy

An Olympus BX51 microscope (Olympus, Shinjuku Tokyo, Japan) was used to view the images using brightfield microscopy. The microscope was equipped with a motorized stage (LUDL Electronics, Hawthorne NY) and a z‐encoder (Heidenhain, Shaumburg IL, USA). Images were captured using a MBF CX9000 (Optronics, Goleta, CA) camera using Neurolucida or StereoInvestigator (MBF Bioscience, Williston, VT).

A Leica DM5500B epifluorescence microscope with a Leica DFC345 FX camera (Leica Microsystems, Mannheim, Germany) was used to image the immunofluorescent sections. Alexa fluorophores were excited using the appropriate filters (Alexa 488, L5; Alexa 546, N3). The fluorescent images were acquired in monochrome, and color maps were applied to the images post acquisition. Post hoc linear brightness and contrast adjustment were applied uniformly to the image under analysis.

Estimate of the neuron number in a human layer four finger‐module

We chose to compare the estimated number of neurons in the human area 3b finger representation to neuron number layer 4 barrels of Etruscan shrews, mice, and rats. This comparison was motivated by the following: 1) finger‐related modules have been described in primate area 3b (Jain et al., 1998; Catania and Henry, 2006); and 2) finger‐related barrels are observed in rodents and finger barrels have a similar size in rats as whisker barrels (Waters et al. 1995). We obtained an estimate of the number of layer 4 neurons in a human area 3b finger representation. We computed a number of ∼1,150,000 neurons in a single finger module of layer 4 neurons in the human area 3b finger representation by using the formula:

$$n\hspace{0.17em}=\hspace{0.17em}\frac{\mathrm{N}*\varphi *\lambda *\alpha *\theta }{\mathrm{r}*\mathrm{s}}$$

where n is the number of neurons in a single finger module in layer 4 in the human area 3b finger representation, and N = 20 billion refers to the total number of cortical neurons (Koch, 1999; Pakkenberg and Gundersen, 1997). ϕ = 0.023 refers to the fraction of the total human cortical sheet occupied by areas 3a and 3b, based on functional imaging data (Orban et al., 2004), and λ = 0.67 refers to the approximate fraction of this area corresponding to area 3b. α = 0.16 denotes that ∼16% of this area corresponds to the finger representation based on the Penfield maps (Penfield and Rasmussen, 1950), and θ = 0.23 refers to the fraction of neurons in this finger cortical column present in layer 4, derived from rat data, where layer 4 contributes 23% of neurons in a column (Meyer et al., 2010). This value was normalized by r = 2, to obtain the value for a single hemisphere and s = 5 to obtain the value for a single finger.

RESULTS

Phylogeny and location of entorhinal cortex in five mammalian species

In our comparative analysis of entorhinal architecture, we identified the entorhinal cortex based on previous publications for bats (Schneider, 1966; Gatome et al., 2010; Yartsev et al., 2011), rodents (Blackstad, 1956; van Groen, 2001; Kjonigsen et al., 2011; Boccara et al., 2015), and humans (Sgonina, 1938; Insausti et al., 1995) and on our own work on the Etruscan shrew (Naumann et al., 2012). The remarkably different sizes of the brains under study and their divergence in the phylogenetic tree are illustrated in Figure 1A. The position of entorhinal cortex and its medial (caudal in humans) and lateral (rostral in humans) subdivisions are indicated in Figure 1B.

Figure 1.

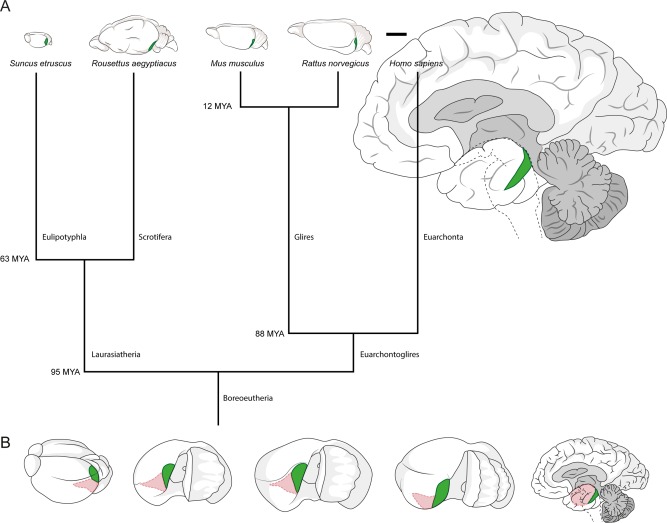
Position of medial and lateral entorhinal cortices and scaling of the brains under study. A: Position of medial/caudal entorhinal cortices containing calbindin patches (highlighted in green) in the brain of the Etruscan shrew, the Egyptian fruit bat, the mouse, the rat and the human (left to right, drawn to scale). Branch points of the tree show estimated divergence time according to Janecka et al. (2007), Hallström et al. (2007), Jacobs and Downs (1994), Jacobs and Flynn (2005), and Waddell et al. (2001). B: Position of entorhinal cortices in the brain of the Etruscan shrew, the Egyptian fruit bat, the mouse, the rat and the human (left to right, not to scale). The brains were rotated to show the surface of the medial/caudal entorhinal cortex (highlighted in green). Remaining entorhinal areas are marked in pink. Scale bar = 5 mm in A.

Laminar architecture of calbindin‐positive cells in entorhinal cortex

Calbindin immunoreactivity identifies a variety of cells in medial entorhinal cortex. As noted in the introduction, the majority of these cells are layer 2 pyramidal neurons, and this neuronal population is what we focus on in the present article. Figure 2 shows cortical lamination in sections perpendicular to the pial plane stained for calbindin, namely, parasagittal sections from a mouse (Mus musculus), rat (Rattus norvegicus), and bat (Rousettus aegyptiacus) and coronal sections from shrew (Suncus etruscus) and human (Homo sapiens) medial entorhinal cortex. Calbindin‐positive cells in the entorhinal cortex form periodic clusters (Fig. 2A,C,E,G,I). Higher magnification views show that these patches contain both calbindin‐positive cells and calbindin‐positive neuropil and are most easily detected in layer 2 (Fig. 2B,D,F,H). Calbindin‐positive cells within patches also show differences in laminar distribution across species. The medial part of the entorhinal cortex in the Etruscan shrew is very thin (∼200 µm), comparable in thickness to single layers in other species, such as layer 3 in rodents. We were able to identify layer 1 and a thin cell‐free layer (lamina dissecans) separating superficial and deep entorhinal layers (Fig. 2A). However, despite the small size of the region, calbindin‐positive cells form a small number of clearly separated clusters in layer 2/3. In rodents, calbindin‐positive cells form clusters only in layer 2 (Fig. 2C–F), whereas in shrews (Fig. 2A,B), bats (Fig. 2G,H), and humans (Fig. 2I) they appear to extend through layer 2 and 3. In addition to the calbindin‐positive pyramidal neurons that are clustered in patches, we observed two other calbindin‐positive cell populations: 1) a scattered population of cells with intense calbindin immunoreactivity and nonpyramidal morphologies, perhaps corresponding to a specific interneuron subpopulation (DeFelipe, 1997); and 2) a population of weakly calbindin‐immunoreactive neurons outside of patches, which are likely to be calbindin‐positive pyramidal neurons. These neurons were differently distributed in the species investigated. In mice, very few weakly calbindin‐positive neurons were found outside of patches, whereas in shrews and rats there was a larger number of such cells outside of patches in the same cortical layer.

Figure 2.

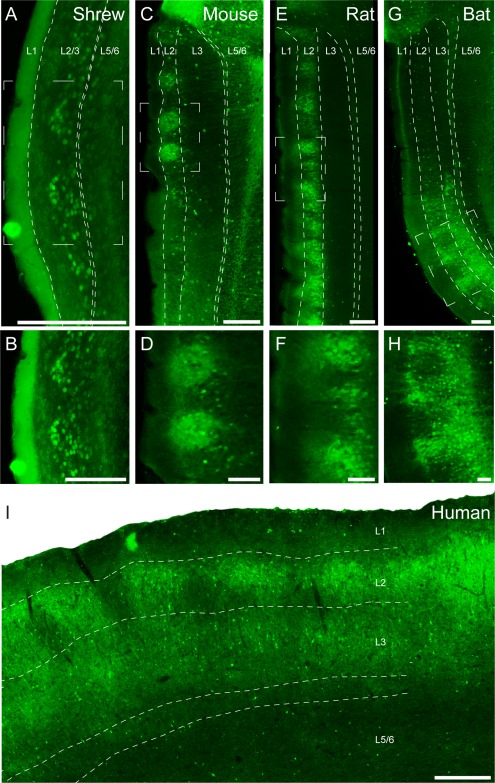
Sagittal and coronal sections through medial/caudal entorhinal cortex of Etruscan shrews, mice, rats, bats, and humans stained for calbindin immunoreactivity revealing patches of pyramidal cells. Calbindin immunoreactivity in the entorhinal cortex reveals patches of calbindin‐positive pyramidal cells, shown in a coronal section in the Etruscan shrew (A) and parasagittal sections in the mouse (C), rat (E), and Egyptian fruit bat (G). B,D,F,H: Higher magnification views of the respective panels above. I: Coronal section of a human caudal entorhinal cortex. White stippled lines indicate laminar borders. White stippled boxes in A, C, E, and G indicate subregions used for higher magnification images in B, D, F, and H. L1, L2, L3, and L5/6 indicate entorhinal layers 1, 2, 3, and 5/6. Scale bar = 200 µm in A; 250 µm in C,E,G; 100 µm in B,D,F,H; 500 µm in I.

Architecture of calbindin‐positive cells in tangential cortical sections

Next we focused on the cross‐species comparison of entorhinal organization in the tangential cortical plane. To this end we stained tangential sections from Etruscan shrew (Fig. 3A), mouse (Fig. 3B), rat (Fig. 3C), bat (Fig. 3D), and human (Fig. 3E) medial/caudal entorhinal cortex for calbindin immunoreactivity. All species display a modular arrangement of calbindin‐positive cells or neuropil (Fig. 3). Bundling of calbindin‐positive dendrites superficial to the patches was prominent in the rat entorhinal cortex (Fig. 2E,F; Ray et al., 2014), but this was not obvious in sections perpendicular to the surface in other species. Even so, we found that calbindin‐positive neuropil contributes to patch architecture in tangential sections and in the shrew we could detect calbindin‐positive neuropil above the calbindin‐positive cells in tangential sections (Fig. 3A).

Figure 3.

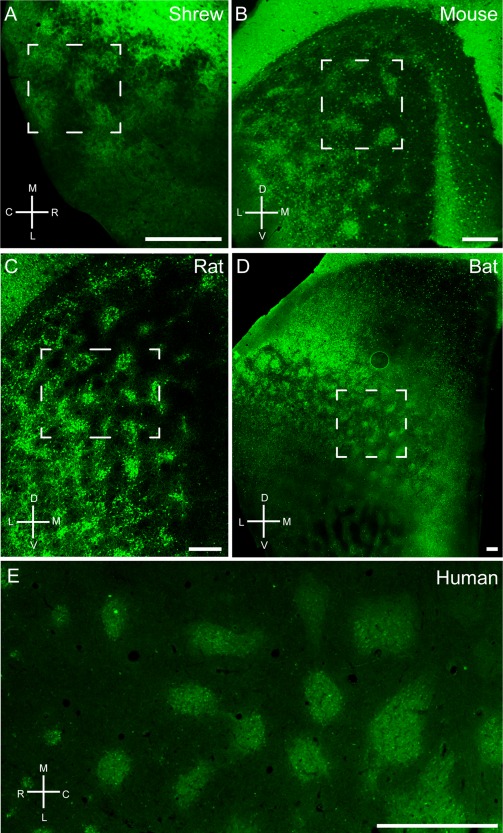
Tangential sections through medial entorhinal cortex of Etruscan shrews (A), mice (B), rats (C), bats (D), and humans (E) stained for calbindin immunoreactivity revealing grid‐like patches of pyramidal cells. Note that, especially in rodents, areas surrounding the entorhinal cortex such as postrhinal cortex and presubiculum contain a high density of calbindin‐positive cells in superficial layers. Stippled boxes indicate the position of higher magnification images in Figure 4. C, caudal; D, dorsal; L, lateral; M, medial; R, rostral; V, ventral. Scale bar = 250 µm in A–D; 1 mm in E.

When comparing the size of individual calbindin patches across species, we observed that individual modules were remarkably similar in size (Fig. 3, Table 4), whereas the size of the entorhinal cortex increased significantly in larger species. The average diameter of an entorhinal calbindin patch was 104 ± 25 µm in the Etruscan shrew, 94 ± 37 µm in the mouse, 145 ± 41 µm in the rat, 250 ± 77 µm in the bat, and 532 ± 197 µm in humans. In contrast, entorhinal cortex volume increased from 0.73 mm³ (area ∼2.81 mm²) in the shrew, to 19 mm³ in rats (Wree et al., 1992), and to ∼1,678 mm³ (517.90 mm²) in humans (Insausti et al., 1998; Velayudhan et al., 2013), an approximately 2,300‐fold increase (184‐fold areal increase). The number of patches also showed an increase, with 14 ± 2 in shrews, 22 ± 7 in mice, 69 ± 17 in rats, 100 ± 1 in bats to 115 ± 16 in humans (Table 4).

Table 4.

Patch Number, Patch Size, and Spacing^a

Species	Total no. of patches in a medial/caudal EC hemisphere	Patch diameter (µm)	Linear patch density (dorsoventral) (No. of patches per mm)	Patch density (No. of patches per square mm)
Shrew	14 ± 2	103 ± 23	25	45
Mouse	22 ± 7	94 ± 37	19	10
Rat	69 ± 17	145 ± 41	17	14
Egyptian fruit bat	100 ± 1	250 ± 77	20	6
Human	115 ± 16	532 ± 197	8	1

^aThe number of neurons in a human finger representation was estimated as described in Materials and Methods. The total number of patches is difficult to estimate because it requires well‐stained and completely analyzable specimen and also relies on accurate assessment of areal boundaries. Estimates of total of total patch number are based on 6 brains and 9 hemisphere in mice, 10 brains in rats, and 2 brains each for shrews, bats, and humans.

Periodicity of calbindin patch pattern in entorhinal cortex

Another species‐invariant feature of the organization of calbindin patches was their spatially periodic grid‐like arrangement. In specimens of medial entorhinal cortex stained for calbindin, periodic arrangements of calbindin patches in the superficial layers can be seen. We analyzed the spatial periodicity of calbindin‐positive patches with a variety of techniques. As shown in Figure 4, we applied two‐dimensional spatial autocorrelation analysis to calbindin‐stained tangential sections (Fig. 4A,C,E,G,I) of medial/caudal entorhinal cortex. Two‐dimensional spatial autocorrelation captured spatially recurring features and revealed a periodic arrangement of calbindin patches in all species (Fig. 4B,D,F,H,J). However, the particular geometry of the layout is difficult to ascertain due to confounding factors like distortions of the surface when the brain is flattened, uneven shrinkage in tissue processing, and incomplete capture of a particular pattern in any single histological section.

Figure 4.

Grid‐like arrangement of calbindin‐positive pyramidal cells in the medial entorhinal cortex. High‐magnification view of a tangential section of Etruscan shrew (A), mouse (C), rat (E), bat (G), and human entorhinal cortex (I). B,D,F,H,J: Two‐dimensional spatial autocorrelation of the respective panels to the left revealing a periodic spatial organization of calbindin‐positive patches. Color scale: –0.5 (blue) through 0 (green) to 0.5 (red), The mouse, rat, and bat samples exhibit hexagonal spatial organization, and their grid scores are 0.63 (C,D), 0.98 (E,F), and 0.82 (G,H), respectively. The Etruscan shrew and human exhibit rectangular spatial organization, and their cartesian scores are 1.39 (A,B) and 0.46 (I,J), respectively. C, caudal; D, dorsal; L, lateral; M, medial; R, rostral; V, ventral. Scale bar = 250 µm in A–J.

Quantification of the periodicity of calbindin patches

To quantify the nature of the periodicity in the samples, we calculated grid scores (Sargolini et al., 2006) to determine hexagonality, and cartesian scores to determine rectangularity. The grid scores were also modified to quantify hexagonality in elliptically distorted hexagons (Barry et al., 2012; see Materials and Methods for details). Grid and cartesian scores vary from −2 to +2, with values >0 indicative of hexagonality and rectangularity, respectively. However, it should be noted that these values only provide an indication of the nature of periodicity and do not provide proof of the absolute geometry without further statistical testing. We observed periodic arrangements in all species and determined grid scores or cartesian scores as indicated for individual images in the figure legend (Fig. 4). In addition, we prepared further sets of tangential sections and computed the following average grid scores (Table 6): shrews (0.73 ± 0.21, n = 2), mice (0.55 ± 0.09, n = 3), rats (0.84 ± 0.23, n = 9), bats (0.81 ± 0.04, n = 3), and humans (1.18 ± 0.10, n = 3). To assess the probability of a chance occurrence of the arrangement of the patches, we employed a shuffling procedure (Krupic et al., 2012; Ray et al. 2014). We found that the strongest Fourier component in each of the samples exceeded that of the 99th percentile of the shuffled data, given preserved local structure, suggesting that such spatial arrangement, regardless of the particular geometry of the arrangement, is unlikely to arise by chance. The number of samples for each individual species was in general not high enough to determine statistically whether the periodicity present was hexagonal or rectangular. However, in rats, in which sufficiently large numbers of samples were present, the grid score was significantly higher than the cartesian score (P = 0.0416, one‐tailed t‐test; Shapiro–Wilk normality test), indicating that in rats the grid‐like layout is rather hexagonal than rectangular. To ensure compatibility we used grid scores without elliptical modifications to compare with cartesian scores.

Table 6.

Grid Scores, Elliptical Grid Scores, and Cartesian Scores^a

Species	Grid scores	Elliptical grid scores	Cartesian scores
Shrew	−0.02 ± 0.84	0.73 ± 0.21	0.58 ± 1.15
Mouse	0.35 ± 0.11	0.55 ± 0.09	0.14 ± 0.30
Rat	0.28 ± 0.43	0.84 ± 0.23	0.00 ± 0.15
Egyptian fruit bat	0.52 ± 0.35	0.81 ± 0.04	0.45 ± 0.42
Human	0.36 ± 0.39	1.18 ± 0.10	0.28 ± 0.39

^aAverage grid scores with and without elliptical modifications and cartesian scores. Scores are represented as mean ± SD and are based on nine samples in rats, two samples in shrews, and three samples each for mice, bats, and humans.

Furthermore, to assess the generality of the grid layout across the medial/caudal entorhinal surface, we introduced a MAUP analysis (Gehlke and Biehl, 1934; Openshaw, 1983). A critical issue while performing a spatial analysis is selecting the size of the region under observation, because analysis at different scales can lead to different outcomes. This issue is known as the scaling problem (Openshaw, 1983). To resolve it, we performed our analysis at two different scales, obtained by dividing the smallest side of the whole entorhinal patch pattern into three and six parts. Another critical issue pertaining to spatial analysis corresponds to selecting the boundaries of the region under analysis (as opposed to size described by the scaling problem). This issue is known as the zoning problem (Schuurman et al., 2007); to cope with it, we performed a sliding window analysis, with 50% overlap between the successive windows, at each of the two scales. We performed these analyses on micrographs of the whole medial/caudal entorhinal cortices from species with large entorhinal cortices (human, bat, and rat), and compared grid scores with cartesian scores. To ensure compatibility, we used grid scores without elliptical modifications to compare with cartesian scores. We counted the number of regions having positive grid scores and cartesian scores and classified them as hexagonal or rectangular grid‐like regions, respectively. In case a region exhibited both positive grid and cartesian scores, then the region was classified as hexagonal, if the value of the grid score was higher than the cartesian score, and rectangular in case the converse was true. We observed that in most cases (five of six across two scales and three species; Table 5), regions were mostly classified as hexagonal rather than rectangular. This indicated that the underlying periodicity was more hexagonal than rectangular. However, the difference between hexagonal and rectangular regions was minor and cannot be used to form conclusions about the particular geometry of the periodicity until larger numbers of samples are analyzed, to increase the power of the analysis.

Periodicity of modular structures in the cortex and colliculus of mammals

Modular structures are a prominent feature of many cortical areas (Kaas, 2012) but also other regions of the mammalian (Roney et al., 1979) and nonmammalian brain (Leise, 1990). In the cerebral cortex, modules are commonly defined as a set of structural features that repeats in a relatively regular fashion in a plane parallel to the surface (Manger et al., 1998). Modules are not necessarily circular in shape but can also take the form of bands or stripes and may be arranged in different patterns. We suggest that spatial autocorrelation analysis can complement manual analysis of patch patterns, and we applied it to tangential sections of other modular cortical structures from rats, monkeys, and humans (Fig. 5). We obtained images of monkey primary and secondary visual cortex stained for cytochrome oxidase (Fig. 5A,C) from Dr. Lawrence C. Sincich and Dr. Jonathan C. Horton (Sincich and Horton, 2002). Autocorrelation analysis of these patterns (Fig. 5B,D) showed similar grid and cartesian scores. Figure 5E shows the NADPH diaphorase staining in the superior colliculus of the rat (Wallace, 1986), and Figure 5G shows the cytochrome oxidase staining pattern in the rat barrel cortex (Woolsey and van der Loos, 1970). Autocorrelation analysis of these patterns (Fig. 5F,H) showed regular patterns with higher cartesian scores than grid scores. Figure 5I shows myelin staining in patches of the presubiculum of the human brain (Sgonina, 1938), and Figure 5K shows the zinc staining pattern in the rat visual cortex (Ichinohe et al. 2003). Autocorrelation analysis of these patterns (Fig. 5J,L) showed patterns more similar to hexagonal patterns of the entorhinal cortex with higher grid scores than cartesian scores. In summary, we found that periodic structures are not unique to the entorhinal cortex, yet the pattern in the entorhinal cortex appears well conserved across different species, in contrast to other structures, like the cytochrome oxidase patterns of monkey visual cortex and rat barrel cortex.

Figure 5.

Structural analysis of different brain regions using spatial autocorrelation. Macaque primary (A) and secondary (C) visual cortex stained for cytochrome oxidase. Pale cytochrome oxidase stripes in V2 receive the richest projection from macaque striate cortex. E: Rat superior colliculus stained for NADPH diaphorase. G: Rat barrel cortex stained for cytochrome oxidase. I: Human presubiculum stained for myelin. K: Rat visual cortex stained for presynaptic zinc ions. B,D,F,H,J,L: Two‐dimensional spatial autocorrelation of the respective panels to the left revealing different types of regular spatial organization. Color scale: −0.5 (blue) through 0 (green) to 0.5 (red), (60‐degree) grid scores are 0.24 (A,B), –0.04 (C,D), 0.31 (E,F), 0.29 (G,H), 0.74 (I,J), and 0.3 (K,L), respectively. Cartesian (90‐degree grid) scores are 0.24 (A,B), 0.09 (C,D), 0.56 (E,F), 0.91 (G,H), 0.08 (I,J), and 0 (K,L), respectively. CO, cytochrome oxidase; V1, primary visual cortex; V2, secondary visual cortex; SC, superior colliculus; NADPH, NADPH diaphorase staining; BaCo, barrel cortex; PrS, presubiculum; Zinc, synaptic zinc staining. A and C are adapted with permission from L.C. Sincich and J.C. Horton, J Comp Neurol 447:18–33. Copyright © 2002 Wiley‐Liss, Inc. Scale bar = 1 mm in A,B; 5 mm in C,D; 250 µm in E,F; 500 µm in G–L.

Acetylcholinesterase staining in relation to calbindin patches

In rodents acetylcholine has diverse effects on medial entorhinal cortex (for review, see Hasselmo, 2006). Ray et al. (2014) have described a preferential cholinergic innervation of calbindin patches in rats. In mice we observed a similar preferential cholinergic innervation of calbindin patches, as shown in a tangential section of mouse entorhinal cortex stained for both acetylcholinesterase activity (Fig. 6A) and calbindin (Fig. 6B), revealing a close match of the two staining patterns, which was confirmed in overlays (not shown). Equivalent observations were made in the rat (Fig. 6C,D). In both species we observed a medial stripe free of calbindin patches (Fujimaru and Kosaka, 1996) that had homogeneous acetylcholinesterase activity similar to the staining pattern in between the calbindin patches. The parasubiculum had high acetylcholinesterase activity and surrounded the dorsal medial entorhinal cortex. A striking species difference in cholinergic innervation was evident, however, when rat and mouse were compared with the bat and human entorhinal cortices. In Egyptian fruit bat, a section stained for acetylcholinesterase showed clusters of increased activity in the dorsal part but little staining in the ventral part (Fig. 7A). The reverse was true for calbindin staining (Fig. 7B). Thus, in contrast to the nearly complete overlap in rats, cholinergic and calbindin patches formed two largely non‐overlapping sets of modules in bats. Finally, in human caudal entorhinal cortex we observed anticorrelated cholinergic and calbindin staining patterns (Fig. 7C,D).

Figure 6.

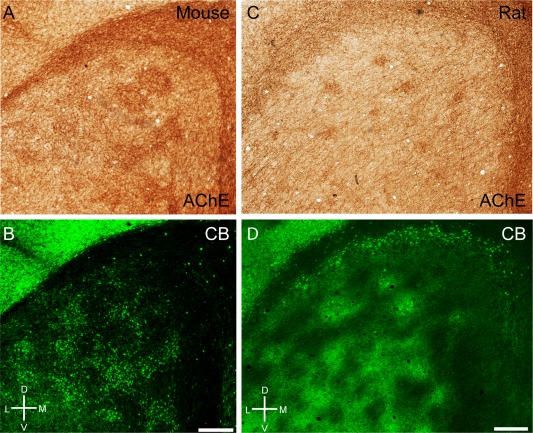
Cholinergic innervation targets calbindin patches in mice and rats. A: Tangential section through mouse entorhinal cortex stained for acetylcholinesterase activity, showing discrete clusters of staining. B: The same section stained for calbindin. C: Tangential section through rat entorhinal cortex stained for acetylcholinesterase activity, showing discrete clusters of staining. D: The same section stained for calbindin. D, dorsal; L, lateral; M, medial; V, ventral. Scale bar = 250 µm in B (also applies to A) and D (also applies to C).

Figure 7.

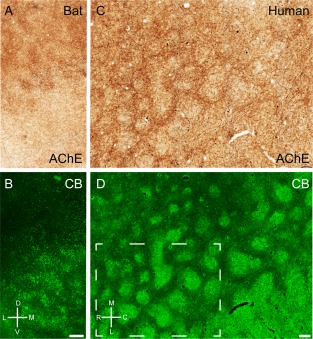
Cholinergic innervation avoids calbindin patches in bats and humans. A: Tangential section through Egyptian fruit bat entorhinal cortex stained for acetylcholinesterase activity, showing discrete clusters of staining. B: The same section stained for calbindin. C: Tangential section through human entorhinal cortex stained for acetylcholinesterase activity, showing discrete clusters of staining. D: The same section stained for calbindin. Stippled box in D indicates the position of higher magnification images in Figure 4. D, dorsal; L, lateral; M, medial; V, ventral. Scale bar = 250 µm in B (also applies to A) and D (also applies to C).

Calbindin patches in the human entorhinal cortex

Modularity of the human entorhinal cortex has been intensely investigated (for review, see Insausti and Amaral, 2011). Because human entorhinal cortex shows a high degree of regional diversity (Sgonina, 1938; Rose, 1927b) and most of this work has focused on so‐called stellate cell islands, we add an overview (Fig. 8), which shows to which entorhinal subregion our conclusions on the arrangement of calbindin patches apply and how these compare with stellate cell islands. Figure 8A shows a ventral view of a human cortical hemisphere; the white box indicates the position of the tangential‐section whole‐mount preparation of flattened entorhinal cortex shown in Figure 8B. We identified putative stellate cell islands by neurofilament immunoreactivity (Fig. 8B, red) and calbindin patches by calbindin immunoreactivity (Fig. 8B, green). In caudal human entorhinal cortex (Fig. 8C), we observed hexagonally (Fig. 8C,D) arranged calbindin patches, which were superimposed onto a spatially scattered population of putative stellate cells (Fig. 8E,F). This arrangement is remarkably similar to the cellular organization of rat medial entorhinal cortex (Ray et al., 2014). Consistent with previous observations (Mikkonen et al., 1997) we observed little calbindin immunoreactivity (Fig. 8G,H) around stellate cell islands in more rostral parts of entorhinal cortex (Fig. 8I). Such islands of stellate cells in the rostral parts of human entorhinal cortex are perhaps the most distinct modular structures in human cortex, and they have a regular but somewhat less periodic organization (Fig. 8J) than calbindin patches in caudal entorhinal cortex (Fig. 8D).

Figure 8.

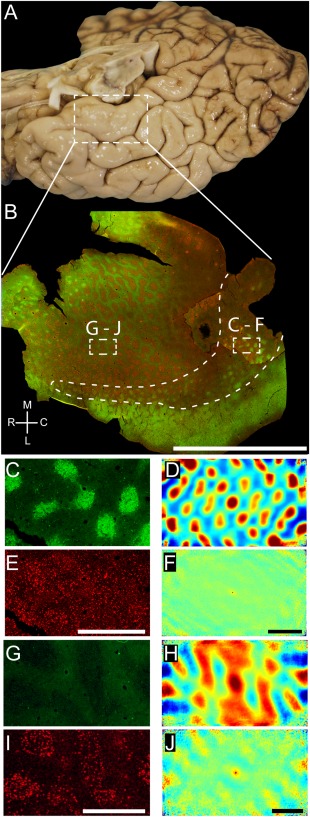
Grid‐like arrangement of calbindin‐positive pyramidal cells in the human entorhinal cortex. A: Overview of the human temporal lobe showing the entorhinal cortex close to the substantia nigra. B: Tangential section through entorhinal cortex oriented as in A and stained for calbindin and neurofilament immunoreactivity (SMI‐32). This figure was assembled from two different sections stained in the same way to show a larger number of calbindin‐positive patches. Stippled boxes indicate the location of panels C–F and G–J. Stippled line surrounds the caudal calbindin patch region and thus marks the caudal border of the entorhinal cortex. C: High‐magnification view of calbindin immunoreactivity in a tangential section of human caudal entorhinal cortex. D: Two‐dimensional spatial autocorrelation of the respective panel to the left revealing a hexagonal spatial organization of calbindin‐positive patches. Grid score is 0.71. E: High‐magnification view of SMI‐32 immunoreactivity in a tangential section of human caudal entorhinal cortex. F: Two‐dimensional spatial autocorrelation of the respective panel to the left revealing a lack of spatial organization. Grid score is –0.03. G: High‐magnification view of calbindin immunoreactivity in a tangential section of human rostral entorhinal cortex. H: Two‐dimensional spatial autocorrelation of the respective panel G revealing a less regular spatial organization than in D. Grid score is –0.18. I: High‐magnification view of SMI‐32 immunoreactivity in a tangential section of human rostral entorhinal cortex. J: Two‐dimensional spatial autocorrelation of the respective panel to the left revealing a little regularity in spatial organization. Grid score is 0.19. A magenta–green version of this figure has been provided as an online supporting file for the assistance of color‐blind readers. C, caudal; L, lateral; M, medial; R, rostral. Scale bar = 1 cm in B; 1 mm in E (also applies to C); 1 mm in F (also applies to D); 1 mm in I (also applies to G); 1 mm in J (also applies to H).

Extent of calbindin patches in entorhinal cortex

In rats, we have observed calbindin patches quite ventrally (4 mm from the dorsal border; Ray et al., 2014). However, the modular architecture of more ventral regions is difficult to assess in tangential sections due to 1) strong local tissue curvature in the rat ventral entorhinal cortex; and 2) variable definitions of ventral areas in the literature (Haug, 1976; Paxinos and Watson, 1998). Coronal sections stained for calbindin in an atlas of the parahippocampal region (Kjonigsen et al., 2011) suggest that the most ventral (anterior) parts of the medial entorhinal cortex do not contain patches but more homogeneous calbindin staining. Thus, the borders of the medial entorhinal cortex as defined by Kjonigsen et al. (2011) do not coincide with the occurrence of patches. Although assessing patch patterns is difficult in coronal sections, as shown by Kjonigsen et al. (2011), our tangential sections do not allow conclusions about patch patterns in the ventral entorhinal cortex. In bats, the dorsal end of the entorhinal region has a wide, calbindin‐free region, putatively corresponding to the parasubiculum (Figs. 2G, 3D). Similar to rodents (Fig. 6), this region has high cholinergic innervation (Fig. 7A).

In humans, we outlined the caudal calbindin patch region and thus marked the caudal border of the entorhinal cortex (Fig. 8B). In the rostral and medial regions the section was too fractured to delineate the borders. However, we think that all or nearly all parts present in the section belong to the entorhinal cortex.

Allometry of calbindin patches

Our species sample, with the Etruscan shrew's brain and the human brain, contained the smallest and one of the largest mammalian brains. Thus, this sample provides an ideal opportunity to analyze how calbindin patches scale with brain size. To approach this question quantitatively, we counted the number of calbindin‐positive cells per patch in all species (Table 2). For an allometric analysis we related this number to brain weight (Table 3). We found that the number of calbindin‐positive cells per patch increased from about 80 calbindin‐positive cells per patch in Etruscan shrews to about 800 neurons in humans (Table 3, Fig. 9). Thus, the number of calbindin‐positive cells increased only 10‐fold from shrews to humans, whereas brain size increased 20,000‐fold. The relatively minor changes in size of calbindin‐positive cells per patch was also apparent, compared with the scaling of layer 4 barrels (in Etruscan shrews, mice, and rats) or the finger representation in humans. In Figure 9, we chose to plot the estimated number of neurons in the human area 3b finger representation together with barrels because: 1) finger‐related modules have been described in primate area 3b (Jain et al., 1998; Kaas, 1998; Catania and Henry, 2006); and 2) finger‐related barrels are observed in rodents and the three barrels per finger have a similar size in rats as a large whisker barrel (Waters et al., 1995; Riddle al., 1992). From Figure 9 it appears that somatosensory module neuron number scales isometrically with brain size, whereas calbindin‐positive cell number scales allometrically and stays relatively constant in evolution.

Table 2.

Neuron Number/Calbindin Patch

Species	Patches counted	Calbindin‐positive neurons/patch
Shrew	10 from 3 brains	79 ± 22
Mouse	11 from 4 brains	107 ± 22
Rat	19 from 4 brains	111 ± 42
Egyptian fruit bat	10 from 2 brains	381 ± 105
Human	8 from 2 brains	837 ± 84

Table 3.

Brain Weight, Neuron Number in Somatosensory Barrels and Total Neuron Number in Entorhinal Cortex

Species	Brain size (mg)	Reference	No. of neurons in a layer 4 barrel/finger representation	Reference	EC no. of neurons	Reference
Shrew	64	Naumann et al., 2012	∼100	This study	1.3 × 105	Naumann et al., 2012
Mouse	453	Williams, 2000	∼2,000 (1,035–2,624)	Lee and Woolsey, 1975	4 × 105	Irizzary et al., 1997
Rat	∼2,000	Donaldson and Hatai, 1931	4,447 ± 439	Meyer et al., 2010	6.8 × 105	Rapp et al., 2002
Egyptian fruit bat	2,157 ± 100	This study
Human	1,320,000	Blinkow and Glezer, 1968	∼1,150,000	Estimate; this study (see text)	7–8 × 106	West and Slomianka, 1998

Figure 9.

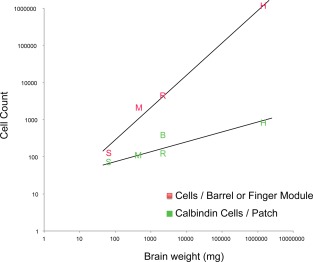
Neuron number in L2 entorhinal calbindin modules, L4 barrel /finger modules, and brain size. Letters indicate barrel cell numbers in somatosensory barrels (red) and entorhinal calbindin patches (green) in S (Etruscan shrews), M (mice), R (rats), B (Egyptian fruit bats), and H (humans) (from left to right).

We identified two factors that seem to contribute to the relatively constant calbindin‐positive cell number per patch across species. First, it appears that the total number of entorhinal neurons does not scale isometrically with brain size (Table 3). Second, we found that the increase of entorhinal cortex across species was associated with an increasing number of calbindin patches (Table 4). Also, the density of patches decreases with increasing entorhinal cortex size (Table 4).

Table 5.

Modifiable Areal Unit Analysis^a

Species	Scale 1 (hexagonal/rectangular/none)	Scale 2 (hexagonal/rectangular/none)
Rat	11/8/6	56/47/29
Egyptian fruit bat	16/13/6	64/68/33
Human	9/7/4	66/37/29

^aNumber of regions having hexagonal periodicity/rectangular periodicity/no periodicity as illustrated by modifiable areal unit analysis of complete entorhinal micrographs of species having large entorhinal cortices.

DISCUSSION

We confirm the existence of calbindin‐positive patches in layer 2 of entorhinal cortex in five mammalian species. Although we observed in all species a periodic modular arrangement of calbindin‐positive patches, we detected major species differences in the cholinergic innervation of these patches. The architecture of calbindin‐positive patches in the entorhinal cortex also showed clear species differences, particularly in terms of lamination, but the organization of calbindin patches was remarkably constant in specific subregions. Anatomical similarity is not sufficient to define homology; however, our findings support earlier conclusions about the correspondence of entorhinal subregions (Insausti, 1993). The number of neurons in a calbindin patch increased only ∼10‐fold over a 20,000‐fold difference in brain size between Etruscan shrew and human (∼2,300 fold difference in volume of entorhinal cortex). In rats, but also in other species, we observed substantial animal to animal variability in the number of calbindin patches, which strongly argues against “identical” calbindin patch maps in individual rats, in contrast to modular structures such as the barrel cortex, which are very similar in every animal.

Entorhinal modules: comparison with neocortical modules and evolutionary perspective

Our results confirm and extend a range of studies describing calbindin‐positive modules in the mammalian entorhinal cortex. Fujimaru and Kosaka (1996) described patches of calbindin‐positive neurons in the mouse dorsal medial entorhinal cortex. Calbindin‐positive cell clusters were also described in monkeys (Suzuki and Porteros, 2002) and humans (Beall and Lewis, 1992). In primates, these calbindin cell clusters are most prominent at the caudal pole of entorhinal cortex, which may correspond to medial entorhinal cortex of rodents (Bakst and Amaral, 1984).

Evidence for columnar organization in superficial layers of the cerebral cortex was obtained from a wide range of cortical areas in a variety of species (Manger et al., 1998; Ichinohe et al., 2003; Rockland and Ichinohe, 2004). Interestingly, commonly studied modules in the neocortex such as barrels and orientation columns are present only in a limited number of species (Kaschube et al., 2010; Keil et al., 2012; Molnar, 2013). In the case of ocular dominance columns, even individuals of the same species show a large variability in the expression of the columnar pattern (Adams and Horton, 2003). Based on our observations in the entorhinal cortex of five species, we speculate that parahippocampal modules may be more conserved across species than neocortical modules. However, although parahippocampal modules are present in a wide range of species, they have been less extensively studied than neocortical modules (Ikeda et al., 1989; Hevner and Wong‐Riley, 1992; Ding and Rockland, 2001; Ichinohe, 2012). For example, the human entorhinal cortex appears to consist of homogeneous modules varying only in size when cytochrome oxidase or pigment staining is used (Hevner and Wong‐Riley, 1992; Braak and Braak, 1995); when markers such as calbindin (Fig. 9) or markers for different neuromodulatory systems are used, different types of modules can be shown (Gaspar et al., 1990; Akil and Lewis, 1994).

Our analysis in five mammalian species shows that the periodic arrangement of patches in layer 2 is present in species that are separated by millions of years in evolution and that differ in size by several orders of magnitude. This indicates a conserved mechanism for generating entorhinal architecture, but anatomical study of further mammalian species such as marsupials is necessary. Of particular interest would be investigating similar brain regions in other amniotes. Interestingly, in adult lizards (Dávila et al., 1999) and during development of the hippocampal region in chickens, modular structures enriched in calbindin (and acetylcholinesterase in chickens) emerge (Kovjanic and Redies, 2003; Suárez et al., 2006); however, the exact correspondence of mammalian and bird hippocampal regions is currently a topic of ongoing research (Herold et al., 2014; Abellán et al., 2014).

Quantification of periodicity in neocortical modules has been challenging, although observations of hexagonality in apical dendritic columns (Gabbott, 2003; Peters and Kara, 1987) have been reported. Our analysis of patch patterns reveals their periodicity across species; however, what the particular geometry of that periodicity might be is less clear. In the rat, we demonstrate that the layout is rather hexagonal than rectangular, and an analysis of a larger number of samples from each species would be required to ascertain the nature of periodicity across species.

Relation of calbindin patches and functional modules

Grid cells form functional modules (Stensola et al., 2012), are anatomically clustered in the medial entorhinal cortex (Heys et al., 2014), and may also be found within the calbindin‐positive cell population in rats (Tang et al., 2014). Therefore, we hypothesized that anatomical and functional modularity may be related in the entorhinal cortex (Brecht et al., 2014). Here we provide evidence for the relatively inelastic scaling of calbindin patch size and for the conserved regular arrangement of calbindin patches across several mammalian species. Although these points are consistent with calbindin patches as structurally preserved functional compartments, they do not provide proof for this concept. However, the functional relevance of most cortical modules is poorly understood (Horton and Adams, 2005), and they have been described as a mere byproduct of cortical development. Resolving these questions will require as a first step knowledge about the connectivity within and between modules such as calbindin patches. Only a few studies have investigated projection patterns of individual pyramidal cells in the entorhinal cortex area (Lorente de No, 1933; Klink and Alonso, 1997). Studies in the superior colliculus have indicated structure–function relationships (Mana and Chevalier, 2001), and future studies will be needed to address whether clustered intrinsic connections similar to those described in other regions of cortex (Rockland and Lund, 1983; Gilbert and Wiesel, 1983; Lund et al., 1993) are present in the entorhinal cortex and how they relate to functional (Barry et al., 2007; Brun et al., 2008; Stensola et al. 2012) and anatomical modules (Burgalossi and Brecht, 2014).

Cholinergic innervation differs across mammalian species

Acetylcholinesterase shows a modular staining pattern at the layer 1/2 border of rodent medial entorhinal cortex (Mathisen and Blackstad, 1964; Slomianka and Geneser, 1991). In primates, increased acetylcholinesterase activity has been described as coinciding either with stellate cell clusters (Solodkin and Van Hoesen, 1996) or with pyramidal cell clusters in between the stellate cells (Bakst and Amaral, 1984), depending on the subregion of entorhinal cortex studied (Bakst and Amaral, 1984). Although the distribution of acetylcholinesterase is similar in mice and rats, in Egyptian fruit bats, there is little overlap between acetylcholinesterase modules and calbindin patches (Fig. 7A,B). Interestingly, the most dorsal aspect of the bat entorhinal cortex (Yartsev et al., 2011) contains very few calbindin‐positive cells, a feature often ascribed to the neighboring parasubiculum in rodents. Further studies will need to investigate whether this type of entorhinal architecture is special to bats or more widespread among mammals. Similarly, it is not known whether the alignment of the patches to layer 1 axons and the parasubiculum described in rats (Ray et al., 2014) applies to all species.

Grid cells in rodents show increased theta rhythmicity compared with other cells in entorhinal cortex (Hafting et al., 2005). Blocking septal inputs to the entorhinal cortex has been shown to abolish grid cell activity (Koenig et al., 2011; Brandon et al., 2011), and it was suggested that in particular the cholinergic septal input to the entorhinal cortex is essential for grid cell firing (Newman et al., 2013). We found that calbindin‐positive cells in rats show increased theta rhythmicity and appear to receive more cholinergic input compared with calbindin‐negative cells (Ray et al., 2014), and that grid cells may preferentially correspond to this calbindin‐positive pyramidal cell population (Tang et al., 2014). In Egyptian fruit bats, grid cells do not oscillate in the theta frequency range (Yartsev et al., 2011). If cholinergic inputs are important for theta rhythmicity, it will be interesting to investigate whether there is a link between the lack of theta oscillations in grid cells in bats and the low amount of overlap between cholinergic inputs and calbindin patches reported here. The preferential cholinergic input to calbindin patches in rodents, as well as the lack thereof in bats and humans, suggests a link between cholinergic inputs and theta modulation of grid cells (Yartsev et al., 2011).

Relation of rodent medial and primate caudal entorhinal cortex

In caudal human entorhinal cortex we observed regularly arranged calbindin patches, which were superimposed onto a spatially scattered population of putative stellate cells. This arrangement is remarkably similar to the cellular organization of the rat medial entorhinal cortex (Ray et al., 2014). This finding supports earlier conclusions (Bakst and Amaral, 1984) that the medial entorhinal cortex of rodents corresponds to the dorsocaudal part of the entorhinal cortex in primates, because both are close to the parasubiculum and presubiculum. Lateral entorhinal cortex is located more rostral and medial entorhinal cortex more caudal in the rat. Larger brains have a greatly enlarged neocortex so that the entorhinal cortex is now on the medial side of the brain, but the topography of medial entorhinal cortex at the caudal end and lateral entorhinal cortex at the rostral end is likely to be conserved (Insausti, 1993).

Quantitative analysis of neuron number in calbindin patches and stellate cell islands in entorhinal cortex

Converging evidence from physiology, anatomy, and cell biology indicates that principal cells in layer 2 of entorhinal cortex divide into at least two very distinct types of principal cells: calbindin‐positive pyramidal cells and stellate cells. As described previously for the rat (Ray et al., 2014) and also shown in Figure 8B and C for the human, medial/caudal entorhinal cortex contains calbindin‐positive pyramidal cell patches and scattered stellate cells (Fig. 8E). These modules are different from the stellate cell islands (Fig. 8B,I) in rostral entorhinal cortex that have been extensively characterized in the human brain. In total, there are on average 121 entorhinal stellate islands in the left hemisphere and 111 modules in the right hemisphere of the human brain (Simic et al., 2005). Simic et al. (2005) also estimated the subset of entorhinal cortex layer 2 cells contained in cellular clusters to be 4.68 × 10⁵ in the left and 4.05 × 10⁵ in the right hemisphere. From these data one can calculate that there may be close to 4,000 neurons in one entorhinal stellate cell island. This number is quite different from our count of ∼800 calbindin‐positive neurons per calbindin patch. In two species of fruit bats, Gatome et al. (2010) estimated a fraction of ∼46% stellate cells, ∼24% pyramidal cells, and ∼29% cells of variable morphology in layer 2 of medial entorhinal cortex. The authors subdivide both stellate and pyramidal cells into two subclasses based on cell shape; however, the relation of these subclasses to immunohistochemical markers is not known. In the mouse, Fujimaru and Kosaka (1996) estimated that there are about 600 calbindin‐positive neurons in the dorsal half of medial entorhinal cortex; ∼75% of these were in layer 2. If we assume that there are five to six calbindin patches in the dorsal half of mouse medial entorhinal cortex (Fig. 3B), our estimates of calbindin‐positive cell number per patch are in agreement with the data of Fujimaru and Kosaka (1996). Peterson et al. (1996) provided the most extensive cell type–specific quantification of rat entorhinal cortex layer 2 neurons. They estimated that ∼32 % of all layer 2 neurons are calbindin‐positive and that of those, ∼88% were glutamatergic. We find a similar fraction of calbindin‐positive neurons (Ray et al., 2014). However, given the total number of calbindin‐positive neurons estimated by Peterson et al. (1996) and our count of patch numbers, one would predict an ∼3‐fold higher number of calbindin‐positive neurons per patch in rats. This may be due to intrinsic variability in patch number or differences in the definition of areal borders. In addition, whereas in the mouse most calbindin‐positive neurons in layer 2 are within patches, in the rat deep layer 2 tangential sections show an almost uniform distribution of calbindin‐positive cells. Neuron density varies up to 5‐fold across the neocortical sheet (Collins et al., 2010) and up to 3‐fold even in well‐defined modules such as barrels (Meyer et al., 2013). Our counts indicate up to 2‐fold differences in the number of calbindin‐positive cells per patch, indicating a similar or lower variability of cell numbers within a species.

Constant size of calbindin patches and allometry of entorhinal cortex

In contrast to the variability of patches observed within species, our analysis suggests that calbindin patches are relatively “inelastic” in evolution and maintain a relatively constant size in mammals. When mammals of different brain sizes are compared, the allocortex takes up a large part of total brain volume in small mammals and a progressively smaller part in larger brained mammals (Stephan, 1983). This is mainly due to the enormous enlargement of the neocortex. When size differences are calculated independent of increased neocortical volume, it becomes clear that the entorhinal cortex, as well as the hippocampus and septum, are progressively enlarged in larger brained species (Stephan, 1983). The opposite is true for the olfaction‐related parts of the allocortex; therefore in small mammals the olfactory bulb is larger than the entorhinal cortex, whereas in primates this relation is reversed (Rose S, 1927). The calbindin patches only show a 10‐fold increase in cell numbers, when the brain shows ∼20,000‐fold increase in volume (∼2,300 fold increase in entorhinal cortex volume). Patches also only show an ∼5‐fold increase in diameter across these species, which is much smaller than the ∼13‐fold increase in size expected if the scaling of the patches is linear to the increase in entorhinal volume (∼2,300‐fold increase) or area (∼180‐fold increase). Earlier studies have also observed the relative inelasticity in the size of certain modules, like insular cortex patches (Manger et al., 1998) and visual cortex patches (Lund et al., 1993; Luhmann et al., 1986; Rockland et al., 1982).

In summary, we describe modular structures in the entorhinal cortex that are largely invariant in size, arrangement, and neuron numbers across five mammalian species; the structures span ∼100 million years of evolutionary divergence and an ∼20,000 fold difference in brain size.

CONFLICT OF INTEREST STATEMENT

The authors declare that they have no conflicts of interest.

ROLE OF AUTHORS

All authors had full access to all the data in the study and take responsibility for the integrity of the data and the accuracy of the data analysis. Study concept and design: RN, SR, MB. Acquisition of data: RN, SR, LL, MB. Analysis and interpretation of data: RN, SR, MB. Drafting of the manuscript: RN, SR, MB. Critical revision of the manuscript for important intellectual content: RN, SR, SP, LL, FLH, MB. Statistical analysis: RN, SR, MB. Obtained funding: FLH, MB. Administrative, technical, and material support: SP, LL, FLH, MB. Study supervision: MB.

Supporting information

All Supporting Information may be found in the online version of this article

Supporting Information

Supporting Information