Highlight
A synthesis of existing data reveals differences in the temperature responses of Rubisco kinetics among higher plants, with important consequences for photosynthesis modeling.
Keywords: Activation energy, adaptation, carboxylation, meta-analysis, photosynthesis, temperature dependences.
Abstract
The present study provides a synthesis of the in vitro and in vivo temperature responses of Rubisco Michaelis–Menten constants for CO2 (Kc) and O2 (Ko), specificity factor (Sc,o) and maximum carboxylase turnover rate () for 49 species from all the main photosynthetic kingdoms of life. Novel correction routines were developed for in vitro data to remove the effects of study-to-study differences in Rubisco assays. The compilation revealed differences in the energy of activation (∆Ha) of Rubisco kinetics between higher plants and other photosynthetic groups, although photosynthetic bacteria and algae were under-represented and very few species have been investigated so far. Within plants, the variation in Rubisco temperature responses was related to species’ climate and photosynthetic mechanism, with differences in ∆Ha for among C3 plants from cool and warm environments, and in ∆Ha for and Kc among C3 and C4 plants. A negative correlation was observed among ∆Ha for Sc/o and species’ growth temperature for all data pooled, supporting the convergent adjustment of the temperature sensitivity of Rubisco kinetics to species’ thermal history. Simulations of the influence of varying temperature dependences of Rubisco kinetics on Rubisco-limited photosynthesis suggested improved photosynthetic performance of C3 plants from cool habitats at lower temperatures, and C3 plants from warm habitats at higher temperatures, especially at higher CO2 concentration. Thus, variation in Rubisco kinetics for different groups of photosynthetic organisms might need consideration to improve prediction of photosynthesis in future climates. Comparisons between in vitro and in vivo data revealed common trends, but also highlighted a large variability among both types of Rubisco kinetics currently used to simulate photosynthesis, emphasizing the need for more experimental work to fill in the gaps in Rubisco datasets and improve scaling from enzyme kinetics to realized photosynthesis.
Introduction
According to the Farquhar, von Caemmerer and Berry (1980) model of C3 photosynthesis (FvCB model; Farquhar et al., 1980; von Caemmerer, 2000), under physiologically relevant conditions, CO2 fixation rates are limited by the carboxylation of ribulose-1,5-bisphosphate (RuBP). RuBP carboxylation in turn is either limited by the regeneration of RuBP (typically by the rate of photosynthetic electron transport) or by the activity of the carboxylating enzyme, RuBP carboxylase/oxygenase (Rubisco). The limitations imposed by Rubisco result from its notorious catalytic inefficiencies, including slow catalysis and imperfect discrimination between CO2 and O2 (Whitney et al., 2011). Due to these inefficiencies, plants need to accumulate high amounts of Rubisco, and lose significant amounts of previously fixed CO2 and NH3 in the process of photorespiration (Keys, 1986). Indeed, a slow rate of catalysis and competitive inhibition by O2 not only limit the rate of CO2 fixation, but also compromise the capacity of photosynthetic organisms for optimal use of water and nitrogen, the key limiting resources. Not surprisingly, Rubisco has been listed among the most obvious targets to improve the photosynthetic capacity of crops (Long et al., 2006; Galmés et al., 2014a). Theoretical estimations indicate that reducing these Rubisco inefficiencies could deliver increases in net photosynthesis of up to 60% in the mid-term (Murchie et al., 2008; Zhu et al., 2010).
The quantitative impacts of Rubisco inefficiencies depend on the environmental conditions during catalysis. For instance, under drought stress conditions, RuBP oxygenation is favored over carboxylation because of the lower concentration of CO2 ([CO2]) at the active sites of Rubisco due to reduced rate of CO2 diffusion through stomata and leaf mesophyll (Chaves et al., 2009; Cornic and Massacci, 2004; Flexas et al., 2004; Niinemets and Keenan, 2014). Furthermore, at any given [CO2], Rubisco catalysis is also strongly affected by temperature. In particular, the maximum carboxylase turnover rate () of Rubisco increases up to 50–55 ºC or even higher for some organisms from extreme environments (Galmés et al., 2015 for a review), while the Rubisco specificity factor (Sc/o) decreases and the Michaelis–Menten constants for CO2 (Kc) and O2 (Ko) increase (Bernacchi et al., 2001). Although the basic patterns of temperature-dependent variation in key Rubisco kinetic characteristics are well known and measured in a number of studies, there is surprisingly limited comparative information of the variability of temperature responses of Rubisco across different photosynthetic groups that evolved at different periods of time, as well as among photosynthetic organisms adapted to different environmental conditions.
Considerable variation exists in the catalytic properties of Rubisco among distant phylogenetic groups with different Rubisco types (Jordan and Ogren, 1981; Keys, 1986; Raven, 2000; Savir et al., 2010; Whitney et al., 2011), but also within closely related taxa (Galmés et al., 2005, 2014b, c; Kubien et al., 2008; Ishikawa et al., 2009). Several lines of evidence suggest that the most likely factor shaping the specialization in Rubisco kinetics among higher plants is the availability of CO2 at the active sites of the enzyme in the chloroplastic stroma (Delgado et al., 1995; Raven, 2000; Young et al., 2012; Galmés et al., 2014b, c). Importantly, optimization of Rubisco kinetic traits to the prevailing [CO2] has inevitably to deal with the trade-off between Rubisco affinity for CO2 and enzyme turnover rate (Badger and Andrews, 1987; Tcherkez et al., 2006; Savir et al., 2010). Thus, evolution in Rubisco catalytic properties in species with the C4 carbon concentration mechanism has led to increased and Kc (Ghannoum et al., 2005; Kubien et al., 2008). In contrast, C3 species with lower [CO2] at the carboxylation site, especially species from dry, warm and saline habitats, are characterized by lower Kc and (Galmés et al., 2005, 2014c).
Similar to the [CO2]-driven evolution of Rubisco, other evidence suggests that the evolution of the enzyme’s catalytic traits has also been driven by the prevailing growth temperature (Sage, 2002; Galmés et al., 2005; Tcherkez et al., 2006; Yamori et al., 2006; Cavanagh and Kubien, 2013). A broad compilation of the temperature dependences of confirmed the existence of a notable natural variation in Rubisco thermal tolerance (Galmés et al., 2015). More importantly, within the land plants, the energy of activation of was positively correlated with the species’ thermal environment. A recent study further provided evidence that the evolutionary adjustment in the temperature sensitivity of Rubisco kinetic properties differed between C3 and C4 species of Flaveria (Perdomo et al., 2015).
From a practical perspective, the accuracy of the FvCB model in simulating temperature responses of leaf photosynthesis for any given species requires information on the species-specific temperature dependences of the Rubisco catalytic constants, in particular, Kc, Ko, Sc/o (or the photosynthetic CO2 compensation point in the absence of mitochondrial respiration, Γ*) and (von Caemmerer, 2000; Bernacchi et al., 2001; Walker et al., 2013). Indeed, recent modeling indicates that the temperature dependence of Rubisco kinetics dictates the optimum temperature for the photosynthetic rate (Galmés et al., 2014a). So far, application of the FvCB model to leaf photosynthesis has used three main datasets of temperature dependences of Rubisco kinetics: Badger and Collatz (1977) for Atriplex glabriuscula (in vitro measurements, used also in the original FvCB model), Jordan and Ogren (1984) for Spinacia oleracea (in vitro measurements) and Bernacchi et al. (2001) for Nicotiana tabacum (determined from in vivo leaf gas-exchange measurements in transgenic lines with reduced Rubisco content where photosynthesis was assumed to be limited by Rubisco under all [CO2] and leaf temperature combinations). These three datasets are widely used in modeling photosynthesis of species, plant stands, landscapes and biomes, whereas the use of any one of the three datasets mainly reflects the historical roots of the given modeling community (e.g. Niinemets et al., 2009a, b; Keenan et al., 2010; Galmés et al., 2011a; Bermúdez et al., 2012; Bernacchi et al., 2013; Bagley et al., 2015; see also Niinemets et al., 2015 for an analysis of the frequency of use of different Rubisco datasets across studies). Implicit in the use of a single species’ temperature response of Rubisco kinetics is that the variability among these responses is small across species spanning biomes with extensive variations in temperature and water availability. However, already comparisons of the in vitro A. glabriuscula and S. oleracea data and N. tabacum in vivo data have indicated that the variability is profound (Bernacchi et al., 2001). More recently, Walker et al. (2013) compared in vivo temperature dependences of Rubisco catalytic constants between Arabidopsis thaliana and N. tabacum and demonstrated that species-dependent differences in Rubisco kinetics do alter simulations of leaf photosynthesis.
Overall, the need for accurate estimations of the temperature dependences of Rubisco kinetic parameters has become apparent as mathematical modelers try to predict the impact of increasing global temperatures on plant productivity (Sage and Kubien, 2007; Gornall et al., 2010). As the natural variation in temperature responses of has been analysed in a recent compilation (see above, Galmés et al., 2015), temperature responses of can be included in models separately for different species groups from warm and cold habitats, but no such synthetic analysis exists for temperature responses of other key Rubisco characteristics, Kc, Ko and Sc/o. Construction of such integrated datasets has been difficult due to limited in vivo data and multiple complications with in vitro measurements. Among such complications for in vitro studies are study-to-study differences in the assay medium composition and in the values of physico-chemical characteristics used in the estimation of the concentrations of CO2 and O2 in the assay medium (e.g. Yokota and Kitaoka, 1985 for highlighting the problem). The present work aims to fill this gap and to provide a comprehensive analysis of the available temperature responses of Rubisco kinetics. The specific objectives of our analysis were: (i) to compile all available temperature responses of Rubisco, and to normalize the temperature parameters of different species to standard conditions for comparative purposes, (ii) to examine differences in the temperature parameters for the Rubisco kinetics from different species, (iii) to determine whether these differences are related to the phylogeny and/or the ecology of the species, (iv) to compare the temperature parameters of Rubisco kinetics derived from in vivo and in vitro measurements, and (v) to quantify the impact of these differences on model estimates of Rubisco-limited photosynthesis.
Methods
Data on the in vitro and in vivo Rubisco kinetic parameters, specificity factor (Sc/o) and Michaelis–Menten constants for CO2 (Kc) and O2 (Ko) at varying temperature were compiled from peer-reviewed literature identified by Thompson-Reuters ISI Web of Science (Philadelphia, PA, USA).
In vitro data compilation
The in vitro database consisted of the following information: article bibliographic data, species name, cultivar name for agricultural plants and strain name for bacteria (where reported), measurement temperature (T) and pH, the ionic composition of the assay buffer, headspace gas composition and, wherever available, the ionic strength of the assay solution and the acidity constant of dissolved CO2 () used to estimate the CO2 concentration in solution () from added bicarbonate concentration at given solution pH. Wherever relevant data were missing, article authors were contacted and obtained information was included in the database (see the Acknowledgements section).
The information about the assay buffer composition was needed to correct for study-to-study differences in the solution CO2 and O2 concentrations. In particular, the key issue with in vitro data is that the solubility of gases and the equilibrium coefficients of bicarbonate, which is commonly used as the source for CO2, depend on solution temperature and composition (Yokota and Kitaoka, 1985). While early studies have often used the O2, CO2 and bicarbonate equilibrium characteristics for pure water, it was later realized that depends on solution ionic strength (Yokota and Kitaoka, 1985) with major implications for estimates of Kc. However, solution composition also affects the solubility of O2 and thereby the estimation of Ko, and both differences in bicarbonate equilibrium and O2 solubility affect estimation of Sc/o. Furthermore, equilibrium constants are needed to convert between gas- and liquid-phase equivalent values of Kc, Ko and Sc/o. This means that major differences among the estimates of these characteristics across studies can simply result from differences in the equilibrium constants used. Although the general importance of physico-chemical characteristics in Rubisco assays is well understood by the Rubisco research community, studies continue using different estimates of physico-chemical characteristics. In this study, the information on assay buffer characteristics was employed to correct for differences in Rubisco characteristics resulting from varying equilibrium coefficients used.
Across all analysed literature reporting in vitro data, the temperature response of Sc/o was obtained from 12 different studies: Badger and Collatz (1977), Jordan and Ogren (1984), Lehnherr et al. (1985), Uemura et al. (1997), Zhu et al. (1998), Galmés et al. (2005), Haslam et al. (2005), Yamori et al. (2006), Gubernator et al. (2008), Boyd et al. (2015), Perdomo et al. (2015) and Hermida-Carrera et al. (2016). These studies provided estimates for 38 species (n=1 for Proteobacteria and Rhodophyta; n=2 for Cyanobacteria; n=4 for Bacillariophyta; n=30 for Spermatophyta).
The temperature response of in vitro Kc was obtained from the following studies: Laing et al. (1974), Badger and Collatz (1977), Badger (1980), Jordan and Ogren (1984), Lehnherr et al. (1985), Castrillo (1995), Wei et al. (1994), Boyd et al. (2015), Perdomo et al. (2015), Young et al. (2015) and Hermida-Carrera et al. (2016) providing information for 21 species (Cyanobacteria, n=1; Bacillariophyta, n=2; Spermatophyta, n=18). Finally, data on the temperature response of in vitro Ko for five species (all Spermatophyta) were obtained from Laing et al. (1974), Badger and Collatz (1977), Jordan and Ogren (1984), Lehnherr et al. (1985) and Boyd et al. (2015).
The specific temperatures at which the Rubisco kinetic parameters were measured differed among the original studies, but compiled studies reported measurements for at least three different temperatures, except the data from Jordan and Ogren (1984) for Rhodospirillum rubrum, and Young et al. (2015) for Thalassiosira weissflogii and Fragilariopsis cylindrus, with two assayed temperatures.
Initially, four additional datasets were incorporated in the database, but were ultimately not used in the analyses due to following reasons. In the case of Triticum aestivum, the data of Hall and Keys (1983) for the temperature response of Sc/o and Mächler and Nösberger (1980) for the temperature response of Kc presented a large scatter. Analogously, Kc temperature response for Agropyron smithii in Monson et al. (1982) had a large scatter and evidence of non-monotonic temperature response (r of only 0.83 for the linear regression between measured and predicted values compared with r>0.95 for all other in vitro Kc data) and was therefore not included in comparison of Kc temperature responses. However, it was used in the comparison between in vitro and in vivo data to highlight the potential uncertainties among different types of data. The Sc/o for Thermococcus kodakariensis of Ezaki et al. (1999) increased with increasing the measurement temperature contrary to all other data, and these data were therefore deemed unreliable.
The temperature responses of from Galmés et al. (2015) for 49 species (Archaea, n=1; Cyanobacteria, n=3; Proteobacteria, n=4; Rhodophyta, n=1; Chlorophyta, n=4; Spermatophyta, n=36) were also included for an integrated analysis of the relationships between the temperature dependence of the different kinetic parameters of Rubisco.
Correction of in vitro data for differences in the equilibrium coefficients used
In the case of Kc, the buffer composition-corrected value (Kc,c) and measured (Kc,m) value depend on the solution pH and used (pKa,u) and buffer composition-corrected (pKa,c) acidity constants of dissolved CO2. For the typical pH ranges used in Rubisco assays, the undissociated carbonic acid concentration is negligible (<10−10 M), and = −log([H+][HCO3−]/), where [H+] is the hydrogen ion concentration and [HCO3−] the bicarbonate concentration. Thus, Kc,c is given as:
| (1) |
Yokota and Kitaoka (1985) have proposed an equation to estimate pKa,c values based on the solution ionic strength and temperature. However, their equation was based on only one study (Harned and Bonner, 1945), and included only three parameters such that it was accurate only over the temperature range of 10–35 °C (Yokota and Kitaoka, 1985). Because Kc,c depends highly non-linearly on pKa,c (Eq. 1), we considered it essential to improve estimation of pKa,c. Thus, we conducted a meta-analysis of published pKa,c values reported for different solution temperatures (0–50 °C) and ionic strengths (0–1.042M). Altogether, 105 estimates of pKa,c were obtained (Shedlovsky and MacInnes, 1935; Harned and Davis, 1943; Harned and Bonner, 1945; Pocker and Bjorkquist, 1977; Schumacher and Smucker, 1983; Yokota and Kitaoka, 1985). To convert the molal concentrations reported in some studies, including Harned and Bonner (1945), to the corresponding molar concentrations, water density at different solute concentrations and temperatures was estimated using a polynomial equation based on data of Weast (1974).
Consistent with the Debye–Hückel theory of non-ideality of solutions, and as common in analytical chemistry studies fitting pKa values of different buffer substances (e.g. Bates et al., 1973; Roy et al., 1998; Roy et al., 2009), we have used a series of log and polynomial terms to describe the dependence of pKa,c on absolute temperature (Tk, K) and solution ionic strength (Is, M) as:
| (2) |
where the values of the empirical coefficients are: a1=16400, a2=211.56, a3=−0.1291, a4=−533.63, s1=0.3252, s2=0.3830, s3=−0.2692, s4=−0.8503. Equation 2 provided an excellent fit to the data (r2=0.9985, mean squared error of 4.8×10−5), i.e. a considerable improvement compared with the equation of Yokota and Kitaoka (1985) (r2=0.981 for the Tk and Is range over which the equation was valid).
The ionic strength of the assay buffer was calculated considering all the ionic species in the solution. For weak acids and bases, including buffer substances, their pKa values were used to estimate the concentration of the ionic species in the solution. Again, multiple regression equations similar to Eq. 2 were developed for individual compounds to consider pKa dependences on Tk and Is based on published data (e.g. Bates et al., 1973; Feng et al., 1989; Roy et al., 2006, 2009, 2011). However, in the case of zwitterionic buffers, e.g. for HEPES (Vega and Bates, 1976; Feng et al., 1989; Roy et al., 2009) and Bicine (Datta et al., 1964; Azab et al., 1994; Roy et al., 2006), the effect of Is was not always important (but see Bates and Hetzer, 1961; Durst and Staples, 1972; Bates and Robinson, 1973; Ramette et al., 1977 for the Is dependence of Tris). Given the pKa dependence on Is and the Is dependence on pKa, Is and pKa for the given buffer solution were ultimately calculated iteratively.
In the case of Ko estimations, the gas-phase oxygen concentration , mol mol−1) was typically varied to achieve variation in the liquid-phase oxygen concentration , mol m−3). Thus, the key issue is how has been converted in . The concentrations in different phases are related through the Henry’s law constant (, Pa m3 mol−1) as:
| (3) |
where P (Pa) is the air pressure. We note that the word ‘constant’ is misleading, because Hpc for the given compound depends on temperature and other solutes that can affect the solubility of the compound of interest (Sander, 2001; Staudinger and Roberts, 2001; Copolovici and Niinemets, 2007). Dependence of Hpc on the presence of solutes has been largely ignored by the Rubisco community. Here, we use different subscripts to clearly denote these effects.
Several different conversion factors taken from physical chemical reference sources had been used across the studies (data not shown), but all of these factors were based on pure water. However, oxygen solubility is importantly driven by the solute concentrations (Tromans, 2000; Gnaiger, 2001; Millero and Huang, 2003). The overall solubility in complex media such as biological assay buffers is difficult to predict due to partly non-additive effects of different solutes (e.g. Gros et al., 1999). Thus, we have employed a simplified approach, and linked Hpc to total concentration of ions in solution. First, the value of Hpc for pure water, Hpc,0, was described in dependence on temperature using a polynomial equation in the form:
| (4) |
where the empirical coefficients have values c1=0.051816, c2=−42.437, c3=12977.3, c4=−1388072.1, which were derived from Millero and Huang (2003) and Millero et al. (2003). The value of Hpc corresponding to different solute concentrations, Cs (Hpc,s) was further described as:
| (5) |
where d1–d6 are empirical coefficients that we initially derived for different electrolytes. As the differences among electrolytes were small and due to difficulties with the non-additivity mentioned above, in this analysis, we used the empirical coefficients d1=1.4565, d2=−178.90, d3=−6.0556, d4=−0.7818, d5=54.240, d6=0.10796 derived for KCl (r2=0.9983 for the complete fit including both the temperature effects on described by Eq. 4 and the denominator) based on the data of Millero and colleagues (Millero et al., 2002, 2003; Millero and Huang, 2003). The implication of Eq. 5 is that the O2 solubility in ionic media is less, ca 3% at 0 °C and 1.5% at 50 °C, than in pure water (the salting-out effect, Table 1). Ultimately, the liquid-phase Ko values reported, Ko,m, were corrected for solute effects as:
Table 1.
Henry’s law constants (Pa m3 mol−1) for conversion of Rubisco kinetic characteristics among gas- and liquid-phase equivalent values (Eqs 8–10)
| Gas | Medium | Temperature (ºC) | |||
|---|---|---|---|---|---|
| 15 | 25 | 35 | 45 | ||
| CO2 | Pure water | 2186 | 2982 | 3867 | 4777 |
| CO2 | Chloroplast | 2230 | 3041 | 3944 | 4873 |
| O2 | Pure water | 67 510 | 82 080 | 97 430 | 113 870 |
| O2 | Chloroplast | 69 260 | 83 950 | 99 370 | 115 840 |
Henry’s law constant (Hpc) is the gas–liquid phase equilibrium partition coefficient and is given as the ratio of the gas partial pressure (Pa) and corresponding liquid-phase concentration (mol m−3, Eq. 3). Because the gas solubility depends on the presence of other solutes (salting-out effect), Hpc typically increases with increasing solute concentration. Equation 4 was used to estimate values of Hpc at different temperatures for pure water, and Eq. 5 for chloroplastic water. In the latter calculation, the dominant solute was assumed to be KCl and the solute concentration was taken as 0.11M. Derivation of Eqs 4 and 5 with supporting references and review of chloroplast solute concentrations is provided in the Methods.
| (6) |
where Hpc,u is the value of the Henry’s law constant used at the given temperature in the original studies.
Estimates of the specificity factor, Sc/o, depend on both differences in pKa values used for the acidity constant of dissolved CO2 (pKa,u) and Henry’s law constant for O2. Thus, the Sc/o measurements, Sc/o,m, were converted to a common set of equilibrium coefficients as:
| (7) |
In vivo database
In the case of in vivo estimates (only available for Spermatophyta), the database included the following: article bibliographic data, species name, cultivar name for agricultural plants, measurement temperature (T) and details of the measurement methods used (e.g. gas exchange combined with chlorophyll fluorescence, gas exchange and carbon isotopic discrimination, gas exchange and 14CO2 uptake, indicating whether the leaf mesophyll conductance and mitochondrial respiration were considered when deriving Rubisco kinetic parameters). Typically, values of Kc, Ko and/or Sc/o were reported for the gas phase (Kc,g, Ko,g, and Sc/o,g), but when available, liquid-phase equivalent values of these characteristics and corresponding values of Henry’s law constants used were also included in the database. The gas-phase estimates of Rubisco characteristics estimated in in vivo studies themselves do not require any standardization, but as the Rubisco reaction takes place in the liquid phase, corresponding liquid-phase estimates are needed to compare Rubisco kinetics among species. The gas-phase estimates of Rubisco kinetic characteristics were converted to liquid-phase equivalent values (Kc,liq, Ko,liq, Sc/o,liq) using the following equations:
| (8) |
| (9) |
| (10) |
where the Henry’s law constant for O2, , is given by Eq. 5 and that for CO2, Hpc,s,CO2, was derived analogously (Table 1 for estimates of Henry’s law constant at different temperatures). For pure water, the temperature dependence of was derived analogously to that for O2 (Eq. 4) using an extensive set of values from published studies (van Slyke et al., 1928; Markham and Kobe, 1940; Harned and Davis, 1943; Umbreit et al., 1972; Rischbieter et al., 1996) to estimate the empirical coefficients as c1=−0.01081, c2=10.1188, c3=− 3065.93 and c4=304097.1 (r2=0.9994). These reference sources were further employed to fit Eq. 5 to solute concentrations, and values of d1=−2.8858, d2=−173.31, d3=18.718, d4=0.41177, d5=−32.719, d6=−0.050167 were derived for KCl (r2=0.9993 for the complete fit including both the temperature effects on as described by Eq. 4 and the denominator). KCl was used as K is the dominant solute in plant cells (Gupta and Berkowitz, 1988; Schröppel-Meier and Kaiser, 1988), but analogous fits using other electrolytes such as NaCl were similar (data not shown). Given that ionic concentrations in chloroplasts of non-stressed leaves are on the order of 0.09–0.15M in non-dissociated salt equivalents used in developing Eq. 5 (Gupta and Berkowitz, 1988; Schröppel-Meier and Kaiser, 1988), we have taken Cs as 0.11M in this analysis. For comparison, an equivalent average value of 0.08M was estimated across the in vitro studies (assuming a non-dissociated salt consisting of two monovalent ions). When in vivo studies reported liquid-phase equivalent values of Rubisco kinetic characteristics, they were again converted to a common set of equilibrium constants. In the case of Kc and Ko, Eq. 6 was used with corresponding Henry’s law constant values for CO2 and O2, while the values of Sc/o were standardized as:
| (11) |
In vivo data on the temperature response of Sc/o were obtained from five different studies: Brooks and Farquhar (1985), Ghashghaie and Cornic (1994), Bernacchi et al. (2001), Viil et al. (2012) and Walker et al. (2013) providing information for six species. The temperature responses of in vivo Kc were obtained from the following studies: Monson et al. (1982), Harley et al. (1985), Bernacchi et al. (2001) and Walker et al. (2013) yielding data for four species. The temperature responses of in vivo Ko for three species were extracted from Harley et al. (1985), Bernacchi et al. (2001) and Walker et al. (2013). Across all these studies, mesophyll conductance (gm) had been considered, and accordingly Rubisco kinetics based on chloroplastic CO2 concentration had been derived, only in the study of Walker et al. (2013). In all other studies, Rubisco kinetics had been derived based on intercellular CO2 concentration. Although Bernacchi et al. (2002) have reported the temperature kinetics of gm, the Rubisco temperature characteristics of Bernacchi et al. (2001) cannot be readily converted to chloroplastic CO2 concentration based estimates using these independent measurements of gm. This is because at any given value of gm, the CO2 drawdown between the intercellular airspace and chloroplasts can vary due to differences in foliage anatomical characteristics and leaf photosynthetic capacity (Niinemets et al., 2009a; Tomás et al., 2013).
Species’ phylogenetic and ecological characteristics grouping
Species were grouped into the main phylogenetic groups Archaea, Proteobacteria, Cyanobacteria, Rhodophyta, Chlorophyta, Bacillariophyta and Spermatophyta. The average optimum growth temperature (Tgrowth) for each species was obtained from the literature or assigned according to the species’ climatic range as in Galmés et al. (2015). Spermatophytes were further classified according to their photosynthetic mechanism and Tgrowth as C3 plants from warm environments (Tgrowth≥25 ºC), C3 plants from cool environments (Tgrowth<25 ºC) and C4 plants. The arbitrary threshold of 25 ºC was based on analogous studies (Sage, 2002; Galmés et al., 2015).
Fitting the temperature responses
The temperature response curves of the kinetic parameters obtained from the original data were fitted for each individual temperature response dataset by an Arrhenius-type temperature response function:
| (12) |
where c is the scaling constant for the parameter, ∆Ha (J mol−1) is the activation energy, T (K) is the temperature and R is the universal gas constant (8.314 J mol−1 K−1). Equation 12 was fitted to the data by iteratively minimizing the sum of squares between the measured and predicted values of each kinetic parameter using the Microsoft Excel Solver function.
The temperature response curves of the kinetic parameters were also fitted by second- and third-order polynomial equations in the form of:
| (13) |
| (14) |
As the actual measurement temperatures differed across studies, the Arrhenius-type and polynomial equations (Eqs 12–14) were further used to calculate the standardized values of each parameter at 5, 15, 25, 35 and 45 ºC for each species. These values were used to obtain the Q10 value over the temperature intervals of 5–15, 15–25, 25–35 and 35–45 ºC. We also reanalysed the temperature data described in Galmés et al. (2015) to calculate the Q10 values.
To compare the different functions, the correlation coefficient (r) was calculated for linear regressions for predicted vs. measured values by SigmaPlot 11.0 (Systat Software, Inc., San Jose, CA, USA) as a measure of goodness of the fits.
Simulation of temperature responses of Rubisco-limited photosynthesis
We used the photosynthesis model of Farquhar et al. (1980) to quantify the importance, in terms of Rubisco-limited CO2 gross assimilation rate (ARubisco), of different thermal sensitivities of Rubisco kinetics from C3 plants from cool and warm environments. ARubisco only provides the potential estimate of photosynthesis rate supported by a given set of Rubisco characteristics under RuBP-saturated conditions (Farquhar et al. 1980). The extent to which this potential is realized depends on the rate of RuBP regeneration, which in turn is driven by the actual light level, the capacity of RuBP regeneration (typically determined by the capacity for photosynthetic electron transport) and the temperature dependence of RuBP regeneration (Farquhar et al. 1980; Galmés et al. 2014a). Although this complicates interpretation of differences in ARubisco temperature responses, we note that over the ambient temperature range of 15–40 ºC, Rubisco characteristically operates in RuBP-saturated conditions at higher light (photosynthetic quantum flux density greater than ca 400 μmol m−2 s−1) and lower CO2 concentrations (chloroplastic CO2 concentration, Cc, less than ca 200 μmol mol−1) with the actual crossover between Rubisco-limited and RuBP-limited conditions depending on combinations of light, Cc, temperature and temperature responses of ARubisco and RuBP regeneration (Farquhar et al. 1980; Galmés et al. 2014a). In these simulations, group-specific average temperature parameters for Sc/o, Kc and were used (Table 3), while the temperature dependence parameters of Ko were considered invariable among plant functional types. They were obtained as the average of the four reported in vitro values for C3 plants (c=9.9 and ∆Ha=9.7 kJ mol−1, see Table 2 for single species data). A value of of 2.5s−1 at 25 ºC and a leaf Rubisco content of 2g m−2 (equivalent to a concentration of 29 μmol catalytic sites m−2) were used for all plant functional types. The values of the deactivation energy (∆Hd) and the entropy term (∆S) for used for the different plant functional types were taken from Galmés et al. (2015): C3 plants from cool habitats, ∆Hd=305 kJ mol−1, ∆S=929 J mol−1 K−1; C3 plants from warm habitats, ∆Hd=220 kJ mol−1, ∆S=664 J mol−1 K−1; C3 average, ∆Hd=258 kJ mol−1, ∆S=782 J mol−1 K−1.
Table 3.
Average temperature dependence parameters of the in vitro-measured Rubisco specificity factor for CO2/O2 (Sc/o), the Michaelis–Menten constant for CO2 (Kc) and the Rubisco maximum carboxylase turnover rate ()
| Group | n | c | ∆Ha
(kJ mol−1) |
Tgrowth
(ºC) |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sc/o | ||||||||||||
| Proteobacteria | 1 | −5.2 | −18.8 | 0.75 | 0.77 | 33 | ||||||
| Cyanobacteria | 2 | −6.9±6.0 | −27.4±15.6 | 0.68±0.16 | 0.70±0.15 | 0.71±0.14 | 0.73±0.14 | 50.5±5.5 | ||||
| Rhodophyta | 1 | −10.3 | −38.7 | 0.56 | 0.58 | 0.60 | 0.62 | 45 | ||||
| Bacillariophyta | 4 | −4.2±1.0 | −21.3±2.3 | 0.73±0.02 | 0.74±0.02 | 0.76±0.02 | 0.77±0.02 | 7.8±4.6 | ||||
| Spermatophyta | 30 | −4.2±0.2 | −21.5±0.4 | 0.73±0.01 | 0.74±0.01 | 0.75±0.01 | 0.77±0.01 | 25.0±0.7 | ||||
| Spermatophyta (C3 plants) | 24 | −4.1±0.2 | −21.4±0.4 | 0.73±0.01 | 0.75±0.01 | 0.76±0.01 | 0.77±0.01 | 24.0±0.8 | ||||
| Spermatophyta (C3 plants from cool habitats) | 8 | −3.5±0.3b | −19.9±0.6b | 0.74±0.01b | 0.77±0.01b | 0.78±0.01b | 0.79±0.01b | 19.5±0.5a | ||||
| Spermatophyta (C3 plants from warm habitats) | 16 | −4.4±0.2a | −22.0±0.5ab | 0.72±0.01a | 0.74±0.01a | 0.75±0.01a | 0.76±0.01a | 26.3±0.6b | ||||
| Spermatophyta (C4 plants) | 6 | −4.8±0.5a | −22.3±1.2a | 0.72±0.01a | 0.73±0.01a | 0.75±0.01a | 0.76±0.01a | 29.2±0.8c | ||||
| Kc | ||||||||||||
| Cyanobacteria | 1 | 20.8 | 38.8 | 1.79 | 1.72 | 1.66 | 1.61 | 35 | ||||
| Bacillariophyta | 2 | 19.4±1.7 | 39.0±4.1 | 1.80±0.11 | 1.73±0.10 | 13.5±8.5 | ||||||
| Spermatophyta | 18 | 19.2±0.9 | 41.1±2.3 | 1.85±0.06 | 1.77±0.06 | 1.70±0.05 | 1.64±0.05 | 25.3±1.1 | ||||
| Spermatophyta (C3 plants) | 12 | 20.0±0.8 | 43.8±2.2 | 1.91±0.07 | 1.82±0.06 | 1.75±0.06 | 1.68±0.06 | 23.9±1.4 | ||||
| Spermatophyta (C3 plants from cool habitats) | 6 | 18.8±1.2a | 40.5±3.2ab | 1.79±0.09a | 1.71±0.09a | 1.64±0.09a | 1.58±0.08a | 19.3±0.7a | ||||
| Spermatophyta (C3 plants from warm habitats) | 7 | 20.9±1.1a | 46.1±2.8b | 2.01±0.09a | 1.92±0.08a | 1.84±0.07a | 1.77±0.06a | 27.9±1.0b | ||||
| Spermatophyta (C4 plants) | 5 | 17.2±2.0a | 34.7±4.7a | 1.70±0.13a | 1.64±0.11a | 1.59±0.10a | 1.54±0.09a | 29.0±1.0b | ||||
| Archaea | 1 | 15.2 | 37.2 | 1.75 | 1.68 | 1.63 | 1.58 | 85.0 | ||||
| Proteobacteria | 4 | 18.5±1.5 | 45.9±4.1 | 2.00±0.13 | 1.91±0.11 | 1.83±0.10 | 1.76±0.09 | 33.8±5.5 | ||||
| Cyanobacteria | 3 | 16.3±3.5 | 40.1±8.9 | 1.86±0.26 | 1.78±0.23 | 1.71±0.21 | 1.66±0.19 | 46.7±7.3 | ||||
| Rhodophyta | 1 | 30.8 | 76.3 | 3.14 | 2.91 | 2.71 | 2.55 | 57.0 | ||||
| Chlorophyta | 4 | 10.8±0.4 | 26.7±0.9 | 1.49±0.02 | 1.45±0.02 | 1.42±0.02 | 1.39±0.02 | 15.5±5.5 | ||||
| Spermatophyta | 36 | 23.5±0.7 | 58.1±1.7 | 2.43±0.07 | 2.28±0.06 | 2.16±0.05 | 2.06±0.05 | 24.9±0.9 | ||||
| Spermatophyta (C3 plants) | 26 | 24.3±0.9 | 60.2±2.3 | 2.51±0.09 | 2.35±0.08 | 2.23±0.07 | 2.11±0.06 | 23.1±1.0 | ||||
| Spermatophyta (C3 plants from cool habitats) | 12 | 22.3±0.8a | 55.3±2.0a | 2.30±0.07a | 2.18±0.06a | 2.07±0.05a | 1.98±0.05a | 18.3±0.8a | ||||
| Spermatophyta (C3 plants from warm habitats) | 14 | 26.0±1.4b | 64.5±3.5b | 2.68±0.15b | 2.51±0.13b | 2.36±0.11b | 2.23±0.10b | 27.2±0.7b | ||||
| Spermatophyta (C4 plants) | 10 | 21.3±0.5a | 52.8±1.3a | 2.22±0.05a | 2.10±0.04a | 2.00±0.03a | 1.91±0.03a | 29.6±0.4b |
The original data for Sc/o and Kc were taken from Table 2 and those for from Galmés et al. (2015). For Spinacea oleracea, Triticum aestivum and Flaveria pringlei, average values from Table 2 were used. The values are means±SE, except when n=1. Within Spermatophyta, significant differences among C3-cool, C3-warm and C4 species (P<0.05 according to one-way ANOVA followed by Duncan’s test) are denoted by different letters. The optimum growth temperature (Tgrowth) for each species is shown in Table 2. c, scaling constant; ∆Ha, activation energy; Q10 coefficient over the temperature intervals of 5–15 ºC (), 15–25 ºC (), 25–35 ºC () and 35–45 ºC ().
Table 2.
Temperature dependence parameters of in vitro-measured Rubisco catalytic constants
| Group | Species | Reference |
Tmeas
(ºC) |
c | ∆Ha
(kJ mol−1) |
r | Tgrowth (ºC) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sc/o | |||||||||||||||
| Proteobacteria | Rhodospirillum rubruma | Jordan and Ogren (1984)a | 2–25 | −5.2 | −18.8 | n.d. | 0.75 | 0.77 | 33 | ||||||
| Cyanobacteria | Thermosynechococcus elongatus BP-1 | Gubernator et al. (2008) | 15–45 | −13.0 | −43.0 | 0.998 | 0.52 | 0.55 | 0.57 | 0.59 | 56 | ||||
| Synechococcus lividus | Zhu et al. (1998) | 15–35 | −0.9 | −11.7 | 0.999 | 0.84 | 0.85 | 0.86 | 0.87 | 45 | |||||
| Rhodophyta | Galdieria partita Tokara | Uemura et al. (1997) | 15–45 | −10.3 | −38.7 | 0.991 | 0.56 | 0.58 | 0.60 | 0.62 | 45 | ||||
| Bacillariophyta | Chaetoceros socialis | Haslam et al. (2005) | 10–25 | −3.2 | −18.7 | 0.975 | 0.76 | 0.77 | 0.78 | 0.80 | 10 | ||||
| Skeletonema costatum | Haslam et al. (2005) | 10–25 | −7.1 | −28.1 | 0.992 | 0.66 | 0.67 | 0.69 | 0.71 | 20 | |||||
| Thalassiosira antarctica | Haslam et al. (2005) | 10–25 | −3.8 | −20.3 | 0.963 | 0.74 | 0.75 | 0.77 | 0.78 | −0.5 | |||||
| Thalassiosira hyalina | Haslam et al. (2005) | 10–25 | −2.9 | −18.1 | 0.991 | 0.76 | 0.78 | 0.79 | 0.80 | 2 | |||||
| Spermatophyta (C3 plants from cool habitats) | Atriplex glabriuscula | Badger and Collatz (1977)b | 15–35 | −0.1 | −12.1 | 0.984 | 0.76 | 0.81 | 0.90 | 1.05 | 20 | ||||
| Avena sativa cv. Forridena | Hermida-Carrera et al. (2016)c | 15–35 | −2.9 | −18.4 | 0.998 | 0.76 | 0.77 | 0.79 | 0.80 | 20 | |||||
| Hordeum vulgare ssp. vulgare cv. Morex | Hermida-Carrera et al. (2016)c | 15–35 | −2.5 | −17.4 | 0.997 | 0.77 | 0.78 | 0.80 | 0.81 | 20 | |||||
| Lysimachia minoricensis | Galmés et al. (2005) | 15–35 | −4.2 | −21.4 | 0.989 | 0.73 | 0.74 | 0.76 | 0.77 | 20 | |||||
| Mentha aquatica | Galmés et al. (2005) | 15–35 | −4.2 | −21.4 | 0.996 | 0.73 | 0.74 | 0.76 | 0.77 | 20 | |||||
| Spinacea oleracea | Uemura et al. (1997) | 15–35 | −3.5 | −19.8 | 0.996 | 0.74 | 0.76 | 0.77 | 0.78 | 16 | |||||
| Spinacea oleracea | Zhu et al. (1998) | 15–35 | −2.6 | −17.6 | 0.999 | 0.77 | 0.78 | 0.79 | 0.81 | 16 | |||||
| Spinacea oleracea | Jordan and Ogren (1984) | 7–25 | −3.8 | −20.5 | 0.999 | 0.77 | 0.75 | 0.74 | 0.74 | 16 | |||||
| Spinacea oleracea cv. Torai | Yamori et al. (2006)d | 5–45 | −1.4 | −14.7 | 0.987 | 0.80 | 0.81 | 0.83 | 0.84 | 16 | |||||
| Spinacea oleracea | Average | −3.3 | −19.3 | 0.77 | 0.78 | 0.78 | 0.79 | 16 | |||||||
| Triticum aestivum | Haslam et al. (2005) | 10–25 | −3.7 | −20.5 | 0.997 | 0.74 | 0.75 | 0.76 | 0.78 | 20 | |||||
| Triticum aestivum | Hermida-Carrera et al. (2016)c | 15–35 | −3.4 | −19.7 | 0.999 | 0.74 | 0.76 | 0.77 | 0.79 | 20 | |||||
| Triticum aestivum | Average | −3.6 | −20.0 | 0.74 | 0.75 | 0.77 | 0.78 | 20 | |||||||
| Urtica atrovirens ssp. bianorii | Galmés et al. (2005) | 15–35 | −4.1 | −21.1 | 0.999 | 0.73 | 0.74 | 0.76 | 0.77 | 20 | |||||
| Spermatophyta (C3 plants from warm habitats) | Beta maritima ssp. marcosii | Galmés et al. (2005) | 15–35 | −4.4 | −22.0 | 0.999 | 0.72 | 0.73 | 0.75 | 0.76 | 25 | ||||
| Beta maritima ssp. maritima | Galmés et al. (2005) | 15–35 | −4.5 | −22.4 | 0.994 | 0.71 | 0.73 | 0.75 | 0.76 | 25 | |||||
| Diplotaxis ibicensis | Galmés et al. (2005) | 15–35 | −5.6 | −24.9 | 0.998 | 0.69 | 0.71 | 0.72 | 0.74 | 25 | |||||
| Flaveria cronquistii | Perdomo et al. (2015) | 10–40 | −3.5 | −19.5 | 0.985 | 0.75 | 0.76 | 0.77 | 0.79 | 30 | |||||
| Flaveria pringlei | Zhu et al. (1998) | 15–35 | −3.0 | −18.9 | 0.999 | 0.75 | 0.77 | 0.78 | 0.79 | 30 | |||||
| Flaveria pringlei | Perdomo et al. (2015) | 10–40 | −4.0 | −20.8 | 0.991 | 0.73 | 0.75 | 0.76 | 0.77 | 30 | |||||
| Flaveria pringlei | Average | −3.5 | −19.8 | 0.7 | 0.8 | 0.8 | 0.8 | 30 | |||||||
| Hypericum balearicum | Galmés et al. (2005) | 15–35 | −4.7 | −22.6 | 0.999 | 0.71 | 0.73 | 0.74 | 0.76 | 25 | |||||
| Kundmannia sicula | Galmés et al. (2005) | 15–35 | −4.9 | −23.2 | 0.996 | 0.71 | 0.72 | 0.74 | 0.75 | 25 | |||||
| Limonium gibertii | Galmés et al. (2005) | 15–35 | −5.1 | −24.1 | 0.999 | 0.70 | 0.71 | 0.73 | 0.74 | 25 | |||||
| Limonium magallufianum | Galmés et al. (2005) | 15–35 | −5.2 | −24.3 | 0.998 | 0.69 | 0.71 | 0.73 | 0.74 | 25 | |||||
| Pistacia lentiscus | Galmés et al. (2005) | 15–35 | −4.4 | −22.0 | 0.999 | 0.72 | 0.74 | 0.75 | 0.76 | 25 | |||||
| Rhamnus alaternus | Galmés et al. (2005) | 15–35 | −4.7 | −22.8 | 0.998 | 0.71 | 0.73 | 0.74 | 0.76 | 25 | |||||
| Rhamnus ludovici-salvatoris | Galmés et al. (2005) | 15–35 | −5.2 | −24.0 | 0.993 | 0.70 | 0.71 | 0.73 | 0.74 | 25 | |||||
| Trifolium repens (native ecotype) | Lehnherr et al. (1985) | 10–25 | −2.8 | −18.0 | 0.983 | 0.76 | 0.78 | 0.79 | 0.80 | 25 | |||||
| Urtica membranacea | Galmés et al. (2005) | 15–35 | −3.7 | −20.4 | 0.998 | 0.74 | 0.75 | 0.77 | 0.78 | 25 | |||||
| Flaveria angustifolia (C3–C4) | Perdomo et al. (2015) | 10–40 | −4.3 | −21.6 | 0.978 | 0.72 | 0.74 | 0.75 | 0.77 | 30 | |||||
| Flaveria floridana (C3–C4) | Perdomo et al. (2015) | 10–40 | −3.8 | −20.4 | 0.989 | 0.74 | 0.75 | 0.77 | 0.78 | 30 | |||||
| Spermatophyta (C4 plants) | Amaranthus hybridus | Jordan and Ogren (1984) | 5–35 | −7.0 | −27.9 | 0.998 | 0.66 | 0.68 | 0.69 | 0.71 | 30 | ||||
| Flaveria bidentis | Perdomo et al. (2015) | 10–40 | −3.8 | −20.0 | 0.994 | 0.74 | 0.76 | 0.77 | 0.78 | 30 | |||||
| Flaveria trinervia | Perdomo et al. (2015) | 10–40 | −4.3 | −21.4 | 0.999 | 0.73 | 0.74 | 0.76 | 0.77 | 30 | |||||
| Saccharum officinarum | Hermida-Carrera et al. (2016)c | 15–35 | −4.9 | −23.0 | 0.997 | 0.71 | 0.72 | 0.74 | 0.75 | 30 | |||||
| Setaria viridis | Boyd et al. (2015) | 10–40 | −4.6 | −21.3 | 0.950 | 0.73 | 0.74 | 0.76 | 0.77 | 25 | |||||
| Zea mays cv. Carella | Hermida-Carrera et al. (2016)c | 15–35 | −3.6 | −20.1 | 0.999 | 0.74 | 0.75 | 0.77 | 0.78 | 30 | |||||
| Kc | |||||||||||||||
| Cyanobacteria | Anabaena variabilis M3 | Badger (1980) | 15–40 | 20.8 | 38.8 | 0.989 | 1.79 | 1.72 | 1.66 | 1.61 | 35 | ||||
| Bacillariophyta | Fragilariopsis cylindrus | Young et al. (2015)e | 0–20 | 17.7 | 34.9 | n.d. | 1.69 | 1.63 | 5 | ||||||
| Thalassiosira weissflogii | Young et al. (2015)e | 0–20 | 21.1 | 43.0 | n.d. | 1.91 | 1.83 | 22 | |||||||
| Spermatophyta (C3 plants from cool habitats) |
Atriplex glabriuscula | Badger and Collatz (1977) | 5–35 | 15.9 | 32.4 | 0.987 | 1.63 | 1.57 | 1.53 | 1.49 | 20 | ||||
| Avena sativa cv. Forridena | Hermida-Carrera et al. (2016)c | 15–35 | 20.2 | 44.2 | 0.999 | 1.94 | 1.86 | 1.78 | 1.72 | 20 | |||||
| Espeletia schultzii | Castrillo (1995)f | 5–35 | 11.9 | 23.7 | 0.988 | 1.50 | 1.38 | 1.31 | 1.26 | 20 | |||||
| Hordeum vulgare ssp. vulgare cv. Morex | Hermida-Carrera et al. (2016)c | 15–35 | 16.2 | 34.6 | 0.999 | 1.68 | 1.62 | 1.57 | 1.53 | 20 | |||||
| Spinacia oleracea | Jordan and Ogren (1984) | 7–35 | 22.4 | 50.2 | 0.994 | 2.12 | 2.02 | 1.93 | 1.85 | 16 | |||||
| Triticum aestivum cv. Cajeme | Hermida-Carrera et al. (2016)c | 15–35 | 19.0 | 41.3 | 0.990 | 1.86 | 1.78 | 1.72 | 1.66 | 20 | |||||
| Spermatophyta (C3 plants from warm habitats) | Flaveria cronquistii | Perdomo et al. (2015) | 10–40 | 22.9 | 51.8 | 0.996 | 2.18 | 2.07 | 1.97 | 1.89 | 30 | ||||
| Flaveria pringlei | Perdomo et al. (2015) | 10–40 | 17.7 | 38.6 | 0.983 | 1.78 | 1.72 | 1.66 | 1.60 | 30 | |||||
| Glycine max cv. Wayne | Laing et al. (1974) | 15–35 | 17.8 | 37.0 | 0.963 | 1.74 | 1.68 | 1.62 | 1.57 | 25 | |||||
| Oryza sativa indica×japonica hybrid | Wei et al. (1994) | 20–40 | 25.6 | 58.4 | 0.978 | 2.40 | 2.26 | 2.15 | 2.05 | 25 | |||||
| Trifolium repens (native ecotype) | Lehnherr et al. (1985) | 10–25 | 22.5 | 48.9 | 0.999 | 2.08 | 1.98 | 1.90 | 1.82 | 25 | |||||
| Flaveria angustifolia (C3–C4) | Perdomo et al. (2015) | 10–40 | 20.0 | 44.0 | 0.998 | 1.93 | 1.85 | 1.78 | 1.71 | 30 | |||||
| Flaveria floridana (C3–C4) | Perdomo et al. (2015) | 10–40 | 19.9 | 44.1 | 0.999 | 1.94 | 1.85 | 1.78 | 1.72 | 30 | |||||
| Spermatophyta (C4 plants) | Flaveria bidentis | Perdomo et al. (2015) | 10–40 | 15.4 | 31.6 | 0.993 | 1.61 | 1.56 | 1.51 | 1.47 | 30 | ||||
| Flaveria trinervia | Perdomo et al. (2015) | 10–40 | 15.4 | 31.7 | 0.992 | 1.61 | 1.56 | 1.51 | 1.47 | 30 | |||||
| Saccharum officinarum | Hermida-Carrera et al. (2016)c | 15–35 | 17.8 | 35.8 | 0.998 | 1.71 | 1.65 | 1.60 | 1.55 | 30 | |||||
| Setaria viridis | Boyd et al. (2015) | 10–40 | 24.7 | 51.8 | 0.990 | 2.17 | 2.06 | 1.97 | 1.89 | 25 | |||||
| Zea mays cv. Carella | Hermida-Carrera et al. (2016)c | 15–35 | 12.6 | 22.9 | 0.971 | 1.41 | 1.38 | 1.35 | 1.32 | 30 | |||||
| Ko | |||||||||||||||
| Spermatophyta (C3 plants from cool habitats) | Atriplex glabriuscula | Badger and Collatz (1977) | 15–35 | 19.7 | 34.6 | 0.996 | 1.68 | 1.62 | 1.57 | 1.53 | 20 | ||||
| Spinacia oleracea | Jordan and Ogren (1984)g | 7–35 | 6.2 | 0.0 | 1.00 | 1.00 | 1.00 | 1.00 | 16 | ||||||
| Spermatophyta (C3 plants from warm habitats) | Glycine max cv. Wayne | Laing et al. (1974) | 15–35 | 3.7 | −5.5 | 0.989 | 0.92 | 0.93 | 0.93 | 0.94 | 25 | ||||
| Trifolium repens (native ecotype) | Lehnherr et al. (1985) | 10–25 | 10.1 | 9.3 | 0.927 | 1.15 | 1.14 | 1.13 | 1.12 | 25 | |||||
| Spermatophyta (C4 plants) | Setaria viridis | Boyd et al. (2015) | 10–40 | 4.5 | −4.0 | 0.738 | 0.94 | 0.95 | 0.95 | 0.95 | 25 |
Species were assigned to different phylogenetic groups. One phylogenetic group, Spermatophyta, was further divided into C3 and C4 species, and C3 species were further divided into warm- and cool-temperature species according to their optimum growth temperature (Tgrowth). The two C3–C4 intermediate species Flaveria angustifolia and F. floridana were assigned to the group of C3 plants from warm habitats because they present C3-like Rubisco kinetics (Perdomo et al., 2015). The optimum growth temperature (Tgrowth) for each species was either obtained from literature or assigned according to their climate of origin. For Spinacea oleracea, Triticum aestivum and F. pringlei, individual reports’ values and average values for Sc/o of different reports are given. c, scaling constant; ∆Ha, activation energy; Kc, Michaelis–Menten constant for CO2; Ko, Michaelis–Menten constant for O2; r, correlation coefficient for linear regressions between measured vs. predicted (Microsoft Excel Solver function) values of each kinetic parameter at the assayed temperatures; Q10, coefficient over the temperature intervals of 5–15 ºC (), 15–25 ºC (), 25–35 ºC () and 35–45 ºC (); Sc/o, Rubisco specificity factor for CO2/O2; Tmeas, range of measurement temperature.
n.d.: r was not determined because measurements consisted in only two assay temperatures.
a Data from Jordan and Ogren (1984) for Rhodospirillum rubrum consisted of only two measurement temperatures (2 and 25 ºC) and, therefore, and were not calculated.
b Due to poor convergence in the Excel Solver (low degree of explained variance), c and ∆Ha for this report were not considered in determining the group averages, and Q10 values were obtained from second-order polynomial fits. Due to high scatter at higher temperature, values of and from polynomial fits were also unreliable and were therefore not considered for group averages.
c Data from Hermida-Carrera (2016) consisted of measurements at three temperatures (15, 25 and 35 ºC), and the assays were performed following the procedures described in Galmés et al. (2014b).
d Low adjustment of the Excel Solver; c and ∆Ha for this report were not considered in calculating the averages for Spinacea oleracea.
e Young et al. (2015) consists of only two measurement temperatures (0 and 20 ºC); and were not calculated.
f Low adjustment of the Excel Solver; c and ∆Ha of this report were not considered for group averages.
g r is not provided given the large scattering between measured vs. predicted values.
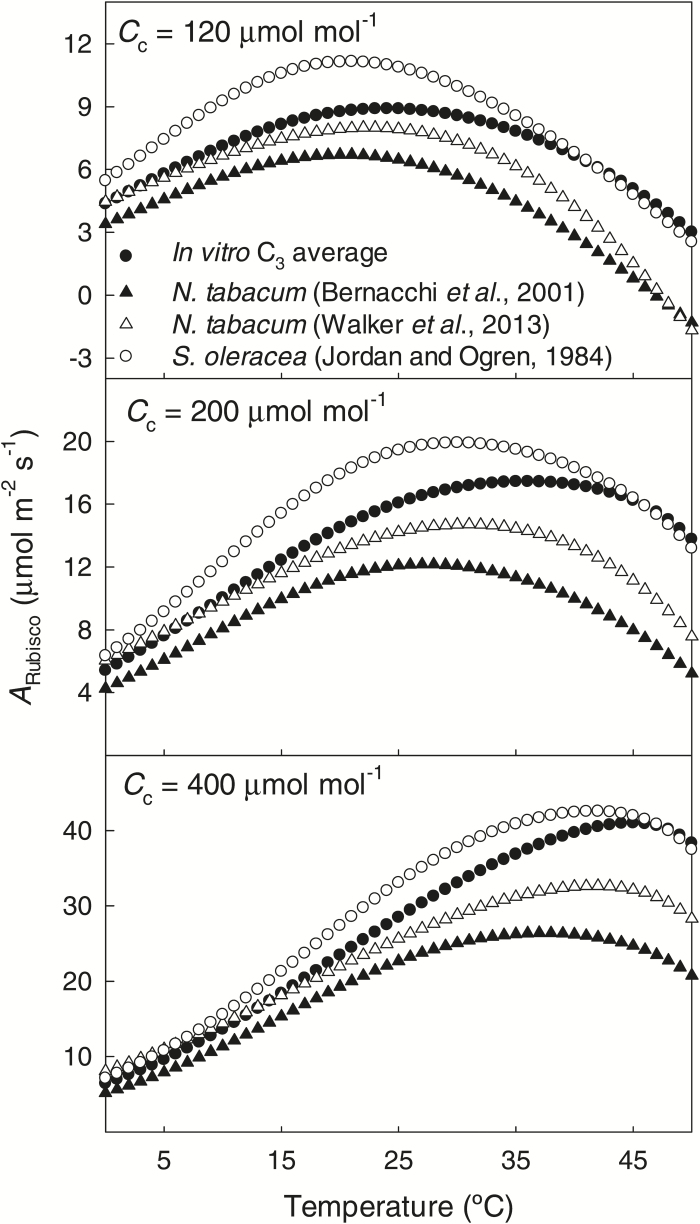
Analogous simulations were conducted to compare the average C3 in vitro temperature response functions developed here and three different temperature functions widely used in the literature in simulating photosynthesis, i.e. in vivo Rubisco temperature responses for Nicotiana tabacum (Bernacchi et al., 2001; Walker et al., 2013) and in vitro Rubisco temperature responses for Spinacia oleracea (Jordan and Ogren, 1984). To quantitatively compare different simulated temperature response curves, warm vs. cool C3 plants and temperature response curves currently in use in the modeling community, mean absolute (σA) and root mean squared (σS) differences between different model estimates (Willmott and Matsuura, 2005; Niinemets et al., 2013) were calculated through the modeled temperature range of 5–50 ºC. The mean absolute difference was calculated as:
| (15) |
where ARubisco,f1(Ti) is the estimated ARubisco for the first function at temperature Ti and ARubisco,f2(Ti) is the corresponding ARubisco value for the second function. The root mean squared differences was further calculated as:
| (16) |
Statistical analysis and tests for phylogenetic signals and trait correlations
Conventional statistical analyses consisted of one-way ANOVA and correlation and linear regression analyses. For all the parameters studied, a univariate model of fixed effects was assumed. The univariate general linear model for unbalanced data (Proc. GLM) was applied and significant differences among groups of species were revealed by Duncan’s test. To avoid type II errors due to limited data, only groups with at least five species were statistically compared. In particular, the limited data available on the in vitro temperature dependence of Ko impeded the comparative analysis among groups of species for temperature responses of this characteristic. Modeled temperature responses of ARubisco were compared by pairwise t-test over temperature ranges of 5–20 and 30–50 ºC. In addition, paired t-tests were used to compare the mean absolute and root mean squared differences in model estimates among different groups of model datasets (in vitro warm vs. cool C3 dataset developed in this study vs. three currently widely used model datasets, comparisons conducted for four different simulations with chloroplastic CO2 concentrations of 120, 150, 200 and 400 μmol mol−1). These analyses were conducted with the IBM SPSS Statistics 20 software package (IBM, Armonk, NY, USA).
In order to test phylogenetic signal strength on trait correlations (the theoretical background of these analyses followed the framework set in Galmés et al. (2015)), complete phylogeny was assembled for all the species in this study. For this, we used RbcL and 16S ribosomal RNA (for species with no available RbcL) sequences from GenBank (http://www.ncbi.nlm.nih.gov). Where genetic data were not available for the given species, we obtained data from GenBank for functionally similar species from the same genus that had overlapping distribution. Phylogeny was constructed in MEGA6 (Tamura et al., 2013), using standardized methods of aligning multiple sequences: Muscle (Edgar, 2004) and constructing maximum likelihood phylogenetic tree (Chor and Tuller, 2005). Phylogenetic independent contrasts, indicative of the strength of phylogenetic signal, were calculated in R using packages ‘ape’ (Paradis et al., 2004), ‘nlme’ (Pinheiro et al., 2014) ‘geiger’ (Harmon et al., 2008) and ‘phytools’ (Revell, 2012). The effects of phylogenetic signal on trait correlations were assessed by analysis of covariance (ANCOVA) and by calculating Pagel’s lambda (λ) based on phylogenetic independent contrasts values (Pagel, 1999). All statistical differences were considered significant at P<0.05.
Results
Standardization of in vitro data
The default value of acidity constant of dissolved CO2, , for pure water used in early studies was commonly taken as 6.35–6.37 at 25 °C (with reference to e.g. Harned and Bonner, 1945; Umbreit et al., 1972). Across the studies, the average ionic strength of the assay medium (Is) at 25 ºC was 0.117±0.006M (range 0.066–0.165M), and the predicted true value of (Eq. 2) corresponding to this average estimate of Is is 6.112, while the equation of Yokota and Kitaoka (1985) suggests a value of 6.118. Given further that the average pH used in Kc assays at 25 ºC was 8.17±0.04 (range 8.0–8.5), using the estimates of pure water would overestimate Kc by 1.75-fold (and 1.015-fold for the equation of Yokota and Kitaoka (1985)). At 35 °C, the for pure water is 6.32 (Harned and Bonner, 1945), while the predicted true value for the average Is is 6.067 (predicted overestimation by 1.78-fold), and the value predicted according to Yokota and Kitaoka (1985) is 6.076 (predicted overestimation 1.021-fold). In our analysis, across all data (different species and temperatures pooled) the average error (±SE) in Kc estimates (Kc,c for standardized and Kc,m for measured Kc values), 100(Kc,c–Kc,m)/Kc,m was −19.8±1.6% (range −50 to 10%). For comparison, the overall variation in Kc,c values across species and temperatures was 206-fold (average±SE=31±5 μM, coefficient of variation of 179%).
In the case of Ko, differences among the estimates can result both from the effects of solutes on Hpc for oxygen and from differences in Hpc,0 values used among the studies to estimate O2 concentration in solutions (Eqs 4–6), while differences in Sc/o can include both differences in and oxygen solubility calculations (Eq. 7). Equations 4 and 5 predict an value of 83950 Pa m3 mol−1 at 25 ºC for the average ion concentration observed in our study, while the typical value of Hpc,0,O2 used in original studies was 80040 Pa m3 mol−1. As Eq. 6 indicates, the use of the default value of Henry’s law constant would lead to 4.9% underestimation in Ko at 25 ºC. In our database, across all species and temperature combinations, the average error (±SE) in Ko estimates was −4.6±0.3% (range −2.4 to −6.6%), whereas the variation in standardized Ko values across species and temperatures was 28-fold (average±SE=560±100mM, coefficient of variation of 119%). In the case of Sc/o where both bicarbonate equilibrium and O2 solubility play a role, average estimate deviation for all species and temperature combination was −3.5±0.7% (range −10.2 to 66.3%), whereas the variation in standardized Sc/o values across species and temperatures was 32-fold (average±SE=92.3±2.6mol mol−1, coefficient of variation of 39%).
Comparison of different functions in capturing the Rubisco temperature responses
Both the exponential and the polynomial functions used to fit the temperature responses of Rubisco characteristics (Eqs 12–14) provided a good fit to the data, with most r values (for predicted vs. measured trait values) for individual relationships greater than 0.950 (Tables 2 and 4, and data not shown). With some exceptions indicated in Table 2, differences between r values from second- and third-order polynomial equations (Eqs 13–14) and the Arrhenius-type function (Eq. 12) were minor (for instance, average r values for in vitro Ko were 0.951, 0.974 and 0.913, respectively). For all kinetic parameters, significant correlation was found between polynomial- and Arrhenius-derived values of and (data not shown). To the contrary, the relationship between polynomial- and Arrhenius-derived values of and was non-significant for some kinetic parameters. This fact indicates that second- and especially third-order polynomial equations are problematic in predicting kinetics values out of the range of assayed temperatures. Therefore, we suggest using the Arrhenius-type function in capturing the Rubisco temperature responses.
Table 4.
Temperature dependence parameters of in vivo-measured Rubisco catalytic constants for Spermatophyta
| Group | Species | Reference |
Tmeas
(ºC) |
c | ∆Ha
(kJ mol−1) |
r |
Tgrowth
(ºC) |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sc/o | |||||||||||||||
| C3 plants from cool habitats | Epilobium hirsutumSpinacia oleracea hybrid 102 | Ghashghaie and Cornic (1994)Brooks and Farquhar (1985) | 16–2815–30 | −11.8−4.5 | −40.8−22.3 | 0.9780.993 | 0.540.72 | 0.570.73 | 0.590.75 | 0.610.76 | 18.016.0 | ||||
| Triticum aestivum cv. Saratovskaya 29 | Viil et al. (2012) | 5–41 | −6.1 | −25.2 | 0.997 | 0.69 | 0.70 | 0.72 | 0.73 | 20.0 | |||||
| Arabidopsis thaliana cv. Columbia | Walker et al. (2013) | 15–35 | −3.8 | −20.9 | 0.956 | 0.73 | 0.75 | 0.76 | 0.77 | 22.0 | |||||
| C3 plants from warm habitats | Nicotiana tabacum cv. W38 | Bernacchi et al. (2001) | 10–40 | −8.2 | −31.4 | 0.997 | 0.62 | 0.64 | 0.66 | 0.68 | 25.0 | ||||
| Nicotiana tabacum | Walker et al. (2013) | 15–35 | −9.2 | −34.2 | 0.950 | 0.60 | 0.62 | 0.64 | 0.66 | 25.0 | |||||
| Phaseolus vulgaris | Ghashghaie and Cornic (1994) | 12–32 | −10.3 | −36.8 | 0.973 | 0.58 | 0.60 | 0.62 | 0.64 | 25.0 | |||||
| Kc | |||||||||||||||
| C3 plants from cool habitats | Arabidopsis thaliana cv. Columbia | Walker et al. (2013) | 15–35 | 14.8 | 31.4 | 0.946 | 1.60 | 1.55 | 1.51 | 1.47 | 22 | ||||
| C3 plants from warm habitats | Agropyron smithiiGlycine max cv. P61–22 | Monson et al. (1982) | 10–40 | 10.1 | 17.1 | 0.933 | 1.29 | 1.27 | 1.25 | 1.23 | 25 | ||||
| Harley et al. (1985) | 20–40 | 10.0 | 18.0 | 0.993 | 1.31 | 1.29 | 1.27 | 1.25 | 25 | ||||||
| Nicotiana tabacum cv. W38 | Bernacchi et al. (2001) | 10–40 | 26.6 | 59.5 | 0.995 | 2.44 | 2.30 | 2.18 | 2.07 | 25 | |||||
| Nicotiana tabacum | Walker et al. (2013) | 15–35 | 17.5 | 37.6 | 0.991 | 1.76 | 1.69 | 1.64 | 1.59 | 25 | |||||
| Ko | |||||||||||||||
| C3 plants from cool habitats | Arabidopsis thaliana cv. Columbia | Walker et al. (2013) | 15–35 | 11.9 | 16.0 | 0.734 | 1.27 | 1.25 | 1.23 | 1.22 | 22 | ||||
| C3 plants from warm habitats | Nicotiana tabacum cv. W38 | Bernacchi et al. (2001) | 10–35 | 15.7 | 24.6 | 0.991 | 1.45 | 1.41 | 1.38 | 1.35 | 25 | ||||
| Nicotiana tabacum | Walker et al. (2013) | 15–35 | 15.3 | 24.1 | 0.935 | 1.44 | 1.40 | 1.37 | 1.34 | 25 | |||||
| Glycine max cv. P61–22 | Harley et al. (1985) | 20–40 | 18.3 | 31.5 | 0.988 | 1.60 | 1.55 | 1.51 | 1.47 | 25 |
Species were classified as C3 and C4 species, and C3 species were further divided among warm- and cool-temperature species according to their optimum growth temperature (Table 2). c, scaling constant; ∆Ha, activation energy; Kc, Michaelis–Menten constant for CO2; Ko, Michaelis–Menten constant for O2; Q10, coefficient over the temperature intervals of 5–15 ºC (), 15–25 ºC (), 25–35 ºC () and 35–45 ºC (); r, correlation coefficient for linear regressions between measured vs. predicted (Microsoft Excel Solver function) values of each kinetic parameter at the assayed temperatures; Sc/o, specificity factor for CO2/O2; Tmeas, range of measurement temperature.
Overall variability of the Rubisco in vitro temperature response parameters for Sc/o, Kc and Ko
Among all 38 species, the energy of activation (∆Ha) for Sc/o ranged between −43.0 kJ mol−1 for the Thermosynechococcus elongatus and −11.7 kJ mol−1 for Synechococcus lividus (Table 2). With regard to Kc, Zea mays had the lowest (∆Ha=22.9 kJ mol−1) and Oryza sativa the highest (∆Ha=58.4 kJ mol−1) temperature-dependent increases in Kc among the 20 species (Table 2). For both Sc/o and Kc, a high correlation was observed between ∆Ha and the Q10 coefficients calculated at specific ranges of measurement temperatures (r>0.995), so that the extremes of the range for Q10 were generally represented by the same species as for ∆Ha (Table 2).
The in vitro temperature response of Ko is the least documented trait of Rubisco with data only available for five land plant species (Table 2). Moreover, the values of the temperature dependence parameters for these five species are contradictory. Hence, Badger and Collatz (1977) for Atriplex glabriuscula, and Lehnherr et al. (1985) for Trifolium repens reported positive values of ∆Ha for Ko (i.e. Ko increasing with temperature of measurement); Laing et al. (1974) for Glycine max, and Boyd et al. (2015) for Setaria viridis reported negative values of ∆Ha for Ko (i.e. Ko decreasing with increases of the temperature of measurement); and Jordan and Ogren (1984) reported that Spinacia oleracea Ko was insensitive to temperature of measurement (∆Ha=0 kJ mol−1). Data standardization did not change the direction of Ko temperature responses in any of the cases.
Comparison of the in vitro temperature response parameters for Sc/o, Kc and among groups of species
Across all the measurement temperatures analysed, average Sc/o values for Spermatophyta were lower than those for Rhodophyta (Galdieria partita), higher than those for Proteobacteria (Rhodospirillum rubrum), and similar to Bacillariophyta and Cyanobacteria (Fig. 1A). The divergence between the two Cyanobacteria species, Synechococcus lividus and Thermosynechococcus elongates, resulted in large standard errors at ≤25 ºC for this group. In all phylogenetic groups, Rubisco Sc/o decreased with increasing the assay temperature, but the extent of such decrease differed among groups. Hence, average ∆Ha for Sc/o of Spermatophyta (−21.5 kJ mol−1) was similar to the values reported for Proteobacteria and Bacillariophyta, and 44% lower compared with Rhodophyta (in absolute values, Table 3). The comparison of average ∆Ha for Sc/o of Spermatophyta with that of Cyanobacteria depended on the species (1.8-fold higher compared with Synechococcus lividus and 50% lower compared with Thermosynechococcus elongatus).
Fig. 1.
Values of the Rubisco specificity factor for CO2/O2 (Sc/o) in liquid phase at a range of temperatures in different phylogenetic groups of photosynthetic organisms (A) and in land plants only (B). (A) Open upward triangles and short-dashed line, Proteobacteria; open circles and dash-dotted line, Cyanobacteria; filled circles and long-short-dashed line, Bacillariophyta (diatoms); empty diamond and long-dashed line, Rhodophyta (red algae); filled squares and solid line, Spermatophyta (plants). Sample number n=4 for Bacillariophyta and n=30 for Spermatophyta; no replication was available for Proteobacteria, Cyanobacteria and Rhodophyta. The inset in shows the values of Sc/o for Rhodophyta. (B) Open downward triangles and dotted line, C3 plants from cool habitats (n=8); open upward triangles and long-dashed line, C3 plants from warm habitats (n=16); open circles and solid line, C4 plants (n=6). Different letters denote statistically significant differences by Duncan’s analysis (P<0.05) among plant functional and photosynthetic groups. All data for Sc/o correspond to in vitro measurements at discrete temperatures from data shown in Table 3 after applying Eq. 12, and were standardized to a common set of liquid-phase CO2 and O2 physico-chemical characteristics by Eqs 1–7. For CO2, these equations correct for study-to-study differences in assumed bicarbonate equilibrium as dependent on solution pH, temperature and ionic strength and when pertinent study-to-study differences in the value of Henry’s law constant used. For O2, these equations standardize for differences in the value of Henry’s law constant used. Means and standard errors are provided when n≥2. Table 1 provides Henry’s law constants that can be used to convert the Rubisco kinetic characteristics to gas-phase equivalent values.
Within Spermatophyta, C4 plants had lower Sc/o values than C3 plants from cool and warm habitats at all assay temperatures (between 5 and 45 ºC), while non-significant differences were found between C3 plants from cool and warm habitats (Fig. 1B). The temperature response of Sc/o also differed within Spermatophyta, with higher thermal sensitivity of Sc/o (i.e. more negative ∆Ha and lower Q10) in C4 plants compared with C3 plants from cool habitats (Table 3). C3 plants from warm habitats presented intermediate values of ∆Ha for Sc/o, and similar Q10 values to C4 plants (Table 3).
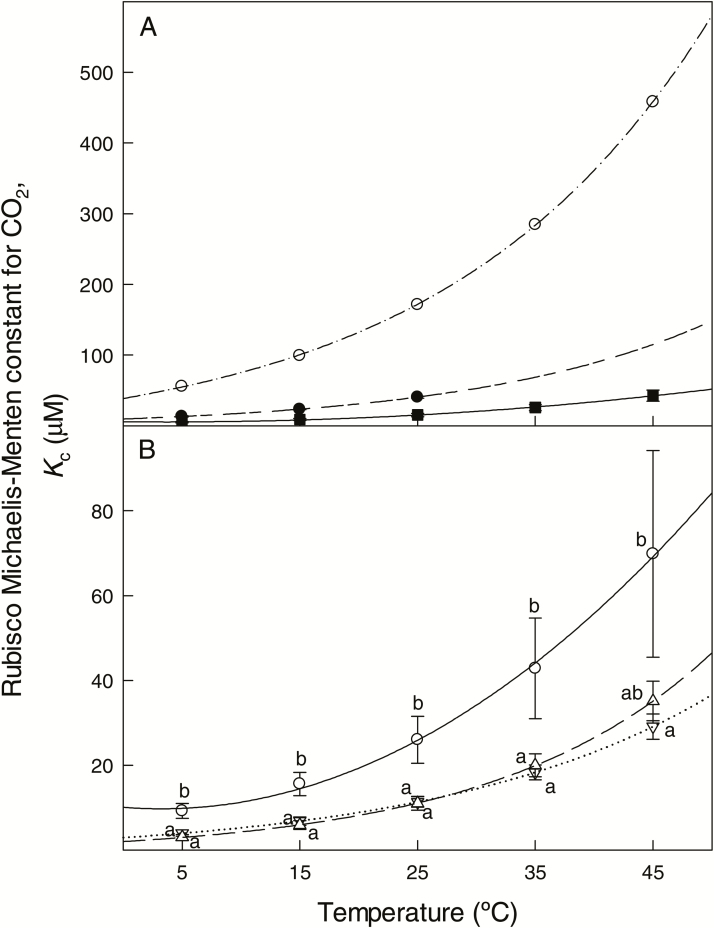
Rubisco from Spermatophyta had a higher affinity for CO2 (i.e. lower Kc) than Rubiscos from Bacillariophyta and Cyanobacteria throughout the range of temperatures of measurement (Fig. 2A). For the three phylogenetic groups with available data, Kc values from in vitro measurements increased with the temperature of measurement, and the values of ∆Ha and Q10 for Kc were similar among the groups (Table 3). Within land plants, Rubisco from C4 plants displayed higher Kc values compared with Rubiscos from C3 plants, at all temperatures of measurement except 45 ºC (Fig. 2B). Differences in Kc between C3 plants from cool and warm habitats were non-significant across the range of temperatures of measurement. The temperature dependence of Kc varied within Spermatophyta, with Rubisco from C4 plants presenting lower values of ∆Ha compared with C3 plants from warm habitats, while differences between C3 plants from cool and warm habitats were non-significant (Table 3). Differences in Q10 for Kc among higher plants groups were non-significant.
Fig. 2.
Values of the Rubisco Michaelis–Menten constant for CO2 (Kc) in liquid phase at a range of temperatures in different phylogenetic groups (A) and in land plants only (B). (A) Open circles and dash-dotted line, Cyanobacteria; filled circles and dashed line, Bacillariophyta (diatoms); filled squares and solid line, Spermatophyta (plants). Sample number n=2 for Bacillariophyta and n=17 for Spermatophyta; no replication was available for Cyanobacteria. (B) Open downward triangles and dotted line, C3 plants from cool habitats (n=5); open upward triangles and dashed line, C3 plants from warm habitats (n=7); open circles and dotted line, C4 plants (n=5). Values for Kc correspond to in vitro measurements at discrete temperatures from data shown in Table 3 after applying Eq. 12, and were standardized to a common set of CO2 liquid-phase physico-chemical characteristics as explained in Fig. 1 (Table 1 for Henry’s law constants for CO2 and O2 that can be used to convert the values reported to gas-phase equivalents). Data presentation as in Fig. 1.
Reanalysing the data compilation of Galmés et al. (2015) in terms of Q10, we note that in the comparisons of the temperature response of among Spermatophyta, Rubisco from C4 plants presented lower values of ∆Ha and Q10 than C3 plants from warm habitats (Table 3). Similarly to the Sc/o temperature dependence, of C3 plants from warm environments was more sensitive to increases in temperature (i.e. higher ∆Ha or Q10) than those of C3 plants from cool environments (Table 3).
The calculated values for ∆Ha integrate all data of the temperature response curve, while Q10 values refer to specific thermal ranges of the curve. With the exception of ∆Ha vs. Q10 for Kc in the comparison among higher plant groups, the trends observed for Q10, in terms of species or groups comparison, are identical to those described for ∆Ha (Table 3) in all kinetic parameters. Due to the changes in scaling exponent of the temperature response of Rubisco kinetics, values of Q10 for Sc/o increase from to , while they decrease for Kc and , in all groups of species.
Phylogenetic signals were not significant in ANCOVA models (P-values for Sc/o, Kc and within Spermatophyta were 0.519, 0.114 and 0.742, respectively). This fact indicates that when corrected for the phylogenetic signal, the comparison of Sc/o and Kc values at given temperatures (Figs 1B and 2B), as well as the differences in temperature dependence parameters for Sc/o, Kc and among Spermatophyta groups (Table 3), were qualitatively identical to the conventional statistics (ANOVA).
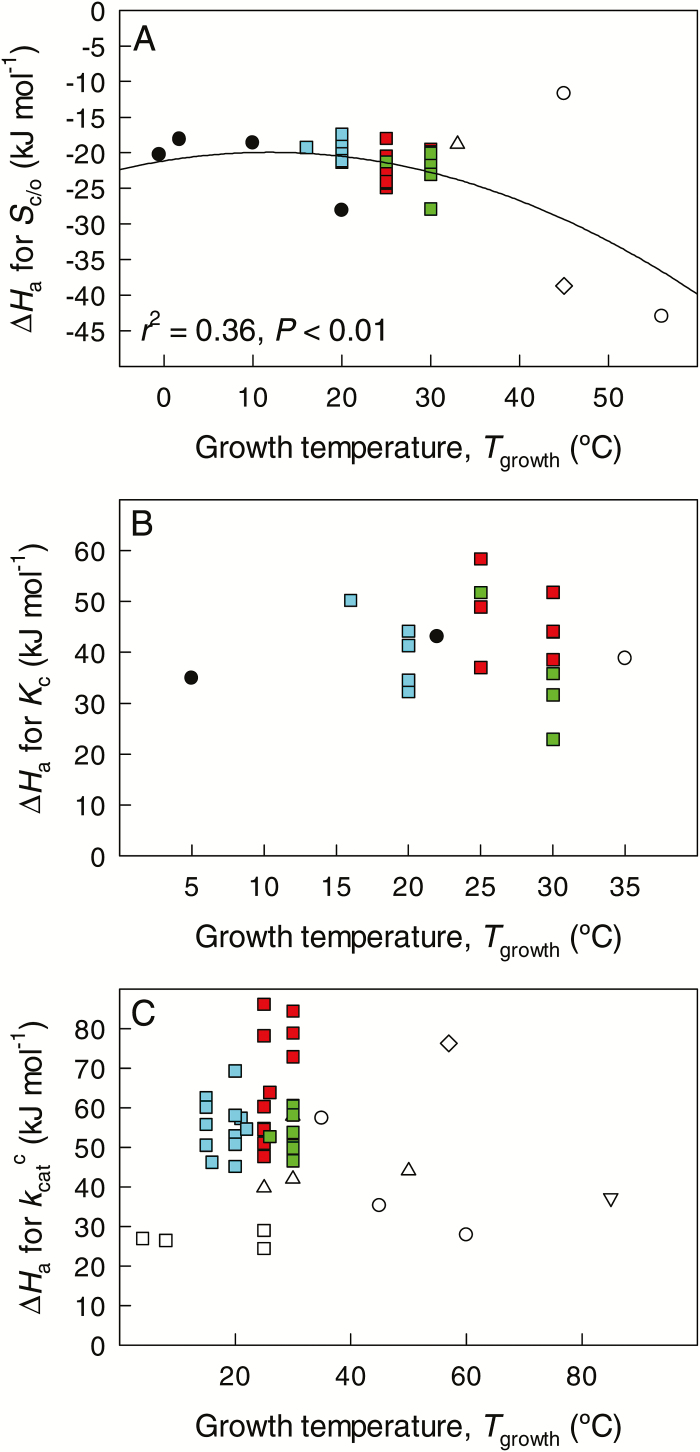
Relationship between the energies of activation of Rubisco catalytic traits and the species optimum growth temperature
An inverse relationship was found between ∆Ha for Sc/o and the species average optimum growth temperature (Tgrowth), suggesting that Sc/o values of Rubisco from species inhabiting hot environments present a higher sensitivity to changes in temperature (Fig. 3A). Although this relationship was significant and not affected by the species’ phylogeny (Pagel’s λ=0.575), it was substantially influenced by the values of the thermophiles Thermosynechococcus elongatus (Cyanobacteria) and Galdieria partita (Rhodophyta), which presented the highest Tgrowth and the lowest ∆Ha for Sc/o. Furthermore, Synechococcus lividus, with the same Tgrowth as Galdieria partita (45 ºC), had the highest ∆Ha for Sc/o among all the species studied. Nevertheless, when the data were reanalysed without these three species with Tgrowth>40 ºC, there was still a significant correlation between ∆Ha for Sc/o and Tgrowth (r2=0.175, P<0.02 for a second-order polynomial regression). Clearly, there is evidence of common trends in temperature scaling of Sc/o across disparate phylogenetic groups, indicating that convergent evolution has led to similar functional responses. In contrast, the relationships between Tgrowth and ∆Ha for Kc and were non-significant (Figs 3B, C). The relationships were analogous with Q10 values (data not shown).
Fig. 3.
The relationship between the growth temperature (Tgrowth) and the energy of activation (∆Ha) for (A) the Rubisco specificity factor for CO2/O2 (Sc/o) in liquid phase, (B) the Rubisco Michaelis–Menten constant for CO2 (Kc) in liquid phase, and (C) the Rubisco maximum carboxylase turnover rate (). Each symbol corresponds to individual species (Table 2 for data sources). Open upward triangles, Proteobacteria; open circles, Cyanobacteria; black circles, Bacillariophyta (diatoms); open squares, Chlorophyta (green algae); open diamond, Rhodophyta (red algae); blue squares, C3 plants from cool habitats; red squares, C3 plants from warm habitats; green squares C4 plants. In vitro estimates at discrete temperatures were standardized for study-to-study differences in physico-chemical characteristics for CO2 and O2 used as in Figs 1 and 2 and the temperature responses were fitted by Eq. 12. In (A), the data were fitted by a non-linear equation in the form y=−20.911+0.207x–0.009x2. In (B) and (C), data fits by linear and different monotonic non-linear equations were statistically not significant (best r2 values were 0.090 for (B) and 0.115 for (C), P>0.1 for both).
When considering group averages, a negative relationship was found between ∆Ha for Sc/o and ∆Ha for in all groups except the Cyanobacterium T. elongatus (Fig. 4). This relationship was significant both when all plants were averaged and when plant functional and photosynthetic groupings were separately considered, and was not affected by the phylogenetic signal (Pagel’s λ=−0.936, and ANCOVA P=0.21, respectively).
Fig. 4.
The relationship between the energies of activation (∆Ha) for the Rubisco maximum carboxylase turnover rate () and the Rubisco specificity factor for CO2/O2 (Sc/o) in liquid phase across domains of life and photosynthetic and ecological groupings of plants (symbols as in Fig. 3). Data were separately fitted by linear regressions across domains of life (all plants averaged; solid line, r2=0.952, P<0.01) and across all groupings (plant functional and photosynthetic groupings, C3 cool and warm and C4, separately considered; dashed line, r2=0.846, P<0.01). In Rhodophyta, the value of ∆Ha for Sc/o is from Galdieria partita, while that of ∆Ha for is from Cyanidium caldarium. For the other phylogenetic groups, data correspond to averages±SE from different numbers of species (Table 3 for data sources). Data for Thermosynechococcus elongatus (Cyanobacteria) with vastly different Rubisco kinetics (Figs 1 and 2) were not considered in the regression analysis.
Temperature dependence of in vivo-estimated Rubisco kinetics and the relationship with the temperature parameters derived from in vitro measurements
In the six species with available data, in vivo-estimated Sc/o decreased with increasing temperature, although important differences existed among the species in the rate of decrease (Fig. 5A). As a consequence, ∆Ha for Sc/o varied 2-fold between Arabidopsis thaliana (−20 kJ mol−1) and Epilobium hirsutum (−40.8 kJ mol−1; Table 4). The average values of in vitro Sc/o for C3 plants fell within the lower range of the in vivo-estimated values, and the in vitro-based ∆Ha for Sc/o (−21.4 kJ mol−1, Table 3) was similar to that estimated in vivo for A. thaliana and S. oleracea (Fig. 5A).
Fig. 5.
Values of the Rubisco specificity factor for CO2/O2 (Sc/o) (A) and the Michaelis–Menten constants for CO2 (Kc) (B) and O2 (Ko) (C) at a range of temperatures. Values for these parameters were obtained at discrete temperatures from in vivo gas-phase data (shown in Table 4) after applying Eq. 12 and converted to the liquid phase by Eqs 8–10 (Table 1 for corresponding Henry’s law constants to convert between liquid-phase and gas-phase equivalents). For comparative purposes, in vitro C3 average values for Sc/o and Kc have been also included (using data shown in Table 3). In (C), in vitro Ko data for Atriplex glabriuscula (Badger and Collatz 1977, shown in Table 2) that have been widely used to model leaf photosynthesis (see Introduction) have been also included.
An increase in the in vivo Kc with increasing temperature of measurement was observed for all the species (Fig. 5B), but the ∆Ha for Kc varied three-fold between 17.1 kJ mol−1 for Agropyron smithii (Monson et al., 1982) and 59.5 kJ mol−1 for Nicotiana tabacum (Bernacchi et al., 2001) (Table 4). The average (±SE) energy of activation for in vitro Kc in C3 plants was 43.8±2.2 kJ mol−1 (Table 3), i.e. higher than all the in vivo-based values except that for N. tabacum described in Bernacchi et al. (2001).
The temperature response of in vivo-estimated Ko has been reported for N. tabacum, A. thaliana and Glycine max (Table 4). In contrast to some in vitro data (Table 2), all in vivo data exhibited a positive scaling of Ko with temperature (Fig. 5C). Compared with the in vivo Ko values, the in vitro Ko of the C3 plant Atriplex glabriuscula (Badger and Collatz, 1977) presented lower values at temperatures below 25 ºC and higher values at temperatures above 25 ºC. The higher thermal sensitivity of the in vitro Ko of A. glabriuscula resulted in a higher ∆Ha for Ko (34.6 kJ mol−1, Table 2) compared with the in vivo-based values for ∆Ha of other plants (Table 4).
In the case of in vivo data, only the study of Walker et al. (2013) considered the leaf mesophyll conductance, i.e. used the ‘true’ chloroplastic CO2 concentration in the derivation of Rubisco characteristics by inverting the FvCB photosynthesis model. Indeed, Sc/o and Kc temperature characteristics for A. thaliana estimated in this study are closer to C3 average in vitro data than most of the other estimates (Fig. 5A, B). However, in N. tabacum, Sc/o in vivo temperature characteristics estimated without mesophyll conductance in the study of Bernacchi et al. (2001) are actually closer to C3 average estimates than N. tabacum in vivo characteristics estimated by considering mesophyll conductance in the study of Walker et al. 2013 (Fig. 5).
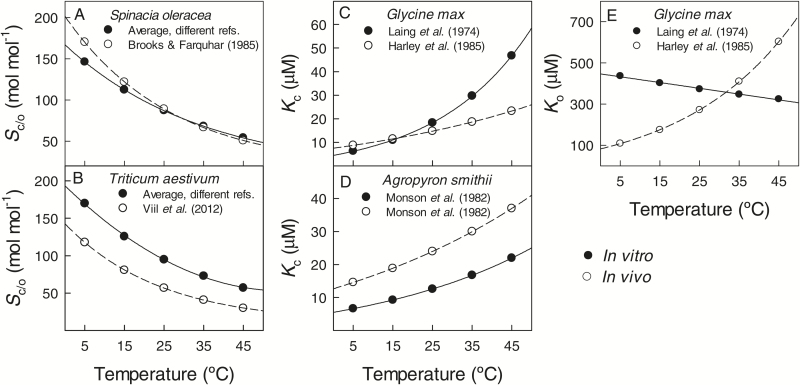
For several species, the temperature responses of Rubisco characteristics had been reported both in vitro and in vivo, whereas all these in vivo analyses had been conducted without considering mesophyll conductance. As for the temperature response of Sc/o, in vitro and in vivo data were available for Spinacia oleracea and Triticum aestivum (Fig. 6A, B). In S. oleracea, in vitro (average from different references) and in vivo (Brooks and Farquhar, 1985) data for Sc/o were similar over the range of measurement temperatures (Fig. 6A). In T. aestivum, in vitro values (average from different references) were higher than the in vivo ones (Viil et al., 2012) at all temperatures of measurement (Fig. 6B). It should be noted that differently from all other in vivo studies, Viil et al. (2012) used in vivo 14CO2 leaf uptake for Sc/o derivation.
Fig. 6.
Comparisons between in vitro (filled symbols) and in vivo (open symbols) values of the Rubisco specificity factor for CO2/O2 (Sc/o) (A, B) and the Michaelis–Menten constants for CO2 (Kc) (C, D) and O2 (Ko) (E) at a range of temperatures for species with available data. Equation 12 was used to derive estimates for these parameters at discrete temperatures from data in Tables 2 and 4. The in vitro liquid-phase data were standardized for a common set of physico-chemical characteristics of CO2 and O2 as explained in Figs 1 and 2, while the in vivo gas-phase data were converted to the liquid phase as explained in Fig. 5 (Table 1 for pertinent Henry’s law constant to convert between liquid- and gas-phase equivalents). Sc/o data for Spinacia oleracea are averages for the studies Jordan and Ogren (1984), Uemura et al. (1997), Zhu et al. (1998) and Yamori et al. (2006). Sc/o data for Triticum aestivum are averages for studies Haslam et al. (2005) and Hermida-Carrera et al. (2016).
In vitro and in vivo data on the temperature response of Kc have been published for Glycine max and Agropyron smithii (Fig. 6C, D). In G. max, in vitro (Laing et al., 1974) and in vivo (Harley et al., 1985) reported data were similar over the temperature range 5–25 ºC, but at higher temperatures of measurement in vitro values were higher than in vivo values (Fig. 6C). In A. smithii, in vivo estimations for Kc were higher than in vitro values at all temperatures of measurement (Fig. 6D). Glycine max is the unique species for which the temperature response of Ko has been examined both in vitro and in vivo (Fig. 6E). Differently from other comparisons between in vitro and in vivo values for Sc/o and Kc that were at least qualitatively similar, the in vivo values of Ko (Harley et al., 1985) increased exponentially with increasing temperature, but the in vitro values (Laing et al., 1974) tended to decrease.
Variation in the temperature responses of Rubisco kinetics: implications for modeling photosynthesis
The simulation analysis combining all different Rubisco kinetic characteristics indicated that the temperature responses of Rubisco kinetics of C3 plants from cool environments resulted in higher simulated Rubisco-limited gross photosynthesis rate (ARubisco) at lower temperatures than in C3 species from warm environments, while the latter species performed better at higher temperatures (Fig. 7), although the overall differences among the cool and warm C3 species were moderate. The mean absolute difference (σA, Eq. 15) between cool and warm C3 species was 0.39 μmol m−2 s−1 at chloroplastic CO2 concentration (Cc) of 120 μmol mol−1, and 2.9 μmol m−2 s−1 at Cc=400 μmol mol−1, and corresponding root mean squared differences (σS, Eq. 16) were 0.20 μmol m−2 s−1 at Cc=120 μmol mol−1 and 12.5 μmol m−2 s−1 at Cc=400 μmol mol−1.
Fig. 7.
Modeling effect of the different temperature responses of Rubisco kinetic parameters from C3 plants from cool habitats (open downward triangles), C3 plants from warm habitats (open upward triangles) and C3 average (open circles) on the Rubisco-limited gross assimilation rate (ARubisco) at chloroplastic CO2 concentrations (Cc) of 120, 200 and 400 μmol mol−1. To model ARubisco at different temperatures, the values for the temperature dependence parameters of Sc/o, Kc and were taken from Table 3 (see Methods for further details). We simulated gross assimilation here to avoid confounding effects of mitochondrial respiration.
The predicted quantitative differences in simulated ARubisco between C3 plants from cool and warm environments depended on Cc. Hence, at lower temperature, the higher simulated ARubisco for C3 plants from cool environments, compared with that for C3 plants from warm environments, was more evident at Cc of 120 μmol mol−1 (for the temperature range of 5–20 ºC, average±SE ARubisco was 7.7±0.2 μmol m−2 s−1 for C3 cool vs. 7.3±0.3 μmol m−2 s−1 for C3 warm; means are significantly different at P<0.001 according to paired samples t-test). At higher temperature, the enhancement in simulated ARubisco for C3 plants from warm environments was greater at Cc of 400 μmol mol−1 (Fig. 7; for the temperature range of 30–50 ºC, average±SE ARubisco was 36.0±0.4 μmol m−2 s−1 for C3 cool vs. 40.8±0.7 μmol m−2 s−1 for C3 warm; means are significantly different at P<0.001 according to paired samples t-test). Of course, this simulation is only based on two groups of species, and it is further important that there is a significant within group variability in any of the Rubisco temperature traits that is not related to growth temperature (Fig. 3).
An analogous modeling exercise was conducted to compare the potential effects of using the average temperature parameters of C3 Rubiscos (taken from the in vitro compilation, Tables 2 and 3) and any of the three datasets widely used in photosynthesis modeling (Fig. 8). As with the C3 cool vs. warm comparison, the differences among simulated ARubisco by different Rubisco temperature responses depended on the temperature range and Cc, but in general, the in vitro datasets, i.e. in vitro C3 average from the present study and that of S. oleracea from Jordan and Ogren (1984), yielded higher simulated ARubisco than the in vivo datasets based on N. tabacum from Bernacchi et al. (2001) and Walker et al. (2013). Irrespective of Cc, simulated ARubisco of the in vitro C3 average was similar to simulated ARubisco of N. tabacum from Walker et al. (2013) at the lower temperature range (<15 ºC), and similar to that of S. oleracea from Jordan and Ogren (1984) at the higher temperature range (>40 ºC). Between 15 and 40 ºC, simulated ARubisco of the in vitro C3 average was lower than that of S. oleracea (Jordan and Ogren, 1984) and higher than that of N. tabacum (Bernacchi et al., 2001; Walker et al., 2013). At all Cc values used in the simulations, differences between simulated ARubisco of the in vitro C3 average and in vivo estimates (Bernacchi et al., 2001; Walker et al., 2013) became larger at higher temperatures (Fig. 8, according to paired samples t-tests, P<0.001 for all these comparisons mentioned above).
Fig. 8.
Comparison of the Rubisco-limited gross photosynthesis (ARubisco) among average of in vitro data reported for C3 plants and three widely cited datasets at chloroplastic CO2 concentrations (Cc) of 120, 200 and 400 μmol mol−1. The temperature dependence parameters of Sc/o, Kc, and Ko for in vitro average C3 plants (shown in Table 3) were the same as in Fig. 7, while those for in vivo Nicotiana tabacum (Bernacchi et al., 2001; Walker et al., 2013) and in vitro Spinacia oleracea (Jordan and Ogren, 1984) were obtained from the original papers (shown in Tables 2 and 4). Bernacchi et al. (2001), Walker et al. (2013) and Jordan and Ogren (1984) did not report values of the deactivation energy (∆Hd) and the entropy term (∆S) for , and the simulation assumed identical values to those used for the in vitro average C3 plants (indicated in the Methods). Note that Bernacchi et al. (2001) in vivo values have been derived without considering mesophyll conductance, while mesophyll conductance has been included in the in vivo estimates of Walker et al. (2013).
The differences in predicted ARubisco temperature relationships from the three datasets of Rubisco kinetics were extensive. For 12 comparisons with temperature response curves derived for four Cc (120, 150, 200 and 400 μmol mol−1), average σA±SE=4.5±0.8 μmol m−2 s−1 and σS=31±12 μmol m−2 s−1. These differences were much greater than the differences in predicted ARubisco temperature relationships among cool and warm C3 species (Fig. 7 vs. Fig. 8; see above for σA and σS values), and the differences in predicted ARubisco temperature responses for cool and warm C3 species from the ARubisco responses predicted by the mean in vitro data for C3 species (for these eight comparisons, average σA=0.65±0.18 μmol m−2 s−1 and average σS=0.93±0.48 μmol m−2 s−1). Indeed, the average σA and σS values for ARubisco predictions using C3 in vitro kinetics and the average σA and σS values for ARubisco predictions using the three selected Rubisco kinetics datasets were significantly different (P<0.005 according to pairwise t-tests).
Discussion
Rubisco in vitro temperature relationships: caveats and potentials
To our knowledge, the present study provides the most complete dataset of temperature dependences of Rubisco kinetic characteristics including altogether 17 in vitro and seven in vivo studies providing information for 49 species from most autotrophic kingdoms of life (Tables 2 and 4). As with any meta-analysis, creating such a synthetic summary inevitably requires analysing the effects of different experimental protocols on the observed trait values. In the case of Rubisco, one should be particularly careful when comparing data from different labs, due to differences in the assay conditions and the calculation of CO2 concentration in the assay medium.
In our analysis, we have considered all the assay medium conditions and developed appropriate corrections to standardize for study-to-study differences in assay conditions (Eqs 1–7). In addition to the effects of assay medium composition on the equilibrium CO2 concentration, which is known to affect Kc estimations (Yokota and Kitaoka, 1985, Eqs 1 and 2), we have further highlighted the potential problems with O2 solubility that affect Ko estimation (Eqs 3–6). Furthermore, appropriate corrections were provided for Sc/o (Eq. 7), which is potentially affected by both bicarbonate equilibrium and O2 solubility. Although the corrections of Kc, Ko and Sc/o values at any given temperature were large in several cases, the temperature effect on these corrections was relatively weak, such that the absolute trait values at all temperatures were similarly affected. Thus, the overall temperature sensitivity as characterized by the activation energy (∆Ha) and Q10 values was much less affected by the applied corrections (in most cases <5%).
Although part of the compiled variation may still be due to differences in the methodology from the different reports, we argue that with the corrections applied we have overcome discrepancies in the concentration of CO2 and O2 in the assay media. Furthermore, data were filtered as explained in the Methods, with the most problematic reports being excluded from the analyses. Analysis of the data also indicates that (i) independent measurements for the same species yielded similar ∆Ha and Q10 values (see Sc/o for Spinacia oleracea and Flaveria pringlei in Table 2), and (ii) the variability within the main groups of species was low (Tables 2 and 3), suggesting that the approach developed for a posteriori standardization of Rubisco characteristics was sound. Thus, we consider that the temperature responses reported here are robust, and that the data in Tables 2 and 3 mainly reflect biological differences.
We note that, although up to seven phylogenetic groups had temperature responses of Rubisco kinetics, data for some phylogenetic groups (in particular Archaea, Proteobacteria, Cyanobacteria and Rhodophyta) were represented by very few species. We therefore suggest that more species of these phylogenetic groups should be surveyed in the future to confirm the trends observed in the present database. Future surveys should include the analysis of the temperature responses of Rubisco kinetics from non-vascular plant groups (liverworts, hornworts and mosses) and ferns, which have not been studied so far. This would allow gaining deeper insight into the evolutionary trends in the temperature response of Rubisco catalysis.
What do we learn from the compiled dataset? Important species variations in the temperature dependence of Rubisco kinetics suggest adaptation to the thermal environment and photosynthetic mechanism of the species
Among in vitro data, Sc/o (the present study) and (Galmés et al., 2015) are the best documented traits, compared with Kc and especially Ko, in terms of its temperature response (Table 2). With the exception of the excluded study by Ezaki et al. (1999), showing an increase in Sc/o of Thermococcus kodakariensis with increasing temperatures, all compiled reports agree that Sc/o decreases with increasing temperature, while and Kc increase (Figs 1 and 2; Galmés et al., 2015).
Despite general trends, the data indicate that the temperature response of Rubisco kinetics varies among phylogenetic groups (Figs 1A and 2A; Galmés et al., 2015). In this sense, Spermatophyta present higher ∆Ha for Sc/o (in absolute values) than Proteobacteria and lower values compared with Rhodophyta (Table 3). A similar trend has been observed in the comparative analysis of ∆Ha for among these phylogenetic groups (Galmés et al., 2015), indicative of adjustment in the temperature sensitivity of Rubisco kinetics. As for Sc/o, this adjustment seems to be related to the Tgrowth where the species evolved, with those species from warmer environments presenting a higher thermal dependence of Sc/o (Fig. 3A).
The lack of correlation between ∆Ha for and Tgrowth apparently contradicts a co-adjustment of Rubisco kinetics to the prevailing environmental conditions (Fig. 3C), and may be attributed to the different set species included in each correlation. Actually, considering all species, the range of variation in ∆Ha for these two parameters is similar, about 3.5-fold (Table 2 and Galmés et al. 2015). Moreover, excluding the data for the cyanobacterium Thermosynechococcus elongatus, with vastly different Rubisco kinetics, the results suggest a significant correlation between ∆Ha for Sc/o and (Fig. 4). In other words, those Rubiscos with a large increase in with temperature also present a large decrease in Sc/o. This finding may be related to the widely described trade-off between Sc/o and at 25 ºC (Tcherkez et al., 2006), suggesting that this trade-off is also valid at other temperatures. It should be noted that this correlation was made using average data for the different groups, and that different species were used to obtain the group averages. When the same correlation was analysed for the subset of species for which both Sc/o and have been measured at different temperatures (nine Spermatophytes), a non-significant relationship was found (data not shown).
Within Spermatophyta, ∆Ha for and Kc of Rubiscos from C4 plants was lower compared with C3 plants from warm habitats (Table 3), in agreement with recent observations in congeneric species of Flaveria with contrasting photosynthetic mechanism (Perdomo et al., 2015). Differences between C3 plants from cool and warm habitats were significant in ∆Ha for , but not in ∆Ha for Kc. On average, the ratio between ∆Ha for and ∆Ha for Kc was 1.37, 1.40 and 1.52 for C3 plants from cool and warm habitats and C4 plants, respectively. This observation indicates that the carboxylase catalytic efficiency (/Kc) varies with temperature and suggests that /Kc increases more steeply with temperature in C4 plants than in C3 plants. Perdomo et al. (2015) reported the same trend between C3 and C4 Flaveria species, and related these differences to specific structural changes in the C4 Rubisco causing a conformational change that favors product formation (i.e. higher ) at the expense of weaker substrate affinity (i.e. higher Kc).
In spite of the trend for increased ∆Ha for Sc/o (in absolute values) in C3 plants from warm habitats as compared with C3 plants from cool habitats, differences between these two groups averages were non-significant (Table 3). This result is in agreement with Galmés et al. (2005), who reported a tendency for higher temperature dependence for Sc/o in Mediterranean C3 species from warmer habitats, although with some exceptions (e.g. Lysimachia minoricensis from wettest and coolest environments displaying also a high activation energy). On the other hand, the non-significant difference in ∆Ha for Sc/o between C3 and C4 plants is in line with the observations of Perdomo et al. (2015). Overall, differences in the temperature sensitivity between Sc/o and /Kc suggest that the temperature dependences for /Kc and kcato/Ko also differ among C3 and C4 plants.
Given the observed variability, we suggest using the corrected species-specific functions describing the temperature dependence of Rubisco kinetic parameters (shown in Table 2) to model photosynthesis in the different species. If the temperature response of Rubisco kinetic parameters has not been described for the species under study, we recommend using the groups’ average values (presented in Table 3) to increase the accuracy of photosynthesis models in the different functional groups.
The temperature dependence of Ko: apparent contradictions among in vitro data
The temperature response of Ko based on in vitro data is available for five Spermatophyta species (Table 2), with contradictory results. A quantitatively similar value of ∆Ha for Ko to those of ∆Ha for Kc in Spermatophyta has been reported only for Atriplex glabriuscula (Badger and Collatz, 1977). The overall difficulty with Ko estimations is that Rubisco is much less specific for O2 than for CO2, and the oxygenase reaction of Rubisco is not saturated even in a 100% O2 atmosphere. Estimation of Ko over an O2 concentration range exhibiting only a slight non-linearity is extremely sensitive to any errors in gas concentrations. According to the compiled evidence, the temperature dependence of Ko for the other three species is very low compared with that for Kc, with values of ∆Ha for Ko close to zero, or even negative for Glycine max (Laing et al., 1974) and Setaria viridis (Boyd et al., 2015). Apparently, this discrepancy is not due to the specific methods used by the different studies as qualitatively different temperature scaling functions have been observed using the same methodologies, and similar responses with different methodologies: Badger and Collatz (1977) and Lehnherr et al. (1985) measured oxygenase activity using an oxygen electrode, Jordan and Ogren (1984) obtained Ko from the inhibition of carboxylase activity at 50% O2 (i.e. Kc,app), Laing et al. (1974) measured the oxygenase activity at different O2 concentrations by spectrophotometric determination of a P-glycolate derivate, and Boyd et al. (2015) used membrane inlet mass spectrometry to measure the temperature responses of Rubisco kinetics.
Common trends and discrepancies between in vitro and in vivo-based data on the temperature dependence of Rubisco kinetics
In vivo data on the temperature response of Ko agree in that values of ∆Ha for Ko are positive (i.e. Ko increasing with assay temperature, Fig. 5C), although with lower values compared with the in vitro-based trend described for Atriplex glabriuscula (Badger and Collatz, 1977) (Tables 2 and 4). The comparison of the in vitro and in vivo measurements of the temperature response of Ko in Glycine max exemplifies how the discrepancies between in vitro and in vivo are particularly important for this kinetic parameter (Fig. 6E). Presence of some CO2 is inevitable in in vivo measurements due to mitochondrial respiration, which could be affected by [O2] itself. Typically, only two, seldom three, O2 concentrations have been used in Ko estimations, but given the high sensitivity of these measurements to O2 concentration, we argue that both in vivo and in vitro measurements of Ko can be improved by using more O2 concentrations in the assays. Overall, Ko (or the Michaelis–Menten constant of Rubisco for CO2 at atmospheric conditions, ) is needed to model photosynthesis responses to temperature, and therefore, more in vitro and in vivo data on the temperature dependence of Ko are required in a larger number of species to confirm observed trends and solve discrepancies.
Contrary to Ko, in vitro and in vivo determinations of the temperature response of Sc/o and Kc describe similar shapes, with the in vitro averages lying intermediate between in vivo estimates (Fig. 5). In this case, methodological issues associated with in vitro assays and in vivo estimations may determine the degree of agreement between in vitro and in vivo reports. For instance, in vitro and in vivo data on the temperature response of Sc/o in Spinacia oleracea match very well between 15 and 45 ºC (Fig. 6A), with minor differences in the ∆Ha (Tables 2 and 4). The values of ∆Ha for Sc/o in Triticum aestivum are also similar between in vitro (−19.7 kJ mol−1) and in vivo (−25.2 kJ mol−1), although absolute values of in vitro Sc/o are approximately 1.6-fold higher than in vivo ones across the range of measurement temperatures (Fig. 6B).
Both in vitro and in vivo data on Rubisco kinetics present concerns implicitly linked to the specific methodologies. Since Monson et al. (1982), the first study discussing the possible reasons for discrepancies between in vitro and in vivo data, other studies have added to the debate on whether in vitro or in vivo data are more reliable and should be used in photosynthesis models (Ghashghaie and Cornic, 1994; von Caemmerer et al., 1994; Rogers et al., 2001; Galmés et al., 2011b; Díaz-Espejo, 2013; Walker et al., 2013). The main concerns related to in vitro measurements are that assay conditions may not be representative of the solute-rich environment of a chloroplast stroma where Rubisco operates, and that the extraction may not be fully efficient in terms of enzyme recovery and activation (Monson et al., 1982; Rogers et al., 2001; Galmés et al., 2011b; Díaz-Espejo, 2013). The latter, however, will have no consequences for Sc/o, Kc and Ko assays since they are independent of Rubisco concentration. Furthermore, as we have observed, the differences in assay conditions have only a moderate effect on ∆Ha and Q10 values. In turn, difficulties in the in vivo estimations are mainly related to the quantification of the actual concentration of CO2 at the site of carboxylation (Cc) and the rate of mitochondrial respiration in the light (Rlight), in addition to the concerns associated with the leaf mesophyll heterogeneity in terms of photosynthetic capacity, CO2 concentration and light reaching the chloroplasts (Ghashghaie and Cornic, 1994; von Caemmerer et al., 1994; Díaz-Espejo, 2013; Walker et al., 2013). The accurate quantification of Cc depends on the estimation of the leaf mesophyll conductance (gm), which relies on a series of assumptions (see for instance Tholen et al., 2012; Busch et al., 2013; Loriaux et al., 2013; Gu and Sun, 2014). The incorporation of gm in photosynthesis models has resulted in an improvement of the in vivo estimates of Rubisco kinetics and partially reconciled in vitro and in vivo data (von Caemmerer et al., 1994; Walker et al., 2013). In addition to technical difficulties in both in vitro and in vivo measurements, we note that there has not been much attention on how to conduct valid comparisons among in vivo and in vitro data. As our methodological analysis demonstrates, the comparison is not trivial because the conversion of kinetic characteristics among gas (in vivo data) and liquid (in vitro data) phases is strongly dependent on equilibrium constants used (Eqs 8–10).
A principal problem with in vivo measurements is that derivation of Rubisco kinetics using inverse modeling techniques becomes increasingly challenging at the physiological limits, e.g. leaf temperatures above 35–40 °C and below 10–15 °C, and especially in conditions leading to heat (above ca 45 °C) and cold stress (below ca 5 °C). Under higher temperatures, enhanced mitochondrial respiration, inactivation of Rubisco, closure of stomata and unclear response of gm preclude any accuracy of derivation of Rubisco kinetics (Crafts-Brandner and Salvucci, 2000; Atkin and Tjoelker, 2003; von Caemmerer and Evans, 2015). At lower temperatures, the challenges are associated with overall low gas-exchange fluxes due to low stomatal conductance and enzymatic capacities and again unclear effects of gm (Ensminger et al., 2012). Even if gm, mitochondrial and stomatal effects could be accounted for, the principal problem still remaining is that Rubisco-limited photosynthesis under such conditions is driven by combined effects of Rubisco activase and Rubisco. In the case of heat and cold stress conditions, the situation is further complicated because of time-dependent reductions in enzymatic capacities (Niinemets and Keenan, 2014). On the other hand, the problems associated with in vitro assays at low and high temperatures can originate from low reaction rates and changes in the substrate concentration in the assay media due to evaporation, respectively, which may increase the error associated with these measurements. It may well be that the lower Q10 values for Kc at higher temperatures observed for in vivo data compared with in vitro data (Fig. 5B) reflect the outlined problems with measurements at higher temperature. We suggest that both in vivo and in vitro measurements provide informative insight into the potential and actual in vivo kinetics of Rubisco and we call for more comparative measurements of in vivo and in vitro Rubisco kinetics in economically and ecologically relevant species.
Modeling Rubisco-dependent photosynthesis: how much do all the observed differences in temperature kinetics matter?
Although statistically important differences were observed in a number of Rubisco kinetic characteristics determined in in vitro studies (Table 3), the differences were relatively small, and the key question is how much do these differences matter when considered together? A comparison of simulated Rubisco-dependent photosynthesis among C3 cool and warm species demonstrates that the temperature adaptation indeed improves modeled photosynthesis of C3 cool species under lower temperatures, especially at lower chloroplastic CO2 concentration, while the temperature adaptation increases modeled photosynthesis of C3 warm species under higher temperatures, especially at higher chloroplastic CO2 concentration (Fig. 7). This is an important outcome, suggesting that in addition to higher-level cellular, whole leaf and whole plant adaptation responses (e.g. Björkman et al., 1980; Silim et al., 2010; Muhl et al., 2011), enzyme-level adaptation can lead to significant modifications in realized leaf photosynthesis in plants adapted to different climates. Of course, it is only a simulation for two groups of species that have relatively similar Rubisco characteristics and only considers the potential Rubisco-limited photosynthesis. Nevertheless, across all species, the activation energy for Sc/o (Fig. 3A) and the deactivation energy for kcat scaled with the growth temperature (Galmés et al., 2015), indicating that the simulations shown for C3 cool and warm species constitute a part of a broad trend of Rubisco temperature acclimation. Combining temperature responses of Rubisco-limited and RuBP-regeneration-limited photosynthesis further indicates that Rubisco-limited photosynthesis is a key driver of realized photosynthesis over much of the ambient temperature response for a large fraction of physiologically relevant quantum flux densities and chloroplastic CO2 concentrations (Galmés et al. 2014a).
The difference among C3 cool and warm plants was predicted to increase with increasing CO2 concentration (Fig. 7). This difference in Rubisco temperature characteristics is expected to enhance the competitive potential of C3 warm species relative to C3 cool species in future climates with higher atmospheric CO2 concentration and air temperature (Kirtman et al., 2013). We believe that for realistic simulation of carbon gain in future climates, models of C3 photosynthesis need to be modified to incorporate different Rubisco temperature kinetics of broad species groups to reflect modifications in Rubisco temperature kinetics to species’ growth environment. Even by doing this, we still need to recognize the inherent variability in species’ Rubisco temperature responses within species groups that we cannot explain by species’ growth environment or by phylogenetic relationships (Fig. 3). Such a variability is of particular significance when species group averages need to be used for simulation of photosynthesis for any given species lacking measured Rubisco kinetic traits (or for derivation of FvCB photosynthesis model parameters). However, it is likely of less concern for simulating photosynthesis of multi-species canopies where species-specific effects average out and average kinetics for species groups are more appropriate.
In fact, the problem of selecting ‘the appropriate’ set of kinetic parameters for modeling C3 photosynthesis has a long history starting with the publication of the FvCB photosynthesis model (Farquhar et al., 1980). Early model applications used in vitro measurements for Atriplex glabriuscula (Badger and Collatz, 1977) or Spinacia oleracea (Jordan and Ogren, 1984), while today researchers increasingly use the in vivo dataset based on N. tabacum (Bernacchi et al., 2001). While further in vivo datasets are becoming available (Walker et al., 2013), in vitro parameters from either Badger and Collatz (1977) or Jordan and Ogren (1984) remain widely used today. In fact, according to Thomson Reuters Web of Science (accessed 3 May 2016), Farquhar et al. (1980), the paper with the FvCB model, has been cited 3563 times (232 times in 2015), while Bernacchi et al. (2001) has been cited 442 times (42 times in 2015) (see also Niinemets et al. (2015) for an analysis of the frequency of use of different Rubisco kinetics for a subset of studies using the FvCB model in simulating canopy photosynthesis). The comparison of the three datasets, in vitro Jordan and Ogren (1984), in vivo Bernacchi et al. (2001) and in vivo Walker et al. (2013), with the in vitro C3 average dataset derived in our study demonstrated significant differences in predicted Rubisco-limited photosynthesis (Fig. 8). Further, the variability among the photosynthesis estimates derived by the three kinetics datasets is much greater than the variability among the estimated photosynthesis derived by the in vitro average kinetics for C3 cool and warm datasets developed in the current study.
A detailed examination of differences among model estimates indicated that both in vivo datasets provided lower estimates of Rubisco-limited photosynthesis than the C3-average and Jordan and Ogren (1984) in vitro datasets (Fig. 8). This is an important difference for interpretation of the FvCB model’s parameters, in particular Vcmax, the maximum carboxylase activity of Rubisco, derived from gas-exchange data (Rogers, 2014). Use of the in vivo kinetics of Bernacchi et al. (2001) to derive Vcmax from net assimilation vs. CO2 response curves leads to much higher, even more than 50% higher, estimates of Vcmax at 25 °C than use of the in vitro Jordan and Ogren (1984) kinetics. This difference is not fully appreciated by the modeling community, especially by modelers working at canopy, landscape, regional and global levels. Obviously, part of the large difference of the in vitro Jordan and Ogren (1984) and in vivo Bernacchi et al. (2001) kinetics could reflect lack of mesophyll diffusion conductance in parameter estimation in the study of Bernacchi et al. (2001), especially given the important temperature effects on mesophyll conductance (Bernacchi et al., 2002). This is partly confirmed by the smaller differences in in vitro and in vivo estimates from the dataset of Walker et al. (2013) that is derived considering mesophyll conductance. Nevertheless, as our study demonstrates, there are species-specific differences in Rubisco temperature kinetics, and this comparison again emphasizes the principal problem of using a single Rubisco temperature kinetics to simulate photosynthesis of all C3 species. Researchers should be fully aware about the limitations and associated uncertainties of using a single Rubisco temperature dataset.
Concluding remarks
The purpose of our study was two-fold: to summarize all the existing information on Rubisco temperature kinetics and analyse the relationships between Rubisco temperature kinetics within and among the phylogenetic and functional groups. We have standardized all the available in vitro Rubisco temperature data and constructed an extensive database that allows for direct comparison of Rubisco temperature kinetics without possible study-to-study differences due to assay buffer composition. We believe that in addition to identification of what is available, a key strength of this analysis is recognition of the gaps in data coverage. Too often relevant research is not conducted because there is a feeling in the community that ‘all this has already been measured’. As our analysis demonstrates, at least concerning Rubisco temperature kinetics, this opinion is an illusion and the coverage of several species groups is poor, suggesting that there clearly is room for high quality Rubisco temperature kinetic measurements over the years to come. This new research could potentially challenge some of the relationships developed here.
The other widespread opinion is that in vitro data coming from different labs and obtained using somewhat different methodologies cannot be used for broad analyses. We believe that the standardization functions developed by us largely solve this issue. Furthermore, we observed that activation energies and Q10 values that describe the magnitude of temperature-dependent change of given Rubisco kinetics are not very sensitive to the corrections developed, suggesting that our analysis of Rubisco temperature trait covariation is robust. However, we strongly advise against uncritical use of data by simply pooling the information without paying due attention to the experimental details.
From an immediate practical perspective, we provide separate average Rubisco temperature kinetics for C3 species from cool and warm habitats and argue that use of separate kinetics is warranted in models of carbon gain, especially for simulation of future conditions. Comparison of Rubisco temperature kinetics widely used so far further suggests that the modeling community needs to rethink the concept of ‘single species Rubisco fits all’. In fact, the variability in photosynthesis predictions from widely used single species datasets was much bigger than the variability between photosynthesis predictions by C3 cool and warm datasets developed here. Although we acknowledge the inertia in the modeling community, at least uncertainties of using single species models need consideration in simulating photosynthesis from leaf to globe.
Acknowledgements
The study was financially supported by the Spanish Ministry of Science and Innovation (AGL2009-07999 and AGL2013-42364-R), the Estonian Ministry of Science and Education (grants IUT-8-3 and PUT 607) and the European Commission through the European Regional Fund (the Center of Excellence EcolChange). The authors thank Asaph B. Cousins, Ryan Boyd, Carl J. Bernacchi, Gerald E. Edwards, Alfred J. Keys, Russell K. Monson and Berkley Walker for sending original data and/or for providing information about their experimental protocols. Alfred J. Keys is also acknowledged for his precious comments on the manuscript. The authors have no conflict of interest to declare.
References
- Atkin OK, Tjoelker MG. 2003. Thermal acclimation and the dynamic response of plant respiration to temperature. Trends in Plant Science 8, 343–351. [DOI] [PubMed] [Google Scholar]
- Azab HA, Khafagy ZA, Hassan A, El-Nady AM. 1994. Medium effect on the second-stage dissociation constant of N,N-bis(2-hydroxyethyl)glycine. Journal of Chemical and Engineering Data 39, 599–601. [Google Scholar]
- Badger MR. 1980. Kinetic properties of ribulose 1,5-bisphosphate carboxylase/oxygenase from Anabaena variabilis. Archives of Biochemistry and Biophysics 201, 247–254. [DOI] [PubMed] [Google Scholar]
- Badger MR, Andrews TJ. 1987. Co-evolution of Rubisco and CO2 concentrating mechanisms. In: Biggens J, ed. Progress in Photosynthesis Research, Vol. III Dordrecht: Martinus Nijhoff Publishers, 601–609. [Google Scholar]
- Badger MR, Collatz GJ. 1977. Studies on the kinetic mechanism of ribulose-1,5-bisphosphate carboxylase and oxygenase reactions, with particular reference to the effect of temperature on kinetic parameters. Carnegie Institution of Washington Yearbook 76, 355–361. [Google Scholar]
- Bagley J, Rosenthal DM, Ruiz-Vera UM, Siebers MH, Kumar P, Ort DR, Bernacchi CJ. 2015. The influence of photosynthetic acclimation to rising CO2 and warmer temperatures on leaf and canopy photosynthesis models. Global Biogeochemical Cycles 29, 194–206. [Google Scholar]
- Bates RG, Hetzer HB. 1961. Dissociation constant of the protonated acid form of 2-amino-2(hydroxymethyl)-1,3-propanediol [tris-(hydroxymethyl)-aminomethane] and related theromodynamic quantities from 0 to 50 ºC. Journal of Physical Chemistry 65, 667–671. [Google Scholar]
- Bates RG, Robinson RA. 1973. Tris(hydroxymethyl)aminomethane – a useful secondary pH standard. Analytical Chemistry 45, 420. [DOI] [PubMed] [Google Scholar]
- Bates RG, Roy RN, Robinson RA. 1973. Buffer standards of tris(hydroxymethyl)methylglycine (“tricine”) for the physiological range pH 7.2 to 8.5. Analytical Chemistry 45, 1663–1666. [DOI] [PubMed] [Google Scholar]
- Bermúdez MA, Galmés J, Moreno I, Mullineauz PM, Gotor C, Romero LC. 2012. Photosynthetic adaptation to length of day is dependent on S-sulfocysteine synthase activity in the thylakoid lumen. Plant Physiology 160, 274–288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernacchi CJ, Bagley JE, Serbin SP, Ruiz-Vera UM, Rosenthal DM, Vanloocke A. 2013. Modeling C3 photosynthesis from the chloroplast to the ecosystem. Plant, Cell and Environment 36, 1641–1657. [DOI] [PubMed] [Google Scholar]
- Bernacchi CJ, Portis AR, Nakano H, von Caemmerer S, Long SP. 2002. Temperature response of mesophyll conductance. Implications for the determination of Rubisco enzyme kinetics and for limitations to photosynthesis in vivo. Plant Physiology 130, 1992–1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernacchi CJ, Singsaas EL, Pimentel C, Portis AR, Long SP. 2001. Improved temperature response functions for models of Rubisco-limited photosynthesis. Plant, Cell and Environment 24, 253–259. [Google Scholar]
- Björkman O, Badger MR, Armond PA. 1980. Response and adaptation of photosynthesis to high temperatures. In: Turner NC, Kramer PJ, eds. Adaptation of plants to water and high temperature stress. New York: John Wiley and Sons, 233–249. [Google Scholar]
- Boyd RA, Gandin A, Cousins AB. 2015. Temperature responses of C4 photosynthesis: biochemical analysis of rubisco, phosphoenolpyruvate carboxylase, and carbonic anhydrase in Setaria viridis. Plant Physiology 169, 1850–1861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brooks A, Farquhar GD. 1985. Effect of temperature on the CO2/O2 specificity of ribulose-1,5-bisphosphate carboxylase/oxygenase and the rate of respiration in the light. Planta 165, 397–406. [DOI] [PubMed] [Google Scholar]
- Busch FA, Sage TL, Cousins AB, Sage RF. 2013. C3 plants enhance rates of photosynthesis by reassimilating photorespired and respired CO2 . Plant, Cell and Environment 36, 200–212. [DOI] [PubMed] [Google Scholar]
- Castrillo M. 1995. Ribulose-1,5-bis-phosphate carboxylase activity in altitudinal populations of Espeletia schultzii Wedd. Oecologia 101, 193–196. [DOI] [PubMed] [Google Scholar]
- Cavanagh AP, Kubien DS. 2013. Can phenotypic plasticity in Rubisco performance contribute to photosynthetic acclimation? Photosynthesis Research 119, 203–214. [DOI] [PubMed] [Google Scholar]
- Chaves MM, Flexas J, Pinheiro C. 2009. Photosynthesis under drought and salt stress: regulation mechanisms from whole plant to cell. Annals of Botany 103, 551–560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chor B, Tuller T. 2005. Maximum likelihood of evolutionary trees: hardness and approximation. Bioinformatics 21 (suppl 1), i97–i106. [DOI] [PubMed] [Google Scholar]
- Copolovici L, Niinemets Ü. 2007. Salting-in and salting-out effects of ionic and neutral osmotica on limonene and linalool Henry’s law constants and octanol/water partition coefficients. Chemosphere 69, 621–629. [DOI] [PubMed] [Google Scholar]
- Cornic G, Massacci A. 2004. Leaf photosynthesis under drought stress. In: Baker NR, ed. Photosynthesis and the environment. Advances in Photosynthesis and Respiration, 5. Dordrecht, The Netherlands: Kluwer Academic Publisher, 347–366. [Google Scholar]
- Crafts-Brandner SJ, Salvucci ME. 2000. Rubisco activase constrains the photosynthetic potential of leaves at high temperature and CO2 . Proceedings of the National Academy of Sciences of the United States of America 97, 13430–13435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Datta SP, Grzybovvski AK, Bates RG. 1964. Second acid dissociation of N,N-di (2-hydroxyethyl)glycine and related thermodynamic quantities from 0 to 55º. Journal of Physical Chemistry 68, 275–279. [Google Scholar]
- Delgado E, Medrano H, Keys AJ, Parry MAJ. 1995. Species variation in Rubisco specificity factor. Journal of Experimental Botany 46, 1775–1777. [Google Scholar]
- Díaz-Espejo A. 2013. New challenges in modeling photosynthesis: temperature dependencies of Rubisco kinetics. Plant, Cell and Environment 36, 2104–2107. [DOI] [PubMed] [Google Scholar]
- Durst RA, Staples BR. 1972. Tris/Tris.HCl: a standard buffer for use in the physiologic pH range. Clinical Chemistry 18, 206–208. [PubMed] [Google Scholar]
- Edgar RC. 2004. MUSCLE: multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Research 32, 1792–1797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ensminger I, Berninger F, Streb P. 2012. Response of photosynthesis to low temperature. In: Flexas J, Loreto F, Medrano H, eds. Terrestrial photosynthesis in a changing environment: a molecular, physiological, and ecological approach. Cambridge: Cambridge University Press, 272–289. [Google Scholar]
- Ezaki S, Maeda N, Kishimoto T, Atomi H, Imanaka T. 1999. Presence of a structurally novel type ribulose-bisphosphate carboxylase/oxygenase in the hyperthermophilic archaeon, Pyrococcus kodakaraensis KOD1. Journal of Biological Chemistry 274, 5078–5082. [DOI] [PubMed] [Google Scholar]
- Farquhar GD, von Caemmerer S, Berry JA. 1980. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 149, 78–90. [DOI] [PubMed] [Google Scholar]
- Feng D, Koch WF, Wu YC. 1989. Second dissociation constant and pH of N-(2-hydroxyethy1)piperazine-N’-2-ethanesulfonic acid from 0 to 50 ºC. Analytical Chemistry 61, 1400–1405. [Google Scholar]
- Flexas J, Bota J, Loreto F, Cornic G, Sharkey TD. 2004. Diffusive and metabolic limitations to photosynthesis under drought and salinity in C3 plants. Plant Biology 6, 269–279. [DOI] [PubMed] [Google Scholar]
- Galmés J, Andralojc PJ, Kapralov MV, Flexas J, Keys AJ, Molins A, Parry MAJ, Conesa MÀ. 2014b Environmentally driven evolution of Rubisco and improved photosynthesis and growth within the C3 genus Limonium (Plumbaginaceae). New Phytologist 203, 989–999. [DOI] [PubMed] [Google Scholar]
- Galmés J, Conesa MÀ, Díaz-Espejo A, Mir A, Perdomo JA, Niinemets Ü, Flexas J. 2014a Rubisco catalytic properties optimized for present and future climatic conditions. Plant Science 226, 61–70. [DOI] [PubMed] [Google Scholar]
- Galmés J, Conesa MA, Ochogavía JM, Perdomo JA, Francis D, Ribas-Carbó M, Savé R, Flexas J, Medrano H, Cifre J. 2011a Physiological and morphological adaptations in relation to water use efficiency in Mediterranean accessions of Solanum lycopersicum. Plant, Cell and Environment 34, 245–260. [DOI] [PubMed] [Google Scholar]
- Galmés J, Flexas J, Keys AJ, Cifre J, Mitchell RAC, Madgwick PJ, Haslam RP, Medrano H, Parry MAJ. 2005. Rubisco specificity factor tends to be larger in plant species from drier habitats and in species with persistent leaves. Plant, Cell and Environment 28, 571–579. [Google Scholar]
- Galmés J, Kapralov MV, Andralojc PJ, Conesa MÀ, Keys AJ, Parry MAJ, Flexas J. 2014c Expanding knowledge of the Rubisco kinetics variability in plant species: environmental and evolutionary trends. Plant, Cell and Environment 37, 1989–2001. [DOI] [PubMed] [Google Scholar]
- Galmés J, Kapralov MV, Copolovici LO, Hermida-Carrera C, Niinemets Ü. 2015. Temperature responses of the Rubisco maximum carboxylase activity across domains of life: phylogenetic signals, trade-offs, and importance for carbon gain. Photosynthesis Research 123, 183–201. [DOI] [PubMed] [Google Scholar]
- Galmés J, Ribas-Carbó M, Medrano H, Flexas J. 2011b Rubisco activity in Mediterranean species is regulated by the chloroplastic CO2 concentration under water stress. Journal of Experimental Botany 62, 653–665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghannoum O, Evans JR, Chow WS, Andrews TJ, Conroy JP, von Caemmerer S. 2005. Faster Rubisco is the key to superior nitrogen-use efficiency in NADP-malic enzyme relative to NAD-malic enzyme C4 grasses. Plant Physiology 137, 638–650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghashghaie J, Cornic G. 1994. Effect of temperature on partitioning of photosynthetic electron flow between CO2 assimilation and O2 reduction and on the CO2/O2 specificity of RubisCo. Journal of Plant Physiology 143, 643–650. [Google Scholar]
- Gnaiger E. 2001. Oxygen solubility in experimental media. OROBOROS Bioenergetics Newsletter 63, 1–6. [Google Scholar]
- Gornall J, Betts R, Burke E, Clark R, Camp J, Willett K, Wiltshire A. 2010. Implications of climate change for agricultural productivity in the early twenty-first century. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences 365, 2973–2989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gros JB, Dussap CG, Catté M. 1999. Estimation of O2 and CO2 solubility in microbial culture media. Biotechnology Progress 15, 923–927. [DOI] [PubMed] [Google Scholar]
- Gu L, Sun Y. 2014. Artefactual responses of mesophyll conductance to CO2 and irradiance estimated with the variable J and online isotope discrimination methods. Plant, Cell and Environment 37, 1231–1249. [DOI] [PubMed] [Google Scholar]
- Gubernator B, Bartoszewski R, Kroliczewski J, Wildner G, Szczepaniak A. 2008. Ribulose-1,5-bisphosphate carboxylase/oxygenase from thermophilic cyanobacterium Thermosynechococcus elongatus. Photosynthesis Research 95, 101–109. [DOI] [PubMed] [Google Scholar]
- Gupta AS, Berkowitz GA. 1988. Chloroplast osmotic adjustment and water stress effects on photosynthesis. Plant Physiology 88, 200–206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall NP, Keys AJ. 1983. Temperature dependence of the enzymic carboxylation and oxygenation of ribulose 1,5-bisphosphate in relation to effects of temperature on photosynthesis. Plant Physiology 72, 945–948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harley PC, Weber JA, Gates DM. 1985. Interactive effects of light, leaf temperature, CO2 and O2 on photosynthesis in soybean. Planta 165, 249–263. [DOI] [PubMed] [Google Scholar]
- Harmon LJ, Weir JT, Brock CD, Glor RE, Challenger W. 2008. GEIGER: investigating evolutionary radiations. Bioinformatics 24, 129–131. [DOI] [PubMed] [Google Scholar]
- Harned HS, Bonner FT. 1945. The first ionization of carbonic acid in aqueous solutions of sodium chloride. Journal of the American Chemical Society 67, 1026–1031. [Google Scholar]
- Harned HS, Davis R., Jr 1943. The ionization constant of carbonic acid in water and the solubility of carbon dioxide in water and aqueous salt solutions from 0 to 50º. Journal of the American Chemical Society 65, 2030–2037. [Google Scholar]
- Haslam RP, Keys AJ, Andralojc PJ, Madgwick PJ, Andersson I, Grimsrud A, Eilertsen HC, Parry MAJ. 2005. Specificity of diatom Rubisco. In: Omasa K, Nouchi I, De Kok LJ, eds. Plant Responses to Air Pollution and Global Change. Tokyo: Springer-Verlag, 157–164. [Google Scholar]
- Hermida-Carrera C, Kapralov MV, Galmés J. 2016. Rubisco catalytic properties and temperature response in crops. Plant Physiology, doi: 10.1104/pp.16.01846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishikawa C, Hatanaka T, Misoo S, Fukayama H. 2009. Screening of high kcat Rubisco among Poaceae for improvement of photosynthetic CO2 assimilation in rice. Plant Production Science 12, 345–350. [Google Scholar]
- Jordan DB, Ogren WL. 1981. Species variation in the specificity of ribulose biphosphate carboxylae/oxygenase. Nature 291, 513–515. [Google Scholar]
- Jordan DB, Ogren WL. 1984. The CO2/O2 specificity of ribulose 1,5-bisphosphate carboxylase/oxygenase. Dependence on ribulosebisphosphate concentration, pH and temperature. Planta 161, 308–313. [DOI] [PubMed] [Google Scholar]
- Keenan T, Sabate S, Gracia C. 2010. The importance of mesophyll conductance in regulating forest ecosystem productivity during drought periods. Global Change Biology 16, 1019–1034. [Google Scholar]
- Keys AJ. 1986. Rubisco: its role in photorespiration. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences 313, 325–336. [Google Scholar]
- Kirtman B, Power SB, Adedoyin JA, et al. 2013. Near-term climate change: projections and predictability. In: Stocker TF, Qin D, Plattner G-K, Tignor M, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, Midgley PM, eds. Climate change 2013: The physical science basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge, New York: Cambridge University Press, 953–1028. [Google Scholar]
- Kubien DS, Whitney SM, Moore PV, Jesson LK. 2008. The biochemistry of Rubisco in Flaveria. Journal of Experimental Botany 59, 1767–1777. [DOI] [PubMed] [Google Scholar]
- Laing WA, Ogren WL, Hageman RH. 1974. Regulation of soybean net photosynthetic CO2 fixation by the interaction of CO2, O2, and ribulose 1,5-diphosphate carboxylase. Plant Physiology 54, 678–685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehnherr B, Mächler F, Nösberger J. 1985. Influence of temperature on the ratio of ribulose bisphosphate carboxylase to oxygenase activities and on the ratio of photosynthesis to photorespiration of leaves. Journal of Experimental Botany 168, 1117–1125. [Google Scholar]
- Long SP, Zhu X-G, Naidu SL, Ort DR. 2006. Can improvement in photosynthesis increase crop yields? Plant, Cell and Environment 29, 315–330. [DOI] [PubMed] [Google Scholar]
- Loriaux SD, Avenson TJ, Welles JM, McDermitt DK, Eckles RD, Riensche B, Genty B. 2013. Closing in on maximum yield of chlorophyll fluorescence using a single multiphase flash of sub-saturating intensity. Plant, Cell and Environment 36, 1755–1770. [DOI] [PubMed] [Google Scholar]
- Mächler F, Nösberger J. 1980. Regulation of ribulose bisphosphate carboxylase activity in intact wheat leaves by light, CO2, and temperature. Journal of Experimental Botany 125, 1485–1491. [Google Scholar]
- Markham AE, Kobe KA. 1940. The solubility of carbon dioxide and nitrous oxide in aqueous salt solutions. Industrial and Engineering Chemistry Analytical Edition 12, 449–454. [Google Scholar]
- Millero FJ, Huang F. 2003. Solubility of oxygen in aqueous solutions of KCl, K2SO4, and CaCl2 as a function of concentration and temperature. Journal of Chemical and Engineering Data 48, 1050–1054. [Google Scholar]
- Millero FJ, Huang F, Graham TB. 2003. Solubility of oxygen in some 1–1, 2–1, 1–2, and 2–2 electrolytes as a function of concentration at 25 ºC. Journal of Solution Chemistry 32, 473–487. [Google Scholar]
- Millero FJ, Huang F, Laferiere AL. 2002. Solubility of oxygen in the major sea salts as a function of concentration and temperature. Marine Chemistry 78, 217–230. [Google Scholar]
- Monson R-K, Stidham MA, Williams GJ, III, Edwards GE, Uribe EG. 1982. Temperature dependence of photosynthesis in Agropyron smithii Rydb. Plant Physiology 69, 921–928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muhl QE, Du Toit ES, Robbertse PJ. 2011. Leaf adaptation to temperature regimes in Moringa oleifera (horseradish tree). International Journal of Agriculture and Biology 13, 1021–1024. [Google Scholar]
- Murchie EH, Pinto M, Horton P. 2008. Agriculture and the new challenges for photosynthesis research. New Phytologist 181, 532–552. [DOI] [PubMed] [Google Scholar]
- Niinemets Ü, Ciccioli P, Noe SM, Reichstein M. 2013. Scaling BVOC emissions from leaf to canopy and landscape: how different are predictions based on contrasting emission algorithms? In: Niinemets Ü, Monson RK, eds. Biology, controls and models of tree volatile organic compound emissions. Berlin: Springer, 357–390. [Google Scholar]
- Niinemets Ü, Díaz-Espejo A, Flexas J, Galmés J, Warren CR. 2009b Importance of mesophyll diffusion conductance in estimation of plant photosynthesis in the field. Journal of Experimental Botany 60, 2271–2282. [DOI] [PubMed] [Google Scholar]
- Niinemets Ü, Keenan TF. 2014. Photosynthetic responses to stress in Mediterranean evergreens: mechanisms and models. Environmental and Experimental Botany 103, 24–41. [Google Scholar]
- Niinemets Ü, Keenan TF, Hallik L. 2015. Tansley review. A worldwide analysis of within-canopy variations in leaf structural, chemical and physiological traits across plant functional types. New Phytologist 205, 973–993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niinemets Ü, Wright IJ, Evans JR. 2009a Leaf mesophyll diffusion conductance in 35 Australian sclerophylls covering a broad range of foliage structural and physiological variation. Journal of Experimental Botany 60, 2433–2449. [DOI] [PubMed] [Google Scholar]
- Pagel M. 1999. Inferring the historical patterns of biological evolution. Nature 401, 877–884. [DOI] [PubMed] [Google Scholar]
- Paradis E, Claude J, Strimmer K. 2004. APE: analyses of phylogenetics and evolution in R language. Bioinformatics 20, 289–290. [DOI] [PubMed] [Google Scholar]
- Perdomo JA, Cavanagh AP, Kubien DS, Galmés J. 2015. Temperature dependence of in vitro Rubisco kinetics in species of Flaveria with different photosynthetic mechanisms. Photosynthesis Research 124, 67–75. [DOI] [PubMed] [Google Scholar]
- Pinheiro J, Bates D, DebRoy S, Sarkar D. 2014. nlme: linear and nonlinear mixed effects models. R package version 3.1–117, http://CRAN.R-project.org/package=nlme. [Google Scholar]
- Pocker Y, Bjorkquist DW. 1977. Stopped-flow studies of carbon dioxide hydration and bicarbonate dehydration in H2O and D2O. Acid-base and metal ion catalysis. Journal of the American Chemical Society 90, 6537–6543. [Google Scholar]
- Ramette RW, Culberson CH, Bates RG. 1977. Acid-base properties of tris(hydroxymethyl)aminomethane (Tris) buffers in seawater from 5 to 40 ºC. Analytical Chemistry 49, 867–870. [Google Scholar]
- Raven JA. 2000. Land plant biochemistry. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences 355, 833–846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Revell LJ. 2012. Phytools: an R package for phylogenetic comparative biology (and other things). Methods in Ecology and Evolution 3, 217–223. [Google Scholar]
- Rischbieter E, Schumpe A, Wunder V. 1996. Gas solubilities in aqueous solutions of organic substances. Journal of Chemical and Engineering Data 41, 809–812. [Google Scholar]
- Rogers A. 2014. The use and misuse of Vc,max in Earth System Models. Photosynthesis Research 119, 15–29. [DOI] [PubMed] [Google Scholar]
- Rogers A, Ellsworth DS, Humphries SW. 2001. Possible explanation of the disparity between the in vitro and in vivo measurements of Rubisco activity: a study in loblolly pine grown in elevated pCO2 . Journal of Experimental Botany 52, 1555–1561. [DOI] [PubMed] [Google Scholar]
- Roy LN, Roy RN, Denton CE, LeNoue SR, Roy CN, Ashkenazi S, Williams TB, Church DR, Fuge MS, Sreepada KN. 2006. Second dissociation constant of bis-[(2-hydroxyethyl)amino]acetic acid (BICINE) and pH of its buffer solutions from 5 to 55 ºC. Journal of Solution Chemistry 35, 605–624. [Google Scholar]
- Roy LN, Roy RN, Wollen JT, Harmon MA, Stegner JM, Shah AA, Henson IB. 2011. Buffer standards for the biological pH of the amino acid N-[2-hydroxyethyl]piperazine-N’-[3-propanesulfonic acid], HEPPS, from (278.15 to 328.15) K. Journal of Chemical and Engineering Data 56, 4126–4132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy RN, Cramer J, Randon V, Willard D, Walter JL, Good WS, Kilker A, Roy LN. 1998. Buffers for the physiological pH range: thermodynamics of the second dissociation of N-(2-hydroxyethyl)piperazine-N’-2-hydroxypropanesulfonic acid from 5 to 55 °C. Journal of Solution Chemistry 27, 425–434. [Google Scholar]
- Roy RN, Roy LN, Ashkenazi S, Wollen JT, Dunseth CD, Fuge MS, Durden JL, Roy CN, Hughes HM, Morris BT, Cline KL. 2009. Buffer standards for pH measurement of N-(2-hydroxyethyl)piperazine-N’-2-ethanesulfonic acid (HEPES) for I=0.16 mol·kg−1 from 5 to 55 °C. Journal of Solution Chemistry 38, 449–458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sage RF. 2002. Variation in the kcat of Rubisco in C3 and C4 plants and some implications for photosynthetic performance at high and low temperature. Journal of Experimental Botany 53, 609–620. [DOI] [PubMed] [Google Scholar]
- Sage RF, Kubien DS. 2007. The temperature response of C3 and C4 photosynthesis. Plant, Cell and Environment 30, 1086–1106. [DOI] [PubMed] [Google Scholar]
- Sander R. 2001. Henry’s law constants. In: Linstrom PJ, Mallard WG, eds. NIST chemistry WebBook. NIST standard reference database, 69. Gaithersburg, MD: National Institute of Standards and Technology, http://webbook.nist.gov. [Google Scholar]
- Savir Y, Noor E, Milo R, Tlusty T. 2010. Cross-species analysis traces adaptation of Rubisco toward optimality in a low-dimensional landscape. Proceedings of the National Academy of Sciences of the United States of America 107, 3475–3480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schröppel-Meier G, Kaiser WM. 1988. Ion homeostasis in chloroplasts under salinity and mineral deficiency. I. Solute concentrations in leaves and chloroplasts from spinach plants under NaCl or NaNO3 salinity. Plant Physiology 87, 822–827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schumacher TE, Smucker AJM. 1983. Measurement of CO2 dissolved in aqueous solutions using a modified infrared gas analyzer system. Plant Physiology 72, 212–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shedlovsky T, MacInnes DA. 1935. The first ionization constant of carbonic acid, 0 to 38º, from conductance measurements. Journal of the American Chemical Society 57, 1705–1710. [Google Scholar]
- Silim SN, Ryan N, Kubien DS. 2010. Temperature responses of photosynthesis and respiration in Populus balsamifera L.: acclimation versus adaptation. Photosynthesis Research 104, 19–30. [DOI] [PubMed] [Google Scholar]
- Staudinger J, Roberts PV. 2001. A critical compilation of Henry’s law constant temperature dependence relations for organic compounds in dilute aqueous solutions. Chemosphere 44, 561–576. [DOI] [PubMed] [Google Scholar]
- Tamura K, Stecher G, Peterson D, Filipski A, Kumar S. 2013. MEGA6: Molecular Evolutionary Genetics Analysis version 6.0. Molecular Biology and Evolution 30, 2725–2729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tcherkez GGB, Farquhar GD, Andrews TJ. 2006. Despite slow catalysis and confused substrate specificity, all ribulose bisphosphate carboxylases may be nearly perfectly optimized. Proceedings of the National Academy of Sciences of the United States of America 103, 7246–7251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tholen D, Ethier G, Genty B, Pepin S, Zhu X-G. 2012. Variable mesophyll conductance revisited: theoretical background and experimental implications. Plant, Cell and Environment 35, 2087–2103. [DOI] [PubMed] [Google Scholar]
- Tomás M, Flexas J, Copolovici L, Galmés J, Hallik L, Medrano H, Tosens T, Vislap V, Niinemets Ü. 2013. Importance of leaf anatomy in determining mesophyll diffusion conductance to CO2 across species: quantitative limitations and scaling up by models. Journal of Experimental Botany 64, 2269–2281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tromans D. 2000. Modeling oxygen solubility in water and electrolyte solutions. Industrial and Engineering Chemistry Research 39, 805–812. [Google Scholar]
- Uemura K, Anwaruzzaman M, iyachi S, Yokota A. 1997. Ribulose-1,5-bisphosphate carboxylase/oxygenase from thermophilicred algae with a strong specificity for CO2 fixation. Biochemical and Biophysical Research Communications 233, 568–571. [DOI] [PubMed] [Google Scholar]
- Umbreit WW, Burris RH, Stauffer JF. 1972. Manometric and biochemical techniques. A manual describing methods applicable to the study of tissue metabolism, 5th edn Minneapolis: Burgess Publishing Company. [Google Scholar]
- van Slyke DD, Sendroy J, Jr, Hastings B, Neill JM. 1928. Studies of gas and electrolyte equilibria in blood. X. The solubility of carbon dioxide at 38º in water, salt solution, serum, and blood cells. Journal of Biological Chemistry 78, 765–799. [Google Scholar]
- Vega CA, Bates RG. 1976. Buffers for the physiological pH range: thermodynamic constants of four substituted aminoethanesulfonic acids from 5 to 50 ºC. Analytical Chemistry 48, 1293–1296. [DOI] [PubMed] [Google Scholar]
- Viil J, Ivanova H, Pärnik T. 2012. Specificity factor of Rubisco: estimation in intact leaves by carboxylation at different CO2/O2 ratios. Photosynthetica 50, 247–253. [Google Scholar]
- von Caemmerer S. 2000. Biochemical Models of Leaf Photosynthesis. Canberra: CSIRO Publishing. [Google Scholar]
- von Caemmerer S, Evans JR. 2015. Temperature responses of mesophyll conductance differ greatly between species. Plant, Cell and Environment 38, 629–637. [DOI] [PubMed] [Google Scholar]
- von Caemmerer S, Evans JR, Hudson GS, Andrews TJ. 1994. The kinetics of ribulose-1,5-bisphosphate carboxylase/oxygenase in vivo inferred from measurements of photosynthesis in leaves of transgenic tobacco. Planta 195, 88–97. [Google Scholar]
- Walker B, Ariza LS, Kaines S, Badger MR, Cousins AB. 2013. Temperature response of in vivo Rubisco kinetics and mesophyll conductance in Arabidopsis thaliana: comparisons to Nicotiana tabacum. Plant, Cell and Environment 36, 2108–2119. [DOI] [PubMed] [Google Scholar]
- Weast RC. 1974. CRC handbook of chemistry and physics. A ready-reference book of chemical and physical data, 55th edn Boca Raton: CRC Press, Inc. [Google Scholar]
- Wei J-C, Wang R-L, Cheng G-Y. 1994. Studies on the kinetic properties of ribulose-1, 5-bisphosphate carboxylase from of F1 hybrid rice. Acta Phytophisiologica Sinica 20, 55–60. [Google Scholar]
- Whitney SM, Houtz RL, Alonso H. 2011. Advancing our understanding and capacity to engineer nature’s CO2-sequestring enzyme, Rubisco. Plant Physiology 155, 27–35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willmott CJ, Matsuura K. 2005. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Climate Research 30, 79–82. [Google Scholar]
- Yamori W, Suzuki K, Noguchi K, Nakai M, Terashima I. 2006. Effects of Rubisco kinetics and Rubisco activation state on the temperature dependence of the photosynthetic rate in spinach leaves from contrasting growth temperatures. Plant, Cell and Environment 29, 1659–1670. [DOI] [PubMed] [Google Scholar]
- Yokota A, Kitaoka S. 1985. Correct pK values for dissociation constant of carbonic acid lower the reported Km values of ribulose bisphosphate carboxylase to half. Presentation of a monograph and an equation for determining the pK values. Biochemical and Biophysical Research Communications 131, 1075–1079. [DOI] [PubMed] [Google Scholar]
- Young JN, Goldman JAL, Kranz SA, Tortell PD, Morel FMM. 2015. Slow carboxylation of Rubisco constrains the rate of carbon fixation during Antarctic phytoplankton blooms. New Phytologist 205, 172–181. [DOI] [PubMed] [Google Scholar]
- Young JN, Rickaby REM, Kapralov MV, Filatov DA. 2012. Adaptive signals in algal Rubisco reveal a history of ancient atmospheric carbon dioxide. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences 367, 483–492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu XG, Jensen RG, Bohnert HJ, Wildner GF, Schlitter J. 1998. Dependence of catalysis and CO2/O2 specificity of Rubisco on the carboxy-terminus of the large subunit at different temperatures. Photosynthesis Research 57, 71–79. [Google Scholar]
- Zhu X-G, Long SP, Ort DR. 2010. Improving photosynthetic efficiency for greater yield. Annual Review of Plant Biology 61, 235–261. [DOI] [PubMed] [Google Scholar]