Skip to main content
PMC home page
Wiley Open Access Collection logoLink to Wiley Open Access Collection
. 2015 Aug 10;42(15):6170–6179. doi: 10.1002/2015GL064955

Near‐Earth injection of MeV electrons associated with intense dipolarization electric fields: Van Allen Probes observations

Lei Dai 1,2,✉, Chi Wang 1, Suping Duan 1, Zhaohai He 1, John R Wygant 2, Cynthia A Cattell 2, Xin Tao 3, Zhenpeng Su 3, Craig Kletzing 4, Daniel N Baker 5, Xinlin Li 5, David Malaspina 5, J Bernard Blake 6, Joseph Fennell 6, Seth Claudepierre 6, Drew L Turner 6, Geoffrey D Reeves 7, Herbert O Funsten 7, Harlan E Spence 8, Vassilis Angelopoulos 9, Dennis Fruehauff 10, Lunjin Chen 11, Scott Thaller 2, Aaron Breneman 2, Xiangwei Tang 2
PMCID: PMC5014237  PMID: 27656009

Abstract

Substorms generally inject tens to hundreds of keV electrons, but intense substorm electric fields have been shown to inject MeV electrons as well. An intriguing question is whether such MeVelectron injections can populate the outer radiation belt. Here we present observations of a substorm injection of MeV electrons into the inner magnetosphere. In the premidnight sector at L ∼ 5.5, Van Allen Probes (Radiation Belt Storm Probes)‐A observed a large dipolarization electric field (50 mV/m) over ∼40 s and a dispersionless injection of electrons up to ∼3 MeV. Pitch angle observations indicated betatron acceleration of MeV electrons at the dipolarization front. Corresponding signals of MeV electron injection were observed at LANL‐GEO, THEMIS‐D, and GOES at geosynchronous altitude. Through a series of dipolarizations, the injections increased the MeV electron phase space density by 1 order of magnitude in less than 3 h in the outer radiation belt (L > 4.8). Our observations provide evidence that deep injections can supply significant MeV electrons.

Keywords: substorm injection, substorm dipolarization, radiation belt electrons, electric fields

Key Points

  • Unambiguous evidence of deep injections of MeV electrons from multispacecraft

  • Extremely large electric fields (50 mV/m) associated with the dipolarization

  • Strong dipolarizations may supply significant MeV electrons to radiation belts

1. Introduction

Substorm dipolarization is known to inject energetic electrons into the radiation belts. Injected electrons are usually in the energy range from tens of keV to hundreds of keV. Observations and model results from the last two decades, however, indicate that dipolarizations sometimes inject MeV electrons, as well. In test particle simulations, Kim et al. [2000] showed that dipolarizations can contribute to MeV electrons enhancements in the outer radiation belt. Ingraham et al. [2001] provided observational evidence that strong substorms continuously inject MeV electrons to the geosynchronous altitude. Using data from the Akebono spacecraft, Nagai et al. [2006] identified rapid enhancements of MeV electrons associated with storm time substorm dipolarizations in the outer radiation belt. Modeling results from Fok et al. [2001] and Glocer et al. [2011] attributed rapid enhancements of MeV electrons in their modeling results to dipolarization electric fields. Using data from multiple spacecraft that tracked the electron phase space density (PSD) at different radial locations, Dai et al. [2014] showed that strong dipolarization electric fields injected MeV electrons by pushing magnetotail electrons to the geosynchronous altitude. Su et al. [2014] provided evidence from the Van Allen Probes (Radiation Belt Storm Probes (RBSP)) measurements that substorm injections of MeV electrons, as well as acceleration by chorus waves, contribute to the outward extension of the outer belt.

Substorm injections of MeV electrons are interesting from several perspectives. Their contribution to the energization of MeV electron in the radiation belt is relatively underexplored. The efficiency of this energization under different solar wind conditions and various levels of geomagnetic activity is unclear. Much of the physics of MeV electron injection remains to be explored. It now appears that only a small portion of substorm dipolarizations can inject MeV electrons. The special conditions under which substorm dipolarizations can inject MeV electrons are unknown. Furthermore, injections have been considered to provide the seed population needed for the local energization through wave‐particle interactions. Injections of MeV electrons provide a harder spectrum of seed populations than injections of tens to hundreds of keV electrons.

The electric field associated with dipolarizations, in which magnetic field lines collapse from a tail‐like shape to a more dipole‐like shape [Baker et al., 1996], is believed to drive particle acceleration and injections [Birn et al., 2013]. In observations, dipolarization electric fields are time varying, are azimuthally localized, and can be from mV/m to tens of mV/m [e.g., Cattell and Mozer, 1984; Fairfield et al., 1998; Tu et al., 2000; Dai et al., 2014]. Inspired by the injection front model [Moore et al., 1981], Li et al. [1998] constructed a model of an earthward propagating electric field pulse to simulate the substorm injection. In the model of Li et al. [1998], the electric field pulse is associated with a rapid increase in B z to represent the dipolarization. The model can produce signals of injections at different radial distances [Li et al., 1998; Sarris et al., 2002; Li et al., 2003; Zaharia et al., 2004; Liu et al., 2009]. Gabrielse et al. [2012] developed a similar model, adding the ingredient of twin vortices and their dawnward electric fields that are adjacent to the edge of the earthward flow. Alternative approaches to model the electric field and plasma dynamics of substorm dipolarizations involve MHD simulations [Birn et al., 1998; Fok et al., 2006; Birn et al., 2013; Ashour‐Abdalla et al., 2011] and Rice Convection Model(RCM)‐based simulations [Zhang et al., 2009; Yang et al., 2011].

Injected particles are trapped on closed orbits as the dipolarization electric field is reduced or diminished. As a result, deep injections can directly supply energetic particles to the center of the outer radiation belt. Using the CRRES data set, Friedel et al. [1996] showed that injections can penetrate to L = 4. Such near‐Earth injection events are also manifested as penetrating electric fields [Rowland, 2002]. Sergeev et al.[1998] documented short‐duration injections that correlate with dawn‐dusk electric fields at a radial distance of ∼5Re. In a study of multiple events, Reeves et al. [1996] showed that the injection region traveled earthward at an average of 24 km/s from the geosynchronous altitude to the CRRES satellite. Turner et al. [2015] provided evidence of substorm‐associated injections observed down to L = 2.5.

The orbit of Van Allen Probes (RBSP) [Mauk et al., 2012] is suitable for studying near‐Earth injections. To better understand MeV electron injections in the RBSP data set, we need to investigate the spatial scales of the injection region, the properties of the electric fields and magnetic fields, the characteristics of MeV electrons, and how many MeV electrons are injected during the dipolarizations. In this paper, we present detailed field and particle observations from RBSP, Time History of Events and Macroscale Interactions during Substorms (THEMIS), Los Alamos National Laboratory (LANL)‐GEO, and GOES of a MeV electron injection event in the inner magnetosphere. Previous observations of MeV electron injections has one limitation—only dispersionless injections were observed. In this study, we provide an unambiguous injection signature of the dispersed and drifting electron population up to ∼3 MeV. This event is notable because of an extremely large dipolarization electric field 50 mV/m that is rarely seen in previous models and observations.

2. Observations of Near‐Earth Injection of MeV Electrons

2.1. Overview of RBSP‐A Observations on 26 April 2013

With its apogee near midnight, RBSP‐A spent several hours at L = 5–6 in the nightside on 26 April 2013. RBSP‐B is not in an ideal orbit location to be relevant for this study. Figure 1 shows solar wind conditions, geomagnetic conditions, and an overview of fields and energetic particles from RBSP‐A from 03 UT to 09 UT on 26 April 2013. As shown in Figure 1a, the solar wind dynamic pressure was steady. The SYM‐H index from −20 to −50 covered part of the main phase and the recovery phase in a moderate storm (see Figure 1b). The AE index increased from 400 to ∼1000 at around 0510 UT. The substorm around 0510 UT is selected for analysis. Intuitively, intense solar wind and large geomagnetic storms may have more free energy to drive MeV electron injection events. However, this event and similar events in previous studies indicate frequent occurrence of MeV electron injections during moderate activity, suggesting a complex chain of processes through which MeV electron injections can drain free energy from the magnetosphere.

Figure 1.

Figure 1

Open in a new tab

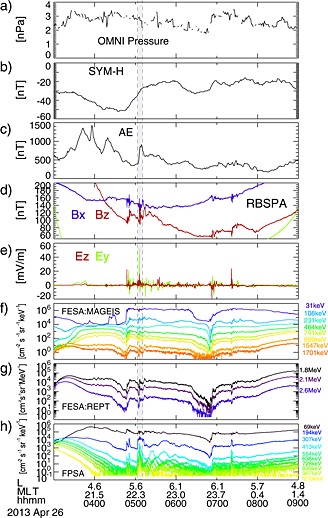
Overview of solar wind conditions, the geomagnetic activity and RBSP‐A observations on 26 April 2013. (a) One minute OMIN data of the solar wind dynamic pressure. (b) The SYM‐H index. (c) AE index. (d) One second resolution B x and B z components in GSM from RBSP‐A. (e) Spin fit E y and E z in MGSE from RBSP‐A. (f) The different flux of energetic electrons from MagEIS onboard RBSP‐A. (g) The different flux of energetic electrons from REPT onboard RBSP‐A. (h) The different flux of energetic ions from MagEIS onboard RBSP‐A.

Figures 1d and 1e show the DC magnetic field and electric field from RBSP‐A. The magnetic field data are the 1 s resolution data from the Electric and Magnetic Field Instrument Suite and Integrated Science (EMFISIS) fluxgate magnetometer [Kletzing et al., 2013]. The typical dipolarization signal is a rapid increase in B z that is often associated with a decrease in B x. In Figure 1d, several dipolarizations with different time scales can be clearly identified from about 0440 UT to 0740 UT. The spin resolution electric field from the Electric Field and Waves (EFW) instrument [Wygant et al., 2013] in the modified GSE coordinates is shown in Figure 1e. E z and E y are in the spin plane and close to the GSE z and GSE y within 20∘. In the regime of DC and ULF wave measurement, the electric field component E x along the spin axis can be deduced from the E·B = 0 assumption if the angle between B, and the spin plane is larger than 15∘ [Dai et al., 2013]. Electric field pulses of more than 20 mV/m were frequently seen during dipolarizations on this day. In particular, the duskward electric field was as large as 50 mV/m during the dipolarization around 0505 UT.

Figures 1f, 1g, and 1h show the electron and ion flux from the RBSP Energetic Particle, Composition, and Thermal Plasma (ECT) [Spence et al., 2013]. Figure 1f shows the electron differential flux from Magnetic Electron Ion Spectrometer (MagEIS) [Blake et al., 2013] in the 31 keV to 1.7 MeV energy range. Electron of 10–100 keV can increase by 2 orders of magnitude during dipolarizations. Figure 1g shows the electron differential flux in the first three energy channels (1.8 MeV, 2.1 MeV, and 2.6 MeV) from Relativistic Electron‐Proton Telescope (REPT) [Baker et al., 2013]. Figure 1h shows the differential flux of energetic ions from 69 keV to 1.2 MeV from MagEIS. In the substorm dipolarization near 0505 UT, injected MeV ions were followed up by drift echos signals.

2.2. Dipolarization Front and the Dispersionless Injection at RBSP

Figures 2a–2h present an expanded view of the substorm injection at RBSP‐A from 0445 UT to 0515 UT. An abrupt increase from 100 nT to 140 nT in the northward magnetic component B z, usually referred to as a dipolarization front (DF) [Nakamura et al., 2002; Runov et al., 2009; Ge et al., 2011; Fu et al., 2011; Hwang et al., 2011; Zhou et al., 2014], is identified around 0506 UT in Figure 2b and marked by the gray bar. The DF, which lasted about 40 s from 05:05:40 UT to 05:06:20 UT, was accompanied by an extremely large dawn‐dusk electric field E y and a rapid increase in 30 keV to 2.6 MeV electrons. The dawn‐dusk dipolarization electric field corresponded to a large earthward E × B in panel Figure 2d. Even though it decelerates in the near‐Earth region,a high‐speed bursty bulk flow [Angelopoulos et al., 1992] may occasionally penetrate deep into the inner magnetosphere. Because of the large B x in the inner magnetosphere, the DF was also related to a large V z(∼−E y/B x) toward the equatorial plane. In addition, E z corresponded to a flow deflected toward flanks at about 100 km/s, likely due to the rising pressure in the inner magnetosphere.

Figure 2.

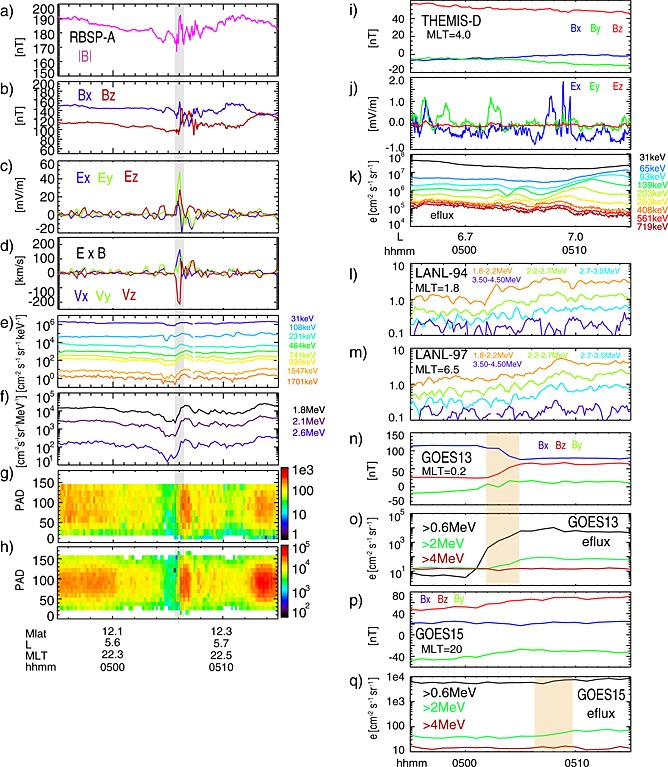
Figure 2

Open in a new tab

The 20 min expanded view of the injection event from 0445 UT to 0515 UT. RBSP‐A measurements of (a) the magnitude of B, (b) B x and B z in GSM, (c) the spin fit electric field in GSM (the spin axis electric field is obtained from the E·B = 0 assumption), (d) the E ×B drift velocity in GSM, (e) fluxes of energetic electrons from MagEIS, (f) fluxes of energetic electrons from REPT, (g) PAD of 0.9 MeV electrons from MagEIS, (h) PAD of 1.8 MeV electrons from REPT. THEMIS‐D measurements of (i) the spin resolution magnetic field in GSM, (j) the spin resolution electric field in GSM, (k) differential energy fluxes of energetic electrons from SST. (l and m) Counts per second of MeV electrons (averaged over 20 s) measured from LANL 94 and LANL 94, respectively. (n and o) GOES 13 measurements of three magnetic field components in GSM and the integral flux of energetic electrons. (p and q) are GOES 15 measurements of three magnetic field components in GSM and the integral flux of energetic electrons.

The electron injection of electrons at RBSP‐A was dispersionless (Figures 2e and 2f). As shown in Figures 2g and 2h, the pitch angle distribution (PAD) of injected MeV electrons was more concentrated around 90∘ at the DF and thereafter spread out in a more isotropic distribution. The major acceleration mechanisms of electrons in dipolarizations, betatron acceleration and Fermi acceleration, are characterized by an energy increase associated with the perpendicular and parallel velocities, respectively [Northrop, 1963; Birn et al., 2013; Fu et al., 2011]. The PAD observations thus indicates that the acceleration of MeV electrons at the DF is mostly caused by betatron acceleration. Before the DF, energetic electrons appear to drop out due to the stretching of field lines. Behind the dipolarization front from 05:06:10 UT to 05:07:10 UT was the high B z region, usually referred to as the dipolarizing flux bundle (DFB) [Liu et al., 2013]. The DFB was associated with an elevated flux of energetic electrons.

2.3. The Dispersive Injection at THEMIS‐D

Figures 2i–2k present the simultaneous observations form THEMIS‐D from 0445 UT to 0515 UT in the predawn sector (MLT = 4) at L ∼ 7. Because of the dipolarization's azimuthal localization, THEMIS‐D did not observe the dipolarization signals. After 0506 UT, THEMIS‐D observed an increase in 720 keV electrons fluxes followed by increases in lower energy electron fluxes, usually referred to as a dispersed injection. Such dispersion signals result from the energy dependence of electron drift velocities after electrons are released simultaneously from an injection region [e.g., Reeves et al., 1991]. From the timing difference of the initial flux increases, the injected electrons at THEMIS‐D corresponded to a release of dispersionless electrons at ∼MLT = 2–3 around 0505–0506 UT.

2.4. Signals of MeV Electron Injection From LANL‐GEO and GOES at Geosynchronous Altitude

The LANL 94 and LANL 97 spacecraft were at MLT∼1.8 and ∼6.5, respectively. Figures 2l and 2m show MeV electrons observations from these two spacecraft. LANL 94 was near the eastern edge of the injection region, and LANL 97 was outside the injection region. Starting from 0502 UT, LANL 94 observed an injection of MeV electrons. The onset time was close to that at GOES 13 shown in Figure 2o. Dispersed, drifting electron populations up to 3 MeV, an unambiguous signature of MeV electron injections, were clearly seen by LANL 97 from 0506 UT.

The GOES 13 and GOES 15 spacecraft were on the nightside, monitoring the injection at the geosynchronous altitude. Figures 2n–2q show GOES 13 and GOES 15 observations of the magnetic fields and energetic particles. Starting from ∼0502 UT, GOES 13, which was at the midnight within the injection region, observed a sustained dipolarization associated with injection of >0.6 MeV and >2.0 MeV electrons. The dipolarization at GOES 13 involved a increase of B z toward an elevated level. This type of dipolarization is usually thought of as a global dipolarization that is possibly related to but distinct from a dipolarization front [Nakamura et al., 2011].

Based on the 2–3 min timing difference of the maximum electron flux increases at GOES 13 and RBSP‐A, we obtain a 40–60 km/s earthward propagation velocity of the injection region from GOES 13 to RBSP‐A. This slow earthward propagation of the injection region is consistent with those in previous statistical studies by Moore et al. [1981] and Reeves et al. [1996]. Similar to THEMIS‐D, GOES 15 was located outside the injection region. Dipolarization signals were absent at GOES 15. From 0507 UT to 0508 UT, the injection started to populate the electrons at the geosynchronous altitude. As a result, GOES 15 observed a persistent increase in >0.6 MeV and >2.0 MeV electron fluxes.

2.5. Increases of MeV Electron PSD in the Outer Radiation Belt

Several injections occurred between 05 UT and 08 UT on 26 April. Figure 3 presents the electron PSD as a function of the first and second adiabatic invariant from RBSP‐A in 5 h before and after the injections. The electron PSD is plotted at the fixed second adiabatic invariant K = 0.1 ± 0.02 G1/2 km and first adiabatic invariant μ = 1000 ± 20,1500 ± 20,2000 ± 20 MeV/G. The PSD is presented in the Geospace Environment Modeling units (c/MeV/cm)3 [Chen et al., 2005]. The parameter K is evaluated based on the T04 models [Tsyganenko and Sitnov, 2005] and available from the Ephemeris data files on the RBSP ECT website. Note that there is uncertainty (10–20%) in K due to the inaccuracy of the magnetic field model near the injection region. This magnitude of uncertainty in K is expected to produce very little difference in Figure 3. The selected set of μ and K approximately corresponds to 1–2 MeV electrons mirrored at low magnetic latitude at the geosynchronous altitude. Before the injections, the PSD at μ = 1000MeV/G is 10−9–10−8(c/MeV/cm)3 at L = 4–5.5. After the injections, the electron PSD at μ = 1000 MeV/G increased by an order of magnitude from 10−9 to 10−8(c/MeV/cm)3 at L = 4.8–5.6. The PSD of higher energy electrons at μ = 1500 MeV/G and μ = 2000 MeV/G increased by 1 order of magnitude as well. The increases of MeV electrons at L = 4.8–5.7 were detected between 08 UT and 09 UT, indicating that the acceleration of MeV electrons was finished before 08 UT, fewer than 3 h after the injection. The 3 h time scale is generally less than that characterized by whistler wave‐driven acceleration (∼10 h) or radial diffusion (∼1 day).

Figure 3.

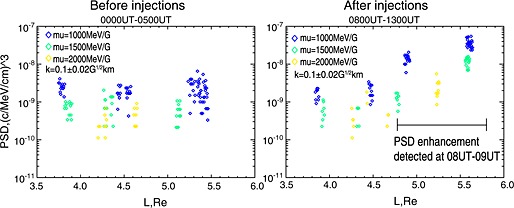
Figure 3

Open in a new tab

The electron PSD at fixed K and μ (left) before the injections and (right) after the injections.

In the following, we examine if whistler wave‐driven acceleration or radial diffusion can be responsible for the enhancement in Figure 3. We first estimate the wave power needed to produce the observed fast acceleration (∼3 h) by local wave acceleration. The time scale for the energization can be estimated as 1/(D EE/E 2), where D EE is the diffusion coefficient in the energy space and E is the energy of particles. D EE is proportional to the wave power Bw2 of the whistler waves. According to a previous whistler wave model by [Horne et al., 2005], it took ∼20 h for whistler waves with amplitude 50–100 pT to increase the flux of 1 MeV electrons by 1 order of magnitude. In our event, the acceleration occurs within less than 3 h. For wave acceleration to be viable in this event, we need a continuous presence of strong whistler waves with amplitude >200 pT. Assume a few hundred Hz bandwidth of the whistler waves, the required wave power is larger than 10−4 nT2/Hz. Figure 4 shows the observed wave power Bw2 from RBSP‐A and THEMIS‐E. At the nightside, RBSP‐A did not see the required strong whistler wave activity. Lower band (<0.5fce) whistler waves are sparsely observed from 0520 UT to 0600 UT and from 0730 UT to 0840 UT. The power of whistler waves was mostly less than 10−6nT2/Hz, more than 2 orders of magnitude less than that of the whistler waves considered to effectively energize MeV electrons [Su et al., 2014]. At the dawnside, THEMIS‐D was at large L (L = 6.7–9.8) from 05 UT to 08 UT; THEMIS‐E encountered L = 4–5.7 at dawn around 0630 UT–0710 UT and did not observe strong whistler waves (Figure 4d). According to the statistical result Li et al. [2009], strong (>100 pT) whistler waves have a higher occurrence rate at nightside and dawnside. With an absence of continuous strong whistler waves at nightside (RBSP‐A) and dawnside (THEMIS‐E) in this event, it is highly unlikely to have strong whistler waves at other locations during this 3 h time period. Thus, we conclude that whistler wave‐driven acceleration is unlikely to produce the electron enhancement in Figure 3.

Figure 4.

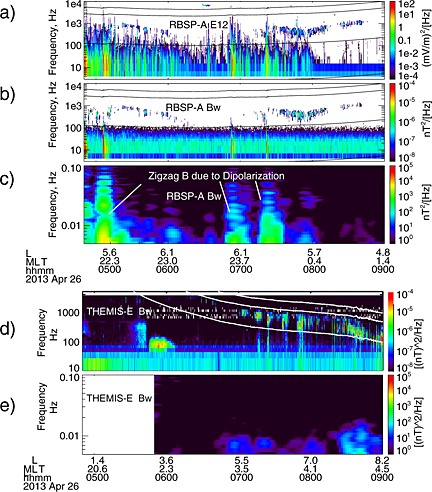
Figure 4

Open in a new tab

The observations of wave power spectra from RBSP‐A and THEMIS‐E. (a and b) RBSP‐A observations of the wave power spectra (10–104 Hz) of one electric field component (E12) and one magnetic field component (B w) from EFW burst data in VLF frequency range. (top to bottom) The three horizontal black lines in each panel represent the local electron gyrofrequency (fce), half fce, and the lower hybrid frequency. (c) RBSP‐A observations of the power spectra in the ULF frequency band. (d and e) THEMIS‐E observations of wave power spectra in the VLF frequency and ULF frequency band. The black region in Figure 4e is the inner radiation belt with strong DC magnetic fields.

Now we estimate whether radial diffusion is possible to produce the acceleration. How quickly radial diffusion can occur is proportional to the power of random wave fields in the ULF frequency band. ULF waves can be driven by solar wind or sources internal to the magnetosphere. Figures 4c and 4e show the ULF power spectra from RBSP and THEMIS for this event. At RBSP‐A, most Fourier power from 05 UT to 08 UT is due to the zigzag shape of B in dipolarizations. A zigzag shape naturally corresponds to a broadband Fourier power spectrum. But these broadband power spectra are not random fluctuations which can lead to radial diffusion. Only around 06 UT and 08 UT there were some ULF wave spectra (102–103 nT2/Hz) that may cause radial diffusion. The ULF wave power observed by THEMIS‐E is 101–102 nT2/Hz, 1 order magnitude smaller. The observed ULF wave spectra, which are comparable to or less than those in past statistic results [Ozeke et al., 2012], are too weak and sporadic to cause fast radial diffusion in less than 3 h in this event.

Based on the above estimates, whistler wave‐driven acceleration and radial diffusion are unlikely responsible for the MeV electron enhancement in Figure 3. We conclude that substorm injection is primarily responsible for increases of MeV electrons at L > 4.8 in this event. The PSD increase reflects a high PSD of source populations that were directly transported to RBSP. The inferred source of high PSD may relate to a positive gradient of PSD in radial direction [e.g., Turner et al., 2010] or a transient process.

2.6. Schematic: The Dipolarization and Injection of MeV Electrons

The main dipolarization and injection observations are summarized in the schematic in Figure 5. Located at the nightside geosynchronous altitude, GOES 13 and LANL 94 first encountered the injection region at around 0502 UT. The dipolarization at GOES 13 was a large‐scale dipolarization in which Bz and energetic electron fluxes increase to an elevated level. At 0506 UT, RBSP‐A observed a small‐scale dipolarization front. From the timing difference (3–4 min) of the dispersionless injection at GOES 13 and RBSP‐A, the injection region propagated earthward at 30–40 km/s, consistent with previous statistic studies [Moore et al., 1981; Reeves et al., 1996]. The different characteristics of dipolarizations at these two spacecraft reflect a strong inhomogeneity of the injection region across the azimuthal direction and/or the radial direction. The observation of this event suggests a patchy, rapidly varying injection region.

Figure 5.

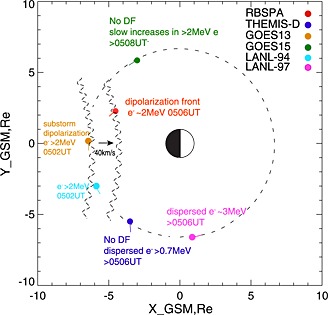
Figure 5

Open in a new tab

The xy plane schematic of RBSP‐A, LANL‐94, LANL‐97, THEMIS‐D, GOES 13, and GOES 15 during the dipolarization and injection of MeV electrons.

As the injection region propagated earthward inside the geosynchronous altitude, the dipolarization electric field presumably was reduced at L = 6.8. Gradient B drift gradually became dominant, and particles started to drift away from the injection region. By 0506 UT when the injection region reached RBSP, large amounts of energetic electrons were released from the injection region. Outside the injection region, LANL 97 observed dispersed and drifting MeV electrons; THEMIS observed the energy‐dispersive drifting electrons >700 keV, and GOES 15 observed slow MeV electrons increases. Based on the PSD results in Figure 3, the injection region may penetrate to L = 4.8.

3. Summary and Discussion

We present observations of an MeV electron injection event measured by RBSP at L = 5.5 and THEMIS, LANL‐GEO, and GOES at geosynchronous altitude. This MeV electron injection event is particularly interesting because it featured a large (50 mV/m) duskward electric field pulse associated with a dipolarization front at RBSP‐A. Pitch angle observations indicated that betatron acceleration of the MeV electrons was operating at the dipolarization front. Dispersed, drifting MeV electrons were observed at LANL‐GEO. Corresponding signals of MeV electron injection were also observed by GOES and THEMIS at the geosynchronous altitude. The injection region propagated earthward at a speed of 30–40 km/s inside the geosynchronous altitude. After a series of injections, the PSD of MeV electrons increased by an order of magnitude at L > 4.8 in less than 3 h. We show evidence that whistler wave‐driven acceleration and radial diffusion are unlikely responsible for the MeV electron enhancement in this event. Our observations indicate that the deep injection associated with strong dipolarization electric fields can supply significant MeV electrons to the outer radiation belt.

Substorm injection can be thought of as a coherent radial transport process. The electric field must be intense and nonrandom during its interaction with particles for such coherent radial transport to be effective. A one to tens of MeV electron injection caused by shock‐induced electric fields is an example of coherent transport [Blake et al., 1992; Li et al., 1993; Wygant et al., 1994]. The intensity and structure of dipolarization electric fields may be important in differentiating injections of MeV electrons from injections of subrelativistic electrons. The large magnitude of the dipolarization electric field (∼50 mV/m) in this event far exceeded the values (several mV/m) used in most injection models. Regarding the electric field structure, our observations suggested that the injection region (and probably the dipolarization electric field) is likely to be patchy and/or rapidly‐varying. These observations may shed lights on future efforts to model injections of MeV electrons.

Another important factor in MeV electron injections is the source population. During near‐Earth injections, energetic electrons are transported earthward and trapped in the inner magnetosphere. The increase of PSD in Figure 3 reflects a high PSD of the source populations that were directly transported to the outer radiation belt. The high PSD of the source population needed for MeV electron injection may be from the high‐energy tail of the plasma sheet populations, a temporal source in the magnetotail (e.g., reconnection), or accumulated from previous substorms.

Acknowledgments

This work was supported by NNSFC grant 41231067 and in part by the Specialized Research Fund for State Key Laboratories of China. Work at UMN was supported by a contract from APL for the development of RBSP/EFW. EMFISIS is supported by a JHU/APL contract 921647. L.C. would like to acknowledge the support of the NASA grant NNX15AF55G. D.L.T., G.D.R., and X.L. are thankful for the support from the International Space Science Institute's (ISSI) International Teams program. L.D. greatly appreciates Judy Hohl from UCLA for editorial help. The RBSP EMFISIS data are available at http://emfisis.physics.uiowa.edu/Flight/. The RBSP EFW data are available at http://rbsp.space.umn.edu/data/rbsp/. The RBSP ECT data are available at http://www.rbsp-ect.lanl.gov/. THEMIS data are available at http://themis.ssl.berkeley.edu/data/themis/. LANL‐GEO data are provided by Geoffrey D. Reeves. GOES data are available at http://satdat.ngdc.noaa.gov/sem/goes/data/. The OMNI data are available at CDAWeb. The SYM‐H data are provided by the World Data Center for Geomagnetism, Kyoto.

The Editor thanks two anonymous reviewers for their assistance in evaluating this paper.

Dai, L. , Wang C., Duan S., He Z., Wygant J. R., Cattell C. A., Tao X., Su Z., Kletzing C., Baker D. N., et al. (2015), Near‐Earth injection of MeV electrons associated with intense dipolarization electric fields: Van Allen Probes observations, Geophys. Res. Lett., 42, 6170–6179, doi:10.1002/2015GL064955.

References

  1. Angelopoulos, V. , Baumjohann W., Kennel C. F., Coronti F. V., Kivelson M. G., Pellat R., Walker R. J., Luehr H., and Paschmann G. (1992), Bursty bulk flows in the inner central plasma sheet, J. Geophys. Res., 97, 4027–4039, doi:10.1029/91JA02701. [Google Scholar]
  2. Ashour‐Abdalla, M. , El‐Alaoui M., Goldstein M. L., Zhou M., Schriver D., Richard R., Walker R., Kivelson M. G., and Hwang K.‐J. (2011), Observations and simulations of non‐local acceleration of electrons in magnetotail magnetic reconnection events, Nat. Phys., 7, 360–365, doi:10.1038/nphys1903. [Google Scholar]
  3. Baker, D. N. , Pulkkinen T. I., Angelopoulos V., Baumjohann W., and McPherron R. L. (1996), Neutral line model of substorms: Past results and present view, J. Geophys. Res., 101, 12,975–13,010, doi:10.1029/95JA03753. [Google Scholar]
  4. Baker, D. N. , et al. (2013), The Relativistic Electron‐Proton Telescope (REPT) instrument on board the Radiation Belt Storm Probes (RBSP) spacecraft: Characterization of Earth's radiation belt high‐energy particle populations, Space Sci. Rev., 179, 337–381, doi:10.1007/s11214-012-9950-9. [Google Scholar]
  5. Birn, J. , Thomsen M. F., Borovsky J. E., Reeves G. D., McComas D. J., Belian R. D., and Hesse M. (1998), Substorm electron injections: Geosynchronous observations and test particle simulations, J. Geophys. Res., 103, 9235–9248, doi:10.1029/97JA02635. [Google Scholar]
  6. Birn, J. , Hesse M., Nakamura R., and Zaharia S. (2013), Particle acceleration in dipolarization events, J. Geophys. Res. Space Physics, 118, 1960–1971, doi:10.1002/jgra.50132. [Google Scholar]
  7. Blake, J. , et al. (2013), The Magnetic Electron Ion Spectrometer (MagEIS) instruments aboard the Radiation Belt Storm Probes (RBSP) spacecraft, Space Sci. Rev., 1–39, doi:10.1007/s11214-013-9991-8. [Google Scholar]
  8. Blake, J. B. , Kolasinski W. A., Fillius R. W., and Mullen E. G. (1992), Injection of electrons and protons with energies of tens of MeV into L less than 3 on 24 March 1991, Geophys. Res. Lett., 19, 821–824, doi:10.1029/92GL00624. [Google Scholar]
  9. Cattell, C. A. , and Mozer F. S. (1984), Substorm electric fields in the Earth's magnetotail, in Magnetic Reconnection in Space and Laboratory Plasmas, pp. 208–215, AGU, Washington, D. C. [Google Scholar]
  10. Chen, Y. , Friedel R. H. W., Reeves G. D., Onsager T. G., and Thomsen M. F. (2005), Multisatellite determination of the relativistic electron phase space density at geosynchronous orbit: Methodology and results during geomagnetically quiet times, J. Geophys. Res., 110, A10210, doi:10.1029/2004JA010895. [Google Scholar]
  11. Dai, L. , et al. (2013), Excitation of poloidal standing Alfvén waves through drift resonance wave‐particle interaction, Geophys. Res. Lett., 40, 4127–4132, doi:10.1002/grl.50800. [Google Scholar]
  12. Dai, L. , Wygant J. R., Cattell C. A., Thaller S., Kersten K., Breneman A., Tang X., Friedel R. H., Claudepierre S. G., and Tao X. (2014), Evidence for injection of relativistic electrons into the Earth's outer radiation belt via intense substorm electric fields, Geophys. Res. Lett., 41, 1133–1141, doi:10.1002/2014GL059228. [Google Scholar]
  13. Fairfield, D. H. , et al. (1998), Geotail observations of substorm onset in the inner magnetotail, J. Geophys. Res., 103, 103–118, doi:10.1029/97JA02043. [Google Scholar]
  14. Fok, M.‐C. , Moore T. E., and Spjeldvik W. N. (2001), Rapid enhancement of radiation belt electron fluxes due to substorm dipolarization of the geomagnetic field, J. Geophys. Res., 106, 3873–3882, doi:10.1029/2000JA000150. [Google Scholar]
  15. Fok, M.‐C. , Moore T. E., Brandt P. C., Delcourt D. C., Slinker S. P., and Fedder J. A. (2006), Impulsive enhancements of oxygen ions during substorms, J. Geophys. Res., 111, A10222, doi:10.1029/2006JA011839. [Google Scholar]
  16. Friedel, R. H. W. , Korth A., and Kremser G. (1996), Substorm onsets observed by CRRES: Determination of energetic particle source regions, J. Geophys. Res., 101, 13,137–13,154, doi:10.1029/96JA00399. [Google Scholar]
  17. Fu, H. S. , Khotyaintsev Y. V., André M., and Vaivads A. (2011), Fermi and betatron acceleration of suprathermal electrons behind dipolarization fronts, Geophys. Res. Lett., 38, L16104, doi:10.1029/2011GL048528. [Google Scholar]
  18. Gabrielse, C. , Angelopoulos V., Runov A., and Turner D. L. (2012), The effects of transient, localized electric fields on equatorial electron acceleration and transport toward the inner magnetosphere, J. Geophys. Res., 117, A10213, doi:10.1029/2012JA017873. [Google Scholar]
  19. Ge, Y. S. , Raeder J., Angelopoulos V., Gilson M. L., and Runov A. (2011), Interaction of dipolarization fronts within multiple bursty bulk flows in global MHD simulations of a substorm on 27 February 2009, J. Geophys. Res., 116, A00I23, doi:10.1029/2010JA015758. [Google Scholar]
  20. Glocer, A. , Fok M.‐C., Nagai T., Tóth G., Guild T., and Blake J. (2011), Rapid rebuilding of the outer radiation belt, J. Geophys. Res., 116, A09213, doi:10.1029/2011JA016516. [Google Scholar]
  21. Horne, R. B. , Thorne R. M., Glauert S. A., Albert J. M., Meredith N. P., and Anderson R. R. (2005), Timescale for radiation belt electron acceleration by whistler mode chorus waves, J. Geophys. Res., 110, A03225, doi:10.1029/2004JA010811. [Google Scholar]
  22. Hwang, K.‐J. , Goldstein M. L., Lee E., and Pickett J. S. (2011), Cluster observations of multiple dipolarization fronts, J. Geophys. Res., 116, A00I32, doi:10.1029/2010JA015742. [Google Scholar]
  23. Ingraham, J. C. , Cayton T. E., Belian R. D., Christensen R. A., Friedel R. H. W., Meier M. M., Reeves G. D., and Tuszewski M. (2001), Substorm injection of relativistic electrons to geosynchronous orbit during the great magnetic storm of March 24, 1991, J. Geophys. Res., 106, 25,759–25,776, doi:10.1029/2000JA000458. [Google Scholar]
  24. Kim, H.‐J. , Chan A. A., Wolf R. A., and Birn J. (2000), Can substorms produce relativistic outer belt electrons?, J. Geophys. Res., 105, 7721–7736, doi:10.1029/1999JA900465. [Google Scholar]
  25. Kletzing, C. , et al. (2013), The Electric and Magnetic Field Instrument Suite and Integrated Science (EMFISIS) on RBSP, Space Sci. Rev., 179, 127–181, doi:10.1007/s11214-013-9993-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Li, W. , Thorne R. M., Angelopoulos V., Bortnik J., Cully C. M., Ni B., LeContel O., Roux A., Auster U., and Magnes W. (2009), Global distribution of whistler‐mode chorus waves observed on the THEMIS spacecraft, Geophys. Res. Lett., 36, L09104, doi:10.1029/2009GL037595. [Google Scholar]
  27. Li, X. , Roth I., Temerin M., Wygant J. R., Hudson M. K., and Blake J. B. (1993), Simulation of the prompt energization and transport of radiation belt particles during the March 24, 1991 SSC, Geophys. Res. Lett., 20, 2423–2426, doi:10.1029/93GL02701. [Google Scholar]
  28. Li, X. , Baker D. N., Temerin M., Reeves G. D., and Belian R. D. (1998), Simulation of dispersionless injections and drift echoes of energetic electrons associated with substorms, Geophys. Res. Lett., 25, 3763–3766, doi:10.1029/1998GL900001. [Google Scholar]
  29. Li, X. , Sarris T. E., Baker D. N., Peterson W. K., and Singer H. J. (2003), Simulation of energetic particle injections associated with a substorm on August 27, 2001, Geophys. Res. Lett., 30(1), 1004, doi:10.1029/2002GL015967. [Google Scholar]
  30. Liu, J. , Angelopoulos V., Runov A., and Zhou X.‐Z. (2013), On the current sheets surrounding dipolarizing flux bundles in the magnetotail: The case for wedgelets, J. Geophys. Res. Space Physics, 118, 2000–2020, doi:10.1002/jgra.50092. [Google Scholar]
  31. Liu, W. L. , Li X., Sarris T., Cully C., Ergun R., Angelopoulos V., Larson D., Keiling A., Glassmeier K. H., and Auster H. U. (2009), Observation and modeling of the injection observed by THEMIS and LANL satellites during the 23 March 2007 substorm event, J. Geophys. Res., 114, A00C18, doi:10.1029/2008JA013498. [Google Scholar]
  32. Mauk, B. H. , Fox N. J., Kanekal S. G., Kessel R. L., Sibeck D. G., and Ukhorskiy A. (2012), Science objectives and rationale for the Radiation Belt Storm Probes mission, Space Sci. Rev., 179, 3–27, doi:10.1007/s11214-012-9908-y. [Google Scholar]
  33. Moore, T. E. , Arnoldy R. L., Feynman J., and Hardy D. A. (1981), Propagating substorm injection fronts, J. Geophys. Res., 86, 6713–6726, doi:10.1029/JA086iA08p06713. [Google Scholar]
  34. Nagai, T. , Yukimatu A. S., Matsuoka A., Asai K. T., Green J. C., Onsager T. G., and Singer H. J. (2006), Timescales of relativistic electron enhancements in the slot region, J. Geophys. Res., 111, A11205, doi:10.1029/2006JA011837. [Google Scholar]
  35. Nakamura, R. , et al. (2002), Motion of the dipolarization front during a flow burst event observed by Cluster, Geophys. Res. Lett., 29(20), 1942, doi:10.1029/2002GL015763. [Google Scholar]
  36. Nakamura, R. , et al. (2011), Flux transport, dipolarization, and current sheet evolution during a double‐onset substorm, J. Geophys. Res., 116, A00I36, doi:10.1029/2010JA015865. [Google Scholar]
  37. Northrop, T. G. (1963), Adiabatic charged‐particle motion, Rev. Geophys. Space Phys., 1, 283–304. [Google Scholar]
  38. Ozeke, L. G. , Mann I. R., Murphy K. R., Rae I. J., Milling D. K., Elkington S. R., Chan A. A., and Singer H. J. (2012), ULF wave derived radiation belt radial diffusion coefficients, J. Geophys. Res., 117, A04222, doi:10.1029/2011JA017463. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Reeves, G. D. , Belian R. D., and Fritz T. A. (1991), Numerical tracing of energetic particle drifts in a model magnetosphere, J. Geophys. Res., 96, 13,997–14,008, doi:10.1029/91JA01161. [Google Scholar]
  40. Reeves, G. D. , Henderson M. G., McLachlan P. S., Belian R. D., Friedel R. H. W., and Korth A. (1996), Radial propagation of substorm injections, in International Conference on Substorms, vol. 389, edited by Rolfe E. J. and Kaldeich B., pp. 579–584, ESA Spec. Publ, Paris. [Google Scholar]
  41. Rowland, D. (2002), The electrodynamics of the inner magnetosphere during major geomagnetic storms, PhD thesis, Univ. Of Minnesota, Minnesota.
  42. Runov, A. , Angelopoulos V., Sitnov M. I., Sergeev V. A., Bonnell J., McFadden J. P., Larson D., Glassmeier K.‐H., and Auster U. (2009), THEMIS observations of an earthward‐propagating dipolarization front, Geophys. Res. Lett., 36, L14106, doi:10.1029/2009GL038980. [Google Scholar]
  43. Sarris, T. E. , Li X., Tsaggas N., and Paschalidis N. (2002), Modeling energetic particle injections in dynamic pulse fields with varying propagation speeds, J. Geophys. Res., 107(A3), 1033, doi:10.1029/2001JA900166. [Google Scholar]
  44. Sergeev, V. A. , Shukhtina M. A., Rasinkangas R., Korth A., Reeves G. D., Singer H. J., Thomsen M. F., and Vagina L. I. (1998), Event study of deep energetic particle injections during substorm, J. Geophys. Res., 103, 9217–9234, doi:10.1029/97JA03686. [Google Scholar]
  45. Spence, H. E. , et al. (2013), Science goals and overview of the Radiation Belt Storm Probes (RBSP) Energetic Particle, Composition, and Thermal Plasma (ECT) suite on NASA's Van Allen Probes mission, Space Sci. Rev., 179, 311–336, doi:10.1007/s11214-013-0007-5. [Google Scholar]
  46. Su, Z. , et al. (2014), Quantifying the relative contributions of substorm injections and chorus waves to the rapid outward extension of electron radiation belt, J. Geophys. Res. Space Physics, 119, 10,023–10,040, doi:10.1002/2014JA020709. [Google Scholar]
  47. Tsyganenko, N. A. , and Sitnov M. I. (2005), Modeling the dynamics of the inner magnetosphere during strong geomagnetic storms, J. Geophys. Res., 110, A03208, doi:10.1029/2004JA010798. [Google Scholar]
  48. Tu, J.‐N. , Tsuruda K., Hayakawa H., Matsuoka A., Mukai T., Nagano I., and Yagitani S. (2000), Statistical nature of impulsive electric fields associated with fast ion flow in the near‐Earth plasma sheet, J. Geophys. Res., 105, 18,901–18,908, doi:10.1029/1999JA000428. [Google Scholar]
  49. Turner, D. , et al. (2015), Energetic electron injections deep into the inner magnetosphere associated with substorm activity, Geophys. Res. Lett., 42, 2079–2087, doi:10.1002/2015GL063225. [Google Scholar]
  50. Turner, D. L. , Li X., Reeves G. D., and Singer H. J. (2010), On phase space density radial gradients of Earth's outer‐belt electrons prior to sudden solar wind pressure enhancements: Results from distinctive events and a superposed epoch analysis, J. Geophys. Res., 115, A01205, doi:10.1029/2009JA014423. [Google Scholar]
  51. Wygant, J. , Mozer F., Temerin M., Blake J., Maynard N., Singer H., and Smiddy M. (1994), Large amplitude electric and magnetic field signatures in the inner magnetosphere during injection of 15 MeV electron drift echoes, Geophys. Res. Lett., 21, 1739–1742, doi:10.1029/94GL00375. [Google Scholar]
  52. Wygant, J. R. , et al. (2013), The electric field and waves instruments on the Radiation Belt Storm Probes mission, Space Sci. Rev., 179, 183–220, doi:10.1007/s11214-013-0013-7. [Google Scholar]
  53. Yang, J. , Toffoletto F. R., Wolf R. A., and Sazykin S. (2011), RCM‐E simulation of ion acceleration during an idealized plasma sheet bubble injection, J. Geophys. Res., 116, A05207, doi:10.1029/2010JA016346. [Google Scholar]
  54. Zaharia, S. , Birn J., Friedel R. H. W., Reeves G. D., Thomsen M. F., and Cheng C. Z. (2004), Substorm injection modeling with nondipolar, time‐dependent background field, J. Geophys. Res., 109, A10211, doi:10.1029/2004JA010464. [Google Scholar]
  55. Zhang, J.‐C. , Wolf R. A., Spiro R. W., Erickson G. M., Sazykin S., Toffoletto F. R., and Yang J. (2009), Rice convection model simulation of the substorm‐associated injection of an observed plasma bubble into the inner magnetosphere: 2. Simulation results, J. Geophys. Res., 114, A08219, doi:10.1029/2009JA014131. [Google Scholar]
  56. Zhou, X.‐Z. , Angelopoulos V., Liu J., Runov A., and Li S.‐S. (2014), On the origin of pressure and magnetic perturbations ahead of dipolarization fronts, J. Geophys. Res. Space Physics, 119, 211–220, doi:10.1002/2013JA019394. [Google Scholar]

Articles from Geophysical Research Letters are provided here courtesy of Wiley

RESOURCES