Bidirectional cargo transport: Moving beyond tug-of-war

Preface

Vesicles, organelles and other intracellular cargo are transported by kinesin and dynein motors, which move in opposite directions along microtubules. This bidirectional cargo movement is frequently described as a “tug-of-war” between oppositely-directed motors attached to the same cargo. However, although many experimental and modeling studies support the tug-of-war paradigm, numerous knockout and inhibition studies in a variety of systems have found that inhibiting one motor leads to diminished motility in both directions, which is a “paradox of codependence” that challenges it. In an effort to resolve this paradox, three classes of bidirectional transport models, termed microtubule tethering, mechanical activation, and steric disinhibition, are proposed and a general mathematical modeling framework for bidirectional cargo transport is put forward to guide future experiments.

Introduction

Long distance transport in neurons is carried out by the motor proteins kinesin and cytoplasmic dynein that bind to cargo (vesicles, organelles, and protein and mRNA complexes) and transport them along axonal and dendritic microtubules^{1, 2}. Almost all cargo have both plus-end directed kinesin motors (responsible for anterograde transport toward the cell periphery) and minus-end directed cytoplasmic dynein motors (responsible for retrograde transport back to the cell body) simultaneously attached^3–9. While individual motors move unidirectionally along microtubules, the directional transport of intracellular cargo is generally achieved through back-and-forth movements with an overall net directionality toward the proper destination. It has been hypothesized that the selective advantage of this seemingly inefficient transport behavior is to facilitate motors in maneuvering around roadblocks in the form of organelles or microtubule associated proteins, or to provide a type of “proofreading” mechanism whereby cargo destination is achieved by a directional bias that is reinforced over many passes rather than an ‘all-or-nothing’ decision that is determined by the initial directionality^10–12. The importance of understanding the molecular mechanisms underlying bidirectional transport is highlighted by its potential role in neurodegenerative diseases. Alzheimer’s disease, for example, is characterized by tangles of the microtubule binding protein tau¹³ that inhibit axonal transport, and Amyotrophic Lateral Schlerosis (ALS), Huntington’s disease and Parkinson’s disease are all thought to involve deterioration in anterograde and/or retrograde axonal transport^14–18.

In vitro reconstitution of microtubule-based transport, structural studies, and biochemical investigations have uncovered many of the molecular details of motor protein function. However, there remains a significant gap between the insights into motor behavior at the single-molecule level and a comprehensive understanding of cargo transport in living cells. In contrast to the relatively simple model of a single motor moving along an individual microtubule, cargo transport in vivo involves multiple motors of both directionalities transporting cargos of diverse geometries through crowded cytoplasm, along microtubules that harbour diverse post-translational modifications and that are decorated by microtubule associated proteins (MAPs). Hence, a key challenge in the field is to bridge the knowledge gap between single-motor function in vitro and intracellular transport in vivo.

Bidirectional cargo movement is frequently described as a “tug-of-war” between oppositely-directed motors attached to the same cargo. However, while the “tug-of-war” model is consistent with many experimental observations, numerous knockout and inhibition studies in a variety of systems have found that inhibiting one motor leads to diminished motility in both directions, in direct conflict with predictions from this paradigm. This Review begins with an overview of bidirectional cargo transport and a description of experimental and modeling studies that support the tug-of-war model. A critique of the model and an exploration of the experiments that conflict with it follows. Finally, in an effort to resolve this paradox of codependence, three classes of bidirectional transport mechanisms, microtubule tethering, mechanical activation, and steric disinhibition, are defined and a general modeling framework put forward to guide future experiments.

Diversity in bidirectional transport

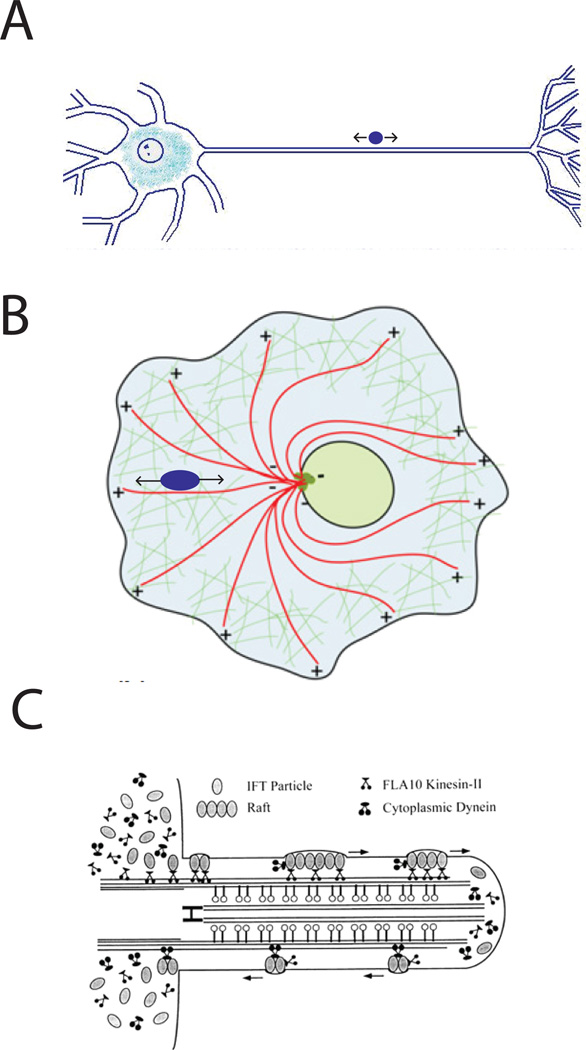
Cargo with a range of geometries and intracellular functions move bidirectionally along microtubules, and important model systems have emerged to study these phenomena. For the purposes of the present discussion, cargo that are transported bidirectionally will be separated into three general groups; neuronal vesicles, larger organelles, and intraflagellar transport (Figure 1). These model systems have been reviewed in detail¹¹, and a number of informative reviews have been written on the general topic of bidirectional transport^{10, 19–24}.

Figure 1. Three classes of bidirectional transport in cells.

A: Neurons contain numerous membrane-bound vesicles that are transported bidirectionally by kinesin and dynein motors in both axons and dendrites. B: In many diverse cell types, larger organelles such as mitochondria, melanosomes, peroxisomes, and lipid droplets are transported bidirectionally along microtubules. C: Intraflagellar transport (IFT) involves the bidirectional transport of proteins (IFT particles) along axonemal microtubules in cilia and flagella by kinesin-2 (KIF3) and dynein-2 (IFT dynein) motors that are attached to the cargo.

Neurons have a long history as a model system for studying bidirectional transport, and the prevalence of human neurodegenerative diseases makes a complete understanding of bidirectional transport in neurons clinically important^{1, 14}. Axons and dendrites contain a diverse array of bidirectionally transported vesicles, generally ranging in size from a few tens to a few hundred nanometers. These include secretory vesicles^25–27, lysosomal vesicles^{7, 28}, autophagosomes²⁹, and vesicles containing amyloid precursor protein (APP)^30–32 and mammalian prion protein⁸. Transport of these diverse neuronal cargo involves different motors, adaptors, and regulatory proteins, but in general, similar conceptual models have been applied to understanding the molecular mechanisms underlying bidirectional transport.

Larger organelles (with sizes ranging from a few hundred nanometers to a few microns) such as mitochondria^{20, 22}, melanosomes^{3, 4, 33–39}, peroxisomes^{12, 40}, and lipid droplets²³ constitute a second class of cargo that are transported bidirectionally and have emerged as model systems for understanding the underlying molecular mechanisms of bidirectional transport. Mitochondria move bidirectionally in axons, transported by kinesin-1 family members and cytoplasmic dynein motors^{20, 22, 41, 42},. Melanosomes, which are transported by the kinesin-2 KIF3A/B and dynein (along with myosin V) are another well-studied system that has revealed important molecular details^{3, 4, 33–39}. And the bidirectional transport of lipid droplets in Drosophila melanogaster embryos has proven to be a very fruitful model system, especially because the particles can be manipulated using optical tweezers and the molecular mechanisms can be dissected using the tools of fly genetics^{23, 43–49}.

A third category of bidirectional transport is intraflagellar transport (IFT), in which protein complexes in cilia and flagella are transported along axonemal microtubules by kinesin-2 (KIF3 complex) and dynein-2 (IFT dynein)^50–60. One hallmark of IFT is that, instead of the directional switching and pausing seen in most bidirectional transport, the cargo move unidirectionally without pause until reaching the end, and then after some time turn around and make a similar return journey^{50, 59–61}. This behavior implies a different mechanism of regulation, though like most of these bidirectional transport examples, the molecular details of directional switching are not entirely clear. Directional switching in IFT will be left for later reviews, and the focus of the discussion here will be on vesicle and organelle transport.

These diverse cargo range in size from a few tens of nm to nearly ten microns. For small cargo, steric constraints will set an upper limit for the number motors that can simultaneously attach, whereas for large cargo, the forces required to move through the viscous cytoplasm may set a lower bound for the number of motors required. Furthermore, different cargo are transported by different kinesins (primarily members of the kinesin-1, 2 and 3 families), and these different motors move at different speeds, have different degrees of processivity, and respond differently to external loads – while kinesin-1 members can walk against sustained loads, kinesin-2 and kinesin-3 motors tend to detach under load^62–68. Cytoplasmic dynein (hereafter referred to simply as dynein) contains two heavy chains and numerous intermediate and light chains. Its complex structure allows for numerous avenues of regulation, and a number of dynein regulatory molecules such as Klar, Halo, Lis1 and NudE have been identified^{11, 19, 31, 44, 47, 49, 69–81}. In the face of this diversity, it is important to exercise appropriate caution when trying to unify these phenomena into a common model to describe bidirectional transport. However, despite their different intracellular functions and the involvement of different molecular players, most of these cargo display qualitatively similar transport behavior, specifically stochastic directional switching interspersed by pauses. Thus, while future progress will inevitably lead to dividing the mechanisms that underlie bidirectional transport into distinct sub-classes, at the present moment, it is still instructive to approach these questions in terms of finding common mechanisms, and that has generally been the approach taken in the field.

Tug-of-War

The tug-of-war model for bidirectional transport (also called a mechanical competition model) describes the mechanical competition between antagonistic kinesin and dynein motors bound to the same cargo. While the term was used previously by Salmon and Reider to describe opposing poleward forces on sister kinetochores during mitosis⁸², and the concept of directional switching due to the forces of opposing kinesin and dynein motors was explored by Vale and colleagues⁸³, the use of “tug-of-war” to describe bidirectional transport along microtubules was originally coined by Welte, Gross, and co-workers in 1998 to describe lipid droplet transport in D. melanogaster embryos⁴⁸. Over the ensuing 15 years, numerous experimental and theoretical studies have used the tug-of-war framework to analyze intracellular transport of neuronal vesicles, mitochondria, lysosomes, and melanosomes in cells, as well as precisely engineered multi-motor complexes in vitro^{4, 7, 46, 84–90}.

Experimental support for the model

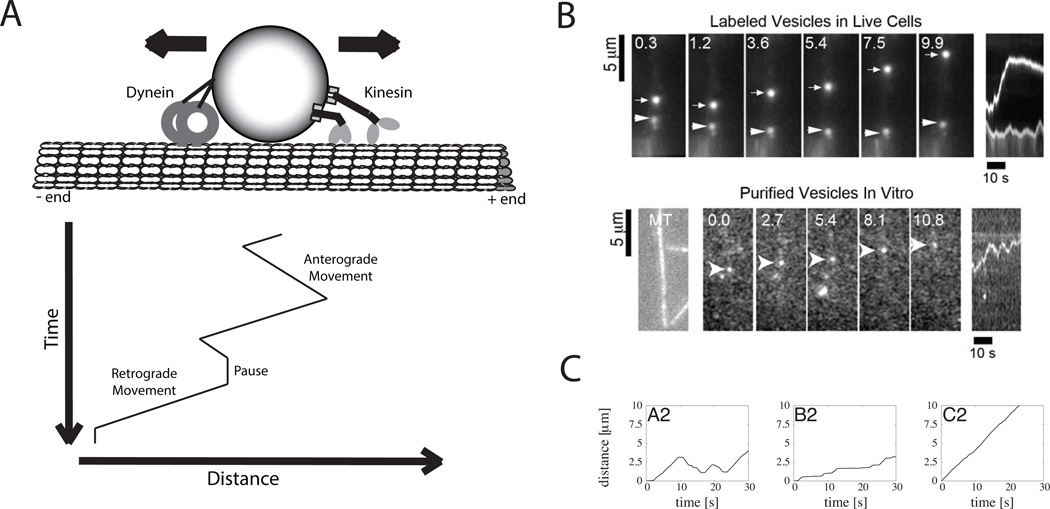
The use of tug-of-war models for interpreting experimental data was greatly facilitated by the development of a mean-field computational model put forth by Müller, Lipowsky and colleagues^{84, 88, 91}. Using experimentally-derived parameters for motor velocity, run length, stall force and detachment rate, the Müller tug-of-war model was able to qualitatively, and in some cases quantitatively recapitulate the back-and-forth vesicle trajectories observed in vivo. An excellent demonstration of the utility of the model was its application to kinesin and dynein-driven vesicle transport in neurons⁷. In this work, the authors estimated the number of kinesin-1 family, kinesin-2 family and dynein motors on purified vesicles that moved bidirectionally on isolated microtubules in vitro. When the specific motor parameters for kinesin-1, kinesin-2, and cytoplasmic dynein were input into the model along with estimated motor numbers per vesicle, the simulated cargo trajectories included distinct runs in either direction punctuated by pauses, nicely matching the experimental results (Figure 2). Furthermore, anti-dynein antibody inhibition experiments could be recapitulated in the model by reducing the number of dyneins per vesicle.

Figure 2. The tug-of-war model.

A: Schematic of bidirectional transport showing cargo with bound dynein motors that move to the minus-ends of microtubules (retrograde transport) and kinesin motors that move to the plus-ends of microtubules (anterograde transport). Cargo move bidirectionally with runs interrupted by periodic pauses. The bottom plot is a sketch of a typical kymograph, which is created by stacking line-scans from successive frames in a movie of bidirectional transport. Shallow lines denote fast movement and vertical lines denote no movement. B: Experimental observations of bidirectional transport. In this experiment by Hendricks and colleagues⁷, bidirectional transport of neuronal vesicles was visualized both by live-cell imaging in neurons and by in vitro reconstitution on immobilized microtubules. (Top) Montage of six images taken over 10 seconds and the resulting kymograph (far right) showing the bidirectional transport of Lyso-Tracker-labeled vesicles in neurons. While the upper vesicle takes long runs in both directions, the lower vesicle shows only small fluctuations. (Bottom) Similar results are seen for purified vesicles containing dynactin-GFP moving along immobilized microtubules in vitro. Image of rhodamine-labeled microtubules is shown at left, followed by a montage of five images taken over 11 seconds, and the resulting kymograph. C: Results from simulations of a theoretical tug-of-war model. Simulations by Müller and colleagues⁸⁴ show that model-generated bidirectional transport dynamics can recapitulate experimental data and that the specific transport characteristics depend strongly on the choice of parameters and numbers of motors used. In these simulations, six kinesin and six dynein motors were modeled, with the motor parameters estimated from lipid droplet experiments. Simulation A2 used the default parameters and show robust runs in both directions analogous to those observed experimentally. In B2 the dynein stall force was reduced by a factor of 2.4 and the dynein dissociation rate constant was reduced by 12%, resulting in net plus-end movement with occasional stalls. In C2, the dynein stall force was also reduced by a factor of 2.4, but the dynein dissociation rate constant was increased by a factor of 2, resulting in smooth plus-end movement (dominated by kinesin).

Support for the tug-of-war model also comes from a study investigating the transport of endosomes in Dictyostelium discoideum cells and on isolated microtubules in vitro⁹⁰. Directional switching of endosomes was observed to involve a phase of slower velocity during which vesicles elongated, consistent with being pulled by opposing motors (similar deformations have been observed for mitochondria⁹²). Optical trapping was used to quantify parameters for the kinesin-3 family member DdUNC104 and Dictyostelium cytoplasmic dynein, and these parameters input into a computational model (similar to the Müller model⁸⁴) that was able to recapitulate the observed directional switching behavior. The simulations suggest that each kinesin is balanced by 4–8 dynein motors in this system. A related optical tweezer study⁹³ found that, compared to beads with only kinesin attached, both intracellular cargo and artificial beads having both dynein and kinesin attached had lower stall forces, suggesting that motors attached to the same cargo mechanically compete as predicted by the tug-of-war model.

Hence, it is clear that in some systems bidirectional switching can be qualitatively and quantitatively accounted for by a tug-of-war model. And, based on the fact that motors generally remain attached to their cargo during directional switching^3–9, it seems unavoidable that mechanical competition between opposed kinesins and dyneins will occur during bidirectional transport. There are really two questions here. First: Is mechanical competition, as delineated by the tug-of-war model, the dominant mechanism underlying bidirectional transport, or are these experimental tug-of-war examples isolated exceptions? And second: Is the tug-of-war model, as quantitatively described by current computational models, really an accurate description of the underlying molecular mechanisms? While the agreement between simulations and experiments is clearly impressive, it is important to remember that demonstrating the agreement of a 14-parameter model with experimental results does not prove that model to be correct. Hence, because the Müller mean-field model performs so well in recapitulating experimental data, it is worth examining the underlying model assumptions before moving forward.

Critiquing the model

The first critique of the Müller model is how the force-dependence of motor detachment was taken into account. Because transport direction is determined by the number of attached plus- and minus-end directed motors, as well as their mechanical strengths, the kinetics of detachment under load is the most important factor defining model behavior. Consistent with standard theory^{94, 95}, the force-dependent off-rate is defined as k_off(F)=k_off(0)e^F/Fdetach., where k_off(0) is the motor detachment rate at zero load and F_detach is the key scaling parameter that defines the sensitivity of the motor-microtubule bond to load. A simple problem arises from the fact that the motor detachment rate from the microtubule is equal to the motor velocity divided by the distance a motor moves before detaching (k_off = velocity/run length). The first issue is that hindering loads (exerted by oppositely-directed motors attached to the same cargo, for instance) are known to reduce both the kinesin motor velocity and run length^{62, 68, 96}, so their ratio is expected to be a complex function of load. The second issue is that directional switching involves motors transitioning from forward walking (when force is below the stall-force) to backwards walking (when force exceeds the stall-force) with a transition point at the stall force where velocity is zero Optical tweezer experiments on kinesin-1 family members confirm that motor behavior differs significantly under in “substall” and “superstall” loads^{68, 96}, and cytoplasmic dynein experiments point to even more complex “catch bond” behavior at high loads⁹⁷. Thus, because detachment kinetics are such an important determinant of model behavior, the load-dependence of motor dissociation must be modeled as a more complex function than simply an exponential dependence (as has been done by others^{90, 96}), and it is vital that the governing parameters are tightly constrained by experiments.

A second critique of the Müller approach is the assumption that load is shared equally between all motors of a given type (kinesin or dynein) (what is known as the mean-field approximation). This approximation would be valid if every motor were a clock-like stepper (that is, they all stepped in synch) and there was no motor-cargo compliance. However, the region of motor proteins connecting the microtubule binding site to the cargo binding site acts as nonlinear elastic tether, and motors step stochastically, sometimes waiting short times between steps and sometimes waiting long times⁹⁸. Thus, as a motor diverges from the pack due to fluctuations in stepping rates, it will stretch and shoulder a greater proportion of the load, which will decrease its velocity and increase its detachment rate. One result of this phenomenon is that two motors attached to a single cargo don’t work nearly as well as one might expect, an issue that has been explored extensively through both experiments and modeling^{86, 87, 89, 96, 99–104}.

One model system where experimental results are not well described by the tug-of-war model is the bidirectional transport of lipid droplets in D. melanogaster embryos. Quantitative characterization of the transport kinetics, switching rates, and in vivo and in vitro forces governing lipid droplet transport have instead favored a “coordination model” between kinesin and dynein to account for bidirectional switching. A number of potential regulatory proteins have been put forward as potential “coordinators” of motor activity, including Klar, Halo, Lis1, NudE, and dynactin^{10, 11, 19, 44–49, 75}, but the precise molecular mechanism underlying coordination of kinesin and dynein motors in this system remain elusive. To more fully challenge whether lipid droplet transport can be quantitatively described using a tug-of-war framework, the Müller mean-field model was expanded into a stochastic model that included motor-cargo tethers, stochastic motor stepping, and experimentally-determined force-dependent off-rates for kinesin and dynein⁹⁶. Despite this significant expansion of the model, which addresses essentially all of the Müller model critiques described above, the experimental data could still not be fit by a tug-of-war framework, effectively ruling out this mechanism for describing bidirectional transport in the lipid droplet system.

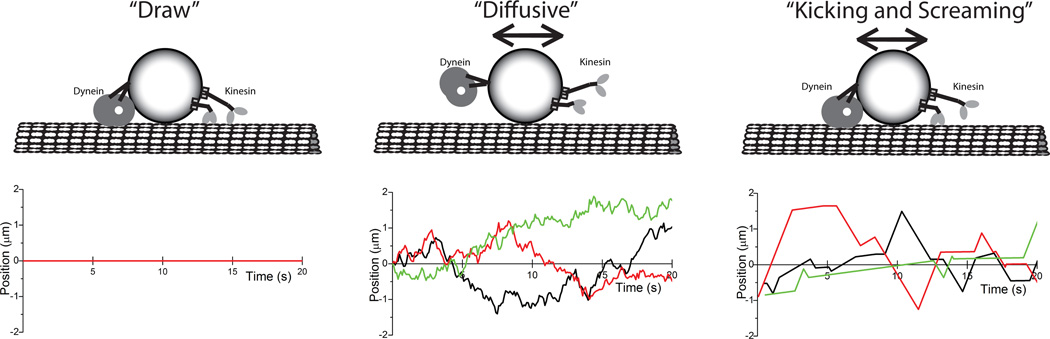
A final detail of bidirectional transport that warrants further experimental work is the definition of the pause state. A consistent feature of many bidirectional transport measurements in cells is that the cargo spends a significant amount of time in a paused or static state^{8, 31, 46, 105, 106}. These pauses could be due to three underlying mechanisms (Figure 3). The first possibility is that the motors are pulling with equal and opposite forces, such that all motors are stalled (a “draw”). Microtubule binding by a cargo-bound protein other than kinesin or dynein could achieve a similar non-motile stall state. The second possibility is that all motors are detached and the cargo is actually diffusing freely, but at a sufficiently slow rate as to appear static. The third possibility is that motors are engaged but moving only very slowly and/or are rapidly switching directions, resulting in a velocity close to zero (the “kicking and screaming model”⁸¹). The Müller mean-field model actually makes very specific and falsifiable predictions about this pause state. Specifically, it postulates that apparent pauses are due to slow backward motion resulting from the very slow superstall velocities of attached kinesin and dynein motors (see the “kicking and screaming” model in Figure 3). Experimental characterization of cargo kinetics during pauses is hindered by limits in spatial resolution (due to inherent fluctuations in cells and potential artifacts from using centroid tracking on deformable cargo, for instance) and temporal resolution (due to finite frame rates and inherent difficulties in calculating instantaneous velocities, for instance). However, these information-rich fluctuations provide important constraints for testing specific transport models, and experimental efforts aimed at enhancing the spatial and temporal resolution of these fluctuation measurements are of high importance for the field.

Figure 3. Different mechanisms for the “pause” state.

A: In the “Draw” state, both motors are engaged and stalled. The resulting static position of the cargo in the pause state is represented as a line at position of zero in the corresponding plot. B: In the “Diffusive” state, both motors are detached and cargo is diffusing. The corresponding plot shows 1D diffusion of three simulated cargo, each having a diffusion constant 0.05 µm²/s. As can be seen, diffusion can result in substantial excursions of the cargo in both directions. C: In the “Kicking and Screaming” state⁸¹, both motors are engaged and moving slowly due to their inherently slow reverse walking speeds. The plot shows results from a stochastic simulation of tug-of-war between 1 kinesin-1 family member and 7 dyneins using the modeling framework and kinesin-1 and dynein parameters from Müller et al.⁸⁴. Three 20 second periods of minimal displacement are shown, highlighting that although the displacements are generated by a different mechanism, they can appear qualitatively similar to the excursions seen in the Diffusive state.

The paradox of codependence

A consistent feature of all existing tug-of-war models is that, because the two motor types are in competition, inhibiting one motor should lead to enhanced motility in the opposite direction. As detailed above, this is what has been observed in many studies^{7, 77, 90, 93, 107, 108}. However, despite the intuitive nature and widespread acceptance of tug-of-war models, a number of investigations over many years have found precisely the opposite result – inhibiting one motor diminishes transport in both directions. These puzzling observations, which I refer to as “the paradox of codependence,” call into question the validity of the tug-of-war modeling framework in explaining in vivo bidirectional transport and point to a need for developing new quantitative models of bidirectional transport. Before describing novel mechanisms that could explain the paradox of codependence, this section reviews some of the key studies that demonstrate it.

Over 30 years ago, even before the discovery of kinesin, it was observed in Aplysia that axonal injection of an inhibitor of the retrograde transport motor dynein surprisingly inhibited anterograde vesicle transport¹⁰⁹. Later studies in extruded squid axoplasm showed that antibody inhibition of either kinesin or the p150^Glued subunit of the dynein adaptor protein dynactin led to a strong reduction in bidirectional vesicle movement on isolated microtubules^{110, 111}. A series of studies in transgenic D. melanogaster larvae extended these findings. Mutating dynein was found to result in the same phenotype as a kinesin knockout — axonal swellings filled with immobilized cargo rather than cargo accumulation at either the cell body or periphery¹¹². Mutating UNC104, the kinesin-3 family motor responsible for the anterograde transport of synaptic vesicles in flies, resulted in vesicles moving with slower velocities and shorter run lengths in both the anterograde and retrograde directions²⁷. Importantly, the dynamics of both mitochondria and neurosecretory vesicles, which are transported by motors other than UNC104 were unaffected in this study, confirming that the phenomenon was not simply a result of global effects on the microtubule cytoskeleton.

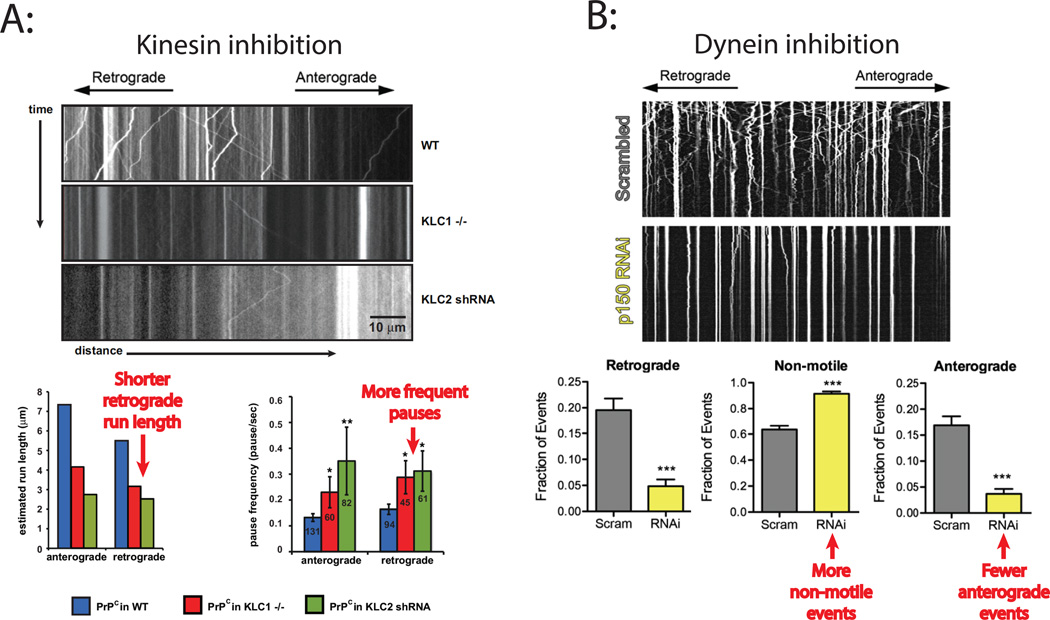
Similar results were observed for fluorescently labeled prion-protein (PrP^c) vesicles in mouse hippocampal neurons⁸. Knocking out kinesin light chain 1 (KLC1) or shRNA knockdown of kinesin light chain 2 (KLC2) (both of which are involved in linking kinesin-1 to PrP^c vesicles) diminished vesicle run lengths and increased the pause frequency in the retrograde direction, the opposite of what was expected (Figure 4 Panel A). Similarly, knockdown of dynein heavy chain in this study resulted in shorter runs and more frequent pauses in both the retrograde and anterograde directions. Because knockdown of a kinesin-1 was previously shown to alter microtubule dynamics¹¹³, it is important to confirm that the results are not due to off-target effects. To this end, it was shown that knockdown of KIF5B, which increased pausing of PrP^c vesicles, did not alter synaptophysin vesicle transport, arguing that the results cannot be explained by a global repression of microtubule-based transport.

Figure 4. Examples of antagonistic motor codependence.

A: The anterograde motor kinesin was inhibited in mouse neurons by knocking out kinesin light-chain 1 (KLC1−/−) or by knocking down light-chain 2 (KLC2 shRNA), both of which are involved in linking kinesin-1 to PrP^c vesicles. Vesicles were labeled by YFP-PrP^c and their transport dynamics analyzed by kymographs. The wild-type kymograph (top) shows left and right diagonal tracks, indicative of retrograde and anterograde cargo transport, respectively, as well as some vertical lines indicative of stationary vesicles. In contrast, the kinesin inhibition kymographs (middle and bottom) show very little transport in either the retrograde or anterograde directions, and many stationary vesicles. Schematic plots of the data demonstrate that while kinesin inhibition was expected to result in longer retrograde run lengths and fewer pauses during retrograde movement, the opposite was observed. (While the observed results in the schematic approximate the published data, the expected results are only qualitative estimates for comparison). Figures adapted from Encalada et al.⁸. B: Dynein in mouse neurons was inhibited by knocking down the p150 subunit of the dynein adaptor protein dynactin that links dynein to vesicles. Vesicles were labeled by RFP-LAMP1 and their transport analyzed by kymographs. In the control kymograph at top (scrambled RNAi), numerous bidirectional transport events (diagonal lines) were observed, while following dynein inhibition (p150 RNAi) very little transport in either direction was observed and almost all vesicles were stationary (vertical lines). Schematic plots of the data show that while dynein inhibition is expected to result in more anterograde transport events and fewer non-motile events, the opposite was observed. Figure adapted from Moughamian and Holzbaur¹⁰⁶.

In mouse dorsal root ganglia, knockdown of the p150 subunit of the dynein adaptor protein dynactin decreased the number of anterograde transport events, countering expectations, and increased the number of vesicles remaining in paused states (Figure 4 Panel B)¹⁰⁶. In a different study, deletion of the Arp1 dynactin subunit in D. melanogaster neurons led to slower vesicle transport velocities in both anterograde and retrograde directions and a substantial increase in the number of paused vesicles¹¹⁴.

To investigate the role of motor forces in bidirectional transport, fluorescently-labeled peroxisomes were tracked in D. melanogaster S2 cells in different genetic backgrounds¹². Inhibition of either kinesin-1 (KHC) or dynein (DHC) arrested cargo transport (as opposed to causing mis-localization to the microtubule plus- or minus-ends, which would be predicted by tug-of-war models). The next question was whether this arrest was due to the inhibition of the specific motor species or the specific motor activity. In the kinesin-1 knockdown, bidirectional motility could be rescued by the kinesin-3 UNC104, but not by a non-motile kinesin-1. Similarly, in the dynein knockdown, bidirectional transport could be rescued by the minus-end-directed kinesin-14, ncd. Hence, in this system a specific motor activity and not the particular motor species is key to maintaining bidirectional transport.

The finding that inhibiting one motor also inhibits the activity of the oppositely-directed motor suggests some sort of codependence – the activity of one is required for the activity of the other. I call this paradox ‘Codependence Among Antagonistic Motors’. In addition to the above studies, this apparent codependence has also been observed for the bidirectional transport of lipid droplets⁴⁶, melanophores³³, mitochondria^{22, 42, 112, 115}, neurofilaments¹¹⁶, and ribonucleotide granules¹¹⁷. Because the dominant paradigm in the field, the tug-of-war model, cannot explain this large body of results, there is a need for new models of bidirectional transport that go beyond existing frameworks and are able to account for the large body of disparate data.

Mechanisms to explain codependence

In an effort to resolve the paradox of codependence between kinesin and dynein, three hypothetical mechanisms of bidirectional transport are proposed below (Figure 5). The approach advocated here follows Platt’s “strong inference” method to scientific inquiry^{118, 119}: propose multiple hypotheses to describe a phenomenon, devise and carry out crucial experiments to falsify one or more of the hypotheses, and repeat as necessary. Because of the complexity of bidirectional transport, progress forward requires a tight integration of modeling and experiments. To provide more rigor to the conceptual mechanisms presented in Figure 5, a modeling framework for developing these (and other) hypothetical mechanisms into quantitative models is presented in Figure 6. The general mathematical framework can be thought of as a collection of kinesin and dynein motors that can exist in different states (such as stepping, diffusing, stalled, inhibited, and so on). Transition rates between states depend on motor properties and the current state of the system (such as the number of motors attached, cargo velocity, the forces being generated by motors, and so on). In this way, the model structure is not unlike the Müller tug-of-war model, but the key differences are the definition of the on- and off-states, and how parameters that control the transition rates are specified.

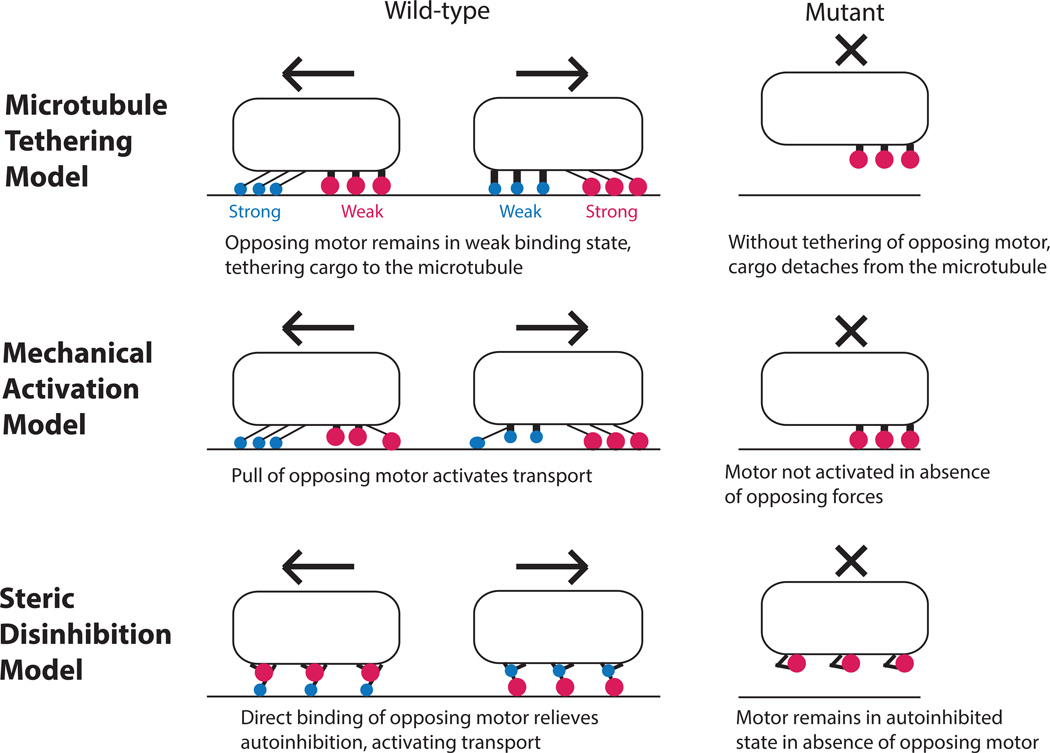
Figure 5. Three hypothetical mechanisms for resolving the paradox of codependence.

In the microtubule tethering mechanism, motors are proposed to transition between a strong-binding state when the motor is walking and a weak-binding state in which the motor is inactive but remains tethered to the microtubule. Diminished cargo transport in mutants results from a lack of tethering. In the mechanical activation mechanism, motors are posited to be in an inactive state until an opposing force pulls on and activates them. The absence of one class of motors in a mutant diminishes cargo transport because the opposing motor is not mechanically activated. In the steric disinhibition mechanism, motors are proposed to remain in an inhibited state even when bound to their cargo. Direct binding by opposing motors or other regulatory proteins relieves inhibition, resulting in transport. The diminished cargo transport in mutants results from motors remaining in their inhibited state.

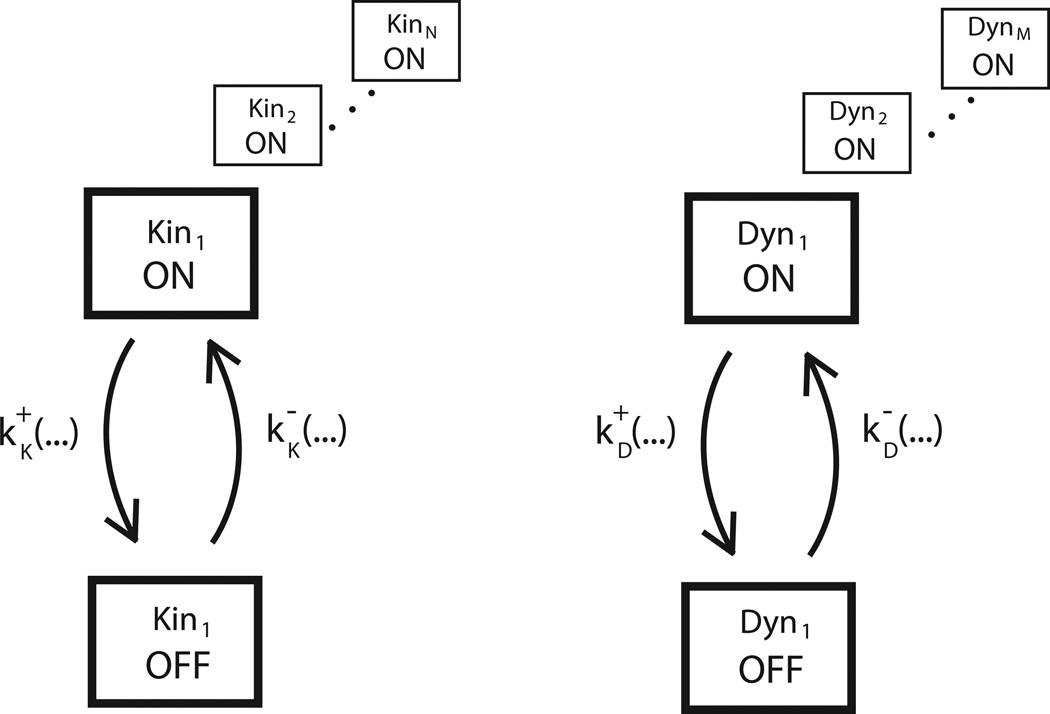
Figure 6. Mathematical modeling framework for bidirectional transport models.

Hypothetical mechanisms can be explored and quantitatively tested using mathematical models of cargo transport by kinesin and dynein motors. On a given cargo, there are N kinesin motors (Kin₁ to Kin_N) and M dynein motors (Dyn₁ to Dyn_M). Motor states are defined generically as On and Off, with different hypothetical mechanisms having different definitions of the on- and off-states (given at the right in order: microtubule tethering, mechanical activation, and steric disinhibition). For each motor, the rate constant k⁺ defines the rate that the motor switches from the off-state to the on-state, and the rate constant k defines the rate that the motor switches from the on-state to the off-state. These switching rates depend on different variables in the system (such as the force acting on that motor, the cargo position, or the activity of the opposing motors), and the switching rate magnitudes and parameter dependencies are the principal determinants of overall model behavior. The different hypothetical mechanisms presented in Figure 5 will have different dependencies for their switching rates; for example, the k⁺ dependencies for the three hypothetical mechanisms are given at the right. These models readily lend themselves to standard Monte Carlo (Gillespie Stochastic Simulation Algorithm¹⁶⁴) approaches.

Microtubule tethering mechanism

The first mechanism that may account for the paradox is the microtubule tethering mechanism, where the key characteristic is that instead of simply attaching and detaching, motors switch between states of directed transport and a weak-binding or diffusive transport. Motors are generally characterized in vitro by their run length, the distance they move along the microtubule before detaching¹²⁰. However, there are many documented cases where motors diffuse one-dimensionally along microtubules. This 1D diffusion is often compared to DNA binding proteins, which are known to bind electrostatically to the negatively charged DNA and diffuse until finding the proper sequence, at which time they switch to a strongly bound state^121–123. The kinesin-3 family member UNC104/KIF1A was the first kinesin to clearly display this 1D diffusional movement; it was shown that an engineered monomeric KIF1A moved processively along microtubules in low ionic strength buffer by a combination of diffusive and directed transport^{64, 124, 125}. The noncovalent forces keeping the motor associated with the microtubule were mapped to the positively charged “K-loop” of the motor and the negatively-charged C-terminal tail of tubulin. Although it was subsequently shown that in vivo kinesin-3 family motors dimerize through cargo binding or other mechanisms^{63, 126, 127}, KIF1A serves as an important model of motor transport where continuous transport is achieved by the motor switching between a motile state and a diffusive state, while continuing to remain bound to the microtubule.

Subsequent to the work on KIF1A, others have shown that the mitotic motor Eg5 (kinesin-5 family) switches between diffusive and motile states¹²⁸, and that at low ionic strengths mouse KIF5B (kinesin-1 family) alternate between stepping and diffusing along the microtubule¹²⁹. Furthermore, dynein links to cargo through the adaptor protein dynactin, and dynactin can bind and diffuse along microtubules¹³⁰. Hence, there is clear support from in vitro studies that motors (or motor-adaptor complexes) can diffuse along microtubules. What is not clear is what triggers the switch between the diffusive and the directed transport states. Furthermore, the implications of extrapolating these diffusive properties of isolated motors up to the motor–cargo complex, have not been explored in detail.

One prediction from the microtubule tethering mechanism is that, in the paused state, one or both sets of motors remain attached to the microtubule in a weakly-bound state. This situation contrasts with the active stall (where both sets of motors are attached and their forces balanced) inherent in tug-of-war models. In this framework, the reason that inhibiting one motor diminishes cargo transport by the opposing motor is that the tethering of the cargo to the microtubule is diminished and the cargo tends to then dissociate from the microtubule (Figure 5).

In the modeling framework of Figure 6, the simplest formulation is that the on-state is stepping, the off-state is diffusing, and the transition rates depend on the number of motors in the stepping and diffusive states. A slightly more complex model would include a second off-state (distinct from the diffusive state) in which the motor is completely shut-off or detached.

Mechanical activation mechanism

The mechanical activation hypothesis postulates that motors are, at low load forces, predominantly in an inhibited state due to tight binding with the microtubule, failure to properly engage with the microtubule, or another reason. The forces generated by opposing motors bound to the same cargo pull the motor out of this inhibited state, freeing it for active motion. According to this paradigm, the reason that inhibiting one motor diminishes transport in both directions is that in the absence of opposing forces, the remaining motors are generally in an inactive state (Figure 5).

Despite the fact that beads with a uniform population of attached motors move robustly in vitro, there is experimental support for mechanical activation as a mechanism to control motor activity. First, from optical trap experiments in which beads are dragged back and forth along immobilized microtubules, it has been shown that the dissociation of kinesin motors from microtubules depends not only on the magnitude of the external load but also on its direction, with dissociation being faster when the load is pulling in the assisting (plus-end) than in the hindering (minus-end) direction^{68, 131–133}. Furthermore, a recent optical trapping study that analyzed both phagosomes in intact cells as well as artificial beads in vitro found that the duration that dynein motors stalled increased with increasing stall forces, reminiscent of a catch-bond⁹⁷. A similar study using rat brain dynein on polystyrene beads also found that at superstall forces, the binding duration of dynein increased with increasing load⁹⁶. Granted, these studies demonstrated enhanced attachment and not necessarily activation due to opposing motor forces, so evidence is still lacking for the precise mechanism underlying activation. Notably, the principal result from the aforementioned study of fluorescent peroxisomes in D. melanogaster S2 cells¹² was that, following knockdown of KHC or dynein, bidirectional transport could be rescued by any motor as long as it was functional and pulled in the appropriate direction. While it doesn’t settle the mechanism, this result is exactly what the mechanical activation mechanism would predict.

In terms of the modeling framework in Figure 6, the on- and off-states in the mechanical activation mechanism would be walking and inactive (which could mean stuck, weak-binding, or fully detached), respectively, and transitions between the states would be regulated primarily by the forces generated by the competing motors. Another possibility is that the mechanical activation results from other mechanisms than motor effects per se. For instance, when opposed teams of motors are simultaneously pulling on a cargo, there will be an attractive force toward the microtubule surface, which will bring motors and microtubules in closer proximity and enhance on-rates following motor dissociation. This normal force will be diminished when one set of motors is inhibited.

Steric disinhibition mechanism

Kinesin motors exist in autoinhibited conformations in which the tail folds back to shut down the motor activity^{127, 134–141}. Activation is thought to result from binding to cargo, or binding by regulatory proteins^{142, 143}. While there is no clear autoinhibition mechanism for dynein, there are regulatory proteins that control its activation^{79, 80}, and it has been shown that the nucleotide state of their secondary AAA domains can also alter dynein processivity and microtubule affinity¹⁴⁴. Hence, it is reasonable to hypothesize that the motor activity of kinesin and dynein motors can be altered even while the motors remain bound to their cargo. The steric disinhibition mechanism holds that motors remain in their autoinhibited state even after cargo binding, and that transport results from activation of one or the other motors. This activation could result from direct binding of one motor to the other or through a regulatory protein that relieves this autoinhibition through direct binding, phosphorylation, or some other mechanism. Hence, the reduced motility following inhibition of one motor results from the fact that the opposing motor is no longer activated (Figure 5).

In support of this model, there is evidence that kinesin-1 family members directly bind to dynein⁶ and that both the kinesin-2 accessory protein KAP3 and dynein bind directly to dynactin³³. [Recent work showed that the adaptor protein JIP1 directly binds to and relieves the autoinhibition of kinesin-1 (KHC), and that it also binds to dynactin, leading to speculation that JIP1 differentially regulates the two motors, perhaps acting as the master control switch³¹. Perhaps the strongest support for this type of mechanism involves the mitochondrial Rho-GTPase Miro and the Milton/TRAK adaptor protein, which link kinesin-1 motors and dynein to mitochondria in a Ca²⁺ dependent manner, resulting in mitochondria being positioned at sites of elevated [Ca²⁺] in neurons. In D. melanogaster both the dynein/dynactin complex and DmKHC bind directly to Milton and in the presence of Ca²⁺, Miro binds to the KHC heads, inhibiting motor activity and resulting in arrest of transport^{115, 145}. Thus, low [Ca²] acts as a disinhibitor of KHC. While similar high [Ca²⁺] arrest is observed in mammalian neurons, experiments suggest that mammalian KIF5 binds directly to Miro at low [Ca²⁺] but dissociates at high [Ca²⁺], suggesting that the same ends are achieved through a different mechanism¹⁴⁶.

In terms of the modeling framework in Figure 6, the motor on- and off-states would be disinhibited and inhibited, respectively, and transitions between states would be regulated by binding of oppositely-directed motors or adaptor proteins, or possibly by phosphorylation.

Other considerations

To build a comprehensive picture of bidirectional microtubule-based transport in cells, it is also important to take into account possible roles of the actin cytoskeleton and myosin motors. For instance, it has been shown that in addition to kinesin and dynein, myosin V motors are also attached to melanosomes, and that dispersion and aggregation involve both actin filaments and microtubules^{4, 36, 147, 148}. In particular, the cortical actin network appears to be important for anchoring cargo at the periphery, as depolymerization of actin leads to melanosome aggregation. This spatial segregation between the roles of actin and microtubules, with actin-based mechanisms dominating at the periphery, is also thought to play a role in endocytosis and the subsequent trafficking of endosomes²¹. In other cellular systems, however, depolymerizing the actin cytoskeleton has minor effects on microtubule-based cargo transport^{97, 149}. Finally, myosin V interacts with microtubules and enhances kinesin processivity in vitro, suggesting another potential crosstalk between actin and microtubule-based transport^150–152. Hence, in the context of the three hypothetical mechanisms discussed above, actin and myosin likely play minimal roles in bidirectional cargo transport in neurons, but may play a significant role in organelle dynamics in other systems, particularly transport and docking at the cell cortex.

While their connection to antagonistic disinhibition isn’t entirely clear, there are other regulatory molecules that have been shown to alter the activities of kinesin, dynein or both, and thereby alter bidirectional transport. For instance, the protein huntingtin, which is mutated in Huntington’s disease, facilitates bidirectional transport, most likely by acting as a scaffold for binding motors and/or motor binding partners ^{108, 153–155}. C-Jun N-terminal Kinases (JNKs) and JNK-interacting proteins (JIPs) are important regulators of bidirectional transport in neurons, with JIPs acting as scaffolding proteins that link motors to cargo and JNK phosphorylation leading to some combination of reduced cargo binding, reduced activity, and diminished mechanical performance of kinesin-1 motors^{16, 31, 156–159}. JNK kinases are also thought to enhance microtubule dynamics and promote microtubule stability, providing another avenue for altering transport^160–163.

Another issue in uncovering mechanisms controlling bidirectional transport is the question of timescales. Direct measurements of transport, such as visualizing vesicle deformations and transient pauses, provide potentially a very different readout than the behavior of cargo following hours or days of inhibition. For instance, the injection of dynein antibody into non-neuronal cells resulted in rapid anterograde vesicle movement in the short term, followed by diminished overall transport at later times⁷⁷.

The way forward

The value of using models to uncover biological mechanisms is that they provide testable hypotheses for designing experiments and a framework for interpreting data. Distilled to its core, the fundamental concept of the tug-of-war model – that motors of opposite directionality mechanically compete during bidirectional transport – seems unavoidable. Furthermore, for some specific model systems, bidirectional cargo transport can be explained well both qualitatively and quantitatively using the tug-of-war model. However, for the large number of intracellular cargo that demonstrate the paradox of codependence among antagonistic motors, experiments are not consistent with the tug-of-war. These conflicts require development of new models to describe bidirectional cargo transport in cells.

An important step towards defining new models is to generate experimentally testable model predictions. Table 1 lists the three mechanisms proposed above along with the tug-of-war model, and defines three key characteristics for each – the termination of a unidirectional run, the description of the pause state, and the resumption of movement following a pause. These characteristics provide the first round of qualitative model predictions that can be addressed experimentally. For instance, a preliminary model classification can be achieved by making high temporal and spatial resolution measurements of cargo dynamics in the paused state and determining whether the data are best fit by a Diffusive model (characterized by a linear mean-squared displacement (MSD) versus time profile), a Draw (normally distributed experimental noise, giving a flat MSD profile), or a Kicking and Screaming model (data consisting of a series of slow runs) (Figure 3). The next step is to build a mathematical framework (such as that proposed in Figure 6, though others are possible), use these mathematical models to generate quantitative experimental predictions such as the switching rate, pause duration, or other metrics, and then challenge these predictions with targeted experiments.

Table 1.

Mechanisms by which different models account for experimentally observed cargo behavior.

Model	Experimentally Observed Cargo Behavior
	End of run	Pause state	Rescue from pause
Tug-of-War	Stall due to stochastic motor detachment or attachment of opposing motor	Both motors stalled in “a draw” (with potential cargo deformation).	One motor wins, other motor detaches or backsteps (with potential recoil of cargo)
Microtubule Tethering	Motor switches to diffusive state	Both motors bound in diffusive state	Motor switches to moving state
Mechanical Activation	Motor switches into inactive state	Either both detached or both bound and stalled	Thermal or motor-driven mechanical activation
Steric Disinhibition	Motor switches into inhibited state	Both detached, or one or both attached but inactive	Release from inhibited state

When modeling a biological system there is always a tradeoff between simplicity (parsimony) and complexity. Although the Müller tug-of-war model contains 14 parameters, the model is actually quite parsimonious when considering the details of the underlying motors and the complex dynamics of the system it is describing. It is likely that new bidirectional models will necessarily be more complex; but because existing simpler models cannot account for the experiments, this added complexity is warranted. Further biological features of intracellular transport that may impact cargo behavior include microtubule heterogeneity (resulting from microtubule associated proteins and tubulin post-translational modifications), cargo geometry (including cargo size, compliance of the motor-cargo linkage, and ability of cargo-bound motors to laterally diffuse and thus locally concentrate in the membrane), and regulatory proteins that alter motor activity and binding to cargo. Because of the complexity of the biology, an important task is to delineate the specific details that impact transport characteristics from those that play only minor roles and can be left out of models. Fortunately, the influence of these variables can be addressed by combinations of knockdown and inhibition studies in cells, along with creative reconstitutions of bidirectional motility in vitro.

Different cargo (for example lysosomes, secretory vesicles, mitochondria, lipid droplets and melanosomes) have different transport requirements and in many cases are transported by different sets of motors. Hence, it is expected that different mechanisms may apply to different intracellular transport systems. By defining classes of bidirectional transport models and focusing in on characterizing the key transport parameters underlying model behavior, a combined experimental and computational approach to these problems should yield significant new insights into this fascinating problem.