Fast, Exact Bootstrap Principal Component Analysis for p > 1 million

Abstract

Many have suggested a bootstrap procedure for estimating the sampling variability of principal component analysis (PCA) results. However, when the number of measurements per subject (p) is much larger than the number of subjects (n), calculating and storing the leading principal components from each bootstrap sample can be computationally infeasible. To address this, we outline methods for fast, exact calculation of bootstrap principal components, eigenvalues, and scores. Our methods leverage the fact that all bootstrap samples occupy the same n-dimensional subspace as the original sample. As a result, all bootstrap principal components are limited to the same n-dimensional subspace and can be efficiently represented by their low dimensional coordinates in that subspace. Several uncertainty metrics can be computed solely based on the bootstrap distribution of these low dimensional coordinates, without calculating or storing the p-dimensional bootstrap components. Fast bootstrap PCA is applied to a dataset of sleep electroencephalogram recordings (p = 900, n = 392), and to a dataset of brain magnetic resonance images (MRIs) (p ≈ 3 million, n = 352). For the MRI dataset, our method allows for standard errors for the first 3 principal components based on 1000 bootstrap samples to be calculated on a standard laptop in 47 minutes, as opposed to approximately 4 days with standard methods.

1 Introduction

Principal component analysis (PCA) (Jolliffe, 2005) is a dimension reduction technique that is widely used fields such as genomics, survey analysis, and image analysis. Given a multidimensional dataset, PCA identifies the set of basis vectors such that the sample subjects' projections onto these basis vectors are maximally variable. These new basis vectors are called the sample principal components (PCs), and the subjects' coordinates with respect to these basis vectors are called the sample scores. The sample PCs can be thought of as estimates of the population PCs, or the eigenvectors of the population covariance matrix. It has been shown that, as dimension increases, whether or not the sample PCs converge to their population counterparts depends on the rate of sample size growth, the rate of dimension growth, and the spacing of the eigenvalues of the population covariance matrix (Shen et al. (2012a), for a recent literature review, see Koch (2013)). Nadler (2008) and Shen et al. (2012a) discuss PC consistency under the “spike covariance” model introduced by Johnstone (2001), where the first several eigenvalues of the population covariance matrix are assumed to be much larger than the remaining eigenvalues. Jung and Marron (2009) introduced consistency conditions for cases where sample size is fixed, dimension grows, and groups of eigenvalues grow with dimension at different rates. Shen et al. (2013) discuss consistency conditions for sparse PCA, when the first eigenvector of the population covariance matrix can be assumed sparse. Consistency conditions for the n-length, right singular vectors of high dimensional sample data matrices are discussed by Leek (2011) and Shen et al. (2012b).

A fundamental drawback of the PCA algorithm is that it is purely descriptive – there is no clear method for estimating the sampling variability of the scores, the PCs, or proportion of variance that each PC explains. Analytically derived, asymptotic confidence intervals for PCs typically require the assumption of normally distributed data (Girshick, 1939; Tipping and Bishop, 1999), or existence and computation of fourth order moments which results in O(p⁴) complexity (Kollo and Neudecker, 1993, 1997; Ogasawara, 2002), where p is the sample dimension. As an alternative to analytical, asymptotic confidence intervals, Diaconis and Efron (1983) proposed bootstrap based confidence intervals for PCA results. Hall and Hosseini-Nasab (2006) gave a theoretical justification for using bootstrap confidence regions to estimating sampling variability of functional PCA output. Goldsmith et al. (2013) applied a bootstrap procedure in functional PCA to estimate confidence bands for subject-level underlying functions, accounting for additional uncertainty coming from the PC decomposition. Salibián-Barrera et al. (2006) use the bootstrap in the context of a robust PCA procedure. There, the authors applied an eigenvalue decomposition to a robust estimate of the population shape matrix, which is a scaled version of the population covariance matrix. The bootstrap has also been discussed in the context of factor analysis (Chatterjee, 1984; Thompson, 1988; Lambert et al., 1991), and in the context of determining the number of nontrivial components in a dataset (Lambert et al., 1990; Jackson, 1993; Peres-Neto et al., 2005; Hong et al., 2006). However, when applying the bootstrap to PCA in the high dimensional setting, the challenge of calculating and storing the PCs from each bootstrap sample can make the procedure computationally infeasible.

To address this computational challenge, we outline methods for exact calculation of PCA in high dimensional bootstrap samples that are an order of magnitude faster than the current standard methods. These methods leverage the fact that all bootstrap samples occupy the same n-dimensional subspace, where n is the original sample size. Importantly, this leads to bootstrap variability of the PCs being limited to rotational variability within this subspace. To improve computational efficiency, we shift operations to be computed on the low dimensional coordinates of this subspace before projecting back to the original p-dimensional space.

There has been very little work applying bootstrap to PCA in the high dimensional context, largely due to computational bottlenecks. The methods we propose drastically reduce these bottlenecks, allowing for simulation studies of PCA in high dimensions, and for further study of bootstrap PCA in real world, high dimensional scientific applications.

Our methods can also be directly applied to determine the resampling-based variability of any model that depends on a singular value decomposition of the sample data matrix. For example, in Independent Component Analysis (ICA, Bell and Sejnowski, 1995), the first step is typically to use PCA to represent the data on a low dimensional space (Calhoun et al., 2001). Other examples include bootstrap and cross-validation variability for principal component regression (PCR), ridge regression, and, more generally, regression with quadratic penalties.

The remainder of this paper is organized as follows. Section 1.1 presents some initial mathematical notation, and gives a basic summary of PCA and the bootstrap procedure. Section 1.2 outlines the intuition for fast bootstrap PCA. Section 2 discusses two motivating data examples – one based on sleep electroencephalogram (EEG) recordings, and one based on brain magnetic resonance images (MRIs). Section 3 presents the full details of our methods for fast, exact bootstrap PCA. The computation complexity of our methods depends on the final sampling variability metric of interest. For example, pointwise standard errors for the PCs can be calculated more quickly than the full, high dimensional bootstrap distribution of the PCs. Section 4 uses simulations to demonstrate coverage rates for confidence regions around the PCs. Section 5 applies fast bootstrap PCA to the EEG and MRI datasets.

1.1 A brief summary of PCA, SVD, the bootstrap, and their accompanying notation

In the remainder of this paper, we will use the notation X_[i,k] to denote the element in the i^th row and k^th column of the matrix X. The notation X_[,k] denotes the k^th column of X; X_[k,] denotes the k^th row of X; X_[,1:k] denotes the first k columns of X; and X_[1:k,1:k] denotes the block of matrix X defined by the intersection of the first k columns and rows. The notation v_[j] denotes the j^th element of the vector v, the notation 1_k denotes the k-length vector of ones, and the notation I_k denotes the k × k identity matrix. We will also generally use the term “orthonormal matrix” to refer to rectangular matrices with orthonormal columns.

In order to create highly informative feature variables, PCA determines the set of orthonormal basis vectors such that the subjects' coordinates with respect to these new basis vectors are maximally variable (Jolliffe, 2005). These new basis vectors are called the sample principal components (PCs), and the subjects coordinates with respect to these basis vectors are called the sample scores.

Both the sample PCs and sample scores can be calculated via the singular value decomposition (SVD) of the sample data matrix. Let Y be a full rank, p × n data matrix, containing p measurements from n subjects. Suppose that the rows of Y have been centered, so that each of the p dimensions of Y has mean zero. The singular value decomposition of Y can be denoted as VDU′, where V is the p × n matrix containing the orthonormal left singular vectors of Y, U is the n × n matrix containing the right singular vectors of Y, and D is a n × n diagonal matrix whose diagonal elements contain the ordered singular values of Y. The principal component vectors are equal to the ordered columns of V, and the sample scores are equal to the n × n matrix DU′. The diagonal elements of (1/(n − 1))D² contain the sample variances for each score variable, also known as the variances explained by each PC. Approximations of Y using only the first K principal components can be constructed as $\widehat{\mathbf{Y}}:={\sum }_{k=1}^K{\mathbf{V}}_{[,k]}{(\mathbf{\text{DU}}\prime )}_{[k,]}$. Existing methods for fast, exact, and scalable calculation of the SVD in high dimensional samples are discussed in the supplemental materials.

The sampling variability of PCA can be estimated using a bootstrap procedure. The first step of this procedure is to construct a bootstrap sample, by drawing n observations, with replacement, from the original demeaned sample. PCA is reapplied to the bootstrap sample, and the results are stored. This process is repeated B times, until B sets of PCA results have been calculated from B bootstrap samples. We index the bootstrap samples by the superscript notation b, so that Y^b denotes the b^th bootstrap sample. Variability of the PCA results across bootstrap samples is then used to approximate the variability of PCA results across different samples from the population. Unfortunately, recalculating the SVD for all B bootstrap samples has a computation complexity of order O(Bpn²), which can make the procedure computationally infeasible when p is very large.

1.2 Fast bootstrap PCA – resampling is a low dimensional transformation

It's important to note that the interpretation of principal components (PCs) depends on the coordinate vectors on which the sample is measured. Given the sample coordinate vectors, the PC matrix represents linear transformation that aligns the coordinate vectors with the directions along which sample points are most variable. When the number of coordinate vectors (p) exceeds the number of observations (n), this transformation involves first reducing the coordinate vectors to a parsimonious, orthonormal basis of n vectors¹ whose span still includes the sample data points, and then applying the unitary transformation that aligns this basis with the directions of maximum sample variance. The first step, of finding a parsimonious basis, is more computationally demanding than the alignment step. However, if the number of coordinate vectors is equal to the number of data points, then the transformation obtained from PCA consists of only an alignment.

The key to improving computational efficiency of PCA in bootstrap samples is to realize that all resampled observations are contained in the same low dimensional subspace as the original sample. Because the span of the principal components V includes all observations in the original sample, the span of V also includes all observations in any bootstrap sample. Thus, in each bootstrap sample, Y^b, we can skip the computationally demanding dimension reduction step of the PCA by first representing Y^b in terms of the parsimonious, orthonormal basis V. Viewing the bootstrap procedure as a loop operation over several bootstrap samples, we see that the low dimensional subspace on which all sample points lie is loop invariant.

To translate this intuition into the calculation of the SVD for bootstrap samples, we first note that Y^b can be represented as YP^b, where ${\mathbf{P}}_{[i,j]}^b=1$ If ${\mathbf{Y}}_{[,j]}^b={\mathbf{Y}}_{[,i]}$ and zero otherwise. In each bootstrap sample, we then calculate its SVD, denoted by V^bD^bU^b′, via the following steps

$$\begin{array}{l}{\mathbf{Y}}^b=\mathbf{Y}{\mathbf{P}}^b\text{where}{\mathbf{P}}^b\text{represents a resampling operation}\\ =\mathbf{V}\mathbf{D}\mathbf{U}\prime {\mathbf{P}}^b\text{where}\mathbf{D}\mathbf{U}\prime {\mathbf{P}}^b\text{is the matrix of resampled scores}\\ =\mathbf{V}({\mathbf{A}}^b{\mathbf{S}}^b{\mathbf{R}}^{b\prime })\text{where}{\mathbf{A}}^b{\mathbf{S}}^b{\mathbf{R}}^{b\prime }:=\mathit{svd}(\mathbf{D}\mathbf{U}\prime {\mathbf{P}}^b)\\ =(\mathbf{V}{\mathbf{A}}^b){\mathbf{S}}^b({\mathbf{R}}^b)\prime \text{where}(\mathbf{V}{\mathbf{A}}^b)\text{and}({\mathbf{R}}^b)\text{are orthonormal},\text{and}{\mathbf{S}}^b\text{is diagonal}\\ =\mathit{svd}({\mathbf{Y}}^b)\end{array}$$

Rather than directly decomposing the p-dimensional bootstrap sample Y^b, we reduce the problem to a decomposition of the n-dimensional resampled scores, svd(DUP^b) =: A^bS^bR^b′. Because V and A^b are both orthonormal, their product VA^b is orthonormal as well. Since S is diagonal and R^b is orthonormal, (VA^b)S^b(R^b) is equal to the SVD of Y^b. The singular values, and right and left singular vectors of the Y^b can then be written respectively as D^b = S^b, U^b = R^b, and V^b = VA^b. If only the first K principal components are of interest, then it is sufficient to calculate and store A^b, U^b, and D^b as the matrices containing only the first K singular vectors and values of DU′P^b. Full details of our proposed methods for bootstrap PCA are discussed in section 3.

Daudin et al. (1988) applied an equivalent result to eigen-decompositions of bootstrap co-variance matrices in the p < n setting, but this result has not been widely used, nor has it been generalized to the p ≫ n setting. Daudin et al. (1988) suggested that, rather than decomposing the p × p covariance matrix, a more computationally efficient approximation is to decompose the covariance matrix of the k leading resampled score variables. The eigenvectors of this k × k covariance matrix can then be projected onto the p-dimensional space to approximate the eigenvectors of the full p × p covariance matrix. In the p ≫ n setting, however, if k is set equal to n, then the approximation becomes exact. Note also that in the p ≫ n setting, it is the projection onto the p-dimensional space that is most computationally demanding step (computational complexity O(KBpn)), rather than the n-dimensional decompositions (computational complexity O(KBn²)).

To gain intuition for why that the columns of VA^b are the principal components of Y^b, note that the resampled scores, DU′P^b, are equivalent to the resampled data, Y^b, expressed in terms in terms of the coordinate vectors V. This implies that the principal components of the resampled scores, A^b, give the transformation required to align the coordinate vectors of the scores, V, with the directions along which the resampled scores are most variable. Applying this transformation yields VA^b – the bootstrap principal components in terms of the sample's original, native coordinate vectors.

Random orthogonal rotations comprise the only possible way that the fitted PCs can vary across bootstrap samples. Because of this, the bootstrap procedure will not be able to directly estimate PC sampling variability in directions orthogonal to the observed sample, not unlike how a bootstrap mean estimate must be a weighted combination of the observed data points. However, when the inherent dimension of the population is small, the sampling variability of the PCs will generally be dominated by variability in a handful of directions, and these directions will generally be well represented by the span of the bootstrap PCs. Variability in directions not captured by the bootstrap procedure will tend to be of a much smaller magnitude.

The rotational variability of the bootstrap PCs is directly represented by the A^b matrices. More specifically, information about random rotations within the K leading PCs is captured by the ${\mathbf{A}}_{[1:K,1:K]}^b$ block matrices, which show how much each of the K leading bootstrap PCs weight on each of original K leading components. When the majority of bootstrap PC variability is due to rotations within the K leading PCs, the ${\mathbf{A}}_{[1:K,1:K]}^b$ matrices provide a parsimonious description of this dominant form of variability.

Decomposing V^b into an alignment operation, A^b, applied to the original sample components, V, can drastically reduce the storage and memory requirements required for the bootstrap procedure, making it much more amenable to parallelization. Using this method, we're able to store all the information about the variability of V^b only by storing the A^b matrices, which can later be projected onto the high dimensional space. Calculating the A^b matrices only requires the low dimensional matrices DU′ and P^b, and does not require either operations on the p × n matrix Y^b, or access to the potentially large data files storing Y. In the context of parallelizing the bootstrap procedure, this allows for minimal memory, storage, and data access requirements for each computing node.

Furthermore, in many cases, it is not even necessary to calculate and store the p-dimensional components, ${\mathbf{V}}_{[,1:K]}^b$. Instead we can calculate summary statistics for the bootstrap distribution of the low dimensional matrices A^b, and translate only the summary statistics to the high dimensional space. For example, we can quickly calculate bootstrap standard errors for V_[,1:K] by first calculating the bootstrap moments of A^b, and projecting these moments back onto the p-dimensional space (see section 3.2). Joint confidence regions for the PCs can also be constructed solely based on the bootstrap distribution of A^b (see section 3.3). Similar complexity reductions are available when calculating bootstrap distribution of linear functions of the components, such as the the arithmetic mean of the k^th PC (i.e. $(1/p)1_p^{\prime }{\mathbf{V}}_{[,k]}^b$). For any bootstrap statistic of the form $\mathbf{q}\prime {\mathbf{V}}_{[,k]}^b=(\mathbf{q}\prime \mathbf{V}){\mathbf{A}}_{[,k]}^b$, where q is a p-length vector, the n-length vector q′V can be pre-calculated, and the complexity of the bootstrap procedure will be limited only by n.

2 Motivating data

In this section we apply standard PCA to a dataset of sleep EEG recordings (p=900), and to a dataset of preprocessed brain MRIs (p=2,979,666). A bootstrap procedure is later applied in section 5, to estimate sampling variability for the fitted PCs.

There has been demonstrated interest in the population PCs corresponding to both datasets (Di et al., 2009; Crainiceanu et al., 2011; Zipunnikov et al., 2011a,b). For our purposes, the functional EEG data form an especially useful didactic example, as the sample PCs are also functional, and easily visualizable. We include the MRI dataset primarily to demonstrate computational feasibility of the bootstrap procedure when dimension (p) is large.

2.1 Sleep EEG

The Sleep Heart Health Study (SHHS) is a multi-center prospective cohort study designed to analyze the relationships between sleep-disorder breathing, sleep metrics, and cardiovascular disease (Quan et al., 1997). Along with many other health and sleep measurements, EEG recordings were taken for each patient, for an entire night's sleep. An EEG uses electrodes placed on the scalp to monitor neural activation in the brain, and is commonly used to describe the stages of sleep. Our goal in this application is to estimate the primary patterns in EEG signal that differentiate among healthy subjects, and to quantify uncertainty in these estimated patterns due to sampling variability.

To reflect this goal, we selected a subsample of 392 healthy, comparable controls from the SHHS (n = 392). Our sample contained only female participants between ages 40 and 60, with no sleep disordered breathing, no history of smoking, and high quality EEG recordings for at least 7.5 hours of sleep. In order to more easily register EEG recordings across subjects, only the first 7.5 hours of EEG data from each subject were used. Although the EEG recordings consist of measurements from two electrodes, we focus for simplicity only on measurements from one of these electrodes (from the left side of the top of the scalp).

To process the raw EEG data, each subject's measurements were divided into thirty second windows, and the proportion of the signal in each window attributable to low frequency wavelengths (0.8-4.0 Hz) was recorded. This proportion is known as normalized δ power (NP_δ), and is particularly relevant to deep stage sleep (NREM Stage 3). The preprocessing procedure used here to transform the raw EEG data into NP_δ is the same as the procedure used by Crainiceanu et al. (2009). A lowess smoother was then applied to each subject's NP_δ function, as a simple means of incorporating the assumption that the underlying NP_δ process is a smooth function. This preprocessing procedure resulted in 7.5 hours × (60 minutes/hour) × (2 thirty second windows/minute) = 900 measurements of NP_δ per subject (p = 900).

The left panel of Figure 1 shows examples of NP_δ functions for five subjects, as well as the mean NP_δ function across all subjects, denoted by μ. The first five principal components of the NP_δ data are shown in the right panel of Figure 1. The first PC (PC1) appears to be a mean shift, indicating that the primary way in which subjects differ is in their overall NP_δ over the course of the night. The remaining four PCs (PC2, PC3, PC4, and PC5) roughly correspond to different types of oscillatory patterns in the early hours of sleep. These components are fairly similar to the results found by (Di et al., 2009), who analyze a different subset of the data, and employ a smooth multilevel functional PCA approach to estimate eigenfunctions that differentiate subjects from one another.

Figure 1.

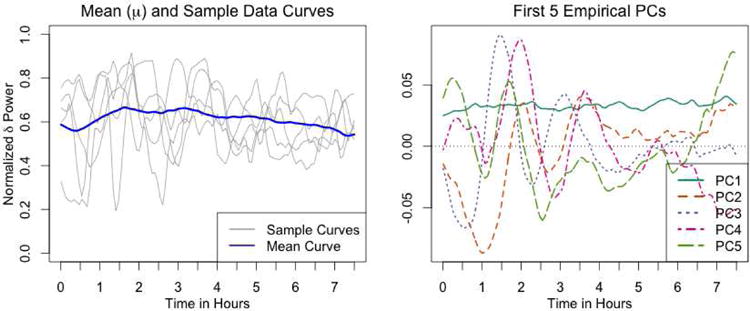
Summary of EEG dataset - The left panel shows examples of normalized δ power (NP_δ) over the course of the night for five subjects, as well as the mean NP_δ function across all subjects (μ). The right panel shows the first five PCs of the dataset.

Collectively, the first five PCs explain approximately 55% of the variation, and the first ten PCs explain approximately 76% of the variation (see scree plot in supplemental materials). These estimates for the variance explained by each component are much lower than the estimates from Di et al. (2009). The difference is most likely due differences in how the MFPCA method employed by Di et al. (2009) incorporates the assumption of underlying smoothness in NP_δ.

2.2 Brain magnetic resonance images

We also consider a sample data processed using voxel based morphometry (VBM) (Ashburner and Friston, 2000), a technique that is frequently used to study differences in the size of brain regions across subjects, or within a single subject over time. Our data came from an epidemiological study of former organolead manufacturing workers (Stewart et al., 2006; Schwartz et al., 2007, 2010; Bobb et al., 2014). We focused on the baseline MRIs from the 352 subjects for which both baseline and followup MRIs were recorded.

VBM images were constructed based on brain MRIs. The original MRIs were stored as 3-dimensional arrays, with each array element corresponding to tissue intensity in a voxel, or volumetric pixel, of the brain. Creating VBM images typically begins by registering each subject's brain MRI to a common template image, using a non-linear warping. The number of voxels mapped to each voxel of the template image during the registration process is recorded. This information is used to create subject-specific images on the template space, where each voxel's intensity represents the size of that voxel in the subject's original MRI. The VBM images used here were processed using a generalization of the regional analysis of volumes examined in normalized space (RAVENS) algorithm (Goldszal et al., 1998; Davatzikos et al., 2001), and are the same as the baseline visit images used in (Zipunnikov et al., 2011b,a).

To create a single p × n data matrix, each subject's VBM image was vectorized, omitting the background voxels that did not correspond to brain tissue. The vector for each subject contained 2,979,666 measurements (p=2,979,666). Because the resulting data matrix was 3.5 Gb, it is difficult to store the entire data matrix in working memory, and block matrix algebra is required to calculate the sample PCs (see supplemental materials).

A central slice from each of the first three PCs is shown in the first row of Figure 3. PC1 appears to roughly correspond with grey matter, indicating that the primary way in which subjects regions tend to differ is in their overall grey matter volume. Together, the first 30 PCs explain approximately 53.3% of the total sample variation (see scree plot in supplemental materials).

Figure 3.

Bootstrap PC variability - Each column of plots corresponds to a different PC, either the first, second or third. The top row shows the fitted principal components on the original high dimensional space (V_[,k] for k = 1, 2, 3), along with pointwise confidence intervals, and 30 draws from the bootstrap distribution. The bottom row shows the same information, but for the low dimensional representation of the bootstrap PCs ( ${\mathbf{A}}_{[,k]}^b$ for k = 1, 2, 3). In the bottom row, the thick black line corresponds to the case when ${\mathbf{A}}_{[,k]}^b={\mathbf{I}}_{n[,k]}$, where I_n[,k] is the k^th column of the n × n identity matrix, such that ${\mathbf{V}}_{[,k]}^b=\mathbf{V}{\mathbf{A}}_{[,k]}^b={\mathbf{V}}_{[,k]}$.

In the remainder of this paper, we refer to this dataset primarily as to demonstrate the computational feasibility of bootstrap PCA in especially high dimensions. Additional interpretation of the sample PCs is given in (Zipunnikov et al., 2011b,a).

3 Full description of the bootstrap PCA algorithm

In this section we outline calculation methods for bootstrap standard errors, bootstrap confidence regions, and for the full bootstrap distribution of the principal components (PCs). The overall computational complexity of the procedure depends on the bootstrap metric of interest, but the initial steps of all our proposed methods are the same.

Building on the notation of sections 1.1 and 1.2, let K be the number of principal components that are of interest, which typically will be less than n – 1. For simplicity of presentation, we assume that each dimension of the bootstrap sample Y^b has mean zero. Manually recentering Y^b however will not add any high dimensional complexity to the procedure, as this is equivalent to recentering the n × n matrix of resampled scores DU′P^b (see supplemental materials).

For each bootstrap sample, we begin by calculating the leading K singular vectors and singular values of the resampled scores DU′P^b. As noted in section 1.2, the leading left and right singular vectors of DU′P^b are stored as solutions for the n × K matrices A^b and U^b respectively. The leading singular values of DU′P^b are the solutions for the diagonals of the K × K matrix D^b. In the typical case where K is less than or equal to the rank of DU′P^b, the first K singular values of DU′P^b are positive and unique, and the solutions for the columns of A^b and U^b are unique up to sign changes. Arbitrary sign changes in the columns of A^b will ultimately result in arbitrary sign changes in the bootstrap PCs. Adjusting for these arbitrary changes is discussed in section 3.1.

We find in approximately 4% of bootstrap samples from the MRI dataset, that although a solution to the SVD of DU′P^b exists, the SVD function fails to converge. We handle these cases by randomly preconditioning the matrix DU′P^b, reapplying the SVD function, and appropriately adjusting the results to find the SVD of the original matrix. The full details of this procedure are described in the supplement materials.

These baseline steps require a computational complexity of order O(KBn²). They are sufficient for calculating the leading K bootstrap scores and the variance explained by the leading K bootstrap PCs.²

When moving on to describe the bootstrap distribution of the PCs, we have several options, each requiring a different level of computational complexity:

• Standard errors for the PCs can be calculated based on the bootstrap mean and variance of the columns of A^b (see section 3.2). These standard errors can be used to create pointwise confidence intervals (see section 3.3.1). This option requires additional computational complexity of order O(Kpn² + KBn²).

• Joint confidence regions for the PCs and for the principal subspace can be constructed using the methods in section 3.3.3. This option requires no additional computational complexity on the high dimensional scale.

• The full bootstrap distribution of PCs can be calculated by projecting the principal components of the bootstrap scores onto the p-dimensional space (i.e. ${\mathbf{V}}_{[,1:K]}^b=\mathbf{V}{\mathbf{A}}^b$). The bootstrap PC vectors ( ${\mathbf{V}}_{[,1:K]}^b$) can then be used to create pointwise percentile intervals for the PCs (see section 3.3.1). If p is sufficiently large such that the matrix V cannot be held in working memory, block matrix algebra can be used to break down the calculation of VA^b into a series low memory operations (see supplemental materials). Calculation of all bootstrap PCs requires additional computational complexity of order O(KBpn). If K is set equal to n−1, then the computational complexity of this method is roughly equivalent to that the standard methods (O(Bpn²)). The total computation time, however, will still be approximately half the time of standard methods, as the matrices Y^b′ Y^b need not be calculated (see supplemental materials).

3.1 Adjusting for axis reflections of the principal components

Because the singular vectors of Y^b are not unique up to sign, arbitrary sign changes, also known as reflections across the origin, will induce variability in both the sampling and bootstrap distributions of the principal components (V^b). These reflections, however, do not affect the interpretation of the PCs, and so their induced variability will cause us to overestimate sampling variability of the patterns decomposed by PCA (Efron and Tibshirani, 1993, see section 7.2; Mehlman et al., 1995; Jackson, 1995; Milan and Whittaker, 1995). For example, arbitrary sign changes can cause the confidence interval for any element of any principal component to include zero, even if the absolute value of that element is nearly constant and nonzero across all bootstrap samples.

To isolate only the variation that affects the interpretation of the PCs, we adjust the sign of the columns of V^b so that the dot products ${\mathbf{V}}_{[,k]}^{b\prime }{\mathbf{V}}_{[,k]}$ are positive for k = 1, 2, …, K. Note that because V^b = VA^b, sign changes in the columns of V^b are equivalent to sign changes in the columns of A^b. For the same reason, sign adjustments for the columns of V^b are equivalent to sign adjustments for the columns of A^b, which can be simpler to compute. Here, the dot products ${\mathbf{V}}_{[,k]}^{b\prime }{\mathbf{V}}_{[,k]}$ for k = 1, 2, …, K actually do not require any additional calculations, as they can be found on the diagonal elements of V′V^b = V′VA^b = A^b. Independent of our work, this calculation simplification is also noted by Daudin et al. (1988). Whenever ${\mathbf{A}}_{[k,k]}^b$ is negative, we declare that an arbitrary sign change has occurred, and adjust by multiplying ${\mathbf{A}}_{[,k]}^b$ and ${\mathbf{U}}_{[,k]}^b$ by -1. The resulting PCs and scores are still valid solutions to the PCA algorithm.

Since ${\mathbf{V}}_{[,k]}^b$ and V_[,k] each have norm equal to one, their dot product is equal to the cosine of the angle between them. As a result, using the dot product ${\mathbf{V}}_{[,k]}^{b\prime }{\mathbf{V}}_{[,k]}$ to adjust for sign will ensure that the angle between ${\mathbf{V}}_{[,k]}^b$ and V_[,k] is between −π/2 and π/2. This range of angles is exactly the range that affects our interpretation of the bootstrapped PCs. Using these dot products for sign adjustment is also equivalent to choosing the sign of ${\mathbf{V}}_{[,k]}^b$ that minimizes the Frobenius distance $\Vert {\mathbf{V}}_{[,k]}^b-{\mathbf{V}}_{[,k]}\Vert$, a method that has been previously suggested (Lambert et al., 1991; Milan and Whittaker, 1995).

It has also been suggested that the sign of each PC should be switched based on the correlation between the columns of V^b and the columns of V, rather than the dot products ${\mathbf{V}}_{[,k]}^{b\prime }{\mathbf{V}}_{[,k]}$ (Jackson, 1995; Babamoradi et al., 2012).³ We advocate against this correlation method, in favor of the cross product method. Of course, the two methods are very similar, as the correlation method is equivalent to applying a cross product operation after first centering and scaling the two vectors. Pre-scaling has no practical effect, as only the sign of the correlation is retained. However, pre-centering removes information that is potentially relevant to the sign switch decision. For example, consider the case where V_[,k] is proportional to a sine wave, shifted up by 2, and scaled appropriately to have norm 1. Furthermore, let ${\mathbf{V}}_{[,k]}^b$ be proportional to the same sine wave, shifted down by 2, and similarly scaled to have norm 1. Note that V_[,k] has all positive elements, and ${\mathbf{V}}_{[,k]}^b$ has all negative elements. These two vectors will be positively correlated, but have a negative crossproduct. The correlation rule will not result in a sign change, which can yield a bimodal bootstrap PC distribution with PCs clustered on either side of the zero line. Alternatively, the cross product rule will result in a sign change, making a bimodal bootstrap distribution less likely. In the supplemental materials, we illustrate such cases in more detail, and further argue for the use of the cross product over the correlation.

3.2 Bootstrap moments of the principal components

Traditional calculation of the mean and variance of ${\mathbf{V}}_{[,k]}^b$ requires first calculating the bootstrap distribution of ${\mathbf{V}}_{[,k]}^b$, and then taking means and variances over all B bootstrap samples. However, using our characterization of V^b as VA^b, and properties of expectations, the same result can achieved without calculating or storing ${\mathbf{V}}_{[,k]}^b$.

Specifically, the bootstrap mean $E({\mathbf{V}}_{[,k]}^b)$ can be found via $E(\mathbf{V}{\mathbf{A}}_{[,k]}^b)=\mathbf{V}E({\mathbf{A}}_{[,k]}^b)$, where the operation E is the expectation with respect to the bootstrap distribution. The bootstrap variance of ${\mathbf{V}}_{[i,k]}^b$ can be found via

$$\mathit{Var}({\mathbf{V}}_{[i,k]}^b)=\mathit{Cov}{({\mathbf{V}}_{[,k]}^b)}_{[i,i]}=\mathit{Cov}{(\mathbf{V}{\mathbf{A}}_{[,k]}^b)}_{[i,i]}={[\mathbf{V}\mathit{Cov}({\mathbf{A}}_{[,k]}^b)\mathbf{V}\prime ]}_{[i,i]}=({\mathbf{V}}_{[i,]})\prime \mathit{Cov}({\mathbf{A}}_{[,k]}^b)({\mathbf{V}}_{[i,]})$$

Where Var and Cov are variance operators with respect to the bootstrap distribution. The total computational complexity of finding $\mathit{Cov}({\mathbf{A}}_{[,k]}^b)$ and then $\mathit{Var}({\mathbf{V}}_{[i,k]}^b)$ for each combination of i = 1, 2, …, p and k = 1, …, K is only O(Kpn² + KBn²)).⁴

This improvement in computation speed comes from pre-collapsing the complexity induced by having a large number of bootstrap samples before transforming to the high dimensional space. This allows us to separate calculations of order B from calculations of order p. Similar speed improvements are attainable whenever summary statistics or parametric models for the bootstrap distribution of A^b can be translated into summary statistics or parametric models for the high dimensional components V^b.

3.3 Construction of confidence regions

Several types of confidence regions can be constructed based on the bootstrap distribution the PCs. In this section, we specifically discuss (1) pointwise confidence intervals (CIs) for the PCs, based on either the bootstrap moments or bootstrap percentiles; (2) confidence regions (CRs) for the individual PCs; and (3) CRs for the principal subspace. Only the pointwise percentile intervals require calculation of the full bootstrap distribution of the high dimensional PCs. All other CRs can be calculated solely based on the bootstrap distribution of the low dimensional A^b matrices.

3.3.1 Pointwise confidence intervals for the principal components

The simplest pointwise confidence interval for the principal components is the moment-based, or Wald confidence interval. For the i^th element of the k^th PC, the moment-based CI is defined as $E({\mathbf{V}}_{[i,k]}^b)\pm \sigma ({\mathbf{V}}_{[i,k]}^b)z_{(1-\alpha /2)}$, where α is the desired alpha level, z_(1–α/2) is the 100(1 – α/2)^th percentile of the standard normal distribution, and the E and σ functions capturing the mean and standard deviation of ${\mathbf{V}}_{[i,k]}^b$ across bootstrap samples. Both $E({\mathbf{V}}_{[i,k]}^b)$ and $\sigma ({\mathbf{V}}_{[i,k]}^b)$ can be attained without calculating or storing the full bootstrap distribution of ${\mathbf{V}}_{[i,k]}^b$ (see section 3.2).

Another common pointwise interval for ${\mathbf{V}}_{[i,k]}^b$ is the bootstrap percentile CI, defined as $(q({\mathbf{V}}_{[i,k]}^b,\alpha /2),q({\mathbf{V}}_{[i,k]}^b,1-\alpha /2))$ where $q({\mathbf{V}}_{[i,k]}^b,\alpha )$ denotes the 100α^th percentile of the bootstrap distribution of ${\mathbf{V}}_{[i,k]}^b$. Unlike the moment-based CI, the percentile CI does require calculation of the full bootstrap distribution of ${\mathbf{V}}_{[i,k]}^b$.

Estimating the percentile interval tends to require more bootstrap samples (e.g. B=1000-2000) than estimating the moment-based interval (e.g. B=50-200), as the quantile function is more affect affected by the tails of the bootstrap distribution than the moments are (Efron and Tibshirani, 1993). Interpretation of both these pointwise CIs is discussed further in section 5.

Our methods can also be used to quickly calculate bias corrected and accelerated (BC_a) CIs (Efron, 1987), as others have suggested (Timmerman et al., 2007;Salibián-Barrera et al., 2006).

3.3.2 Confidence regions for the principal components

Each principal component can be represented as a point in p-dimensional space. More specifically, because of the norm 1 requirement for the PCs, the parameter space for the principal components is restricted to the p-dimensional unit hypersphere, S_p = {x ∊ R^p : x′x = 1}. To create p-dimensional CRs for each PC, Beran and Srivastava (1985) suggest so-called confidence cones on the unit hypersphere, of the form

$$\{\mathrm{x}\in S_p:|\mathrm{x}\prime {\mathbf{V}}_{[,k]}|\ge q(|{\mathbf{V}}_{[,k]}^{b\prime }{\mathbf{V}}_{[,k]}|,\alpha )=q(|{\mathbf{A}}_{[k,k]}^b|,\alpha )\}$$

Here, q(a^b, α) is the quantile function denoting the 100α^th bootstrap percentile of the statistic a^b. As noted in section 3.1, the calculation of ${\mathbf{V}}_{[,k]}^{b\prime }{\mathbf{V}}_{[,k]}$ can be simplified to ${\mathbf{V}}_{[,k]}^{b\prime }{\mathbf{V}}_{[,k]}={\mathbf{A}}_{[k,k]}^b$. Geometrically, the dot product condition of this CR is equivalent to a condition on the angle between x and V_[,k]. Note that this CR automatically incorporates the sign adjustments described in section 3.1. Beran and Srivastava (1985) provide a theoretical proof for the coverage of CRs constructed in this way.

It is also possible to create joint confidence bands (jCBs) for the PCs according the method outlined by Crainiceanu et al. (2012). However, such bands will also contain vectors that do not have norm 1, and may even exceed 1 in absolute value for a specific dimension. As a result, many vectors contained within the jCBs will not be valid principal components, which complicates interpretation of the jCBs.

3.3.3 Confidence regions for the principal subspace

To characterize the variability of the subspace spanned by the first K PCs, also known as the principal subspace, it is not sufficient to simply combine the individual CRs for each PC. This is because the sampling variability of the individual fitted PCs is influenced by random rotations of the fitted PC matrix ${\mathbf{V}}_{[,1:K]}^b$, while the sampling variability of the subspace is not. Similarly, most models whose fit depends on the leading PCs are unaffected by random rotations.

To characterize the sampling variability of the principal subspace, we first note that any bootstrap principal subspace can be defined by the p × K matrix with columns equal to the leading K PCs. Any such matrix must be contained within the set of all of p × K orthonormal matrices. This set can be written as the Stiefel manifold M_K(R^P) := {X ∈ F^p×K : X′X = I_K}, where F^p×K is the set of all p × K matrices. To create CRs for the principal subspace, we can use the following generalization of CRs for the individual PCs

$$\{\mathbf{X}\in M_K(R^p):\Vert \mathbf{X}\prime {\mathbf{V}}_{[,1:K]}\Vert \ge q(\Vert {\mathbf{V}}_{[,1:K]}^{b\prime }{\mathbf{V}}_{[,1:K]}\Vert ,\alpha )=q(\Vert {\mathbf{A}}_{[1:K,1:K]}^b\Vert ,\alpha )\}$$

Here, the norm operation refers to the Frobenius norm. Beran and Srivastava (1985) suggest CRs of this form to characterize variability of a set of sample covariance matrix eigenvectors whose corresponding population eigenvalues are all equal. However, the CR construction method can also be applied in the context of estimating the principal subspace. As with CRs for the individual PCs, we can make the simplification that ${\mathbf{V}}_{[,1:K]}^{b\prime }{\mathbf{V}}_{[,1:K]}={\mathbf{A}}_{[1:K,1:K]}^b$. Note that such CRs automatically adjust for random rotations of the first K principal components – if R is a K × K orthonormal transformation matrix, then ‖(XR)′V‖ = ‖X′V‖.

3.4 Maintaining informative rotational variability

When several of the leading eigenvalues of the population covariance matrix are close, the fitted PCs in any sample may be a mixtures the leading population PCs. In these cases, the bootstrap PCs will often be approximate rotations of the leading sample PCs. Others have argued if the parameter of interest is the principal subspace or the model fit, then the bootstrap PCs should be adjusted to correct for rotational variability, as the principal subspace is unaffected by rotations among the leading PCs. Specifically, it has been suggested to use a Procrustean rotation to match the bootstrap PCs to the original sample PCs (Milan and Whittaker, 1995), and to then create pointwise confidence intervals (CIs) based on the rotated PCs (Timmerman et al., 2007; Babamoradi et al., 2012).⁵ We argue however that bootstrap rotational variability is informative of genuine sampling rotational variability, and that adjusting for rotations is not an appropriate way to represent sampling variability of the principal subspace, or the sampling variability of model fit. This is because pointwise CIs are not designed to estimate the sampling variability of the principal subspace. The pointwise CIs generated from rotated bootstrap PCs also do not capture the sampling variability of standard PCs, as the rotated PCs are not valid solutions to the PCA algorithm.

Rather than rotating towards the sample, it has also been proposed to rotate both the sample and bootstrap PCs towards a p × K target matrix T, which is pre-specified before collecting the initial sample Y (Raykov and Little, 1999; Timmerman et al., 2007).⁶ The target matrix T may be based on scientific knowledge, or previous research. Such an approach can also be used to test null hypotheses about the principal subspace by rotating ${\mathbf{V}}_{[,1:K]}^b$ toward a null PC matrix V₀ (Raykov and Little, 1999), and checking if elements of V₀ are contained in the resulting CRs.

Our opinion is that if investigators are interested in the sampling variability of the output from a model that uses PCA, then it is the model output, and not the principal components, for which CRs should be calculated. If the sampling variability of the subspace is of interest, than CRs specifically designed for the subspace should be used (see section 3.3.3), rather than adjusted CIs for the elements of the PCs. Rotating towards a pre-specified target matrix T can also be a useful approach, although it may be more interpretable to calculate the bootstrap distribution of the variance explained by the columns of T,⁷ rather than the bootstrap distribution of the fitted PCs after a rotation towards T.

4 Coverage rate simulations

In this section we present simulated coverage rates for the CRs described in section 3.3. In order to make these simulations as realistic as possible, we simulated data using the empirical PC vectors of the EEG dataset as the true population basis vectors. As a baseline simulation scenario we set the sample size (n) equal to 392, and the true number of basis vectors in the population (denoted by K₀) equal to 5.

Measurement vectors for each subject were simulated according to the model ${\mathbf{y}}_i={\sum }_{k=1}^{K_0}{s}_{ik}{\mathbf{\Psi }}_k+{∊}_i$, where y_i is a p-length vector of simulated measurements for the i^th subject; Ψ_k is the k^th true underlying basis vector, which is set equal to the k^th empirical PC of the EEG dataset; s_ik is a random draw from the empirical, univariate distribution of the scores for the k^th PC; and ∊_i is a vector of independent random normal noise variables, each with mean 0 and variance σ²/p. Setting the variance of ∊_i equal to σ²/p implies that the total variance attributable to the random noise will be approximately equal to σ², and will not depend on the number of measurements (p). The parameter σ² was set equal to the sum of the variances of the K₀ + 1 to n^th empirical score variables, implying that for each simulated sample, the first K₀ basis vectors (Ψ₁, Ψ₂, …, Ψ_K0) were expected to explain approximately the same proportion of the variance that they explained in the empirical sample. For each simulated subject, y_i, the K₀ score variables s_i1, …, s_iK0 were all drawn independently. Coverage was compared across 1000 simulated samples. For each simulated sample, the number of bootstrap samples created for estimation (B) was set to 1000.

As comparison simulation scenarios, we increased the number of measurements (p) to 5000 and to 20000, by interpolating the empirical EEG data and recalculating the principal components and scores. We also compared against simulated sample sizes (n) of 100 and 250. Because much of the variability in fitting principal components is determined by the spacing of eigenvalues in the population, we simulated separate scenarios where the empirical score distribution was scaled so that each basis vector explained half as much variance as the preceding basis vector. In other words, we scaled true population distribution of scores such that the vector of variances of the 5 score variables was proportional to the vector (2⁴, 2³, 2², 2¹,1). The total variance of the first 5 score variables was kept constant across all simulations. We refer to the modified eigenvalue spacing as the “parametric spacing” simulation scenario, and refer to the original eigenvalue spacing as the “empirical spacing” simulation scenario. Finally, we also simulated scenarios where the total variance due to the random noise (σ²) was scaled up 50%, and where it was scaled down by 50%. Considering all combinations of eigenvalue spacing, random noise level, sample size, and number of measurements, we conducted 2 × 3 × 3 × 3 = 54 sets of simulations. Thus, our simulation study required the calculation of 54 × 1000 × 1000 = 54 million principal component decompositions, with the ranges for p and n mentioned above.

The total elapsed computation time for these 54 simulations was 28 hours. The simulations were run as a series of parallel jobs on an ×86-based linux cluster, using a Sun Grid Engine for management of the job queue. As many as 200 jobs were allowed to run simultaneously. Each job required between approximately .5Gb and 2Gb maximum virtual memory, depending on the scenario being simulated.

4.1 Simulation results

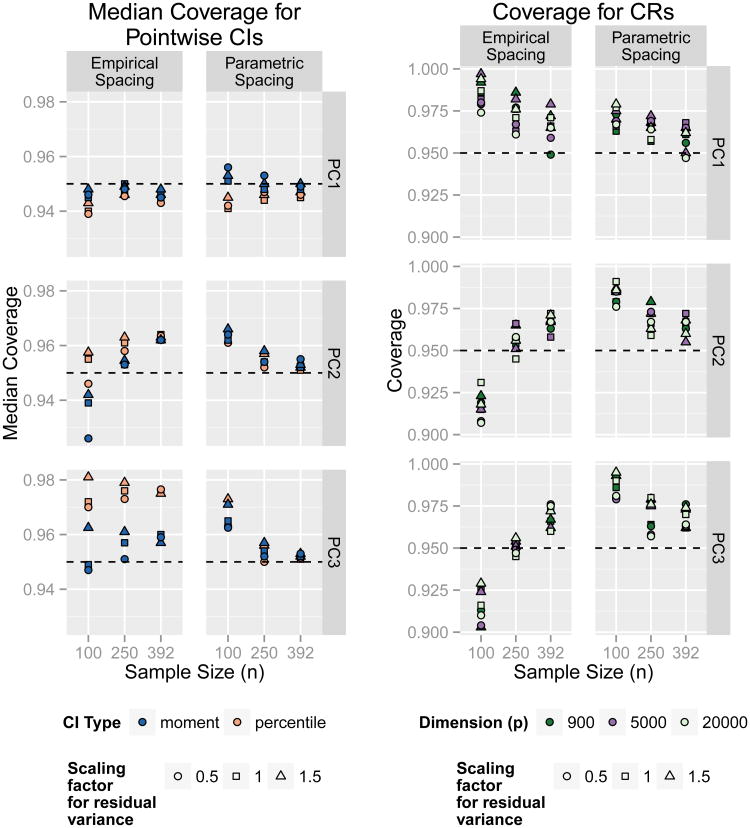
The left of Figure 2 compares simulation results across different levels of residual variance, sample size, and eigenvalue spacing. In this 3 × 2 array of plots we fix p at 900, but results were similar for alternate values of p. For each simulation scenario, we calculated the median pointwise CI coverage across all 900 measurements. Both the moment-based and percentile intervals generally perform well, with all 54 simulation scenarios (including those not shown here) having median coverage rates between 92.4% and 98.1%. When the eigenvalues of the estimated PCs are well spaced (e.g. for PC1 in the empirical spacing scenario, or PCs 1-3 in the parametric spacing scenario), the coverage rates converge to 95% as the sample size increases. However, when the eigenvalues are not clearly differentiated, higher sample sizes can lead to slightly overly conservative CIs.

Figure 2.

Coverage across simulation scenarios - The (3 × 2) array of plots on the left shows the median coverage rate across all p estimated CIs for the PC elements (p = 900). Rows correspond to the PC being estimated. Simulation cases using the empirical eigenvalue spacing are shown on the left column, and simulation cases where where each PC explains half as much as the previous PC are shown on the right column. The (3 × 2) array of plots on the right shows coverage for CRs for the PCs.

In the supplemental materials we further explore coverage by examining the full distribution of coverage rates across each of the p dimensions of the PCs, rather than summarizing by taking the median. We find that for both PC2 and PC3, the moment-based intervals give close to 95% coverage, but that the percentile intervals may give poor coverage in certain regions.

The right side of Figure 2 shows coverage rates of confidence cones for the principal components (section 3.3.2). Coverage appears to improve when the eigenvalues are well spaced and when sample size increases. Differences in coverage are also more noticeable here than in the median coverage rates for pointwise intervals. Coverage rates of CRs for the principal subspace (section 3.3.3) are shown in the supplemental materials, and follow the same general pattern as CRs for the individual PCs.

To more formally summarize our simulation results for the confidence cones, we modeled PC coverage rate as a function of the sample dimension, sample size, eigenvalue spacing, and residual noise variance. Specifically, we considered the ordinary linear regression model |Coverage–.95| = β₀ + β₁log(p) + β₂n + β₃s + β₄f + e, where s is an indicator of the parametric spacing for the eigenvalues, f is the scaling factor applied to the variance of the residual noise in the simulation, and e is a random normal error accounting for unmodeled variability in coverage. We separately fit this model on coverage rates for each PC, treating the all coverage rates as having independent and identically distributed random errors. For PC1, larger sample sizes and the parametric eigenvalue spacing both significantly improved coverage (βˆ₂ = −5.1 × 10⁻⁵, βˆ₃ = .0097, with 95% CIs: (−6.5 × 10⁻⁵, −3.8 × 10⁻⁵) and (−0.013, −0.0064) respectively), and higher levels of residual noise significantly worsened coverage (βˆ₄ = 0.0084, 95% CI: (0.0045,0.012)). For PC2 and PC3, larger sample sizes also significantly improved coverage (βˆ₂ estimates 6.1 × 10⁻⁵ and −6.1 × 10⁻⁵ respectively, with 95% CIs: (−8.0 × 10⁻⁵, −4.2 × 10⁻⁵) and (−8.5 × 10⁻⁵, −3.5 × 10⁻⁵)), but no other variables had significant effects.

We also studied coverage of parameters relevant to the first three score variables. Because the scores themselves are subject-specific random effects rather than population parameters, we focused on coverage of best linear unbiased predictors (BLUPs) for the score variables (Robinson, 1991). We calculated the true BLUPs conditional on the observed data matrix being equal to ΨS, where S is the matrix from which we draw the score variables (s_i1, s_i2,…, s_iK0), and Ψ is the matrix of first K₀ true population PCs. In each bootstrap sample we then calculated the empirical BLUPs (EBLUPs) for the scores (Fitzmaurice et al., 2012), and used the bootstrap distribution of the EBLUPs to calculate percentile and moment-based CIs.

Coverage rates for the BLUP CIs generally followed a similar pattern as coverage rates for the pointwise PC CIs, although the coverage was worse when the sample size was small and the residual noise was high. In the smallest sample size tested, coverage of BLUPs was as low as 85% coverage for the percentile CIs, and 90% for the moment-based CIs. Poorer coverage in these scenarios is to be expected though, as the EBLUPs depend not only on estimates of the PCs, but also on estimates of the eigenvalues of the population covariance matrix, which are known to be biased (Daudin et al., 1988). Note that if we had instead focused on estimates of Ψ′yi then proper coverage would have been implied by proper coverage of the pointwise CIs for the PCs, as both parameters are projections of the true basis vectors. A full description of coverage rates for the BLUPs, as well as the calculation procedure for the BLUPs and EBLUPs, is given in the supplemental materials.

As a secondary analysis, we also looked at the distribution of the angles between the sample PCs and the true population PCs. In general, when the k^th eigenvalue of the population covariance matrix was on a different order of magnitude than the other eigenvalues, the k^th sample PC tended to be close to the k^th population PC. This was the case for PC1 in the empirical spacing scenario, and PCs 1 through 3 in the parametric spacing scenario. When the leading five eigenvalues of the population covariance matrix were not well separated from each other but were well separated from the remaining eigenvalues, the individual sample PCs were not necessarily close to their corresponding population PCs but did tend to be close to the subspace spanned by the leading population PCs. This was the case for PCs 2 and 3 in the empirical spacing scenario. These results are all consistent with what we would expect based on Theorem 2 of Jung and Marron (2009). Because we fixed the proportion of variability explained by each PC, regardless of dimension, our increases in dimension correspond to the case described in Shen et al. (2012a) where the dimension and the leading eigenvalues all grow at the same rate. In this context, Theorem 4.1 of Shen et al. (2012a) suggests that our sample PCs should converge to their population counterparts as n increases, regardless of dimension. This is indeed what we see in our results (see section 6.4 in the supplemental materials).

5 Applying fast bootstrap PC A

5.1 Sleep EEG

When applying fast bootstrap PCA to the EEG dataset, we find that bootstrap estimates of PC1 exhibit minimal variability. PC2 and PC3 are estimated with considerably more variability, but most of this variability is due to random rotations among PCs 2 through 4, all of which roughly correspond with oscillatory patterns.

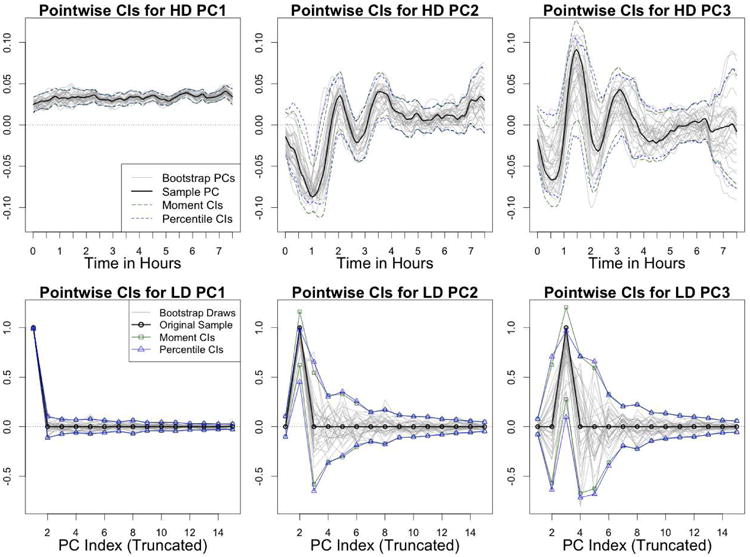
Figure 3 shows the results of this analysis. The first row shows 95% pointwise intervals for each dimension of each of the three PCs. A random subsample of 30 draws from the bootstrap distribution of each PC are shown in gray. We see that the moment-based and percentile intervals generally agree, although they tend to differ more when the fitted PC elements are further from zero. Since the width of the percentile and moment-based CIs are fairly similar, disagreements between the two types of intervals are reflective of skewness in the underlying bootstrap distribution.

The sets of pointwise intervals shown in the top row of Figure 3 form bands around the fitted sample PCs. It's important to note these bands are only calibrated for pointwise 95% coverage – they are not expected to simultaneously contain the true population PC in 95% of samples. Statements about the overall shape of the population PCs that are based on these intervals will be somewhat ad hoc. Furthermore, many curves contained within these bands do not satisfy the norm 1 requirement for principal components, and are not valid solutions to PCA. For example, the upper and lower boundaries of the bands do not have norm 1, and thus are not in the parameter space for the PCs. Similarly, the zero vector is also not in the parameter space.

The top row of Figure 3 shows that both sets of intervals for PC1 are fairly tight, implying that there is little sampling variability in PC1. The pointwise CIs for PC2 are wider, especially in the first four hours of the night. If examined alone, this feature of the CIs might erroneously lead readers to think that the oscillatory pattern in V_[,2] is artificial, and not present in the population PC. However, if we also look at a subsample of draws from the bootstrap distribution of PC2 (shown in gray), we see that the negative spike in hour 1 and the positive spike in hour 2 are often shifted in bootstrap samples. Pointwise variability in the oscillatory pattern is better explained by a simultaneous shift of both peaks than by a magnitude change in either peak. Those bootstrap draws of ${\mathbf{V}}_{[,2]}^b$ that are most shifted tend to bear a closer resemblance to V_[,3].

This resemblance is shown more directly in the bottom row of Figure 3, which shows pointwise CIs summarizing the distribution of ${\mathbf{A}}_{[,k]}^b$ for k = 1, 2, 3. Recall that the bootstrap PCs are equal to V^b = VA^b, such that ${\mathbf{A}}_{[j,k]}^b$ represents the weight that the k^th PC of the b^th bootstrap sample ( ${\mathbf{V}}_{[,k]}^b$) places on the j^th PC of the original sample (V_[,j]). Low bootstrap variability for the k^th PC is generally characterized by ${\mathbf{A}}_{[k,k]}^b$ being close to 1, and all other elements of ${\mathbf{A}}_{[,k]}^b$ being close to zero. While this is the case for bootstrap variability in PC1 (bottom-left panel of Figure 3), the bootstrap draws of PC2 tend to place high weight on V_[,3], in addition to V_[,2]. Equivalently put, bootstrap draws for both ${\mathbf{A}}_{[2,2]}^b$ and ${\mathbf{A}}_{[3,3]}^b$ tend to have high absolute values (bottom-center panel of Figure 3). A similar pattern is shown for PC3. Overall, the bottom row of Figure 3 shows that the majority of the variation in PCs 2-3 is due to rotations among the leading PCs.

Note that the moment-based CIs shown on the right column of Figure 3 can exceed one in absolute value, which will surely violate the norm condition for PCs. In practice, such violations should be accounted for by truncating the CIs at -1 and 1, but we keep the violation for illustrative purposes in Figure 3. It is also worth noting that the percentile CIs for ${\mathbf{A}}_{[k,k]}^b$ will rarely include the value 1, which can be thought of as the fitted value of ${\mathbf{A}}_{[k,k]}^b$ in the original sample (shown in black in Figure 3). The low dimensional percentile CIs for the elements of A^b also fully contain the information required to create confidence cones for each PC (section 3.3.2).

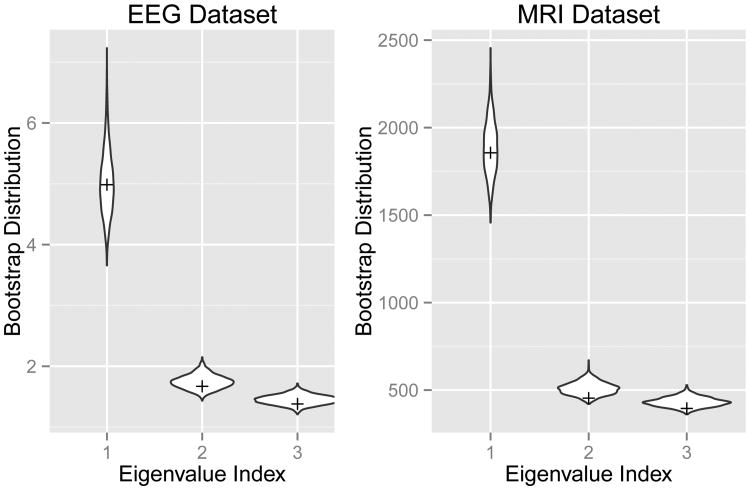
Figure 4 shows the bootstrap distribution of the first three eigenvalues of the sample covariance matrix (the diagonals of (1/(n − 1))(D^b)²). In general, there is a known upward bias in the first eigenvalue of the sample covariance matrix, relative to the first eigenvalue of the population covariance matrix (Daudin et al., 1988). The amount of bias can be estimated using bias in the bootstrap distribution of covariance matrix eigenvalues. Each bootstrap sample can be seen as a simulated draw from the original sample, in which the eigenvalues are known. Here, we define the percent bias in the bootstrap eigenvalues as the difference between the average eigenvalue across all bootstrap samples and the eigenvalue in the original sample, divided by the eigenvalue of the original sample. For the first three covariance matrix eigenvalues in the EEG dataset (Figure 4), there is only a slight upward bias in the bootstrap estimates (percent bias = 1.1%, 4.5%, and 5.0% respectively).

Figure 4.

Bootstrap eigenvalue distribution - For both the EEG and MRI datasets, we show bootstrap distribution for the first three eigenvalues of the sample covariance matrix. Tick marks show the eigenvalues from the original sample covariance matrix.

5.2 Brain MRIs

We also apply our bootstrap procedure to estimate sampling variability of the PCs from the brain MRI dataset. This is primarily included as an example to show the computational feasibility of our method in the high dimensional setting. A deeper interpretation of the sample PCs is provided by (Zipunnikov et al., 2011b,a).

Our results imply that PC1 is estimated with fairly low sampling variability, but that sampling variability is higher for PC2 and PC3. The first two rows of Figure 5 respectively show the fitted sample PCs and the bootstrap standard errors for the PCs. For PC1, the standard errors are generally of a lower order of magnitude than the corresponding fitted values. A direct comparison is given in the bottom row of Figure 5, which shows the fitted sample PCs divided by their pointwise bootstrap standard errors. These ratios can be interpreted as Z-scores under the element-wise null hypotheses that the value of any one element of the population PC is zero. Z-scores with absolute value less than 1.96 are omitted from the display.

Figure 5.

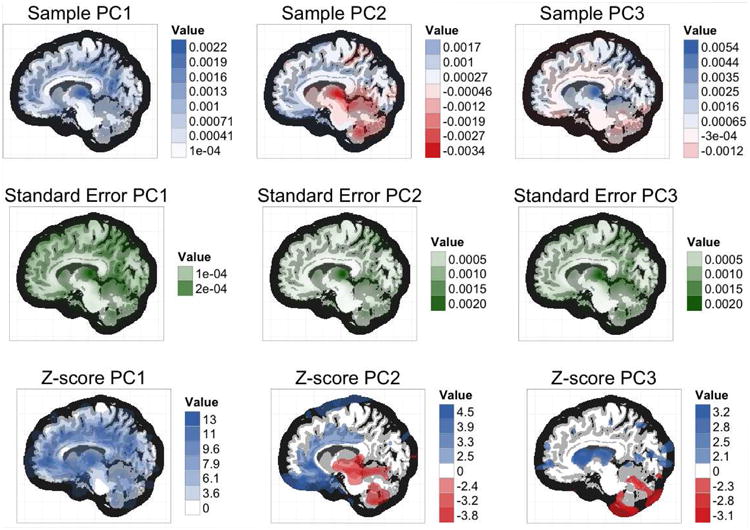
Fitted sample values, bootstrap standard errors, and Z-scores for the MRI PCs - The voxelwise values for the PCs and Z-scores (top and bottom rows) have been binned, and shaded according to the value of their corresponding bin's midpoint. This allows us to visually show both sign (color) and magnitude (opacity). Because the standard errors (middle row) are always positive, the binning procedure is not necessary, and the voxels are shaded on a continuous scale.

To estimate sampling variability due to rotations of the leading population PCs, Figure 6 shows pointwise confidence intervals for the truncated vectors ${\mathbf{A}}_{[,k]}^b$, for k = 1, 2, 3. These intervals are analogous to the intervals shown in the bottom row of Figure 3. A substantial proportion of the bootstrap variability for the second two PCs is due to random rotations between them.

Figure 6.

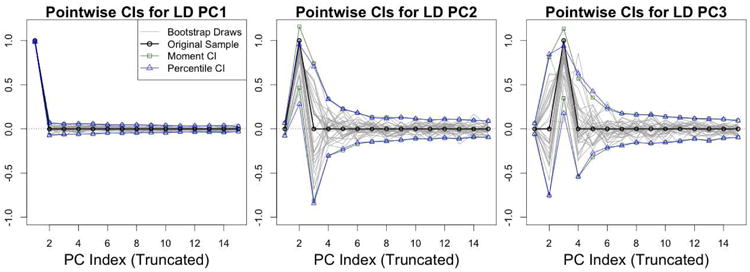
Low dimensional CIs for the MRI PCs - Moment-based CIs, percentile CIs, and 30 random bootstrap draws for ${\mathbf{A}}_{[1:15,k]}^b$, where k = 1, 2 and 3.

The second panel of Figure 4 shows the bootstrap distribution of the eigenvalues of sample covariance matrix. Relative to the fitted eigenvalues in the original sample, the bootstrap eigenvalues show a small, but notable upward bias (percent bias = 1.7%, 12.2%, and 9.2% respectively). Figure 4 also illustrates that, for both datasets, the first eigenvalue is well separated from the second and third eigenvalues. This makes the relatively small variability in PC1, and the largely rotational variability in PCs 2 and 3, consistent with what we would expect from Theorem 2 of Jung and Marron (2009).

6 Discussion

In this paper we outline methods for fast PCA in high dimensional bootstrap samples, based on the fact that all bootstrap samples lie in the same low dimensional subspace. We show computational feasibility by applying this method to a sample of sleep EEG recordings (p = 900), and to a sample of processed brain MRIs (p =2,979,666). Bootstrap standard errors for the first three components of the MRI dataset were calculated on a commercial laptop in 47 minutes, as opposed to approximately 4 days with standard methods (see supplemental materials for computational comparisons against standard methods for different values of p and n).

Ultimately, the usefulness of high dimensional bootstrap PCA will depend not on its speed, but on its demonstrated ability to capture sampling variability. We found that the bootstrap performed well in the simulation settings presented here (section 4). However, bootstrap PCA has rarely been applied to high dimensional data in the past, and its theoretical properties in high dimensions are still not well understood. Specifically, to our knowledge, the theoretical coverage of bootstrap-based confidence intervals have not been well studied. The lack of study on this topic is likely due, in part, to the computational bottlenecks of standard bootstrap PCA, which are compounded in theoretical research that includes simulation studies. Our hope is that the methods presented here will expand the use of bootstrap PCA, and allow for theoretical properties of the bootstrap PCA procedure to be studied and verified via simulations.

When interpreting the results of bootstrap PCA, we find it particularly useful to generate confidence intervals around elements of the low dimensional A^b matrices (Figures 3 and 6). These CIs are a parsimonious way to display the dominant directions in PC bootstrap variability which often correspond to rotations among the leading sample PCs. Calculating these CIs also does not require operations on the p-dimensional scale, beyond the initial SVD of the sample. Another potential way to summarize the dominant directions of PC bootstrap variability would be to create elliptical CRs constrained to the p-dimensional hypersphere, a topic which we discuss in the supplementary materials.

Interpretation of bootstrap PCA results is complicated by the fact that many PCA results are interdependent. For example, each PC is only defined conditionally on the preceding PCs. If we want to isolate only the variability of the k^th PC that affects this conditional interpretation, it can be useful to first assume that the first k − 1 PCs are estimated without error. Logistically, we can condition on the leading k – 1 PCs by resampling from the residuals after projecting the dataset onto the matrix V_[,1:(k−1)]. This is equivalent to setting the first k − 1 score variables to zero before starting the resampling process. Alternatively, we could assume that the first PC is a mean shift, and estimate the sampling variability of the remaining PCs by resampling from the residuals after projecting the dataset onto a constant, flat basis vector. This general approach requires the strong assumption that the leading PCs are known, but the procedure can still be useful in exploring the sources of PC variability.