Nonparametric Analysis of Bivariate Gap Time with Competing Risks

Summary

This article considers nonparametric methods for studying recurrent disease and death with competing risks. We first point out that comparisons based on the well-known cumulative incidence function can be confounded by different prevalence rates of the competing events, and that comparisons of the conditional distribution of the survival time given the failure event type are more relevant for investigating the prognosis of different patterns of recurrence disease. We then propose nonparametric estimators for the conditional cumulative incidence function as well as the conditional bivariate cumulative incidence function for the bivariate gap times, that is, the time to disease recurrence and the residual lifetime after recurrence. To quantify the association between the two gap times in the competing risks setting, a modified Kendall’s tau statistic is proposed. The proposed estimators for the conditional bivariate cumulative incidence distribution and the association measure account for the induced dependent censoring for the second gap time. Uniform consistency and weak convergence of the proposed estimators are established. Hypothesis testing procedures for two-sample comparisons are discussed. Numerical simulation studies with practical sample sizes are conducted to evaluate the performance of the proposed nonparametric estimators and tests. An application to data from a pancreatic cancer study is presented to illustrate the methods developed in this article.

1. Introduction

This research is motivated by a pancreatic adenocarcinoma study conducted at the Johns Hopkins Hospital, in which the medical records of 209 consecutive patients who underwent pancreatectomy between 1998 and 2007 were retrospectively reviewed and the patterns of cancer recurrences were documented. While the majority of resected pancreatic adenocarcinoma recurs within 5 years of resection, the prognosis of different patterns of recurrence after surgical resection has not been well studied. An objective of this study is to investigate whether patients with lung metastasis have better overall survival than those with metastatic recurrent disease at other sites and whether the time to the initial diagnosis of metastatic disease is correlated with the residual lifetime after metastasis. Because patients may or may not develop metastasis before death and the metastasis can occur in different sites of the body, it is natural to treat death without or with metastasis in different sites as competing events. In the pancreatic cancer study, direct comparisons in the overall survival of the following three competing events are of interest to the study investigators: death with metastasis in lung only, death with metastasis at other sites, and death without metastasis.

When analyzing competing risks data, a common practice is to estimate the cumulative incidence functions (CIFs), that is, the cumulative probability of a subject failing from a specific event over time accounting for the fact that patients can fail from other events. Most statistical methods focus on evaluating the covariate effects on the CIF of a particular competing event (see Gray, 1988; Lin, 1997) or comparing CIFs of different competing events (Kochar, 1995 ; Carriere and Kochar, 2000). However, these CIF-based approaches do not properly address the research question in the pancreatic cancer study, because the difference in CIFs can be confounded by different prevalence rates of the competing events. In our study, the CIF for death with lung metastasis is expected to be smaller than that for death with metastatic disease at other sites because of a smaller proportion of patients with lung metastasis. To investigate disease progression after surgery for different type of metastatic patterns, the comparison of interest is the conditional distribution of overall survival given the type of recurrence pattern, that is, the conditional cumulative incidence function (CCIF). In contrast to CIF, the methods and theories for CCIF have not been well-studied. This research fills the gap by constructing a consistent estimator for the CCIF, establishing the asymptotic properties of the estimated CCIF, and formulating testing procedures to compare the CCIFs of different competing events.

Another objective of the pancreatic cancer study is to evaluate the association between the time from pancreatectomy to metastatic recurrent disease and the residual lifetime after the initial diagnosis of metastasis. We consider nonparametric analysis of the joint distribution of the bivariate gap time under the setting of competing risks. In the absence of competing events, this is known as bivariate gap time data. Various nonparametric and semiparametric methods have been proposed to estimate the joint distribution of the bivariate gap time under right censoring (Stute, 1993; Huang and Louis, 1998; Wang and Wells, 1998; Lin et al., 1999; Huang, 2002 ; Lawless and Yilmaz, 2011). For two-sample comparisons, Lin and Ying (2001) and Chang (2000) proposed nonparametric tests to compare the bivariate gap time distribution. Lakhal-Chaieb et al. (2010) studied Kendall’s tau-type of association measure for bivariate gap time. These methods are different than the conventional approaches for multivariate survival time data in that they need to account for the unique sequential ordering structure of bivariate gap time (Lin et al., 1999 ; Huang and Wang, 2005). To our knowledge, nonparametric estimation of the bivariate gap time distribution and the association measure in the setting of competing risks has never been formally studied in the literature.

This article is organized as follows. In Section 2, we study nonparametric estimation of the conditional cumulative incidence function (CCIF) and present a nonparametric hypothesis testing procedure to compare the CCIFs of different competing events. Nonparametric estimation of the joint distribution and the association of the bivariate gap times in the setting of competing risks are considered in Sections 3 and 4. We present results of simulation studies in Section 5 and illustrate the proposed methods with data from the Johns Hopkins pancreatic cancer study in Section 6. Some concluding remarks are given in Section 7.

2. Conditional Cumulative Incidence Functions

Denote by T the time to a failure event of interest. Suppose the study participants can potentially experience any of several, say J, different types of failure events. Let ε = 1, …, J indicate the failure event type. In the pancreatic cancer study, T is the time from surgical resection of pancreatic adenocarcinoma to death. We set ε = 1 for patients who had only lung metastasis, ε = 2 for other sites of recurrence, and ε = 3 if no recurrent metastasis before death. Define the cumulative incidence function (CIF) for the jth competing event

$$F_j(t)=\text{pr}(T\le t,\epsilon =j),j=1,\dots ,J.$$

The focus of this paper is the conditional cumulative incidence function (CCIF)

$$G_j(t)=\text{pr}(T\le t\mid T\le \eta ,\epsilon =j),t\in [0,\eta ],j=1,\dots ,J,$$

where, in practice, the value of η is determined based on scientific interest as well as the length of the study, and, ideally, it should be a large enough value to cover the time period of interest. Note that the value of η may depend on the failure type, and one could choose, say, η_j for failure type j so long as pr(T ≥ η_j, ε = j) > 0. In this paper, we apply the same value of η to different failure types for the purpose of comparing different event types. In the pancreatic cancer study, we set η = 120 (months) because the 10-year survival probability is known to be very low in pancreatic cancer and because the entire follow-up period of this retrospective study exceeds 10 years. In this case, G_j(t) is almost identical to the conditional distribution function pr(T ≤ t | ε = j).

The CCIF G_j(t) characterizes disease progression among those who experience the jth competing event before time η. Our research interest is placed on the comparison of G₁(t) and G₂(t) instead of that of F₁(t) and F₂(t), because the result of latter can be misleading when the prevalence rates of ε = 1 and ε = 2 are different. It follows directly from the equality G_j(t) = F_j(t)/F_j(η) that a consistent estimator for G_j(t) can be constructed by dividing the consistent estimator of F_j(t) by its value evaluated at time η. In what follows, we briefly review the nonparametric CIF estimator and establish the asymptotic properties of the proposed corresponding CCIF estimator.

The observation of T is subject to right censoring, denoted by C. In many applications, it is reasonable to assume that the censoring time C is independent of (T, ε). Let Y = min(T, C) denote the follow-up time until failure or censoring, and let Δ = I(T ≤ C) be the indicator of failure. For ease of discussion, we assume that the distribution functions of the failure time T and the censoring time C are absolutely continuous throughout the paper. The observed data {(Y_i, Δ_i, Δ_iε_i), i = 1, …, n} on n patients are assumed to be i.i.d. copies of (Y, Δ, Δε).

Define the functions $F_j^{uc}(t)=\text{pr}(\mathrm{\Delta }=1,Y\le t,\epsilon =j)$ and S_Y(t) = pr(Y ≥ t). We also define S(t) = pr(T ≥ t) and S_C(t) = pr(C ≥ t) for random variables T and C respectively. Under independent censoring, it can be verified that ${dF}_j^{uc}(t)={dF}_j(t)·S_C(t)$ and S_Y(t) = S(t)S_C(t). Hence the CIF can be reexpressed as

$$F_j(t)={\int }_0^{t}S(u)\frac{{dF}_j^{uc}(u)}{S_Y(u)}.$$ (1)

It is worthwhile to point out the failure type indicator ε can be viewed as a mark variable for the failure time T, where the value of the mark variable can be observed when T is uncensored (Stute, 1993; Huang and Louis, 1998; Huang, 1999; Gilbert et al., 2008). Replacing S(u) with its Kaplan-Meier estimator Ŝ(t) and replacing $F_j^{uc}(u)$ and S_Y(u) with their corresponding empirical measures $n^{-1}{\sum }_{i=1}^n{\mathrm{\Delta }}_{i}I(Y_i\le t,{\epsilon }_i=j)$ and $n^{-1}{\sum }_{i=1}^{n}I(Y_i\ge t)$, we have

$${\widehat{F}}_j(t)={\int }_0^t\widehat{S}(u)\frac{n^{-1}{\sum }_{i=1}^n{dN}_{ij}(u)}{n^{-1}{\sum }_{k=1}^n{R}_k(u)},$$ (2)

where N_ij(u) = Δ_iI(Y_i ≤ u, ε_i = j) is the counting process for the uncensored failure event of type j and R_i(u) = I(Y_i ≥ u) is the at risk process. It is known that F_j(t) is not nonparametrically identifiable outside the support of Y = min(T, C). Hence pr(ε = j) may not be estimable if the support of C does not cover the support of T. We set η to be a prefixed time point that lies inside the support of Y, that is, pr(Y ≥ η) > 0, so that both F_j(t), t ≤ η, and π_j = pr(T ≤ η, ε = j) are estimable.

Define the stochastic process $M_{ij}(t)=N_{ij}(t)-{\int }_0^t{R}_i(u)d{\mathrm{\Lambda }}_j(u)$ for failure type j, where Λj(t) is the cause-specific cumulative hazard function given by ${\mathrm{\Lambda }}_j(t)={\int }_0^t{\lambda }_j(u)du$ with the cause-specific hazard function λ_j(u) = lim_dt→0 pr{T ∈ [u, u + dt), ε = j | T ≥ u}/dt. Gray (1988) showed that M_i1, …, M_iJ are orthogonal martingales; moreover, Lin (1997) established the asymptotically i.i.d. representation ${\widehat{F}}_j(t)-F_j(t)=n^{-1}{\sum }_{i=1}^n{\varphi }_{ij}(t)+o_p(n^{-1/2})$ and proved weak convergence of n^1/2{F̂_j(t) − F_j(t)}, where

$${\varphi }_{ij}(t)={\int }_0^t\frac{S(u){dM}_{ij}(u)-\{F_j(t)-F_j(u)\}{\sum }_{k=1}^J\{{dM}_{ik}(u)\}}{S_Y(u)}.$$ (3)

It is easy to see that π_j and G_j(t) are consistently estimated by π̂_j = F̂_j(η) and Ĝ_j(t) = F̂_j(t)/F̂_j(η). Applying the functional delta method, we have the asymptotically i.i.d. representation

$${\widehat{G}}_j(t)-G_j(t)=n^{-1}\sum _{i=1}^n\left\{\frac{{\varphi }_{ij}(t)}{F_j(\eta )}-\frac{F_j(t){\varphi }_{ij}(\eta )}{F_j{(\eta )}^2}\right\}+o_p(n^{-1/2}).$$ (4)

Thus, provided π_j > 0, the stochastic process n^1/2{Ĝ_j(t) − G_j(t)} converges in distribution to a zero-mean Gaussian process with variance-covariance function

$$\sigma {(s,t)}^2=E\left[\left\{\frac{{\varphi }_{ij}(s)}{F_j(\eta )}-\frac{F_j(s){\varphi }_{ij}(\eta )}{F_j{(\eta )}^2}\right\}\left\{\frac{{\varphi }_{ij}(t)}{F_j(\eta )}-\frac{F_j(t){\varphi }_{ij}(\eta )}{F_j{(\eta )}^2}\right\}\right]$$

for s, t ∈ [0, η]. The weak convergence of Ĝ_j(t) follows directly from that of F̂_j(t). Details of the proof are given in Web Appendix.

To compare the CCIF of different failure types j ≠ k, we consider the following class of stochastic processes

$$Q(t)=K(t)\{{\widehat{G}}_j(t)-{\widehat{G}}_k(t)\},$$

where K(t) is a weight function. The stochastic process Q(t) − K(t){G_j(t) − G_k(t)} has the asymptotically i.i.d. representation

$$n^{-1}\sum _{i=1}^{n}K(t)\left[\left\{\frac{{\varphi }_{ij}(t)}{F_j(\eta )}-\frac{F_j(t){\varphi }_{ij}(\eta )}{F_j{(\eta )}^2}\right\}-\left\{\frac{{\varphi }_{ik}(t)}{F_k(\eta )}-\frac{F_k(t){\varphi }_{ik}(\eta )}{F_k{(\eta )}^2}\right\}\right]+o_p(n^{-1/2}).$$

For a formal test, we propose to use the supremum test statistic

$$\underset{t\in [0,\eta ]}{sup}\mid Q(t)\mid ,$$

an omnibus test that is consistent against any alternatives under which G_j(t) ≠ G_k(t) for some t ∈ [0, η].

An approximate p-value corresponding to the supremum test statistic can be obtained by applying the technique of permutation tests. Under one-sample setting, patients with different failure events are subject to the same mechanism of censoring. As a result, the observations of different subjects are exchangeable under the null. Hence the permutation test is expected to yield valid inferential results. Specifically, at each permutation, failure event types are rearranged among individuals with ε = j, k and the proposed test statistic is calculated using the rearranged data. Repeat this procedure a large number of times. The distribution of the test statistics from the permuted samples approximates the null distribution of the test statistic under the hypothesis G_j(t) = G_k(t). The p-value can then be obtained by the empirical probability that the value of the test statistic derived from the observed data exceeds the value of the test statistic derived from a permuted sample.

3. Bivariate Gap Time Distribution With Competing Risks

In the pancreatic cancer study, additional information about metastasis, if any, is also available. For patients with recurrent metastatic disease, let V be the time from surgery to the initial diagnosis of metastasis and let W be the residual lifetime from metastasis to death, so that V + W gives the total survival time T. Note that, given the first gap time V being uncensored, the observable region of the second gap time W is restricted to C–V. Because the two gap times W and V are usually correlated, the second gap time W is subject to induced informative censoring C–V (Visser, 1996 ; Wang and Wells, 1998 ; Lin et al., 1999). As a result, conventional statistical methods can not be applied directly to estimate the marginal distribution of W.

In this section, we consider nonparametric estimation of the cumulative incidence function for the bivariate gap time (V, W), defined by F_j(v, w) = pr(V ≤ v, W ≤ w, ε = j), and the conditional bivariate cumulative incidence function H_j(v, w) = pr(V ≤ v, W ≤ w | T ≤ η, ε = j), where j takes values on 1 and 2 in the pancreatic cancer study to indicate patients who developed metastasis. Because the marginal distribution of T is nonparametrically identifiable up to η, the two functions are identifiable in the region {(v, w) : v + w ≤ η}.

It is easy to observe that the joint distribution function of (V, W, ε) is determined by (T, V, W, ε) through the identity pr(V ≤ v, W ≤ w, ε = j) = pr(T ≤ v + w, V ≤ v, W ≤ w, ε = j). With a slight abuse of notation, we define the CIF of (T, V, W) as F_j(t, v, w) = pr(T ≤ t, V ≤ v, W ≤ w, ε = j). Following Huang and Louis (1998) and Huang and Wang (2005), we propose to treat (V, W, ε) as a vector of mark variables for the failure time T and estimate the joint distribution of T and the corresponding mark variables. Define the function $F_j^{uc}(t,v,w)=\text{pr}(\mathrm{\Delta }=1,Y\le t,V\le v,W\le w,\epsilon =j)$. Under independent censoring, it can be verified that $F_j^{uc}(dt,v,w)=F_j(dt,v,w)·S_C(t)$. Together with the equality S_Y(t) = S(t)S_C(t), we have the following representation

$$F_j(t,v,w)={\int }_0^{t}S(u)\frac{F_j^{uc}(du,v,w)}{S_Y(u)}.$$

Define the marked counting process for uncensored failure time N_ij(t, v, w) = Δ_iI(Y_i ≤ t, V_i ≤ v, W_i ≤ w, ε_i = j) so that N_ij(t, ∞, ∞) reduces to N_ij(t) defined in the previous section. Replacing $F_j^{uc}(u,v,w)$ and S_Y(u) with the corresponding empirical measures and replacing S(u) with its Kaplan-Meier estimator, we propose to estimate F_j(t, v, w) by

$${\widehat{F}}_j(t,v,w)={\int }_0^t\widehat{S}(u)\frac{n^{-1}{\sum }_{i=1}^n{N}_{ij}(du,v,w)}{n^{-1}{\sum }_{k=1}^n{R}_k(u)}$$ (5)

and the cumulative incidence function of (V, W) by F̂_j(v, w) = F̂_j(v + w, v, w). It is easy to see that F̂_j(t, ∞, ∞) reduces to the estimated CIF given by (2).

By the functional delta method and the asymptotic equivalence of S(t) and exp{−Λ(t)}, we can establish the asymptotically iid representation ${\widehat{F}}_j(t,v,w)-F_j(t,v,w)=n^{-1}{\sum }_{i=1}^n{\varphi }_{ij}(t,v,w)+o_p(n^{-1/2})$, where

$${\varphi }_{ij}(t,v,w)={\int }_0^t\frac{S(u)M_{ij}(du,v,w)-\{F_j(t,v,w)-F_j(u,v,w)\}{\sum }_{k=1}^J\{{dM}_{ik}(u)\}}{S_Y(u)}$$ (6)

and $M_{ij}(t,v,w)=N_{ij}(t,v,w)-{\int }_0^t{R}_i(u){\mathrm{\Lambda }}_j(du,v,w)$ with Λ_j(t, v, w) being the cause-specific cumulative hazard function given by ${\mathrm{\Lambda }}_j(t,v,w)={\int }_0^t{\lambda }_j(u,v,w)du$ with

$${\lambda }_j(u,v,w)=\underset{dt\to 0}{lim}\frac{1}{dt}\text{pr}\{T\in [u,u+dt],V\le v,W\le w,\epsilon =j\mid T\ge u\}.$$

Arguing as in Gray (1988), one can show that, for fixed v, w, M_i1(t, v, w), …, M_iJ(t, v, w) are orthogonal martingales. The function ϕ_ij(t, v, w) reduces to ϕ_ij(t) in (3) when (v, w) = (∞, ∞). Details of the proof of the weak convergence of n^1/2{F̂_j(t, v, w) − F_j(t, v, w)} can be found in Web Appendix.

Next, it is natural to estimate H_j(v, w) by

$${\widehat{H}}_j(v,w)={\widehat{F}}_j(v+w,v,w)/{\widehat{F}}_j(\eta ,\infty ,\infty )={\widehat{F}}_j(v+w,v,w)/{\widehat{F}}_j(\eta ).$$

Applying the functional delta method, for v + w ≤ η, we have

$$\begin{array}{l}{\widehat{H}}_j(v,w)-H_j(v,w)=\frac{{\widehat{F}}_j(v+w,v,w)-F_j(v+w,v,w)}{F_j(\eta )}-\frac{F_j(v+w,v,w)\{{\widehat{F}}_j(\eta )-F_j(\eta )\}}{F_j{(\eta )}^2}+o_p(n^{-1/2})\\ =n^{-1}\sum _{i=1}^n\left\{\frac{{\varphi }_{ij}(v+w,v,w)}{F_j(\eta )}-\frac{F_j(v+w,v,w){\varphi }_{ij}(\eta )}{F_j{(\eta )}^2}\right\}+o_p(n^{-1/2}).\end{array}$$ (7)

Thus, provided π_j > 0, the stochastic process n^1/2{Ĥ_j(v, w) − H_j(v, w)} converges in distribution of a zero-mean Gaussian process with variance-covariance function σ{(v₁, w₁), (v₂, w₂)}² = E[{ϕ_ij(v₁ + w₁, v₁, w₁)F_j(η)⁻¹ − F_j(v₁ + w₁, v₁, w₁)ϕ_ij(η)F_j(η)⁻²}{ϕ_ij(v₂ + w₂, v₂, w₂)F_j(η)⁻¹ − F_j(v₂ + w₂, v₂, w₂)ϕ_ij(η)F_j(η) ⁻²}] for v₁ + w₁ ≤ η and v₂ + w₂ ≤ η. Details of the proof can be found in Web Appendix.

To compare the joint distribution functions H_j(v, w) and H_k(v, w) of different failure types j ≠ k, we consider the supremum test sup_v+w≤η | Q^*(v, w) | based on the following class of processes

$$Q^{\ast }(v,w)=K^{\ast }(v,w)\{{\widehat{H}}_j(v,w)-{\widehat{H}}_k(v,w)\},$$

where K^*(v, w) is a prespecified weight function. The stochastic process Q^*(v, w) − K^*(v, w){H_j(v, w) − H_k(v, w)}, has the asymptotically i.i.d. representation

$$\begin{array}{l}{n}^{-1}\sum _{i=1}^n{K}^{\ast }(v,w)[\{{\varphi }_{ij}(v+w,v,w)F_j{(\eta )}^{-1}-F_j(v+w,v,w){\varphi }_{ij}(\eta )F_j{(\eta )}^{-2}\}\\ -\{{\varphi }_{ik}(v+w,v,w)F_k{(\eta )}^{-1}-F_k(v+w,v,w){\varphi }_{ik}(\eta )F_k{(\eta )}^{-2}\}]+o_p(n^{-1/2}).\end{array}$$

The approximate p-value can be obtained by applying the technique of permutation tests described in Section 2.

4. Nonparametric Association Measure for the Bivariate Gap Time With Competing Risks

In cancer research, it is of interest to evaluate whether the time from surgery to metastasis is associated with the residual lifetime after the initial diagnosis of metastasis. A popular nonparametric measure of the association between two random variables is Kendall’s tau statistic, defined as the probability of concordance among two pairs of survival times minus the probability of discordance. Estimation of Kendall’s tau with bivariate gap time data is not straightforward, because the second gap time is observed only when the first gap time is uncensored. Lakhal-Chaieb et al. (2010) proposed an inverse probability of censoring weighted estimator for Kendall’s tau with right-censored bivariate gap time data; however, their method applies only to bivariate gap time data without competing risks.

A cause-specific Kendall’s tau for failure type ε = j can be defined as

$${\tau }_j=\text{pr}(V_1>V_2,W_1>W_2\mid {\epsilon }_1=j,{\epsilon }_2=j)-\text{pr}(V_1>V_2,W_1<W_2\mid {\epsilon }_1=j,{\epsilon }_2=j)=4\times \text{pr}(V_1>V_2,W_1>W_2\mid {\epsilon }_1=j,{\epsilon }_2=j)-1.$$

It is easy to see that − 1 ≤ τ_j ≤ 1, where τ_j = 1 (−1) indicates perfect positive (negative) correlation between V and W and τ_j = 0 when V and W are independent among individuals with the jth competing event. In the pancreatic cancer study, we consider the association measure for j = 1, 2. Note that, in the absence of right censoring, pr(V₁ > V₂, W₁ > W₂, ε₁ = j, ε₂ = j) and pr(ε₁ = j, ε₂ = j) can be estimated by their empirical measures

$$\frac{1}{n(n-1)}\sum _{i=1}^n\sum _{i=1}^{n}I(V_i>V_k,W_i>W_k,{\epsilon }_i=j,{\epsilon }_k=j)$$

and

$$\frac{2}{n(n-1)}\sum _{i=1}^n\sum _{k=i+1}^{n}I({\epsilon }_i=j,{\epsilon }_k=j)=\frac{1}{n(n-1)}\left[{\left\{\sum _{i=1}^{n}I({\epsilon }_i=j)\right\}}^2-\sum _{i=1}^{n}I({\epsilon }_i=j)\right].$$

Thus cause-specific Kendall’s tau can be estimated by

$$\frac{4}{n_j(n_j-1)}\sum _{i=1}^n\sum _{k=1}^{n}I(V_i>V_k,W_i>W_k,{\epsilon }_i=j,{\epsilon }_k=j)-1$$

where $n_j={\sum }_{i=1}^{n}I({\epsilon }_i=j)$.

In the presence of right censoring, the type of failure is unknown for censored subjects and the probability pr(ε₁ = j, ε₂ = j) is not nonparametrically estimable if η is smaller than the maximum support of the failure time T = V + W. Thus we consider a modified Kendall’s tau measure that is estimable with observed data

$${\tau }_j^{\ast }=4\times \text{pr}(V_1>V_2,W_1>W_2\mid V_1+W_1\le \eta ,V_2+W_2\le \eta ,{\epsilon }_1=j,{\epsilon }_2=j)-1.$$

It is easy to see that ${\tau }_j^{\ast }$ takes values between −1 and 1, and ${\tau }_j^{\ast }=0$ when the conditional independence of V and W given V +W ≤ η holds among individuals with the jth competing event. Assuming that V and W are continuous random variables, by definition, we have

$$\begin{array}{l}\text{pr}(V_1>V_2,W_1>W_2\mid V_1+W_1\le \eta ,V_2+W_2\le \eta ,{\epsilon }_1=j,{\epsilon }_2=j)\\ =\int \int I(v_1>v_2,w_1>w_2)H_j({dv}_1,{dw}_1)H_j({dv}_2,{dw}_2)=\int \int H_j(v,w)H_j(dv,dw)\end{array}$$ (8)

A straightforward estimator of ${\tau }_j^{\ast }$ can be obtained by replacing H_j with Ĥ_j in (8), that is,

$${\widehat{\tau }}_j^{\ast }=4\int \int {\widehat{H}}_j(v^{-},w^{-}){\widehat{H}}_j(dv,dw)-1.$$

Define ψ_ij(v, w) = ϕ_ij(v + w, v, w)/F_j(η) − F_j(v + w, v, w)ϕ_ij(η)/F_j(η)² so that ${\widehat{H}}_j(v,w)-H_j(v,w)=n^{-1}{\sum }_{i=1}^n{\psi }_{ij}(v,w)+o_p(n^{-1/2})$. The strong consistency of ${\widehat{\tau }}_j^{\ast }$ for ${\tau }_j^{\ast }$ follows directly from the strong consistency of Ĥ_j for H_j. Moreover, applying the functional delta method, it follows from the weak convergence of n^1/2{Ĥ_j(v, w) − H_j(v, w)} that

$$\begin{array}{l}{n}^{1/2}({\widehat{\tau }}_j^{\ast }-{\tau }_j^{\ast })=4n^{1/2}\left\{\int \int {\widehat{H}}_j(v^{-},w^{-}){\widehat{H}}_j(dv,dw)-\int \int H_j(v,w)H_j(dv,dw)\right\}\\ =4\int \int n^{1/2}\left\{{\widehat{H}}_j(v^{-},w^{-})-H_j(v,w)\right\}{H}_j(dv,dw)-4\int \int H_j(v,w)n^{1/2}\left\{{\widehat{H}}_j(dv,dw)-H_j(dv,dw)\right\}+o_p(1)\\ =4n^{-1/2}\sum _{i=1}^n\left\{\int \int {\psi }_{ij}(v,w)H_j(dv,dw)-\int \int H_j(v,w){\psi }_{ij}(dv,dw)\right\}+o_p(1),\end{array}$$

which can be shown to converge weekly to the mean-zero normal random variable with variance-covariance matrix E[{∫ψ_ij(v, w)H_j(dv, dw) − ∫H_j(v, w) ψ_ij(dv, dw)}²].

The modified Kendall’s tau is constructed using ideas similar to the conditional Kendall’s tau for truncated and censored data. It is known that Kendall’s tau is not directly applicable in this situation. As an extension, a conditional Kendall’s tau has been widely used for tests of quasi-independence for survival data under truncation based on comparability of truncated data (Tsai, 1990 ; Martin and Betensky, 2005). In a similar manner, our modified Kendall’s tau tests quasi-independence in the estimable region defined by V + W ≤ η.

5. Numerical Studies

In this section, we conduct a serial of numerical studies to evaluate the proposed non-parametric estimators and hypothesis testing procedures. Two types of failure events (J = 2) are considered for the simulation studies. Given ε = j (j = 1, 2), we generate the bivariate gap time (V, W) from Clayton’s multivariate failure time distribution (Clayton, 1978; Oakes, 1989) with joint survivorship function

$$S^{\ast }(v,w\mid \epsilon =j)={\left\{S_{V,j}{(v)}^{1-{\theta }_j}+S_{W,j}{(w)}^{1-{\theta }_j}-1\right\}}^{\frac{1}{1-{\theta }_j}},$$

where

$$\begin{array}{lll}\hfill S_{V,j}(v)& =\hfill & \text{pr}(V>v\mid \epsilon =j)=exp(-v/{\lambda }_j),\hfill \\ \hfill S_{W,j}(w)& =\hfill & \text{pr}(W>w\mid \epsilon =j)=exp(-w/{\gamma }_j).\hfill \end{array}$$

Thus V and W each marginally follows an exponential distribution and the parameter θ_j (θ_j ≥ 1) determines the degree of association between the bivariate gap times V and W among individuals with failure type ε = j.

We consider three simulation scenarios. In Scenario I, we set θ₁ = θ₂ = 2, λ₁ = λ₂ = 2, and γ₁ = γ₂ = 1 so that the two types of failure events have identical underlying distributions. In Scenario II, we set θ₁ = 2, θ₂ = 9, λ₁ = λ₂ = 2 and γ₁ = γ₂ = 1, so that the two types of failure event have the same marginal distributions for V and W but different degrees of association between V and W. Finally, in Scenario III, we set θ₁ = 2, θ₂ = 9, λ₁ = 2, λ₂ = 4, γ₁ = 1 and γ₂ = 2, so that the two types of failure events have different distributional patterns of V and W as well as different degrees of association between V and W. For ε = 1, the true median survival is about 1 for all scenarios. For ε = 2, the true median survival is 1 for Scenarios I and II, and is 0.5 for Scenario III. The corresponding Kendall’s tau coefficient of concordance for the bivariate gap times are 0.33 and 0.80 when θ_j = 2 and 9, respectively. In all three scenarios, the prevalence rates of the the two competing events are set at π₁ = 0.6 for ε = 1 and π₂ = 0.4 for ε = 2. The censoring time, C, is simulated independently from an exponential random variable with mean 6. The censoring rates in the three scenarios are about 20%.

For all simulation studies, we generate 1000 datasets, each with 200 and 500 subjects. For each scenario, two different values of η = 3 and 5 are considered. When η = 3, P(T ≤ η | ε = 1) ≈ 088 in all three scenarios, and P(T ≤ η | ε = 2) = 0.89, 0.86, and 0.98 in Scenarios I~III. When η = 5, we have P(T ≤ η | ε = j) > 0.96, j = 1, 2, in all scenarios. Table 1 summarizes the empirical bias and empirical standard deviation for Ĝ_j(t) at time points t = 0.6, 1.4. The empirical bias and empirical standard deviation for Ĥ_j(v, w) at four selected grid points (v, w), where v and w take values 0.4 and 0.8, are reported in Table 2, and the estimated associations between V and W measured by modified Kendall’s tau are reported in Table 3.

Table 1.

Summary of the simulation results for conditional cumulative incidence functions. Bias and MCSD are the empirical bias (×1000) and the empirical standard deviation (×1000) of the 1000 estimated conditional cumulative incidence functions.

SCE	Size	η	t	ε = 1			ε = 2
				G1(t)	Bias	MCSD	G2(t)	Bias	MCSD
I	200	3.0	0.6	0.31	5	49	0.31	5	58
			1.4	0.69	4	51	0.69	5	60
		5.0	0.6	0.28	9	46	0.28	8	55
			1.4	0.63	13	51	0.63	13	60
	500	3.0	0.6	0.31	3	30	0.31	4	39
			1.4	0.69	2	32	0.69	4	41
		5.0	0.6	0.28	4	27	0.28	5	36
			1.4	0.63	5	32	0.63	7	41
II	200	3.0	0.6	0.31	3	50	0.38	3	62
			1.4	0.69	3	50	0.70	9	60
		5.0	0.6	0.28	6	47	0.34	9	59
			1.4	0.63	10	51	0.63	18	59
	500	3.0	0.6	0.31	1	31	0.38	3	40
			1.4	0.69	2	31	0.70	0	40
		5.0	0.6	0.28	2	29	0.34	5	37
			1.4	0.63	5	31	0.63	5	40
III	200	3.0	0.6	0.31	6	48	0.56	4	61
			1.4	0.69	9	49	0.86	1	45
		5.0	0.6	0.28	11	46	0.55	5	61
			1.4	0.63	22	50	0.85	4	46
	500	3.0	0.6	0.31	2	29	0.56	3	37
			1.4	0.69	2	32	0.86	1	28
		5.0	0.6	0.28	4	27	0.55	3	37
			1.4	0.63	8	32	0.85	2	29

Table 2.

Summary of the simulation results for conditional bivariate cumulative incidence functions. Bias and MCSD are the empirical bias (×1000) and the empirical standard deviation (×1000) of the 1000 estimated conditional bivariate cumulative incidence functions.

Scenario	n	η	v	w	ε = 1			ε = 2
					H1(v, w)	Bias	MCSD	H2(v, w)	Bias	MCSD
I	200	3.0	0.4	0.4	0.28	5	47	0.28	3	58
			0.4	0.8	0.44	7	52	0.44	3	64
			0.8	0.4	0.35	4	51	0.35	4	60
			0.8	0.8	0.58	5	53	0.58	5	63
		5.0	0.4	0.4	0.26	8	44	0.26	6	55
			0.4	0.8	0.40	12	50	0.40	8	61
			0.8	0.4	0.32	9	48	0.32	8	56
			0.8	0.8	0.53	12	51	0.53	12	61
	500	3.0	0.4	0.4	0.28	2	29	0.28	3	38
			0.4	0.8	0.44	2	33	0.44	4	42
			0.8	0.4	0.35	2	31	0.35	3	40
			0.8	0.8	0.58	2	33	0.58	5	41
		5.0	0.4	0.4	0.26	3	26	0.26	4	35
			0.4	0.8	0.40	3	31	0.40	5	39
			0.8	0.4	0.32	3	28	0.32	5	38
			0.8	0.8	0.53	4	32	0.53	7	40
II	200	3.0	0.4	0.4	0.28	3	48	0.38	3	62
			0.4	0.8	0.44	3	53	0.59	7	63
			0.8	0.4	0.35	4	52	0.38	3	62
			0.8	0.8	0.58	4	52	0.64	8	62
		5.0	0.4	0.4	0.26	6	44	0.34	8	59
			0.4	0.8	0.40	8	50	0.53	15	61
			0.8	0.4	0.32	7	49	0.34	8	59
			0.8	0.8	0.53	10	50	0.57	16	61
	500	3.0	0.4	0.4	0.28	1	30	0.38	2	39
			0.4	0.8	0.44	1	32	0.59	2	42
			0.8	0.4	0.35	1	33	0.38	2	39
			0.8	0.8	0.58	1	33	0.64	1	42
		5.0	0.4	0.4	0.26	2	28	0.34	4	36
			0.4	0.8	0.40	3	31	0.53	6	41
			0.8	0.4	0.32	2	31	0.34	4	36
			0.8	0.8	0.53	4	33	0.57	5	41
III	200	3.0	0.4	0.4	0.28	6	47	0.56	3	61
			0.4	0.8	0.44	10	54	0.80	2	52
			0.8	0.4	0.35	6	51	0.56	3	61
			0.8	0.8	0.58	10	53	0.81	2	51
		5.0	0.4	0.4	0.26	11	44	0.55	5	61
			0.4	0.8	0.40	18	52	0.78	5	53
			0.8	0.4	0.32	13	48	0.55	5	61
			0.8	0.8	0.53	21	53	0.80	4	52
	500	3.0	0.4	0.4	0.28	1	28	0.56	4	37
			0.4	0.8	0.44	2	33	0.80	2	32
			0.8	0.4	0.35	1	31	0.56	4	37
			0.8	0.8	0.58	1	33	0.81	2	31
		5.0	0.4	0.4	0.26	3	26	0.55	4	37
			0.4	0.8	0.40	5	32	0.78	2	32
			0.8	0.4	0.32	4	29	0.55	4	37
			0.8	0.8	0.53	6	32	0.80	2	31

Table 3.

Summary of the simulation results for modified Kendall’s tau. Bias and MCSD are the empirical bias (×1000) and empirical standard deviation (×1000) of the 1000 estimated modified Kendall’s tau.

Scenario	n	η	ε = 1				ε = 2
			${\tau }_1^{\ast }$	Bias	MCSD	CR	${\tau }_2^{\ast }$	Bias	MCSD	CR
I	200	3.0	0.20	−13	68	0.947	0.26	−21	83	0.943
		5.0	0.30	−26	68	0.923	0.31	−33	79	0.942
	500	3.0	0.20	−4	43	0.945	0.26	−8	53	0.925
		5.0	0.30	−8	42	0.939	0.31	−14	52	0.937
II	200	3.0	0.20	−16	70	0.925	0.77	−35	41	0.947
		5.0	0.30	−26	68	0.921	0.79	−38	36	0.918
	500	3.0	0.20	−7	42	0.947	0.77	−13	24	0.952
		5.0	0.30	−12	42	0.935	0.79	−15	22	0.939
III	200	3.0	0.20	−14	67	0.947	0.80	−27	35	0.934
		5.0	0.30	−33	65	0.920	0.80	−28	35	0.927
	500	3.0	0.20	−8	44	0.932	0.80	−11	20	0.942
		5.0	0.30	−17	43	0.922	0.80	−12	20	0.944

With a moderate sample size of 200, all the proposed nonparametric estimators are close to their estimands, as indicated by the small empirical bias over 1000 simulations. Note that, due to a lower prevalence rate of failure type ε = 2, the degree of uncertainty measured by the empirical standard error for ε = 2 is larger than that for ε = 1 even when the two competing events have identical distributions in Scenario I. The uncertainty in Ĝ_j(t) and Ĥ_j(v, w) does not systematically vary with η; instead, the variability of the estimators depends on the true conditional probabilities. We also report in Table 3 the performance of the bootstrap confidence intervals for modified Kendall’s tau. The 95% bootstrap confidence interval is obtained by applying the nonparametric bootstrap method that repeatedly samples subjects with replacement. For each simulated dataset, we repeat the resampling procedure 1000 times and use the 2.5th and 97.5th percentiles of the empirical distribution based on these 1000 estimated value of the modified Kendall’s tau as the 95% bootstrap confidence interval. The coverage probabilities of the bootstrap confidence intervals are very close to the nominal levels (95%), suggesting that the bootstrap method works reasonably well.

We also evaluate the performance of the proposed supremum test statistics for comparing the conditional cumulative incidence functions and the conditional bivariate distribution functions for different competing events. For each dataset, the p-values for testing the null hypotheses H₀ : G₁(t) = G₂(t) and H₀ : H₁(v, w) = H₂(v, w) are computed by the empirical probabilities that the values of the test statistics sup_t≤η | Q(t) | and sup_v+w≤η| Q^*(v, w) | with identity weight functions derived from the observed data exceed that derived from 1000 permuted samples.

At a significance level of 0.05, the average rejection rates in the 1000 simulated datasets are reported in Table 4. Under the null hypothesis (Scenario I), the estimated size of both tests are close to the nominal level. In Scenario II, where the bivariate gap time (V, W) for the two competing events have the same marginal distributions but different degrees of associations, hypothesis testing of H₀ : H₁(v, w) = H₂(v, w) achieves relatively big power with a large sample size, while the testing of H₀ : G₁(t) = G₂(t) requires a sample size larger than 500 to achieve appropriate power. On the other hand, sufficient power is achieved with a sample size of 500 for Scenario III, when both the underlying marginal distribution and the association for V and W are different for ε = 1 and 2. As expected, in Scenarios II and III, the power to reject the null hypothesis H₀ : H₁(v, w) = H₂(v, w) is higher compared to that for testing H₀ : G₁(t) = G₂(t). We also observe that the power does not systematically vary with η.

Table 4.

Estimated power for sumpremum tests, with a significance level of 0.05. Results are the percentages of rejected null hypotheses G₁(t) = G₂(t) and H₁(v, w) = H₂(v, w) among 1000 replications

Scenario	n	η	Rejection Rate
			G1(t) = G2(t)	H1(v, w) = H2(v, w)
I	200	3.00	0.063	0.057
		5.00	0.065	0.068
	500	3.00	0.050	0.055
		5.00	0.055	0.058
II	200	3.00	0.134	0.409
		5.00	0.110	0.347
	500	3.00	0.303	0.796
		5.00	0.229	0.694
III	200	3.00	0.925	0.998
		5.00	0.968	0.999
	500	3.00	1.000	1.000
		5.00	1.000	1.000

6. Data Application

Pancreatic cancer has a very poor prognosis and is highly resistant to chemotherapy and radiation therapy. Despite recent advances in cancer therapies, the prognosis for patients with pancreatic ductal adenocarcinoma (PDAC), the most common form of pancreatic malignancy, remains extremely poor. Radical surgical resection is considered to be the only curative option for PDAC. Unfortunately, less than 20% of pancreatic cancer patients have surgically resectable disease at the time of diagnosis, and the majority of resected pancreatic cancer recurs within 5 years of resection while over 60% develop metastatic recurrent diseases within 2 years. The clinical outcomes of patients with different recurrence patterns are very heterogeneous; moreover, different types of recurrences may benefit from different treatments. In the literature, however, only a few studies have investigated the patterns of recurrence following surgery. The prognosis of different patterns of recurrence has not been well studied.

We apply the proposed methods to the data from 209 consecutive patients who had surgical resection of pancreatic adenocarcinomas and had postoperative follow-up at the Johns Hopkins Hospital between January 9th, 1998 and June 13th, 2007. The median follow-up time is 16.0 months (range, 0.8–142.9), and the median overall survival for all 209 patients was 17.5 months (95% CI, 14.9–19.3). As of last follow-up date, 174 patients had metastatic recurrent diseases; among them, 163 died after disease recurrence. Based on clinical observation, the study investigators hypothesized that patients with metastasis limiting to lung only had better overall survival and longer residual lifetime after the initial diagnosis of metastasis, and that the two gap times are positively correlated within each recurrence pattern. Specifically, three failure event types are of interest in our data analysis: death with metastasis limited to lung only (ε = 1); death with metastasis that involves any other sites, such as liver, peritoneum and local site (ε = 2); death without disease recurrence (ε = 3). Among the 190 observed deaths, 25 had metastasis limited to lung, 138 had metastasis in other site, and 27 died without recurrence. We set η = 120 (months) because “very long-term survivors” (VLTS) of PDAC (defined as patients with ≥ 10-year survival following resection) are quite uncommon. The estimated survival probability at months 120 is close to 0, with Ŝ(120) = 0.04, in our retrospective cohort study.

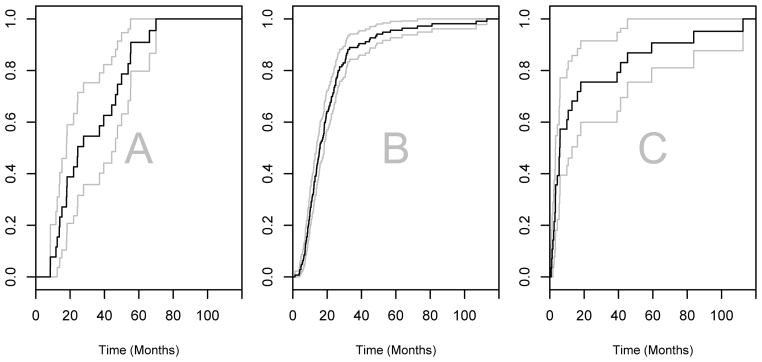
Figures 1 and 2 show the estimated CIF and the estimated CCIF for different competing events together with the corresponding pointwise 95% confidence intervals, where all CIs reported hereafter are based on 2,000 bootstrap samples. It is easy to see that the CIF for ε = 2 is significantly higher than that for the other two competing events because of a higher proportion of individuals with metastasis at other sites. Hence the comparison of CIFs does not shed light on the potential differences in the prognosis of patients with different recurrence patterns. The estimated conditional median overall survival is 25.5 months (95% CI, 17.7–45.3) for deaths with metastasis only in lung, 15.6 months (95% CI, 13.7–18.2) for deaths with metastasis at other sites, and 5.6 months (95% CI, 3.0–12.5) for deaths without recurrent disease. The conditional 5-year cumulate incidence rate is 0.91 (95% CI, 0.80–1.0) for deaths with recurrence limited to lung, 0.96 (95% CI, 0.93–0.99) for deaths with recurrence involving any other sites, and 0.91 (95% CI, 0.80–1.00) for deaths without recurrent disease.

Figure 1.

The cumulative incidence functions (CIF) for death with metastasis limited to lung only (ε = 1, Panel A), death with metastasis in other sites (ε = 2, Panel B), and death without disease recurrence (ε = 3, Panel C). The gray lines in Panels A–C represent the pointwise 95% confidence interval.

Figure 2.

The conditional cumulative incidence functions (CCIF) for death with metastasis limited to lung only (ε = 1, Panel A), death with metastasis in other sites (ε = 2, Panel B), and death without disease recurrence (ε = 3, Panel C). The gray lines in Panels A–C represent the pointwise 95% confidence interval.

Based on 2000 permutations, the overall hypothesis testing for H₀ : G₁(t) = G₂(t) = G₃(t), that is, the conditional cumulative incidence functions for the three competing events are identical, is significant with p < 0.001. Pairwise comparisons are further conducted. Specifically, the p-value for testing the null hypothesis H₀ : G₁(t) = G₂(t) is 0.01. The p-values for testing the null hypotheses H₀ : G₁(t) = G₃(t) and H₀ : G₂(t) = G₃(t) are < 0.001. We conclude that there exists significant differences in the conditional cumulative incidence functions between deaths with metastasis only in lung, deaths with metastasis in any other sites, and deaths without recurrence. Additionally, for bivariate gap time analysis, we test the null hypothesis H₀ : H₁(v, w) = H₂(v, w), that is, the the two competing events ε = 1, 2 have identical conditional bivariate cumulative incidence functions. Based on 2000 permutations, the result of the supremum test shows that the difference between H₁(v, w) and H₂(v, w) is significant with p = 0.003.

We also apply the proposed estimator for the conditional bivariate distribution to investigate the risk of death after metastasis. Specifically, for competing events ε = 1, 2, we estimate the conditional probabilities pr(W ≤ 12 | V ≤ 12, V + W ≤ 120, ε = j) and pr(W ≤ 12 | 12 < V ≤ 60, V + W ≤ 120, ε = j); that is, among patients whose survival time is shorter than 10 years after surgery, the probability that a patient will die within 12 months after the diagnosis of metastasis conditioning on that the metastasis occurred within 12 months or between 12 and 60 months after surgery. For patients with metastasis in lung only (ε = 1), the probabilities are 0.69 (95% CI, 0.41–0.92) and 0.48 (95% CI, 0.20–0.79), respectively. For patients with metastasis at other sites (ε = 2), the probabilities are 0.89 (95% CI, 0.83–0.95) and 0.74 (95% CI, 0.61–0.86), respectively. The results suggest that patients with early onset of metastatic disease tend to have worse prognosis, and that metastasis in lung only is associated with a better 1-year survival after the initial diagnosis of metastasis.

For competing events ε = 1, 2, we summarize the association between the time from surgery to the initial diagnosis of metastasis and the residual lifetime after recurrence using modified Kendall’s tau. The value of modified Kendall’s tau is estimated to be 0.03 (95% bootstrap CI, −0.31–0.28) for death after recurrence limited to lung only, and 0.09 (95% CI,−0.05–0.20) for death after recurrence involving any other sites. The two association measures are not significantly different from 0, indicating that the time from surgery to metastasis is not significantly correlated with the residual lifetime after the diagnosis of recurrent metastatic disease for both competing events. Note that modified Kendall’s tau measures the overall association between V and W in the region V + W ≤ η, hence it may not coincide with the the result of subgroup comparisons (e.g. V ≤ 12 vs. 12 < V ≤ 60, as discussed before).

We repeat the same analyses with a different value of η = 60 (months), as 5-year survival of pancreatic cancer after pancreatectomy is of major interest to medical oncologists. The hypothesis testing yields the same conclusions, with p < 0.001 for the overall null hypohtesis H₀ : G₁(t) = G₂(t) = G₃(t), and p = 0.02, p < 0.001, and p < 0.001 for the pairwise comparisons of H₀ : G₁(t) = G₂(t), H₀ : G₁(t) = G₃(t), and H₀ : G₂(t) = G₃(t), respectively. The hypothesis testing for H₀ : H₁(v, w) = H₂(v, w) is also significant with p = 0.008. The value of modified Kendall’s tau is estimated to be −0.06 (95% CI, −0.39–0.29) for death after recurrence limited to lung only, and 0.08 (95% CI, −0.05–0.19) for death after recurrence involving any other sites. The findings are similar to those obtained by setting η = 120.

As pointed out by a reviewer, in general the conditional cumulative incidence functions, conditioning on the failure type, may not be suitable for the purpose of prediction because failure type is known at the time when the event occurs (Andersen and Keiding, 2012). However, the CCIF might be useful in our data example, because disease recurrence is in fact an intermediate event before death. The result of the study will have the potential in helping understand the biology of recurrent disease and may help guide follow-up and therapy for recurrent disease to improve overall survival. This study will also highlight the need and the value to identify tumor characteristics and biomarkers that bestow favorable prognosis of lung recurrence.

7. Remarks

This research aims to provide statistically appropriate methods to study overall survival in cancer patients with different recurrence patterns. In our experience, many medical and statistical practitioners fail to recognize that disease recurrence pattern is stochastically defined and that the recurrence pattern may not be observed before lost to follow-up. A common mistake is to group subjects according to their observed recurrence patterns. In this case, patients with recurrent disease can be misclassified as no recurrence if they are censored before disease recurrence. Moreover, analyses of overall survival in patients with known recurrence patterns using Kaplan-Meier estimators and log-rank tests are biased, because these patients tend to progress faster.

In this article, we consider nonparametric estimation of the conditional cumulative incidence function and the conditional bivariate cumulative incidence function and propose a modified Kendall’s tau measure for quantifying the association between the two successive gap times in the competing risks setting. It is important to point out that the second gap time is subject to induced informative censoring, as gap times of the same subject are usually correlated. As the result, conventional methods for bivariate survival time data can not be applied directly. Interestingly, the proposed nonparametric estimators and association measures can also be viewed as inverse probability censoring weighted (IPCW) estimators, where the weights used in correcting the bias in the uncensored failure events are inversely proportional to the probability of being uncensored and occurring before η. Regression analyses can be developed along the same line and will be investigated elsewhere.