Skip to main content
PMC home page
Clinical Orthopaedics and Related Research logoLink to Clinical Orthopaedics and Related Research
. 2016 Jun 22;474(10):2246–2253. doi: 10.1007/s11999-016-4930-0

Is Model-based Radiostereometric Analysis Suitable for Clinical Trials of a Cementless Tapered Wedge Femoral Stem?

Sanaz Nazari-Farsani 1, Sami Finnilä 1, Niko Moritz 1, Kimmo Mattila 2, Jessica J Alm 1, Hannu T Aro 1,✉
PMCID: PMC5014820  PMID: 27334320

Abstract

Background

In clinical trials of THA, model-based radiostereometric analysis (RSA) techniques may be less precise than conventional marker-based RSA for measurement of femoral stem rotation. We verified the accuracy and clinical precision of RSA based on computer-aided design models of a cementless tapered wedge femoral stem.

Questions

We asked: (1) Is the accuracy of model-based RSA comparable to that of marker-based RSA? (2) What is the clinical precision of model-based RSA?

Methods

Model-based RSA was performed using combined three-dimensional computer-aided design models of the stem and head provided by the implant manufacturer. The accuracy of model-based RSA was compared with that of marker-based RSA in a phantom model using micromanipulators for controlled translation in three axes (x, y, z) and rotation around the y axis. The clinical precision of model-based RSA was evaluated by double examinations of patients who had arthroplasties (n = 24) in an ongoing trial. The clinical precision was defined as being at an acceptable level if the number of patients needed for a randomized trial would not differ from a trial done with conventional marker-based RSA (15–25 patients per group).

Results

The accuracy of model-based RSA was 0.03 mm for subsidence (translation along the y axis) (95% CI for the difference between RSA measurements and actual displacement measured with micrometers, −0.03–0.00) and 0.39° for rotation around the y axis (95% CI, −0.41 to −0.06). The accuracy of marker-based RSA was 0.06 mm for subsidence (95% CI, −0.04–0.01; p = 0.728 compared with model-based RSA) and 0.18° for the y axis rotation (95% CI, −0.23 to −0.07; p = 0.358). The clinical precision of model-based RSA was 0.14 mm for subsidence (95% CI for the difference between double examinations, −0.02–0.04) and 0.79° for the y axis rotation (95% CI, −0.16–0.18).

Conclusions

The accuracy of model-based RSA for measurement of the y axis rotation was not quite as high as that of marker-based RSA, but its clinical precision is at an acceptable level.

Clinical relevance

Model-based RSA may be suitable for clinical trials of cementless tapered wedge femoral stem designs.

Introduction

Radiostereometric analysis (RSA) is a unique method for assessment of translational and rotational micromovement of implant components in randomized clinical trials of THAs [7, 12, 18]. Because of its high accuracy and precision, trials of RSA are powered with relatively few subjects (approximately 15–25 patients) [24]. However, standard RSA techniques have the major disadvantage of requiring attachment of at least three tantalum markers on the implant surface (marker-based RSA), requiring expensive manufacture of implants with approved modifications. Model-based RSA techniques were introduced to solve this problem [11].

Model-based RSA techniques use surface models of implant components based on computer-aided design (CAD) models [10, 11, 20], reverse-engineered implant models [11, 23], or elementary geometric shapes [10, 14, 20]. However, a new issue of reduced precision has emerged. The large variation in contemporary cementless femoral component designs [13] has proved to be a challenge because the shape of a stem can largely dictate the precision of model-based RSA [20]. Differences between actual projection of the implant and the virtual contour of three-dimensional surface models also might produce methodologic inaccuracies [20, 23]. As a consequence, model-based RSA has shown larger SDs than conventional marker-based RSA, especially with measurement of stem rotation [10, 14, 23]. This lower precision has been partly solved by adding the surface model of the femoral head in the stem model [20]. Owing to these technical issues, a validation experiment of accuracy and precision is recommended before starting a model-based RSA trial [10, 20, 23]. Accuracy is related to measurement errors and is defined as the closeness of agreement between the test result with RSA imaging and the direct measurement of implant position using a highly accurate measurement tool, which has a resolution substantially better than RSA [21]. Validation of accuracy requires the use of a phantom model in which accurate translations and rotations can be controlled by means of micromanipulators [4, 16, 19, 22]. Validation studies of model-based RSA have focused on measuring “the accuracy of zero motion” in phantom models [10, 20], when there is no controlled micromotion of the implant, but the whole phantom is subjected to repeated RSA imaging in different positions. Precision is synonymous with repeatability [24]. The clinical precision of RSA is assessed by double examinations of trial patients.

Tapered-wedge femoral stems have become popular owing to their clinical results [5, 15], and one of these was selected to evaluate the success of cementless THA in our randomized clinical trial of postmenopausal women with osteoporosis (ClinicalTrials.gov NCT01926158). Before starting the RSA trial, we decided to assess the accuracy and clinical precision of model-based RSA for the selected tapered wedge femoral stem (Accolade® II, Stryker® Orthopaedics, Mahwah, NJ, USA) using the advantages of state-of-the-art RSA technology (combined stem–head models) and access to high-quality CADs of the stem provided by the implant manufacturer.

Therefore, (1) we determined the accuracy of model-based RSA for the selected femoral stem in a phantom study and compared the results with those of the gold standard (marker-based RSA), and (2) evaluated the clinical precision of model-based RSA in trial subjects.

Materials and Methods

This study was designed to verify the relevance of model-based RSA for measurement of translational and rotational migration of a cementless tapered wedge femoral stem. Before starting the trial, we followed recommendations [10, 20, 23] and performed a phantom experiment to validate the accuracy of model-based RSA. In the phantom experiment (Fig. 1), the accuracy of model-based RSA was compared directly with that of standard marker-based RSA. Subsequently, clinical precision of model-based RSA was evaluated in trial subjects.

Fig. 1A–C.

Fig. 1A–C

Open in a new tab

(A) The original phantom model consisted of a total hip prosthesis and a plastic model of the human proximal femur with six tantalum RSA bone-markers. (B) To achieve unrestricted motion of the stem, the femur model was replaced by a plastic tube with tantalum markers (open circles). Only the plastic tube model was applied in the current phantom study. For marker-based RSA, three implant markers (arrows) were attached by plastic studs in a configuration similar to that in clinical RSA-marked stems. (C) The implant construct was rigidly fixed to the base plate, forming the nonmovable portion of the phantom. The plastic femur/tube was distally attached to an x, y, z translation stage and a y rotation stage with micrometers (arrows) for highly controlled simulation of stem migration in relation to the surrounding bone.

Phantom Study

The physical phantom model replicated an RSA-marked cementless THA (Fig. 1A). The model had no simulated soft tissue envelope (such as immersion in simulated physiologic fluid) owing to the limited influence on accuracy [22]. The phantom consisted of a plastic model of the right human proximal femur (model 2021; Sawbone AG, Karlihof, Switzerland) with an inserted femoral stem component (Accolade® II, size 6 with 127° neck angle; Stryker®), a metallic head (LFITTM anatomic cobalt-chrome femoral head, size 36 mm; Stryker®), and an acetabular component (titanium cup with polyethylene insert; Stryker®), placed in the proper anatomic position and fixed rigidly to a base plate. Six tantalum beads with a diameter of 1 mm (RSA BioMedical Innovations AB, Umeå, Sweden) were attached to the greater and lesser trochanters of the plastic bone (Fig. 1A). The femoral stem had three tantalum 1 mm diameter RSA markers attached by plastic studs: one in the shoulder, one in the collar, and one in the distal tip (Fig. 1B). This distribution of the implant markers simulated the typical marker configuration in clinical RSA trials. The plastic femur was attached distally to a high-precision x, y, z translation stage (M-460A-XYZ, Newport Corporation, Irvine, CA, USA) and a high-precision rotation stage (M-UTR80, Newport Corporation) instrumented with three SM-13 Vernier Micrometers (Newport Corporation). According to the manufacturer, the micrometers were accurate to 1 µm for translation with an angular deviation less than 0.009° and accurate to 1/60° for rotation with a wobble of ± 0.003°. The implant construct and the translation stage were rigidly fixed to the base plate. The implant construct formed the nonmovable portion of the phantom while the plastic femur was the moving part. Because contact-free relative motion of the femoral stem and the plastic femur was difficult to secure, the plastic femur was replaced by an 80-mm diameter transparent plastic tube (Fig. 1B). The positions of the RSA markers in the proximal part of the tube were kept as close as possible to the positions of the markers in the plastic femur model. This experimental setup (Fig. 1C) eventually was used in the whole phantom study and the data of the plastic femur model were not applied. The plastic tube model allowed simulation of relative migration of the stem in a highly controlled manner in relation to the surrounding bone along the three axes (x, y, z) of the linear movements and around the longitudinal axis (y) of the angular movement. The inserted markers defined distinct rigid body segments (femoral stem, simulated proximal femur). According to the definition described by Karrholm et al. [12], migration of the femoral stem was considered to be the relative displacement of rigid body segments between the femoral stem and the simulated bone.

Clinical Trial

The clinical precision of model-based RSA was determined at the planned 3-month interim analysis of the first 24 trial patients (mean age ± SD, 68.3 ± 5.4 years; BMI ± SD, 26.8 ± 3.7 kg/m2).

RSA Imaging

Image analyses were performed according to the RSA guidelines [24]. A uniplanar RSA arrangement was used, with one ceiling-mounted radiograph unit (Philips Optimus 50; Philips Medical Systems DMC GmbH, Hamburg, Germany) and one portable radiograph unit (Siemens Mobilett Plus; Siemens-Elema AB, Solna, Sweden). A uniplanar calibration cage (Cage 43; RSA BioMedical Innovations AB) was placed under the examination table. The radiograph tubes were positioned to make the radiograph beams cross each other at a 40° angle at the site of the hip implant. The film–focus distance was set at 165 cm. The radiograph tubes were operated simultaneously to obtain paired images (stereoradiographs). During repeated RSA imaging of the phantom, paired images were taken at various settings simulating different amounts of stem migration in terms of translations along three axes (x, y, z) and rotations around the y axis. This was achieved one axis at a time by turning one of the micrometers to a predefined value while the others were set to zero. First, two sets of image pairs were taken with all micrometers set to zero, to serve as the baseline measurements. To determine accuracy in the measurements of translation, the image pairs were taken at 25-µm, 50-µm, 150-µm, 1-mm, and 6-mm translations along each axis. To determine the accuracy in measurements of rotation around the longitudinal y axis, the image pairs were taken at 0.5°, 1°, 2°, 5°, and 10° right-handed rotations (simulated retroversion of the stem). In total, 42 image pairs were obtained from the phantom for comparative model-based and marker-based RSA.

Model-based RSA was performed using a combination of three-dimensional CAD models of the stem and the head, as described [20]. The combined stem–head models increase the precision of model-based RSA for rotation about the longitudinal axis [20]. The CAD models were provided by the implant manufacturer (Stryker Europe). These models were converted to the model-based format (Leiden Biomechanics and Imaging Group, Leiden University Medical Center, Leiden, The Netherlands). Model-based RSA measurements were performed using MBRSA software (Version 3.34; Medis Specials BV, Leiden, The Netherlands). With marker-based RSA the images were analyzed with the marker-mode of the MBRSA software application. As a reference, the images also were analyzed using UmRSA® software (Version 6.0; RSA BioMedical Innovations AB). In both measurements of MBRSA and UmRSA®, the center of the femoral head was used as an additional marker to obtain better scatter of the stem segment and to increase reliability of the measurements. The setup for the clinical RSA imaging of trial patients, originally standardized in previous phantom [17] and clinical [1] studies, did not differ from that of the phantom study.

The adequate spatial distribution of bone RSA markers was assessed using the condition number [24]. RSA software calculates the condition number based on the distance between each marker and an arbitrary straight line passing through the cluster of markers in the rigid body. A high condition number indicates that markers are spaced close to a line, whereas low condition numbers (≤ 100–150) indicate appropriate wide marker distribution for reliable determination of implant migration. The condition number was low in the clinical trial (median, 26; range, 23–98). The condition number of bone markers in the phantom model varied between nine and 38, depending on the software used. The condition number of implant markers in the phantom model was 35. The in vivo stability of bone markers, assessed by calculating the mean error of rigid body fitting [24], was less than the recommended upper limit of 0.35 in the clinical trial (median, 0.08; range, 0.01–0.32).

Statistical Analyses

The accuracy and precision were calculated according to the recommendations [6, 21]. The accuracy was calculated as t × SD/√2, where t is the critical value of the two-tailed 95% t-distribution with eight degrees of freedom and SD is the standard deviation of the differences between the values measured by RSA and the actual displacements induced by micrometers (Table 1). As recommended by Bland and Altman [3], direct comparison of the established technique (marker-based RSA) and model-based RSA was performed using Bland–Altman plots with 95% limits of agreement (mean difference ± 1.96 × SD) (Fig. 2). This approach was selected because correlation analyses are not recommended for comparison of two methods [9]. Bland–Altman plots assess the degree of agreement between two quantitative measurements. The difference between the two paired measurements is plotted against the mean of the two measurements. The graphic approach shows any systematic difference between the two measurements (the bias) and the range of agreement. Bland–Altman plots do not directly show if agreement between the two methods is sufficient. The normal distribution of accuracy data was verified and the statistical comparison of the two methods for the two main endpoints (the measurements of y axis translation and y axis rotation) was performed using a t-test for independent samples. Clinical precision of model-based RSA was determined from the results of double examinations of trial patients (Table 2). The clinical precision was calculated as t × SD, where t is the critical value of the two-tailed 95% t-distribution with 23 degrees of freedom and SD is the standard deviation of the differences between the paired measurements of double examinations. The clinical precision of model-based RSA was defined as being at an acceptable level if a power analysis indicates the number of patients needed for a randomized trial will not differ from a trial done with conventional marker-based RSA. Randomized trials of marker-based RSA have required 15–25 patients per group [24]. Statistical analyses were performed using IBM SPSS Statistics Version 23.0 (IBM Corporation, Armonk, NY, USA).

Table 1.

Accuracy of model-based and marker-based RSA (phantom model)

RSA method Translation (mm) Translation (mm) Translation (mm) Rotation (degrees)
x axis y axis z axis y axis
Model-based RSA
 Mean difference −0.01 −0.01 0.02 −0.23
 95% CI (−0.02 to −0.01) (−0.03–0.00) (−0.04–0.07) (−0.41 to −0.06)
 Accuracy 0.02 0.03 0.13 0.39
Marker-based RSA
 Mean difference 0.00 −0.02 −0.02 −0.15
 95% CI (−0.01–0.01) (−0.04–0.01) (−0.03 to −0.01) (−0.23 to −0.07)
 Accuracy 0.02 0.06 0.03 0.18
Marker-based RSA (UmRSA®)
 Mean difference −0.01 −0.01 −0.02 −0.04
 95% CI (−0.02–0.00) (−0.01–0.00) (−0.04–0.00) (−0.17–0.10)
 Accuracy 0.02 0.01 0.04 0.30
Open in a new tab

Mean difference = paired difference between micrometer-measured actual displacements and RSA-measured values; accuracy = t × SD/√2.

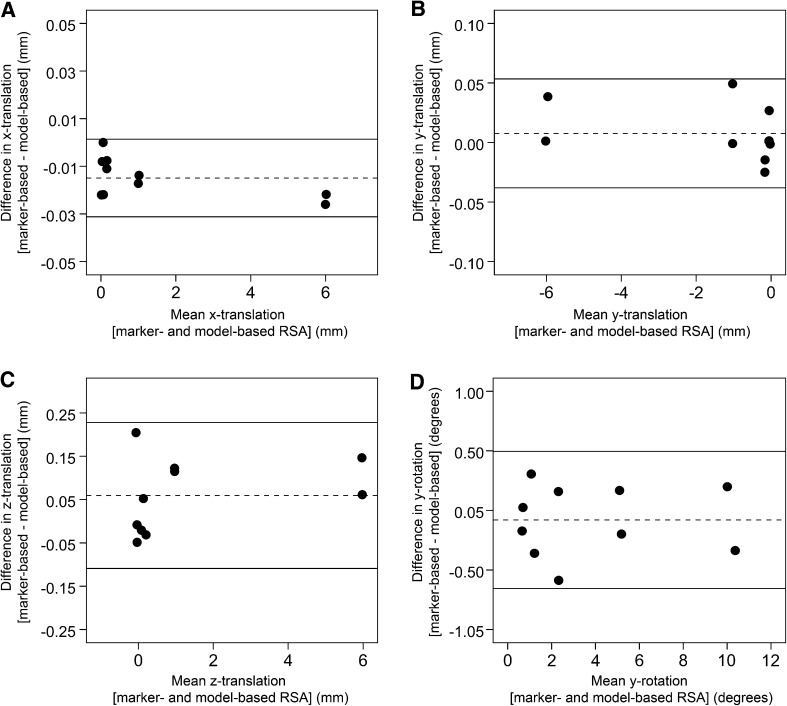
Fig. 2A–D.

Fig. 2A–D

Open in a new tab

Bland–Altman plots comparing model-based and marker-based RSA (MBRSA software) for measurement of micromanipulator-induced stem translation and rotation in the phantom model are shown. The difference between the model-based RSA and marker-based RSA measurements (y axis) was calculated for each increment of micromovement and plotted against the mean of the two measurements (x axis). The two methods showed good global agreement for measurement of (A) x axis translation, (B) y axis translation, (C) z axis translation, and (D) y axis rotation. The dashed line represents the mean of the differences, which was close to zero in each comparison, suggesting that model-based RSA measurements were not biased. The two solid lines represent the 95% limits of agreement.

Table 2.

Clinical precision of model-based RSA in 24 trial patients

RSA method Translation (mm) Translation (mm) Translation (mm) Rotation (degrees) Rotation (degrees) Rotation (degrees)
x axis y axis z axis x axis y axis z axis
Model-based RSA
 Mean difference −0.01 0.01 −0.03 0.01 0.01 −0.01
 95% CI −0.04–0.02 −0.02–0.04 −0.07–0.013 −0.08–0.10 −0.16–0.18 −0.09–0.08
 Clinical precision 0.13 0.14 0.47 0.41 0.79 0.39
Open in a new tab

Mean difference = paired difference between the measurements of double examinations; 95% CI = for the mean difference; clinical precision = t × SD.

Results

The accuracy of model-based and marker-based RSA was high and, based on Bland-Altman plots (Fig. 2), the results of the two methods showed high agreement.

The accuracy of model-based RSA was 0.03 mm for measurement of subsidence (translation along the y axis) (95% CI for the difference between RSA measurements and actual displacement measured with micrometers, −0.03 to 0.00), and accuracy for measurement of rotation around the y axis was 0.39° (95% CI, −0.41 to −0.06) (Table 1). Accuracy of the marker-based RSA was 0.06 mm for measurement of subsidence (translation along the y axis) (95% CI, −0.04 to 0.01; p = 0.728 compared with model-based RSA) and 0.18° for rotation around the y axis (95% CI, −0.23 to −0.07; p = 0.358). The marker-based modes of MBRSA and UmRSA® software showed similar accuracy.

Double examinations of trial patients (Table 2) confirmed a relevant clinical precision of model-based RSA. Clinical precision was 0.14 mm for the measurement of subsidence (translation along the y axis) (95% CI for the paired difference of double examinations, −0.02 to 0.04) and 0.79° for rotation around the y axis (95% CI, −0.16 to 0.18).

Based on the least precise axis (rotation around the y axis) and assuming a difference of 0.4° in stem rotation between two groups, the calculated number of patients required for a randomized model-based RSA trial will be 13 per group, which is at the acceptable level.

Discussion

In clinical studies of cementless THAs, applications of model-based RSA may have low precision owing to unfavorable surface geometries of the femoral stems, such as tapered round shapes [13], and inaccuracies of the available CAD models [10, 11]. Therefore, we followed the international guidelines for standardization of RSA research [24], which recommend validation of RSA accuracy in a phantom model and documentation of the clinical precision. We improved precision of measurement of stem rotation by using a combined stem–head model [20]. We also gained access to the high-quality CADs of the implant manufacturer to overcome possible problems related to the quality of CAD models [10, 23]. Attention also was paid to numerous factors that dictate the intralaboratory precision of any RSA [22], including a standardized radiographic setup and accurate patient positioning [8, 17], and the number and configuration of bone markers [16, 22]. This approach allowed us to address our research questions regarding the accuracy and clinical precision of model-based RSA for the selected femoral stem design under optimal conditions.

We acknowledge limitations to our study. First, we did not perform the phantom study using different configurations of bone markers. Such an experiment could confirm our assumption that precision of model-based RSA is sensitive to correct configuration of bone markers, and high condition number is a risk factor for inaccuracies. We also did not analyze the effect of simulated soft tissues on RSA accuracy. Second, the phantom model included analysis of rotation only around the y axis, because simulated stem rotations around the x axis (rotation forward) and z axis (varus–valgus) are technically challenging. However, our clinical precision measurements included measurement of rotation around all three axes, and, as in previous studies [10, 14, 20, 23], the results confirmed that the y axis is the least precise in model-based and marker-based RSA. Thus, the focus of RSA research should be on the y axis. Third, we did not perform a clinical comparison of model-based and marker-based RSA for the Accolade® II stem. The manufacturing and regulatory processes for an RSA-marked Accolade® II stem would have been unrealistic just for the needs of the planned trial. Fourth, the results of our model-based RSA are relevant only for the stem design under investigation and are not directly applicable to different designs of cementless femoral stems. However, it is likely that adherence of the principles of our protocol makes it possible to successfully apply model-based RSA for various designs of cementless tapered femoral stems. Finally, the quality of the CAD models provided by the manufacturer was not tested against high-resolution reverse-engineered models of the stems, because the comparison would have required purchase of a whole spectrum of stems of different sizes and different neck angles and offsets for scanning the reverse-engineered surface models. In addition, we did not analyze the results using the elementary geometric shape mode of the MBRSA software, which is one of the model-based RSA techniques. Although elementary geometric shape-based RSA seems to be a good alternative to marker-based RSA for certain stem designs [11], in a clinical trial of a tapered wedge femoral stem [14] the method showed low precision in measuring stem rotation.

Model-based RSA was highly accurate for measurement of translation (20–130 µm), corresponding to the level of accuracy (10–60 µm) observed in our marker-based RSA and in previous phantom model studies of marker-based RSA [4, 19, 23]. The Bland–Altman plots showed the closeness of the model-based and marker-based measurements. Accuracy of model-based RSA for measurement of rotation around the longitudinal y axis was relatively high (0.39°) and corresponded to the phantom RSA results obtained with low- and high-resolution reverse-engineered models [23], but still was lower than the level (0.18°–0.30°) achieved with marker-based RSA. However, it is evident that the difference in rotational accuracy between model-based and marker-based RSA was not seen in the clinical precision measurement of stem rotation.

Determination of clinical RSA precision is mandatory before a trial [24]. Double examinations must be made for each patient in marker-based and model-based RSA trials, because each patient has a unique bone marker configuration. Model-based RSA had similar clinical precision with measurement of translation along three axes (variation, 0.13–0.47 mm) than in clinical trials of different RSA-marked femoral stems, including the Taperloc® stem (Biomet, Warsaw, IN, USA) (0.11–0.33 mm) [14], the VerSys® stem (Zimmer Inc, Warsaw, IN, USA) (0.10–0.19 mm) [2], and the Furlong® stem (JRI Ltd, London, UK) (0.08–0.12 mm) [25]. Model-based RSA also had an acceptable clinical precision (0.79°) for measurement of rotation around the y axis, which was similar to results of recent clinical trials of RSA-marked Taperloc® (0.62°) [14], VerSys® (0.98°) [2], and Furlong® stems (0.30°) [25]. Our successful clinical application of model-based RSA probably reflects sufficient quality of the applied CAD models and optimal distribution of RSA bone markers. The median condition number was 26, which is well below the recommended upper limit of 100 or 150 for hip prostheses.

Our results support the concept [10] that model-based RSA may be suitable for clinical trials of cementless tapered wedge femoral stems. For other stem designs, the key is to verify the quality of stem–head CAD models in a phantom model. It is important to have proper configuration of bone markers to ensure a low condition number and high precision. At best, the clinical precision of model-based RSA can match that of marker-based RSA, and therefore the number of patients needed for a randomized trial will not differ from a trial done with conventional marker-based RSA.

Acknowledgments

We thank radiologic technicians Johanna Rinne and Larissa Lamberg (Department of Diagnostic Radiology, Turku University Hospital) for help with RSA imaging of the patients and the Leiden Biomechanics and Imaging Group for conversion of the CAD models to MBRSA format.

Footnotes

The institution of the authors (SNF, SF, NM, KM, JJA, HTA) has received funding from Academy of Finland, Amgen Inc, and the Government of Finland.

Each author certifies that he or she, or a member of his or her immediate family, has no funding or commercial associations (eg, consultancies, stock ownership, equity interest, patent/licensing arrangements, etc) that might pose a conflict of interest in connection with the submitted article.

All ICMJE Conflict of Interest Forms for authors and Clinical Orthopaedics and Related Research ® editors and board members are on file with the publication and can be viewed on request.

Each author certifies that his or her institution approved or waived approval for the reporting of this investigation and that all investigations were conducted in conformity with ethical principles of research.

This work was performed at Turku University Hospital and University of Turku (Turku, Finland).

A comment to this article is available at http://dx.doi.org/10.1007/s11999-016-5016-8.

References

  • 1.Aro HT, Alm JJ, Moritz N, Mäkinen TJ, Lankinen P. Low BMD affects initial stability and delays stem osseointegration in cementless total hip arthroplasty in women: a 2-year RSA study of 39 patients. Acta Orthop. 2012;83:107–114. doi: 10.3109/17453674.2012.678798. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Baad-Hansen T, Kold S, Olsen N, Christensen F, Søballe K. Excessive distal migration of fiber-mesh coated femoral stems. Acta Orthop. 2011;82:308–314. doi: 10.3109/17453674.2011.574562. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;1:307–310. doi: 10.1016/S0140-6736(86)90837-8. [DOI] [PubMed] [Google Scholar]
  • 4.Bragdon CR, Malchau H, Yuan X, Perinchief R, Kärrholm J, Börlin N, Estok DM, Harris WH. Experimental assessment of precision and accuracy of radiostereometric analysis for the determination of polyethylene wear in a total hip replacement model. J Orthop Res. 2002;20:688–695. doi: 10.1016/S0736-0266(01)00171-1. [DOI] [PubMed] [Google Scholar]
  • 5.Casper DS, Kim GK, Restrepo C, Parvizi J, Rothman RH. Primary total hip arthroplasty with an uncemented femoral component: five- to nine-year results. J Arthroplasty. 2011;26:838–841. doi: 10.1016/j.arth.2011.02.010. [DOI] [PubMed] [Google Scholar]
  • 6.Derbyshire B, Prescott RJ, Porter ML. Notes on the use and interpretation of radiostereometric analysis. Acta Orthop. 2009;80:124–130. doi: 10.1080/17453670902807474. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Flatøy B, Röhrl SM, Bøe B, Nordsletten L. No medium-term advantage of electrochemical deposition of hydroxyapatite in cementless femoral stems: 5-year RSA and DXA results from a randomized controlled trial. Acta Orthop. 2016;87:42–47. doi: 10.3109/17453674.2015.1084768. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Gascoyne TC, Morrison JB, Turgeon TR. The effect of patient positioning on the precision of model-based radiostereometric analysis. J Biomech. 2014;47:1914–1917. doi: 10.1016/j.jbiomech.2014.03.034. [DOI] [PubMed] [Google Scholar]
  • 9.Giavarina D. Understanding Bland Altman analysis. Biochem Med (Zagreb). 2015;25:141–151. doi: 10.11613/BM.2015.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Kaptein BL, Valstar ER, Spoor CW, Stoel BC, Rozing PM. Model-based RSA of a femoral hip stem using surface and geometrical shape models. Clin Orthop Relat Res. 2006;448:92–97. doi: 10.1097/01.blo.0000224010.04551.14. [DOI] [PubMed] [Google Scholar]
  • 11.Kaptein BL, Valstar ER, Stoel BC, Rozing PM, Reiber JH. A new model-based RSA method validated using CAD models and models from reversed engineering. J Biomech. 2003;36:873–882. doi: 10.1016/S0021-9290(03)00002-2. [DOI] [PubMed] [Google Scholar]
  • 12.Kärrholm J, Herberts P, Hultmark P, Malchau H, Nivbrant B, Thanner J. Radiostereometry of hip prostheses: review of methodology and clinical results. Clin Orthop Relat Res. 1997;344:94–110. [PubMed] [Google Scholar]
  • 13.Khanuja HS, Vakil JJ, Goddard MS, Mont MA. Cementless femoral fixation in total hip arthroplasty. J Bone Joint Surg Am. 2011;93:500–509. doi: 10.2106/JBJS.J.00774. [DOI] [PubMed] [Google Scholar]
  • 14.Li Y, Röhrl SM, Bøe B, Nordsletten L. Comparison of two different Radiostereometric analysis (RSA) systems with markerless elementary geometrical shape modeling for the measurement of stem migration. Clin Biomech (Bristol, Avon) 2014;29:950–955. doi: 10.1016/j.clinbiomech.2014.06.007. [DOI] [PubMed] [Google Scholar]
  • 15.Lombardi AV, Jr, Berend KR, Mallory TH, Skeels MD, Adams JB. Survivorship of 2000 tapered titanium porous plasma-sprayed femoral components. Clin Orthop Relat Res. 2009;467:146–154. doi: 10.1007/s11999-008-0568-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Madanat R, Mäkinen TJ, Moritz N, Mattila KT, Aro HT. Accuracy and precision of radiostereometric analysis in the measurement of three-dimensional micromotion in a fracture model of the distal radius. J Orthop Res. 2005;23:481–488. doi: 10.1016/j.orthres.2004.07.002. [DOI] [PubMed] [Google Scholar]
  • 17.Mäkinen TJ, Koort JK, Mattila KT, Aro HT. Precision measurements of the RSA method using a phantom model of hip prosthesis. J Biomech. 2004;37:487–493. doi: 10.1016/j.jbiomech.2003.09.004. [DOI] [PubMed] [Google Scholar]
  • 18.Olofsson K, Digas G, Kärrholm J. Influence of design variations on early migration of a cemented stem in THA. Clin Orthop Relat Res. 2006;448:67–72. doi: 10.1097/01.blo.0000224020.73163.28. [DOI] [PubMed] [Google Scholar]
  • 19.Önsten I, Berzins A, Shott S, Sumner DR. Accuracy and precision of radiostereometric analysis in the measurement of THR femoral component translations: human and canine in vitro models. J Orthop Res. 2001;19:1162–1167. doi: 10.1016/S0736-0266(01)00039-0. [DOI] [PubMed] [Google Scholar]
  • 20.Prins AH, Kaptein BL, Stoel BC, Nelissen RG, Reiber JH, Valstar ER. Handling modular hip implants in model-based RSA: combined stem-head models. J Biomech. 2008;41:2912–2917. doi: 10.1016/j.jbiomech.2008.07.035. [DOI] [PubMed] [Google Scholar]
  • 21.Ranstam J, Ryd L, Onsten I. Accurate accuracy assessment: review of basic principles. Acta Orthop Scand. 2000;71:106–108. doi: 10.1080/00016470052944017. [DOI] [PubMed] [Google Scholar]
  • 22.Ryd L, Yuan X, Löfgren H. Methods for determining the accuracy of radiostereometric analysis (RSA) Acta Orthop Scand. 2000;71:403–408. doi: 10.1080/000164700317393420. [DOI] [PubMed] [Google Scholar]
  • 23.Seehaus F, Emmerich J, Kaptein BL, Windhagen H, Hurschler C. Dependence of model-based RSA accuracy on higher and lower implant surface model quality. Biomed Eng Online. 2013;12:32. doi: 10.1186/1475-925X-12-32. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Valstar ER, Gill R, Ryd L, Flivik G, Börlin N, Kärrholm J. Guidelines for standardization of radiostereometry (RSA) of implants. Acta Orthop. 2005;76:563–572. doi: 10.1080/17453670510041574. [DOI] [PubMed] [Google Scholar]
  • 25.Weber E, Sundberg M, Flivik G. Design modifications of the uncemented Furlong hip stem result in minor early subsidence but do not affect further stability: a randomized controlled RSA study with 5-year follow-up. Acta Orthop. 2014;85:556–561. doi: 10.3109/17453674.2014.958810. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Clinical Orthopaedics and Related Research are provided here courtesy of The Association of Bone and Joint Surgeons

RESOURCES