Abstract
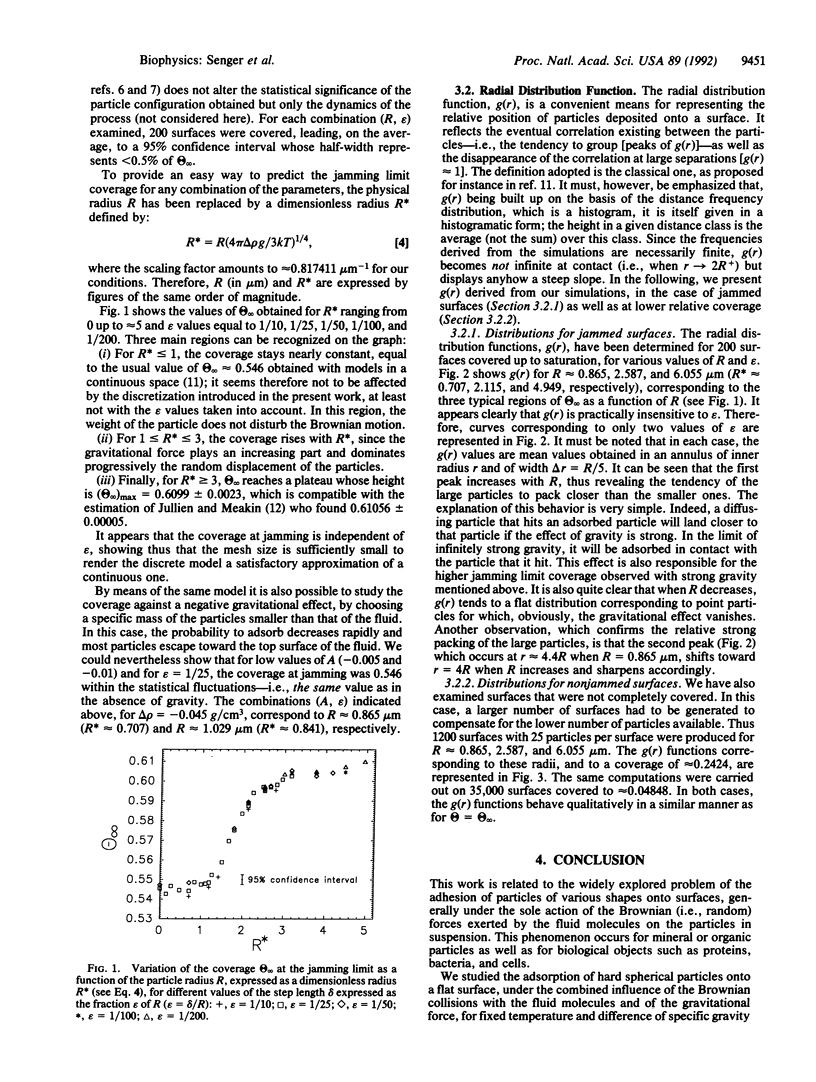
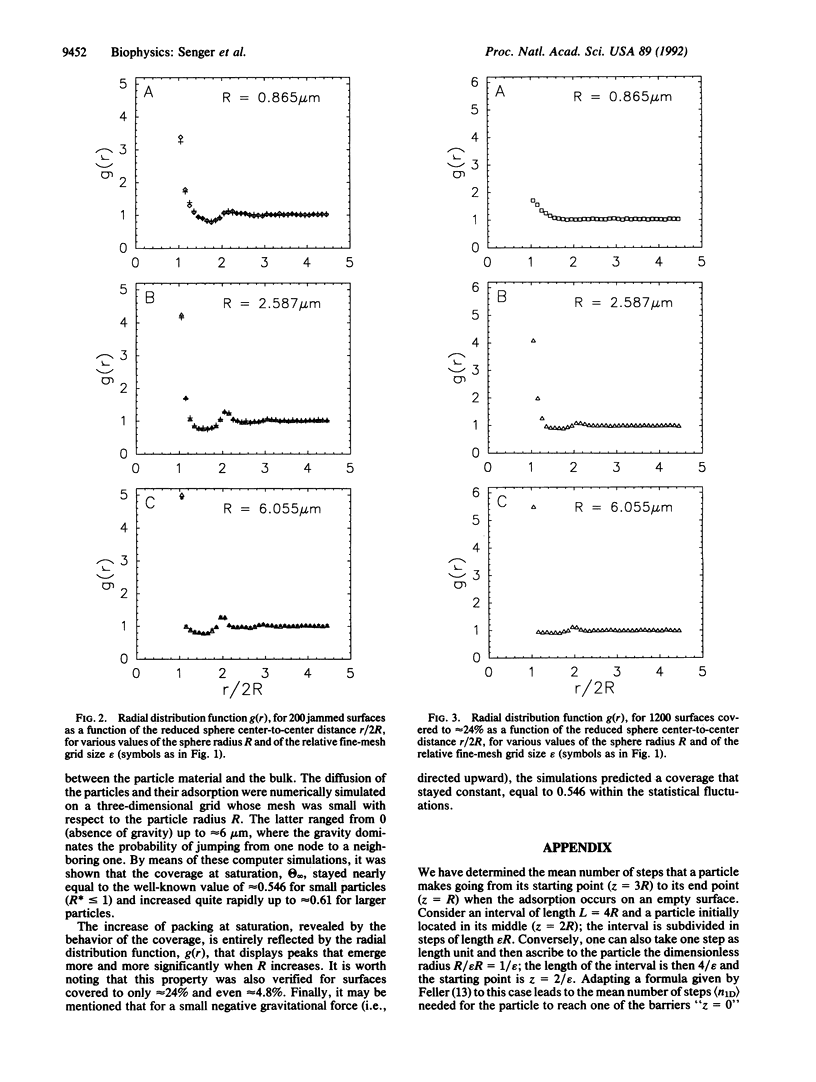
The deposition and adhesion of particles on a solid surface are governed by a great number of interplaying forces. In this paper we analyze, by means of computer simulations, the influence of (i) the short-range repulsive forces, modeled by hard sphere interactions, (ii) the gravitational forces, and (iii) the diffusion process of the particles in the fluid on the structure of the surface covered by the particles. In particular, the evolution of the limiting coverage, [symbol, see text] infinity (where [symbol, see text] is the reduced relative surface coverage), and the radial distribution, g(r), at the jamming limit, are determined as a function of the gravitational forces. These forces play an important role in many experiments performed on latex beads. Our results should stimulate new experiments in this field and, thus, be directly experimentally tested. It is shown, for example, that for polystyrene particles [symbol, see text] infinity is constant and equal to the random sequential adsorption jamming limit value for radii R not larger than 1 micron. It increases for 1 </= R </= 3 micron and tends, for higher R, to a plateau, whose value is approximately equal to 0.61. The tendency to a closer packing when R is large, and thus large gravitational forces, is confirmed by the shape of the radial distribution function. This phenomenon occurs not only for jammed surfaces but also for unsaturated surfaces.
Full text
PDF


Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Huang YB, Somasundaran P. Discrete modeling of sedimentation. Phys Rev A Gen Phys. 1988 Dec 15;38(12):6373–6376. doi: 10.1103/physreva.38.6373. [DOI] [PubMed] [Google Scholar]
- Onoda GY, Liniger EG. Experimental determination of the random-parking limit in two dimensions. Phys Rev A Gen Phys. 1986 Jan;33(1):715–716. doi: 10.1103/physreva.33.715. [DOI] [PubMed] [Google Scholar]
- Selinger RB, Stanley HE. Percolation of interacting diffusing particles. Phys Rev A. 1990 Oct 15;42(8):4845–4852. doi: 10.1103/physreva.42.4845. [DOI] [PubMed] [Google Scholar]
- Senger B, Voegel J, Schaaf P, Johner A, Schmitt A, Talbot J. Properties of jamming configurations built up by the adsorption of Brownian particles onto solid surfaces. Phys Rev A. 1991 Nov 15;44(10):6926–6928. doi: 10.1103/physreva.44.6926. [DOI] [PubMed] [Google Scholar]
- Tarjus G, Viot P. Generalized car-parking problem as a model for particle deposition with entropy-activated rate process. Phys Rev Lett. 1992 Apr 13;68(15):2354–2357. doi: 10.1103/PhysRevLett.68.2354. [DOI] [PubMed] [Google Scholar]


