Abstract
Photo-induced charge transfer at molecular heterojunctions has gained particular interest due to the development of organic solar cells (OSC) based on blends of electron donating and accepting materials. While charge transfer between donor and acceptor molecules can be described by Marcus theory, additional carrier delocalization and coherent propagation might play the dominant role. Here, we describe ultrafast charge separation at the interface of a conjugated polymer and an aggregate of the fullerene derivative PCBM using the stochastic Schrödinger equation (SSE) and reveal the complex time evolution of electron transfer, mediated by electronic coherence and delocalization. By fitting the model to ultrafast charge separation experiments, we estimate the extent of electron delocalization and establish the transition from coherent electron propagation to incoherent hopping. Our results indicate that even a relatively weak coupling between PCBM molecules is sufficient to facilitate electron delocalization and efficient charge separation at organic interfaces.
Absorption of sunlight in OSCs primarily creates neutral molecular excitations, while their conversion to electron-hole (e-h) pairs occurs at the heterojunction between electron donating (polymers or small molecules) and electron accepting (fullerenes or their derivatives) materials. Electron-hole pairs split into free charge carriers on a femtosecond time scale and despite the strong Coulomb interaction between the charges this process is known to be often close to 100% efficient. Although several often conflicting models have been proposed, to this day it remains unclear what mechanism is responsible for efficient charge separation at organic heterojunctions. Several explanations were suggested for this initial dissociation stage, for example: charge carrier delocalization over several polymer segments and/or fullerene molecules1, hot interfacial charge-transfer (CT) states with delocalized wave functions2,3, or, alternatively, with electron and/or hole wavefunctions localized on molecules situated at large distances from the interface4. Recently, a partially coherent model, assuming electron delocalization over the entire aggregated fullerene domain5, and a hybrid model of a 1D polymer/fullerene lattice with semi-classical dynamics at short time scales and Redfield relaxation theory at long time scales6, have been proposed. Consequently, charge separation on an ultrafast time scale is often considered to be predominantly coherent. However, carrier delocalization and coherent propagation, their extent and temporal evolution have only been qualitatively postulated. Although the later time scales of charge separation have been successfully described by incoherent hopping7, a consistent model at the earliest time scales, describing the coherent propagation of charge and the gradual transition into the classical hopping regime, is still absent. As a consequence, the role of coherence remains elusive.
To elucidate the role of delocalization and coherence in charge separation a full quantum mechanical description is necessary. Here, we use the stochastic Schrödinger equation (SSE) to describe the charge separation process by the principles of open quantum systems. This approach allows us to evaluate the interplay between coherent dynamics and bath induced dephasing8,9, and predict the importance of delocalization in systems with a wide range of intermolecular couplings, leading to different charge separation scenarios. Our model predictions are consistent with experimentally measured charge carrier separation dynamics on an ultrafast time scale, as confirmed by a recently developed experimental technique10. This article thus reveals the role of delocalization and coherence in aiding charge separation at organic interfaces.
We consider charge separation at the heterojunction of a conjugated polymer and an aggregate of the fullerene derivative PCBM. Our results are also applicable to small molecule donors and pristine fullerenes. It has been recently experimentally demonstrated that mainly electron motion in PCBM is responsible for the initial evolution of the charge separation process – hole motion is significantly slower5,11,12. Therefore, in our treatment we consider the hole to be immobile. Consequently, we construct a finite cubic lattice of acceptors and a single donor site for the hole (see the Methods section for details and a schematic). The variable size of acceptor aggregates and the overall complexity of interfaces in the hierarchical morphology of the bulk heterojunction blend is reflected by a variation of couplings between the acceptor sites. In order to model photo-excitation in the donor phase, we initially place both the electron and the hole at the donor site and let the electron propagate in the electrostatic field of the stationary hole. We set simulation parameters typical for polymer-PCBM solar cells (see Supplementary Information), however, we find that the most important parameter governing the coherent (<500 fs) dynamics of the electron is the inter-acceptor coupling JA. Variations of other parameters: donor site excitation energy εD, CT state energy εCT, donor-acceptor interaction energy JDA and system-bath interaction energy λ only slightly affect the evolution of the system – while the dynamics at later times (>500 fs) somewhat differ, they remain qualitatively the same, see Supplementary Information. Hence, in most of our analysis we keep the parameters fixed, except for the inter-acceptor coupling JA, which was varied. We find that within these ranges our model gives quite a narrow spectrum of possible charge separation scenarios. All of them lead to charge separation kinetics which qualitatively agree with experimental results. This means that the simulation results presented below are suggestive of the underlying physical phenomena occurring in operating organic solar cells.
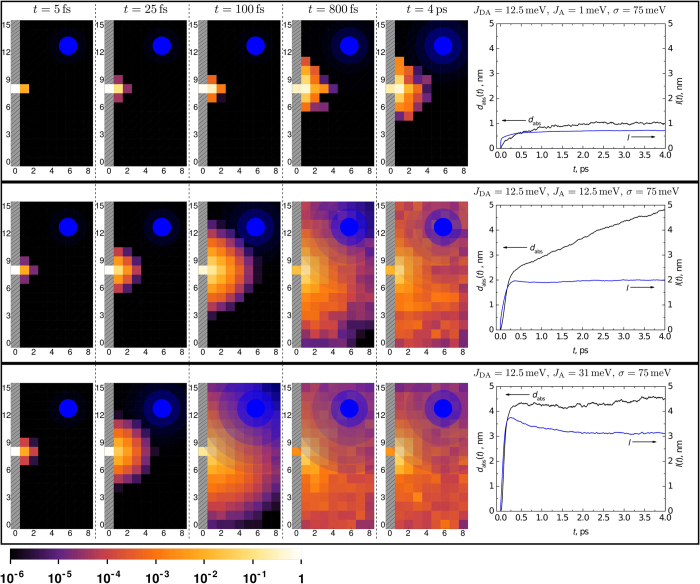
Figure 1 shows the simulated temporal evolution of electron density for the indicated values of inter-acceptor electron coupling JA. Data are projected in the plane perpendicular to the donor/acceptor interface. External electric field is not applied to highlight the effects of delocalization. Our results show that the electron is transferred from the donor site to a nearby pool of coherently coupled acceptor sites within ~300 fs. The number of accessible sites in a given time interval grows with increasing intermolecular (inter-acceptor) coupling, allowing for the electron to transfer to more distant sites already at very early times. Electron transfer is quantitatively characterized in the rightmost column of Fig. 1, where the kinetics of the absolute e-h separation distance, dabs(t) (Fig. 1 black traces) and the electron delocalization radius, l(t) (Fig. 1, blue traces), are shown (details on these parameters are given in the Methods section). The extent of electron delocalization is visualized by the blue circles. These results only weakly depend on the donor excitation energy εD (see Supplementary Information), in agreement with experimental studies of charge separation efficiency versus excitation energy13.
Figure 1. Ensemble-averaged evolution of electron probability density in the plane perpendicular to the donor (grey area) and acceptor (8 × 16 × 16 nm3 domain) interface at different times following photoexcitation for the indicated values of inter-acceptor coupling JA.
The rightmost column shows the corresponding absolute charge separation distance dabs(t) (black traces) and delocalization radius l(t) (blue traces). Filled blue circles illustrate the extent of electron coherence at a given time. The color scale at the bottom describes the probability of finding the electron at the indicated distance from the interface.
The kinetics of both dabs(t) and l(t), for different JA exhibit a similarly rapid initial rise. For very weak coupling both electron delocalization and initial electron transfer distance are small, and thus the electron is only transferred from the donor to the nearest acceptor site. For intermediate coupling the initial transfer distance is increased and the electron is more, although still weakly, delocalized. In this regime at later times >500 fs the average electron distance increases while its delocalization remains constant. In case of strong coupling, the electron is strongly delocalized, we thus observe the largest electron transfer distance at early times, whereas the later part of the transfer process is mainly determined by time-dependent localization. Note that for strong couplings electron delocalization is confined by the size of the acceptor lattice in our model, chosen to correspond to the expected PCBM domain size (8 × 16 × 16 nm3) in efficient polymer-PCBM blends (see the Methods section). Despite similar probability distributions at long times in the second and third rows of Fig. 1, the extent of delocalization of individual electrons and, consequently, the character of their motion is very different.
To determine which regime corresponds to real polymer-PCBM blends, we have compared our model prediction to experimentally measured carrier drift dynamics probed by a recently developed experimental technique, time-resolved electric-field induced second harmonic generation (TREFISH), enabling ultrafast measurements. We have chosen a bulk heterojunction solar cell based on P3TI-PC71BM. This system is of particular interest due its exceptionally low driving force ΔE ~ 0.1 eV for charge separation14, nevertheless leading to an internal quantum efficiency (IQE) of 90%. Transient absorption spectroscopy also indicates ultrafast photo-induced charge transfer on a <100 fs time scale, see Supplementary Information. Charge separation in P3TI-PC71BM is thus expected to rely on charge delocalization and coherent electron propagation.
Figure 2 shows the experimental and simulated average e–h separation along the direction of the electric field of 5.7 × 105 V/cm, created by applied voltage and the built-in field of the OSC (see the Methods section and the Supplementary Information for a more detailed description). Using transient absorption spectroscopy we observe no signatures of delayed charge transfer due to exciton diffusion, only prompt photo-induced charge transfer at a time scale of <100 fs, see Supplementary Information. Thus, the experimental EFISH data in Fig. 2 directly monitors the motion of the photo-induced electron away from the donor/acceptor interface. The experiment shows a fast ≈500 fs initial rise to a charge separation distance of 0.4 nm. The later part of the charge separation process is considerably slower – separation distance gradually rises up to 0.9 nm in 3.5 ps.
Figure 2. Time dependence of the charge separation distance dF along the direction of the electric field F of 5.7 × 105 V/cm for the indicated inter-acceptor coupling values JA.
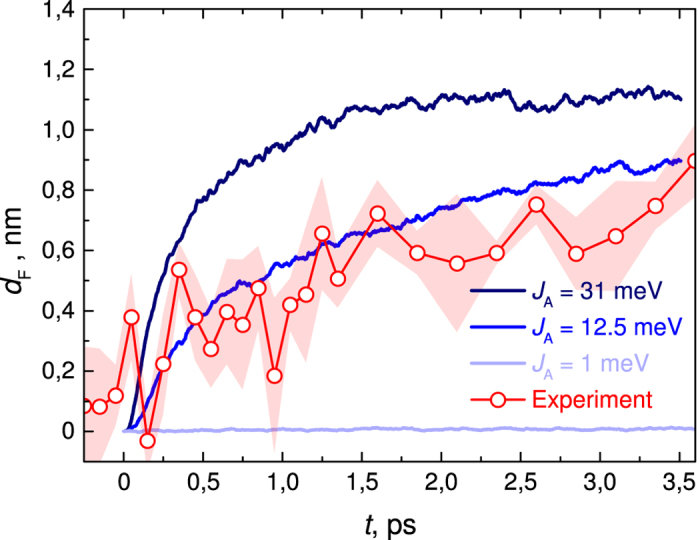
Symbols - experiment, shaded area – standard error in experiment, solid colored lines – simulations at different values of JA.
To simulate the experiment we have added an external electric field to the model and have also taken into account the fact that donor-acceptor interfaces can be arbitrarily oriented with respect to the direction of the field. We reproduce this situation by performing simulations with a randomly oriented electric field and averaging the obtained e-h separation distance projected along the direction of the field. Our model with JA = 12.5 meV (intermediate coupling) reproduces the experiment (see Fig. 2) and points to an absolute carrier separation distance of 2.5 nm in 500 fs as shown in Fig. 1. It is considerably smaller than the 4 nm distance evaluated in Ref. 5 for PCDTBT:PC61BM. The latter corresponds to our model prediction in the strong coupling regime where we also obtain a carrier separation distance of 4 nm (Fig. 1c). However, at least for the case of P3TI-PC71BM, comparison with experiment indicates that such coupling and initial separation are overestimated. Given that P3TI-PC71BM operates at an IQE of 90%, we thus suggest that intermediate couplings, leading to electron delocalization just over two lattice sites (Fig. 1), are already sufficient to facilitate efficient charge separation at organic interfaces.
To further support our results we calculate electron mobilities using the same set of parameters. The obtained values are 0.03, 0.37 and 1.26 cm2V−1s−1 for JA = 1, 12.5 and 31.5 meV respectively. The predicted mobility at JA = 12.5 meV is in excellent agreement with the experimentally measured electron mobility value of 0.3 cm2V−1s−1 in PCBM at the picosecond time scale15.
Classical hopping models have been used extensively to describe electron-hole separation and subsequent charge motion in organic materials7. The simulations rely on the initial e-h distance distribution following photoexcitation, which is difficult to access experimentally. Initial charge separation distances of 3–4 nm have been estimated16. Our present simulations allows us to visualize the formation of the e-h distance distribution with high spatio-temporal resolution. We find that coherent electron transfer lasts up to ~500 fs and is responsible for shaping the “initial” electron-hole distance distribution. Following the coherent propagation stage charge separation kinetics gradually switch to the slower phase (see e.g. the rightmost column of Fig. 1b where the dabs(t) trace features a two-phase evolution), which effectively corresponds to the incoherent-hopping phase. Thus, 500 fs marks the transition from coherent electron propagation to incoherent hopping where classical hopping models become valid.
Figure 3 shows the temporal evolution of e-h distance distribution without external electric field in the intermediate coupling regime. The electron gets completely transferred from the donor site to the acceptor lattice in ~500 fs, however, it is still strongly bound to the hole. Further charge separation is facilitated by incoherent electron hopping as outlined in ref. 17. The resulting e-h distance distribution at 800 fs can be approximated as an exponential (red dashed line in Fig. 3) and could be used in classical hopping models as the initial distribution.
Figure 3. Radial distribution of (e-h) separation distance at early times.
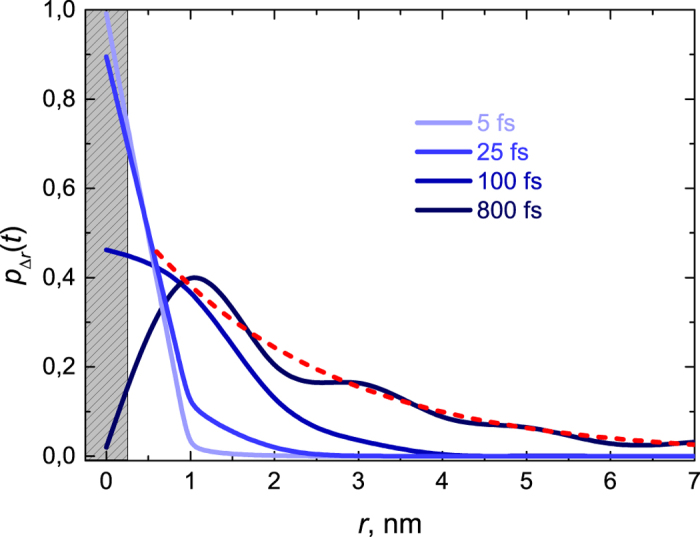
The shaded grey area indicates the position of the donor site. Dashed red line represents the exponential character of the e-h distance distribution after 800 fs.
Before we conclude, we have to point out that our model does not include geminate recombination, which although considered insignificant in efficient OSC systems, is necessary for a complete description. The extent of electron delocalization, as elucidated here, may be one of the key factors minimizing geminate recombination18.
In conclusion, our results suggest a complex coherence dynamics and their role in photo-induced electron transfer at organic interfaces: electron delocalization occurs on a femtosecond time scale, during which the electron wavefunction spreads in the acceptor phase. Although the extent of the electron wavefunction in PCBM is limited to only several molecules, it is already sufficient to facilitate an average electron-hole separation distance of ~2.5 nm on a femtosecond time scale. Coherent propagation also shapes the “initial” e-h distance distribution, which can be implemented in classical hopping models that are valid at time scales >500 fs – the transition time from coherent propagation to incoherent hopping. Finally, it should be noted that our proposed model is not specific to OSCs and may be generalized to explain charge transfer not only at any molecular interface but also in other collectively coupled molecular systems.
Methods
Experimental
Sample preparation
A monolayer of poly(3,30-([(90,90-dioctyl-9H,90H-[2,20-bifluorene]-9,9-diyl)bis(4,1-phenylene)]bis(oxy))bis(N,N-dimethylpropan-1-amine)) (PFPA-1) interface material was deposited on ITO coated glass substrates that were TL-1 treated. Poly[N,N′-bis(2-hexyldecyl)isoindigo-6,6′-diyl-alt-thiophene-2,5-diyl] (P3TI) and [6,6]-phenyl-C71-butyric acid methyl ester (PC71BM) (D/A 2:3 w/w) were then spin-coated from a 20 g/l o-dichlorobenzene (ODCB) solution with 2.5% (vol%) of 1,8-Diiodooctane (DIO). The thickness of the active layer (~70 nm +/− 10 nm) was determined by a Dektak surface profilometer. PEDOT:PSS PH1000 with a layer thickness of 110 nm was deposited from an aqueous solution mixed with 5% (vol%) of dimethyl sulfoxide and 0.5% (vol%) Zonyl FS 300 as the surfactant, and then annealed at 60C to remove residual water. The device was then encapsulated by a glass lid.
Experiment
The time-resolved electric-field-induced second harmonic generation (TREFISH) technique has been described elsewhere10. Briefly, we use the Electric Field-Induced Second Harmonic (EFISH) generation effect to monitor the temporal evolution of the electric field strength in the bulk of the OSC active layer. Photogenerated charge carriers partially screen the applied electric field, leading to a reduction of the 2nd harmonic intensity and allowing for their motion to be evaluated optically with sub-picosecond time resolution. We have used 130 fs, 800 nm, 1 kHz repetition rate pulses, generated by a Ti-Sapphire laser (Quantronix Integra-C) to excite the blend biphotonically. A fraction of the same laser pulse was used as the probe for the second harmonic (at 400 nm) intensity in the active layer. The 2nd harmonic intensity transient can be related to changes in electric field strength in the active layer by I2h ~ E2 10. Electric field dynamics with sub-picosecond time resolution were obtained by varying the time delay between the excitation and the probe pulse, which was achieved by a mechanical delay stage. The intensity of the pump was set such that the electric field change caused by the optical excitation itself was significantly smaller than the electric field created by external voltage and the built-in field of the OSC. To avoid sample degradation external voltage was applied by reverse bias pulses of 10 μs duration, synchronized to those of the laser pump. The carrier separation distance along the direction of the electric field was determined as described in ref. 7. Standard error in experiment (Shaded area in Fig. 2.) was estimated as 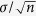 , where σ is the standard deviation and n is the number of collected data points at a particular pump-probe time delay.
, where σ is the standard deviation and n is the number of collected data points at a particular pump-probe time delay.
Simulations
We describe the acceptor medium with the donor site as a quantum system characterized by the lattice Hamiltonian
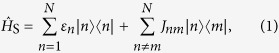 |
where εn is the electron energy on the n-th site and Jnm is the electron hopping energy between sites n and m (only one-particle states are included); state |n〉 denotes the electron on site n. The environment (heat bath) consists of harmonic oscillators (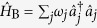 ). Here ωj is the frequency of the j-th oscillator,
). Here ωj is the frequency of the j-th oscillator, 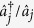 are the bosonic creation/annihilation operators of j-th bath mode and ℏ = 1. We assume only linear coupling between the system and the environment characterized by the interaction Hamiltonian
are the bosonic creation/annihilation operators of j-th bath mode and ℏ = 1. We assume only linear coupling between the system and the environment characterized by the interaction Hamiltonian 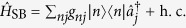 ). Here gnj are constants describing the coupling strength between the n-th site and the j-th bath oscillator.
). Here gnj are constants describing the coupling strength between the n-th site and the j-th bath oscillator.
The heat bath consists of an infinite number of oscillators whose distribution is described by spectral density C′′(ω) = ∑j|gnj|2δ(ω − ωj). We use the environment model based on the Debye spectral density which has the form of an overdamped Lorentzian9.
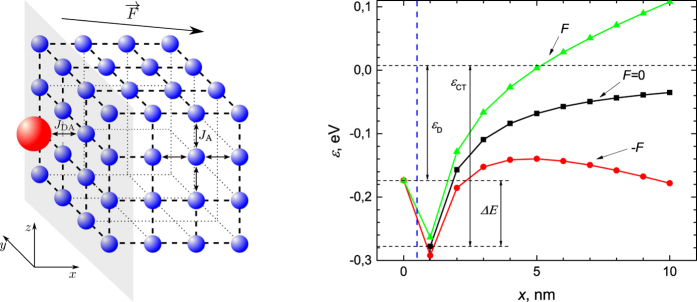
The model is implemented on a 3D cubic lattice of 8 × 16 × 16 sites (Fig. 4 (a)). This lattice size corresponds to the expected size of a PCBM aggregate in well-intermixed bulk heterojunction solar cells. Transmission electron microscopy images of P3TI:PC71BM14 indicate a well-intermixed morphology, in agreement with our assumption. Each site of the acceptor (molecule) can be free or occupied by an electron. The CT state is obtained when the electron is transferred from the donor to the neighboring acceptor site. At all times the donor site remains occupied by a hole, i.e., the donor site is merely the source of the electrostatic Coulomb field and the electron is described quantum mechanically using the SSE.
Figure 4. Model description.
(a) Schematic of the donor - acceptor interface model. Red sphere denotes the donor site; blue spheres denote the acceptor sites; F denotes the arbitrary direction of the external electric field reflecting the averaging procedure over all possible CT interface orientations with respect to F, see the main text; JDA and JA denote the interaction energies between the donor and the nearest acceptor site and between the nearest neighbor acceptor sites respectively. (b) Energy profile in the direction perpendicular to the donor/acceptor interface plane (dashed blue line), parameter values are given in the Supplementary Information. The red and green curves represent the shift of the Coulomb potential due to the applied external electric field 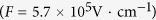 , the black curve - the shifted Coulomb potential when a net zero electric field is applied. The donor site corresponds to x = 0. εD is the donor site excitation energy, εCT denotes the state energy of the CT exciton and ΔE is the driving force.
, the black curve - the shifted Coulomb potential when a net zero electric field is applied. The donor site corresponds to x = 0. εD is the donor site excitation energy, εCT denotes the state energy of the CT exciton and ΔE is the driving force.
Site energies εn in the Hamiltonian 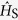 (Eq. 1) are given by
(Eq. 1) are given by
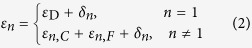 |
Here εD is the electron self-energy on the donor site (it is the molecular excitation energy since the hole is localized on this site as well), while self-energies of the acceptor sites are zero, εn,C is the Coulomb interaction energy between the hole and the electron, εn,F is the energy contribution due to some external electric field and δn - the contribution due to the static energetic disorder of electron energies in the lattice. δn is taken as a Gaussian random number, characterized by the standard deviation σ, and the results must be averaged over this parameter. Interaction energy Jnm in the system Hamiltonian is equal to JDA if n and m denote the donor and the nearest-neighbor acceptor site, otherwise, Jnm = JA if n and m denote nearest-neighbor acceptor sites.
Coulomb potential between the hole and the electron has the form 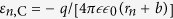 , where q is the electron charge, ∈0 and ∈ are the dielectric constants of empty-space and of material, respectively, rn is the distance between the n-th site of the lattice and the donor site, parameter b accounts for the finite size of the donor and acceptor molecules shifting up the CT exciton energy according to the experimentally determined binding energy. The energy term
, where q is the electron charge, ∈0 and ∈ are the dielectric constants of empty-space and of material, respectively, rn is the distance between the n-th site of the lattice and the donor site, parameter b accounts for the finite size of the donor and acceptor molecules shifting up the CT exciton energy according to the experimentally determined binding energy. The energy term 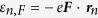 is due to the external electric field F. Using Eq. 2 and expressions for εn,C and εn,F we can visualize the energy profile in the x direction, perpendicular to the donor - acceptor interface as presented in Fig. 4 (b). Here, the energy profile is given for three different cases: when the external electric field is applied perpendicular to the donor/acceptor interface (with positive values of F pointing from the donor to the acceptor phase), in the opposite direction (negative F values) and with no external electric field. Using our model we calculate the electron probability density
is due to the external electric field F. Using Eq. 2 and expressions for εn,C and εn,F we can visualize the energy profile in the x direction, perpendicular to the donor - acceptor interface as presented in Fig. 4 (b). Here, the energy profile is given for three different cases: when the external electric field is applied perpendicular to the donor/acceptor interface (with positive values of F pointing from the donor to the acceptor phase), in the opposite direction (negative F values) and with no external electric field. Using our model we calculate the electron probability density 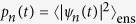 and the absolute e-h separation distance dabs(t) =〈∑n|ψn(t)|2|rn − rD|〉ens. Here ψn(t) is the electron amplitude on lattice site n, the sum runs over all system sites and 〈…〉ens denotes ensemble averaging. We also introduce the average coherence radius of the electron
and the absolute e-h separation distance dabs(t) =〈∑n|ψn(t)|2|rn − rD|〉ens. Here ψn(t) is the electron amplitude on lattice site n, the sum runs over all system sites and 〈…〉ens denotes ensemble averaging. We also introduce the average coherence radius of the electron 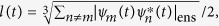 which denotes the linear extent of delocalization. Finally, we calculate the electon-hole drift separation distance
which denotes the linear extent of delocalization. Finally, we calculate the electon-hole drift separation distance 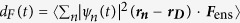 along the direction of the applied external electric field. Using the calculated drift distance we are also able to estimate the electron mobility
along the direction of the applied external electric field. Using the calculated drift distance we are also able to estimate the electron mobility 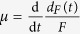 .
.
Additional Information
How to cite this article: Abramavicius, V. et al. Role of coherence and delocalization in photo-induced electron transfer at organic interfaces. Sci. Rep. 6, 32914; doi: 10.1038/srep32914 (2016).
Supplementary Material
Acknowledgments
We thank Arkady Yartsev at Lund University for the help with transient absorption measurements. The work was partly financed by Research Council of Lithuania, projects MIP-090/2015 (simulations) and MIP-085/2015 (experiment). Studies of organic photovoltaics in Linköping are funded by the Swedish Science Council and the Knut and Alice Wallenberg foundation through a Wallenberg Scholar grant to O.I. All theoretical calculations were performed using resources at the High Performance Computing Center of the Lithuanian National Center of Physical and Technology Sciences (HPC Sauletekis).
Footnotes
Author Contributions V.A. and D.A. performed simulations, V.P. and V.G. performed experiments, A.M. prepared samples. V.A. and A.M. wrote the manuscript. All authors commented on the manuscript.
References
- Deibel C., Storbel T. & Dyakonov V. Origin of the efficient polaron-pair dissociation in polymer-fullerene blends. Phys. Rev. Lett. 103, 036402 (2009). [DOI] [PubMed] [Google Scholar]
- Bakulin A. A. et al. The role of driving energy and delocalized states for charge separation in organic semiconductors. Science 335, 1340–1344 (2012). [DOI] [PubMed] [Google Scholar]
- Grancini G. et al. Hot exciton dissociation in polymer solar cells. Nat. Mater. 12, 29−33 (2013). [DOI] [PubMed] [Google Scholar]
- Jailaubekov A. E. et al. Hot charge-transfer excitons set the time limit for charge separation at donor/acceptor interfaces in organic photovoltaics. Nat. Mater. 12, 66–73 (2013). [DOI] [PubMed] [Google Scholar]
- Gélinas S. et al. Ultrafast long-range charge separation in organic semiconductor photovoltaic diodes. Science, 343, 512–516 (2014). [DOI] [PubMed] [Google Scholar]
- Lee M. H., Aragó J. & Troisi A. Charge Dynamics in Organic Photovoltaic Materials: Interplay between Quantum Diffusion and Quantum Relaxation. J. Phys. Chem. C 119, 14899–14998 (2015). [Google Scholar]
- Vithanage D. A. et al. Visualizing charge separation in bulk heterojunction organic solar cells. Nat. Commun. 4, 2334 (2013). [DOI] [PubMed] [Google Scholar]
- Abramavicius V. & Abramavicius D., Excitation transfer pathways in excitonic aggregates revealed by the stochastic Schrödinger equation. J. Chem. Phys. 140, 065103 (2014). [DOI] [PubMed] [Google Scholar]
- Valkunas L., Abramavicius D. & Mančal T. Molecular Excitation Dynamics and Relaxation: Quantum Theory and Spectroscopy (John Wiley & Sons, 2013). [Google Scholar]
- Devizis A., Serbenta A., Meerholz K., Hertel D. & Gulbinas V. Ultrafast dynamics of carrier mobility in a conjugated polymer probed at molecular and microscopic length scales. Phys. Rev. Lett. 103, 027404 (2009). [DOI] [PubMed] [Google Scholar]
- Pranculis V. et al. Charge carrier generation and transport in different stoichiometry APFO3:PC61BM solar cells. J. Am. Chem. Soc. 136, 11331–11338 (2014). [DOI] [PubMed] [Google Scholar]
- Melianas A. et al. Dispersion-dominated photocurrent in polymer:fullerene solar cells. Adv. Funct. Mater. 24, 4507–4514 (2014). [Google Scholar]
- Vandewal K. et al. Efficient charge generation by relaxed charge-transfer states at organic interfaces. Nat. Mater. 13, 63–68 (2014). [DOI] [PubMed] [Google Scholar]
- Vandewal K. et al. Quantification of Quantum Efficiency and Energy Losses in Low Bandgap Polymer:Fullerene Solar Cells with High Open-Circuit Voltage. Adv. Funct. Mater. 22, 3480–3490 (2012). [Google Scholar]
- Devižis A., Hertel D., Meerholz K., Gulbinas V. & Moser J. A. Time-independent, high electron mobility in thin PC61BM films: Relevance to organic photovoltaics. Org. Electron. 15, 3729–3734 (2014). [Google Scholar]
- Barker A. J., Chen K. & Hodgkiss J. M. Distance Distributions of Photogenerated Charge Pairs in Organic Photovoltaic Cells. J. Am. Chem. Soc. 136, 12018–12026 (2014). [DOI] [PubMed] [Google Scholar]
- van Eersel H., Janssen R. A. J. & Kemerink M. Mechanism for Efficient Photoinduced Charge Separation at Disordered Organic Heterointerfaces. Adv. Funct. Mater. 22, 2700–2708 (2012). [Google Scholar]
- Murthy D. H. K. et al. Origin of reduced bimolecular recombination in blends of conjugated polymers and fullerenes. Adv. Funct. Mater. 23, 4262–4268 (2014). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.