A Large-Scale Computational Analysis of Corneal Structural Response and Ectasia Risk in Myopic Laser Refractive Surgery (An American Ophthalmological Society Thesis)

Abstract

Purpose:

To investigate biomechanical strain as a structural susceptibility metric for corneal ectasia in a large-scale computational trial.

Methods:

A finite element modeling study was performed using retrospective Scheimpflug tomography data from 40 eyes of 40 patients. LASIK and PRK were simulated with varied myopic ablation profiles and flap thickness parameters across eyes from LASIK candidates, patients disqualified for LASIK, subjects with atypical topography, and keratoconus subjects in 280 simulations. Finite element analysis output was then interrogated to extract several risk and outcome variables. We tested the hypothesis that strain is greater in known at-risk eyes than in normal eyes, evaluated the ability of a candidate strain variable to differentiate eyes that were empirically disqualified as LASIK candidates, and compared the performance of common risk variables as predictors of this novel susceptibility marker across multiple virtual subjects and surgeries.

Results:

A candidate susceptibility metric that expressed mean strains across the anterior residual stromal bed was significantly higher in eyes with confirmed ectatic predisposition in preoperative and all postoperative cases (P≤.003). The strain metric was effective at differentiating normal and at-risk eyes (area under receiver operating characteristic curve ≥ 0.83, P≤.002), was highly correlated to thickness-based risk metrics (as high as R² = 95%, P<.001 for the percent of stromal tissue altered (PSTA)), and predicted large portions of the variance in predicted refractive response to surgery (R² = 57%, P<.001).

Conclusions:

This study represents the first large-scale 3-dimensional structural analysis of ectasia risk and provides a novel biomechanical construct for expressing structural risk in refractive surgery. Mechanical strain is an effective marker of known ectasia risk and correlates to predicted refractive error after myopic photoablative surgery.

INTRODUCTION

Corneal ectatic disease is a major cause of impaired vision-related quality of life in the United States^1,2 and is one of the leading indications for corneal transplantation.³ While post-refractive surgery ectasia is uncommon with a reported incidence of 0.04% to 0.6%,^4,5 LASIK is one of the most commonly performed procedures worldwide, and identifying at-risk patients is a major focus of refractive surgery screening exams.⁶ Like the spontaneously occurring forms of the disease, post-refractive surgery ectasia is characterized by progressive local steepening, increasing refractive error with irregular astigmatism, and potential loss of best-corrected visual acuity^7,8 related to structural failure of the load-bearing layers of the cornea.^9–13 While clinical features such as preoperative topographic irregularity, high myopic correction, young age and absolute or relative depth of surgical disruption have been identified as risk factors for post-LASIK ectasia,^4,5,7,14,15 aggregating such information into a clinical decision regarding risk propensity remains one of the most challenging issues for practicing refractive surgeons.

The Ectasia Risk Scoring System⁴ introduced a useful semi-quantitative approach to screening that integrates multiple risk factors in a straightforward grading scheme. In addition to its practical utility, the analysis it is based upon was a critical step in the effort to understand which intrinsic (patient) and extrinsic (surgical) variables relate to the presence or absence of ectasia. Risk models based on historical data are limited, however, in the sense that they are statistical constructs based only on the available measures of disease and risk factors.^16,17 Issues include 1) a scarcity of cases due to the rarity of the condition itself, an ascertainment bias in obtaining cases for analysis due to medicolegal ramifications or loss of follow-up, and lack of a centralized registry process for reporting cases, 2) sparsity of data for documented cases, where missing risk drivers can skew predictive models or lead to poorly conditioned models with low external validity, 3) a binary rather than continuous approach to risk assessment due to models built on disease presence rather than disease severity or susceptibility, and 4) a phenomenological rather than mechanistic approach to risk assessment, in which the resulting statistical relationships are conditioned to fit the data but do not necessarily represent the mechanistic relationships between factors. This confounds attempts to make de novo inferences in new patients with novel combinations of risk factors or to develop strategies to mitigate risk.

With the goal of better characterizing ectasia risk and addressing each of these barriers to traditional clinical investigation, a computational mechanics approach was applied. The purpose of this study was to investigate biomechanical strain as a structural susceptibility metric for corneal ectasia in a large-scale computational trial. To accomplish this objective, we tested the hypothesis that strain is greater in known at-risk eyes than in normal eyes, evaluated the ability of a candidate strain variable to differentiate eyes that were empirically disqualified as LASIK candidates on the basis of clinical topographic and 3D tomographic analysis, and compared the performance of common risk variables as predictors of this novel susceptibility marker across multiple virtual subjects and surgeries.

METHODS

PATIENT SELECTION

Retrospective chart review was performed under an IRB-approved research protocol (Cleveland Clinic protocol #13-213). A total of 40 eyes of 40 patients were selected for serial simulation. In addition to the group-specific characteristics that follow, inclusion criteria included availability of Scheimpflug-based corneal tomography with at least 10 diametric millimeters of anterior corneal elevation data and absence of prior ocular surgery. Ten eyes of 10 consecutive patients were selected that were deemed normal candidates for LASIK (Group 0), ultimately underwent treatment for myopia or low myopic astigmatism at the Cleveland Clinic Cole Eye Institute, and were followed for a year postoperatively with no refractive regression or topographic change to suggest ectasia. Eight more eyes from 8 patients with atypical corneal topographic features such as asymmetric bowtie and against-the-rule astigmatic patterns, including an eye with pellucid marginal degeneration, made up Group 1. Ten eyes of 10 patients that were disqualified as LASIK candidates based on topographic/tomographic features by an experienced refractive surgeon at another institution (see Acknowledgements) were included as an empirically classified high-risk group (Group 2). Finally, 12 eyes of 12 patients with manifest keratoconus from the Cole Eye Institute with a range of disease severities were included as a positive control group representing known high-risk status (Group 3). To avoid statistical bias related to the use of both eyes of a patient, a single eye was selected from each of these 40 patients for modeling by a coin toss. The modeling results are agnostic to anything other than the patient-specific corneal geometries used to drive the simulations, the material assumptions, and the case-specific surgical parameters. Accordingly, patient characteristics such as age, race and gender were not abstracted from the chart review and are not considered explicitly as variables in these simulations.

CORNEAL MATERIAL MODEL

For modeling purposes, the cornea was represented as a nonlinear, anisotropic, hyperelastic, nearly incompressible tissue with depth-dependent material properties.^13,18,19 To simulate this spectrum of behavior, a microstructural fiber-reinforced material model representing corneal collagen fibers was combined with an isotropic Neo-Hookean solid extrafibrillar matrix to produce a composite corneal stroma.²⁰ Collagen crimping behavior was accounted for by representing each collagen fibril as a three-dimensional spring as proposed by Freed et al^20,21 where H is the axial distance between two turns of the helix, R is the radius of the helix, and r is the radius of the fiber thickness. The microstructural helical spring model requires three parameters: H_o/R₀, the ratio between initial axial distance between two turns within the helix and the initial radius of the helix, R₀/r₀, the initial radius of the helix and the radius of the fiber thickness, and E_f, the elastic modulus of the fiber when fiber is uncrimped and takes on more linear stress/strain behavior²⁰. The resulting fiber behavior was calculated using the algorithm given elsewhere by Freed et al.²¹

Corneal material strength is dependent on corneal collagen fiber distributions and their preferred orientations.^22–25 To enhance the microstructural fidelity of the model, the fiber behavior algorithm summarized above was combined with a formulation given by Pinsky et al.¹⁹ for representing the stroma’s preferred collagen orientation in the strain energy density (W) equations that define the material response of the cornea (Equations 1–4). The equations are reproduced in part here primarily to illustrate how fiber and matrix components are accounted for in the overall strain energy density function (Equation 1) and how the fiber component is defined using angular probability density functions (Φ) to describe the presence of fiber populations as a function of rotational angle (θ) and radial distance from the corneal center (R) (Equations 2–4). The separate treatment of fiber orientation for central (Equation 3) and peripheral (Equation 4) cornea allows representation of the transition from predominantly orthogonal to more circumferential/tangential orientations near the limbus.^26,27 The terms n, c₁, and c₂ in Equations 3 and 4 represent an exponential term and 2 constants, respectively, which are used to modify the angular fiber distribution. At each integration point within the model, spatial splay of fibers was modeled and angularly integrated to represent a gradual change in fiber orientation from the center to the periphery of cornea to represent the increased number of transverse fibers observed in those regions. Depth-dependent dependent properties of the cornea^28,29 were simulated by linearly scaling the ground matrix material constant, C₁₀, down to 50% from anterior to posterior stroma. The material model was implemented in an Abaqus v611 UMAT subroutine (Dassault Systemes Simulia Corp., Providence, RI). The pre-treatment corneal material constants were obtained for each eye through individual inverse finite element analyses using published experimental inflation and tensile test data from a 50 year-old excised human cornea.^30,31 Pre-operative material constants were defined as follows: the elastic modulus of the isotropic ground matrix C₁₀ = 0.04 MPa, the compressibility constant D = 0.0001 MPa⁻¹, the ratio of the axial length of the collagen fibers spring to the diameter of the collagen fiber H₀r₀ = 30.5, the unit-less ratio of radial diameter of the collagen fiber to the diameter of the collagen fiber R₀r₀ = 1.51, and the elastic modulus of the collagen fibers E_f = 32 MPa. Epithelium was modeled as a uniformly thick 50 µm isotropic hyperelastic neo-Hookean material. The shear modulus of the epithelium was set as 1% of the shear modulus of the stroma, and the fiber component was omitted due to absence of continuous collagen elements and the epithelium’s negligible contribution to the corneal structural response.³²

• 1)
  $$W=W_{\mathit{isotropic}}+W_{\mathit{fiber}}+W_{\mathit{volumetric}}$$
• 2)
  $$W_{\mathit{fiber}}=\frac{1}{\mathrm{\Pi }}\underset{0}{\overset{\mathrm{\Pi }}{\int }}\mathrm{\Phi }\left(R_{\mathit{cornea}},\phi ;\theta \right)W_{\mathit{fiber}}\left(R,\phi ;\theta \right)d\theta$$
• 3)
  $$\begin{array}{ll}\mathrm{\Phi }\left(R_{\mathit{cornea}},\phi ;\theta \right)={\text{cos}}^{2n}(\theta )+{\text{sin}}^{2n}(\theta )+c_1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hfill & \text{for}\hspace{0.17em}0<{\text{R}}_{\text{cornea}}<4.5\text{mm}\hfill \end{array}$$
• 4)
  $$\begin{array}{ll}\mathrm{\Phi }\left(R_{\mathit{cornea}},\phi ;\theta \right)={\text{sin}}^{2n}(\theta -\varphi )+c_2\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hfill & \text{for}\hspace{0.17em}4\text{mm}<{\text{R}}_{\text{cornea}}<5.5\text{mm}\hfill \end{array}$$

PATIENT-SPECIFIC PREOPERATIVE MODEL GENERATION

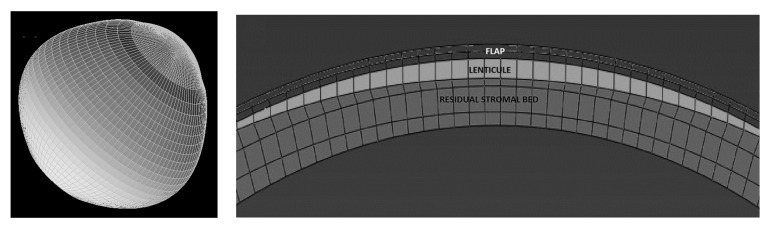
Patient-specific pre-operative Cartesian coordinates of the anterior and the posterior surfaces were exported from Pentacam (v. HR, Oculus Optikgerate GmbH, Germany) as grid-format comma separated value files. The data were interpolated and meshed with 8-node hexahedral brick elements (Figure 1 Left) using custom meshing software (SpecifEye, v0.1, OptoQuest, Cleveland, OH).³³ Each pre-operative corneal geometry was divided into 3 or 4 regions in depth (Figure 1 Right) depending on whether PRK or LASIK was modeled: epithelium (50 μm, uniform thickness), stromal component of the LASIK flap (0, 50 or 110 μm depending on whether PRK, LASIK with a 100 μm flap, or LASIK with a 160 μm flap was modeled), stromal interface wound (10 μm, LASIK only), and residual stroma (encompassing the remaining patient-specific corneal thickness). ³⁴ A generic sclera, with anterior edge thickness matched to the patient-specific corneal peripheral thickness, was modeled to form the posterior portion of the eye to allow for physiological deformations at the limbus.^33,35 The interior surface of each globe was then subjected to a homogenous intraocular pressure (IOP) of 15 mmHg.

FIGURE 1.

An example of a corneo-scleral mesh (A) and defined regions within the mesh for simulation of myopic photoablative surgery (B). The flap includes epithelial and stromal components, the lenticule represents the area that is removed according to a wavefront-optimized ablation algorithm for the specified dioptric correction, and the residual stromal bed represents the unaltered posterior stroma.

SIMULATION OF MYOPIC PRK AND LASIK PROCEDURES

Myopic ablations were modeled as spherical treatments of either 4 or 8 D and were translated from the spectacle plane to the corneal plane (3.80 and 7.27 D, respectively). Each treatment was modeled as a 9mm diameter (6.5mm optical zone) wavefront-optimized ablation profile derived from the equations given by Mrochen et al³⁶ and resulted in central ablation depths of 113.8 and 59.6 µm, respectively, which were used for case-specific calculations of postoperative residual stromal bed (RSB)¹⁴ and percent tissue altered (PTA)³⁷ variables used in a later analysis of risk variables. Finite element analyses were run using a commercial finite element solver (Abaqus v6.11, Dassault Systemes Simulia Corp., Providence, RI). The amount of simulated ablation was calculated for each node in the 3D finite element model and the nodes were repositioned according to their ablation magnitudes to generate the ablation profile with a custom Python script. Since clinical Scheimpflug tomography images were acquired while each eye was subjected to a physiological IOP, the stress-free geometries for each eye had to be calculated with an iterative technique^18,38 and applied as described previously ^39,40 to provide a preoperative model that represented the clinical tomography accurately.

The wound regions surrounding the flap were also simulated.⁴¹ The flap was modeled as a 9mm diameter flap of uniform thickness with a 90-degree (perpendicular to the surface) flap side cut angle. The side cut wound region was defined as a 305° arc (360° minus hinge width of 55°) with a 10um thickness. The side cut was simulated with a 50% weakening in the isotropic component and omitting the fiber component of the strain energy equation (Equation 5). The flap was simulated by omitting the fiber component of the strain energy equation (Equation 6).³⁴ Hinge width was defined as 550 for all LASIK cases at 12 o’clock position. All simulations conformed to these reported surgical parameters for each patient. A wound region beneath the flap was also defined in LASIK models with 90% weakening of the isotropic region and omission of the fiber component from the strain energy equation (Equation 7).^42–44 The material constants of the residual stroma were not altered for surgical simulations. PRK was modeled with identical ablation parameters but with a no flap component, no lamellar stromal wound interface, and no flap side cut wound.

• 5)
  $$W_{\mathit{cutwound}}=0.5\times W_{\mathit{isotropic}}+W_{\mathit{volumetric}}$$
• 6)
  $$W_{\mathit{flap}}=W_{\mathit{isotropic}}+W_{\mathit{volumetric}}$$
• 7)
  $$W_{\mathit{wound}}=0.1\times W_{\mathit{isotropic}}+W_{\mathit{volumetric}}$$

EXTRACTED VARIABLES, ANALYSIS AND STATISTICAL APPROACH

Simulations of 6 different surgical combinations (PRK 4D, PRK 8D, 100 µm flap LASIK 4D, 100 µm flap LASIK 8D, 160 µm flap LASIK 4D and 160 µm flap LASIK 8D) were performed in each of 40 eyes for a total of 280 total simulations including preoperative models. Complete material solutions including displacements, stresses, strains and corneal surface coordinates were exported for selective analysis. All preoperative and postoperative geometries were exported directly from Abaqus to SpecifEye for calculation of geometric variables. Geometric variables were defined primarily for use in univariate linear regression analyses to assess their value as predictors of the mechanical strain once a strain candidate variable was selected, and best-subset regression was performed to assure that no combination of predictors performed significantly better than one-predictor models. These variables included the mean anterior tangential curvature over the central 3mm region (K_mean), the difference between the average curvature of the steepest meridian and the average curvature of the flattest meridian (Anterior Corneal Astigmatism), maximum tangential curvature value (K_max), distance of this point from the corneal vertex (K_max Distance, expressed as the resultant vector of the x and y coordinate vectors), central corneal thickness (CCT, measured as the distance between the anterior and posterior corneal surfaces along a normal to an anterior surface tangent at the corneal vertex), Thinnest Point Value (the local corneal thickness at its thinnest point), and the Thinnest Point Distance (a resultant vector calculated in the same way as K_max Distance). A previously described clinical risk variable, percent tissue altered (PTA = ((flap thickness + ablation depth)/preoperative central corneal thickness) × 100%),³⁷ indicates the depth of surgical tissue disruption as a percentage of total preoperative corneal thickness calculated at the center of the cornea. This metric was modified to properly account for the negligible structural contribution of the corneal epithelium. The new variable, percent stromal tissue altered (PSTA), is also calculated in the central cornea but is expressed as 100% x (flap thickness – epithelial thickness + ablation depth)/(preoperative central corneal thickness – epithelial thickness) for LASIK and 100% x (stromal ablation depth)/(preoperative central corneal thickness – epithelial thickness) for PRK where in both equations the denominator is the preoperative stromal thickness. The surgically induced change in K_mean (postoperative – preoperative) was calculated for each PRK and LASIK simulation and subtracted from the programmed refractive change at the corneal plane to derive the degree of myopic over- or undercorrection predicted by each simulation. Two-sided heteroscedastic Student’s t tests for independent samples were performed to test for significant differences between the normal and keratoconus groups in this response. The criterion for statistical significance criterion was defined as P<0.05 for all comparisons.

Maximum principal strain (MPS) was computed during finite element analysis for every point in the structure and exported for analysis. MPS represents the maximum amount of tensile strain at that material point under the modeled loading conditions, and higher strains are associated with a higher risk of material failure when subjected to tensile deformations.⁴⁵ Strain is a dimensionless quantity that expresses tissue displacement as a function of initial position. Six MPS-derived summary variables were defined for analysis: Mean MPS (individual MPS values averaged over one of 3 regions of interest) and 3 Highest MPS quantities (describing the value of the highest MPS value within one of 3 regions of interest). The 3 analyzed regions were 1) a 9mm wide surface along the anterior residual stromal bed, 2) a 9mm wide surface along the posterior residual stroma, or 3) a 3-dimensional zone encompassing the full thickness of the cornea and spanning the central 5mm diameter. All strain summary variables used the same MPS data as a source and differed only in how these data were summarized.

A comparison of these strain variables was performed by testing for statistical differences between MPS values for the negative controls (Group 0, normal LASIK candidates) and positive controls (Group 3, keratoconus). Comparisons were performed across all 6 candidate variables as defined above with 2-sided heteroscedastic Student’s t-tests for independent samples. Comparisons involving Groups 1 and 2 were not performed to minimize unnecessary comparisons and because those groups were not necessarily defined for the purpose of creating a continuous risk spectrum for the study of ectasia risk. Candidate strain variables were then down-selected using a best-subsets regression analysis to identify the strain variable with the highest coefficient and R-squared value. This variable was then subjected to a discriminative test (Receiver Operating Characteristic (ROC) analysis) for differentiating strain behavior first between Groups 0 and 3, then between Group 0 and Group 2, which represented clinically suspicious eyes disqualified from LASIK by an independent expert surgeon.

All statistical analyses were performed with Minitab (v17, State College, PA) except ROC analyses, which were performed with MedCalc Statistical Software (v15.11.4, MedCalc Software bvba, Ostend, Belgium).

RESULTS

GEOMETRIC RESULTS

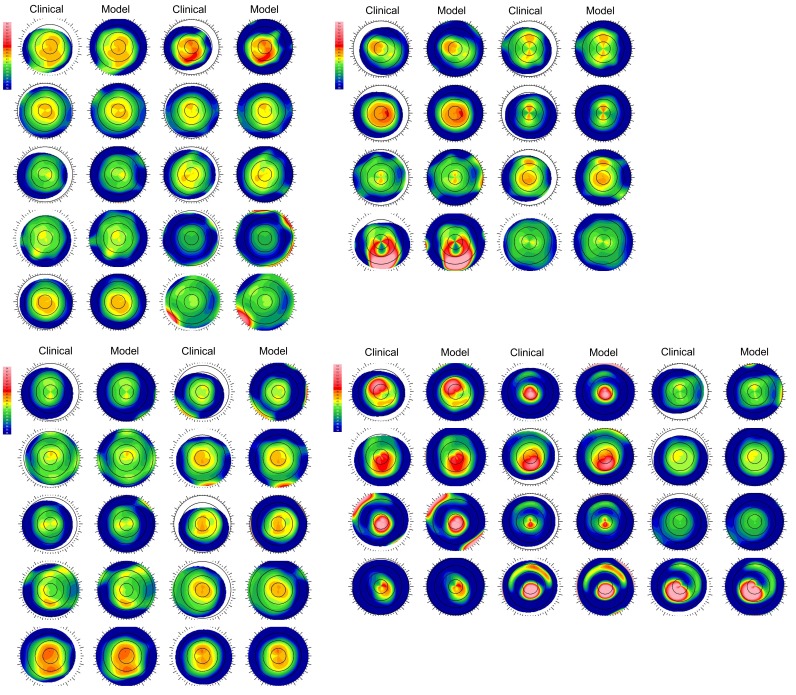
A summary of geometric variables for the 40 preoperative models is presented by group in Table 1. As expected, models derived from keratoconus eyes demonstrated higher average curvature and astigmatism values than normal preoperative LASIK candidates, thinner corneas, more eccentric thinnest and steepest points. Complete anterior surface tangential curvature maps for each eye are available in the Appendix as Figure 8 to facilitate a qualitative comparison of the types of eyes included in each group and an assessment of the agreement in curvature between each preoperative computational model and its corresponding clinical map. Each model is depicted after meshing, merging with a scleral geometry, and determination of the stress-free state as described in the Methods.

TABLE 1.

PREOPERATIVE CORNEAL CURVATURE AND THICKNESS CHARACTERISTICS OF MODEL EYES BY ENROLLMENT GROUP^*

	NORMAL (GROUP 0) n = 10	ATYPICAL (GROUP 1) n = 8	DISQUALIFIED (GROUP 2) n = 10	KERATOCONUS (GROUP 3) n = 12
Kmax (D)	44.14 ± 1.70	45.84 ± 1.93	44.61 ± 1.29	52.27 ± 8.09
	40.46 - 46.92	43.48 - 49.43	43.23 - 46.75	41.65 - 67.82
Kmax Distance (mm)	0.90 ± 0.59	1.99 ± 1.48	0.83 ± 0.61	1.09 ± 0.77
	0.22 - 2.29	0.68 - 4.90	0.13 - 1.99	0.14 - 2.38
Kmean (D)	43.23 ± 1.62	43.40 ± 1.40	43.65 ± 1.34	45.62 ± 3.26
	39.72 - 45.42	41.64 - 46.02	41.91 - 45.95	40.68 - 50.23
Anterior Corneal Astigmatism (D)	0.82 ± 0.40	3.14 ± 3.16	0.90 ± 0.56	2.79 ± 2.63
	0.31 - 1.41	0.34 - 9.32	0.25 - 2.10	0.22 - 9.82
CCT (µm)	567 ± 32	565 ± 26	510 ± 26	510 ± 56
	515 - 624	519 - 590	458 - 543	419 - 628
Thinnest Point Value (µm)	563 ± 32	559 ± 28	505 ± 27	494 ± 63
	514 - 623	511 - 583	458 - 541	406 – 619
Thinnest Point Distance (mm)	0.65 ± 0.24	1.15 ± 0.95	0.82 ± 0.30	1.03 ± 0.43
	0.35 - 1.17	0.64 - 3.49	0.48 - 1.50	0.40 - 1.71

^*D = Diopters, µm = micrometers, mm = millimeters from the corneal vertex calculated as the absolute magnitude of the resultant vector of the x and y decentration of the curvature or thickness feature, CCT = central corneal thickness (at vertex). Values displayed are mean ± standard deviation and range (minimum – maximum).

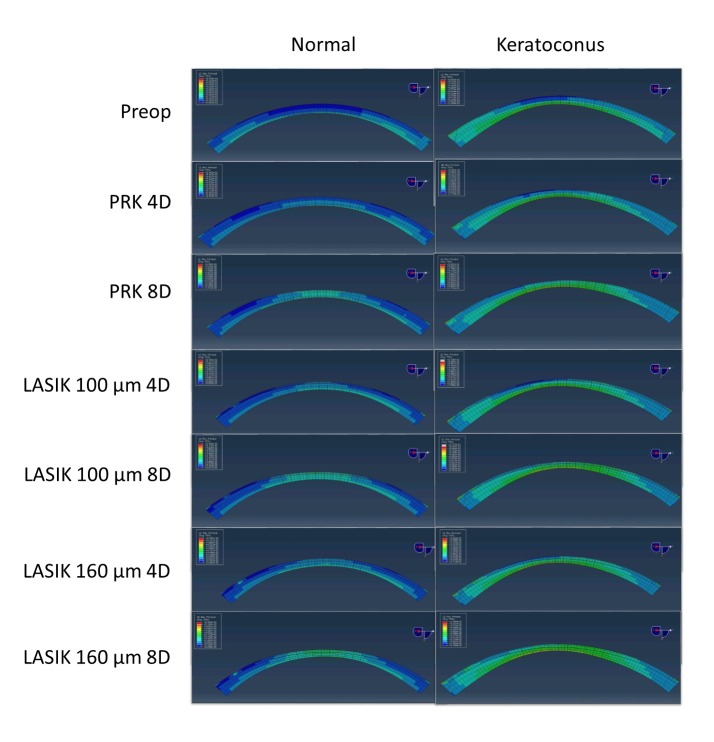
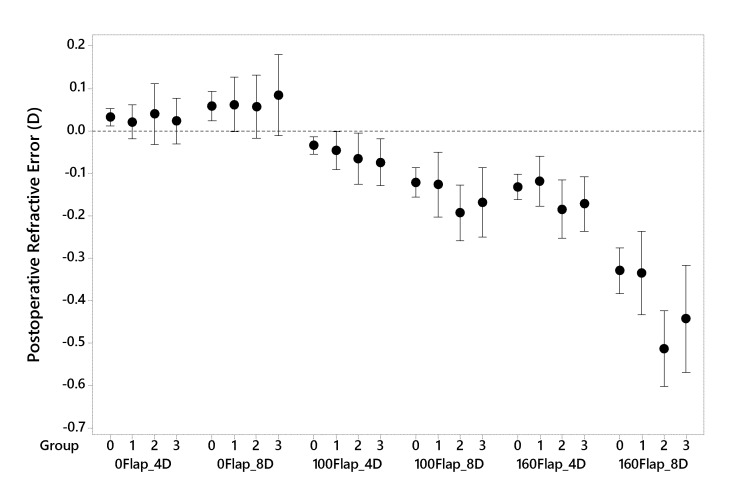
Figure 2 shows examples of cross-sectional strain (MPS) maps for a normal eye and a keratoconic eye as each progressed through the modeling sequence exposing each eye to every surgical combination. This process was repeated for all 40 study eyes across the 4 enrollment groups to generate a clinically relevant range of responses for analysis. Differences in the strain magnitudes and distributions between the eyes are evident in the preoperative state and with every surgical comparison that follows. In Figure 3, the postoperative refractive error calculated from the central 3mm tangential curvature data is plotted for every simulation as a function of group and surgical procedure. Simulated PRK and LASIK resulted in central corneal curvature changes that closely approximated the programmed change, and differences in response to each surgical perturbation were not significantly different between the normal and keratoconic groups (P>.09 in all cases, Table 2). A trend toward myopic undercorrection with more invasive surgical procedures was observed.

FIGURE 2.

Illustrative maps of maximum principal strain values in central cross sections of serial surgical simulations on a normal pre-LASIK eye (left column) and a keratoconic eye (right column). Higher strains are evident in the keratoconic eye across all surgical procedures and in the preoperative model. D = Diopters of myopic treatment, µm = micrometers of flap thickness. Color scales are normalized across all images for comparability, and simulations were performed at a standardized intraocular pressure load (15 mmHg) with an assumption of identical material property constants in all eyes. Cool colors (blue) indicate lower strain values while warmer colors (green) indicate higher strain values.

FIGURE 3.

Difference in programmed vs. achieved refractive result for simulated PRK and LASIK procedures for 4 or 8 Diopters of myopia using mean central (3mm) tangential curvature change as a metric. D = Diopters, 0Flap = PRK, 100Flap = LASIK with a 100 micrometer flap thickness, 160Flap = LASIK with a 160 micrometer flap thickness. Clinical groupings of the patient cohort are represented on the x axis as follows: 0 = normal refractive surgery candidates who eventually underwent LASIK, 1 = atypical topographic patterns not categorized as keratoconus suspects, 2 = suspicious topographic patterns not characterized as manifest keratoconus but disqualified from LASIK, and 3 = manifest keratoconus. Means and 95% confidence intervals are displayed.

TABLE 2.

COMPARISON OF NORMAL AND KERATOCONIC GROUP RESPONSES TO SIMULATED MYOPIC REFRACTIVE SURGERY (DEVIATION FROM PROGRAMMED CURVATURE CHANGE AND STRAIN VARIABLES)^*

	GROUP	PREOP	PRK 4D	PRK 8D	100 µM FLAP LASIK 4D	100 µM FLAP LASIK 8D	160 µM FLAP LASIK 4D	160 µM FLAP LASIK 8D
Postop Refractive Error (D)	Norm (Group 0, n=10)	--	0.03 ± 0.03‡	0.06 ± 0.05‡	−0.03 ± 0.03‡	−0.12 ± 0.05‡	−0.13 ± 0.04‡	−0.33 ± 0.08‡
	KC (Group 3, n=12)	--	0.02 ± 0.09‡	0.08 ± 0.15‡	−0.07 ± 0.09‡	−0.17 ± 0.13‡	−0.17 ± 0.10‡	−0.44 ± 0.20‡
	P‡	--	.7‡	.6‡	.2‡	.2‡	.2‡	.09
Mean MPS† Anterior	Norm	2.07 ± 0.10	2.31 ± 011	2.60 ± 0.13	2.50 ± 012	2.79 ± 0.14	2.66 ± 0.14	2.94 ± 0.16
	KC	2.30 ± 0.20	2.56 ± 0.21	2.88 ± 0.24	2.77 ± 0.27	3.09 ± 0.30	2.99 ± 0.33	3.33 ± 0.40
	P	.003	.003	.003	.007	.007	.006	.008
Highest MPS Anterior	Norm	2.38 ± 0.23	2.53 ± 0.18	2.91 ± 0.15	2.71 ± 0.16	3.09 ± 0.16	2.85 ± 0.15	3.26 ± 0.18
	KC	2.73 ± 0.37	2.83 ± 0.31	3.21 ± 0.32	3.00 ± 0.31	3.44 ± 0.37	3.22 ± 0.38	3.80 ± 0.70
	P	.01	.01	.009	.01	.01	.009	.02
Mean MPS Posterior	Norm	2.78 ± 0.18	2.83 ± 0.18	2.93 ± 0.18	2.90 ± 0.18	3.01 ± 0.18	3.01 ± 0.20	3.14 ± 0.19
	KC	3.14 ± 0.38	3.21 ± 0.39	3.31 ± 0.40	3.29 ± 0.39	3.41 ± 0.40	3.44 ± 0.44	3.60 ± 0.51
	P	.008	.008	.008	.008	.008	.008	.01
Highest MPS Posterior	Norm	3.03 ± 0.37	3.05 ± 0.38	3.14 ± 0.38	3.09 ± 0.35	3.22 ± 0.33	3.20 ± 0.37	3.34 ± 0.35‡
	KC	3.53 ± 0.55	3.55 ± 0.55	3.66 ± 0.61	3.59 ± 0.54	3.72 ± 0.66	3.75 ± 0.60	4.22 ± 1.48‡
	P	.02	.02	.03	.01	.02	.02	.07‡
Overall Mean MPS	Norm	2.25 ± 0.10	2.43 ± 0.11	2.66 ± 0.12	2.42 ± 0.11	2.59 ± 0.12	2.54 ± 0.12	2.72 ± 0.13
	KC	2.48 ± 0.24	2.69 ± 0.25	2.94 ± 0.27	2.69 ± 0.25	2.88 ± 0.27	2.85 ± 0.29	3.06 ± 0.33
	P	.008	.006	.004	.004	.004	.005	.006
Overall Highest MPS	Norm	2.77 ± 0.23	2.84 ± 0.23	3.02 ± 0.22	4.21 ± 0.69‡	4.20 ± 0.69‡	4.47 ±0.65	4.47 ± 0.61
	KC	3.16 ± 0.47	3.23 ± 0.47	3.43 ± 0.45	5.01 ± 1.30‡	5.05 ± 1.31‡	5.87 ± 1.61	5.81 ± 1.62
	P	.02	.02	.02	.08‡	.07‡	.02	.02

^*µm = micrometers, D = Diopters, Norm = normal group, KC = keratoconus group, MPS = maximum principal strain, Mean = average value over analyzed region, Highest = highest value over analyzed region, Anterior = anterior surface of residual stromal bed with a 9mm analysis diameter, Posterior = posterior surface of corneal stroma with a 9mm analysis diameter, Overall = a 3-dimensional analysis zone with a depth encompassing the full thickness of the cornea and spanning the central 5mm diameter.

^†Strain values are dimensionless and are given as strain ×10² to provide a % strain. All values reported as mean ± standard deviation.

^‡Indicate comparisons of normal and KC groups for which independent samples 2-sided heteroscedastic Student’s t tests yielded P values > 0.05 (not significant).

ANALYSIS AND SELECTION OF A PRIMARY SUSCEPTIBILITY METRIC BASED ON STRAIN

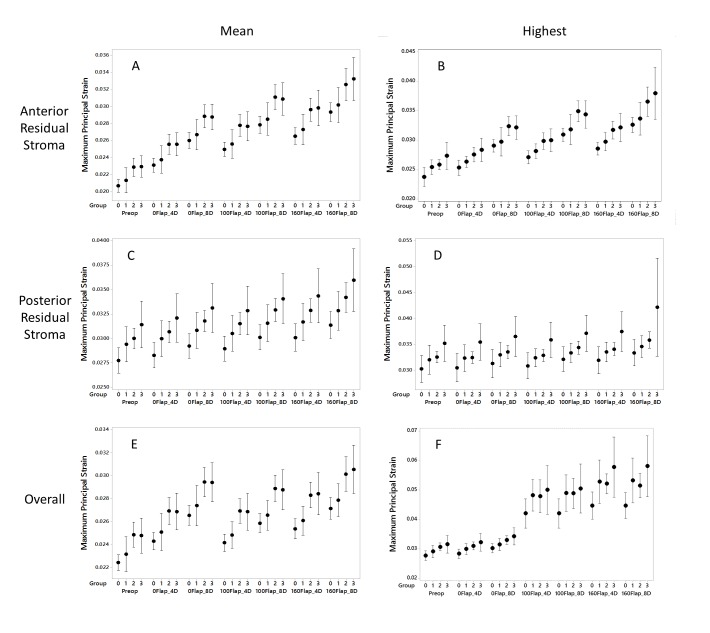
Figure 4 summarizes the strain behavior across all groups and surgical types as reflected by the 6 structural susceptibility variable candidates. Table 2 presents the same strain data, but only for groups 0 (normal, negative control for ectasia susceptibility) and 3 (keratoconic, positive control for ectasia susceptibility) and includes accompanying statistical tests for differences between surgical interventions and groups. Figure 4 and Table 2 are both organized from left to right in approximate order of surgical invasiveness with data from the preoperative (unoperated) model on the left, PRK procedures in the middle, and LASIK procedures on the right. Table 2 also presents the biomechanically mediated over- or under-correction of refractive error calculated from the model-based surgical change in anterior corneal curvature. In Figure 4, most of the strain variables demonstrated roughly linear increasing strains as group number increased from 0 (normal) to 3 (keratoconic), but strain levels on the posterior stromal surface were far less sensitive to the type of surgery performed than anterior stromal bed strains. Variability of strain responses was generally higher in keratoconic eyes and probably related to greater variations in initial corneal geometries for that group.

FIGURE 4.

Maximum principle strain values (dimensionless) for simulated PRK and LASIK procedures across 4 patient groups. Mean values (A, C and E) report the average of all maximal principal strain values across the specified analysis region, and highest values (B, D and F) provide the peak maximum principal strain value from each analysis region. Analyzed regions are either a 9mm wide surface along the anterior (A and B) or posterior (C and D) residual stroma or a 3-dimensional zone encompassing the full thickness of the cornea and spanning the central 5mm diameter (E and F). D = Diopters of attempted correction at the spectacle plane, Preop = preoperative models not yet subjected to surgical simulation, 0Flap = PRK, 100Flap = LASIK with a 100 micron flap, 160Flap = LASIK with a 160 micron flap. Clinical groupings of the patient cohort are represented on the x axis as follows: 0 = normal refractive surgery candidates who eventually underwent LASIK, 1 = atypical topographic patterns not categorized as keratoconus suspects, 2 = suspicious topographic patterns not characterized as manifest keratoconus but disqualified from LASIK, and 3 = manifest keratoconus. Means and 95% confidence intervals are displayed.

As seen in Table 2 and Figure 4, strain values increased from the unoperated state to PRK and from PRK to LASIK for comparable myopic corrections. However, as evidenced both by individual results and analysis of the mean values, PRK did not universally result in lower strains than LASIK, nor did thin-flap LASIK universally result in lower strains than LASIK with a thicker flap. For example, strains were lower on average for the 4D, 100-um LASIK simulations than the 8D PRK simulations, and a similar trend was seen when comparing 4D, 160-um LASIK and 8D, 100-um LASIK. These results suggest a complex interplay between surgical variables that is addressed further in the Discussion. Strains were of a higher magnitude in the posterior residual stroma than at the anterior stromal bed. This behavior is consistent with the depth-dependent decrease in corneal elastic modulus^28,44,46,47 incorporated into the stromal material model as described in the Methods. In Table 2, every strain metric demonstrated statistically significant differences between the normal and keratoconic groups based on preoperative loading alone (P≤.02), and the large majority of comparisons in post-operative models were significantly different as well. Refractive undercorrection of myopia was observed as the depth of LASIK treatment increased. and indicates that a steeper postoperative cornea was predicted than simple geometric subtraction of the ablation zone tissue would predict. For LASIK simulations, the overall highest MPS increased markedly when moving from PRK to LASIK. Based on a separate analysis that identified the location of the highest MPS, this could be explained by the locus of highest strain moving from anterior stroma to the flap. This behavior rendered the metric less sensitive to dioptric correction under the flap.

The responses of 3 of the 6 strain variables—particularly those emphasizing anterior stromal bed behavior—were similar, but inspection of the 95% confidence intervals suggested that mean MPS at the anterior stromal bed would be a more effective differentiator of the normal and keratoconus groups. A binary logistic regression on preoperative strain data with stepwise selection of all candidate variables confirmed that mean MPS at the anterior stromal bed performed marginally better at predicting the odds ratio of manifest ectasia than other metrics. However, the difference between this metric and the next best metric, overall mean MPS, was not significant (pairwise ROC comparison, P=0.9). An ROC analysis of the preoperative mean MPS at the anterior stromal bed for differentiating normal (n=10) from keratoconus (n=22) on the basis of strain alone produced an area under the ROC curve of 0.83 (95% CI 0.61 – 0.95, P=.002). When applied to the problem of differentiating normal eyes from the disqualified eyes (Group 2, n=10), the performance of the strain metric was marginally better (AUROC = 0.90, 95% CI 0.68 – 0.99, P<.001).

ECTASIA RISK FACTORS AND RELATIONSHIP TO A STRAIN-BASED SUSCEPTIBILITY METRIC

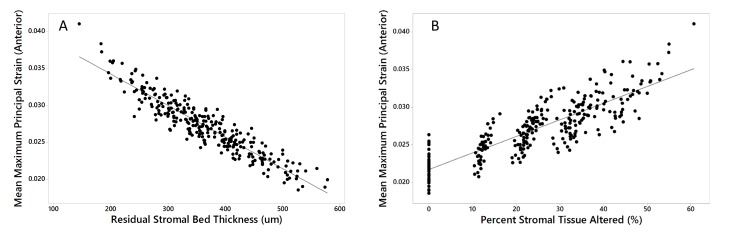
Regression analyses were performed across all 40 eyes and 280 simulations to determine which geometric risk factors are the most important drivers of structural susceptibility across the entire range of responses. The factors investigated are listed in Table 3 along with their univariate linear regression results, including the sign and magnitude of the coefficients describing their relationships to strain. Flap thickness (0 for PRK, 100, or 160um) and attempted refraction correction (0, 4 or 8D) were initially included and demonstrated a significant relationship to strain. However, these variables are clustered due to the fact that only 3 discrete levels for each were simulated and are therefore not well-suited for analysis as continuous variables. Moreover, these factors are implicit in the combined variables RSB and PSTA and because of their covariance with these, fell out of stepwise regression models. Preoperative curvature variables were of little value in predicting strains across preoperative and postoperative models (Table 3). The strongest predictor of strain was RSB, and a second order (quadratic) term was significant, though it only marginally added to the R-squared value so was excluded. Fitted line plots for the relationships between the mean MPS values at the anterior residual bed, where the highest strains of the RSB were concentrated in most simulations, and RSB and PSTA are presented in Figure 5.

TABLE 3.

RELATIONSHIP OF PATIENT AND SURGERY-SPECIFIC ECTASIA RISK VARIABLES TO ABSOLUTE STRAIN IN THE ANTERIOR RESIDUAL STROMA ACROSS ALL MYOPIC SURGICAL SIMULATIONS (N = 280)^*

LINEAR REGRESSION MODEL AND RESULTS:	CONSTANT	COEFFICIENT	P VALUE	R-SQUARED
Kmax (D)	0.01770	0.000203	<.001	9.0%
Kmax Distance (mm)	0.02734	−0.000087	.7	0%
Anterior Corneal Astigmatism (D)	0.02651	0.000385	<.001	4.9%
CCT (µm)	0.05112	−0.000045	<.001	29.5%
Thinnest Point Value (µm)	0.04882	−0.000041	<.001	29.9%
Thinnest Point Distance (mm)	0.02594	0.001437	.001	3.9%
Residual Stromal Bed Thickness, RSB (µm)	0.04282	−0.000043	<.001	86.7%
Percent Stromal Tissue Altered, PSTA (%)	0.02172	0.000221	<.001	71.7%

^*D = Diopters, µm = micrometers, mm = millimeters from the corneal vertex calculated as the absolute magnitude of the resultant vector of the x and y decentration of the curvature or thickness feature, CCT = central corneal thickness (at vertex). Strain = mean maximum principal strain in the anterior residual stroma acquired from finite element analyses of all preoperative and postoperative models

FIGURE 5.

Linear regression demonstrating the strongest predictors of absolute strain across all myopic surgical simulations and preoperative cases. A) Residual stromal bed (RSB) thickness (R-squared = 86.7%, P<.001) and B) percent stromal tissue altered (PSTA, R-squared = 71.7%, P<.001)). In the context of preoperative cases, RSB refers to the total (unaltered) stromal thickness and PSTA = 0%.

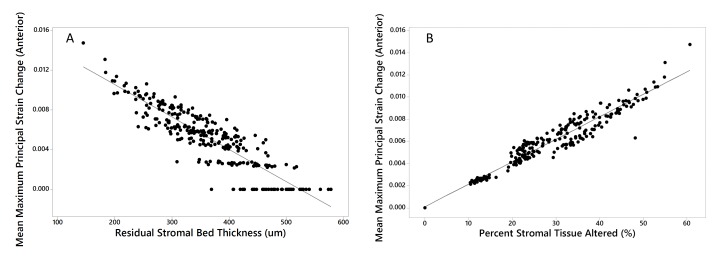
After the results in Table 3 and Figure 5 were obtained, it was hypothesized that PSTA, which is a relative measure of structural impact based on thickness change, might be more strongly correlated to the change in strain than the absolute strain at each simulation endpoint. As illustrated in Figure 6, linear regression analysis of the mean MPS in the anterior stromal bed across all preoperative and postoperative models with case-specific PSTA calculations revealed a strong correlation with 95.6% of variance in strain change (R-squared) explained by PSTA (Strain change = 0.000108 + 0.000203 PSTA, P<0.001). RSB was a strong predictor of surgically induced strain change as well, but PSTA was a better predictor of the increase in strain with myopic refractive surgery than RSB.

FIGURE 6.

Linear regression demonstrating the strongest predictors of preoperative-to-postoperative strain change (rather than absolute strain) across all preoperative and myopic surgical simulations. A) Residual stromal bed (RSB) thickness (R-squared = 79.7%, P<.001) and B) percent stromal tissue altered (PSTA, R-squared = 95.6%, P<.001). In the context of preoperative cases, RSB refers to the total (unaltered) stromal thickness and PSTA = 0%.

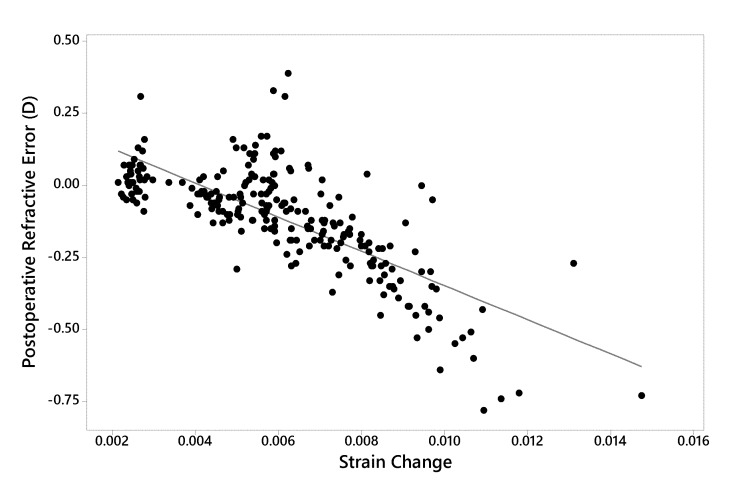
Finally, in Figure 7, the relationship between postoperative refractive error and surgically induced strain change is presented. Refractive error was strongly related to the strain change measured at the anterior residual bed, which predicted 56% of the variance in predicted refractive error (R-squared). A nonlinear trend toward increasing myopic undercorrection was observed with greater strain increases.

FIGURE 7.

Linear regression analysis demonstrating the relationship between postoperative refractive error (achieved – attempted) and strain change (postoperative – preoperative, dimensionless units) across all preoperative and myopic surgical simulations (R-squared = 56.7%, P<.001). D = Diopters. Strain quantity = mean maximum principal strain at the anterior residual stromal bed surface.

DISCUSSION

This computational study provides insight into the complex clinical problem of post-refractive surgery ectasia while circumventing some of the barriers that prevent large-scale clinical investigations of this rare complication. Through patient-specific modeling and iterative surgical simulation on a virtual library of eyes, simulation helped to mitigate the problem of scarcity of cases by generating large datasets from a smaller number of independent patient samples while offering optimal control of variables. A simulation-based approach also allowed for a provocative experimental design in which virtual LASIK and PRK procedures were performed not only in normal refractive surgery candidates but also in atypical eyes, eyes of patients counseled against LASIK, and in keratoconic subjects. The ability to model these procedures in patients with known ectatic predisposition was critical for establishing a spectrum of normal to abnormal strain responses, and such data may be useful as a reference in future simulations for assessing patient-specific risk with a particular procedure.

The use of clinical tomography as the modeling substrate addresses the problem of data sparsity that can afflict statistical models of ectasia risk by incorporating the entire 3-dimensional configuration of each cornea and a precisely specified surgical intervention. In this study, these rich datasets were used in finite element analyses that depend entirely on physics-based interactions, producing results that are implicitly mechanistic and useful for understanding the physical interactions between tissue and surgery. These data structures were then interrogated to extract several risk and outcome variables, and enabled an exploratory analysis of simulation results in normal and at-risk eyes to identify a strain-based susceptibility metric and test the hypothesis that strain is differentially higher in eyes predisposed to ectasia. These steps address the lack of a continuous susceptibility metric, which was then used as a dependent variable to identify key risk drivers for increased ectasia susceptibility.

Strain is an important factor in the tensional homeostasis that drives cellular responses and extracellular matrix maintenance and remodeling in human connective tissues. Cells are exposed to cytoskeletal tension and possess stretch-activated ion channels, integrins and other components that allow the cell to sense and react to strain.⁴⁸ Changes in matrix strain have been shown in corneal stromal keratocyte cultures to activate mechanobiological pathways that normalize matrix tension,⁴⁹ and recent cyclic stretching experiments with corneal fibroblasts have shown that strain magnitude alters the balance of expression of matrix metalloproteinases (MMPs) and tissue inhibitors of MMPs (TIMPs) such that tissue degradation is favored with higher strains.⁵⁰ The same loads in corneas with abnormally low material strength (as in keratoconus or possibly after refractive surgery) would results in higher strains than in normal corneas⁴⁹ and would promote greater activation of destructive pathways in the corneal stroma. It is in this sense that strain is a potentially important predictor of the degradative pathways that promote ectasia.

The hypothesis that mechanical strain is higher in eyes with known ectasia susceptibility is strongly supported by the current study. Furthermore, strain increased as a function of surgical invasiveness. The additional finding that surgically induced strain changes were highly correlated to predicted postoperative refractive error has implications for a priori estimation of biomechanical sources of outcome variability and optimization of surgical planning. The design decision to start with a larger set of candidate strain expressions then select a single variable for subsequent analyses was made to minimize unnecessary statistical comparisons and further burdening the interpretation of the results. However, it is evident from this study that some of the other strain representations may perform equally well, and those that are more sensitive to peak strains could afford more sensitivity (but perhaps less specificity) that could be advantageous in certain screening applications or surgical comparisons. Most strain variables demonstrated reasonable predictive mapping to risk state, but the mean MPS of the anterior stromal bed was selected based on its marginally stronger discriminative performance and the rationale that the residual stromal bed is the critical layer for resisting creep after ablative surgery. Group 1 served to ensure that the overall virtual cohort had a sufficient range of clinical geometries to drive an effective sensitivity analysis and to specifically include eyes that fall outside the spectrum of normal but do not overlap with diagnostic criteria for keratoconus. Group 2 was utilized as an independent clinical sample for which the computational analysis and the investigators were agnostic to the decision parameters regarding refractive surgery candidacy. This group served as a “group of interest” for relating structural risk parameters to the clinical process of decision making. An ROC analysis demonstrated that with nothing more than preoperative strain behavior from the IOP-loaded model, these disqualified cases without overt evidence of manifest ectasia could be differentiated from normal LASIK candidates. The group sizes used to generate this conclusion were small (n=20) but represent an important initial observation linking an objective, model-derived measure of strain susceptibility to the expert clinical decision making process.

A prior finite element modeling study of LASIK from our group demonstrated that undercorrection of myopia could be produced by reducing preoperative corneal material strength while holding all other variables constant.³⁵ The same study abstracted anterior chamber depth data from the model results and attributed myopic undercorrection to a forward corneal apical displacement and central corneal steepening that undermined a full myopic correction. It was hypothesized that this occurs in response to an increased tensile load borne across a residual stroma with weaker properties than the otherwise identical corneal model with higher corneal elastic modulus.³⁵ However, that study based all simulations on a single preoperative corneal geometry and could not offer conclusions about the importance of geometric variation in a surgical population. By contrast, the current study treated material properties as constant across the study sample rather than introduce arbitrary patient-specific material properties as confounding variables, and instead performs a large-scale sensitivity analysis emphasizing the interaction of surgical variables across a diverse library of clinical geometries. The increasing tendency toward myopic undercorrection with more invasive surgery in this study is related to a similar central structural weakening of the cornea, increased localized strain, and forward displacement under the force of the intraocular pressure. Taken together, this and prior computational modeling studies suggest that geometry and corneal biomechanical properties, when varied independently, can influence the instantaneous shape response to tissue removal. The current study is the first to quantify mechanistic relationships between corneal shape features and mechanical strain and to directly link surgically induced strain changes to refractive outcome.

The large-scale analysis of clinical geometric ectasia risk factors demonstrated much stronger correlations between strain and thickness-based metrics than preoperative curvature metrics such as K_max or anterior corneal astigmatism. Regression analysis produced physically plausible relationships, with strain increasing with higher preoperative K_max, higher corneal astigmatism, lower central corneal thickness, lower thinnest point-thickness, lower RSB thickness, and higher PSTA. Even across a cohort of eyes with significant variation in corneal geometry, preoperative anterior corneal astigmatism was only weakly correlated to strain behavior as measured by the mean MPS across the 9mm anterior residual stromal bed. A potential caveat in interpreting the relative performance of these clinical risk factors is that individual differences in corneal elastic properties were not accounted for. To the extent that material property differences are intrinsic to or associated with corneal curvature features,^51,52 or to the extent that they are associated with native corneal thickness differences, the relative predictive value of these metrics could be different in practice. One rationale for incorporating eyes with a variety of astigmatic patterns was a supposition that meridional shape asymmetry might lead to meridional strain asymmetries that are amplified after the cornea is thinned by photoablative surgery. Metrics that average strains across the anterior RSB would mask meridional strain differentials, and additional analysis with the Highest MPS variable or with meridional strain analyses comparing the steep and flat axes of astigmatism are planned to better characterize meridional strains in the setting of preoperative astigmatism and to investigate their relationship to surgically induced astigmatism in this dataset. The study groups (particularly with inclusion of Groups 1 and 3) were designed to contain eyes with a diversity of corneal astigmatism magnitudes and orientations to ensure that astigmatic effects were incorporated in the responses, but it is important to point out that all simulated treatments were spherical. As alluded to earlier, spherical myopic treatment magnitude was varied in this study without incorporating astigmatic correction so the impact of preoperative corneal geometry (including corneal astigmatism) on strain responses could be isolated. A follow-up study on this cohort of eyes is planned to investigate the effects of spherocylindrical treatments on astigmatic geometries, and it is expected that corneal astigmatism will be a stronger predictor of postoperative strain when analyzed in the context of a proportionate astigmatic correction. Other measures of ectasia risk related to mechanical stress, which is closely related to strain but may be more closely related to local curvature, will also be investigated.

A weakness of this study and of computational modeling in general is the need to estimate the material properties of the various components of the eye for finite element analysis. While the assumption of identical properties across subjects has been leveraged here to investigate measurable or calculable geometric drivers of outcomes, eventual incorporation of patient-specific corneal biomechanical properties based on clinical measurement is likely to add sensitivity and specificity to surgical simulations, whether the goal is refractive outcome prediction or ectasia risk assessment. The current modeling results assume the normative material properties of a 50-year-old cornea, but these properties are distributed through the thickness of the cornea in a patient-specific manner as described in the Methods. Since most refractive surgery candidates and emerging corneal ectasia patients are younger than 50 years of age,⁵³ the stiffness of the cornea may be overestimated for the application to refractive surgery and ectasia risk. Furthermore, the group of eyes with manifest keratoconus would be expected to have significant focal reductions in material properties relative to the other groups.^12,51,52,54 The error associated with these assumptions would tend to underestimate the degree of myopic undercorrection and strain generation, especially in more invasive procedures and high-risk patients, and would cast a conservative bias on the results. For the purpose of identifying a susceptibility candidate variable, this is arguably preferable over assuming inappropriately weak material properties that might exaggerate differences. As with any statistical analysis, the relationships observed should not be extrapolated beyond the variable space included in this study. Although a wide range of geometries and treatment magnitudes were included, nonlinear increases in strain with higher treatment magnitudes or with weaker corneal material assumptions are possible.

The material formulation used in this study does not explicitly incorporate time-dependent strain related to viscoelastic properties such as creep or related wound healing processes that may play a role in the progressive shape change that is a hallmark of ectasia.^13,53,55 However, higher instantaneous strains are a reasonable proxy risk factor for time-dependent creep, which is most likely to occur in areas of strain maxima. Thus, the maximum principle strains emphasized in this study are proposed as a risk factor with a magnitude and a location that may be extrapolated to chronic risk of progression. While presence of higher values in a sample of eyes known to already have manifested ectasia even without ablative refractive surgery is a strength of the study, further validation as a risk predictor in eyes that have gone on to develop post-refractive surgery ectasia is desirable.

An adaption of the risk variable PTA, percent stromal tissue altered (PSTA), was introduced in this study. The standard construct of percent tissue altered does not discriminate between the biomechanically negligible epithelium and the collagenous stroma. PSTA accounts for the central epithelial thickness and calculates only the stromal impact of the programmed flap and ablation parameters. This adjustment was thought to be important in the context of this study in which a major aim was to quantify the relationships between several surgical parameters and strain behavior. The modification is particularly critical with comparisons between PRK and LASIK where treating the epithelium as if it were stroma would introduce an important error, and the modification to PSTA is likely to be helpful with further efforts to assess the risk of LASIK and surface ablation on a continuum. RSB and PSTA are both centrally biased expressions that correlate highly to strain behavior in myopic LASIK and PRK. Local PSTA outside of the central cornea could be important in LASIK cases with abnormally deep peripheral flap dimensions, but in a separate analysis of strain location in the current simulation dataset, strains tended to concentrate centrally as myopic treatment magnitude increased. Centrally defined metrics such as RSB and PSTA or PTA are therefore suitable as a clinical metric for risk especially in higher myopic treatments, but will be less representative of local strain behavior and ectasia risk in lower myopic corrections, high astigmatism correction, and hyperopic ablations.

The parametric design of this study also provides new insight into the relative importance of specific surgical variables and illustrated the hazards of generalizing the relative risk of PRK and LASIK. As noted earlier in reference to Table 2 and Figure 4, the interaction of the LASIK flap (whether absent, 100 um, or 160 um thick) and magnitude of refractive correction (which is directly related to central ablation depth and either 60 um for a 4D correction or 114 um for 8D) does not support the conclusion that flapless surgery (PRK in this study) is universally lower in risk than LASIK, at least in terms of strain-based susceptibility across the chosen parameter space. The apparent discontinuity in strain behavior from higher PRK treatments to lower LASIK treatments and from higher thin-flap LASIK treatments to lower thick-flap treatments is not wholly accounted for by the central thinning effect of surgery as measured by the centrally biased variables PTA, PSTA, or RSB. As an illustration, groupwise strain values were higher for 8D LASIK with a 100-um flap than for 4D LASIK with a 160-um flap despite a greater central stromal disruption depth of 214 um and 220 um, respectively. This suggests that the ablation profile is a relatively strong driver of ectasia susceptibility, perhaps stronger than the presence of a flap or the thickness of that flap. Such nuances can be captured in a 3-dimensional computational model that accounts for the different spatial characteristics of the surgical insults: for example, a flap of uniform thickness distributed evenly across the treatment zone as opposed to a myopic ablation profile that preferentially affects the thinner central cornea and may promote local strain maxima. This observation is consistent with a previous clinical study comparing myopic and hyperopic (peripherally biased) ablations in LASIK with equivalent flap creation parameters that showed less biomechanical impact from hyperopic treatments than myopic treatments.⁵⁶

CONCLUSION

This study represents the first large-scale 3-dimensional structural analysis of ectasia risk and provides a novel biomechanical construct and reference data for expressing structural risk in refractive surgery. Mechanical strain is an effective marker of known ectasia risk and correlates to predicted refractive error after myopic photoablative surgery. Efforts to translate this approach to a software-based, patient-specific tomography-driven modeling tool and validate risk thresholds in known post-LASIK ectasia cases are underway.

APPENDIX.

FIGURE 8:

Tangential curvature maps of the anterior cornea for all eyes included in Group 0 (patients determined clinically to be LASIK candidates, n=10)(Top Left), Group 1 (atypical/irregular eyes, n=8)(Top Right), Group 2 (disqualified refractive surgery screening eyes, n=10)(Bottom Left), and Group 3 (manifest keratoconus, n=12)(Bottom Right). The left member of each pair is derived directly from clinical tomography. The right member of each pair is the computational representation of the eye after the finite element meshing process. The color scale in diopters is identical for all maps and is presented in the upper left corner.