Thermodynamic free energy methods to investigate shape transitions in bilayer membranes

Abstract

The conformational free energy landscape of a system is a fundamental thermodynamic quantity of importance particularly in the study of soft matter and biological systems, in which the entropic contributions play a dominant role. While computational methods to delineate the free energy landscape are routinely used to analyze the relative stability of conformational states, to determine phase boundaries, and to compute ligand-receptor binding energies its use in problems involving the cell membrane is limited. Here, we present an overview of four different free energy methods to study morphological transitions in bilayer membranes, induced either by the action of curvature remodeling proteins or due to the application of external forces. Using a triangulated surface as a model for the cell membrane and using the framework of dynamical triangulation Monte Carlo, we have focused on the methods of Widom insertion, thermodynamic integration, Bennett acceptance scheme, and umbrella sampling and weighted histogram analysis. We have demonstrated how these methods can be employed in a variety of problems involving the cell membrane. Specifically, we have shown that the chemical potential, computed using Widom insertion, and the relative free energies, computed using thermodynamic integration and Bennett acceptance method, are excellent measures to study the transition from curvature sensing to curvature inducing behavior of membrane associated proteins. The umbrella sampling and WHAM analysis has been used to study the thermodynamics of tether formation in cell membranes and the quantitative predictions of the computational model are in excellent agreement with experimental measurements. Furthermore, we also present a method based on WHAM and thermodynamic integration to handle problems related to end-point-catastrophe that are common in most free energy methods.

1 Introduction

Surfactant molecules self assemble into mesoscale structures (characteristic lengths are in the order of hundreds of nanometer) when their concentration in an aqueous solvent exceeds a threshold value, generally called the critical micelle concentration (CMC). Examples of these mesoscale entities include simple structures like a monolayer of surfactants at the air-water/air-oil interface or more complex structures like a micelle and a bilayer of surfactants in the bulk. The stability of a given mesoscale structure is in turn is governed by the geometry and chemistry of the individual surfactant molecules [1]. Characteristic energies of a self assembled surfactant interface are comparable to the thermal energy k_BT, where k_B is the Boltzmann constant and T is the equilibrium temperature, and a result the spatial organization of the molecules, which is characterized at the mesoscale by the morphology and topology of the interface, is susceptible to thermal fluctuations in the solvent.

A similar but a more complex system that is of importance to cell biology is the lipid bilayer membrane, formed by the self assembly of lipid molecules, which defines the outer boundaries of most mammalian cells and their organelles. Lipid molecules are fatty acids synthesized within the cell and like a surfactant molecule they also have a hydrophilic head group and a hydrophobic tail—commonly occurring lipids include glycerol based lipids such as DOPC, DOPS and DOPE, sterol based lipids like cholesterol, and ceramide based lipids like sphingomyelin [2]. The cell membrane is formed by the self assembly of these different types of lipid molecules along with other constituents namely proteins and carbohydrates, and the composition of these building blocks differ across different cell membranes [3–5]. Being the interface of the cell, the lipid membrane plays a dominant role in a number of biophysical processes either by virtue of its surface chemistry at the molecular scale or through modulations in its physical properties at the mesoscale: the most obvious examples of the latter include inter- and intracellular trafficking [6–9], membrane mediated aggregation of cell signaling molecules [10, 11] and cell motility [12–14]. Hence, it is natural to expect an inherent feedback between the physical properties of the cell membrane and the biophysical processes it mediates. The primary aim of this article is to review theoretical and computational approaches at the mesoscale that can be used to develop an understanding of this feedback. In particular, our focus is to show how thermodynamic free energy methods employed in a variety in a contexts in condensed matter physics can be applied to the theoretical models for membranes at the mesoscale.

In equilibrium statistical mechanics, the ground state of a system whose intensive or extensive variables are coupled to the environment, and hence can exchange for instance heat or area or volume or number with the bath, is governed by its thermodynamic potential which is also called the free energy of the system. The various thermodynamic observables can be determined by measuring the suitable thermodynamic potential that depends on the ensemble in which the system is defined [15]. Excellent introduction to the implementations and applications of the various free energy methods for molecular systems is provided by Frenkel and Smit [16].

2 Continuum models for cell membranes

The spatial and temporal resolution of the various biophysical processes observed in cell membranes can be classified into two broad classes, namely (a) biochemical processes in which the dynamics of the system is primarily determined by the chemistry of the constituent molecules and (b) biophysical processes where collective phenomena and macroscopic physics govern the behavior of the membrane. These two class of processes have disparate time and length scales. The large separation in the time and length scales allows one to decouple the slower degrees of freedom from the faster ones and this feature can be exploited in constructing physical models at multiple scales for the cell membrane. Molecular scale models such as all-atom or coarse grained molecular dynamics are faithful to the underlying chemistry and are hence more appropriate for investigating membrane processes in the sub cellular length and nanoscopic time scales. In the other limit, phenomenology based field theoretic models neglect the membrane dynamics at the nanoscale and instead focus on how the collective effects of these molecular motions manifest at length and time scales comparable to those accessed in conventional experiments like light microscopy and mechanical measurements of cells. More rigorous discussions on the formulation of multiscale models for membranes can found in a number of review articles on this topics [17–24]. In this article, we will use the thermodynamic formalism of membrane biophysics to demonstrate how free energy methods can extended to the study of diverse class of problems involving the cell membrane at the mesoscale.

The phenomenology based approach focuses primarily on the conformational states of the bilayer membrane at length scales (>100 nm) that are large compared to the thickness of the membrane (~5 nm). In this approach the membrane is treated as a thin elastic sheet of a highly viscous fluid with nearly constant surface area (the number of lipids under consideration is assumed to be constant). This sheet is representative of the neutral surface of a membrane bilayer: it is defined as the cross sectional surface in which the in-plane strains are zero upon a bending transformation, see references [17, 23, 24] for details. The thermodynamic weights of the conformational state of the membrane is governed by the well known Canham–Helfrich energy functional [25, 26] commonly written as,

$$\mathcal{H}=\underset{\mathbf{S}}{\int }d\mathbf{S}\left\{\frac{\kappa }{2}{(2H-H_0)}^2+{\kappa }_{G}G+\sigma \right\}+\underset{V}{\int }dV\mathit{\Delta }p.$$ (1)

If c₁ and c₂ are the principal curvatures at every point on the membrane surface S then H = (c₁ + c₂)/2 and G = c₁c₂ are its mean and Gaussian curvatures respectively. The elastic moduli κ and κ_G are the isotropic and deviatoric bending moduli. Experimental measurements on lipid and cell membranes have estimated their bending stiffness κ to be in the range 10–100k_BT [27, 28], with the lower values corresponding to model membrane structures like giant unilamellar vesicles. The deviatoric modulus is normally taken to κ_G = −κ [17, 23, 29] but the Gaussian energy term can be neglected, by virtue of the Gauss–Bonnet theorem [30] if the topology of the membrane does not change during the analysis. The surface area of the membrane A and the volume V are coupled to their respective conjugate variables namely the surface tension σ and osmotic pressure Δp. Reported values of membrane surface tension (combined contributions from both the lipids and the underlying cytoskeleton) varies between 3–300 μN/m depending on the cell type [27, 28]. The osmotic pressure difference Δp is a function of the difference in the osmolyte concentration between the inside and outside of the cell.

The spontaneous curvature H₀ denotes an induced curvature which can arise in a number of context such as defects in lipid packing, the presence of intrinsic degrees of freedom in the constituent lipids, interactions of the membrane with non-lipid molecules like proteins or nanoparticles and also due to the coupling of the membrane with the underlying cytoskeleton [31–34]. Since the spontaneous curvature is an important parameter in most of our discussions later, it is important to have a closer look at how its impacts the conformational states of the membrane. When H₀ = 0, the energy given by the first term in Eq. (1) is quadratic in the mean curvature H and hence the probability of finding a membrane conformation with a given curvature H^* is a Gaussian peaked around H = 0, with its width being proportional to the bending stiffness κ [35]. On the other hand, when the membrane has a non-zero spontaneous curvature the peak of the probability distribution now shifts to a value H = H₀ and as a result highly curved membrane regions are observed with much larger probabilities.

For purposes of computer simulations, a number of discretizations based on Eq. (1) have been introduced in the literature. The free energy methods for membranes presented in the later sections are based on the Dynamical Triangulation Monte Carlo technique which has been reviewed in brief below.

The two dimensional membrane surface is discretized into an interconnected set of T triangles that intersect at N vertices (nodes) forming L independent links. The values of N, T, and L define the topology of the membrane surface in terms of Euler characteristic as χ = N + T − L. The degrees of freedom of the discretized membrane are the position vectors of the N vertices given by {X} = [x₁ ··· x_N] and the triangulation map given by {𝒯} = [𝒯₁ ··· 𝒯_T]. The discrete form of the elastic Hamiltonian is thus a sum over the curvature energies at every vertex in the triangulated surface given by,

$$\mathcal{H}=\sum _{v=1}^N{A}_v\left\{\frac{\kappa }{2}{(c_{1,v}+c_{2,v}-H_{0,v})}^2+\sigma \right\}+\mathit{\Delta }pV.$$ (2)

The index v denotes a vertex on the triangulated surface and c_1,v and c_2,v are respectively its principal curvatures, H_0,v is the local spontaneous curvature, and A_v denotes the surface area associated with the vertex. The principal curvatures are computed using the methods introduced by Ramakrishnan et. al. [36]. The spontaneous curvature at a vertex is expressed using the general form:

$$H_{0,v}=\sum _{v=1}^N{C}_0\mathcal{D}(v,v^{\prime }),$$ (3)

with C₀ being the magnitude of the induced curvature and 𝒟(v, v′) the functional form of the curvature contribution at vertex v′ due to a curvature field at vertex v. The various forms of 𝒟(v, v′)relevant in different contexts have been discussed in references [23, 37–40]. While 𝒟(v, v′) can take any arbitrary form depending on the protein, we focus mainly on proteins that induce isotropic curvature fields with a Gaussian profile given by

$$\mathcal{D}(v,v^{\prime })=exp\left(-\frac{{\mid {\mathbf{x}}_v-{\mathbf{x}}_{v^{\prime }}\mid }^2}{2{\epsilon }^2}\right).$$ (4)

The choice of isotropic curvature profiles is primarily motivated by our earlier all atom molecular studies of ENTH domains, where we have shown that the form of 𝒟(v, v′) for ENTH domains follows a Gaussian like decay. Here C₀ denotes the magnitude of the spontaneous curvature field and ε² denotes its range. We have chosen the above form to account for the long range nature of the induced curvature field where a protein at vertex v can induce a non-zero spontaneous curvature at a far vertex v′. Evidences for the non-local nature of the spontaneous curvature field has been seen in molecular simulations of proteins interacting with a bilayer membrane [41, 42]. We denote the set of all protein fields as {ϕ} = [ϕ₁ ··· ϕ_N].

In addition to the elastic potential given in Eq. (2) the membrane vertices are also subjected to a repulsive hard-sphere potential in order to enforce self avoidance. If the vertices of the membrane are taken to spheres of diameter a₀ then the length ℰ of the links, connecting any two vertices, obey the constraint $a_0\le \mid \mathcal{E}\mid <\sqrt{3}{a}_0$. Detailed discussions on this topic can be found in reference [43]. The conformational state of the triangulated membrane is given by η = [{X}, {𝒯}, {ϕ}] and a new state η′ can be accessed by varying any of {X}, {𝒯}, and {ϕ}. The various states in the conformational space are sampled using a set of three Monte Carlo moves: (i) a vertex move in which a randomly chosen vertex is displaced to new location that leads to change in state [{X}, {𝒯}, {ϕ}] → [{X′}, {𝒯}, {ϕ}], (ii) a link flip wherein two previously unconnected nodes of a randomly chosen quadrilateral on the triangulated surface are connected to form a new set of triangulation leading to [{X}, {𝒯}, {ϕ}] → [{X}, {𝒯′}, {ϕ}], and (iii) a field exchange move to simulate diffusion of the protein field in which the protein field at vertex v is exchanged with that at vertex v′ that leads to a change in state [{X}, {𝒯}, {ϕ}] → [{X}, {𝒯}, {ϕ′}]. The various Monte Carlo moves are accepted using Metropolis scheme [44] given by P_acc = min {1, exp (−β(ℋ(η′) − ℋ(η)))}, where β = 1/k_BT denotes the temperature of the system. More details on the implementation and usage of Dynamical Triangulation Monte Carlo techniques can be found in reference [23].

3 An overview of free energy methods to study membrane deformations

As noted in the introduction, the thermodynamic free energy of a system is a fundamental quantity in equilibrium statistical mechanics since it contains all the information about the thermodynamic variables of the system. However, the free energy landscape of many body systems is a very complex quantity and the complexity arises primarily from the large number of degrees of freedom associated with such systems—for example an N particle system in one dimensions has a conformational free energy landscape that is N dimensional. In most problems in condensed matter physics, computational biology, and computational chemistry the free energy landscape in the conformational space of the atoms/molecules is an over representation of the system and hence the problem of large number of dimensions can be overcome through coarse graining or representing the system in terms of a fewer macroscopic variables generally called order parameters. The use of the computational methods to delineate free energy landscape is highly optimal in such coarser representations. The problem of protein induced curvature remodeling of membranes is one such problem that is amenable to the use to free energy methods. The partition function of the triangulated membrane surface with n protein fields is defined in terms of the thermodynamic state η as,

$$Q_n=\sum _{\varphi \in \{\mathit{\varphi }\}}\sum _{\mathcal{T}\in \{\mathcal{T}\}}\int d\{\mathbf{X}\}exp(-\beta \mathcal{H}(\mathbf{x},\mathcal{T},\varphi )).$$ (5)

The partition trace in Eq. (5) is performed over all vertex positions and triangulations of the discrete surface and also over all possible configurations of the n proteins on the membrane. The absolute free energy of the membrane with n proteins is thus:

$${\mathcal{F}}_n=-k_{B}Tln{Q}_n.$$ (6)

Computing the absolute free energy F_n requires the calculation of the partition function Q_n which is a problem that requires extensive sampling of the infinitely large conformational states of the membrane-protein system—Metropolis Monte Carlo is not suitable for such purposes since it can only sample the configurational states close to the free energy minimum and the higher energy states can instead be sampled using rare event Monte Carlo techniques which are described later in the context of umbrella sampling. On the other hand, the relative free energy of state m with respect to state n, i.e. the quantity ℱ_m − ℱ_n, does not require the knowledge of Q_n and can be computed with less expensive computations.

In the remainder of this section, we will describe three different methods namely the Widom insertion, thermodynamic integration (TI), and Bennett Acceptance method (BAM) to essentially perform the same calculation — to compute Δℱ= ℱ_n+1 − ℱ_n, the free energy difference between a membrane with n and n + 1 proteins.

3.1 Widom insertion technique

The Widom particle or test-particle insertion method is a computational technique to probe the chemical potential of a system [45]. It is known from statistical mechanics that the total chemical potential of a system is defined as the change in its free energy in response to a change in the system size. In the case of membrane-protein systems, the total chemical potential of the membrane with n proteins (μ_P) is essentially the required free energy difference, i.e. μ_P = Δℱ/Δn.

The total chemical potential can be separated into an ideal and an excess part such that

$${\mu }_P={\mu }_P^{id}+{\mu }_P^{ex}.$$ (7)

The excess part of the chemical potential ${\mu }_P^{ex}$ can be computed using Widom insertion technique in which a virtual test (ghost) protein field is inserted at a randomly chosen location on the membrane. The configurational component of the ideal part can be shown to be ${\mu }_P^{id}=k_{B}Tln\rho$ ln ρ, where ρ is the protein density. If Δℋ be the change in the elastic energy due to the insertion of a test protein field then the excess chemical potential is given by,

$${\mu }_P^{ex}=-k_{B}Tln\int \langle exp(-\beta \mathit{\Delta }\mathcal{H})\rangle P_{\text{uniform}}(s_{n+1})d{s}_{n+1}.$$ (8)

The ensemble average 〈 · 〉 is taken over the configurational space of the partition function, see Eq. (5). Here, s_n+1 = x_p, with p = n + 1, is the position of the n + 1th protein field on the membrane surface, and P_uniform(s_n+1) denotes a uniform probability distribution from which the coordinates of the n + 1th particle/field is drawn. Theintegral over s_n+1 amounts to the sum over all Widom test particle/field insertion trials, and P_uniform(s_n+1) equals the reciprocal of the total number of trials. For conciseness, we represent the right-hand-side term in Eq. (8) as −k_BT ln〈exp(−βΔℋ)〉_n and here the subscript n denotes that the ensemble average is taken on a membrane with n proteins. The form of the excess chemical potential given in Eq. (8) has been derived by treating all insertion sites on the membrane to be homogeneous, while the local excess chemical potential which depends on the spatial location x on the membrane surface is given by,

$${\mu }_P^{ex}(\mathbf{x})=-k_{B}Tln{\langle exp(-\beta \mathit{\Delta }\mathcal{H}(\mathbf{x}))\rangle }_n.$$ (9)

In Eq. (9), Δℋ(x) denotes the change in energy due to the insertion of a protein field at spatial location x. The inhomogeneous chemical potential and the spatially uniform chemical potential ${\mu }_P^{ex}$ can be used to determine the inhomogeneous, scaled spatial density of the proteins using the relation:

$$\rho (\mathbf{x})=exp(\beta {\mu }_P)exp(-\beta {\mu }_P^{ex}(\mathbf{x})),$$ (10)

3.2 Thermodynamic integration (TI) method

Thermodynamic integration is perturbative technique that can be used to determine the relative free energy difference between any two thermodynamic states A and B, provided there exists a continuous path 𝒞 that connects state A to B; in the context of protein induced membrane remodeling the states A and B correspond to a membrane with n and n + 1 proteins respectively. If ℋ_n and ℋ_n+1 be the energies of these two states then the various intermediate states of the membrane along the path 𝒞 can be obtained by varying the coupling parameter 0 ≤ λ ≤ 1 such that the energy of any intermediate state is given by ℋ (λ), subject to the boundary condition ℋ (0) = ℋ_n and ℋ (1) = ℋ_n+1. The energy of an intermediate state with a given value of λ can be expressed in terms of the energies of the end states as [16]:

$$\mathcal{H}(\lambda )=(1-\lambda ){\mathcal{H}}_n+\lambda {\mathcal{H}}_{n+1}.$$ (11)

The free-energy change along this path can expressed in its integral form as,

$$\mathit{\Delta }{\mathcal{F}}_{\text{TI}}={\mathcal{F}}_{n+1}-{\mathcal{F}}_n={\int }_0^1\frac{\partial \mathcal{F}(\lambda )}{\partial \lambda }d\lambda .$$ (12)

Using the definitions of the partition function and the free energy, given in Eqs. (5) and (6), in the above equation the relative free energy Δℱ_TI can be shown to be

$$\mathit{\Delta }{\mathcal{F}}_{\text{TI}}={\int }_0^1\langle \frac{\partial \mathcal{H}(\lambda )}{\partial \lambda }\rangle d\lambda .$$ (13)

In practice, the integrand in Eq. (13) is estimated from independent simulations of the system at pre-determined, sufficiently small intervals of λ and the relative free energy ΔF_TI is then estimated through numerical integration of Eq. (13).

3.3 Bennett acceptance ratio method (BAM)

Bennett acceptance method is another perturbative technique that can be used to approximate the free-energy difference between two states close to each other in their conformational space [46]. The microscopic reversibility for the transition of the membrane-protein system between the two states with n and n + 1 proteins, also called detailed balance condition, can be stated as

$$M({\mathcal{H}}_{n+1}-{\mathcal{H}}_n)exp(-\beta {\mathcal{H}}_n)=M({\mathcal{H}}_n-{\mathcal{H}}_{n+1})exp(-\beta {\mathcal{H}}_{n+1}),$$ (14)

where M is some function that defines the distribution of the acceptance probability for a transition of the membrane from a state with n proteins to a state with n + 1 proteins and vice versa. First, integrating both sides of Eq. (14) over the entire conformational space over which the partition trace of Eq. (5) is defined, and then multiplying and dividing both sides with their corresponding partition functions the above equation can be rewritten as,

$$\frac{Q_n\int d\mathit{\eta }M({\mathcal{H}}_{n+1}-{\mathcal{H}}_n)exp(-\beta {\mathcal{H}}_n)}{Q_n}=\frac{Q_{n+1}\int d\mathit{\eta }M({\mathcal{H}}_n-{\mathcal{H}}_{n+1})exp(-\beta {\mathcal{H}}_{n+1})}{Q_{n+1}},$$ (15)

Here, for conciseness we use the state variable η, to denote integration over all the conformational states of the triangulated surface. Using the definition of thermodynamic averages, the above equation can be reduced to the form

$$\frac{Q_{n+1}}{Q_n}\equiv exp{\left(\frac{-\mathit{\Delta }{\mathcal{F}}_{\text{BAM}}}{k_{B}T}\right)}_{A\to B}=\frac{{\langle M({\mathcal{H}}_{n+1}-{\mathcal{H}}_n)\rangle }_n}{{\langle M({\mathcal{H}}_n-{\mathcal{H}}_{n+1})\rangle }_{n+1}},$$ (16)

which gives an exact expression for the relative free energy difference denoted as Δℱ_BAM, which can be exactly computed if the form of the transition function M is known. A common choice of M is the Metropolis function M(x) = min(1, exp(−βx)), which defines the acceptance probability according to a Boltzmann distribution. In Eq. (16), the angular bracket 〈 · 〉_m represents the ensemble average of the variable M when the membrane transitions from state m to state m + 1.

3.4 Umbrella sampling and weighted histogram analysis method

In a number of scenarios it is desirable to determine the statistical weight and the associated free energy of a particular state of a system. Canonical simulation techniques based on equilibrium Monte Carlo or Molecular dynamics are not well suited for such purposes if the desired state of the system has a large energy barrier with respect to its equilibrium; Arrhenius’ law predicts negligibly small transition rates across this energy barrier and hence one would require infinitely long trajectories of the system in order to generate extensive samples of the state with higher energy. Such at transition event is called a rare event and there are a number of techniques, such as Rosenbluth sampling, Wang-Landau sampling, and umbrella sampling, that can be used to access the rare states of the system within acceptable simulation times. In this article, we only focus on the umbrella sampling technique along with the Weighted Histogram Analysis Method (WHAM) [47] to study the thermodynamics of large deformations in cell membranes.

In general, let ζ denote an atomistic or a molecular or a continuum or a collective variable of a system with an equilibrium probability distribution 𝒫(ζ) which is peaked around the equilibrium value ζ = ζ^* — conventionally the variable ζ is called a reaction coordinate. Umbrella sampling involves the simulation of the system in N_ℬ different windows in the presence of an additional harmonic biasing potential

$${\mathcal{B}}_i(\mathit{\zeta })=\frac{k_{\text{bias}}}{2}{(\zeta -{\zeta }_i)}^2,$$ (17)

such that ζ_i denotes the preferred value of ζ in the ith window and 𝒫_i(ζ) its probability distribution. k_bias is the strength of the biasing spring which is chosen such that the probability distributions from neighboring windows show considerable overlap. The probability distributions 𝒫_i(ζ) computed across multiple simulations windows can be combined together using the Weighted Histogram Analysis method to estimate the free energies of all intermediate states, with respect to the first window. The free energy is computed by self-consistently solving the two WHAM equations, for the unknowns 𝒫(ζ) and ℱ_i, given by:

$$\mathcal{P}(\mathit{\zeta })=\frac{{\displaystyle \sum _{i=1}^{N_{\mathcal{B}}}}{\mathcal{N}}_i{\mathcal{P}}_i(\mathit{\zeta })}{{\displaystyle \sum _{i=1}^{N_{\mathcal{B}}}}{\mathcal{N}}_{i}exp(-\beta ({\mathcal{B}}_i(\mathit{\zeta })-{\mathcal{F}}_i))},$$ (18)

where 𝒩_i is the number of samples in the ith window and

$${\mathcal{F}}_i=-k_{B}Tln\left(\sum _{j=1}^{\mathit{nbins}}\mathcal{P}({\mathit{\zeta }}_j)exp(-\beta {\mathcal{B}}_i({\mathit{\zeta }}_j))\right)+C.$$ (19)

Here nbins denotes the number of used over which the free energy is discretized and C is an arbitrary constant.

4 Predicting transition from curvature sensing to curvature inducing behavior using Widom insertion

An important question in the area of protein driven curvature remodeling of membranes is “when does a cluster of proteins behave in a cooperative manner?” in vitro experiments on a number of curvature inducing proteins such as BAR domains, ENTH domains, and Exo70 domains have shown that these proteins when at low concentrations localize to high curvature regions on the membrane generated by thermal undulations—commonly known as the curvature sensing behavior—while at high concentrations they aggregate into clusters and spontaneously generate membrane curvature to form highly curved membrane morphologies such as tubules and blebs—a characteristic of curvature inducing behavior. Delineating this transition regime is a challenge in experiments but computational models based on free energy methods are well suited for this purpose. The relative free energy of the membrane is an excellent marker for the curvature sensing to transition behavior. It was pointed out in Sect. 3 that the relative free energy to introduce the n + 1th protein in a membrane with n proteins can be computed using Widom insertion or thermodynamic integration or Bennett-acceptance-method. Here we use the computationally less expensive Widom insertion technique to determine the relative free energies to insert a protein on a membrane with n = 0 (i.e. a pure lipid membrane).

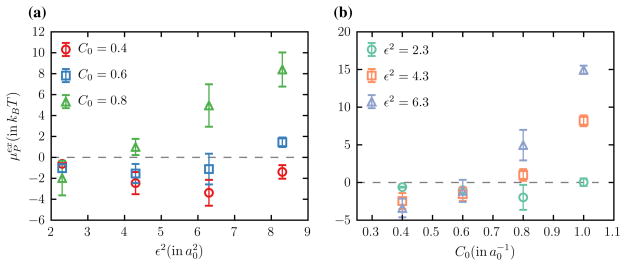
In the continuum description a protein is represented as a curvature field with a Gaussian profile that is parameterized using two variables namely the maximum spontaneous curvature (C₀) and the extent of the curvature field (ε²), see Eqs. (3) and (4). We express both C₀ and ε² in units of a₀, which represents the hard sphere diameter associated with a vertex of the triangulated surface. The excess chemical potentials ${\mu }_P^{ex}$ as a function of ε² (for fixed values of C₀) and C₀ (for fixed values of ε²) are shown in Fig. 1a, b respectively. It can be seen that ${\mu }_P^{ex}$ is negative for small values of C₀ and ε² which indicates that the free energy of the system is reduced upon introduction of the protein. Assuming the entropic contribution to be negligible, this implies that the total bending potential given by Eq. (2) is smaller in the presence of the protein which is only possible when H ≈ C₀. Since the Widom test particle method only probes the membrane curvature and does not deforms the surface it is clear that the equilibrium curvature profile of the membrane matches that of the inserted protein field, which is characteristic of curvature sensing behavior. On the other hand when C₀ and ε² are larger (C₀ > H) ${\mu }_P^{ex}$ become large and positive and since such states are thermodynamically unstable any such proteins associated with the membrane would tend to to generate local curvatures that match their intrinsic curvature profile and this regime where the protein induces curvature. The results presented in Fig. 1 only focus on the thermodynamic stability of a single protein but even weakly curving proteins can transition from curvature sensing to inducing behavior, when their concentration exceeds a critical value. The effect of the cooperative behavior, due to the self- and membrane-mediated interactions of the proteins, on the curvature inducing properties of membrane associated proteins has been recently studied in the context of ENTH domains [40, 42].

Fig. 1.

Excess chemical potential, in units of k_BT, to insert a protein field with maximum spontaneous curvature C₀ and extent of curvature ε² on a membrane with zero proteins—both C₀ and ε² are expressed in units of a₀. a ${\mu }_P^{ex}$ as a function of ε² for fixed values of $C_0=0.4a_0^{-1},0.6a_0^{-1}$ and $0.8a_0^{-1}$ and b ${\mu }_P^{ex}$ as a function of C₀ for fixed values of ${\epsilon }^2=2.3a_0^2,4.3a_0^2$, and $6.3a_0^2$

5 Comparing predictions from Widom insertion, TI, and BAM

The excess chemical potential is reflective of the underlying free energy landscape as shown in Fig. 1 and in this section we compare these predictions to the corresponding relative free energy levels obtained using thermodynamic integration and Bennett-acceptance-method. The free energies determined using TI and BAM (see Eqs. (13) and (16)) are related to the total chemical potential ${\mu }_P={\mu }_P^{id}(\rho )+{\mu }_P^{ex}$ as:

$$\mathit{\Delta }{F}_{\text{TI}}=\mathit{\Delta }{F}_{\text{BAM}}={\mu }_P.$$ (20)

Since the Widom insertion technique can only be used to determine the excess part of the chemical potential the various free energies can be compared only if the total chemical potential can be determined. ${\mu }_P^{id}(\rho )$ is the entropic configurational component of μ_P and depends on the number of conformational states visited by a single particle or protein-field. The number of conformational states accessible to the n + 1th protein on a membrane with n proteins can in turn be determined using the trajectories obtained using TI. In TI, the additional protein field is grown from a non-existent entity to a full-existent object by varying the parameter λ from 0 to 1. The degree of localization changes with change in λ and when λ → 1 the protein does not explore all the conformational states but is instead confined to the minimum of the free energy well, and this minimum in the triangulated surface model corresponds to a subset of vertices on the surface. The required correction ${\mu }_P^{id}(\rho )$ can be calculated from the number of unique vertices N_ψ visited by a protein field in various TI simulations with λ ~ 1 as:

$${\mu }_P^{id}(\rho )=-k_{B}Tln\left(\frac{2{\sigma }_{\psi }}{N}\right).$$ (21)

Here N is the total number of vertices on the triangulated surface and the standard deviation σ_ψ of the distribution of unique vertices is computed as,

$${\sigma }_{\psi }={\left(\sum _{\upsilon =1}^{N_{\psi }}{\upsilon }^2{P}_{\upsilon }-{\left(\sum _{\upsilon =1}^{N_{\psi }}\upsilon P_{\upsilon }\right)}^2\right)}^{\frac{1}{2}},$$ (22)

with P_ν being the probability of a protein to visit the νth unique vertex.

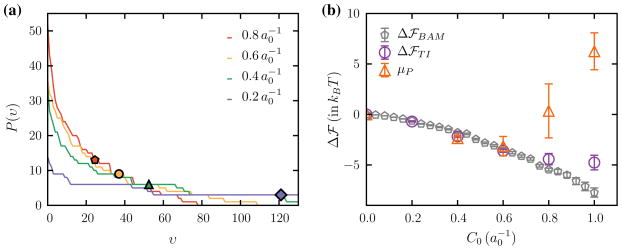
The probability distribution of the number of unique vertices, for four different values of C₀, is shown in Fig. 2a and the symbols shown alongside correspond to the value of σ_ψ. The total chemical potential that compares the entropic configurational part is compared against the relative free energies computed using TI and BAM in Fig. 2b. It can be seen from Fig. 2b that all three methods agree well for low values of C₀ while Widom insertion deviates from the other methods above $C_0>0.6a_0^{-1}$. The deviation of TI and Widom insertion methods at high C₀ is well known since efficient sampling of ${\mu }_P^{ex}$ suffers for large perturbations in energy or higher densities.

Fig. 2.

a Distribution of the number of unique vertices P(ν), visited in a TI simulation with λ ~ 1, for four different values of C₀. The points shown alongside each curve correspond to the standard deviation σ_ψ. b Comparison of the relative free energies to add one protein to a membrane with zero proteins computed using TI, BAM, and Widom insertion

6 In silico tether pulling experiments

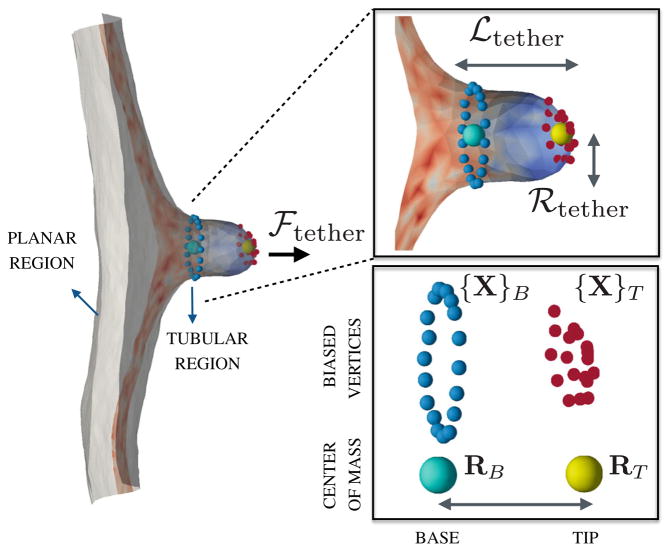
Extraction of cylindrical protrusions (tethers) from the surface of a cell membrane, using optical tweezers or functionalized AFM tips or through attachment of magnetic beads, is a useful method to characterize its mechanical properties such as the bending stiffness, surface tension, and degree of cytoskeletal pinning. A tether is characterized by its radius ℛ_tether, its length ℒ_tether and the force required for its extraction denoted by ℱ_tether, as shown in the illustration in Fig. 3. In order to clearly delineate the role of the various parameters characterizing a cell membrane in a typical in vivo tether extraction assay, it is essential to develop physical models that allow us to gain an understanding at a fundamental level.

Fig. 3.

(left panel) A snapshot of a tether extracted from a patch of a planar membrane. (right panel) A closer view of the tubular region of length ℒ_tether and radius ℛ_tether with the colors denoting the mean curvature of the surface—the tubular region has a positive mean curvature and the neck region has a negative mean curvature. The tip and base regions on the membrane tether are represented by the marked vertices on the tubular membrane along with the position of their center of mass

In this section, we present an in silico tether extraction assay by combining the triangulated surface membrane with umbrella sampling techniques and the weighted histogram analysis method. In order to stabilize a membrane tether of length ℒ_tether, we apply an umbrella sampling biasing potential on a set of macroscopic variables which are defined as follows. The tip of the tubular region is represented by a set of pre-determined vertices {X}_T with center of mass R_T and the base of the tether is represented by another set of of vertices {X}_B with center of mass R_B, such that ℒ_tether = |R_T − R_B| and each vertex in {X}_B with position vector x_B obeys the constraint |R_T − x_B| ≤ 1.5 ℒ_tether. The macroscopic positions of the tip and base of the membrane tether R_T and R_B define an order parameter which is subjected to a harmonic biasing potential in the n^th window given as:

$${\mathcal{B}}_n({\mathbf{R}}_T,{\mathbf{R}}_B)=\frac{k_{\text{bias}}}{2}{(\mid {\mathbf{R}}_T-{\mathbf{R}}_B\mid -{\mathcal{L}}_{\text{tether}}^{\ast })}^2$$ (23)

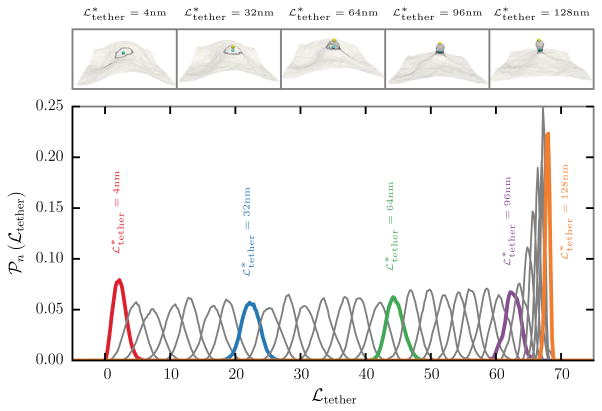
k_bias is the strength of the biasing potential and ${\mathcal{L}}_{\text{tether}}^{\ast }$ denotes the preferred tether length. The conformational state of the membrane patch is evolved using the Dynamical Triangulation Monte Carlo technique with the total potential ℋ_tot = ℋ + ℬ_n. The conformations of a membrane, with fixed values of κ = 20k_BT, ℒ = 510 nm, and A_ex = 10 %, in five different biasing windows with ${\mathcal{L}}_{\text{tether}}^{\ast }=4$, 32, 64, 96, and 128 nm are shown in the top panel of Fig. 4. The positions of the center of masses corresponding to the biasing vertices, R_T and R_B respectively, are also shown alongside and it can be seen that tether like structures are readily formed at larger values of ${\mathcal{L}}_{\text{tether}}^{\ast }$.

Fig. 4.

(top panel) Snapshots of a membrane subject to a biasing potential, along with the positions of the center of masses, for five different values of the preferred tether length ${\mathcal{L}}_{\text{tether}}^{\ast }=4$, 32, 64, 96, and 128 nm. (bottom panel) 𝒫_n(ℒ_tether), the probability distribution of the tether length ℒ_tether in 32 different biasing windows with a window size of 4 nm. The curve corresponding to the snapshots in the top panel are shown as solid colored lines along with the corresponding values of the preferred tether length

The probability distribution of the tether length ℒ_tether in 32 different sampling windows, with a window size of 4 nm, are shown in the bottom panel of Fig. 4. 𝒫_n(ℒ_tether) shows a normal distribution in each of the 32 windows and the peak of the distribution shifts to a higher value of ℒ_tether with increasing ${\mathcal{L}}_{\text{tether}}^{\ast }$ and the strength of the biasing potential k_bias was chosen so that distributions from adjacent windows show a good overlap as seen in Fig. 4. It can also be seen that 𝒫_n(ℒ_tether) becomes narrower following the formation of the tether at ${\mathcal{L}}_{\text{tether}}^{\ast }\approx 96\text{nm}$.

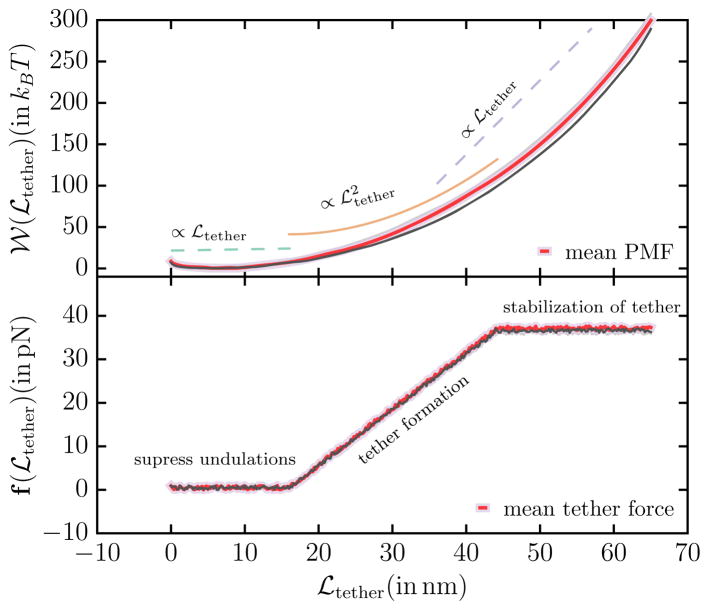
The potential of mean force 𝒲 (ℒ_tether) which denotes the energy required to extract a tether of length ℒ_tether, computed by combining the histograms in Fig. 4 using WHAM, is shown in the top panel of Fig. 5. The PMF shows three distinct regimes which are also shown alongside the PMF in Fig. 5: (1) an initial weakly linear regime (∝ ℒ_tether), (2) an intermediate quadratic regime ( $\propto {\mathcal{L}}_{\text{tether}}^{\ast }$), and (3) a final linear regime (∝ ℒ_tether). These three regimes have a significance in the formation and stabilization of the membrane tether. When a force is applied to an undulating membrane the short wavelength undulations in the membrane conformation are suppressed in the linear response regime and this response characterizes the initial linear regime. The tubular structures nucleate and grow in the intermediate quadratic regime until all the undulations in the membrane are ironed out and are drawn into the tubular region—the extent of the quadratic regime changes with change in the membrane excess area which sets the intensities of the characteristic undulations in the membrane [48]. In the final linear regime the tether does not extends considerably and all the applied force (i.e. the biasing potential in the current context) is primarily used to stabilize the length of membrane tether and this leads to reduced undulations in the tether length which is seen in the narrow distribution of ℒ_tether at large values of ${\mathcal{L}}_{\text{tether}}^{\ast }$. The force required to extract a tether can be determined from the PMF as f(ℒ_tether) = −∇ℒ_tether 𝒲. Numerical differentiation of the PMF can lead to large errors in the estimates for the tether force and hence we use an alternate method where we utilize the scaling relations to determine f(ℒ_tether). The tether force determined using the scaling relations are shown in the bottom panel of Fig. 5 and the constant force in the final regime is taken to be the tether force that can be compared to that obtained in tether pulling experiments. We have shown that the estimates for force and the radius of the membrane tether computed using the continuum in silico assay described here are in excellent agreement with those reported in the literature for cells with similar mechanical properties [48], and have also leveraged the tether pulling technique to determine the excess area in membrane regions between cytoskeletal pinning points.

Fig. 5.

(top panel) Potential of mean force (PMF) 𝒲_tether, in units of k_BT, as a function of the tether length ℒ_tether. The PMF shows three distinct scaling regimes — an initial linear regime followed by a quadratic regime which crosses over to a final linear regime—and the scaling relations are also shown alongside. (bottom panel) The force ℱ_tether, in units of pN, required to extract the tether

7 Bridging techniques using WHAM and TI

The PMF of a system determined using WHAM analysis is accurate only upto an additive constant, as shown in Eq. (19), and hence can only be used to determine the relative energy differences between the various states. Furthermore, the umbrella sampling technique and WHAM also suffer from the problem of end-point-catastrophe, which is a well known phenomenon in alchemical energy methods commonly used to study the free energy landscapes of biomolecular systems. In such systems, the free energy estimates close to the end points of the order parameter are erroneous due to the numerical instabilities arising from the divergence of the interaction potential—a case point being the free energy calculation involving two atoms, interacting via a Lennard-Jones potential, with their separation r → 0. WHAM also suffers from such shortcomings at the end points albeit for a different reason. An end point is defined as the value of the order parameter beyond which the potential of mean force vanishes since the various underlying interaction potentials vanish. In this regime, where the strength of the PMF is very weak (compared to the strength of the fluctuations), the signal to noise ratio is very small and hence conventional sampling techniques do not yield the correct probability distribution for the order parameter in the windows close to the end point. As a result the PMF computed using WHAM does not accurately capture the energy landscape of the system close to the end point. The problem of end-point-catastrophe can be overcome either by generating infinitely long samples or by performing the simulations using a stronger biasing potential with much smaller window sizes and both these methods leads to large computational costs. A similar method has been discussed in the context of solvation free energies by Souaille and Roux [49].

In certain class of problems, the thermodynamic integration technique can be used to overcome the end-point-catastrophe mentioned above and also fix the absolute energy levels for the PMF. We demonstrate the idea of bridging the free energies computed using WHAM and TI using the case of a functionalized nanocarrier interacting with receptor molecules expressed on the surface of a flat membrane. We follow the model previously described by Liu et al. [50, 51] to construct the free energy landscape for the interaction of an anti-ICAM functionalized nanocarrier with a membrane surface expressing ICAM receptors. In brief, the nanocarrier is a sphere of radius 50 nm, discretized into 162 vertices, and is functionalized with antibodies, that are represented as radial vectors of length 15 nm. The membrane is represented as a planar substrate on which the receptors molecules are modeled as cylinders of length 19 nm and radius 1.5 nm. The interaction between the tip of an antibody and the tip of a surface receptor is modeled as a Bell bond with a potential:

$$G(d_{ij})=G_0+\frac{k}{2}{d}_{ij}^2.$$ (24)

G₀ is the activation energy gained by the system when a bond is formed, k is the strength of receptor-antibody bond, d_ij is the distance between the tips of the antibody and receptor molecules. d₀ denotes the maximum extension of the antibody-receptor bonds and the bonds break when d_ij > d₀. Typical values for the anti ICAM-ICAM interactions have been shown to be G₀ = −19.4k_BT, k = 1 N/m, d₀ ~ 0.4 nm, and the receptor density being 2000 ICAM/μm² [50].

A functionalized nanocarrier can form multiple simultaneous antibody-receptor bonds and the degree of bonding varies with the position of the nanocarrier (R_NC) with respect to the base of the planar membrane (R_M). The relative distance |R_NC − R_M| is a suitable choice for the reaction coordinate to evaluate the potential of mean force. For the system considered here, it should be noted that the nanocarrier cannot form bonds when |R_NC− R_M| > 84.4 nm¹ and hence the potential of mean force is zero beyond this value of the reaction coordinate. Hence we take the region around |R_NC − R_M| =84.4 nm to represent the regime corresponding to the end point catastrophe.

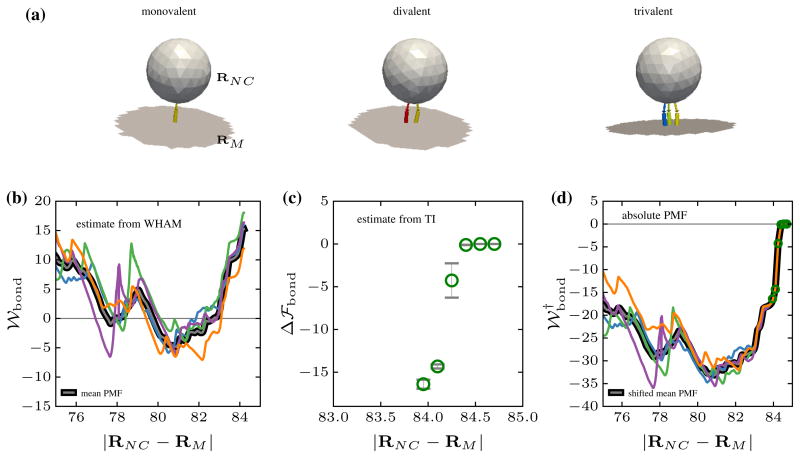
The conformations of a nanocarrier with one, two, and three simultaneous bonds obtained at different values of the reaction coordinates are shown in Fig. 6a (the unbound antibodies and receptors are not shown for clarity). 𝒲_bond, the PMF computed using the umbrella sampling/WHAM techniques, through the application of a biasing potential on the reaction coordinate, is shown in Fig. 6b for four different ensembles of the nanocarrier-membrane system. It can be seen that the potential of mean force obtained from different ensembles are shifted upto an arbitrary constant but the relative energy levels between the various states remain nearly constant, which is reflective of the first shortcoming discussed at the introduction. A closer look at the region between 84.0 and 84.4 nm reveals that the harmonic potential, characteristic of a single antibody-receptor bond with a well depth of 19k_BT, is only partially captured in the WHAM analysis and this is a clear signature of the endpoint catastrophe.

Fig. 6.

a Snapshots of a functionalized nanocarrier forming one, two, and three simultaneous bonds with the receptor molecules expressed on the membrane surface. R_NC and R_M denote the center of mass position of the nanocarrier and membrane respectively. b The potential of mean force 𝒲_bond as a function of |R_NC − R_M| for four different ensembles computed using umbrella sampling and WHAM. c The relative free energy difference Δℱ_bond between a nanocarrier with zero and one antigen-antibody bonds, and d the absolute free energy of the system obtained by combining the PMF obtained using WHAM the relative free energy obtained using TI

On the other hand, as shown in Fig. 6c, the free energy difference close to the end point region computed using TI coupled with WHAM precisely captures both the non-bonded region (|R_NC − R_M| > 84.4 nm) and also the depth of potential well corresponding to a single bond. These results have been obtained using short TI calculations performed in the end point region with an window interval of 0.1 nm. Since the bonded and unbonded states are clearly defined, the relative free energy, computed using TI, can be combined with the PMF, computed using WHAM, to fix the end-point-catastrophe and this allows for a representation of the PMF in the absolute scale. The absolute potential of mean force ( ${\mathcal{W}}_{\text{bond}}^{†}$) obtained by shifting 𝒲_bond with respect to Δℱ_bond through a linear regression fit is shown in Fig. 6d. The absolute PMF obtained by combining WHAM and TI is in excellent agreement with the reported values of the PMF obtained by approximating the PMF in the single bond region to be equal to the harmonic part of Eq. (24) [50]. The bridging technique presented here is very generic and can be applied to even more complex scenarios where the exact form of the effective potential, as a function of the order parameter, is not known.

8 Conclusions

The analysis of the thermodynamic free energy landscape can yield unprecedented levels of insight into the behavior of complex systems. However, it is a challenge in the study of these systems to formulate computational methods to delineate their free energy landscape using physically relevant order parameters. The primary focus of this article is to demonstrate how conventional free energy methods can be adopted to in problems related to morphological transitions in cell membrane. Quantitative predictions based on the relative free energies obtained using these simple but elegant methods reproduce many of the emergent behaviors observed in experiments. Since these methods provide a powerful framework to interpret experimental findings it is essential to develop free energy based models and methods which help in understanding the system at a more fundamental level.