Abstract
Cholesteryl ester transfer protein (CETP) mediates the transfer of cholesteryl esters (CEs) and triglycerides between different lipoproteins. Recent studies have shown that blocking the function of CETP can increase the level of HDL cholesterol in blood plasma and suppress the risk of cardiovascular disease. Hence, understanding the structure, dynamics, and mechanism by which CETP transfers the neutral lipids has received tremendous attention in last decade. Although the recent crystal structure has provided direct evidence of the existence of strongly bound CEs in the CETP core, very little is known about the mechanism of CE/triglyceride transfer by CETP. In this study, we explore the large scale dynamics of CETP by means of multimicrosecond molecular dynamics simulations and normal mode analysis, which provided a wealth of detailed information about the lipid transfer mechanism of CETP. Results show that the bound CEs intraconvert between bent and linear conformations in the CETP core tunnel as a consequence of the high degree of conformational flexibility of the protein. During the conformational switching, there occurred a significant reduction in hydrophobic contacts between the CEs and CETP, and a continuous tunnel traversing across the CETP long axis appeared spontaneously. Thus, our results support the recently proposed “tunnel mechanism” of CETP from cryo-EM studies for the transfer of neutral lipids between different lipoproteins. The detailed understanding obtained here could help in devising methods to prevent CETP function as a cardiovascular disease therapeutic.
Keywords: conformational change, lipid binding protein, lipid transport, lipid-protein interaction, molecular dynamics, cholesteryl ester (CE), cholesteryl ester transfer protein (CETP), free energy, molecular dynamics simulations, tunnel mechanism
Introduction
Coronary heart disease (CHD) 2 is one of the prime causes of an increase in the mortality rate worldwide. Over the past few years, various epidemiological studies have provided ample evidence that increased levels of HDL, by transporting cholesterol from atherosclerotic plaques to liver for excretion, can arrest the progression of CHD (1, 2). Subsequent preclinical studies on overexpression of apolipoprotein A-I (apoA-I), the major protein constituent of HDL, have reported significant reduction in CHD risk (3, 4). Although raising HDL levels is a longstanding strategy for mitigating CHD risk, the current lipid-targeted therapies, including the usage of statins, fibrates, and niacin, have shown reduced therapeutic potential (5–7). Hence, there is a continuous requirement for new strategies that can elevate HDL levels to halt the progression of CHD.
Cholesteryl ester transfer protein (CETP), a plasma glycoprotein with 476 residues, has been found to mediate the transfer of cholesteryl esters (CEs) from HDL to LDL and VLDL as well as the reciprocal transfer of triglycerides (TGs) from LDL and VLDL to HDL (8, 9). The identification of deficient CETP gene levels and correlated high HDL levels in a Japanese population (10–13) brought CETP into focus as a therapeutic target for controlling HDL levels. Preclinical animal model studies have further substantiated these findings by showing an elevated level of HDL in mice with non-expressing CETP (14–16). Since then, the inhibition of CETP activity by small molecule inhibitors has been pursued as an active approach to prevent atherosclerosis with varying levels of success at clinical trial phases (17–20). Given the complexity of lipid metabolism and the pivotal role of CETP in the process, understanding CETP structure, CETP inhibition, and the mechanism by which CETP transfers neutral lipids is of prime importance. The last decade, therefore, has seen the employment of sophisticated techniques, like cryo-EM (21, 22), x-ray (23, 24), and MD simulations (25–28) on this front. Nevertheless, the story of CETP remains far from complete.
The crystal structure of CETP (Protein Data Bank entry 2OBD) has been solved with four bound lipid molecules (23). The structure shows two β-barrel domains at the N and C termini, each with a twisted β-sheet and a long α-helix; a central β-sheet between the two β-barrels; a C-terminal α-helix; and a 60-Å-long hydrophobic tunnel occupied by two CE molecules. Additionally, there were two plug-in dioleoylphosphatidylcholine molecules with polar headgroups exposed to plasma and acyl chains buried in the hydrophobic tunnel of CETP. Interestingly, one of the CEs in the hydrophobic tunnel was in the bent conformation, whereas the second CE molecule was in the linear conformation. Recent cryopositive staining EM and optimized negative-staining electron microscopy (OpNS-EM) protocols combined with CETP C terminus-specific polyclonal antibody studies have suggested that CETP penetrates its C-terminal β-barrel domain into LDL or VLDL and its N-terminal β-barrel domain into HDL to form a ternary complex (21). Further, it was suggested that the aforementioned long continuous hydrophobic tunnel that traverses along the long axis of CETP can connect to the core of HDL and LDL simultaneously to facilitate the transfer of CEs and TGs between the lipoproteins.
Thus, crystal structure has provided a wealth of information about the structure of CETP and the nature of binding of CEs in CETP. However, due to the inherent limitations of the technique, a dynamic phenomenon, such as the time evolution of the protein conformation and its bound substrates, CEs, could not be captured. State-of-the-art molecular dynamics (MD) simulations can capture short to large scale dynamic processes by mapping the interatomic interactions at a resolution as high as 1 fs. Hence, in this study, we have employed multimicrosecond-long atomistic simulations to explore the dynamics of CETP and its bound substrates and to understand the mechanism of lipid transfer by CETP. We have observed high degrees of conformational flexibility of CETP and bound CEs as well as the frequent interconversion of the CEs between the bent and linear conformations, which resulted in the formation of a continuous hydrophobic tunnel spanning the length of CETP.
Results and Discussion
In MD simulations, it is important to ensure that the system is well equilibrated before analyzing the simulation trajectory. A simple strategy is to monitor the mean square displacements of the protein residues from their initial positions. Hence, we plotted the time evolution of the root mean square displacements of Cα atoms of CETP, which is shown in supplemental Fig. S1. The figure depicts the convergence of root mean square displacements only at 130 ns, demonstrating the necessity of long simulation for equilibration. In fact, such a long simulation time is expected, considering the large molecular size of CETP and the intrinsic dynamics of bound lipid molecules in CETP. However, once equilibrated, CETP maintained stability throughout the simulation.
CETP-bound CE Shows Conformational Switching in Nano- to Microsecond Time Scales
Although CETP displayed considerable stability after equilibration, visual inspection of simulation trajectory revealed an interesting conformational switching of the core lipids, CEs, in the hydrophobic tunnel of CETP. Particularly, the N-terminal CE, CEN, exhibited frequent interswitching between the bent and linear conformations, although the C-terminal CE, CEC, maintained a linear conformation throughout the 1-μs simulation run. Recall that in the solved CETP crystal structure, CEN was in the bent conformation, whereas CEC was in the linear form, as shown in Fig. 1a. We will elaborate on this transition of CEs below. It was also evident from the visual inspection that the change in conformation of CEN was effected through the flexibility of oleate chain, whereas the cholesterol moiety maintained a high degree of rigidity. To locate precisely the pivot of CEN bending, we computed the gauche/trans ratio of each dihedral angle in the oleate chain of CEN (supplemental Fig. S2a). For higher accuracy, we divided the whole trajectory into two parts: (a) frames with CEN in the bent conformation and (b) frames with CEN in the linear conformation. Subsequently, we calculated the average fraction of gauche defects for each dihedral angle present in the oleate chain of CEN in both frames. As a control, we also analyzed the gauche fraction in the dihedrals of the oleate chain of CEC. The dihedral angles in the oleate chain are numbered beginning with the C1-C2-C3-C4 fragment and ending with the C15-C16-C17-C18 fragment, as shown in supplemental Fig. S2a. If the dihedral angle falls in the range 120°–240°, it is considered trans, the remainder being gauche (29). From the plotted distributions of dihedral angles in supplemental Fig. S2b, it is evident that the dihedral angle III (C3-C4-C5-C6) and dihedral angle V (C5-C6-C7-C8) in the oleate chain of bent CEN prefer the gauche conformation, whereas the same dihedral angles in CEC and linear CEN oleate chains prefer the trans conformation. Hence, the shift in dihedral angles III and V from gauche to trans is responsible for conformational switching of CEN between bent and linear.
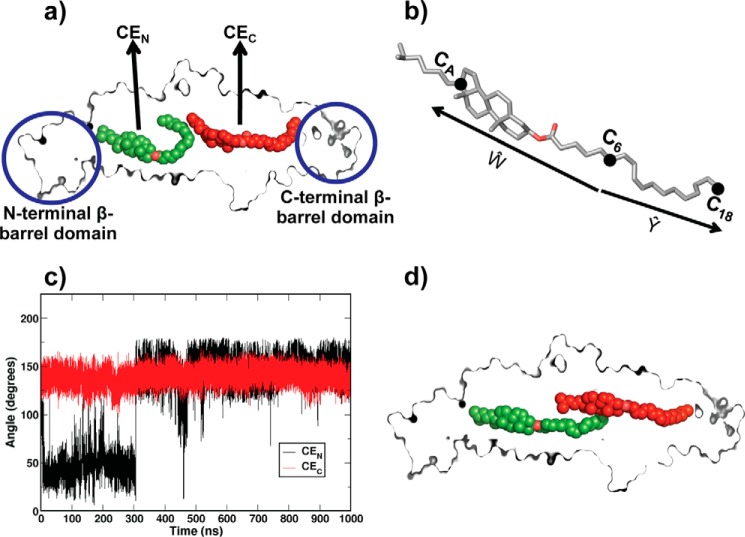
FIGURE 1.
Conformational switching of bound CEs in CETP. a, conformation of the CEs in CETP crystal structure. Two bound CEs are named CEN (green) and CEC (red) and shown in a van der Waals representation. CETP is shown in sliced surface mode. b, molecular structure of CE. Two vectors, Ŵ and Ŷ, directed from C6 to CA and from C6 to C18 atoms are defined to measure the oleate angle. c, time evolution of the CE oleate angle from CETP crystal structure simulation (system 1 in supplemental Table S1). Results are shown for both CEN (black) and CEC (red). d, a representative linear conformation of the CEs in CETP tunnel at 1 μs of simulation time.
Thus, from the gauche fraction of the dihedral angles in the CEN oleate chain, we were able to identify the most flexible region in CE. We specifically found dihedral angle V to exhibit the largest difference in the gauche fraction in the bent CE conformation compared with the linear CE conformation. Further, to determine the extent of bending in CEN, we took C6 of dihedral angle V as the central node to calculate the angle between the oleate chain and cholesterol ring of CE. The angle was estimated by computing the instantaneous angle assumed by two vectors, Ŵ and Ŷ, drawn on the molecular frames. The vector from C6 to CA of the cholesterol ring moiety was termed Ŵ, and the one from C6 to the oleate chain's terminal carbon C18 was termed Ŷ (Fig. 1b). The angle between the two vectors, termed the oleate angle, was then computed as follows.
In order to understand the frequency of CE conformational switching between the bent and linear conformations, we plotted the computed angle against simulation time, as shown in Fig. 1c. The intermittent switching of CEN between the bent and linear conformations was evident. For example, at 305 ns of simulation time, CEN transformed to an extended conformation that was very similar to CEC. Interestingly, this extended conformation lasted for about 170 ns and again adopted back the bent conformation for about 5 ns. After this brief spell of the bent conformation, CEN reverted to a stable linear conformation for rest of the simulation time, as shown in Fig. 1c. Although CEN was flexible in switching conformations between bent and linear, CEC remained in the straight conformation. The extended linear conformations, as attained by both CEN and CEC in the CETP hydrophobic tunnel during the later phase of simulation (0.45–1 μs), are shown in Fig. 1d.
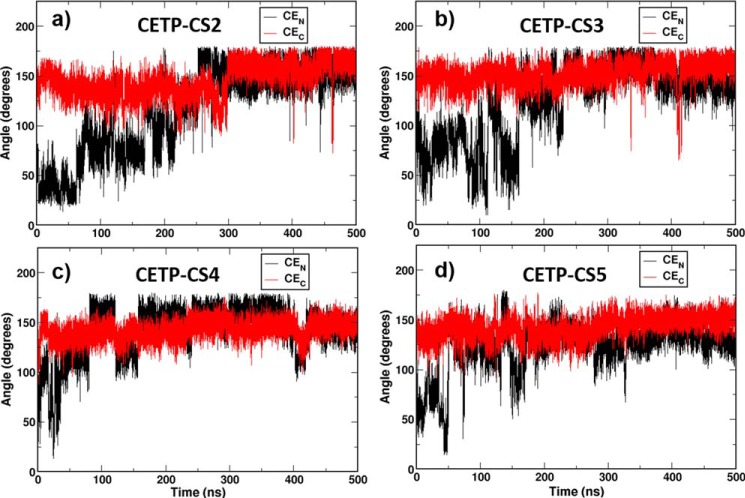
To strengthen our findings of frequent conformational switching of CEN in the CETP tunnel, we performed a new set of MD simulations on the same CE-bound CETP crystal structure but with a different set of initial velocities of the constituent atoms chosen randomly from a Maxwell-Boltzmann distribution (supplemental Table S1). Conformational switching of CEN was again characterized by calculating the bending angle of the CE oleate chain, as discussed above. Interestingly, all of these replica simulations have displayed significant flexibility in CEN conformation despite the stable and linear CEC conformation (Fig. 2). More importantly, CEN interswitches between the bent and linear conformations, very similar to those of the primary system, CETP-CS1. However, the switching time and frequency of CEN varies from system to system due to their different initial conditions. For example, whereas systems 2 and 3 required a prolonged 200–300-ns simulation time to transform CEN from bent to linear, system 4 does it rather quickly in about 100 ns. The conformational transition of CEN in system 5 is most interesting, where the lipid exhibits a back-and-forth motion between the two conformations during the first 200 ns and then settles to the linear conformation at a longer time. Thus, in solution, the bound CEN in the CETP tunnel interswitches between bent and linear conformations with a particular preference for the linear form.
FIGURE 2.
Conformational switching of bound CEs in the replica simulations of CETP crystal structure. Time evolutions of the oleate angle of CEN (black) and CEC (red) are shown in the replica systems: CETP-CS2 (a), CETP-CS3 (b), CETP-CS4 (c), and CETP-CS5 (d). For system definition, see supplemental Table S1.
Normal Mode Analysis Revealed More Frequent Conformational Switching of CE
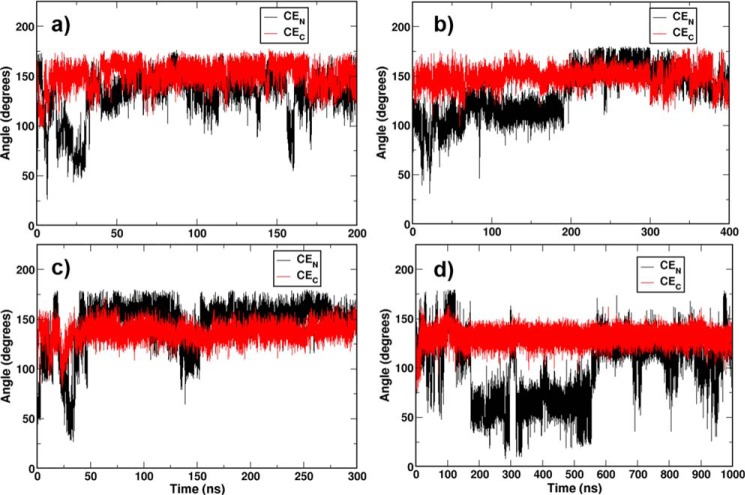
As Figs. 1 and 2 indicate, the N-terminal CE of CETP has a tendency to shuttle between the bent and linear conformations. However, this transition appears to be somewhat restricted. One of the reasons could be the short length and time scales covered under MD simulations. The changes that CETP undergoes in plasma and particularly when bound to lipoprotein would presumably be at much larger scales. To capture such large scale conformational changes, we performed normal mode analysis (NMA) on the CETP structure. NMA is a well tested time-dependent technique that identifies slow, large amplitude motions by investigating the low frequency vibrational modes of a protein described by an elastic network (30). From the NMA results, we extracted four CETP conformations that exhibited the largest variations from the CETP crystal structure. They were (a) normal mode 1 with CETP in an elongated or stretched conformation having a bending angle of 160°, named CETP-NM1 (bending angle in crystal structure 139°); (b) normal mode 2 with CETP in a curved conformation having a bending angle of 131°, named CETP-NM2; (c) normal mode 3 with the CETP N-terminal β-barrel domain torsionally twisted by ∼15°, named CETP-NM3; and (d) normal mode 4 with both ∼9° torsionally twisted N-terminal β-barrel domain and elongated CETP with a bending angle of 148°, named CETP-NM4. To see the conformational transitions of CEs in these NMA-generated CETP structures, we docked two CEs and two phospholipids (PLs) in each of these four structures and performed MD simulations for 200, 400, 300, and 1000 ns, respectively (supplemental Table S1). As Fig. 3 shows, the availability of a larger space in the core of CETP has allowed more frequent interconversion of CEN between bent and linear conformations in these simulations on ANMA-generated structures. This was particularly evident in the CETP-NM4 system, where the bent to linear transition of CEN was more frequent and periodic.
FIGURE 3.
Conformational switching of bound CEs in the MD simulations of NMA-derived relaxed CETP structures. Time evolutions of the oleate angle of CEN (black) and CEC (red) are shown in the CETP-NM1 (a), CETP-NM2 (b), CETP-NM3 (c), and CETP-NM4 (d) systems. For system definition, see supplemental Table S1.
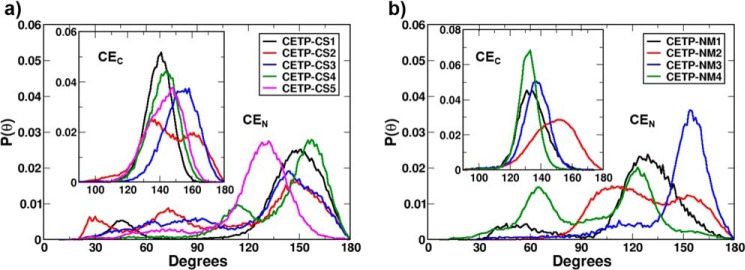
To better quantify the relative occurrences of the bent and linear conformations of CEs, we calculated the probability distributions of the CE oleate angle, P(θ), over the entire simulation trajectories, and the results are presented in Fig. 4. As the figure shows, the N-terminal CE in CETP shuttles between two major conformations, bent and linear, in all systems, suggesting that these two conformations can coexist. This is further supported by the simulation results from ANMA-generated CETP structures, particularly from CETP-NM4, which shows an almost equal propensity for the bent and linear conformations. The C-terminal CE, however, retains its native linear structure with a broad range of angle distribution between 120 and 180° in all systems. To summarize, the linear and bent conformations of CE in CETP coexist in solution. However, there is a particular preference for the linear conformation for both of the CEs in CETP relaxed structures, which might imply that CEs become linear for smooth transfer when CETP attaches to lipoproteins. We will elaborate on this hypothesis below.
FIGURE 4.
Probability distribution of CE oleate angle. Results are shown for CEs in CETP crystal structures (a) and CEs in NMA-derived CETP structures (b). Distribution is computed over the entire simulation time for each system.
Conformational Flexibility of CE Is Assisted by Bending and Twisting Motions of CETP
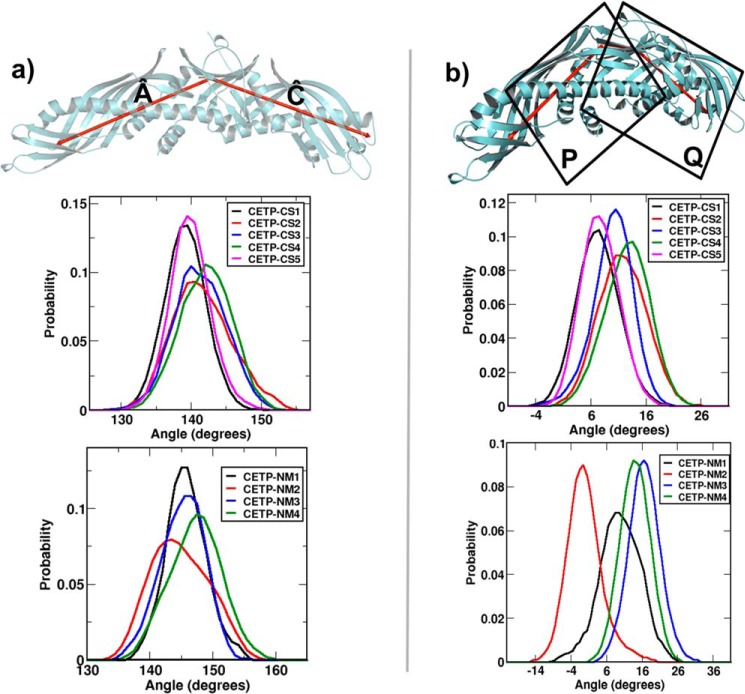
To investigate the possible reason behind the conformational flexibility of CEs and to see whether there is a correlation between CE conformational flexibility and CETP motions, we examined the distribution of bending and twisting angles in CETP. Fig. 5 shows the angular distributions of CETP from the simulation data. The bending motion was estimated by computing the angle between two vectors, Â and Ĉ. The vector from the center of mass (COM) of the central β-sheet to the COM of the N-terminal distal end was termed Â, and the other vector from the COM of the central β-sheet to the COM of the C-terminal distal end was termed Ĉ. The angle subtended by these two vectors was computed using the same formula as in Equation 1.
FIGURE 5.
Quantification of bending and twisting motions in CETP. a, probability distribution of CETP bending angle. Bending was computed from the angle between two vectors, Â and Ĉ, as shown in red on the molecular frame of CETP. b, probability distribution of the CETP twist angle. Twisting was computed by measuring the angle between the two planes, P and Q, as shown.
From the angle distribution profile, it is evident that the CETP crystal structure undergoes significant conformational changes and can extend to a more linear conformation with the bending angle as high as 151° and bend to an arch-like conformation with a bending angle of 131° (the crystal structure angle is 139°), whereas relaxed CETP from NMA displayed relatively high degrees of bending with the bending angle as high as 159° and bent to an arch-like conformation with a bending angle of 135°. In the same context, we estimated twisting-untwisting motion in CETP via relative rotation of N-terminal and C-terminal β-barrel domains with respect to the central β-domain. First, we constructed the axis of CETP as the vector connecting the COMs of N and C termini of the central β-domain and subsequently defined two planes, P and Q, with respect to the axis of CETP. Plane P is constituted by the axis of CETP and COM of the N-terminal β-barrel domain, whereas plane Q is constituted by the axis of CETP and COM of the C-terminal β-barrel domain. The twisting angle (θt) was computed by measuring the angle between the normal vectors n̂1 and n̂2 of these two planes as shown below.
Fig. 5b shows the probability distribution of the twisting angle of CETP, pertaining to the twisting motions with respect to the crystal and normal mode conformations. The figure depicts a Gaussian distribution with an average torsional twist of ∼8–12° in crystal structure simulations and a −2 to 16° twist in ANMA-generated CETP conformations. The average twisting angle observed in crystal conformations is less compared with the twisting observed in the normal modes, which can be attributed to the simplified harmonic description of the protein in ANMA.
The wide distribution of both bending and twisting angles indicates that CETP itself has enough plasticity and had undergone significant conformational changes in solution. To investigate whether these changes can influence the observed conformational switching of CEN, we plotted the time evolution of the bending angle of CETP. As supplemental Fig. S3 shows, although there is no synergy between the motions of CE and CETP, CETP switches its conformation continuously. Moreover, the CETP conformation appeared to be more strained when CEN was in the bent form. Thus, as supplemental Fig. S3 (a and b) indicates, the bending motion in CETP is more rapid, up to 300–500 ns, until when CEN was undergoing a vigorous back-and-forth motion between the bent and linear conformation. After that time when CEN became stabilized in the linear conformation, CETP bending also became less rapid. This was even more evident from the angle evolution of system CETP-CS4, where CETP bending was better stabilized at an earlier time of 250 ns in response to the early stability of CEN to linear conformation (supplemental Fig. S3c). We further confirmed these findings of CETP influence on CE conformational switching by restraining the motion of CETP in a new test simulation (system 10 in supplemental Table S1). As supplemental Fig. S4 indicates, when CETP was restrained, the motions of CEs were completely restricted, with CEN frozen into the original bent conformation. On the other hand, when CEs were kept fixed (system 11 in supplemental Table S1), CETP motion was found to be minimally hampered, as shown in supplemental Fig. S5. Thus, we conclude that CETP structure has sufficient plasticity, and the inherent dynamics of CETP greatly induces the conformational switching of its substrates, the cholesteryl esters.
CE Switching Enlarges CETP Core Tunnel
Because we observed a great deal of conformational flexibility of CEs within CETP, it was necessary to ascertain whether these frequent conformational changes in CEs affected the stability of secondary structural elements of CETP. Hence, we analyzed the evolution and stability of the whole secondary structural content and of local secondary structural elements of CETP around CEN. We found that, although there were significant conformational changes in CEs in the core of CETP, the protein maintained a stable secondary structure throughout the simulation. The total number of residues that constitute different structural elements of the protein remained unchanged throughout the simulation time, suggesting no significant disruption of the CETP secondary elements (supplemental Fig. S6a). More specifically, the local secondary structural elements around CEN, the central β-sheet (constituted by residues 11–16, 227–231, 261–266, and 456–461), helix A (residues 26–31), C-terminal region of helix B (residues 186–206), part of the N-terminal β-barrel twisted sheet (constituted by residues 81–86, 124–130, and 135–139), and the C-terminal region of helix B′ (residues 432–441) were completely stable during the entire course of a 1-μs simulation in the primary system (supplemental Fig. S6b). Analysis of secondary structure was performed by the GROMACS utility program do_dssp, which assigns secondary structure by analyzing the hydrogen bonding pattern between the protein residues.
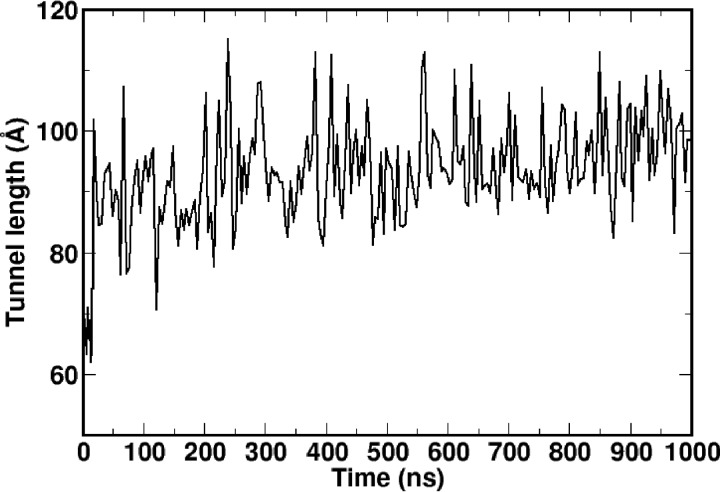
As mentioned previously, the substrate-bound CETP crystal structure was seen to possess a hydrophobic tunnel of length 60 Å and volume 2560 Å3 occupied by the two CEs and two dioleoylphosphatidylcholine molecules (23). The observed conformational flexibility of CEs and the inherent plasticity of CETP have impelled us to examine the plausible changes in the CETP hydrophobic tunnel. Hence, we examined the evolution of the CETP core tunnel across the 1-μs simulation run in the primary CETP system. Very interestingly, as Fig. 6 shows, the CETP tunnel significantly elongates from the crystal conformation and stabilized to an extended length of ∼95 Å during the final 500-ns simulation time when CEN was linear. This finding is consistent with the recent EM structure of CETP bound to HDL and LDL, which suggested a more continuous hydrophobic tunnel, compared with the shorter 60-Å central cavity observed in the CETP crystal structure (21). We speculate that the constricted tunnel found in the CETP crystal structure is a consequence of the crystal packing effects, as was also observed in the crystal structures of other proteins (e.g. HIV-1 protease) (31). Thus, it appears that the otherwise flexible CE was trapped in a bent conformation in the crystal that corresponds to a strongly packed complex of CEN and CETP (further discussed below). In our simulations, as the CETP-CE complex was provided a higher temperature (310 K versus 100 K in crystal) and also the solution phase, the system relaxed to an energetically more favorable conformation, with CEN turning to linear. The computed energy difference between the average structure of linear CE-bound CETP and the crystal conformation is −6.53 kcal/mol (ΔElinear_CE = −85.74 ± 1.2 kcal/mol; ΔEcrystal = −79.21 kcal/mol). The small difference in energetics is again suggestive of their coexistence in solution.
FIGURE 6.
Time evolution of the CETP core tunnel along the 1-μs simulation run in the primary system (system 1). The CETP tunnel significantly elongated from the crystal conformation and stabilized to an extended length of ∼95 Å during the final 500 ns of simulation time when CEN became linear.
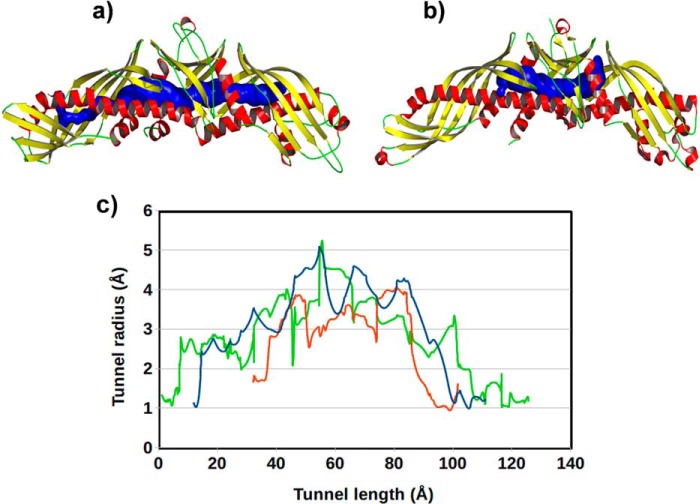
To have a clearer visualization of the CETP core tunnel, we extracted all CETP conformations with tunnel length ≥95 Å from the final 500-ns simulation data. The average conformation of CETP from this ensemble of structures is presented in Fig. 7a. The continuous tunnel traversing from the N- to C-terminal end of CETP is evident from this figure. In contrast, the 60-Å tunnel in the crystal conformation is confined at the central domain of the protein (Fig. 7b). We have also quantified the radius across the tunnel length and computed the total tunnel volume. The existence of a finite radius across the tunnel confirms that the protein indeed creates a continuous tunnel traversing from the N- to C-terminal end (Fig. 7c). The tunnel volume of the ensemble-averaged structure was 3536 Å3, and the radius was 1.4–2.1 Å wider than the crystal conformation. For comparison, we have also done the same analysis on the simulation trajectory of the CETP-NM4 system, and the results are included in Fig. 7c. A more elongated and continuous tunnel traversing up to the C-terminal edge is consistent with the more relaxed nature of this conformation of CETP. In parallel, to check the effect of CE linearization on tunnel length, we measured the CETP tunnel in a new simulation system (system 12 in supplemental Table S1), where CEN was restrained in the bent conformation. As supplemental Fig. S7 shows, the CETP tunnel remained constricted to 65 Å, suggesting that the conformational switching of CE greatly assists the formation of a continuous tunnel across CETP. Taken together, it appears that the inherent plasticity in CETP structure and the induced linearization of bound CEs produce a long continuous tunnel spanning from the N- to C-terminal ends of CETP, which could facilitate the transfer of lipids between lipoproteins. The associated large scale conformational changes in CETP and CE can happen in solution phase and, more prominently, when CETP encounters the lipoproteins, an environment that we attempted to create here by performing normal mode analysis on CETP.
FIGURE 7.
Elongation of the CETP core tunnel during simulations. a, tunnel in the extended CETP structure; b, tunnel in the crystal structure. CETP is shown in a schematic representation, and the tunnel is shown in blue surface mode. c, CETP tunnel radius as a function of tunnel length. Results are shown for CETP in crystal structure (red), CETP in extended conformation from crystal structure simulation (blue), and CETP in extended conformation from simulation of NMA-derived CETP structure (green). Simulation structures are ensemble-averaged over at least 1000 extended conformations of CETP.
Linear CE Loses Contacts with CETP but Gains New Contacts with a Second CE
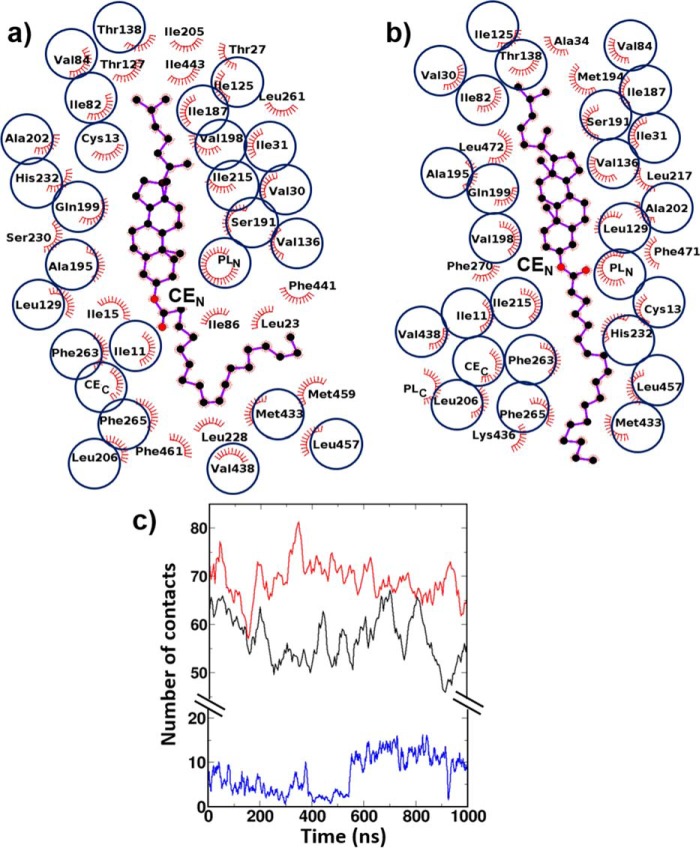
To underscore the possible reason why CEN was trapped in the bent conformation in crystal, we analyzed the interactions of bent CEN with CETP tunnel lining residues and compared that with the interactions of linear CEN. The results are shown in Fig. 8. Unsurprisingly, both bent and linear CEN conformations have many common hydrophobic interactions with CETP residues (e.g. Ile-11 and Cys-13 in strand S1; Val-30 and Ile-31 in helix A; Ile-82 and Val-84 in strand S4; Ile-125 and Leu-129 in strand S5; Val-136 and Thr-138 in strand S6; Ile-187, Ser-191, Ala-195, Val-198, Gln-199, Ala-202, and Leu-206 in helix B; Ile-215 in strand S7; His-232 in strand S8; Phe-263 and Phe-265 in strand S1′; Met-433 and Val-438 in helix B′; Leu-457 in strand S8′). Apart from the CETP residues, CEC and N-terminal phospholipid also maintained similar interactions with both forms of CEN. However, CEN in the linear conformation had lost interactions with other tunnel residues of CETP (e.g. Ile-15 in strand S1; Leu-23 and Thr-27 in helix A; Ile-86 in strand S4; Thr-127 in strand S5; Ile-205 in helix B; Leu-228 and Ser-230 in strand S8; Leu-261 in strand S1′; Phe-441 and Ile-443 in strand S7′; Met-459 and Phe-461 in strand S8′) but gained new hydrophobic contacts with residues Ala-34 in helix A; Met-194 in helix B; Leu-217 in strand S7; Phe-270 in helix A′; Lys-436 in helix B′; Phe-471 and Leu-472 in helix X; and the C-terminal phospholipid, PL-2 (Fig. 8, compare a and b). Thus, there was a net loss of five residue-level contacts due to the linearization of bent CEN, which made 36 residue-level contacts in the crystal, accounting for a net loss of 14% residue-level contacts of linear CE relative to the bent form. In terms of site-site contacts, this loss appears to be even more prominent. A net loss of 20 distinct site-site contacts was observed due to the conformational transition of bent CE to the linear form (Fig. 8c). Site-site contacts were counted by imposing a distance criterion of 5 Å between a pair of protein and CEN atoms. These findings strengthen our inference of crystal packing effects in the solved crystal structure, because the CEN experiences a greater packing (larger contacts) with CETP residues in the bent form. In our simulations, as the CETP-CE complex was provided a higher temperature (310 K versus 100 K in crystal) and also the solution phase, the system relaxed to a thermodynamically more favorable conformation, with CEN turning to linear.
FIGURE 8.
Hydrophobic contacts of different conformation of CEs with CETP. Results are shown for bent CE conformation (a) and linear CE conformation (b). CEs are shown by a ball-and-stick representation, and the protein residues involved in hydrophobic interactions are shown by red spikes. The common interacting CETP residues are highlighted by circles. c, time evolution of the site-site contacts between CEN and CEC (blue), CEN and CETP (black), and CEC and CETP (red).
The other noteworthy feature of Fig. 8c is that despite the significant changes in CEN, CEC maintained very similar contacts with CETP tunnel residues throughout the simulation. More importantly, the oleate chain of CEN tended to form a new set of hydrophobic contacts with the acyl chain of CEC to compensate for its loss of contacts with CETP tunnel residues. Thus, the initial number of 2–10 site-site contacts of CEN with CEC was increased to 10–20 due to the extended linear CEN conformation. From these results, we are tempted to speculate that the reduced contacts of linear CEN with CETP and its increased contacts with CEC reduce the friction of CEs with the CETP tunnel and facilitate the transfer of these neutral lipids through a continuous CETP tunnel. Thus, our MD simulation result could successfully produce the “open state” of CETP, as was speculated by Ren and co-workers (21) from their recent cryo-EM study on the lipid transfer mechanism of CETP.
Straightening of CE Is Boosted by Free Energy Gain
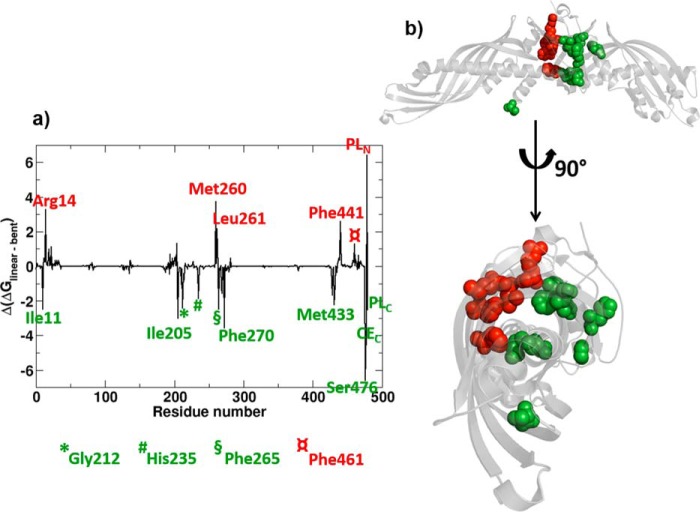
Thus far, we have seen that CETP-bound CE switches conformation from bent to linear, and this process is assisted by the inherent dynamics of CETP and favorable contacts of its tunnel residues. To assess the energetic contribution of individual CETP residues on conformational switching of CEN, we performed a Gibbs free energy calculation and decomposed the total Gibbs energy into residue level. A set of 10,000 frames between 200 and 300 ns, when CEN was in the bent conformation, and another set of 10,000 frames between 600 and 700 ns, when CEN was in linear conformation, were analyzed. Subsequently, free energy gain due to CE conformational change from bent to linear (ΔΔGlinear-bent) was calculated for each CETP residue, and the results are presented in Fig. 9. Free energy contributions are shown only for those CETP residues that pass the free energy difference cut-off of ±0.5 kcal/mol.
FIGURE 9.
a, change in Gibbs free energy of select CETP residues due to the conformational transition of CEN from bent to linear. Residues favoring the CEN linearization are highlighted in green, and those favor bent CEN are highlighted in red. b, location of these CETP tunnel lining residues are shown in the three-dimensional representation of the protein.
As Fig. 9 shows, bent CEN has stronger binding affinity for the central β domain residues (Arg-14, Met-260, Leu-261, Phe-441, and Phe-461) and the N-terminal phospholipid, PLN. On the other hand, CEN in the linear conformation has greater binding strength with the central β domain residues Ile-11, Phe-265, and Phe-270; helix B′ residue Met-433; helix B residue Ile-205; strand S7 residue Gly-212; strand S8 residue His-235; C-terminal residue Ser-476; and the lipids present in the C-terminal hydrophobic pocket, CEC and PLC. This free energy result fits very well with contact analysis data, because most of the strongly interacting CETP residues (e.g. Ile-11, Ile-205, Leu-261, Phe-265, Phe-270, Met-433, Phe-441, and Phe-461) were also found to make contacts with bent or/and linear CEN (compare Figs. 8 and 9). As mentioned above, residues Ile-11, Phe-265, and Met-433 make contacts with both forms of CEN. However, the free energy of binding of these residues with linear CEN is much stronger than with the bent form. Moreover, Phe-270, Gly-212, His-235, Ser-476, etc. engage in specific interactions with linear CEN that are energetically highly favorable. Although the interactions of Arg-14, Met-260, Leu-261, Phe-441, and Phe-461 tend to favor the bent form of CEN, there is a net gain of −5.55 kcal/mol (−85.74 ± 1.2 kcal/mol for linear CE versus −80.19 ± 1.3 kcal/mol for bent CE) for linear CE in the CETP tunnel when in solution.
Interestingly, a subset of our identified residues with significant affinity for linear CEN has recently been reported to be crucial for CE/TG transfer through CETP and CETP stability (23). For example, the mutant M433W exhibited a nearly 2-fold decline in CE transfer activity and a 5-fold decline in TG transfer activity in the site-specific mutagenesis studies (23). Similarly, the mutants F265R and F270R were characterized to be responsible for misfolding and subsequent failure in CETP secretion (23). The deletion of Ser-476 from CETP C-terminal had completely abolished the protein's neutral lipid transfer activity (32). In other words, these reports have pointed out that residues Met-433, Phe-265, Phe-270, and Ser-476 in native CETP maintain the structural integrity and functional activity of the protein. Now, because the functional activity of CETP is the transfer of CE/TG and none of the mutational studies have traced any of our identified CETP residues interacting with the bent form of CE for activity (Fig. 9), it is conceivable that CE remains in the linear conformation in functional CETP, whereas the specific CETP residues (e.g. the green-colored residues in Fig. 9) provide a favorable environment.
Conclusions
Understanding the mechanism of lipid transfer by CETP has received tremendous attention due to its crucial role in maintaining the levels of HDL and LDL. Although the CE-bound CETP crystal structure provided much useful structural information, understanding a dynamic process, such as the transfer of lipids through CETP, remains elusive. In this study, we employed microsecond-long atomistic MD simulations and normal mode analysis to explore the dynamics of CETP and its bound substrates, which provided very important clues about the lipid transfer activity of CETP. Our results suggested unique structural plasticity in the CETP structure, consisting of bending-unbending and twisting motions along its long axis. This inherent dynamics of CETP greatly induces the conformational switching of CEs, which transform to a linear conformation from their bent structure in crystal. We speculate that the bent CE and constricted tunnel found in the CETP crystal structure are the consequence of crystal packing effects, as was also observed in the crystal structures of other proteins (e.g. HIV-1 protease) (31). In our simulations, as the CETP-CE complex was provided a higher temperature (310 K versus 100 K in crystal) and also the solution phase, the system relaxed to a thermodynamically stable conformation, with bound CEs switching to linear. As a consequence of the inherent plasticity of CETP and the induced linearization of bound CEs, a long continuous tunnel spanning from N- to C-terminal ends of CETP is produced, which can facilitate the transfer of lipids between lipoproteins. Thus, our MD simulation results could successfully produce the “open state” of CETP, as was speculated by Ren and co-workers (21) from their recent EM study on the lipid transfer mechanism of CETP.
When this work was in progress, Ren and co-workers (25) reported the transfer pathway of CE through CETP by MD simulation studies. To detect the pathway in a reasonable time, the authors applied an external force to pull a linear CE molecule through a hollow CETP tunnel. Very similar to this study, our results also show the twisting motions in CETP and the formation of a continuous tunnel between the two distal ends of CETP. Moreover, the CETP tunnel lining residues that we found to make favorable interactions with CE (e.g. residues Ile-205, Phe-263, Phe-265, and Met-433) were noted by these authors to facilitate the CE transfer. However, the tunnel length from our CETP crystal structure simulation was found to be shorter by about 15 Å than that in the report by Ren and co-workers (95 Å versus 110 Å), which explicitly included the lipoprotein mimics at both ends of CETP to model the HDL-CETP-LDL ternary complex. Our implicit inclusion of lipoprotein effects by simulating the relaxed CETP generated from NMA, however, produced a continuous core tunnel as lengthy as the aforementioned report. In addition, our study's major focus on the inherent dynamics of CETP shows that, apart from the twisting motion, CETP also undergoes significant bending-unbending that could produce sufficient driving force “within” to induce conformational switching in bound CE and consequently a continuous tunnel across CETP. Although this tunnel could become more prominent when CETP senses the lipoproteins, it can exist in the free form of the protein due to its structural plasticity in solution.
Materials and Methods
A molecular dynamics simulation of the primary CETP system was started from the recently solved x-ray crystal structure of CETP (Protein Data Bank entry 2OBD). The missing residues in the N-terminal region of the crystal structure (Ala-1, Ser-2, Lys-3, and Gly-4) were included using MODELLER9 version 13 (33). Subsequently, the mutations induced in CETP to promote the crystallization (viz. C1A, N88D, C131A, N240D, and N341D) were back-mutated. The charge state of CETP was chosen at pH 7.4 to mimic the physiological conditions. The GROMOS53A6 force field (34) for the protein and Berger lipid parameters (35) for CETP bound lipids were used. Hydrogens for heavy atoms were added by the pdb2gmx module in the GROMACS-4.5.5 simulation package. The protonation states of histidines were determined by the local hydrogen bonding network using the WHAT IF web server (36). The system was subsequently energy-minimized for 2000 steps using the conjugate gradient algorithm and another 2000 steps using the steepest descent algorithm. The structure was solvated using explicit water in a cubic periodic box with water molecules extending 10 Å outside the protein on all sides. Water molecules were described using a simple point charge water model. The system was solvated using 131,251 water molecules, and a salt concentration of 0.15 m was maintained by adding 371 Na+ and 363 Cl− counterions. The system was energy-minimized again and then heated up gradually to reach a temperature of 310 K using a V-rescale thermostat with a coupling constant of 0.1 ps (37). The solvent density was adjusted under isobaric and isothermal conditions at 1 bar and 310 K. A Parrinello-Rahman barostat with isotropic pressure coupling and a coupling constant of 0.1 ps was used to set the pressure at 1 bar (38). The system was equilibrated for 10 ns in the NPT ensemble with a simulation time step of 2 fs. Finally, the production run was carried out for 1000 ns in the NPT ensemble for the primary system (system CETP-CS1 in supplemental Table S1). The long range electrostatic interactions were treated using particle-mesh Ewald sum with a cut-off of 1.0 nm (39). The van der Waals interactions were terminated beyond the cut-off value of 1.0 nm. The LINCS algorithm was used to constrain all bonds involving hydrogen atoms (40). All simulations were performed using the GROMACS-4.5.5 simulation program (41).
The molecular dynamics simulations of CETP crystal structure essentially describe the conformational changes in CETP that occur at short length and time scales. However, the changes that CETP undergoes in plasma and particularly when bound to lipoprotein would be at much larger scales. To capture such large scale conformational changes, we performed NMA on the CETP structure obtained from crystal. NMA is a well tested technique that identifies slow, large amplitude motions by investigating the low frequency vibrational modes of a protein described by an elastic network (30). The anisotropic network model web server, ANM 2.0, was used to perform the NMA (42, 43). In the elastic model of CETP, the maximum interaction range between the Cα atoms (nodes) was set at 15 Å. First the four lowest frequency vibrational modes were picked from NMA, which presumably represent the most relaxed/functionally relevant conformations of CETP as it exists in plasma or when bound to lipoproteins. These four relaxed or functionally relevant CETP conformations were designated CETP-NM1, CETP-NM2, CETP-NM3, and CETP-NM4. Subsequently, to explore the dynamics, the four lipids (two CEs and two PLs) were docked at the requisite locations of the CETP tunnel, and the complex was subjected to long molecular dynamics simulations following the same protocol as described for the primary system. Supplemental Table S1 lists all of the systems studied. Overall, a total of 5.9 μs of atomistic simulation was carried out in this work.
The Caver version 3.0 tool kit was used to identify and characterize the pockets and tunnels in CETP (44). Various conformations of CETP after removing the lipids were given as inputs for tunnel analysis. The probe radius was set to the default of 3 Å to construct the molecular surface of the pocket or tunnel. PyMOL was used to generate all structural figures (45). The LIGPLOT tool was used to map all protein-lipid interactions (46).
Free Energy Calculations
The free energy calculations were performed on the molecular dynamics trajectories using the molecular mechanics Poisson Boltzmann surface area method (47). The GROMACS utility program g_mmpbsa was employed to estimate the free energies (48). Generally, the binding free energy for a ligand bound protein in solvent is estimated as follows,
where Gcomplex, Gprotein, and Gligand are the free energies of the protein-ligand complex, free protein, and free ligand, respectively, in solvent.
The average free energy for each individual component in the above equation is defined as follows,
where TS is the contribution of entropy to the system's free energy at temperature T in vacuum, and 〈EMM〉 is the vacuum potential energy, which includes bonded and non-bonded interaction energies and can be expressed as follows.
〈GS〉 is the solvation free energy and is expressed as follows,
where Gnonpolar and Gpolar represent the contribution of nonpolar and polar solvation energy.
Subsequently, the binding energy for each individual residue (ΔGr) was decomposed as follows,
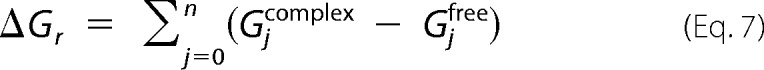 |
where Gjcomplex and Gjfree are the energies of the jth atom from the r residue in complex and free forms, respectively, and n is the total number of atoms in the residue. The vacuum, solute, and solvent dielectric constants were set at 1, 2, and 80, respectively. Bootstrap analysis was performed to obtain S.E. values.
Author Contributions
V. R. C., P. D. R., and S. S. conceived and designed the experiments. V. R. C. and P. D. R. performed the experiments. V. R. C., P. D. R., and S. S. analyzed the data. S. S. contributed reagents, materials, and analysis tools. V. R. C., P. D. R., and S. S. wrote the paper.
Supplementary Material
Acknowledgment
We thank the High Performance Computing Environment (HPCE), Indian Institute of Technology Madras, for computational resources.
The authors declare that they have no conflicts of interest with the contents of this article.

This article contains supplemental Table 1 and Figs. S1–S7.
- CHD
- coronary heart disease
- CETP
- cholesteryl ester transfer protein
- CE
- cholesteryl ester
- MD
- molecular dynamics
- NMA
- normal mode analysis
- PL
- phospholipid
- COM
- center of mass
- ANMA
- anisotropic network model analysis.
References
- 1. Sharrett A. R., Ballantyne C. M., Coady S. A., Heiss G., Sorlie P. D., Catellier D., Patsch W., and Atherosclerosis Risk in Communities Study Group (2001) Coronary heart disease prediction from lipoprotein cholesterol levels, triglycerides, lipoprotein(a), apolipoproteins A-I and B, and HDL density subfractions: the atherosclerosis risk in communities (ARIC) study. Circulation 104, 1108–1113 [DOI] [PubMed] [Google Scholar]
- 2. Luc G., Bard J.-M., Ferrières J., Evans A., Amouyel P., Arveiler D., Fruchart J. C., and Ducimetière P. (2002) Value of HDL cholesterol, apolipoprotein A-I, lipoprotein A-I, and lipoprotein A-I/A-II in prediction of coronary heart disease: The PRIME study. Arterioscler. Thromb. Vasc. Biol. 22, 1155–1161 [DOI] [PubMed] [Google Scholar]
- 3. Zhang Y., Zanotti I., Reilly M. P., Glick J. M., Rothblat G. H., and Rader D. J. (2003) Overexpression of apolipoprotein A-I promotes reverse transport of cholesterol from macrophages to feces in vivo. Circulation 108, 661–663 [DOI] [PubMed] [Google Scholar]
- 4. Tall A. R., Yvan-Charvet L., Terasaka N., Pagler T., and Wang N. (2008) HDL, ABC transporters, and cholesterol efflux: implications for the treatment of atherosclerosis. Cell Metab. 7, 365–375 [DOI] [PubMed] [Google Scholar]
- 5. Cannon C. P., Braunwald E., McCabe C. H., Rader D. J., Rouleau J. L., Belder R., Joyal S. V., Hill K. A., Pfeffer M. A., Skene A. M., and Pravastatin or Atorvastatin Evaluation and Infection Therapy-Thrombolysis in Myocardial Infarction 22 Investigators (2004) Intensive versus moderate lipid lowering with statins after acute coronary syndromes. N. Engl. J. Med. 350, 1495–1504 [DOI] [PubMed] [Google Scholar]
- 6. Robins S. J., Collins D., Wittes J. T., Papademetriou V., Deedwania P. C., Schaefer E. J., McNamara J. R., Kashyap M. L., Hershman J. M., Wexler L. F., Rubins H. B., and VA-HIT Study Group. Veterans Affairs High-Density Lipoprotein Intervention Trial (2001) Relation of gemfibrozil treatment and lipid levels with major coronary events: VA-HIT: a randomized controlled trial. JAMA 285, 1585–1591 [DOI] [PubMed] [Google Scholar]
- 7. Goldberg A., Alagona P. Jr., Capuzzi D. M., Guyton J., Morgan J. M., Rodgers J., Sachson R., and Samuel P. (2000) Multiple-dose efficacy and safety of an extended-release form of niacin in the management of hyperlipidemia. Am. J. Cardiol. 85, 1100–1105 [DOI] [PubMed] [Google Scholar]
- 8. Tall A. R. (1993) Plasma cholesteryl ester transfer protein. J. Lipid Res. 34, 1255–1274 [PubMed] [Google Scholar]
- 9. Barter P. J., Brewer H. B. Jr., Chapman M. J., Hennekens C. H., Rader D. J., and Tall A. R. (2003) Cholesteryl ester transfer protein: A novel target for raising HDL and inhibiting atherosclerosis. Arterioscler. Thromb. Vasc. Biol. 23, 160–167 [DOI] [PubMed] [Google Scholar]
- 10. Zhong S., Sharp D. S., Grove J. S., Bruce C., Yano K., Curb J. D., and Tall A. R. (1996) Increased coronary heart disease in Japanese-American men with mutation in the cholesteryl ester transfer protein gene despite increased HDL levels. J. Clin. Invest. 97, 2917–2923 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Koizumi J., Mabuchi H., Yoshimura A., Michishita I., Takeda M., Itoh H., Sakai Y., Sakai T., Ueda K., and Takeda R. (1985) Deficiency of serum cholesteryl-ester transfer activity in patients with familial hyperalphalipoproteinaemia. Atherosclerosis 58, 175–186 [DOI] [PubMed] [Google Scholar]
- 12. Brown M. L., Inazu A., Hesler C. B., Agellon L. B., Mann C., Whitlock M. E., Marcel Y. L., Milne R. W., Koizumi J., and Mabuchi H. (1989) Molecular basis of lipid transfer protein deficiency in a family with increased high-density lipoproteins. Nature 342, 448–451 [DOI] [PubMed] [Google Scholar]
- 13. Inazu A., Brown M. L., Hesler C. B., Agellon L. B., Koizumi J., Takata K., Maruhama Y., Mabuchi H., and Tall A. R. (1990) Increased high-density lipoprotein levels caused by a common cholesteryl-ester transfer protein gene mutation. N. Engl. J. Med. 323, 1234–1238 [DOI] [PubMed] [Google Scholar]
- 14. Marotti K. R., Castle C. K., Boyle T. P., Lin A. H., Murray R. W., and Melchior G. W. (1993) Severe atherosclerosis in transgenic mice expressing simian cholesteryl ester transfer protein. Nature 364, 73–75 [DOI] [PubMed] [Google Scholar]
- 15. Plump A. S., Masucci-Magoulas L., Bruce C., Bisgaier C. L., Breslow J. L., and Tall A. R. (1999) Increased atherosclerosis in ApoE and LDL receptor gene knock-out mice as a result of human cholesteryl ester transfer protein transgene expression. Arterioscler. Thromb. Vasc. Biol. 19, 1105–1110 [DOI] [PubMed] [Google Scholar]
- 16. Sugano M., Makino N., Sawada S., Otsuka S., Watanabe M., Okamoto H., Kamada M., and Mizushima A. (1998) Effect of antisense oligonucleotides against cholesteryl ester transfer protein on the development of atherosclerosis in cholesterol-fed rabbits. J. Biol. Chem. 273, 5033–5036 [DOI] [PubMed] [Google Scholar]
- 17. Mantlo N. B., and Escribano A. (2014) Update on the discovery and development of cholesteryl ester transfer protein inhibitors for reducing residual cardiovascular risk. J. Med. Chem. 57, 1–17 [DOI] [PubMed] [Google Scholar]
- 18. Sikorski J. A. (2006) Oral cholesteryl ester transfer protein (CETP) inhibitors: a potential new approach for treating coronary artery disease. J. Med. Chem. 49, 1–22 [DOI] [PubMed] [Google Scholar]
- 19. Gotto A. M. Jr., and Moon J. E. (2012) Safety of inhibition of cholesteryl ester transfer protein with anacetrapib: the DEFINE study. Expert Rev. Cardiovasc. Ther. 10, 955–963 [DOI] [PubMed] [Google Scholar]
- 20. Nicholls S. J., Brewer H. B., Kastelein J. J. P., Krueger K. A., Wang M. D., Shao M., Hu B., McErlean E., and Nissen S. E. (2011) Effects of the CETP inhibitor evacetrapib administered as monotherapy or in combination with statins on HDL and LDL cholesterol: a randomized controlled trial. JAMA 306, 2099–2109 [DOI] [PubMed] [Google Scholar]
- 21. Zhang L., Yan F., Zhang S., Lei D., Charles M. A., Cavigiolio G., Oda M., Krauss R. M., Weisgraber K. H., Rye K.-A., Pownall H. J., Qiu X., and Ren G. (2012) Structural basis of transfer between lipoproteins by cholesteryl ester transfer protein. Nat. Chem. Biol. 8, 342–349 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Lauer M. E., Graff-Meyer A., Rufer A. C., Maugeais C., von der Mark E., Matile H., D'Arcy B., Magg C., Ringler P., Müller S. A., Scherer S., Dernick G., Thoma R., Hennig M., Niesor E. J., and Stahlberg H. (2016) Cholesteryl ester transfer between lipoproteins does not require a ternary tunnel complex with CETP. J. Struct. Biol. 194, 191–198 [DOI] [PubMed] [Google Scholar]
- 23. Qiu X., Mistry A., Ammirati M. J., Chrunyk B. A., Clark R. W., Cong Y., Culp J. S., Danley D. E., Freeman T. B., Geoghegan K. F., Griffor M. C., Hawrylik S. J., Hayward C. M., Hensley P., Hoth L. R., et al. (2007) Crystal structure of cholesteryl ester transfer protein reveals a long tunnel and four bound lipid molecules. Nat. Struct. Mol. Biol. 14, 106–113 [DOI] [PubMed] [Google Scholar]
- 24. Liu S., Mistry A., Reynolds J. M., Lloyd D. B., Griffor M. C., Perry D. A., Ruggeri R. B., Clark R. W., and Qiu X. (2012) Crystal structures of cholesteryl ester transfer protein in complex with inhibitors. J. Biol. Chem. 287, 37321–37329 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Lei D., Rames M., Zhang X., Zhang L., Zhang S., and Ren G. (2016) Insights into the tunnel mechanism of cholesteryl ester transfer protein using all-atom molecular dynamics simulations. J. Biol. Chem. 291, 14034–14044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Chirasani V. R., Sankar R., and Senapati S. (2016) Mechanism of inhibition of cholesteryl ester transfer protein by small molecule inhibitors. J. Phys. Chem. B. 10.1021/acs.jpcb.6b01928 [DOI] [PubMed] [Google Scholar]
- 27. Koivuniemi A., Vuorela T., Kovanen P. T., Vattulainen I., and Hyvönen M. T. (2012) Lipid exchange mechanism of the cholesteryl ester transfer protein clarified by atomistic and coarse-grained simulations. PLoS Comput. Biol. 8, e1002299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Äijänen T., Koivuniemi A., Javanainen M., Rissanen S., Rog T., and Vattulainen I. (2014) How anacetrapib inhibits the activity of the cholesteryl ester transfer protein? Perspective through atomistic simulations. PLoS Comput. Biol. 10, e1003987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Senapati S., and Berkowitz M. L. (2003) Molecular dynamics simulation studies of polyether and perfluoropolyether surfactant based reverse micelles in supercritical carbon dioxide. J. Phys. Chem. B 107, 12906–12916 [Google Scholar]
- 30. Alexandrov V., Lehnert U., Echols N., Milburn D., Engelman D., and Gerstein M. (2005) Normal modes for predicting protein motions: a comprehensive database assessment and associated Web tool. Protein Sci. 14, 633–643 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Layten M., Hornak V., and Simmerling C. (2006) The open structure of a multi-drug-resistant HIV-1 protease is stabilized by crystal packing contacts. J. Am. Chem. Soc. 128, 13360–13361 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Wang S., Kussie P., Deng L., and Tall A. (1995) Defective binding of neutral lipids by a carboxyl-terminal deletion mutant of cholesteryl ester transfer protein: evidence for a carboxyl-terminal cholesteryl ester binding site essential for neutral lipid transfer activity. J. Biol. Chem. 270, 612–618 [DOI] [PubMed] [Google Scholar]
- 33. Webb B., and Sali A. (2014) Comparative protein structure modeling using Modeller. Curr. Protoc. Bioinformatics 47, 5.6.1–5.6.37 [DOI] [PubMed] [Google Scholar]
- 34. Schuler L. D., Daura X., and van Gunsteren W. F. (2001) An improved GROMOS96 force field for aliphatic hydrocarbons in the condensed phase. J. Comput. Chem. 22, 1205–1218 [Google Scholar]
- 35. Berger O., Edholm O., and Jähnig F. (1997) Molecular dynamics simulations of a fluid bilayer of dipalmitoylphosphatidylcholine at full hydration, constant pressure, and constant temperature. Biophys. J. 72, 2002–2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Vriend G. (1990) WHAT IF: a molecular modeling and drug design program. J. Mol. Graph. 8, 52–56, 29. [DOI] [PubMed] [Google Scholar]
- 37. Bussi G., Donadio D., and Parrinello M. (2007) Canonical sampling through velocity rescaling. J. Chem. Phys. 126, 014101 [DOI] [PubMed] [Google Scholar]
- 38. Parrinello M., and Rahman A. (1981) Polymorphic transitions in single crystals: a new molecular dynamics method. J. Appl. Phys. 52, 7182–7190 [Google Scholar]
- 39. Essmann U., Perera L., Berkowitz M. L., Darden T., Lee H., and Pedersen L. G. (1995) A smooth particle mesh Ewald method. J. Chem. Phys. 103, 8577–8593 [Google Scholar]
- 40. Hess B., Bekker H., Berendsen H. J. C., and Fraaije J. G. E. M. (1997) LINCS: a linear constraint solver for molecular simulations. J. Comput. Chem. 18, 1463–1472 [Google Scholar]
- 41. Hess B., Kutzner C., van der Spoel D., and Lindahl E. (2008) GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 4, 435–447 [DOI] [PubMed] [Google Scholar]
- 42. Eyal E., Yang L. W., and Bahar I. (2006) Anisotropic network model : systematic evaluation and a new web interface. Bioinformatics 22, 2619–2627 [DOI] [PubMed] [Google Scholar]
- 43. Doruker P., Atilgan A. R., and Bahar I. (2000) Dynamics of proteins predicted by molecular dynamics simulations and analytical approaches: application to α-amylase inhibitor. Proteins 40, 512–524 [PubMed] [Google Scholar]
- 44. Chovancova E., Pavelka A., Benes P., Strnad O., Brezovsky J., Kozlikova B., Gora A., Sustr V., Klvana M., Medek P., Biedermannova L., Sochor J., and Damborsky J. (2012) CAVER 3.0: a tool for the analysis of transport pathways in dynamic protein structures. PLoS Comput. Biol. 8, e1002708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Delano W. L. (2011) The PyMOL Molecular Graphics System, version 1.5.0.4, Schrödinger, LLC, New York [Google Scholar]
- 46. Laskowski R. A., and Swindells M. B. (2011) LigPlot+: multiple ligand-protein interaction diagrams for drug discovery. J. Chem. Inf. Model. 51, 2778–2786 [DOI] [PubMed] [Google Scholar]
- 47. Kumari R., Kumar R., Open Source Drug Discovery Consortium, and Lynn A. (2014) g-mmpbsa: a GROMACS tool for high-throughput MM-PBSA calculations. J. Chem. Inf. Model. 54, 1951–1962 [DOI] [PubMed] [Google Scholar]
- 48. Baker N. A., Sept D., Joseph S., Holst M. J., and McCammon J. A. (2001) Electrostatics of nanosystems: application to microtubules and the ribosome. Proc. Natl. Acad. Sci. U.S.A. 98, 10037–10041 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.