A Statistical Model to Analyze Clinician Expert Consensus on Glaucoma Progression using Spatially Correlated Visual Field Data

Abstract

Purpose

We developed a statistical model to improve the detection of glaucomatous visual field (VF) progression as defined by the consensus of expert clinicians.

Methods

We developed new methodology in the Bayesian setting to properly model the progression status of a patient (as determined by a group of expert clinicians) as a function of changes in spatially correlated sensitivities at each VF location jointly. We used a spatial probit regression model that jointly incorporates all highly correlated VF changes in a single framework while accounting for structural similarities between neighboring VF regions.

Results

Our method had improved model fit and predictive ability compared to competing models as indicated by the deviance information criterion (198.15 vs. 201.29–213.38), a posterior predictive model selection metric (130.08 vs. 142.08–155.59), area under the receiver operating characteristic curve (0.80 vs. 0.59–0.72; all P values < 0.018), and optimal sensitivity (0.92 vs. 0.28–0.82). Simulation study results suggest that estimation (reduction of mean squared errors) and inference (correct coverage of 95% credible intervals) for the model parameters are improved when spatial modeling is incorporated.

Conclusions

We developed a statistical model for the detection of VF progression defined by clinician expert consensus that accounts for spatially correlated changes in visual sensitivity over time, and showed that it outperformed competing models in a number of areas.

Translational Relevance

This model may easily be incorporated into routine clinical practice and be useful for detecting glaucomatous VF progression defined by clinician expert consensus.

Introduction

Glaucomatous vision loss is irreversible, making early detection of the disease and, once detected, prevention of its progression essential. The timely detection of visual field (VF) progression is important since reduction of intraocular pressure (IOP), achieved with medical therapy, laser surgery, and/or incisional surgery, slows the rate of further deterioration.

Once a patient is diagnosed with glaucoma, clinicians must balance the risks and expenses of advancing levels of medical and surgical intervention with the risk of vision loss due to disease progression. The clinician must determine, at regular intervals, whether the disease is stable or not. If the evidence for progression is sufficiently strong and the apparent rate of progression is such that the patient is at risk of symptomatic vision loss in his or her lifetime, the physician must more aggressively lower the IOP. During most stages of the disease, assessment of the VF is the most important factor that must be considered in determining whether the disease process is stable in an individual patient. As a result, much effort has been devoted to determining if damage to an individual's VF is progressing over time at a rate requiring treatment adjustment.

The majority of past studies either model each VF location separately over time or aggregate over the entire VF at each time point when determining progression status.^1–3 Both methods are potentially inefficient and neglect important spatial information contained in the data. We hypothesized that jointly considering changes in sensitivities at each VF location over time when determining progression and identifying regions across the VF where clinicians place increased emphasis when judging progression would preserve important spatial relationships, increasing the explanatory and predictive capabilities of the model. Such an approach increases the amount of available information used in determining progression and more closely resembles the decision-making process used by clinicians who focus on changes across the entire VF and patterns of change as opposed to individual locations separately. The purpose of this study was to develop, implement, and validate a statistical model for detecting glaucoma progression, as defined by the consensus of expert clinicians, and compare its performance to existing approaches.

Our newly developed method for jointly incorporating highly spatially correlated predictors in the modeling framework provides insight into how expert clinicians determine the glaucoma progression status based on observing VF measurements over time for an individual and provides a framework for improved prediction of the outcome for future patients.

Methods

Data Sources

Two VF datasets consisting of reliable VFs (fixation loss rate less than 20% and false-positive and false-negative response rates less than 15%) obtained with the 24-2 Swedish Interactive Thresholding Algorithm (SITA) of the Humphrey Visual Field Analyzer (Carl Zeiss Meditec, Inc., Dublin, CA) were used in this study.^4,5 In the first dataset, each of the VFs were obtained using the SITA standard strategy and VF progression status was determined based on the independent reviews of two expert clinicians. In the case of disagreement, a third clinician was consulted. Reviewers had access to an event-based determination of progression, the Glaucoma Progression Analysis output (GPA; Carl Zeiss Meditec, Inc.), and the print versions of the VF tests over time. Clinicians were instructed to define each series of VF tests as definitely progressing or not.⁴ Table 1 displays the summary information from this modeling dataset.

Table 1.

Data Summaries from the Modeling and Validation Datasets

The second dataset contained approximately 1% of VF tests performed with the full threshold strategy and approximately 1% performed with the 30-2 test pattern. It represents VF series and responses from an independent validation group of glaucoma patients. These data have been described previously.⁵ Progression status was once again determined based on review of the VF series and GPA output for each patient, this time by a different set of five expert clinicians. The intraobserver and interobserver agreements were good to excellent and moderate, respectively.⁵ Table 1 displays the summary information from this validation dataset.

Statistical Model

In our model, the probability that an eye is determined to be progressing based on the clinician expert consensus is a function of the rates of change in sensitivities across time at each VF location, where the contribution of a particular location is related to the contributions at nearby spatially-related locations through the use of a spatially referenced prior distribution. We model the underlying probability associated with the binary clinician expert consensus on glaucoma progression status (yes/no) for a patient/eye as a function of VF sensitivity changes over time at each location on the VF, such that Y_i | β,θ ∼ Bernoulli{p_i(β,θ)}, i = 1,…,n and

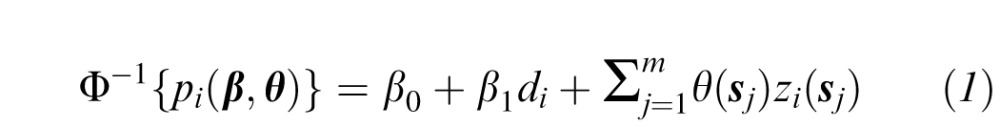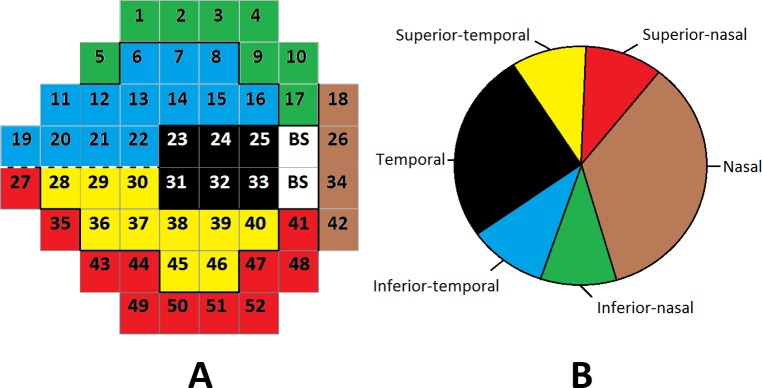
where Y_i is the progression status of patient/eye i, n is the total number of unique patient/eye combinations included in the study (see Table 1), p_i(β,θ) is the probability that patient/eye i is diagnosed as progressing, Φ⁻¹(·) is the inverse cumulative distribution function of the standard normal distribution, d_i is the length of time in years that patient/eye i has been followed in the study, β = (β₀,β₁)^T, β₁ is the parameter describing the association between follow-up time and the probability of being diagnosed as progressing by the clinician expert consensus, β₀ is the intercept parameter, θ = {θ(s₁),…,θ(s_m)}^T, and m = 52 is the number of VF locations (after removing the two locations within the physiologic blind spot; see Fig. 1). We note that progression often occurs at different rates in different eyes of the same individual and that the clinicians assessed progression for each eye individually. Therefore, we chose to model each eye independently.

Figure 1.

Visual field regions (A) mapped to the optic disc (B). The numbers represent the spatial locations associated with the η(s_j) parameters. BS, blind spot.

The z_i(s_j) term is defined as the estimated slope from a simple linear regression analysis of VF sensitivities at VF location s_j for person/eye i. Increasingly negative values of this metric indicate deterioration in vision at a given location while values near zero indicate little change over time. The sum, 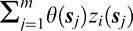, represents the total impact of changes in the VF over time at each of the individual VF locations on the probability of patient/eye i being diagnosed as progressing by the clinician expert consensus.

The main parameters of interest in the study are represented by θ(s_j), j = 1,…,m. These spatially varying regression parameters describe the association between a change in VF sensitivities over time at each location and the probability of interest. Including a separate parameter for each VF location allows for increased modeling flexibility and for the possibility that deterioration in the VF at different locations is more (or less) informative with respect to being diagnosed as progressing by the clinician expert consensus. A priori we assume a constant association between sensitivity changes at each location and the probability of interest along with location-specific deviations such that θ(s_j) = θ₀ + η(s_j), where θ₀ represents the constant mean of the spatial process and η(s_j) is the slope deviation specific to VF location s_j. The constant prior mean reflects our initial beliefs that changes in sensitivities over time at any location should have a similar impact on progression diagnosis by the clinician expert consensus, with the possibility that certain locations are more (or less) meaningful to clinicians being represented by the spatial deviations. The η(s_j) parameters allow for location-specific slopes for each VF location, potentially leading to a model that better describes the process used by clinicians to diagnose glaucoma progression. We allow these parameters to be spatially correlated as detailed in the Prior Specification Subsection so that estimation of their values will depend on the parameter values in surrounding VF locations if necessary. Equation 3 describes how these parameters are related to each other a priori in more detail. Therefore, the probit regression model in Equation 1 can be rewritten as:

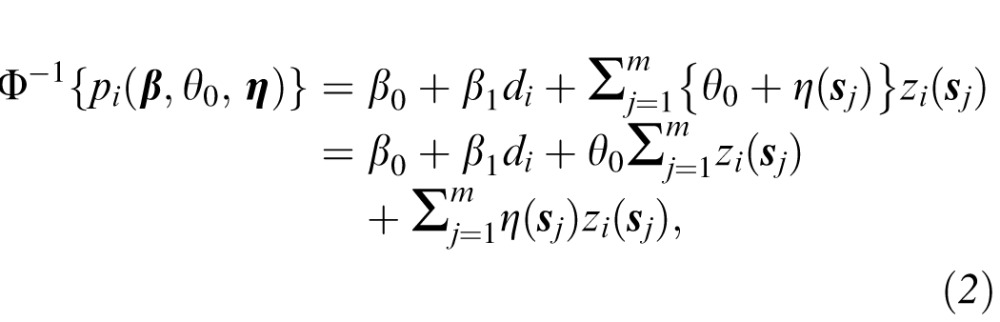where 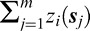represents a measure of the total level of deterioration across the entire VF over time and θ₀ describes the relationship between this measure and the probability of interests.

Prior Specification

We assigned prior distributions to the introduced model parameters to complete the model specification. A spatially referenced prior distribution was required for the introduced location specific deviations, η(s_j). Providing spatial structure in this context helped to control the effect of multicollinearity which often can inflate standard errors and change the sign of parameter estimates. We included a separate predictor at each of the 52 VF locations for a patient/eye with the understanding that sensitivities in similar VF locations are likely positively correlated. Conditional on the spatial proximity matrix, W, which describes the spatial relationship between each of the 52 VF locations, the η(s_j) parameters were jointly assigned a prior distribution that allowed neighboring parameters to share information spatially, if appropriate. We specified an intrinsic conditional autoregressive (ICAR) prior model such that η and

where η = {η(s₁),…,η(s_m)}^T, η(−s_i) = {η(s₁),…,η(s_i−1),η(s_i+1),…,η(s_m)}^T, is the variance parameter for the spatial process, w_ij is the row i, column j entry of W describing the proximity between VF locations s_i and s_j, and w_i+ represents the row i sum of W.⁶

For spatial data on a grid, the neighborhood definition for W is typically specified as w_ij = 1 if s_i and s_j share a common border and w_ij = 0 otherwise. Locations are not considered to be neighbors of themselves, resulting in w_ii = 0 for all i. However, the spatial structure across the VF is more complex due to each location's structural relationship with the optic disc. We, therefore, used a similar proximity matrix to that previously introduced.⁴ In Figure 1, we display the optic disc regions (Fig. 1B) and their spatial association with each location of the VF (Fig. 1A).⁷ Based on this structural mapping, we defined W(δ) as:

with w_ij(δ) = 0 for all i. The δ parameter describes the strength of spatial association between neighboring VF locations in adjacent optic disc regions. A number of past studies also have investigated the use of a partially unknown proximity matrix while working in different settings.^8–10

We selected weakly informative prior distributions for the hyperparameters to allow the data to drive the inference rather than our prior beliefs. The three nonspatial regression parameters were given independent, vague yet proper prior distributions, such that β₀,β₁,θ₀ ∼ N(0,10¹⁰). The variance parameter for the process was given a vague yet proper uniform prior distribution, such that 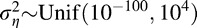. The neighborhood proximity matrix parameter was given a uniform prior distribution such that δ ∼ Unif(0,1).

Computing

Posterior inference is based on 990,000 samples from the posterior distribution of interest after discarding the first 10,000 draws as a burn-in period. The number of samples to obtain was determined based on the calculation of batch means Monte Carlo (MC) standard errors.¹¹ Summaries of the MC standard errors for presented posterior mean estimates are displayed in Table 2 and Figure 2. In Supplementary Figure S1, we present trace plots for all nonspatial parameters and randomly selected spatial deviations (η(s_i)). We noted that these plots are representative of the remaining parameters not displayed. All analyses were done using R Statistical Software and the model fitting details are presented in the Supplementary Material.¹²

Table 2.

Posterior Summaries for the Nonspatial Parameters in Model 1

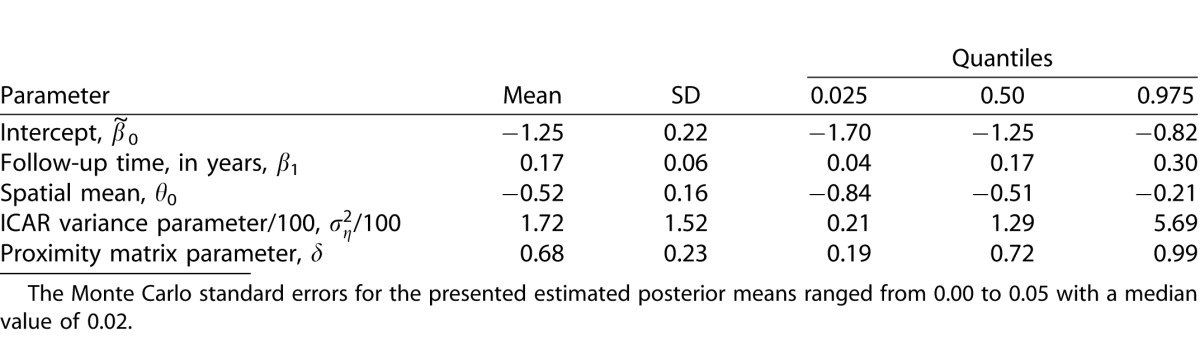
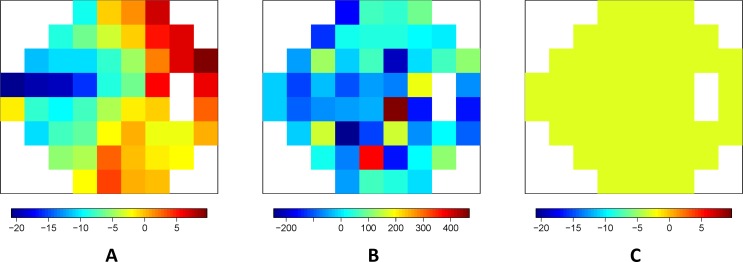
Figure 2.

Posterior means from (A) Model 1, (B) Model 2, and (C) Model 3 for the spatial slopes across the visual field. The posterior standard deviations for the presented parameters ranged from 6.98 to 11.34 with a median value of 8.51 for Model 1, 34.52 to 122.50 with a median value of 56.43 for Model 2, and was 0.75 for Model 3. The Monte Carlo standard errors for the presented estimated posterior means ranged from 0.01 to 0.05 with a median value of 0.02 for Model 1, 0.15 to 1.15 with a median value of 0.39 for Model 2, and was 0.001 for Model 3.

Model Comparisons

The benefits of the newly developed model, referred to as “Model 1” hereafter, are most apparent when results are compared with competing models. We considered the following models in this study:

• Model 1: The newly developed probit regression model for spatially correlated predictors with spatially varying VF parameters modeled using the 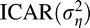prior distribution and partially unknown spatial proximity matrix.

• Model 2: A probit regression model with separate parameters for VF location that are modeled using exchangeable and independent normally distributed prior distributions.

• Model 3: A probit regression model including only a single spatially aggregated predictor without considering location.

• Models P1 to P4: A probit regression model using the first (Model P1), second (Model P2), third (Model P3), and fourth (Model P4) smallest P values from simple pointwise linear regressions (PLRs), fit separately at each location on the VF, as a single predictor.

• Models PS1 to Model PS4: A probit regression model using the first (Model PS1), second (Model PS2), third (Model PS3), and fourth (Model PS4) smallest estimated slopes that are associated with a P value less than or equal to 0.01 from simple PLRs, fit separately at each location in the VF, as a single predictor.

All of the introduced models were fit in the Bayesian setting for comparison purposes. Model 1 represents the newly introduced spatial model previously described. Model 2 uses the same probit regression model form as Model 1 (see Equation 1) while ignoring the spatial structure of the individual parameters. Instead, exchangeable normally distributed prior distributions with common variance were assigned to the parameters. We expected this model to perform poorly due to the lack of sharing of information between the introduced parameters, relatively small sample size, and high correlation between the predictors. This model served as a baseline to investigate what happens when all slopes are included in the model without accounting for spatial correlation.

Model 3 represents a simplified version of Model 1, ignoring the spatial information in the data. Model 3 is nested within Model 1 with 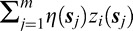removed from Equation 2. Therefore, Model 3 assumes a constant effect (θ₀) across all VF locations. We expected this model to outperform Model 1 if there was no spatial variability across the VF in parameter estimates. This would suggest that clinicians weigh each VF location equally when determining progression status.

Models P1 to P4 represent common analyses in the progression determination setting.¹³ Simple PLR analyses are done at each of the available 52 locations on the VF. From each of these separately run analyses, a frequentist P value is obtained indicating if the regression slope is significantly less than zero. In Model P1, we calculated the minimum P value over the entire VF for a patient and entered it as a predictor in a probit regression model with the progression status, as defined by the consensus of expert clinicians, as the outcome. We then used the second (Model P2), third (Model P3), and fourth (Model P4) smallest P values as predictors separately in their own models and compared results. Models PS1 to PS4 are similar except that they use the slopes from the PLR as the predictor and restrict to only those slopes that have a P value less than or equal to 0.01. Patients who do not have a VF location that meets this P value restriction are given a covariate value of zero to indicate this. These models account for statistical significance through the P value restriction as well as the rate of progression through use of the slope values and, therefore. more closely represent progression methods used in practice.

We considered multiple model comparison and validation measures to differentiate the models in terms of fit and prediction. The deviance information criterion (DIC) is a commonly considered model comparison tool used in the Bayesian setting where the posterior mean of the deviance statistic, D̄, is used to assess model fit while the effective number of parameters, p_D, is used to describe the model complexity. The DIC then is defined as DIC = D̄ + p_D, with smaller values being preferred.¹⁴

D_k is a posterior predictive loss model comparison metric that considers the balance between model fit (G_k) and complexity (P).¹⁵ We work with the deviance of the Bernoulli distribution (with continuity correction) and set k = 10¹⁰ to calculate D_k. As with DIC, smaller values of D_k suggest an improved model fit. D_k is most useful in comparing the predictive performance of a model while DIC is preferred if the model is used mainly for explanatory purposes.

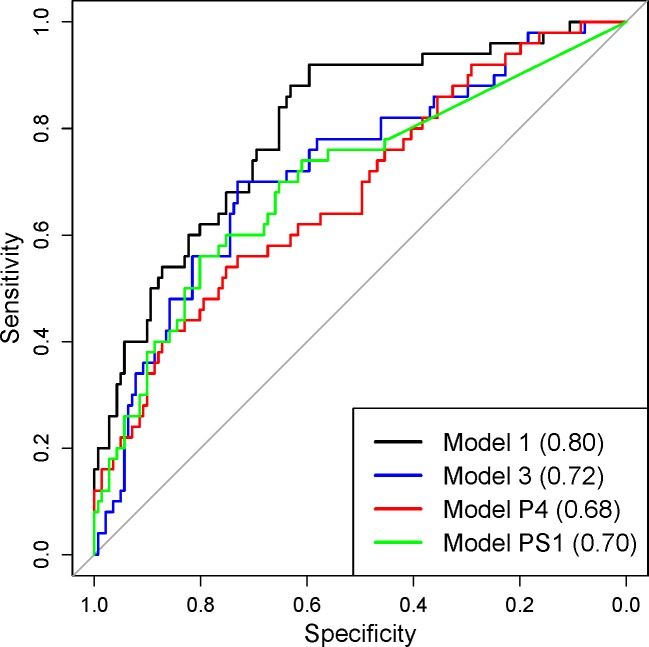
The receiver operating characteristic (ROC) curve also was calculated for each model along with the area under the ROC curve (AUC), the optimal sensitivity, and optimal specificity values. We formally compared the AUC values from the different models using a paired statistical test and reported the P values. The optimal sensitivity and specificity values were determined using Youden's Index.¹⁶

Simulation Study

We carried out a simulation study to demonstrate the ability of our model to efficiently and accurately estimate the individual regression parameters across the VF in a number of different data generation settings and to compare the performance with alternative models. These details and results are presented in the Supplementary Material. The findings suggest that Model 1 is robust to the data generation setting and is preferred most often to the competing models in the simulation framework.

Sensitivity Analyses

We performed a number of sensitivity analyses to assess the adequacy and robustness of our model to the choice of VF predictor (slopes), fixed versus random settings for δ, selected prior distribution, selected neighborhood definition, and choice of the prior distribution. These details and results also are presented in the Supplementary Material. The findings suggested that the observed inference is robust to each of these modeling choices. We also presented an exploratory analysis of the robustness of our findings based on the number of available VF tests in Supplementary Table S5. The results appear to be robust to the number of available VF tests overall.

Model Validation

To validate the newly introduced model, we predicted the probability of being diagnosed as progressing by the clinician expert consensus for patient/eyes in the validation dataset [p̂_i0(β,θ₀,η)] using the posterior predictive distribution. Recall that this dataset was not used in building the predictive model. We similarly predicted these same probabilities using the competing models.

We compared the predicted probabilities with the actual progression determinations for the patient/eyes by defining 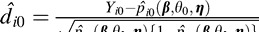, i = 1,…,n₀, where n₀ is number of patient/eyes in the validation dataset (n₀ = 100). Values of d̂_i0 near zero indicate accurate prediction while large values indicate the opposite. We explored the distribution of these diagnostic measures for each model to determine if any outliers exist. We also calculated and compared and 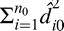for each model to identify which model provides the best predictions overall. Smaller values for these summary measures indicate a model is predicting well.

Results

Analysis of Modeling Dataset

We first applied Model 1 to the modeling dataset. Posterior inference for the nonspatial parameters of Model 1 are shown in Table 2. The 95% credible interval (CI) for β₁ does not include zero and is positive. This indicates that a patient/eye followed for a longer period of time is more likely to be diagnosed as progressing by the group of clinicians. The 95% CI for θ₀ does not include zero and is negative. This indicates that a decrease in any of the VF sensitivities over time (negative slope) leads to an increased probability of being diagnosed as progressing by the clinician expert consensus, regardless of spatial location. In Figure 2A, we display the posterior means for the location-specific slope parameters, θ₀/σ_z + η(s_j), for Model 1. These parameters represent the increase in an individual's latent variable ( ) with a 1 dB decrease in sensitivity per year at the respective VF location for a patient/eye. A significant increase in significantly increases the probability of progression diagnosis. Therefore, more negative estimates of θ₀/σ_z + η(s_j), as shown in the blue and green regions of Figure 2A, indicate that decreases in VF sensitivities over time at these locations have a greater impact on the clinicians' progression determination. Parameter estimates near zero indicate that decreases in these areas have less impact on the progression determination.

In Figure 2A, in the nasal, inferior-nasal, and superior-nasal regions of the optic disc (see Fig. 1) there is very little impact of decreasing sensitivities over time on the probability of diagnosed progression. However, in the temporal, inferior-temporal, and superior-temporal regions of the optic disc, the parameter estimates are further from zero. This indicates that decreasing sensitivities over time in these regions may be more meaningful in terms of glaucoma progression diagnosis. Locations s₁₉, s₂₀, s₂₁, and s₂₂ of the inferior-temporal optic disc region are the only locations to have 95% CIs which fail to include zero [θ₀/σ_z + η(s₁₉): (−43.89, −1.29); θ₀/σ_z + η[s₂₀]: (−37.26, −4.64); θ₀/σ_z + η(s₂₁): (−38.25, −4.48); θ₀/σ_z + η(s₂₂): (−35.37, −1.19)].

The findings in Figure 2A have an anatomic explanation. The retinal verve fiber layer (RNFL) bundle is thickest and converges in the superior-temporal and inferior-temporal regions of the optic disc. As a result, early glaucoma VF loss as well as RNFL defects are predominantly observed in these two regions and, typically, glaucomatous damage to the optic disc advances in a sequence beginning with the same regions.

Model Comparisons

In Figure 2, the posterior means of the location-specific slope parameters are displayed for models 1 to 3. The Model 1 results have been described previously. In Figure 2B, the posterior means for Model 2 are displayed. When compared to Model 1 (Fig. 2A), the range of the means are extreme and the posterior standard deviations are larger at each VF location. Figure 2B also lacks a clear pattern in the means across the VF, unlike in Model 1. These results are expected for Model 2 since multicollinearity is known to change the signs of parameter estimates and inflate standard errors. For Model 3 (Fig. 2C), only one parameter is estimated across the entire VF. Figures 2C and 2A are shown on the same scale for comparison purposes. Recall that if Model 3 was the true underlying model, we would expect Figures 2A and 2C to look similar. However, the plots indicate that there are changes across the VF that Model 3 is unable to account for given its constant effect specification.

In Table 3, we display the model fit/prediction results from all considered models. The ROC curve plots are displayed in Figure 3. For Models P1 to P4 and Models PS1 to PS4, we only display the ROC curve plots for the models with the highest AUC value in each group due to the large number of models being compared. Model 2 has the largest DIC and p_D values, indicating poor overall fit to the data. The predictive measures suggest that Model 2 has improved predictive ability when compared to the other models. However, given the DIC results, Model 2 is likely overfitting the data and resulting in improved predictions as a result. In terms of model fit, Model 1 has the smallest DIC when compared to the competing models. Due to the increased flexibility of Model 1, we now have improved predictive performance when compared to the other models (excluding Model 2) as suggested by G_k, P, and D_k (k = 10¹⁰). The AUC value for Model 1 is significantly larger than the values from all other models (excluding Model 2) with the P vaues from the paired statistical tests ranging from 0.000 to 0.018. Model 1 also has the highest optimal sensitivity among all models. The competing models are outperformed by Model 1 in terms of model fit and prediction, indicating that accounting for spatial variability across the VF is an important feature of the analysis.

Table 3.

Model Fit and Prediction Comparisons between the Considered Models

Figure 3.

Receiver operating characteristic (ROC) curve plots with AUC curves listed in parentheses. Model 2 is omitted due to overfitting.

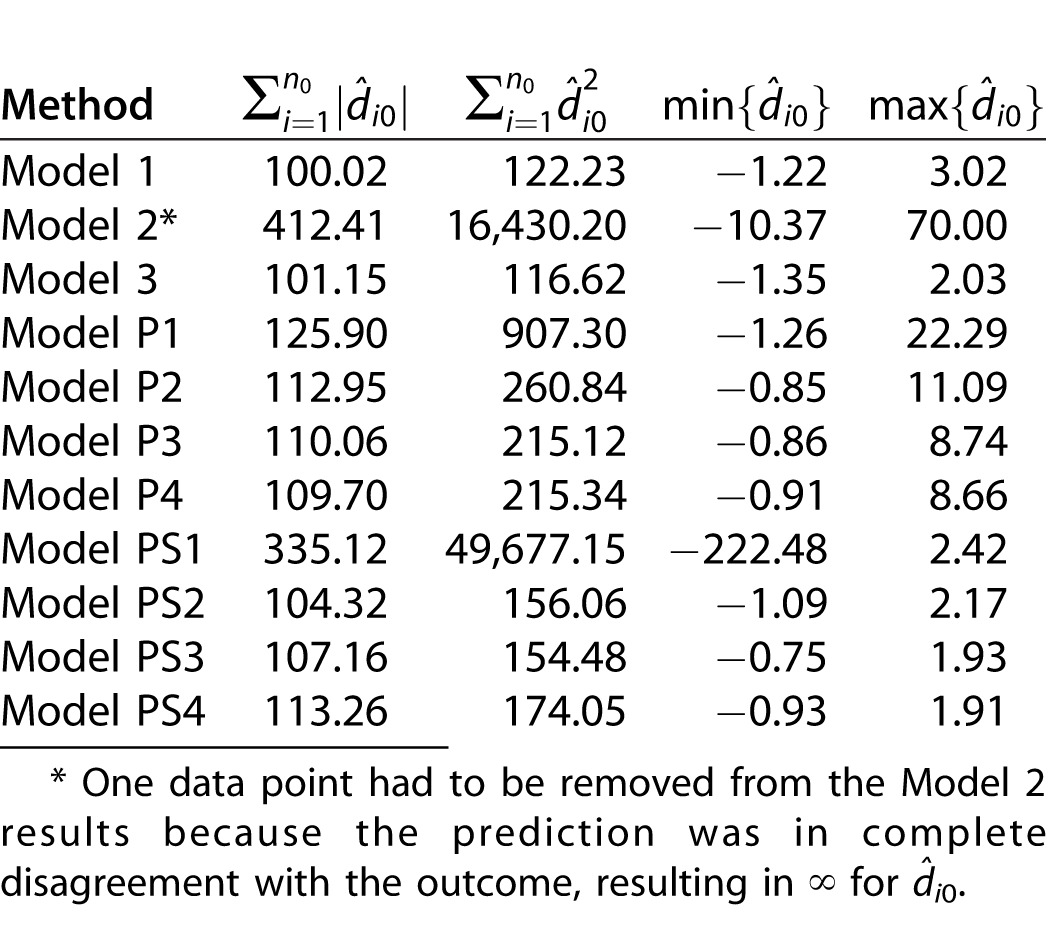
Model Validation

The results from the model validation analyses can be seen in Table 4. As suspected, Model 2 is overfitting and provides extremely poor predictions for the validation dataset. Model 3 provides similar predictive ability to Model 1 overall. Models P1 to P4 result in large outlying values of d̂_i0, indicating poor prediction for those patient/eyes. Models PS2 to PS4 predict slightly better than Models P1 to P4 overall but are still outperformed by Model 1. These results provide further evidence that the newly introduced model is not suffering from overfitting and suggests that it may be clinically useful.

Table 4.

Distribution of Model Validation Measures. Smaller Values Indicate Improved Prediction.

Discussion

Because of the chronic and progressive nature of glaucoma, an important requirement of the long-term follow-up is establishing whether the disease is stable or has progressed, which oftentimes is challenging to the clinician. One of the methods commonly used in clinical practice to judge progression is visual observation of serial automated VF test results along with other clinical and nonclinical information. This approach is quicker and easy to perform for experienced clinicians, but it is subjective without quantification of the change and, therefore, the outcome may be very variable even among glaucoma specialists.^17,18

This has led to the introduction of a number of objective methods to assess VF progression in glaucoma patients. The majority of these methods use statistical modeling in the form of simple linear regression analyses where VF measures collected in frequent follow-up visits are analyzed over time. These measures include the raw sensitivities at individual VF locations as well as global indices, such as the mean deviation (MD), pattern standard deviation (PSD), and visual field index (VFI).^1,2 Following glaucomatous VF over time using these global indices leads to a reduction of the data to a single measure that ignores the spatial nature of VF loss of glaucomatous progression.¹⁹ The pitfall with PLR is that it is based on the erroneous assumption of progression independence between tests locations and only considers test points that show deepening and not enlargement; this assumption is contradicted by available evidence.²⁰ Other studies, such as the Advanced Glaucoma Intervention Study²¹ and the Collaborative Initial Glaucoma Treatment Study,^22,23 have used scoring systems to condense VF data into a single numeric value. The scoring techniques so far have been used only in clinical trials and not in the clinical practice because they display larger long-term variability and fail to provide information with regard to the spatial characteristics of the defects.

Alternative regression models also have been implemented and compared to PLR, including pointwise exponential and quadratic regression.³ Event-based methods, which define progression based on a prespecified level of deterioration, also have been considered.²⁴ Spatial filters have been offered as a method to reduce variability in VF sensitivity measurements before determining progression status.²⁵ Spatial disease mapping techniques also have been used to model the raw VF sensitivities over time with the goal of identifying significant progression.⁴ We proposed a new analytical method that uses the sensitivities of all VF test locations and takes into account their spatial correlation. This model outperformed competing models in terms of model fit and predictive ability in the modeling and validation datasets.

Our newly developed method most closely resembles the previously introduced pointwise methods. In the pointwise methods, a progression determination is made based on the location and severity of decreasing sensitivities across the VF. At each VF location, the slope and/or P value are evaluated and a decision about progression is made based on these 52 values. Our method also attempts to summarize the information contained in these 52 values. However, instead of offering a new deterministic method to make the progression decision, our method uses the introduced statistical model to optimize the decision-making process using all of the information simultaneously. This data-driven method is shown to outperform competing methods with similar forms. We also note that without the use of the spatial prior distribution (Model 2), the method would be essentially ignoring the spatial location of vision deterioration. So while the forms of the model are similar conditional on the spatial random effects, unconditionally Model 1 allows for sharing of information across the VF during estimation. As shown in Figure 2, this results in stable and interpretable spatial patterns that are driven by the observed data as well as our prior understanding of the structure-function correlation between the VF and optic nerve head.

The major limitation of VF testing is short-term (at each test location) and long-term fluctuation (between tests) of the sensitivity thresholds as a result of measurement error and the combination of the psychophysical nature of the test and biological factors. The long-term variability between tests is concerning and becomes an issue when serial VFs are used to monitor disease progression. The fact that reduction of the long-term fluctuation of VF sensitivities is not a component of this analysis may be regarded as a limitation. However, if one considers that there is no standard method for determining glaucoma progression by evaluation of longitudinal VF data and that most widely used methods, such as the GPA and the Octopus EyeSuite (Haag-Streit, Koenig, Switzerland), do not attempt to reduce the long-term variability, our method is acceptable based on its performance. In addition, while developing and validating the model described herein using spatially correlated VF data from clinically confirmed perimetric glaucoma patients only may be viewed also as a limitation, it is, however, important to note that this method also may be used successfully in glaucoma suspects, preperimetric glaucoma patients, and other conditions where VF is used to monitor disease progression, such as nonglaucomatous optic neuropathies. Although we chose the Garway-Heath's map because it is the most widely used based on the good structure-function relationship it yields,²⁶ it is worth noting that a positive attribute of the proposed model is its flexibility as it may be applied easily to other glaucoma VF cluster map schemes. Studies comparing different cluster map schemes may be needed in the future to determine the scheme with the strongest model fit and highest predictive ability to detect glaucoma progression.

The complexity of the model is not a factor when classifying new patients. The VF data for a new patient can easily be entered into the regression framework and a predicted probability of progression, as defined by the consensus of expert clinicians, is calculated within a few seconds using the previously obtained posterior samples from the model parameters. This predicted probability then can be used to classify the new patient based on the optimal threshold value determined during the ROC curve analysis. This speed will allow for real time decision making in the clinical setting, which constitutes a real strength of the proposed model.

In conclusion, we presented and described a tool for the analysis of spatially correlated longitudinal VF data and demonstrated its usefulness in the modeling and validation datasets. With both datasets, we have established that the proposed method outperformed competing models in terms of model fit and predictive ability without sacrificing information. Using the introduced regression modeling framework, our model can be extended in future work to incorporate other covariates, such as RNFL, ganglion cell-inner plexiform layer and optic disc topographic measures, and patient level attributes that could provide additional information for decision making. Our newly developed model was able to jointly consider highly correlated changes across the entire VF when determining the progression status based on clinician expert consensus, similar to the actual process used by expert clinicians. Results from the validation dataset suggest that the model may also be clinically useful.