Nucleated polymerization with secondary pathways III. Equilibrium behavior and oligomer populations

Abstract

We explore the long-time behavior and equilibrium properties of a system of linear filaments growing through nucleated polymerisation. We show that the length distribution for breakable filaments evolves through two well defined limiting cases: first, a steady state distribution determined by the balance of breakage and elongation is reached; upon monomer depletion at the end of the growth phase, an equilibrium length distribution biased towards smaller filament fragments emerges. We furthermore compute the time evolution of the concentration of small oligomeric filament fragments. For frangible filaments, oligomers are present both at early times and at equilibrium, whereas in the absence of fragmentation, oligomers are only present in significant quantities at the beginning of the polymerisation reaction. Finally, we discuss the significance of these results for the biological consequences of filamentous protein aggregation.

I. Introduction

The polymerisation of proteins into fibrillar structures is a type of behavior characteristic of many different systems, both in the context of functional[1–5] and aberrant biological pathways[6–20] in nature. In particular, aberrant protein aggregation is observed in relation with 50 or more disorders associated with formation of amyloid fibrils[14, 16, 21]. A key question characterising such linear growth phenomena is the size of the structures that are formed from the proteins, as this factor can influence the severity of disease or its rate of progression[22–28]. Nucleated polymerisation reactions yield filament populations with highly heterogeneous lengths[22, 29–32], a complexity due to the concurrent action of competing microscopic processes favoring either the lengthening or shortening of individual filaments in the ensemble. In this paper we focus on the behaviour of the size distribution of aggregates for long times, and explore the nature of the equilibrium distribution using numerical solutions to the master equation of filamentous growth, and obtain analytical results for many of the important limiting cases.

II. Master Equation

The starting point for the analysis of the length distribution of filaments is given by the master equation describing the kinetics of breakable filament assembly. Letting f(t, j) denote the number of filaments of size j the master equation reads[32–36]:

$$\frac{\partial f\left(t,j\right)}{\partial t}=2m\left(t\right)k_{+}f\left(t,j-1\right)-2m\left(t\right)k_{+}f\left(t,j\right)+2k_{\text{off}}f\left(t,j+1\right)-2k_{\text{off}}f\left(t,j\right)-k_{-}\left(j-1\right)f\left(t,j\right)+2k_{-}{\displaystyle \sum _{i=j+1}^{\infty }f\left(t,i\right)+k_{n}m{\left(t\right)}^{n_c}{\delta }_{j,n_c}}$$ (1)

The condition f(t, j) = 0 is imposed for all j < n_c, where n_c ≥ 2 is the critical nucleus size for the filament growth; that is, all chains shorter than n_c are unstable. The concentration of monomers in the system is m(t), and the last term in Eq. (1) represents the spontaneous formation of a growth nucleus of size j = n_c. The dynamics of the system are defined by the rate constants k₊ for elongation, k_off for monomer dissociation from fibril ends, k₋ for fragmentation and k_n for primary nucleation. Other processes, such as protein synthesis and degradation[32, 39] can be considered in this framework; here we focus on the intrinsic factors that govern the evolution of the aggregate population. This case corresponds to aggregation phenomena in vitro, or in vivo for cases where aggregate growth dominates the opposing contribution from degradation and results in the pathological deposition of aggregated proteins.

The behavior of the system for k₋ = 0 yields classical linear polymerisation that has been studied previously by Oosawa[1, 29] and is briefly discussed in section V. In order to provide a complete picture of the length distributions in nucleated polymerisation phenomena, in this paper we focus primarily on the other limiting case where filament fragmentation and elongation dominate the evolution of the length distribution and primary nucleation and monomer dissociation are of lesser importance. In this limit, the rate of production of filaments through nucleation, k_nm(∞)^n_c, is negligible in front of the rate of production of filaments through breakage k₋[P(∞) − n_c(n_c − 1)M(∞)]. Similarly the rate of generation of free monomer from aggregates through direct dissociation 2k_off P(∞) is taken to be negligible in front of the contribution from breakage through the creation of unstable filaments with a length smaller than the critical nucleus size k₋n_c(n_c − 1)P(∞). Interestingly, (section III B), intermediate parameter ranges interpolate smoothly between the classical nucleated polymerisation results and the fragmentation dominated case.

III. Filament Growth in a Closed System

A. Principal Moments

In a closed system the total protein concentration in solution m_tot = m(t) + ∑_j j · f(t, j) is constant. Insights into the behavior of the system at long times t → ∞ can be obtained from considering average properties, such as the principal moments of the length distribution. From the master equation, the evolution of the principal moments[1, 37]

$$P(t)={\displaystyle \sum _{j}f\left(t,j\right)M(t)={\displaystyle \sum _{j}j\cdot f\left(t,j\right)}}$$ (2)

have been shown to obey the differential equation [1, 32, 38, 39]:

$$\frac{dP\left(t\right)}{dt}=k_{-}\left[M\left(t\right)-\left(2n_c-1\right)P\left(t\right)\right]+k_{n}m{\left(t\right)}^{n_c}$$ (3)

$$\frac{dM\left(t\right)}{dt}=2\left[m\left(t\right)k_{+}-k_{-}{n}_c\left(n_c-1\right)/2\right]P\left(t\right)+n_c{k}_{n}m{\left(t\right)}^{n_c}$$ (4)

To determine the equilibrium steady state values of P and M, the derivatives are set to zero. In the absence of nucleation, k_n = 0, we identify[32]:

$$M\left(\infty \right)=m_{\text{tot}}-\frac{k_{-}{n}_c\left(n_c-1\right)}{2k_{+}}$$ (5)

$$P\left(\infty \right)=\frac{M\left(\infty \right)}{2n_c-1}=\frac{m_{\text{tot}}-\frac{k_{-}{n}_c\left(n_c-1\right)}{2k_{+}}}{2n_c-1}$$ (6)

$$L\left(\infty \right)=\frac{M\left(\infty \right)}{P\left(\infty \right)}=2n_c-1$$ (7)

These equilibrium values correspond to stable node points of the dynamical system Eqs. (3), (4), whereas the trivial solution, M(0) = P(0) = 0, corresponds to an unstable saddle point. Eqs. (45), (6) and (7), are also to good approximation satisfied even for k_n > 0 in a wide range of parameter space that is relevant to the analysis of experimental data. More formally, we note that for n_c = 1, Eqs. (45), (6) and (7) are exactly verified. For n_c > 1, substituting M(t) = m_tot − m(t), a polynomial equation of order n_c + 1 is found for m(∞) which must be solved. For example, for n_c = 2, defining the dimensionless quantities µ = m(∞)/m_tot, χ_n = k_n/k₊, χ₋ = k₋/(2m_totk₊), we obtain a cubic equation: ${\mu }^3{\chi }_n-{\mu }^2{\chi }_{-}\left(1+2{\chi }_n\right)+\mu {\chi }_{-}\left(1+{\chi }_{-}\right)-{\chi }_{-}^2=0.$ The exact solution to this cubic equation has the leading order terms for small ${\chi }_{-}\ll 1:m(\infty )=k_{-}/k_{+}-3k_{-}^2{k}_n/(m_{\text{tot}}{k}_{+}^3)+𝒪(k_{-}^3{k}_n/(m_{\text{tot}}^3{k}_{+}^4)),$ confirming the accuracy of Eq. (7) for values of k_n such that $k_n\ll m_{\text{tot}}{k}_{+}^2/k_{-}.$

B. Equilibrium Length Distribution

Using the values for the principal moments from the previous section, we can gain more detailed insight into the equilibrium length distribution of an ensemble of breakable filaments under the condition that the total mass in the system is conserved. Qualitatively, we expect the length distribution to be defined by a balance between filament fragmentation, leading to a shortening of filaments, and filament elongation which drives the length distribution towards a longer average value. At equilibrium, the number of fibrils created through fragmentation of long filaments into structures larger than the critical nucleus size is compensated by the destruction of filaments through fragmentation of short filaments to unstable structures smaller than the critical nucleus size which disintegrate into their component monomers.

At steady-state t = ∞, the left hand side of the master equation (1) is zero:

$$0=2m(\infty )k_{+}f(\infty ,j-1)-2m(\infty )k_{+}f(\infty ,j)-k_{-}(j-1)f(\infty ,j)+2k_{-}{\displaystyle \sum _{i=j+1}^{\infty }f(\infty ,i)}$$ (8)

an expression which takes the form of a recursion relation for f(∞, j). In order to solve for f(∞, j) we may rewrite the relation as:

$${\displaystyle \sum _{i=j+1}^{\infty }f(t,i)=P(\infty )}-f(t,j)-f(t,j-1)-{\displaystyle \sum _{j=n_c}^{j-2}f(t,i)}$$ (9)

Eqs. (45) and (6) give m(∞) and P(∞). Substituting these into the master equation and rearranging yields:

$$\frac{f(\infty ,j)}{P(\infty )}=\left(\frac{n_c(n_c-1)-2}{n_c(n_c-1)+(j+1)}\right)\frac{f(\infty ,j-1)}{P(\infty )}+\left(\frac{2}{n_c(n_c-1)+(j+1)}\right)\left(1-{\displaystyle \sum _{i=n_c}^{j-2}\frac{f(\infty ,i)}{P(\infty )}}\right)$$ (10)

This difference equation admits, as can be confirmed by direct substitution, the exact solution:

$$\frac{f(\infty ,j)}{P(\infty )}=\frac{(j-(n_c-1))(j+n_c){(n_c(n_c-1))}^{j-(n_c+1)}(n_c-1)}{{(1+{n_c}^2)(2+{n_c}^2)}_{j-n_c}}$$ (11)

where (a)_n is the Pochhammer symbol defined as (a)_n = a(a + 1) … (a + n − 1) = Γ(a + n)/Γ(a). Equivalently we may write:

$$\frac{f(\infty ,j)}{P(\infty )}=\frac{n_c{\left(\left(n_c-1\right)n_c\right)}^{j-n_c}\left(n_c-n_c^2+j+j^2\right)\left(n_c^2-1\right)!}{\left(1+\left(n_c-1\right)n_c+j\right)!}$$ (12)

where the gamma function can be used instead of the factorials to provide a straightforward continuous extension. Eq. (12) describes the length distribution of a fragmenting filament system in closed form. Since this result is exact, it satisfies exactly ${\displaystyle {\sum }_{j=n_c}^{\infty }\frac{f(\infty ,j)}{P(\infty )}=1}\text{and}{\displaystyle {\sum }_{j=n_c}^{\infty }j\frac{f(\infty ,j)}{P(\infty )}=2n_c-1.}$

Interestingly, Eq. (12), shows that the entire shape of the length distribution at long times, not just the average length, is defined solely by n_c, and does not depend on the rate constants k₊ or k₋, which only serve to scale the long time length distribution by a constant factor.

In order to elucidate more clearly the functional form of the equilibrium length distribution given by Eq. (12), an approximation with a simpler functional form can be given by solving the differential equation which results from considering the difference equation Eq. (8) in the continuum limit:

$$f(\infty ,j-1)\approx f(\infty ,j)-f^{\prime }(\infty ,j)+𝒪(f^{″})$$ (13)

$${\displaystyle \sum _{i=j+1}^{\infty }f(\infty ,i)\approx {\displaystyle {\int }_{j+1/2}^{\infty }f(\infty ,i)di}}$$ (14)

where the lower limit of the integral has been chosen using the midpoint approximation. Substituting these expressions into Eq. (8) and differentiating with respect to j yields:

$$0=n_c(n_c-1)f^{″}(\infty ,j)+(j-1)f^{\prime }(\infty ,j)+f(\infty ,j)+2f(\infty ,j+1/2)$$ (15)

and expanding the final term in Eq. (15):

$$f(\infty ,j+1/2)\approx f(\infty ,j)+\frac{1}{2}{f}^{\prime }(\infty ,j)+\frac{1}{8}{f}^{″}(\infty ,j)+𝒪(f^{‴})$$ (16)

allows us to rewrite Eq. (15) as:

$$0=(n_c(n_c-1)+1/4)f^{″}(\infty ,j)+j{f}^{\prime }(\infty ,j)+3f(\infty ,j)$$ (17)

The general solution to this differential equation Eq. (17) is given, with arbitrary constants A and B, by:

$$f(\infty ,j)=\text{A}{e}^{-\frac{2j^2}{{(1-2n_c)}^2}}\left(4j^2-{(1-2n_c)}^2\right)+\text{B}\frac{4j(-1+2n_c)+2\sqrt{2}(4j^2-{(1-2n_c)}^2)\text{D}\left(\frac{\sqrt{2}j}{1-2n_c}\right)}{8{(-1+2n_c)}^3}$$ (18)

where $\text{D}(x)=e^{-x^2}{\displaystyle {\int }_0^x{e}^{y^2}dy}$ is the Dawson integral.

The second term in Eq. (18) does not contribute significantly for small n_c, and decays quickly with j for large n_c, affecting only the value of f(∞, j) around j = n_c. Accordingly, to first approximation, we set B = 0 and fix A by the normalisation condition ${\displaystyle {\int }_{n_c}^{\infty }f(\infty ,i)di}=P(\infty ).$ These simplifications result in a length distribution in the form of a biased Gaussian distribution:

$$\frac{f(\infty ,j)}{P(\infty )}=\frac{e^{\frac{2(-j^2+n_c^2)}{{(1-2n_c)}^2}}\left[4j^2-{(1-2n_c)}^2\right]}{{\left(1-2n_c\right)}^2{n}_c}$$ (19)

As a control for the quality of the approximations made in the derivation of Eq. (19), we compute the mean, µ, of the approximate continuum length distribution as:

$$\mu =2n_c-1+\frac{1}{4n_c}\approx 2n_c-1n_c\gg 1$$ (20)

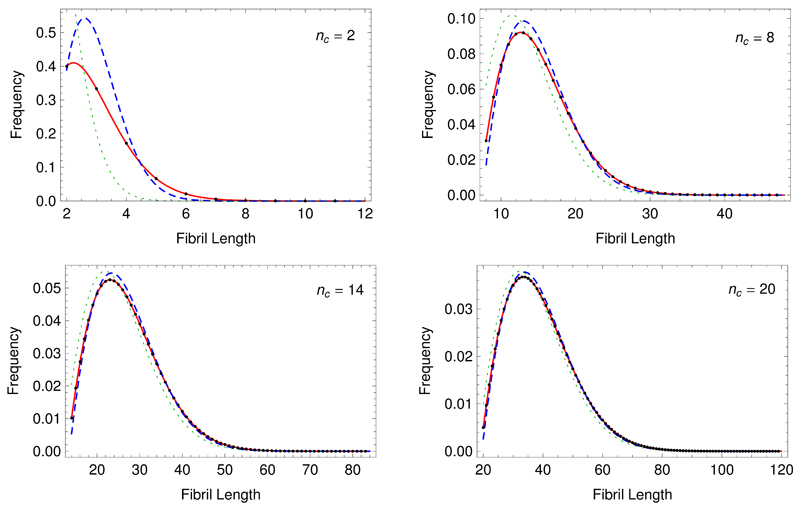
A comparison of this result with the exact value from Eq. (7) indicates that Eq. (19) becomes exact for large n_c, and it is expected that the continuum limit result Eq. (19) will become more accurate as n_c increases. A comparison between numerically generated data, Eq. (19) and Eq. (12) is shown in Fig. 1. The continuum limit gives the correct form – a biased Gaussian function – and matches the exact solution well for large n_c. An approximation of the length distribution which also accounts for the degradation of filaments has been put forward previously by [32] and the results from this approach in the limit of no degradation are also shown in Fig. 1 for comparison.

Fig. 1.

Comparison of solutions to the problem of length distributions for frangible filaments in a closed system. The black dots are calculated numerically from the recursion relation, Eq. (8), while the red continuous line is from the exact solution Eq. (12). The blue dashed line is the continuum limit solution from Eq. (19). The green line shows the solution given by Pöoschel et al. [32] when setting the clearance rate to zero.

The ratio of the standard deviation, σ, to the mean, µ, of the equilibrium length distribution may also be calculated from Eq. (19) in terms of the error function:

$$\frac{\sigma }{\mu }\approx \frac{1}{2}\sqrt{\sqrt{2e\pi }\left(1-\text{erf}\left(\frac{1}{\sqrt{2}}\right)\right)-1}\approx 0.28n_c\gg 1$$ (21)

which is consistent with our previous analytical result[40] that the equilibrium ratio between the standard deviation and the mean filament length in a system of constant mass is independent of the rate constants and approximately equal to $1/(2\sqrt{3})\approx \mathrm{0.29.}$

It is interesting to note that in the domain where the continuum approximation Eq. (19) is valid, the presence of a finite but small dissociation rate k_off > 0 does not, to first approximation, modify the length distribution. Indeed the equilibrium monomer concentration analogous to Eq. (45) becomes[40]:

$$m(\infty )=\frac{k_{-}{n}_c\left(n_c-1\right)}{2k_{+}}+\frac{k_{\text{off}}}{k_{+}}$$ (22)

such that the terms involving k_off cancel in the master equation:

$$0=2m(\infty )k_{+}f(j-1)-2m(\infty )k_{+}f(j)+2k_{\text{off}}f(j+1)-2k_{\text{off}}f(j)-k_{-}(j-1)f(j)+2k_{-}{\displaystyle \sum _{i=j+1}^{\infty }f(i)}$$ (23)

$$=n_c(n_c-1)k_{-}\left[f(j-1)-f(j)\right]+2k_{\text{off}}\left[f(j+1)+f(j-1)-2f(j)\right]-k_{-}(j-1)f(j)+2k_{-}{\displaystyle \sum _{i=j+1}^{\infty }f(i)}$$ (24)

In the continuum limit the second line in Eq.(24) vanishes and therefore we recover Eq. (19) even when k_off > 0.

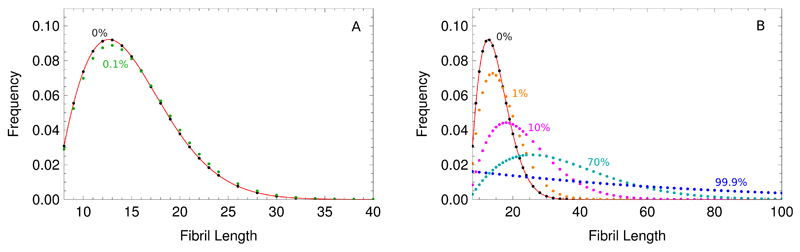
The continuum limit becomes less accurate for increasing k_off as shown in Fig. 2. Furthermore, it can be seen from Fig. 2 that the action of k_off broadens the distribution and shifts the mean to a larger length value. Qualitatively, this change can be understood as the terms proportional to k_off in Eq. (24), f(j + 1) + f(j − 1) − 2f(j), represent a discrete Laplacian, which describes a diffusion-like process acting to broaden the length distribution.

Fig. 2.

Effect of the depolymerisation rate k_off. A shows a small depolymerisation rate in a fragmentation dominated case, 2k_off < n_c(n_c − 1)k₋. B shows the effect of increasing depolymerisation rates to broaden and shift the length distribution towards larger lengths that is described in the main text. The depolymerisation rates are given as percentages of k₊m_tot. The red solid line is the exact solution neglecting the depolymerisation rate and primary nucleation Eq. (12); the blue dashed line is the continuum approximation Eq. (19). The kinetic parameters are: $m_{\text{tot}}=1\mu M,k_{+}=1\cdot {10}^4{M}^{-1}{s}^{-1},k_{-}=2\cdot {10}^{-6}{s}^{-1},k_n{m}_{\text{tot}}^{n_c-1}=1\cdot {10}^{-7}{s}^{-1},n_c=8,M(0)=P(0)=0.$

IV. Filament Growth Under Constant Monomer Concentration

A. Principal moments

In the previous section we derived the length distribution of a closed filament system at equilibrium for t → ∞. A qualitative picture for the evolution of the length distribution at earlier times can be provided by noting that as long as the total mass concentration of fibrils M(t) is much smaller than the concentration of available monomer m(t) = m_tot − M(t) ≈ m_tot, this latter quantity is approximately constant in time. In this section we therefore focus on the growth of filaments in a constant concentration of precursor monomers. Such a situation might arise also, for example, in vivo when biosynthesis and degradation are in balance. In this case, the principal moments, which we label P_e(t) and M_e(t), obey linear moment equations [1, 32, 38, 39]:

$$P_e(t)=C_1{e}^{\kappa t}+C_2{e}^{-\kappa t}-\frac{n_c{k}_n{m}_{\text{tot}}^{n_c-1}}{2k_{+}}$$ (25)

$$M_e(t)=\frac{2m_{\text{tot}}{k}_{+}{C}_1}{\kappa }{e}^{\kappa t}-\frac{2m_{\text{tot}}{k}_{+}{C}_2}{\kappa }{e}^{-\kappa t}-\frac{k_n{m}_{\text{tot}}^{n_c}}{k_{-}}$$ (26)

with the constants defined as:

$$\kappa =\sqrt{2m_{\text{tot}}{k}_{+}{k}_{-}}$$ (27)

and

$$C_{1,2}=\frac{1}{2}\left(P(0)\pm \frac{\kappa }{2k_{+}{m}_{\text{tot}}}M(0)\pm \frac{\kappa k_n{m}_{\text{tot}}^{n_{c^{-1}}}}{2k_{+}{k}_{-}}\right)$$ (28)

The long time limiting forms are, thus, given by:

$$P_e(t)\to C_1{e}^{\kappa t}$$ (29)

$$M_e(t)\to \frac{2C_1{m}_{\text{tot}}{k}_{+}{e}^{\kappa t}}{\kappa }$$ (30)

and the average length L_e = M_e/P_e tends to a constant value that depends only on the ratio of the elongation and fragmentation rates and not on the nucleation rate or on the critical nucleus size:

$$\begin{array}{cc}{L}_e(t)\to \frac{2m_{\text{tot}}{k}_{+}}{\kappa }\approx \sqrt{\frac{2m_{\text{tot}}{k}_{+}}{k_{-}}}& t\to \infty \end{array}$$ (31)

B. Stationary length distribution

As long as there is a constant supply of monomers, the number of breakable filaments increases exponentially, as described by Eq. (29), and we have ∂_tP_e = κP_e(t). If the length distribution approaches a form which does not change over time, we must also have ∂_tf(t, j) = αf (t, j) for a constant α for all values of j; as P_e(t) = ∑_j f(t, j) this condition can only be satisfied if α = κ and the (time independent) distribution sought is:

$$\rho (j)=\underset{t\to \infty }{\text{lim}}f(j,t)e^{-\kappa t}$$ (32)

The master equation Eq. (8) can be rewritten for ρ(j) to yield:

$$\kappa \rho (j)=2m_{\text{tot}}{k}_{+}\rho (j-1)-2m_{\text{tot}}{k}_{+}\rho (j)-k_{-}(j-1)\rho (j)+2k_{-}{\displaystyle \sum _{i=j+1}^{\infty }\rho (i)}$$ (33)

In order to explore how the form of this length distribution compares to the result obtained for the case of conserved mass in section III, we again consider the continuum limit via the approximations Eqs. (13), (14) and (16). Defining the dimensionless constant ξ:

$$\xi =\frac{2k_{+}{m}_{\text{tot}}}{k_{-}}$$ (34)

results in a differential equation with the form:

$$0=\left(\xi +1/4\right){\rho }^{″}(j)+\left(j+\sqrt{\xi }\right){\rho }^{\prime }(j)+3\rho (j)$$ (35)

This expression is formally analogous to Eq. (17) obtained for systems with conserved total mass. Contrary to the case of constant mass, however, the individual rate constants enter the differential equation. Using the same arguments as above, a normalised solution satisfying ${\displaystyle {\int }_{n_c}^{\infty }\rho \left(i\right)di}=1$ is given by:

$$\rho (j)=\frac{e^{-\frac{2(j-n_c)(2\sqrt{\xi }+j+n_c)}{1+4\xi }}\left(-1+4j\right)(2\sqrt{\xi }+j))}{(1+4\xi )(\sqrt{\xi }+n_c)}$$ (36)

The mean length, µ, can be evaluated as a consistency check:

$$\begin{array}{cc}\mu =n_c+\frac{1+4\xi }{4\left(\sqrt{\xi }+n_c\right)}\approx \sqrt{\xi }& \xi \gg n_c\end{array}$$ (37)

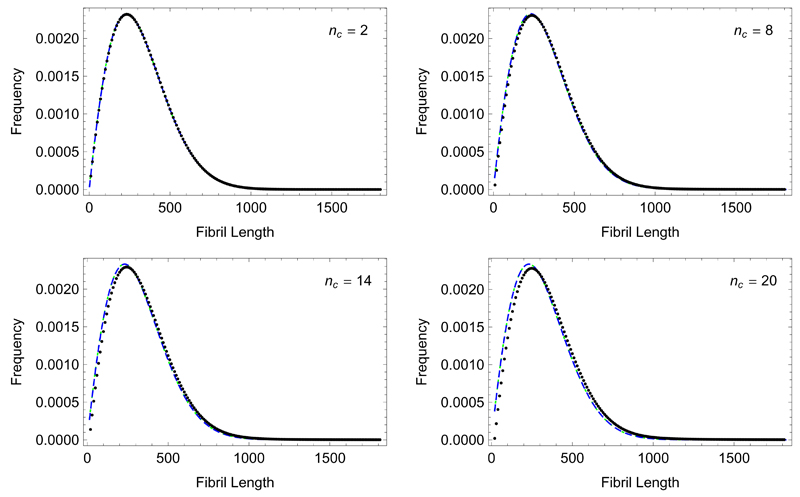
a result which agrees with the exact result in Eq. (31) in the limit ξ ≫ n_c; as n_c is of order unity and ξ, giving the ratio between the elongation and breakage processes is typically ξ » 1 in order for long filaments to be present in the system, the approximation ξ ≫ n_c is likely to be accurate for most cases of practical interest. Fig. 3 shows this result in comparison to the numerical solution. As expected, the continuum limit is seen to become slightly less accurate as n_c increases.

Fig. 3.

Length distribution in the long time limit for increasing nc in the case of constant monomer concentration. The black dots are calculated numerically from the recursion relation, Eq. (33), while the blue dashed line is the continuum limit solution from Eq. (36). The parameters used m_tot = 1µM, k₊ = 1 · 10⁴M⁻¹s⁻¹, k₋ = 2 · 10⁻⁷s⁻¹, giving ξ = 10⁵. The green line shows the solution given by Pöschel et al. [32] when setting the clearance rate to zero.

Interestingly, the ratio of the standard deviation, σ, to the mean, µ, can also be determined from Eq. (36) in terms of an error function:

$$\begin{array}{cc}\frac{\sigma }{\mu }\approx \sqrt{\sqrt{2e\pi }\left(1-\text{erf}\left(\frac{1}{\sqrt{2}}\right)\right)-1}\approx 0.56& \xi \gg n_c\end{array}$$ (38)

which is consistent with our more general analytical result[40] that the ratio between the standard deviation and mean of the filament length distribution in a system of constant monomer concentration is constant and equal approximately to $1/\sqrt{3}\approx 0.58$ throughout the reaction time course.

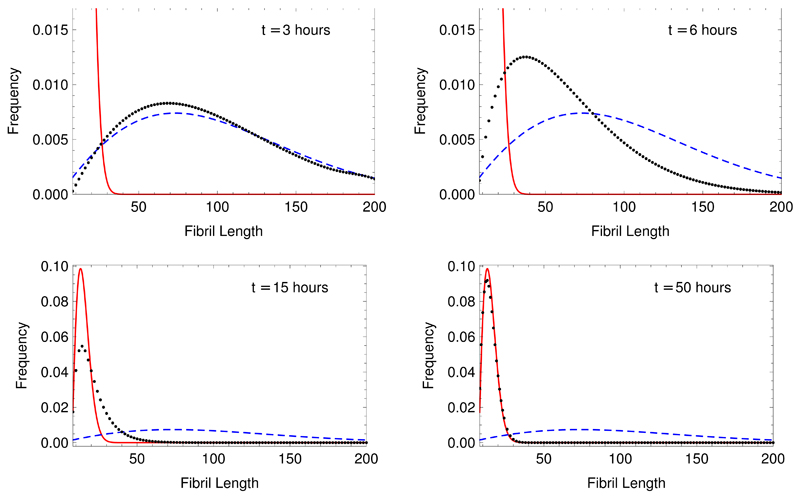
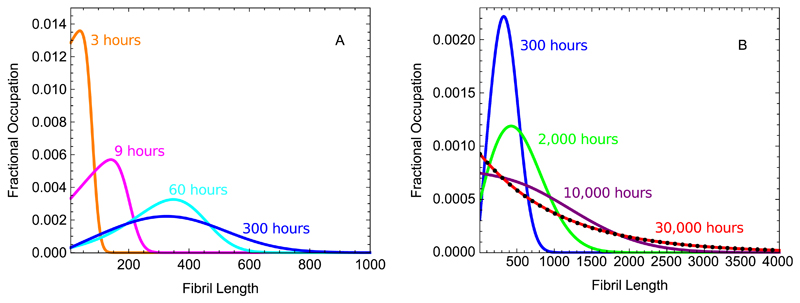
The results for the behavior in the long-time limit both in the case of constant monomer concentration Eq. (36) and in the case of mass conservation Eq. (19) allow an understanding to be developed of the full time evolution of the length distribution of filaments growing in a closed system conserving total mass. Considering that the monomer concentration is approximately constant at a value m_tot at early times in the polymerisation reaction, even for closed systems, we expect that the length distribution will first develop approximately into the biased Gaussian found as the equilibrium behavior for this case, given by Eq. (36), before shifting at later times into the substantially narrower biased Gaussian describing the equilibrium behavior of the constant mass case given in Eq. (19). Numerical evaluation of the master equation verifies this conclusion, and strikingly shows the evolution of the length distribution from the steady state behavior of constant monomer systems at early times to the equilibrium behavior of closed systems at late times as illustrated in Fig. 4.

Fig. 4.

Time evolution of the fibril length distribution in the constant mass case. The black dots are calculated numerically from the master equation Eq. (1). The blue dashed line is the predicted continuum equilibrium length distribution for the constant monomer case given in Eq. (36). The red line is the predicted continuum equilibrium length distribution for the constant mass given in Eq. (19). The parameters used are m_tot = 1µM, k₊ = 1 · 10⁴M⁻¹s⁻¹, k₋ = 2 · 10⁻⁶s⁻¹, k_n = 0, n_c = 8, M(0) = 0.01µM, P(0) = 0.001µM. The mass loss from the system in the numerical solution, due to solving a finite number of equations, is zero to within machine precision.

V. Comparison with Infrangible Filament Systems

The development of the length distribution in the case of infrangible filaments has been studied by Oosawa[1, 29]. It has been shown[1, 29] that the length distribution initially develops into a Poisson distribution in the time taken for the monomer-polymer equilibrium to be established, before relaxing over a longer timescale, in a diffusion-like process, into a (decaying) exponential distribution. In particular this equilibrium length distribution emerging for long times has been shown[1, 29] to take the form:

$$f\left(\infty ,j\right)=\frac{k_{n}m{(\infty )}^{n_c}}{2k_{\text{off}}}{\left(\frac{k_{+}m(\infty )}{k_{\text{off}}}\right)}^{j-n_c}$$ (39)

where m(∞) is the equilibrium concentration of soluble monomer, for which a derivation is sketched in the Appendix. There is no peak in this equilibrium length distribution, and Oosawa comments in his textbook[1]: “in polymers growing one-dimensionally, length distributions having a sharp maximum cannot be realized as a true equilibrium”. This time evolution of the length distribution in the absence of fragmentation is shown in Fig. 5. In contrast to the Poisson-to-exponential evolution seen in the case of nucleated polymerisation, introducing the phenomenon of filament breakage fundamentally alters both the evolution and the equilibrium result, and as we have shown, can lead to true equilibrium length distributions having a sharp maximum. A qualitative picture for why Oosawa’s argument for the lack of a maximum in the distribution breaks down in the presence of filament fragmentation can be provided by considering the fact that the master equation for nucleated polymerisation satisfies detailed balance at equilibrium, whereas with breakage only balance is required, allowing thereby the emergence of a length distribution described by a biased Gaussian. It is also interesting to note that the approach to equilibrium is also significantly faster when breakage processes operate. Instead of the Poisson to exponential development, the distribution now moves from one biased Gaussian form to another.

Fig. 5.

Evolution of the fibril length distribution in a system with depolymerisation from the ends of fibrils but no breakage. A shows earlier times, and B shows later times. The kinetic parameters used are m_tot = 1µM, k₊ = 1 · 10⁴M⁻¹s⁻¹, k_off = (2/3)m_tot k₊ s⁻¹, n_c = 8, $k_n{m}_{\text{tot}}^{n_c-1}=1\cdot {10}^{-7}{\text{s}}^{-1},$ M(0) = P(0) = 0.

In contrast to fragmentation, secondary processes that create structures of a single size will generally lead to a distribution of the exponential type. For example, a monomer-dependent secondary process that creates new structures of a critical size n₂ through nucleation on the surface of existing structures[8] results in an additional term of the form $k_{2}m{(t)}^{n_2}M(t){\delta }_{j,n_2}$ in the master equation. If the term describing monomer dependent secondary nucleation is included in the master equations, the equilibrium length distribution is identical to Eq. (39) with the replacement $k_{n}m{(\infty )}^{n_c}\to k_{2}m{(\infty )}^{n_2}+k_{n}m{(\infty )}^{n_c}M(\infty )$ in the prefactor for n₂ = n_c. In general, on mechanistic grounds, it is plausible to suppose n₂ ≈ n_c and therefore the distribution can still be expected to be of a qualitatively similar form as long as both nucleus sizes are approximately equal.

It is interesting to note that in some cases further processes, not explicitly described by the master equation studied in this paper, can affect the length distribution at equilibrium and the time that is taken for the system to reach equilibrium. In particular, for some systems there is evidence for the lateral association of individual filaments at late stages of the growth process to form higher order assemblies[41, 42]. Such an assembly is likely to result in a substantially lower fragmentation rate of the resulting larger diameter compound filaments than that observed for the individual filaments and could substantially increase the time taken to reach equilibrium, and therefore other mechanisms such as monomer exchange from filament ends could become dominant for determining the length distribution in such a system for long times.

VI. Evolution of Oligomer Occupancy

There is increasing interest in the evolution of the population of small aggregated species, known as oligomers, as they are believed to play an important biological role in protein aggregation disorders[23–28]. In general the structures of smaller aggregates can differ from those found in longer fibrils, a further degree of freedom which could be included in the master equation. In this paper, however, we use the unmodified master equation to investigate the population of small aggregates, and the time evolution of this population, in the presence and absence of filament breakage.

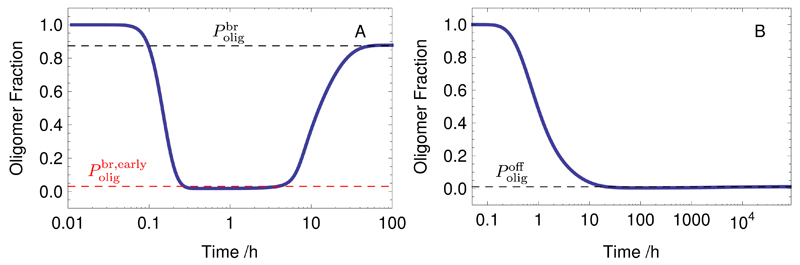
Prior to deriving analytical results further below, we examine the oligomer populations based on numerical solutions to the master equation. The evolution of the number of small species, as a fraction of the total number of fibrils, is shown from numerical calculations in Panel A of Fig. 6 for the cases with breakage, and for comparison for the case without breakage in Panel B. In both cases, at early times all fibrils are small and as time progresses, these fibrils grow and the fractional oligomer occupancy decreases. In the case without breakage, the occupancy drops to very close to the eventual equilibrium level in the time taken for monomer-polymer equilibrium and then equilibrates over a long time scale with only a very small increase in oligomer occupancy. The final state is characterised by the majority of the aggregated material being in larger fibrils rather than small oligomers. In contrast, when breakage is present, oligomer states are re-populated after the monomer-polymer equilibrium is reached as larger fibrils begin to break-up, and the equilibrium state shows that most aggregated material can be in oligomers as opposed to larger fibrils.

Fig. 6.

Evolution of the oligomer population up to size n_max = 20 as a fraction of total fibril population. Panel A shows the case with breakage and Panel B the case without breakage but with an off-rate. The black dashed lines are the analytically predicted equilibrium values from Eqs. (40) and (41). The red dashed line is the early time analytical prediction from Eq. (42). The kinetic parameters used are the same as those in Fig. 4 and Fig. 5 respectively.

Analytical expressions for the equilibrium values of the oligomer populations, P_olig, may be found by integrating the population distributions. If the maximum oligomer size is denoted n_max, then for the case with breakage using Eq. (19) we obtain at equilibrium the result:

$$\begin{array}{l}{P}_{\text{olig}}^{\text{br}}={\displaystyle {\int }_{n_c}^{n_{\text{max}}}\frac{e^{\frac{2(-j^2+{n_c}^2)}{{(1-2n_c)}^2}}\left(4j^2-{(1-2n_c)}^2\right)}{{(1-2n_c)}^2{n}_c}\mathit{\text{dj}}}\\ =1-\frac{n_{\max }}{n_c}{e}^{\frac{2(n_c^2-n_{\max }^2)}{{(1-2n_c)}^2}}\end{array}$$ (40)

In the converse limit, in the absence of breakage in a system including a monomer dissociation rate k_off, we obtain using Eq. (39) the form:

$$\begin{array}{l}{P}_{\text{olig}}^{\text{off}}={\displaystyle {\int }_{n_c}^{n_{\text{max}}}\frac{{\left(\frac{k_{+}M(\infty )}{k_{\text{off}}}\right)}^{-n_c}{k}_{n}M{(\infty )}^{n_c}}{2P(\infty )k_{\text{off}}}}{\left(\frac{k_{+}M(\infty )}{k_{\text{off}}}\right)}^j\mathit{\text{dj}}\\ =\frac{k_{n}M{(\infty )}^{n_c}\left[{\left(\frac{M(\infty )k_{+}}{k_{\text{off}}}\right)}^{n_{\text{max}-n_c}}-1\right]}{2P(\infty )\text{log}\left(\frac{M(\infty )k_{+}}{k_{\text{off}}}\right)k_{\text{off}}}\end{array}$$ (41)

In addition, by making use of the result for the case of breakable filaments that the distribution at an early time corresponds to that found in the presence of a constant monomer concentration, the corresponding early time limit oligomer population can be found from Eq. (36) as the closed form expression:

$$\begin{array}{l}{P}_{\text{olig}}^{\text{br},\text{early}}={\displaystyle {\int }_{n_c}^{n_{\text{max}}}\frac{e^{-\frac{2(j-n_c)(2\sqrt{\xi }+j+n_c)}{1+4\xi }}\left[-1+4j(2\sqrt{\xi }+j)\right]}{(1+4\xi )(\sqrt{\xi }+n_c)}}\mathit{\text{dj}}\\ =1-\frac{e^{-\frac{2(n_{\text{max}}-n_c)(2\sqrt{\xi }+n_{\text{max}}+n_c)}{1+4\xi }}\left(\sqrt{\xi }+n_{\text{max}}\right)}{\sqrt{\xi }+n_c}\end{array}$$ (42)

From these results, Eqs. (40), (42), (41), it is expected that in general the fractional oligomer population begins at unity. For frangible filaments, it then falls to the value given by Eq. (42) before rising to the value given by Eq. (40), whereas in the case without breakage the population falls and remains at around the value given by Eq. (41). The evolution of the respective cases with respect to these analytical limits is shown in Fig. 6. These results highlight the importance of filament fragmentation in the production of small oligomers. It is interesting to speculate that filament fragmentation could therefore be an important factor in the generation of low molecular weight toxic aggregates in protein aggregation disorders[23–28]. In agreement with this idea, it has been observed that strains of prion aggregates with lower stabilities and therefore likely larger fragmentation rates have a tendency to be more infectious[43, 44] and result in higher toxicity[45] to the host organism than strains in which fibers are highly stable.

VII. Conclusion

In this paper we have used the master equation of filament assembly to study the length distribution. We have shown that the classical result of Oosawa for the absence of a maximum in the aggregate length distribution at equilibrium does not hold for breakable filaments. Furthermore we have shown that the time evolution of the length of breakable filaments evolves through two key stages: first the growth proceeds to a length which is determined by the elongation and breakage rates of the filament system and which is typically many orders of magnitude larger than the equilibrium length. In a second slower step, the length distribution shifts towards smaller sizes once the monomer pool is depleted and growth stops, finally to reach an equilibrium length which is solely defined by the critical nucleus size.

Appendix

For a filament system that undergoes primary nucleation, elongation and depolymerisation, the equilibrium length distribution emerging for long times has been shown[1, 29] to take the form:

$$f\left(j,\infty \right)=\frac{k_{n}m{\left(\infty \right)}^{n_c}}{2k_{\text{off}}}{\left(\frac{k_{+}m\left(\infty \right)}{k_{\text{off}}}\right)}^{j-n_c}$$ (43)

We now derive an expression that relates the long time soluble monomer concentration, m(∞) to the total monomer concentration, m_tot, and the kinetic parameters, k₊ and k_n. We note immediately that for k_n = 0, f (j, ∞) = 0 ∀j implying m(∞) = m_tot. In other cases, an expression for m(∞) may be derived from Eq. (43) by noting:

$$m_{\text{tot}}-m\left(\infty \right)={\displaystyle \sum _{j=n_c}^{\infty }j\hspace{0.17em}\cdot \hspace{0.17em}}f\left(t,j\right)$$ (44)

Differentiating the well-known expression for the sum of a geometric series ${\displaystyle {\sum }_{j=m}^{\infty }{\alpha }^j={\alpha }^m/\left(1-\alpha \right)}$ yields the result ${\displaystyle {\sum }_{j=m}^{\infty }j{\alpha }^j=\left(m{\alpha }^m\left(1-\alpha \right)+{\alpha }^{m+1}\right)/\left(1-{\alpha }^2\right)}$ which may be used to evaluate the right-hand side of Eq. (44) to yield:

$$m_{\text{tot}}=m\left(\infty \right)+\frac{\frac{k_{n}m{\left(\infty \right)}^{n_c}}{2k_{\text{off}}}\left(n_c\left(1-\frac{k_{+}m\left(\infty \right)}{k_{\text{off}}}\right)+\frac{k_{+}m\left(\infty \right)}{k_{\text{off}}}\right)}{{\left(1-\frac{k_{+}m\left(\infty \right)}{k_{\text{off}}}\right)}^2}$$ (45)

Eq. (45) is a polynomial equation of order n_c + 1 for m(∞), which may in general only be solved analytically for n_c ≤ 3. Oosawa presented[1] a solution to the special case k_n = 2k₊ and n_c = 2 for which the cubic terms cancel and we are left with a simple quadratic equation for m(∞).

The general behaviour of m(∞) as a function of the total monomer concentration m_tot may be examined without formally inverting Eq. (45). It may be shown by differentiation and inversion that:

$${\frac{dm\left(\infty \right)}{d{m}_{\text{tot}}}|}_{m_{\text{tot}}=0}=1$$ (46)

which in conjunction with the trivial result $m\left(\infty \right){|}_{m_{\text{tot}}=0}=0$ describes the behaviour for low total monomer concentration. In addition, from Eq. (45), the limit as the total monomer concentration becomes large is given by:

$${m\left(\infty \right)|}_{m_{\text{tot}}\to \infty }=\frac{k_{\text{off}}}{k_{+}}$$ (47)

such that the long time soluble monomer concentration tends to a constant as the total monomer concentration becomes large (m_tot ≫ k_off/k₊). Therefore, for small positive k_n → 0, the solution to Eq. (45). must tend towards:

$$\underset{k_n\to 0}{\lim }m\left(\infty \right)=\min \left\{m_{\text{tot}},\frac{k_{\text{off}}}{k_{+}}\right\}$$ (48)

Higher values of k_n lead to a less abrupt transition between the limits where m(∞) = m_tot and m(∞) = k_off /k₊. Interestingly for k_n = 0 we have already seen that the solution is given always by m(∞) = m_tot, implying that the long time free monomer concentration, m(∞), is discontinuous in k_n as k_n → 0.