Perspective: On the importance of hydrodynamic interactions in the subcellular dynamics of macromolecules

Abstract

An outstanding challenge in computational biophysics is the simulation of a living cell at molecular detail. Over the past several years, using Stokesian dynamics, progress has been made in simulating coarse grained molecular models of the cytoplasm. Since macromolecules comprise 20%-40% of the volume of a cell, one would expect that steric interactions dominate macromolecular diffusion. However, the reduction in cellular diffusion rates relative to infinite dilution is due, roughly equally, to steric and hydrodynamic interactions, HI, with nonspecific attractive interactions likely playing rather a minor role. HI not only serve to slow down long time diffusion rates but also cause a considerable reduction in the magnitude of the short time diffusion coefficient relative to that at infinite dilution. More importantly, the long range contribution of the Rotne-Prager-Yamakawa diffusion tensor results in temporal and spatial correlations that persist up to microseconds and for intermolecular distances on the order of protein radii. While HI slow down the bimolecular association rate in the early stages of lipid bilayer formation, they accelerate the rate of large scale assembly of lipid aggregates. This is suggestive of an important role for HI in the self-assembly kinetics of large macromolecular complexes such as tubulin. Since HI are important, questions as to whether continuum models of HI are adequate as well as improved simulation methodologies that will make simulations of more complex cellular processes practical need to be addressed. Nevertheless, the stage is set for the molecular simulations of ever more complex subcellular processes.

I. INTRODUCTION

A grand challenge for computational biophysics in the 21st century is to be able to accurately simulate the biological processes occurring in living cells. If this were possible, in addition to providing fundamental insights into how cells work and the role of molecular specificity versus promiscuity in dictating biochemical and physiological processes, one could model the course of diseases including infections and cancers and suggest optimal and personalized treatments by simulating a virtual model of the cell. Just as rocket engines are now designed in silico,¹ one could design cells to become molecular factories.^2,3 Moreover, one could model the process of cellular evolution and possibly the emergence of living systems from their inanimate components. Of course, now, this is but a dream, but the past decade has seen the emergence of promising early steps towards achieving this goal.^4–13

At present, the most advanced methods do not attempt to simulate all the molecules in a cell from first principles but rather adopt various kinetic schemes. For example, the pioneering E-cell project^14–20 has seen success in the metabolic modeling of human erythrocytes.²¹ Another promising series of flux balance analysis models have been developed by Luthey-Schulten and co-workers.^22–24 They adopt a microscopic kinetics view of individual molecules that interact in a crowded cellular environment modeled as a discretized lattice, where individual macromolecules can hop between lattice sites. These studies are a molecular realization of the phenomenological dynamic flux estimation approaches developed by Voit et al.^25–30 for the analysis of metabolic time series data. Voit reports a number of successes including the ability to reproducing hitherto unexplained observations in glycolytic time course data under anaerobic conditions.

Despite the fact that all the requisite kinetic parameters are not known, kinetic modeling approaches are extremely valuable. They can provide many insights into cellular behavior and are at the cutting edge in treating cellular complexity. However, these methods suffer from the disadvantage that they have to assume a certain kinetic scheme a priori and then examine its consequences. Thus, they require that the fundamental kinetic mechanisms be known in advance. In reality, this is not always the case, and unincluded emergent features would not be discovered (e.g., in metabolic pathway modeling, suppose noncanonical pathways in aggregate contribute a substantial component of the metabolic flux, or certain important correlated motions are ignored). They rely on the ability of kinetic modeler to identify all relevant processes and provide at least order of magnitude estimates of the relevant kinetic parameters. Thus, there is the need for complementary bottom up approaches that can identify the essential fundamental processes involved in intracellular macromolecular dynamics. It is the discussion of the state of the art of such bottom up, molecular simulations of subcellular and cellular processes that is the focus of this Perspective.

A most striking feature of the interior of living cells is just how crowded they are, with macromolecules occupying from 20% to 40% of the total volume.^31,32 Indeed, to a first approximation, the cytoplasm closely resembles the population density of Times Square on New Year’s Eve. In the cytosol, the average intermolecular distance between proteins is of the order of their diameter. Indeed, in bacteria, yeast, and mammalian cells, recent mass spectrometric measurements suggest that there are 2-4 × 10⁶ proteins/μm³ (fL).³³ For such a situation, molecular crowding has been found to exert a significant influence on intracellular protein stability, enzymatic activity, and association kinetics.^34–40 Similarly, one would expect that crowding should affect the dynamics of macromolecular motion in the cytosol. Understanding such elemental processes is necessary before far more complex situations, e.g., reaction kinetics in cells, not to mention physiological processes could be understood from a bottom up perspective.

Diffusion is one of the most elemental and important dynamical processes needed to describe the motion of the molecules themselves as well as their reaction rates. In the crowded environment of a cell, macromolecular motion will be slowed down due to excluded volume effects between molecules. Over the past decade, the diffusion of macromolecules in the cytoplasm has been examined by a variety of experimental techniques including single particle tracking,⁴¹ Fluorescence Recovery After Photobleaching (FRAP),⁴² and Fluorescence Correlation Spectroscopy (FCS).^43–45 The diffusion coefficient of Green fluorescent Protein (GFP) in E. coli measured by FRAP^46,47 shows a reduction of about a factor of 10 relative to that at infinite dilution in water. Thus, macromolecular motion within the cytosol is significantly reduced.

One possible cause of the reduction in diffusion constant is that the viscosity of the cytosol is dramatically less than that of water. However, this early view that the cytosol is gel-like is incorrect; rather its viscosity in eukaryotic cells is quite close to that of pure water.⁴⁸ Given the greater complexity of eukaryotic cells compared to prokaryotic cells, it is a reasonable expectation that this observation will hold for prokaryotic cells as well. Thus, the difference in the viscosity of the cytosol relative to water cannot explain the reduction in macromolecular diffusion. Another possibility consistent with the high volume fraction of macromolecules is steric repulsions between macromolecules. A key question is whether excluded volume effects are sufficient or if other physical interactions are needed.

The early simulations of Ridgway⁴⁹ and Roberts et al.,⁵⁰ suggested that excluded volume effects alone could not account for the reduction in macromolecular diffusion. At first glance, this is somewhat surprising given the very high volume fractions of macromolecules in the cytoplasm. To address these issues, in a pioneering series of studies, McGuffee and Elcock^4,5 performed Brownian dynamics (BD) simulations of a model of the E. coli cytoplasm where protein molecules are described at atomic detail. In Brownian dynamics, the solvent is not explicitly treated, and inertial effects are ignored.⁵¹ Again, crowding/excluded volume was insufficient to describe the reduction in diffusion constant of GFP relative to infinite dilution. Rather, they found that not only were electrostatic interactions needed but also they had to significantly increase the intermolecular van der Waals interaction energy to recover the reduced mobility. Obviously, the van der Waals parameter can be tuned to give whatever diffusion constant between zero (no motion) and the value at infinite dilution that one wants. The key question is whether such enhanced van der Waals interactions are physical or if there are there other interactions at play.

Another effect that is well known both from the study of the dynamics of polymers⁵² and colloidal suspensions is hydrodynamic interactions which describe the perturbation of the solvent flow around a given molecule due to the wake created by other molecules. For polymer dynamics, hydrodynamic interactions (HI) are very important. For example, they change the dependence of the diffusion constant of a polymer from D ∼ n in the absence of HI to D ∼ n^−1/2, with n the number of beads (repeat units) in the polymer.⁵² Thus, intrachain dynamics can be dramatically modified by HI. Similarly, the role of HI in colloidal suspensions has been studied by a variety of computational methodologies including Stokesian dynamics (SD)⁵³ (which includes both HI and short range lubrication forces and is appropriate for low Reynolds numbers⁵⁴), lattice-Boltzmann,⁵⁵ multiparticle collision dynamics,⁵⁶ and dissipative dynamics.⁵⁷ Stokesian dynamics is attractive as it has been shown to reproduce the dynamical properties of high density colloids.⁵⁸ However, with a few exceptions, its use has been mainly limited to monodisperse systems.^59,60 One problem associated with the use of Stokesian dynamics is the scaling of the traditional implementation of the algorithm (see below),^6,7 where the computational cost of each step is of order N³; here, N is the number of system particles. If one desires to simulate large systems containing millions of proteins per fL, methods that reduce the dependence of the scaling with N are needed.

In what follows, we discuss a series of simulations of concentrated macromolecular models of the cytosol designed to elucidate the key factors governing intracellular dynamics. Key questions we address in this Perspective are the following: (1) What is the state of the art of Brownian dynamics based methods to simulate crowded macromolecular solutions? (2) What level of detail is required to simulate translational and rotational motion in crowded macromolecular environments? Specifically, under what conditions can proteins be treated as spheres and when does one need to treat them at atomic detail? (3) What is the relative importance of excluded volume interactions, long and short range (lubrication forces) hydrodynamic interactions, and nonspecific attractive interactions in cellular diffusion? (4) If HI are important, how do they influence the short and long time dynamics of crowded macromolecular solutions? (5) Is there a distance scale, just like in semidilute polymer solutions, where hydrodynamic interactions are screened?⁶¹ (6) What is the distance scale when the granularity of the solvent is important and is a continuum model of the cytosol a good approximation? (7) How does the finite size of a cell affect intracellular macromolecular motion? (8) What role do HI play in the assembly of lipid bilayers that comprise the cell membrane? Finally, we summarize the outlook for the future.

II. SIMULATION METHODOLOGIES

There are a number of algorithms that are routinely used to simulate a collection of Brownian particles. These are summarized in Table I.

TABLE I.

Description of simulation algorithms for crowded macromolecular solutions.

Algorithm	Description	Methodology
SD: Stokesian dynamics	Includes both many-body far-field HI and the near-field lubrication forces at low Reynolds number.54	Original SD algorithm requires an O(N3) matrix inversion and Cholesky factorization of dense matrices.
BD: Brownian dynamics	Includes HI at the level of Oseen62 or RPY tensors.63	Algorithm developed by Ermak and McCammon.51
FD: Free draining	BD without HI; the diffusion matrix is diagonal and constant.	Limiting case of BD.51
FLD: Far field version of SD	Far-field hydrodynamic matrix is approximated by a diagonal matrix, but lubrication forces are explicitly considered.	Developed in Ref. 7. The algorithm scales O(N).

In what follows, we present a summary of the salient features of these algorithms, where for simplicity only particle translations and forces are considered, and rotations and torques are ignored.⁶⁴

A. Stokesian dynamics

The translational motion of N Brownian particles is represented by the Langevin equation^53,65

$${\displaystyle m\frac{du}{dt}={\mathbf{f}}^{\mathbf{H}}+{\mathbf{f}}^{\mathbf{P}}+{\mathbf{f}}^{\mathbf{B}}.}$$ (1)

Here, m is the 3N × 3N mass tensor, u is the particle translational velocity vector of length 3N, and the forces acting on the particles consist of the hydrodynamic forces, f^H, the deterministic non-hydrodynamic forces, f^P, that include electrostatic and van der Waals contributions, and the stochastic Brownian forces f^B. All are vectors of length 3N. For low Reynolds number and without bulk flow, the hydrodynamic forces are given by

$${\displaystyle {\mathbf{f}}^{\mathbf{H}}=-\mathbf{Ru}=\raisebox{1ex}{$-{\mathbf{D}}^{-1}\mathbf{u}$}\!\left/ \!\raisebox{-1ex}{${\text{k}}_{\text{B}}\text{T}$}\right..}$$ (2a)

R (D) is the 3N × 3N configuration dependent hydrodynamic resistance (diffusion) tensor with

$${\displaystyle {\text{k}}_{\text{B}}\text{T}\hspace{0.17em}{\mathbf{R}}^{-1}=\text{D}.}$$ (2b)

The Brownian forces f^B arising from thermal fluctuations are characterized by the fluctuation-dissipation theorem⁶⁶

$${\displaystyle 〈{\mathbf{f}}^{\text{B}}〉=0;〈{\mathbf{f}}^{\text{B}}\left(0\right){\mathbf{f}}^{\text{B}}\left(\text{t}\right)〉={\text{2k}}_{\text{B}}\text{T}\hspace{0.17em}\mathbf{R}\mathrm{\delta }\left(t\right).}$$ (3)

The angle brackets denote the ensemble average, k_B is Boltzmann’s constant, T is the absolute temperature, t is time, and δ(t) is the Dirac delta function.

The time evolution of the particle coordinates given by Ermak and McCammon⁵¹ is obtained by integrating Eq. (1) over a time step Δt larger than the inertial relaxation time (τ_B = m/6πηa, for a particle of radius a and mass m, and solvent viscosity η) but smaller than the time over which the forces relax,

$${\displaystyle \mathbf{r}\left(t+\mathrm{\Delta }\text{t}\right)=\mathbf{r}\left(t\right)+{\text{k}}_{\text{B}}\text{T}\left(\nabla \cdot \mathbf{D}\right)\mathrm{\Delta }\text{t}+{\mathbf{Df}}^{\text{P}}\mathrm{\Delta }\text{t}+\mathbf{x}\left(\mathrm{\Delta }\text{t}\right).}$$ (4)

r is the 3N length position vector, x(Δt) is a random displacement due to Brownian noise. x is calculated from a multivariate Gaussian distribution whose mean and covariance are given by

$${\displaystyle 〈\mathbf{x}\left(\mathrm{\Delta }\text{t}\right)〉=0;〈\mathbf{x}\left(\mathrm{\Delta }\text{t}\right)\mathbf{x}\left(\mathrm{\Delta }\text{t}\right)〉\text{=}2\mathbf{D}\mathrm{\Delta }\text{t}.}$$ (5)

If z is a standard normal vector, then

$${\displaystyle \mathbf{x}=\sqrt{2\mathrm{\Delta }\text{t}}\mathbf{Bz},}$$ (6a)

where

$${\displaystyle \mathbf{D}={\mathbf{BB}}^T.}$$ (6b)

Any B that satisfies Eq. (6b) can be used in Eq. (6a). Thus, all techniques that solve Brownian dynamics require the principal square root or symmetric factorization of D. The simplest way of doing this is to use a Cholesky factorization, an O(N³) operation.⁶ This is the origin of the O(N³) scaling for each time step mentioned above. Another alternative introduced by Fixman is to employ a Chebyshev polynomial approximation.⁶⁷ Recently, we suggested using Krylov subspace methods that are related to the Chebyshev method but do not require eigenvalue estimates and scale roughly as O(N²).⁶ In that regard, a recent comparison of Chebyshev and Krylov subspace methods for polymer dynamics is of note.⁶⁸

B. Hydrodynamic interactions

The matrix D contains the hydrodynamic interactions that are often implemented using the Rotne-Prager-Yamakawa, RPY,⁶³ mobility tensor between the ith and jth spheres at a distance R_ij defined by the following equation:

$${\displaystyle \mathbf{D}\left(\mathit{i},\mathit{j}\right)=\left\{\begin{array}{c}\hfill \frac{{\text{k}}_{\text{B}}\text{T}}{8\pi \eta }\left[\left(\frac{1}{R_{ij}}\mathbf{I}+\frac{{\mathit{R}}_{ij}{\mathit{R}}_{ij}}{R_{ij}^3}\right)+\frac{2a^2}{3R_{ij}^3}\left(\mathbf{I}-\frac{{\mathit{R}}_{ij}{\mathit{R}}_{ij}}{R_{ij}^3}\right)\right]\text{if}{R}_{ij}>2a\hfill \\ \hfill \frac{{\text{k}}_{\text{B}}\text{T}}{6\pi \eta a}\left[\left(\mathbf{I}-\frac{9}{32}\raisebox{1ex}{$R_{ij}\mathit{I}$}\!\left/ \!\raisebox{-1ex}{$a$}\right.\right)+\frac{3}{32a}\frac{{\mathit{R}}_{ij}{\mathit{R}}_{ij}}{R_{ij}}\right]\text{if}{R}_{ij}\le 2a\hfill \end{array}.\right.}$$ (7)

Here, a is the radius of each spherical particle, and I is the 3 × 3 identity matrix. The RPY tensor for D is often used because it is positive definite even for overlapping particles^51,69,70 and ∇ ⋅ D = 0. It contains two-body and long-range contributions to the particle mobility up to order 1/r³. For dilute systems, two-body interactions may suffice. However, for concentrated systems, far-field many-body HI as well as near-field lubrication forces are needed. Thus, SD not only includes the far-field HI but also the many-body and near-field HI contributions.^53,54,71 Here, the resistance tensor R is the sum of the far-field HI and near-field lubrication interactions given by

$${\displaystyle \mathbf{R}={\frac{\left({\mathbf{D}}^{\infty }\right)}{{\text{k}}_{\text{B}}\text{T}}}^{-1}+{\mathbf{R}}_{\mathbf{lub}}}$$ (8)

with

$${\displaystyle {\mathbf{R}}_{\mathbf{lub}}={\mathbf{R}}_{2\text{B}}-{\mathbf{R}}_{2\text{B}}^{\infty }.}$$ (9)

D^∞ is the contribution of many-body, far-field interactions given by the RPY expression of Eq. (7). R_lub contains the near-field lubrication forces of the two-body HI. R_2B represents the exact two-body HI, which includes both near-field and far-field interactions and is calculated using the exact two-body solution of Jeffrey and Onishi.⁷² ${\mathbf{R}}_{2\text{B}}^{\infty }$ is the resistance tensor that represents two-body, far-field interactions and is obtained by inverting the two-body diffusion tensor matrix containing terms to order 1/r. The far-field part has already been included in ${\frac{\left({\mathbf{D}}^{\infty }\right)}{{\text{k}}_{\text{B}}\text{T}}}^{-1}$. To avoid over counting, we must subtract these two-body interactions. This corrects R_lub.

For periodic boundary conditions, D^∞ can be estimated by the Ewald summation of the RPY tensor.⁷³ Due to the long-range nature of HI, use of the Ewald summation technique is often necessary not only for accuracy but also for obtaining positive definite matrices. D^∞ is a dense matrix, and its explicit construction and inversion require O(N²) and O(N³) computations, respectively. Due to the fact that lubrication forces occur at short distances, R_lub is sparse, and using a cut-off method, its construction requires O(N) operations.

III. SIMULATION OF MACROMOLECULAR MOTION IN THE CYTOPLASM

A. Level of detail required to simulate the E. coli cytoplasm

For a concentrated solution of polydisperse protein molecules designed to model the cytoplasm, if one is interested in translational diffusion, what level of detail is required to reproduce the translational self-diffusion constant, D? For the ith molecule, D is given by

$${\displaystyle 〈{\left(r_i\left(t\right)-r_i\left(0\right)\right)}^2〉=6\text{D}\left(t\right)t.}$$ (10)

The long time diffusion constant, D^L, is the limit of Eq. (10) at long times. Similarly, we define the short time diffusion coefficient, D^S, as the initial value of D. To address this issue, Ando and Skolnick⁸ initially performed Brownian dynamics simulations in the absence of hydrodynamic interactions in a model of the E. coli cytoplasm based on the data of Ridgway et al.⁴⁹ Thus, the observed size distribution and relative concentration of macromolecules in the E. coli cytoplasm are reproduced in the simulation. Both molecular-shaped and equivalent sphere systems were considered where only steric interactions were allowed. For each macromolecule, the diffusion constants at infinite dilution, D₀, were calculated at atomic detail from rigid particle theory.^74–76

Examination of the ratio of D^L/D₀ shows that the equivalent sphere and the atomic representations of the macromolecules are well correlated over the entire range of particle radii (20 Å-115 Å) for overall macromolecular concentrations of 300 mg/ml and 350 mg/ml. Only when exceptionally high concentrations of 400 mg/ml of macromolecule are present does the diffusivity of the spherical system become slightly lower than the atomic representation. Thus, with respect to translational motion, treating the macromolecules by their equivalent sphere is a good approximation. This is important in that it enables very large number of particles in the cytoplasm to be simulated. We note that this conclusion likely does not hold for very asymmetric molecules nor for rotational diffusion.^10,77

B. Are steric interactions between macromolecules dominant?

For probe GFP molecules, experiments find that D^L/D₀ is in the range of 0.06-0.09.^78,79 In the model system with just steric interactions, simulated values of D^L/D₀ for GFP from molecule shaped and equivalent sphere systems in 300 mg/ml and 350 mg/ml are 0.41 and 0.38, which is 4-5 times larger than experiment. Even for the molecular-shaped system at 400 mg/ml, for GFP the simulations find that D^L/D₀ is still 2 times larger than experiment. Thus, excluded volume effects only account for at most half of the reduction in the diffusion constant in the cytosol. This result is consistent with the work of McGuffee and Elcock.⁵

C. Are hydrodynamic interactions important?

As shown in Figure 1, using full Stokesian dynamics with steric and hydrodynamic interactions, for GFP, the BD simulation in 350 mg/ml (a value is consistent with experiment³¹) with HI provides a predicted D^L/D₀ of 0.08. This result is in agreement with experiment: D^L/D₀ ranges from 0.09 in DH5α,⁴⁶ 0.07 in BL21(DE3),⁴⁷ to 0.06 in the K-12 strain⁴⁷ grown in rich medium. These results strongly suggest that excluded volume effects and HI are the two major factors which decrease the intracellular diffusivity of macromolecules. As also shown in Figure 1, the predicted D^L/D₀ is in agreement with the experimentally observed values of D^L/D₀ for a series of engineered GFP multimers adapted from Figure 2 of Ref. 80. However, they do not agree with the experimental values obtained from Sourjik et al.⁸¹ who measured the diffusion constants of membrane and DNA binding proteins in E. coli. Interestingly, they find that the mobility of DNA binding proteins depends on their binding specificity, indicative of the possible role of attractive interactions. In all cases, the composition of the simulated cytosol remains fixed.

FIG. 1.

Reduction in the long-time diffusion constant, the relative diffusion constant, D^L/D₀, as a function of radius in the nonspecific interaction model with attractions and steric repulsions (diamonds) compared to the model with steric repulsions and HI (solid circles). The solid triangles show the experimentally observed D^L/D₀ values adapted from Figure 4B of Sourjik et al.⁸¹ who measured the diffusion of membrane and DNA binding proteins in E. coli. The plus signs are the experimentally observed values of D^L/D₀ for a series of engineered GFP multimers adapted from Figure 2 of Ref. 80. The concentration of macromolecules in the simulations is 350 mg/ml, and the dashed line denotes the value for D^L/D₀ of GFP.

Qualitatively different results are seen for the short time diffusion constant depending on whether or not HI are included. For a system without HI, D^S/D₀ = 1. A given macromolecule does not know if it is in a concentrated medium or not until it experiences collisions with other macromolecules. In contrast, with HI, D^S/D₀ ranges from 0.2 for particles with a radius of 20 Å to about 0.1 for particles with a radius of 100 Å. This is an important signature of the presence of hydrodynamic interactions that has been quantitatively confirmed in an elegant study of the self-diffusion of Bovine Serum Albumin (BSA) in a crowded solution at biologically relevant concentrations.⁸²

D. Role of nonspecific attractive interactions in subcellular diffusion

Another possible source of the reduction in diffusivity of macromolecules in the cytosol might be nonspecific attractive interactions as employed in Refs. 5 and 77. To further examine this issue, a number of types of short range nonspecific attractive terms were introduced, and their effects on D^L/D₀ explored. As shown in Figure 1, as might be expected, larger particles having stronger attractive interactions (open diamonds) experience a larger reduction in their long time diffusivity than is found when just HI with steric interactions (solid circles) are included. This is another qualitative difference between systems where HI are important and one where attractive interactions dominate. Further experiments are required to establish the relative importance of nonspecific attractive interactions by measuring the diffusion constants for different size macromolecules. However, we do note that the experiments of Sourjik et al. show an even greater reduction in mobility than that provided by the simulations. This may reflect the fact that some proteins are in the membrane, whereas others might interact with DNA.

In that regard, real proteins mainly form complexes with interactions across a relatively planar interface, with the number of such distinct protein-protein interfaces on the order of about 1000.⁸³ While it was traditionally believed that such interfaces comprised a minor fraction (roughly 1/3) of a protein’s surface, recent work finds that the majority of a protein’s surface (>75%) has the requisite geometry to engage in such nonspecific protein-protein interactions.⁸⁴ However, in addition to having nonspecific attractive interactions, there are residue specific interactions which may be repulsive, neutral, or attractive. The fact that most proteins do not strongly interact (at least as assessed by yeast two hybrid experiments⁸⁵) suggests that nonspecific attractive interactions might be expected to play a fairly minor role in dictating macromolecular dynamics.

E. Hydrodynamic interactions introduce long range spatial and temporal correlations

When HI are included, the short time diffusion coefficient ratio D^S/D₀ in concentrated solutions is macromolecular size dependent. This suggests that the perturbation in solvent motion about a given macromolecule affects individual particle dynamics and raises the question if it induces spatial and temporal correlations. To analyze this correlation, if any, we calculated

$${\displaystyle {\text{C}}_{\text{ij}}\left({\text{d}}_0,\text{t}\right)=\frac{\sum \left|\left({\text{r}}_i\left(t\right)\cdot {\text{r}}_j\left(t\right)\right)\delta ({\text{d}}_0-{\text{d}}_{\text{ij}})\right|}{\sqrt{\sum {\left|\left({\text{r}}_i\left(t\right)\right)\delta ({\text{d}}_0-{\text{d}}_{\text{ij}})\right|}^2\left|\left({\text{r}}_j\left(t\right)\right)\delta ({\text{d}}_0-{\text{d}}_{\text{ij}})\right|}}}$$ (11)

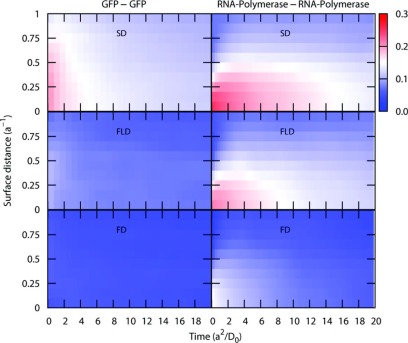
between particles i and j at a distance d₀ at a time t. As shown in Figure 2, for pairs of GFP molecules and RNA polymerases, respectively, in a system with just steric repulsions the correlations are weak and anti-correlated, with GFP experiencing stronger anti-correlations. In contrast, with HI both types of molecule pairs exhibit long lived temporal correlations up to at least 100 ns and spatial correlations up at least to 10 Å. We suspect that such correlations may play an important functional role in cellular processes. Finally, for the nonspecific binding model, the smaller pair has very weak spatial and temporal correlations, while the larger pair of molecules has much stronger, long lived temporal correlations that persist out to 8 Å (that is, are spatially close to the surface of the molecule), rather than at least 10 Å when HI are allowed.

FIG. 2.

Normalized pair correlation function from Eq. (11) averaged over pairs of GFP and RNA polymerase molecules for the three different simulation models at 300 mg/ml. The surface distance is the distance between the surfaces of the pair of proteins.

F. Comparison of hydrodynamic interactions and nonspecific binding models of diffusion

We next summarize the differences when HI as opposed to nonspecific binding dominate the dynamics.

If HI dominate:

If nonspecific binding dominates:

•Decay like 1/r; lubrication forces give repulsion on approach and attraction as pairs of molecules move apart. •Short time diffusion constant, DS, is significantly reduced from D0. •DS/D0 depends on the molecule’s radius. •Long time diffusion constant DL has a much weaker dependence on particle radius. •Spatial and temporal correlations for all size macromolecules; weak dependence on particle size.

•Attractive interactions decay like 1/r2 for spherical macromolecules filled with small van der Waals spheres. •Short time diffusion constant is the same as at infinite dilution, D0. •DS/D0 is independent of molecular radius. •DL is strongly size dependent, with long lived clusters formed with larger macromolecules. •Significant, strongly radius dependent spatial and temporal correlations.

G. Are hydrodynamic interactions in concentrated solutions effectively screened?

Since the long range contribution to HI scales as 1/r between particles, brute force calculations scale as O(N³), with N the number of particles. This can be reduced to roughly O(N²) if Krylov subspace methods are used.⁶ Can the physics of concentrated macromolecular systems help further reduce the scaling? For semidilute solutions of random polymers, de Gennes has shown that HI are screened beyond a polymer concentration dependent length, much like electrostatic interactions in ionic solutions are screened at higher salt concentrations; in such a case, the free draining (FD) limit holds, and polymer dynamics becomes Rouse-like.⁶¹ However, other work suggested that hydrodynamic screening does not occur for freely diffusing particles.⁸⁶ If hydrodynamic interactions were strongly screened, then the far field HI matrix becomes diagonal, and the RPY expression given in Eq. (7) reduces to

$${\displaystyle {\mathbf{D}}^{\infty }\left(\mathit{i,i}\right)=\frac{{\mathrm{k}}_{\mathrm{B}}\mathrm{T}\mathbf{I}}{6\pi {\eta }_{F}a},}$$ (12)

where η_F is the “effective” far field viscosity, and a is the particle radius. Since SD is being employed, and R_lub contains all higher terms, the lubrication term includes the reduction in effective viscosity. Thus, the uncorrected viscosity of the solvent should be used for η_F in Eq. (12). This approximation has been previously employed in fast SD algorithms for both Brownian^87–90 and non-Brownian particles⁹¹ and was termed Fast Lubrication Dynamics, FLD by Bybee.⁸⁹ While monodisperse systems were originally used for algorithm development, Ando et al. considered the validity of FLD for a polydisperse concentrated solution that is a model of the E. coli cytoplasm. In their implementation, the computational cost per time step is of O(N).⁷

The total neglect of all HI as provided by the free draining (both long and short range HI are turned off) approximation grossly overestimates the short and long time diffusion constants by a factor of 4-10. In contrast, the diagonal approximation to D^∞ overestimates the short time diffusion constant D^S by at most 12% for the smallest particles, with a similar overestimate of at most 15% for D^L. Thus, we conclude that with respect to global diffusion at both short and long times, the long distance component of hydrodynamic interactions (see Eq. (7)) is essentially screened. However, as seen in Figure 3, FLD causes a dramatic loss in spatial and temporal correlations, where time and surface distance are normalized by a²/D₀ and a, respectively. For SD simulations, correlated motions are obvious for both pairs. For small pairs (GFP) of particles, the correlated motions (C_ij > 0.2) range up to 2 in time and 0.75 in surface distance (corresponding to 110 ns and 18 Å), respectively. For large particle pairs, the correlation spans 12 in time and 0.4 in surface distance (times of 14 μs and 26 Å, respectively). C_ij from FLD simulations are much smaller for SD and are intermediate between the original SD and FD simulations. This underestimation is obvious for the small particle pairs, as they can readily diffuse away from each other as compared to large particles, and their time to stay near to each other is relatively short. They are sensitive to the absence of cross coupling terms of the far-field HI. This is a clear limitation of using a diagonal approximation for D^∞.

FIG. 3.

Normalized pair correlation function, C_ij from Eq (11) for the 24 Å - 24 Å, GFP, and 66 Å - 66 Å, RNA polymerase pairs of molecules obtained from SD, FLD, and FD simulations. The times and distances are normalized by a²/D₀ and a, respectively.

H. Effects of confinement on models of intracellular macromolecular dynamics

Macromolecules in the cytosol are not in an infinite nor periodic system but rather they are confined within the membrane of the cell. How does such confinement affect intracellular macromolecular dynamics? Can we entirely ignore their effects including the modification of dynamics in the neighborhood of the membrane wall? To address these questions, Chow and Skolnick⁹² simulated a suspension of monodisperse particles in a viscous fluid confined within a spherical shell composed of closely spaced particles that are constrained by a harmonic potential to lie near the rest distance of the spherical shell. For BD, confinement is achieved primarily by steric interactions between the cytoplasmic and the wall particles. For SD, confinement is primarily due to lubrication forces that prevent particles from overlapping. In this idealized model, the radii of all particles are the same (this does not qualitatively change the results, see below). Mimicking the cell interior, the volume fraction of cytoplasmic particles is ϕ = 0.3.

Simulations were performed with 1000 cytoplasm particles in a spherical shell with a radius of approximately 14.4, where the radius of an individual particle is 1. Selected simulations were also done with 20 000 cytoplasm particles in a spherical shell with a radius of approximately 40.0 as well as a system of 500 000 particles with a cell to particle ratio of 119. They also considered a bidisperse system comprised of a relatively small number of particles of radius 4 surrounded by a sea of particles of radius 1, constructed such that the overall volume fraction remains at 0.3. All results were qualitatively the same for these different systems. BD and SD simulations were also performed for periodic conditions to approximate an infinite, unconfined system. Some BD simulations were also performed without HI, to examine the role played by HI.

Particles in the cell interior have qualitatively similar motions to particles in a periodic box with no cell wall. Far enough from the wall, there are no long range correlations due to the wall itself. However, there is an overall slowdown in diffusion due to confinement, which is likely dependent on cell radius. Nevertheless, the qualitative effects of motion in the cell interior can be effectively modeled as an infinite periodic system. Overall, the major effects of confinement are steric. However, the qualitative behavior of systems with and without HI is different. HI generate correlated behavior both far from as well as near the cell wall. SD simulations further show some qualitatively different features than BD simulations with HI, such as a slowdown in diffusion, a reduction in correlated motions of nearby particles, and structure in the velocity profiles that persist farther into the interior of the cell. SD simulations more accurately model the crowded interiors of cells than BD simulations, because they account for lubrication forces.

The results of these simulations might have functional implications. For example, the fact that the model proteins near the model cell wall tend to diffuse along the wall is consistent with the conjecture that there is an increase in macromolecular concentration near the wall.⁹³ These simulations show that the cause is primarily steric and does not require any specific interactions for it to happen. The tendency of protein molecules to diffuse along and remain localized near the membrane might give additional time for signal transduction across a membrane to occur.

IV. IS THE DESCRIPTION OF HYDRODYNAMIC INTERACTIONS IN STOKESIAN DYNAMICS ACCURATE?

In an important study, Morrone et al.⁹⁴ examined the spatial dependence of the friction coefficient in the Brownian limit for two nonpolar bodies. They find that the friction coefficient deviates from continuum hydrodynamic predictions at small separations and depends on the nature of solute-solvent interactions. For purely repulsive spheres, the friction coefficient has a peak at the critical dewetting distance and decreases as the intersolute region dries. For attractive solutes, water is expelled by steric repulsions, and the effects of solvent layering cause a non-monotonic dependence of the friction coefficient on separation. These observations could provide for a better description of the lubrication forces at short distances.

A very important complementary study⁹⁵ compared the Rotne Prager (RP) approach to HI with that obtained in two and three body systems with many centers of friction that accurately account for the many body nature of HI. Surprisingly, when a sufficient number of frictional elements are included, at short distances, then the far field RP approximation provides a description that is in quantitative agreement with the essentially exact numerical scheme. While this is a continuum solvent approach, it does suggest that a combination of modified lubrication forces (which in classical SD non-physically diverge at short distances) and multiple friction centers might provide an accurate description of HI. The disadvantage is the significantly increased computational cost due to multiple centers of friction that might restrict the size of tractable cellular simulations. Clearly, these issues need to be further addressed in the near future.

V. ROLE OF HYDRODYNAMIC INTERACTIONS IN THE KINETICS OF CELL MEMBRANE ASSEMBLY

As shown above, hydrodynamic interactions (HI) give rise to collective motions between molecules in concentrated solutions. The next logical question is to explore their role in the biological self-assembly of large scale molecular aggregates. For example, Ando and Skolnick¹² examined the importance of HI on the kinetics of lipid membrane self-assembly. Using Brownian dynamics (BD) simulations, 1000 coarse-grained lipid molecules in periodic simulation boxes were allowed to assemble into stable bilayers in the presence and absence of intermolecular HI. HI reduce the monomer-monomer association rate by 50%. In contrast, the rate of association of lipid clusters is much faster in the presence of intermolecular HI, with the membrane self-assembly rate 3-10 times faster than that without intermolecular HI. These results suggest that HI greatly influence self-assembly kinetics, and that simulations without HI will significantly underestimate assembly rates. Similar conclusions were reached by Li et al. regarding the importance of HI on the kinetics of assembly of two plates of varying hydrophobicity.⁹⁶ Thus, we suspect that HI may play important roles in many other biologically important self-assembly processes.

VI. CONCLUDING REMARKS AND OUTLOOK FOR THE FUTURE

As mentioned in the Introduction, one of the outstanding computational challenges in the 21st century is the simulation of living cells at molecular detail. However, this is a non-trivial problem. Consider the distance and time scales that are involved. Even for a single cell, one has to describe processes that range over 6-7 orders of magnitude in space and over 12 orders of magnitude in time and involve many millions of macromolecules. Clearly, depending on what is being studied, different levels of molecular description are needed to make the simulations practical and yet retain the appropriate resolution. One of the most elemental dynamical processes is subcellular diffusion. If one cannot adequately represent diffusive motion, it is highly unlikely that more complex biological phenomena will be accurately described. Thus, understanding the nature of macromolecular diffusion in cells is clearly a necessary first step towards the developing the ability to simulate biological cells at molecular detail. In this Perspective, in the context of Brownian and Stokesian dynamics, we explored the relative importance of steric interactions, nonspecific attractive interactions, and hydrodynamic interactions on macromolecular diffusive processes within model cells.

Since 20%-40% of the total volume^31,32 in a cell is occupied by macromolecules, due to steric repulsions with other macromolecules, a slowdown in diffusion relative to that at infinite dilution is anticipated. At first glance, one might guess that this would be the dominant effect. Surprisingly, it only accounts for roughly half of the observed reduction in diffusivity. Next, one might imagine that nonspecific attractive interactions between proteins might dominate. However, a number of factors likely mitigate the importance of this effect. Proteins generally interact across quasi-planar interfaces that have to be spatially and chemically complementary. In practice, for a pair of randomly selected proteins, we estimate that only a tiny fraction of randomly chosen protein pairs (about 10⁻⁵) likely have strongly favorable interactions consistent with such stereochemical interface complementarity.⁹⁷ Thus, we expect that such interactions play a minor role in subcellular dynamics. However, this is not to say that specific interactions between macromolecules are not important, as of course they are. These specific interacting partners might well be enhanced by subcellular localization effects. On the other hand, hydrodynamic interactions are found to be as important as steric interactions in slowing down both the long and short time diffusive processes relative to infinite dilution. They induce cooperative motions between molecules that persist on the order of microseconds and for distances on the order of considerable fraction of a protein’s diameter. HI are also predicted to play an accelerating role in the assembly process of the lipid bilayer and probably in the assembly of large scale molecular aggregates such as tubulin and actin filaments. They might also play important roles in subcellular signaling and in the dynamics of molecular motors, but these effects need to be demonstrated.

Key to the continued success is the development of improved SD sampling methodologies. Since the diffusion matrix is dense, naive implementation of SD scales as O(N³). Some promising, essentially exact methodologies that decrease the computational cost include Krylov subspace methods that scale roughly as O(N²). To further reduce the scaling to O(N), a naive implementation of hydrodynamic screening in SD was developed that simply truncates the long range part of the RPY tensor. This approximation introduces a rather minor error (<15%) in the calculation of the long and short time self-diffusion constants. However, it results in the loss of the dynamic correlations that are likely to be functionally important. One possible way to address this loss of correlation is to employ various cutoff ideas applied to treat electrostatic interactions in molecular dynamics simulations.⁹⁸ Such issues need to be explored in the near future.

What are the likely next steps for molecular simulations of subcellular dynamics? One interesting process that can certainly be addressed is the simulation of macromolecular motion through the E. coli nucleoid, the bacterial region containing chromosomal DNA. Similarly, while simulations suggest that HI play a minor role in protein diffusion along DNA in dilute solution (HI act to retard protein motion along DNA by about 30% relative to the case where they are ignored).¹³ In the nucleoloid, they may significantly modify the motion of proteins (e.g., transcription factors) along DNA. Another area where collective motions could be important is in the mechanism of G-protein signaling across membranes. A third very promising area is to examine the role played by HI in kinesin walking along tubulin in particular and in the mechanism of force generation by molecular motors in general. The key is to identify processes whose general characteristics are sufficiently robust that inaccuracies in the molecular force field and implemented molecular coarse graining have a minor effect on the qualitative behavior. With the advent of GPUs and the needed development of improved sampling approaches, the outlook for simulating ever more complex subcellular process is extremely promising.