Bursting dynamics remarkably improve the performance of neural networks on liquid computing

Abstract

Burst firings are functionally important behaviors displayed by neural circuits, which plays a primary role in reliable transmission of electrical signals for neuronal communication. However, with respect to the computational capability of neural networks, most of relevant studies are based on the spiking dynamics of individual neurons, while burst firing is seldom considered. In this paper, we carry out a comprehensive study to compare the performance of spiking and bursting dynamics on the capability of liquid computing, which is an effective approach for intelligent computation of neural networks. The results show that neural networks with bursting dynamic have much better computational performance than those with spiking dynamics, especially for complex computational tasks. Further analysis demonstrate that the fast firing pattern of bursting dynamics can obviously enhance the efficiency of synaptic integration from pre-neurons both temporally and spatially. This indicates that bursting dynamic can significantly enhance the complexity of network activity, implying its high efficiency in information processing.

Introduction

Bursting activity is widely observed in neural circuits (Selverston and Moulins 1986; Bertram and Sherman 2000; Sohal and Huguenard 2001; Llinás and Steriade 2006) and plays an important role in the communication between neurons (Izhikevich et al. 2003; Lisman 1997; Sherman 2001). In contrast to spike firing, which is a repetitive single firing state, burst firing is two or more spikes followed by a period of quiescence (Izhikevich 2004). Due to the fact that sending a short burst of firings instead of a single firing can overcome synaptic transmission failure, bursting activity can increase the reliability of synaptic transmission (Lisman 1997). Besides, bursting also provides effective mechanisms for selective communication among neurons (Izhikevich et al. 2003), where the inter-spike frequency within the bursts encodes the channel of communication (Izhikevich 2002). It is also found that bursting neurons are easier to achieve synchronization than spiking ones, which means that bursting activities are more important for information transfer in neuronal networks (Shi et al. 2008). Relevant extensive researches about bursting have gained increasing attention in recent years (Kim and Lim 2015b; Meng et al. 2013; Kim and Lim 2015a). However, although functional mechanisms of spiking and bursting dynamics have been broadly investigated, there is rare research focusing on the computational capability of neural networks with bio-realistic neurons firing on these two dynamic patterns.

Spiking neuron model, based on the generation of a single spike, can produce several known types of firing patterns exhibited by real biological neurons. Spiking neural network (so called “third generation” of neural networks) is biologically inspired neural network, where the timing of individual spikes is considered as the means of communication and neural computation instead of analog signals in artificial neural networks, which effectively captures the rich dynamics of real biological networks (Gerstner and Kistler 2002). Thus they are computationally powerful in solving difficult problems in complex. Given that recurrent network can accurately convey and store temporal information, liquid computing is potentially powerful at performing complex computations that are usually conducted in biological organisms (Maass 2007). There are two classic applications of liquid computing which have been widely studied: one is liquid state machines (LSMs) built from spiking neurons and came from computational neuroscience (Maass et al. 2002a); the other is echo state networks (ESNs) built from analog sigmoidal neurons and came from Machine Learning (Jaeger 2001). Instead of online updating all of the synaptic weights in most of the traditional recurrent neural networks (RNN), synaptic connections in the hidden network of liquid computing are usually chosen randomly and fixed during the training process; while only the readout component is trained by using a simple classification/regression technique according to specific tasks (Maass et al. 2002a; Jaeger 2001). In this paper, we focus on liquid computing of LSM based on biologically inspired neuron model. Since proposed by Maass et al in 2002, LSMs have been successfully applied to actual engineering applications, such as controlling a simulated robot arm (Joshi and Maass 2004), modeling an existing robot controller (Burgsteiner 2005) and performing object tracking and motion prediction (Burgsteiner 2005). Additionally, Various ways of constructing reservoir topologies and weight matrices have been developed. For example, in Norton and Ventura (2010), a new method has been develop ed for iteratively refining randomly generated networks, so that the LSM will yield a more effective filter in a fewer epochs than traditional method. Results shown in Schrauwen et al. (2008) have demonstrated that IP rule effectively makes the reservoirs computing more robust. In our previous work (Xue et al. 2013), a novel type of LSM obtained by STDP learning has shown that LSM with STDP learning is able to lead to a better performance than LSM with random reservoir.

In this paper, we make detailed comparisons between spiking and bursting dynamics on the capability of liquid computing. Our results show that neural networks with bursting activity have much better computational performance than those with spike firings. Further analysis of the probability distribution and entropy of network activity demonstrate that the fast firing pattern of bursting dynamics can obviously enhance the efficiency of synaptic integration from pre-neurons both temporally and spatially. The bursting dynamic can significantly enhance the entropy of activity patterns and stochastic resonance (SR) of the entire network, which is beneficial for improving computational capability and information transition efficiency.

Network description

Network architecture

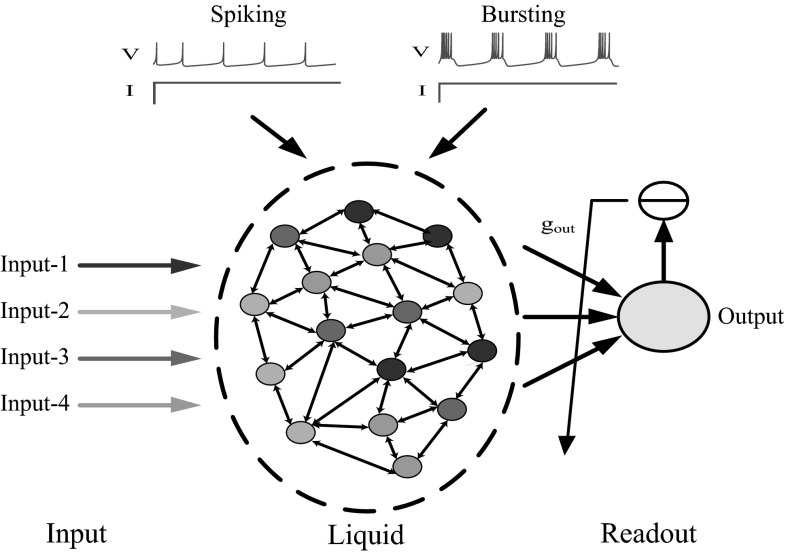
The LSMs is composed of three parts: input component, liquid network (i.e. a randomly connected recurrent neural network), and readout component. In this paper, four different inputs are independently added to four equivalently divided groups in the liquid network, as shown in Fig. 1. Synaptic inputs integrated from the input component are received by the neurons in liquid network and can be expressed in a higher dimensional form called liquid state. For specific tasks (i.e. the polynomial computation of four inputs), liquid network outputs a series of spike trains projecting to the readout component, which acts as a memory-less readout function (Maass et al. 2002a, b). During the computations only readouts are trained by linear regression according to the teaching signal, while connections in the liquid always remain unchanged once the structure is established.Simulations are carried out with the software package CSIM http://www.lsm.tugraz.at/csim/index.html.

Fig. 1.

Schematic diagram of liquid computing. The Input-1, Input-2, Input-3 and Input-4 represent four input components. 400 neurons with spiking or bursting activity in LC are equally connected to four input streams independently. Neurons applied with different inputs are marked with different colors. Arrows in the liquid network represent the directions of synaptic connectivity. The readout neuron is connected to all of the neurons in the liquid with synaptic weights $g_{out}$, which are trained by linear regression for different tasks. (Color figure online)

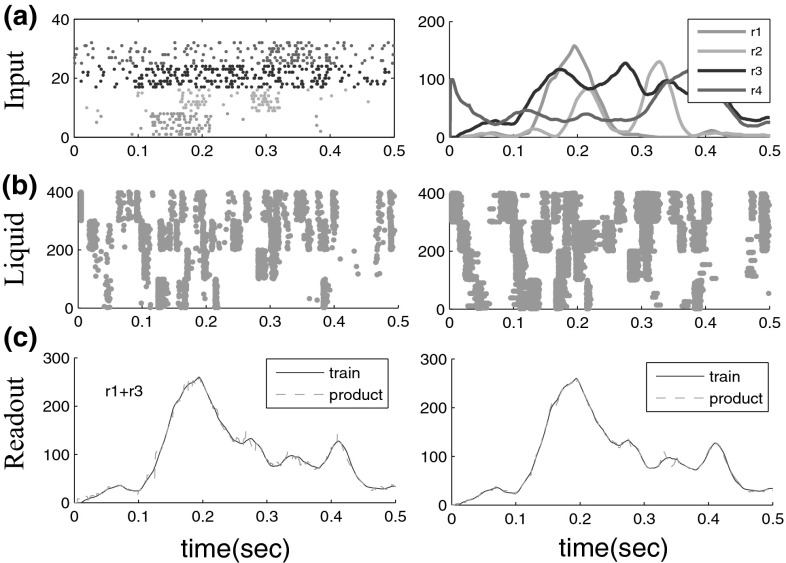
In this paper, the liquid network consists of 400 neurons which are all-to-all bidirectionally connected with synaptic weights randomly distributed in the range of $[0,g_{max}]$. The inputs are four independent signal streams generated by the Poisson process with randomly varying rates $r_i(t),i=1,\dots 4$ , where each input stream consists of eight spike trains (Fig. 2a). The time-varying firing rates $r_i(t)$ of the eight Poisson spike trains were chosen as follows (Maass et al. 2007). The baseline firing rates for streams 1 and 2 are chosen to be 5 Hz, with randomly distributed bursts of 120 Hz for 50 ms. The rates for Poisson processes that generated the spike trains for input stream 3 and 4 are periodically updated, by randomly drawn from the two options 30 and 90 Hz. The curves in Fig. 2a represent the actual firing rates of four input streams. The corresponding responses of liquid neurons with spiking or bursting dynamic and the outputs of readout neuron with respect to the teaching signal $r_1+r_3$ are shown in Fig. reffig:2b, c, respectively. From the results, we can see that the signal of incoming input spike trains could be efficiently transferred into the high-dimensional liquid network, where information can be stored and further amplified by the intrinsic dynamical state of neuronal population, thus resulting in the high precision of computational capability by readouts.

Fig. 2.

a Four independent input streams (left), each consisting of eight spike trains generated by poisson process with randomly varying rates $r_i(t),i=1,\dots 4$; The rates of four input streams are plotted in curves with corresponding colors (right), where all rates are given in the unit of Hz. b The firing activity of 400 neurons in the liquid network with spiking dynamic (left) or bursting dynamic (right). c Corresponding computational performance of the linear readouts (red dashed line) which were trained according to the teaching signal $r_1+r_3$ (blue line). (Color figure online)

Neuron model

In this paper, the two-variable integrate-and-fire (I&F) model of Izhikevich (Izhikevich et al. 2003) is used in the network. It satisfies the following equations:

$$\begin{array}{cc}& \dot{v_i}=0.04v_i^2+5v_i+140-u_i+I+I_i^{syn}\hfill \\ \hfill & \dot{u_i}=a(b{v}_i-u_i)+D{\mathit{\xi }}_i\hfill \end{array}$$ 1

$$\text{if}{v}_i>30\text{mV},\text{then}\left\{\begin{array}{cc}{v}_i\hfill & \leftarrow c\hfill \\ u_i\hfill & \leftarrow u_i+d\hfill \end{array}\right.$$ 2

where $i=1,2,\dots ,N$, $v_i$ represents the membrane potential and $u_i$ is a membrane recovery variable. The variable ${\mathit{\xi }}_i$ is the independent Gaussian noise with zero mean and intensity D that represents the noisy background. The parameters a, b, c, d are dimensionless, various choices of these parameters result in various intrinsic firing patterns (Izhikevich et al. 2003). I stands for the externally applied current, and $I_i^{syn}$ is the total synaptic current through neuron i and is governed by the dynamics of the synaptic variable $s_j$:

$$\begin{array}{cc}\hfill I_i^{syn}=& -{\sum }_{1(j\ne i)}^N{g}_{ji}{s}_j(v_i-v_{syn})\hfill \\ \hfill \dot{s_j}=& \mathit{\alpha }(v_j)(1-s_j)-s_j/\mathit{\tau }\hfill \\ \hfill \mathit{\alpha }(v_j)=& {\mathit{\alpha }}_0/(1+e^{-v_j/v_{shp}})\hfill \end{array}$$ 3

here, the synaptic recovery function $\mathit{\alpha }(v_j)$ can be taken as the Heaviside function. When the presynaptic cell is in the silent state $v_j<0$, $s_j$ can be reduced to $\dot{s_j}=-s_j/\mathit{\tau }$; otherwise, $s_j$ jumps quickly to 1 and acts on the postsynaptic cells. Here the excitatory synaptic reversal potential $v_{syn}$ is set to be 0. Other parameters used in this paper are ${\mathit{\alpha }}_0=3$, $\mathit{\tau }=2$, $V_{shp}=5$, $D=0.1$. In particular, the other parameters are $a=0.02,b=0.2,c=-65,d=6$ for regular spiking neuron and for bursting neuron $a=0.02,b=0.2,c=-50,d=2$ (Izhikevich et al. 2003). The performance of spiking and bursting dynamics on the capability of liquid computing will be discussed in the following section.

Results

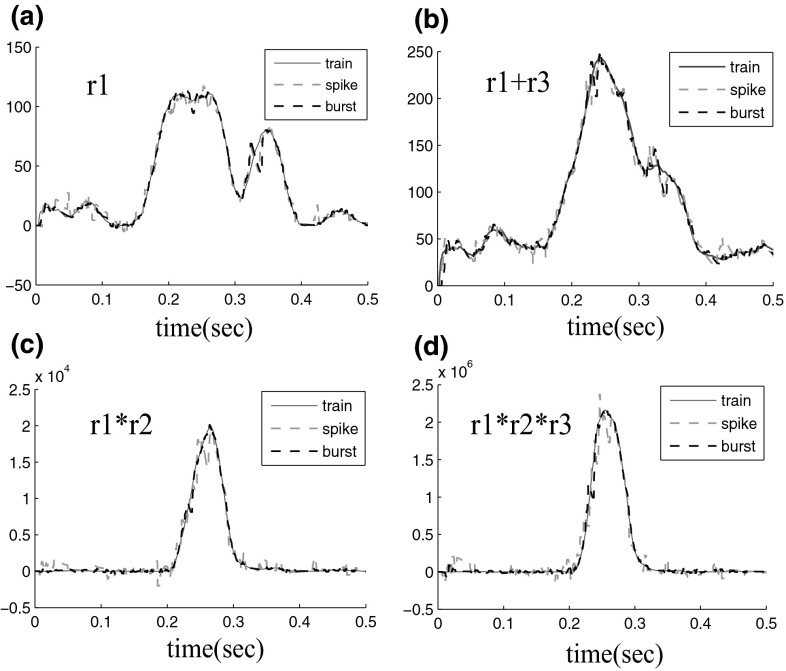
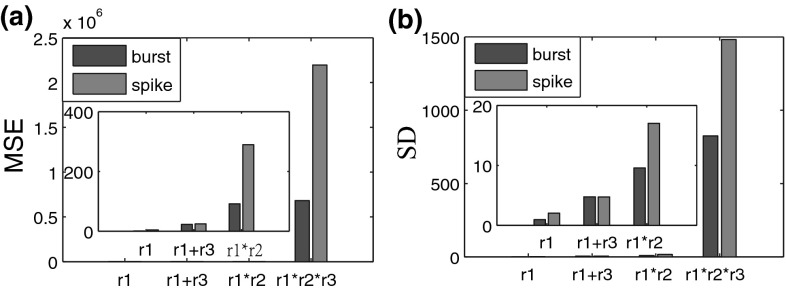
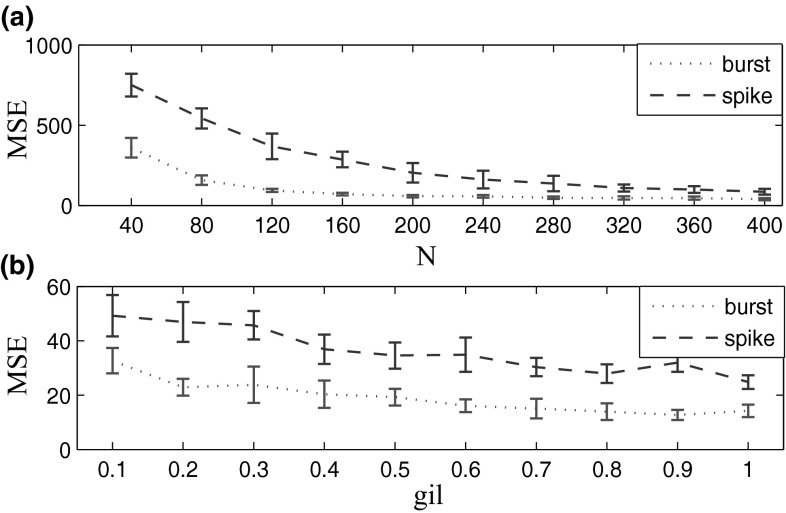
In this section, a list of biologically relevant real-time computational tasks are designed to compare the computational capability of LSMs with spiking or bursting dynamics. In these tasks, target signals are chosen as mathematical functions of the firing rate of the four input streams, i.e. $r_1$, $r_1+r_3$, $r_1\ast r_2$ and $r_1\ast r_2\ast r_3$. The computational results are given in Fig. 3. It shows that readout could be well trained for different computational tasks, even for complex computing with high degree (Fig. 3c, d). Besides, the output curve of LSMs with bursting dynamics (black line) is much smoother with smaller fluctuations than that of LSMs with spiking dynamics (red line), indicating its higher accuracy of output approaching to the target signal. To make it more clear, we use the mean squared error(MSE) and standard deviation (SD) to quantify the general computational capability. Figure 4 shows the MSEs and the SDs for the above four tasks with different degree of complexity. It demonstrates that both MSEs and SDs of the liquid with bursting activity are much smaller than that of liquid with spiking activity, especially when the complexity of computational tasks is increased. This result illustrates that liquid network with bursting activity has better computational capability for real-time computations on complex input streams compared with the spiking case. Further, the influence of network size and synaptic weight from input to liquid network on computational performance are investigated. Results show that computational performance can be improved with the increase of network size and input weights (Fig. 5). The results for each case are the average values from 20 times independent runs. Note that during the whole parameter range, bursting activity always show much better performance than the spiking case, indicating the robust advantage of bursting dynamic on computational capability.

Fig. 3.

Computational performance for different training tasks. Outputs for spike and burst firing are shown as red and blue dashed lines respectively. Without too many large fluctuations as shown in the spiking network, the output for bursting dynamic is much smoother and closer to the target signal. Here, the synaptic weight from input to liquid network is 0.1, the synaptic weight in liquid is 0.001 and the input external current is 3. (Color figure online)

Fig. 4.

Comparison of MSE and SD for the above four tasks. liquid with bursting dynamic has much better performance than the one with spiking dynamic, especially when the complexity of tasks is increased

Fig. 5.

Influence of network size (a) and synaptic weights from input to the liquid (b) on the performance of liquid computing with different firing patterns. The results for each case are the average values from 20 times independent runs. Error bars denote standard error

Dynamic analysis

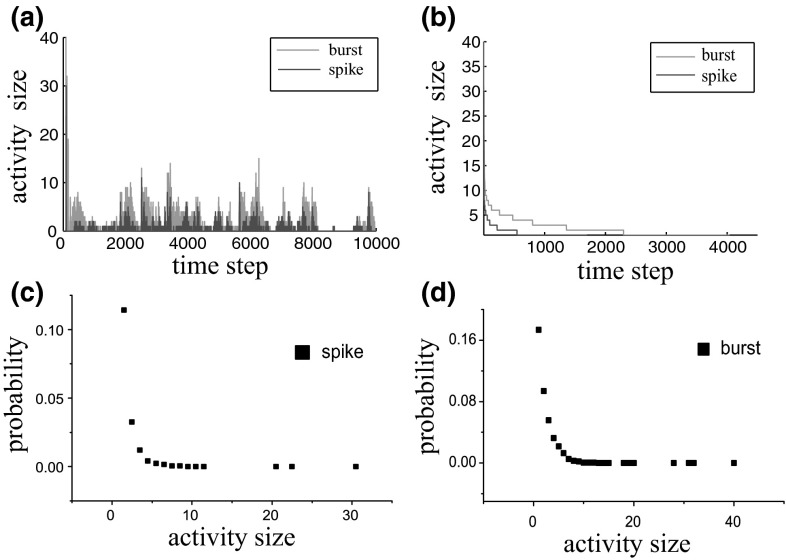
In order to get an insight into the underlying mechanisms of prominent advantage of bursting dynamic, we analyzed the distribution of activity size, which is measured as the number of firing neurons in each time step. Figure 6a compare the activity size of bursting dynamic with the corresponding spiking dynamic. The data are cumulated from 10000 time steps. It can be observed that activity size of burst firing is much larger than that of spike firing. It can also be clearly seen from Fig. 6b after the sorting of activity size. Probability distribution of activity size for two dynamic patterns are shown in Fig. 6c, d. It indicates that the probability of large activity size for bursting dynamic is much larger than that of spiking dynamic, which means that large-scale neuronal firing happens more frequently in the bursting pattern. Indeed, the larger activity size and probability of firings means that more neurons in the liquid are involved in the network activity to better transmit input signal, which is benefit for encoding information and training the readout neuron with high accuracy and leading to efficient computation.

Fig. 6.

Activity size during the whole simulation time steps before sorting (a) and after sorting (b). Probability distribution of activity size for spiking dynamic (c) and bursting dynamic (d). The activity size is defined as the number of firing neurons in each time step

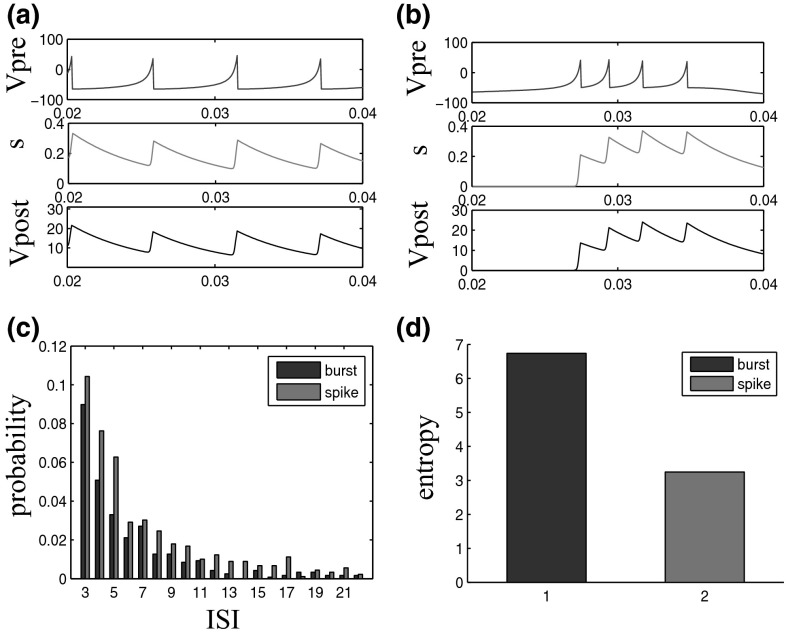
Moreover, the fast firing pattern of bursting activity can obviously enhance the efficiency of synaptic integration from pre-neurons (Fig. 7a, b). Compared with the spiking activity, the post-synaptic potential for bursting neurons can be more easily potentiated with the continuous and fast stimulus from pre-synaptic integrations before the decaying synaptic currents disappear. It means that bursting activity with higher firing frequency from a pre-synaptic neurons can be reliably propagated to the post-synaptic neuron than the spiking activity. That is, bursting dynamic is beneficial for information encoding and propagation. The probability distribution of inter-spike interval (ISI) (i.e. the silent time interval between two neighboring spikes) has been shown in Fig. 7c. It can be clearly seen that the average ISI distribution of bursting dynamic is much smaller than that of spiking dynamic, which results in the more efficient synaptic integration temporally (as shown in Fig. 7a). Besides, the complexity of network activity from these two firing patterns is also compared and measured based on the information entropy (H), which is defined as

$$\begin{array}{c}\hfill H=-\sum _{i=1}^n{p}_i{log}_2{p}_i\end{array}$$ 4

where n is the number of unique binary patterns and $p_i$ is the probability that pattern i occurs (Shew et al. 2011). For calculation convenience, neuronal activities are measured in pattern units consisting of a certain number of neurons. In each time bin, if any neuron of the unit is firing then the event of this unit is active; otherwise it is inactive. Figure 7d shows that network with bursting dynamic has much larger information entropy than that with spiking dynamic. This result further demonstrates that the more efficient synaptic integration for bursting dynamics enhances the diversity of network activity, which benefits for improving the efficiency of information transmission and computational capability.

Fig. 7.

Different degrees of synaptic integration for pre-synaptic neurons with spiking (a) or bursting dynamics (b). The variable s is the fraction of receptors in the open state. c Probability distribution of ISI for two firing patterns. d Comparison of activity entropy for liquid networks with two dynamic activities

The improvement of efficiency in signal processing for networks with bursting dynamic can also be confirmed in the performance on stochastic resonance (SR). SR describes the cooperative effect between a weak signal and noise in a nonlinear system (Benzi et al. 1981), leading to an enhanced response to the periodic force (Wiesenfeld et al. 1995; Kosko and Mitaim 2004; Gammaitoni et al. 1998; Saha and Anand 2003). The neuron model is an excitable system, which can potentially exhibit SR. To evaluate SR, we set the periodic input to be $I_{ex}=Bsin(\mathit{\omega }t)$, with $B=2.5$ and $w=0.03$. The amplitude of the input is small enough to ensure that there is no spiking for all the neurons in the absence of noise. Also, the frequency w is much slower than that of the neurons inherent periodic spiking (Li et al. 2007).

Fourier coefficient Q is used to evaluate the response of out frequency to input frequency. It is defined as (Gammaitoni et al. 1998)

$$\begin{array}{cc}\hfill Q=& \sqrt{Q_{sin}^2+Q_{cos}^2},\hfill \\ \hfill Q_{sin}=& \frac{\mathit{\omega }}{2\mathit{\pi }n}{\int }_0^{\frac{2\mathit{\pi }n}{\mathit{\omega }}}2V_i(t)sin(\mathit{\omega }t)dt,\hfill \\ \hfill Q_{cos}=& \frac{\mathit{\omega }}{2\mathit{\pi }n}{\int }_0^{\frac{2\mathit{\pi }n}{\mathit{\omega }}}2V_i(t)cos(\mathit{\omega }t)dt,\hfill \end{array}$$ 5

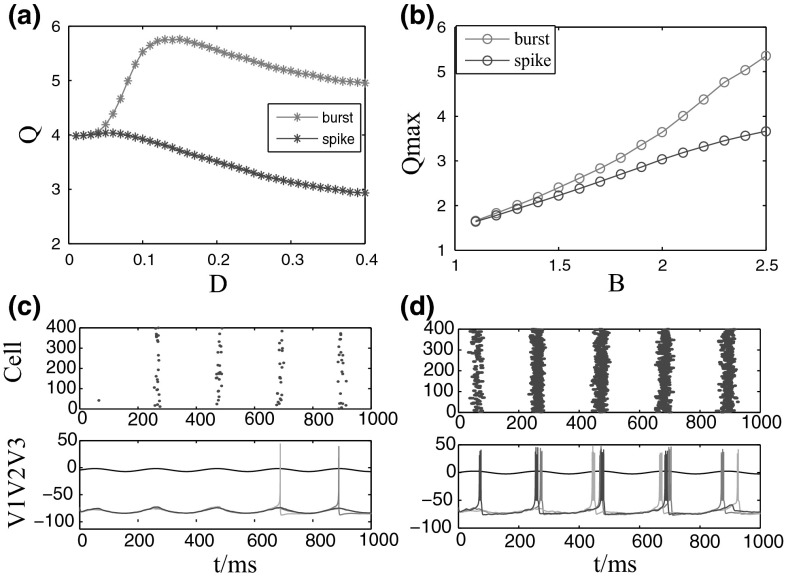
Here, n is the number of periods $\frac{2\mathit{\pi }}{\mathit{\omega }}$ covered by the integration time. $V_i$ is the average membrane potential. The quantity Q measures the component from the Fourier spectrum at the signal frequency $\mathit{\omega }$. The maximum of Q shows the best phase synchronization between input signal and out firing. Again, bursting activity exhibits greater SR than spiking activity (Fig. 8a). And the value of $Q_{max}$ for network with bursting dynamic is also much larger than that of spiking network during the whole range of input intensity (Fig. 8b).The result was obtained by 10 independent trials. Figure 8c, d show that with appropriate noise intensity, bursting network can achieve better phase synchronization between input signal and out firing than spiking network. Thus, bursting activity plays an important role in improving network sensitivity and benefits for signal propagation.

Fig. 8.

Stochastic resonance of liquid network with different dynamic activities. a The performance index Q versus noise intensity D. b The maximum value of Q ($Q_{max}$) versus the amplitude of input signal B. The result was obtained by 10 independent trials. c, d Performance of networks with spiking (D = 0.05), or bursting dynamics (D = 0.15) on SR with intermediate noise intensity. The top figures in (c) and (d) show the spike raster of the 400 neurons in the network. V1, V2, and V3 in bottom represent the membrane potentials of three different neurons. The black line is the input signal

Conclusions

In this paper, detailed comparisons between spiking and bursting dynamics on the capability of liquid computing have been investigated. Our results show that neural networks with bursting activity has much better computational performance than those with spike firings. Both probability and size of bursting activity are much larger than that of spiking activity, meaning that the state of liquid with bursting dynamic can contain much more input information, which is benefit for training readout neuron with high accuracy. Further analysis of the probability distribution and entropy of network activity demonstrate that the fast firing pattern of bursting dynamics can obviously enhance the efficiency of synaptic integration from pre-neurons both temporally and spatially. The bursting dynamic can significantly enhance the entropy of activity patterns and stochastic resonance (SR) of the entire network, implying its high efficiency in information processing. Therefore, It is believed that bursting activity is much efficient in performing signal processing and computational tasks.

The simulation results of this paper have demonstrated that neural networks with bursting dynamic have a better computational performance for polynomial task. Another topic worthy of future studying is the investigation on how the network performs on tasks that require memory as discussed in Dambre et al. (1995).