Cation Interactions and Membrane Potential Induce Conformational Changes in NaPi-IIb

Abstract

Voltage-dependence of Na⁺-coupled phosphate cotransporters of the SLC34 family arises from displacement of charges intrinsic to the protein and the binding/release of one Na⁺ ion in response to changes in the transmembrane electric field. Candidate coordination residues for the cation at the Na1 site were previously predicted by structural modeling using the x-ray structure of dicarboxylate transporter VcINDY as template and confirmed by functional studies. Mutations at Na1 resulted in altered steady-state and presteady-state characteristics that should be mirrored in the conformational changes induced by membrane potential changes. To test this hypothesis by functional analysis, double mutants of the flounder SLC34A2 protein were constructed that contain one of the Na1-site perturbing mutations together with a substituted cysteine for fluorophore labeling, as expressed in Xenopus oocytes. The locations of the mutations were mapped onto a homology model of the flounder protein. The effects of the mutagenesis were characterized by steady-state, presteady-state, and fluorometric assays. Changes in fluorescence intensity (ΔF) in response to membrane potential steps were resolved at three previously identified positions. These fluorescence data corroborated the altered presteady-state kinetics upon perturbation of Na1, and furthermore indicated concomitant changes in the microenvironment of the respective fluorophores, as evidenced by changes in the voltage dependence and time course of ΔF. Moreover, iodide quenching experiments indicated that the aqueous nature of the fluorophore microenvironment depended on the membrane potential. These findings provide compelling evidence that membrane potential and cation interactions induce significant large-scale structural rearrangements of the protein.

Introduction

Two electrogenic members of the SLC34 family of sodium-coupled phosphate cotransporters (SLC34A1 (NaPi-IIa) and SLC34A2 (NaPi-IIb)) catalyze uphill transport of divalent inorganic phosphate (P_i) in mammalian epithelia. Cotransport is coupled to the electrochemical gradient for Na⁺ ions and the transmembrane potential to give a Na⁺:P_i stoichiometry of 3:1. This substrate movement is accompanied by the translocation of one net positive charge per transport cycle (1). The kinetics of cotransport can be modeled as a sequence of partial reactions, the rate constants of which are determined by substrate activity in the external and internal media and the membrane potential. Two partial reactions were identified that determine the voltage-dependent kinetics of the complete (forward, or inward) transport cycle: the first is the inward to outward reorientation of the empty carrier that follows cytosolic substrate release; the second is the binding of the first of two Na⁺ ions to the outward-facing empty carrier preceding P_i binding (0↔1 and 1↔2; Fig. 1 A). The partial reaction involving inward binding/release of the first Na⁺ ion (6↔0; Fig. 1 A) is also thought to be electrogenic, although it has not yet been fully characterized.

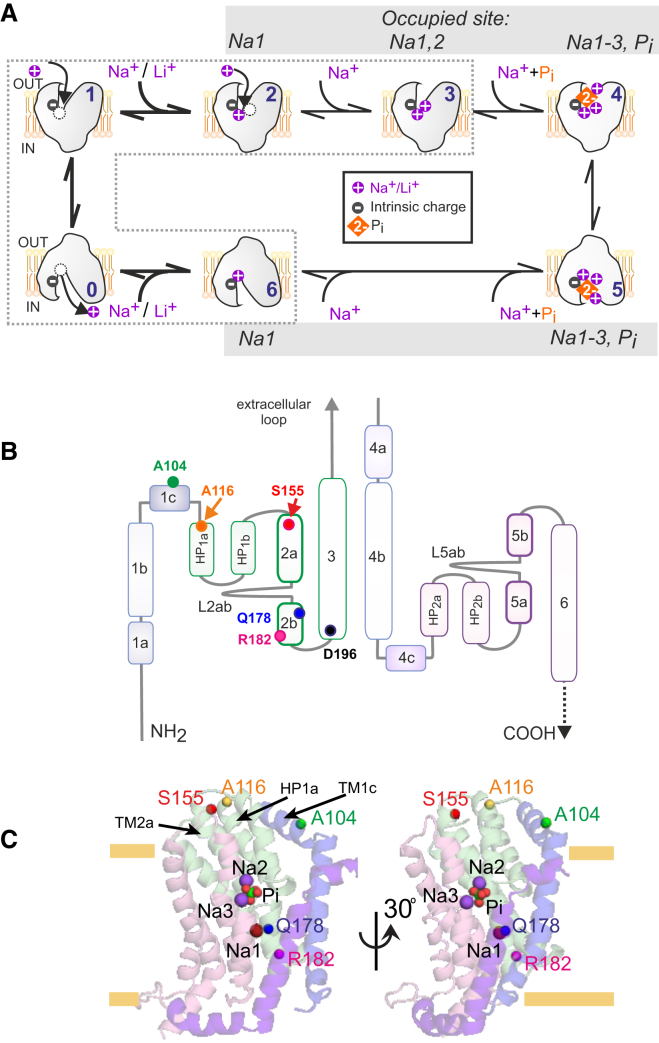
Figure 1.

Transport cycle and structural features of flNaPi-IIb. (A) The transport cycle comprises a sequence of partial reactions between conformational states. Three electrogenic partial reactions (bold arrows: 0↔1, 1↔2, and 0↔6) involve charge displacement and contribute to the electrogenic transport cycle. All other partial reactions are assumed to be electroneutral. For transporters in state 1, a single Na⁺ or Li⁺ ion can access the Na1 site (see C) from the external medium resulting in an intermediate conformation represented by state 2. A second Na⁺ ion (but not Li⁺) can then bind to establish state 3 in the absence of external P_i. (Dashed area) State transitions relevant to this study, i.e., in the absence of P_i. (B) Transmembrane topology of flNaPi-IIb (SLC34A2) based on the structural model of human NaPi-IIa. TM1 through TM3 belong to the first unit in the inverted-topology repeat, while TM4 through TM6 belong to the second repeat unit. Approximate positions for cysteine labeling (104, 116, and 155) and Na1 modifications (178, 182) are indicated. HP: hairpin motif, other α-helices numbered as shown. D196 is critical for electrogenicity. (C) Structural model of flNaPi-IIb based on the structure of VcINDY in an outward conformation in cartoon representation colored according to (B), highlighting the predicted positions of sodium ions (Na1, 2, and 3; purple spheres) and phosphate (P_i, red and green spheres). The Cα atoms of residues A104, A116, S155, Q178, and R182 are shown in green, yellow, red, blue, and magenta spheres, respectively. The approximate position of the membrane boundary is indicated by yellow bars. To see this figure in color, go online.

Experimental evidence for the role of these electrogenic partial reactions in transducing membrane potential was obtained from analysis of presteady-state kinetics. Specifically, exponentially decaying current relaxations can be evoked by rapid changes in membrane potential, in the presence and absence of external cations (see Forster et al. (1)). In general, such so-called presteady-state relaxations may arise from a concerted rearrangement of many charges distributed throughout the protein relative to the low-dielectric barrier provided by the membrane. However, in the case of NaPi-II transporters, there is compelling evidence that a single charged aspartic acid (Asp-196 in the flounder isoform), located close to the Na1 site (Fig. 1 B), is a key determinant of this electrogenicity (2). Moreover, from voltage-clamp fluorometric assays (VCF), evidence has accumulated that the partial reactions involving charge displacements are also accompanied by dynamic molecular rearrangements (3, 4, 5, 6, 7, 8). Nevertheless, the evidence so far remains circumstantial. To assess the role of conformational changes during the transport cycle in more detail, cysteine residues substituted at selected positions are here labeled with fluorophores that report changes in their local environment (e.g., from Ghezzi et al. (5), Patti et al. (6), Virkki et al. (7, 8), and Cha et al. (9)). Notably, we recently showed that the fluorescence intensity changes are unique to each labeling site (3). Moreover, these experimental findings could be matched well with simulations based on a five-state kinetic model for cation interactions, thereby validating our mechanistic scheme (3).

Whereas the kinetics of cotransport have been well described, the absence of a crystal structure for SLC34 proteins has seriously hindered the identification of the structural elements associated with specific steps in the transport cycle, as well as the conformational changes proposed to accompany substrate-binding, translocation, and release. To this end, we developed a three-dimensional structural model for the human NaPi-IIa (hNaPi-IIa) (10), based on homology with the bacterial dicarboxylate cotransporter, VcINDY, whose structure has been reported in Mancusso et al. (11) (Fig. 1, B and C). Using this structural model, we identified a region to which the first sodium ion would bind (designated the Na1 site), which was not apparent from a direct comparison with the VcINDY crystal structure (10). We validated our predictions by mutating side chains at the proposed site, and by examining the steady-state and presteady-state electrogenic kinetics of those single point mutants, which facilitated further structural model refinement (12). The salient kinetic effects of mutagenesis at the sites in the proposed Na1 region were, first, to induce a hyperpolarizing shift in the voltage dependency of the P_i-induced steady-state current; and second, to alter the response to cations. We expect that the kinetic perturbations induced upon mutation also result in altered conformational dynamics, and in turn, these should be experimentally observable as concomitant changes in the fluorophore response to membrane potential.

To test this hypothesis, we now investigate the functional consequences of two mutations predicted to contribute to, or be close to, Na1 made at equivalent positions in the flounder NaPi-IIb (flNaPi-IIb) isoform. This isoform was used because of its high functional expression, and to allow comparison with our previous studies using VCF with fluorophores covalently linked to substituted cysteines at three different positions (104, 116, and 155) (3) (Fig. 1, B and C). Voltage-induced conformational changes were quantitated in terms of presteady-state charge movements and changes in fluorescence intensity of fluorophores linked to the same three sites. According to a homology model of flNaPi-IIb built in this study, these reporter sites are located at the periphery of the protein, external to the transmembrane field (Fig. 1 C); nevertheless, as our previous VCF measurements revealed, their microenvironments change in response to changes in membrane potential and cation interactions. Therefore, a correlation between changes in fluorescence intensity and presteady-state charge movement would provide evidence that the molecular rearrangements proposed to occur within the transmembrane field also extend to the periphery of the protein and accompany critical events in the transport cycle.

Materials and Methods

Alignment of flNaPiIIb and VcINDY

An alignment of the flNaPi-II and VcINDY sequences was obtained by merging the published alignment of hNaPi-IIa with VcINDY (12) together with an alignment between hNaPi-IIa and flNaPi-IIb that was obtained using AlignMe in PS mode (13) (Fig. S1 in the Supporting Material). The sequence identity between flNaPi-IIb and VcINDY was ∼13% in repeat 1 and ∼8% in repeat 2.

Structural models of flNaPi-IIb in outward- and inward-open conformations

A model of flNaPi-IIb in an outward-facing conformation was generated using the structure of VcINDY (Protein Databank (14), PDB: 4F35) as a template. No structure is available for the opposite conformation, although a recently reported repeat-swapped model of VcINDY (15) (Protein Model Database (16), PMDB: PM0080187) represents the opposite state; this repeat-swapped model was therefore used as the template for generating an inward-facing model of flNaPi-IIb.

Both inward- and outward-facing models of flNaPi-IIb were generated using Modeler 9v6 (17), with 2000 iterations of modeling. The final models were chosen from 10 models with the best MolPDF and ProQM scores (18). In addition, both final models were analyzed using Procheck (19). In the case of the outward-facing model, only one residue was found in a disallowed region of the Ramachandran plot (Asp-333), and in the case of the inward-facing model, only two residues were located in that region (Ala-450 and Val-119). All these residues were located in loop regions of the models. The ProQM scores of the final outward- and inward-open models were 0.566 and 0.573, respectively, similar to the scores of the hNaPi-IIa model (0.572 (12)) and only marginally lower than the score of the VcINDY template (0.643). Based on the aforementioned sequence identities, the expected accuracy of the outward-facing model is between 1.5 and 3.5 Å in the Cα positions (20). The outward-facing model is available at the Protein Model Database, PMDB: PM0080462. The accuracy of the inward-facing model is likely to be significantly lower, because its template is itself a model based on swapping the conformations of the repeats (15). This inward-facing model is provided in the Supporting Material.

Solutions and reagents

Oocytes were incubated in Modified Barth’s solution that contained: 88 mM NaCl, 1 mM KCl, 0.41 mM CaCl₂, 0.82 mM MgSO₄, 2.5 mM NaHCO₃, 2 mM Ca(NO₃)₂, 7.5 mM HEPES, adjusted to pH 7.5 with TRIS and supplemented with antibiotics doxycyclin and gentamicin (5 mg/L). The compositions of the superfusing solution were as follows: 100Na solution: 100 mM NaCl, 2 mM KCl, 1.8 mM CaCl₂, 1 mM MgCl₂, 10 mM HEPES, pH 7.4 adjusted with TRIS; 0Na: same as for 100Na solution with equimolar replacement of NaCl with choline Cl. For intermediate Na⁺ concentrations, 100 Na and 0Na were appropriately mixed to maintain the same osmolarity. Inorganic phosphate (P_i) was added to the superfusate from 1 M K₂HPO₄ and KH₂PO₄ stocks that were mixed to give pH 7.4. For the quenching experiments, NaI as powder was added to an equimolar mix of 100 Na and 0Na to give 50 mM I⁻ with 100 mM Na⁺, and KI as powder was added to 100 Ch to give 50 mM I⁻ in zero Na⁺. For some VCF assays, NaMES, LiMES, or NMDG-MES were used instead of NaCl or CholineCl to reduce inward flux through endogenous chloride channels for V > 0. All standard reagents were obtained from either Sigma-Aldrich (St. Louis, MO) or Fluka (Buchs, Switzerland). 2-(trimethylammonium) ethylmethanethiosulfonate bromide and 2-((5(6)-tetramethylrhodamine)carboxylamino) ethyl methanethiosulfonate (MTS-TAMRA) were obtained from Biotium (Hayward, CA).

Site-directed mutagenesis and cRNA preparation

cDNA encoding wild-type (WT) flounder NaPi-IIb (GenBank/EMBL/DDBJ accession No. AAB16821) was subcloned into a vector containing the 5′ and 3′ UTRs from Xenopus β-globin to improve its expression in oocytes. Novel cysteines were introduced using the QuikChange site-directed mutagenesis kit (Agilent Technologies, Santa Clara, CA). The sequence was verified by sequencing (Microsynth, Balgach, Switzerland), linearized with XbaI and cRNA was synthesized in the presence of Cap analog using the T3 Message Machine kit (Ambion, Naugatuck, CT).

Expression in Xenopus laevis oocytes

Animal procedures and preparation of oocytes followed standard procedures (e.g., Patti et al. (6) and Andrini et al. (21)) and were in accordance with the Swiss Cantonal and Federal legislation relating to animal experimentation. Stage V–VI oocytes were selected, maintained in modified Barth’s solution at 16°C, and injected with 50 nL of cRNA (200 ng/μL); experiments were performed 4–5 days after injection.

Two-electrode voltage-clamp

Standard two-electrode voltage-clamp hardware was used (GeneClamp, Model 500; Molecular Devices, Eugene, OR; or TEC-10X; NPI, Tamm, Germany). Voltage-clamp control, data acquisition, and perfusion valve switching was under software control using pClamp Ver. 8-10 software (Molecular Devices).

Voltage-clamp fluorometry

The voltage-clamp fluorometry apparatus comprised a two-electrode voltage-clamp (TEC-10CX; NPI, Tamm, Germany) and a laboratory-built fluorescence microscope as previously described in Virkki et al. (7), with the following changes: 1) we used an XF32 cube set (535DF35 excitation filter, 570DRLP dichroic mirror and 596DF35 emission filter; Omega Optical, Brattleboro, VT); and 2) a green LED (LXHL-PM02; Luxeon, Lumileds, San Jose, CA) driven by a stabilized current source (typically 300 mA) was used for excitation. Oocytes were labeled in the dark at 20°C for 4–5 min by incubating them in 100 μL of 100 Na solution to which was added 0.4 μL of MTS-TAMRA from a 100-mM frozen stock (in DMSO) to give a final concentration of 0.4 mM. We confirmed that the electrogenic behavior of the oocytes after labeling was not significantly affected by the labeling procedure.

Voltage-step protocols and presteady-state analysis

The protocol for recording presteady-state current and simultaneous fluorescence used voltage steps from V_h = −60 mV to voltages in the range −200 mV to +180 mV. Signals were averaged 4–16-fold and filtered at 500 Hz (8-pole Bessel, LPF8; Warner Instruments, Hamden, CT). Presteady-state current relaxations were measured at voltages in the range −180 mV ≤ V ≤ 100 mV, where we could exclude contamination from endogenous Cl⁻ currents. Current relaxations were fitted with a double exponential function. The fastest component represents the linear capacitive charging of the oocyte membrane (typically 0.4 ms, depending on the oocyte) and its time constant showed little voltage dependence. The slower component (time constant, τ >2 ms) was only detected in oocytes expressing NaPi-IIb constructs. To estimate the charge moved (Q) for a step from the holding potential to the test potential, the fitted exponential corresponding to the slower component was numerically integrated from ∼2 ms after the step onset, at which time we estimated the membrane to be >90% charged. The Q-V data were fitted with a Boltzmann function of the form given by Eq. 1:

$$Q=Q_{\text{hyp}}+Q_{\max }/\left(1+\text{exp}\left(z^{Q}e\left(V_{0.5}^Q-V\right)/kT\right)\right),$$ (1)

where V_0.5^Q is the voltage at which the charge is distributed equally between two hypothetical states; z^Q is the apparent valency of an equivalent charge that moves through the whole of the membrane field; Q_max is the total mobile charge available; Q_hyp is the charge of the hyperpolarizing limit and is a function of V_h; and e, k, and T have their usual meanings. Each fluorescence recording was baseline-corrected relative to the value at V_h = −60 mV. After correction for any systematic loss of F as described previously in Virkki et al. (7), data from single oocytes were normalized to the predicted maximum change in fluorescence (ΔF_max) obtained in the solution that gave the highest ΔF and then pooled. ΔF_max was obtained as fits to the ΔF-V data using the Boltzmann equation (Eq. 1, where Q was substituted with ΔF and the corresponding fit parameters are ΔF_max, z^F, and V_0.5^F). The time course of ΔF was described by fitting a single growing exponential function.

Data analysis

Curve fitting using Eq. 1 was performed using GraphPad Prism Ver. 3 for Windows, (GraphPad Software, San Diego, CA; www.graphpad.com). Data points are shown as mean × SE. Error bars are not displayed if smaller than the graphical symbol.

Results

A structural model of flNaPi-IIb in an outward-facing conformation

As mentioned above, a homology model of hNaPi-IIa recently provided a useful structural context for substrate and cation-binding studies (10, 12). However, as also noted, the human isoform has lower functional expression than flNaPi-IIb, making it a poor choice for VCF measurements. Because the human and flounder isoforms share ∼55% identical residues, we considered the possibility that predictions obtained from the available model of human NaPi-IIa might not be directly relevant for designing experiments on the flounder protein. Therefore, to facilitate further studies we constructed a homology model of flNaPi-IIb using a structure of VcINDY as a template (Fig. 1 C; see Materials and Methods). Note that, due to differences in the orientation of the termini, the homology model of flNaPi-II corresponds to an outward-facing conformation, even though it is based on the known structure of VcINDY, which is inward-facing (Fig. 1 C (10)).

As was already clear from their primary sequences, the residues contributing to the predicted P_i- and Na⁺-binding sites are identical in the two isoforms. In the structural model of flNaPi-IIb, despite the other differences in the sequences, these binding residues also adopt similar orientations to those in the hNaPi-IIa model (not shown). The model therefore predicts that residues previously shown to be involved in Na1 binding for hNaPi-IIa will exhibit similar phenotypes upon mutation in flNaPi-IIb.

Functional characterization of Na1 mutants in flNaPi-IIb

Published characterization of the steady-state and presteady-state kinetics of two mutants based on hNaPi-IIa (Q206N and R210A) revealed significant deviations from the WT kinetics (12). To test whether the flNaPi-IIb isoform exhibits the same phenotype, in this study we engineered the corresponding mutants (Q178N, R182A) in flNaPi-IIb. As for the hNaPi-IIa mutants, oocytes injected with cRNA coding for the respective mutants gave robust electrogenic responses to externally applied P_i when voltage-clamped to –50 mV, with P_i-induced currents (I_Pi) usually exceeding –100 nA at –50 mV (in 100Na solution) (data not shown). We confirmed that the mutagenesis had not significantly altered the apparent affinity for P_i (K_0.5^Pi) under standard conditions with 100 mM Na⁺ (100Na solution). Specifically, dose dependence assays yielded values for K_0.5^Pi at –100 mV of 0.03 ± 0.01 mM (Q178N), 0.02 ± 0.01 mM (R182A), and 0.05 ± 0.01 mM (WT) (Fig. S2 A). Despite the similarity of the K_0.5^Pi values, comparison of I-V data in response to 1 mM P_i for the WT flNaPi-IIb and mutants established that the mutagenesis had markedly altered the electrogenic behavior of the mutants, as also observed previously for the equivalent modifications of hNaPi-IIa. That is, whereas the typical WT flNaPi-IIb response to saturating P_i (1 mM P_i) (100Na) showed rate-limiting behavior at the hyperpolarizing extreme (Fig. 2), the normalized I-V data for Q178N and R182A were curvilinear over the entire voltage range explored. Moreover, at 0 mV, the WT I_Pi was ∼50% of that at –100 mV, whereas for both mutants the relative current was only ∼20%.

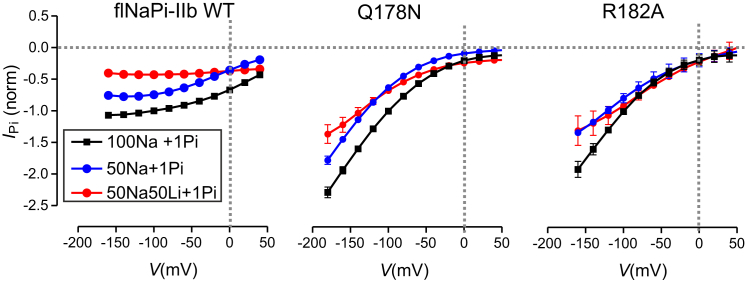
Figure 2.

Steady-state current-voltage relationships for three external superfusing conditions. Comparison of electrogenic response to 1 mM P_i of the WT flNaPi-IIb and mutants Q178N and R182A when superfusing with: 100 mM Na⁺ (100Na); 50 mM Na⁺ (50Na); and 50 mM Na⁺ with 50 mM Li⁺ (50Na50Li). Data were normalized to the response to 1 mM P_i at –100 mV in 100 Na solution. Each data point is mean ± SE for n > 4 cells. To see this figure in color, go online.

As modifications of the Na1 site were expected to alter the response to Li⁺, we also compared the effect of replacing 50% of the external Na⁺ (to 50 mM) with either choline or Li⁺. For WT hNaPi-IIa, we previously reported that this did not alter the normalized response significantly, which suggested that for the human NaPi-IIa, Li⁺ does not substitute significantly for Na⁺ as a driving cation (12, 21). In contrast, for the hNaPi-IIa Na1 mutants (Q206N and R210A), Li⁺ appeared to at least partially substitute for Na⁺ (12, 21). For WT flNaPi-IIb, we found that Li⁺ replacement reduced I_Pi further than when only Na⁺ was removed, whereas, for the corresponding Na1 mutants, there was no evidence of Li⁺ substituting significantly for Na⁺ (Fig. S2 B).

We next investigated the steady-state behavior of double mutants that, in addition to the Na1-site modifications, incorporated a Cys-substitution for fluorophore labeling at position 104, 116, or 155 (Fig. 1, B and C). Constructs containing either Cys-116 or Cys-155 gave robust I_Pi comparable to that of the Na1-site mutants alone (Fig. S3, central panel, and Fig. 2), and the I-V data of the Cys-116 and Cys-155 constructs lacking the Na1-site mutations (Fig. S3, upper panel) were similar to that of WT (Fig. 2, left).

Substitution of Cys at position 104 had more mixed effects: for example, even without the Na1-site mutation, the I-V data for A104C showed a hyperpolarizing shift compared with the WT (Fig. S3, upper panel). Oocytes expressing mutant A104C-Q178N yielded very small I_Pi (typically –20 to –30 nA at –100 mV, data not shown) and this construct was therefore not studied further. For mutant A104C-R182A, the relative I_Pi was approximately fivefold smaller than that of the WT at 0 mV and showed a larger hyperpolarizing shift than A104C, relative to the WT (Fig. S3, lower left).

Importantly, for all double mutants the marked effect on the I-V data seen for Q178N and R182A in response to 1 mM P_i (100Na) was recapitulated, despite the aforementioned effect of the Cys substitutions alone (Fig. S3, center and lower panels). Moreover, after 50% of the external Na⁺ was replaced by choline or Li⁺, the I-V data for the double mutants (Fig. S3, center and lower panels) showed the same altered voltage dependence as Q178N and R182A alone, compared with proteins in which the Na1 site was unmodified (Fig. 2). In particular, A104C-R182A displayed the general phenotype of R182A, and also when Na⁺ was replaced with choline or Li⁺, which established that the Ala→Cys substitution at position 104 was not the major determinant of the altered kinetics (Fig. S3, lower panel).

These steady-state data showed that the two Na1 substitutions led to qualitatively similar cotransport kinetics, and that these properties were insensitive to the presence of the Cys substitutions. However, it was not clear from these data whether the mutagenesis altered the empty carrier kinetics, the Na⁺ interactions, or both, and in particular if removal of charge in the case of the R18A mutant had a specific effect on the kinetics. To gain insight into the underlying changes in their kinetics, we analyzed the charge displaced across the membrane, as reflected by presteady-state relaxations in the absence of P_i, both in the presence and absence of external Na⁺ (100Na, 0Na solutions, respectively) to distinguish between partial reactions that are associated with the empty carrier alone (0Na) and those that additionally involve external cation interactions (100Na). First, we analyzed the Na1-site mutations alone, i.e., in the absence of the Cys substitutions. Representative presteady-state relaxations for the WT, Q178N, and R182A revealed that, for the same hyperpolarizing voltage step, relatively more charge was induced for the mutants compared with the WT (Fig. 3 A) and this difference was observed under both superfusion conditions. The displaced charge (Q) was quantitated as a function of the applied membrane potential (V) by integrating this relaxation attributable to the expressed protein, and the Q-V data were then fit with Eq. 1 (see Materials and Methods). To aid comparison, we normalized the data to the estimated total charge displaced (Q_max, Eq. 1). The superimposed Q-V data show that for Q178N and R182A the fitted curves were shifted in the hyperpolarizing direction relative to the WT by ∼80 mV at the midpoint (Fig. 3 B). Moreover, the maximum slope of the fitted curves, which is a measure of the effective valence (z, in Eq. 1), as reported by a single Boltzmann function at the midpoint of the normalized charge distribution, was reduced for R182A (0.44 ± 0.02) compared with the WT (0.65 ± 0.07). In contrast, for Q178N, the slope factor (0.56 ± 0.02) was closer to that of the WT. In the absence of external Na⁺ (0Na), the Q-V data for Q178N and R182A showed little (Q178N) or no (R182A) evidence of saturation at strong hyperpolarizations compared with the WT (Fig. 3 B, right). Indeed, for R182A, it was not possible to obtain a satisfactory fit using Eq. 1 without incurring a large uncertainty in the fit parameters. In contrast, for Q178N the Q-V data for superfusion with 0Na were satisfactorily fitted, allowing us to determine that the total charge displaced, relative to the estimate in 100Na, was similar to that of the WT (∼60%). This result confirmed our expectations that the neutral Q→N substitution at position 178 should not cause a change in the total displaceable intrinsic charge associated with the empty carrier.

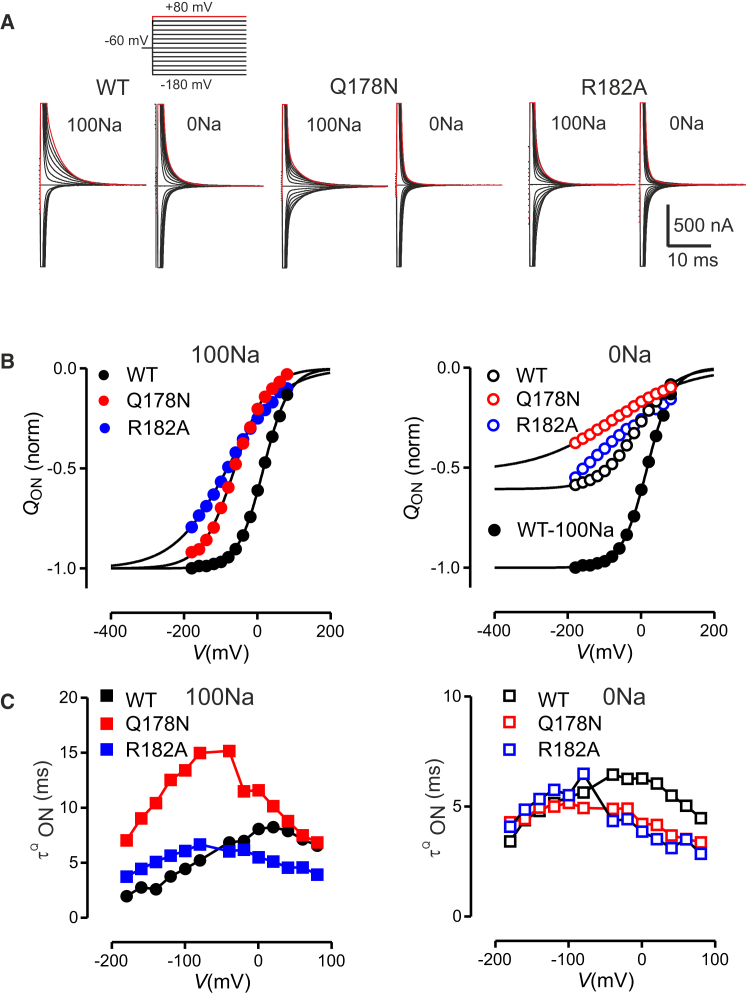
Figure 3.

Comparison of presteady-state properties of Na1 mutants. (A) Representative examples of membrane currents recorded from WT, Q178N, and R182A in response to voltage steps from –60 mV to test potentials in the range –180 to +80 mV (red traces) for two external superfusion conditions, 100 mM Na⁺ (100Na) and 0 mM Na⁺ (0Na). Traces were adjusted to remove the steady-state baseline current arising largely from endogenous currents. (B) Comparison of normalized charge-voltage (Q-V) data for ON steps from –60 mV holding potential for cells shown in (A) when superfusing in 100Na (left) and 0Na (right). To aid comparison, the Q-V data for each cell were fit with a single Boltzmann function (Eq. 1, continuous curves) superimposed at the depolarizing limit and normalized to the predicted Q_max in 100Na. (C) Comparison of main relaxation time constant obtained from exponential fitting the data in A). Note the different ordinate axis scales. Data points joined for clarity only. To see this figure in color, go online.

Next, we compared the effect of sodium on the presteady-state kinetics by analyzing the voltage dependence of the relaxation time constants for the flNaPi-IIb Na1 mutants with that of the WT, superfused with either 0Na or 100Na (Fig. 3 C). For both mutants, and under both conditions, the peak of the τ^Q-V data was shifted toward negative potentials, concomitant with the shift of V_0.5 observed for the Q-V data (Fig. 3 B). Moreover, the peak relaxation time constant for Q178N was significantly slower than for the WT and R182A, but only in the presence of external Na⁺. This finding strongly supported the role of position 178 in Na⁺ ion coordination at Na1, as previously reported for hNaPi-IIa (12). We note that in the absence of external Na⁺, the charge relaxations could not be easily resolved because the signal resolution was reduced, leading to greater uncertainty in the fits. Nevertheless, the shape of the τ^Q-V data for 0 Na superfusion was consistent with having a hyperpolarizing shift compared with the WT.

In summary, both Na1 mutations changed the voltage-dependent distribution of states associated with the empty carrier equilibrium (between states 0 and 1, Fig. 1 A), i.e., in the absence of external Na⁺ ions. These mutations also influenced the presteady-state relaxation kinetics when external Na⁺ ions were present. Notably, oocytes expressing Q178N showed a significant slowing of the relaxation time constant in 100Na that was not seen for R182A. For the double mutants containing Cys substitutions, these features were recapitulated in the corresponding Q-V and τ^Q-V data: namely, when either Na1 mutation was combined with the Cys-104, Cys-116, or Cys-155 substitution, the Q-V data showed a similar hyperpolarizing shift (data not shown) and, like the single Q178N mutant, the peak relaxation time constant in the presence of 100 mM Na⁺ was significantly slower for A116C-Q178N and S155C-Q178N than for the WT or the constructs containing R182A (Fig. S4).

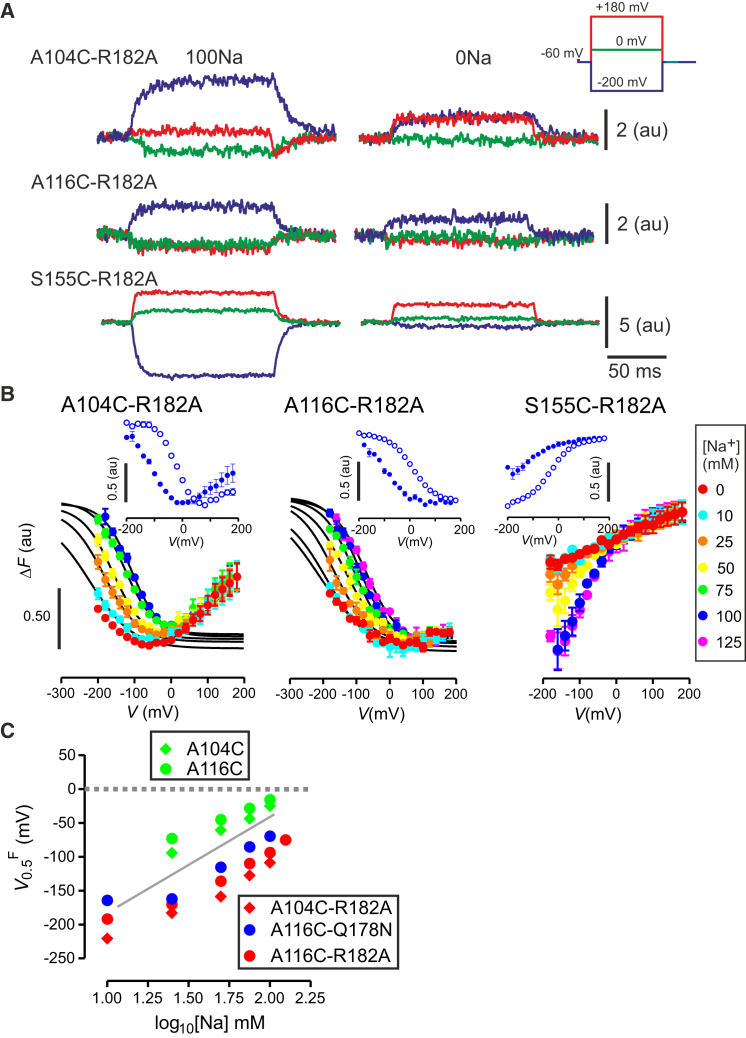
The relationship between V_0.5^Q and [Na⁺] can provide a more detailed understanding of altered cation interactions and therefore, to test whether any other features of the cation interaction were altered by the Cys substitutions, we next analyzed presteady-state relaxations acquired over a range of [Na⁺] from 10 to 125 mM (Fig. 4). For the mutants containing only single Cys-substitutions at positions 116 (Fig. 4 B, green circles) and 155 (Fig. 4 C, green circles), there was a slight depolarizing shift in the V_0.5^Q versus log₁₀ [Na⁺] data relative to the WT, whereas A104C matched the WT characteristic well (Fig. 4 A, green circles). Importantly, and despite the minor effects of the Cys substitutions, the behavior of the respective double mutants resembled that of the single Na1 mutants (Fig. 4, blue/red symbols). Moreover, for all constructs, the limiting slope of the V_0.5^Q versus log₁₀ [Na⁺] data approached the expected ∼120 mV/decade predicted at high [Na⁺] for two Na⁺ ions interacting with a transporter, which confirmed that the stoichiometry of all mutants remained the same as the WT (1, 21, 22).

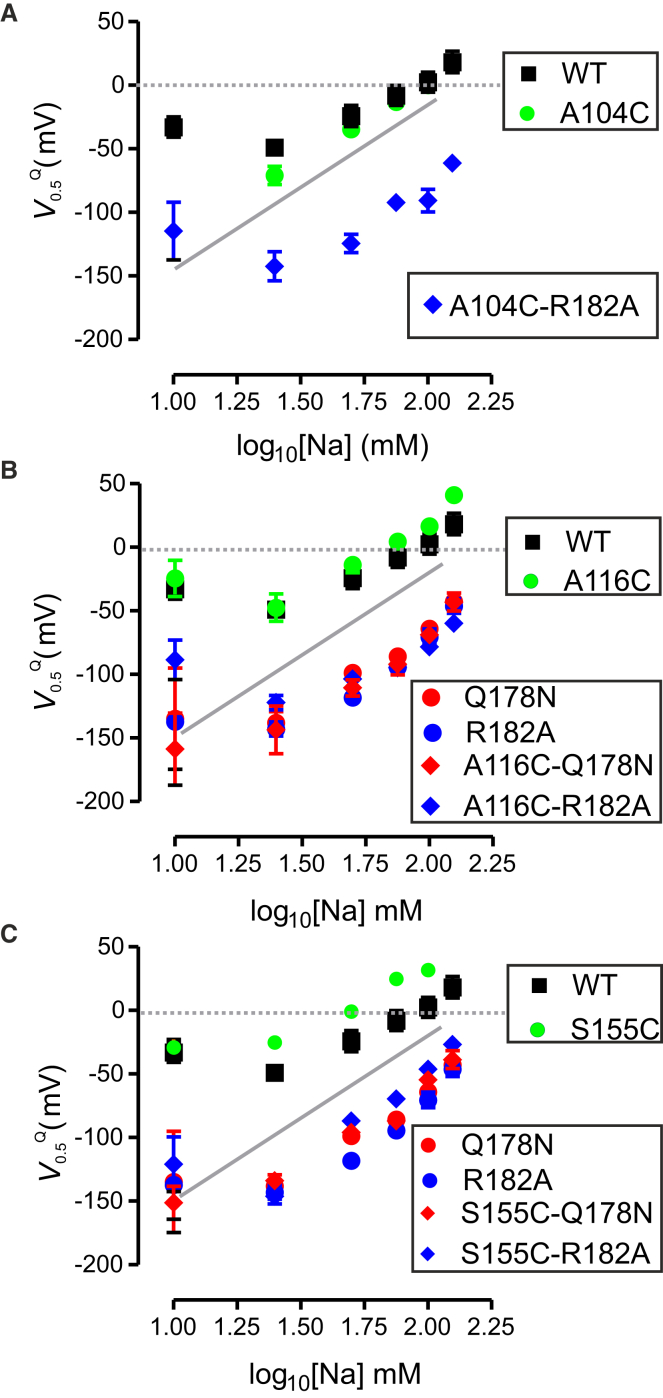
Figure 4.

Dependence of midpoint voltage (V_0.5^Q) on external Na⁺ concentration for single and double mutants. (A) Dependence of V_0.5^Q on [Na⁺] for WT, A104C, and double mutant A104C-R182A. (B) Dependence of V_0.5^Q on [Na⁺] for WT, A116C, single Na1 mutants Q178N and R182A, and double mutants A116C-Q178N and A116C-R182A. (C) Dependence of V_0.5^Q on [Na⁺] for WT, S155C, single Na1 mutants Q178N and R182A, and double mutants S155C-Q178N and S155C-R182C. The continuous shaded line represents the theoretical limiting slope of ∼120 mV/decade predicted for 2 Na⁺ ions binding to protein. Each data point represents mean ± SE for n > 5 cells. To see this figure in color, go online.

Taken together, these findings established that although substituting cysteines at 116 and 155 influenced both steady-state and presteady-state kinetics, the overall effect on the kinetics of the double mutants arose from the Na1 substitutions. This confirmation justified proceeding with voltage-clamp fluorometry assays and using the labeled 104, 116, and 155 sites as potential reporters of the altered kinetics associated with the Na1 mutations.

Changes in fluorescence intensity reported by Cys mutants: steady-state characteristics

Having established that the substitutions at 178 and 182 confer unique changes upon the electrogenic kinetics that largely recapitulate our conclusions derived from studying hNaPi-IIa (12), we then investigated whether these perturbations were detectable as conformational changes, by applying VCF to those mutants. When voltage steps were applied to noninjected oocytes, or to oocytes expressing WT NaPi-IIb, or to the Na1 mutants alone, no voltage-dependent changes in the emitted fluorescence intensity (ΔF) were detected after incubation with the fluorophore MTS-TAMRA (data not shown). However, for the functional double mutants containing Cys substitutions at positions 104, 116, or 155, ΔF was detected after labeling, as shown for the representative recordings from oocytes expressing constructs with the R→A substitution at position 182 (Fig. 5 A). We also confirmed that the steady-state electrogenic behavior of the single Cys mutants was unaffected by the labeling with MTS-TAMRA (data not shown).

Figure 5.

Voltage-clamp fluorometry dependence of ΔF-V on external Na⁺ concentration. (A) Representative recordings of changes in fluorescence (ΔF) in response to voltage steps from the –60 mV holding potential to –200, 0, and +180 mV for oocytes containing the Na1 mutation R182A and a substituted Cys at each of the three reporter positions. Oocytes expressing the respective double mutants were labeled with the fluorophore MTS-TAMRA at Cys-104 (upper); Cys-116 (center), and Cys-155 (lower) and recordings were made in the presence (100Na) and absence (0Na) of external Na⁺ ions. The differences in polarity and magnitude of the change in fluorescence intensity depend on both labeling position and expression levels for the same voltage step. (B) ΔF–V data when superfusing with different [Na⁺] indicated for the three double mutants. All data sets were superimposed at the depolarizing limit. Continuous lines are fits using Eq. 1 to data sets normalized to 100Na data set in each case. Fitting was only applied to data points lying in the monotonic range of ΔF for each [Na⁺]. Fitting was not performed for the S155C-R182A data because of the lack of saturation at hyperpolarizing potentials. Each data point represents mean ± SE for n > 5 cells. (Insets) ΔF-V data obtained from a representative oocyte expressing the respective cysteine-only mutant when superfusing with 100Na (open circles) and 0Na (solid circles). (C) Dependence of V_0.5^Q on [Na⁺] for the single mutants A104C, A116C (data from Patti and Forster (3)) and double mutants A104C-Q178N, A116C-Q178N, and A116C-R182A obtained in this study. (Shaded line) Theoretical limiting slope of ∼120 mV/decade predicted for 2 Na⁺ ions binding to protein. Each data point represents mean ± SE for n > 5 cells. To see this figure in color, go online.

When we replaced external 100 mM Na⁺ with choline, ΔF was still resolved, but was reduced in magnitude for the same voltage step. This showed that cation interactions altered the microenvironments of the three fluorophores and confirmed that their microenvironments also changed in response to membrane potential. The double mutants displayed similar unique ΔF-V phenotypes to those previously reported for the respective single Cys mutants (Fig. 5 B (3)). For example, in the R182A background, labeling Cys-104 yielded a bimodal behavior with increased quenching at intermediate potentials (Fig. 5 B, left panel), whereas labeled Cys-116 and Cys-155 gave monotonic ΔF-V curves with progressively more quenching at depolarizing and hyperpolarizing potentials, respectively (Fig. 5 B, center and right panels). Qualitatively similar findings were obtained for the Q→N substitution at position 178 after labeling at Cys-116 and Cys-155 (data not shown).

To quantitate the fluorometric data, we determined ΔF-V for varying external Na⁺ concentrations (Fig. 5 B). Data were normalized to the response for 100Na and superimposed at the depolarizing limit. The double mutants all displayed a left shift of the ΔF-V data along the voltage axis compared with the corresponding cysteine-only mutants (see insets, Fig. 5 B). For A104C-R182A (Fig. 5 B, left panel), the slope of the ΔF–V data for V > 0 was essentially independent of the external [Na⁺], whereas for V < 0, the data sets deviated, depending on the external [Na⁺]. For A116C-R182A, we observed similar behavior; however the region of increased ΔF at positive potentials was less evident and could be resolved from the signal noise only for V < +50 mV. To facilitate comparison of the sodium dependence, the fluorescence data were fitted with a single Boltzmann function (Eq. 1), starting the fit from the minimum ΔF for each [Na⁺] data set, for three constructs: the Na1 mutant containing Cys-104 (A104C-R182A; Fig. 5 B, left panel); the two mutants containing Cys-116, A116C-R182A (Fig. 5 B, center panel); and A116C-Q178N (data not shown). The voltage at the midpoint of ΔF, V_0.5^F was extracted from those Boltzmann fits, with ΔF_max constrained in the fitting algorithm to the value obtained for 100 Na superfusion. By this analysis, a strong hyperpolarizing shift in V_0.5^F was revealed (Fig. 5 C) that was comparable with the presteady-state parameter V_0.5^Q obtained independently under the same conditions (Fig. 4). Note that for the two Na1 mutants containing Cys-155, the lack of saturation at hyperpolarizing potentials (e.g., Fig. 5 B, right panel) precluded fitting with Eq. 1.

Changes in fluorescence intensity reported by Cys mutants: presteady-state characteristics

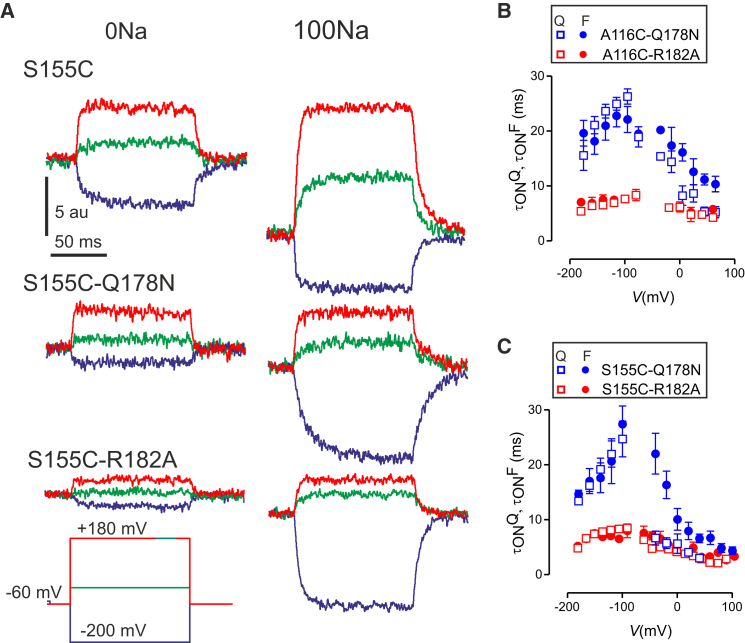
The above results indicated that the conformational changes detected by the fluorophore microenvironment were also affected by the Na1-site modifications. However, it was not clear whether those conformational changes reflected mechanistically relevant events. We therefore examined the time course of ΔF from the onset of the voltage step to see if they were consistent with the time course of the presteady-state current relaxations, for the same condition. Fig. 6 A shows representative fluorescence traces for S155C and the double mutants S155C-Q178N and S155C-R182A for superfusion with 0Na and 100Na solutions. When superfusing with 100Na, it was evident that for S155C-Q178N the change in fluorescence intensity in response to a hyperpolarizing step was significantly slower than for S155C alone, whereas for S155C-R182A, the time course was only slightly slower than for the single mutant (Fig. 6 A, right traces). For superfusion in 0Na, there was no obvious change in the step response except that for S155C-R182A, the magnitude of ΔF was significantly smaller compared with that obtained for either S155C-Q178N or S155C for the same voltage step (Fig. 6 A, left traces). This reduced response could not be attributed to low functional expression levels because when superfusing with 100Na, the magnitude of ΔF was comparable for all three constructs (Fig. 6 A, right traces). Similar findings were also obtained when the Na1-perturbing mutations were combined with Cys-116 (data not shown).

Figure 6.

Time courses of ΔF and presteady-state current relaxations correlate. (A) Representative ΔF recordings from labeled oocytes expressing S155C, S155C-Q178N, and S155C-R182A shown for voltage steps from –60 mV to the indicated potentials. In each case, recordings were made in the absence and presence of 100 mM Na⁺. (B) Comparison of main relaxation time constant from presteady-state current (τ_ON^Q) and from fitting ΔF (τ_ON^F) for the double mutants containing labeled Cys-116 as a reporter, measured in 100Na solution. Each data point is mean ± SE from up to five cells. (C) Comparison of main relaxation time constant from presteady-state current (τ_ON^Q) and from fitting ΔF (τ_ON^F) for the double mutants containing labeled Cys-155 as a reporter, measured in 100Na solution. Each data point is mean ± SE from >5 cells. To see this figure in color, go online.

Quantification of these ΔF time-courses could not be achieved reliably for the double mutants in the absence of sodium, due to the compromised signal/noise. However, for 100Na superfusion, we could successfully fit ΔF from the step onset using a single exponential function to generate τ_ON^F-V relationships (Fig. 6, B and C, solid symbols). Comparing the three constructs labeled with the fluorophore at Cys-116, the τ_ON^F for A116C-Q178N (Fig. 6 B, blue) was significantly slower than that for A116C-R182A (Fig. 6 B, red) and A116C alone (e.g., see Fig. 4 in Patti and Forster (3)), and the peak was shifted in the hyperpolarizing direction. Both these features are consistent with the behavior of the presteady-state current relaxation time constant (τ_ON^Q, open symbols) determined from the same oocytes. This behavior was not unique to the label at position 116, as similar results were obtained upon labeling at Cys-155 (Fig. 6 C), thereby confirming the dominant effect that the Na1 mutation at position 178 had on the dynamic behavior of the protein. We note that for S155C-Q178N, there was a discontinuity in τ_ON^Q-V at test potentials close to the –60 mV holding potential (Fig. 6, B and C) that arises from uncertainties in the double exponential fitting algorithm due to the compromised signal/noise for small voltage steps. Nevertheless, this discontinuity did not affect our ability to detect the increased rates or shifts in peak height due to modifications at position 178.

Iodide quenching experiments indicate a change in the fluorophore microenvironment

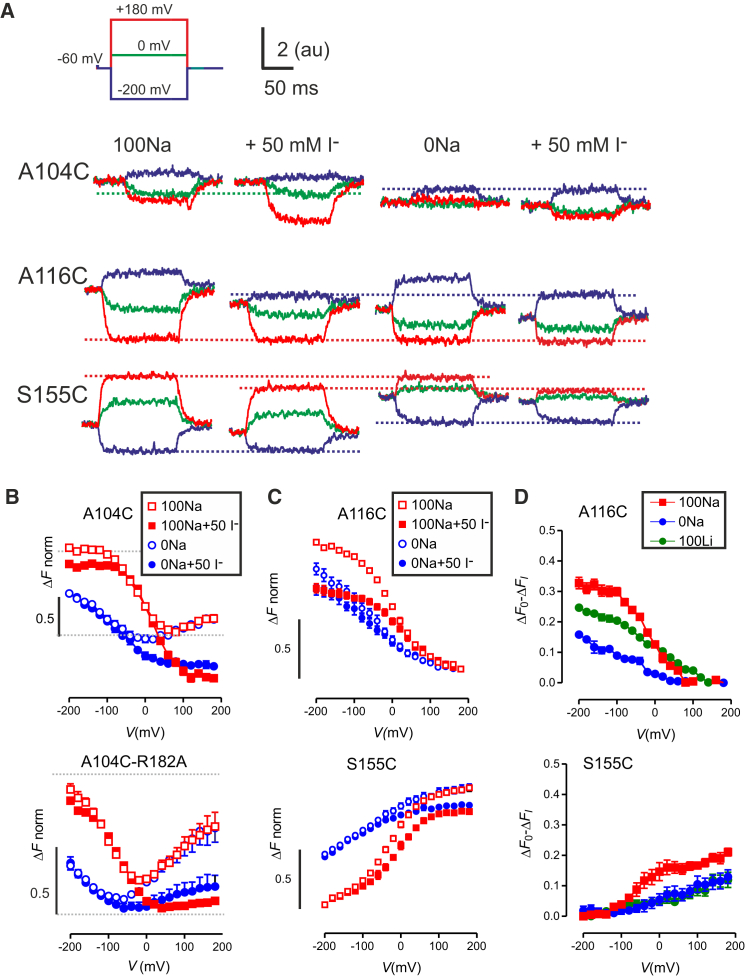
The ΔF-V data reported above indicated a change in environment of the fluorophores at the three positions, but not the nature of those changes, e.g., whether they become more or less buried in the protein. To examine possible changes in solvent accessibility experienced by the fluorophores, we used the collisional quencher iodide in the presence and absence of external cations and compared the ΔF–V behavior after labeling at 104, 116, or 155. We first confirmed that the addition of 50 mM I^– to the external superfusate had a negligible effect on the steady-state electrogenic behavior and on the presteady-state relaxations even in the absence of Na⁺ (0Na + 50 mM KI) (data not shown). However, we noted that at strongly depolarizing potentials (>50 mV), outward currents were evoked by the I^–, presumably resulting from anion influx through endogenous chloride channels (data not shown). Representative examples of I^– fluorescence quenching are shown in Fig. 7 A for oocytes expressing the single mutants A116C (center traces) and S155C (lower traces), both of which exhibit monotonic ΔF–V relationships (Fig. 7 C), as well as for oocytes expressing the single mutant A104C, which displayed a bimodal ΔF–V (Fig. 7 A, upper traces, 7 B, upper panel). In general, in the presence of 50 mM I^–, quenching occurred both with and without external Na⁺ and depended on the membrane potential (Fig. 7, B–D). These effects on ΔF–V were fully reversible (Fig. S5, A and B) and the change in ΔF_max with increasing [I^–] was consistent with the behavior predicted for a collisional quencher according to the Stern-Volmer relation (Fig. S5 C) (e.g., Lakowicz (23)). Significantly, the range of membrane potentials over which detectable quenching occurred was different, depending on labeling position, rather than showing a consistent effect at all positions. That is, for a label at position 155 there was significant quenching for V > 0, whereas for labeling at position 116, quenching occurred only for V < 0 (Fig. 7 C); labeling at position 104 revealed quenching in both ranges (Fig. 7 B). This established that for a given distribution of state occupancies as defined by the membrane potential, the microenvironment of the fluorophore changed according to its position in the protein.

Figure 7.

Quenching fluorescence using iodide. (A) Representative recordings of changes in fluorescence (ΔF) in response to voltage steps from the –60 mV holding potential to –200 mV (blue), 0 mV (green), and +180 mV (red) for oocytes expressing the single mutants A104C, A116C, and S155C before and after exposure to 50 mM I^– in the presence (100Na) and absence (0Na) of external Na⁺. Traces belonging to each data set were baseline-corrected and the data set adjusted to align at the test potentials where we observed no quenching of the transporter-related ΔF (dashed colored lines). For example, mutant S155C shows the same ΔF at the depolarizing extreme (red traces) for 100Na and 0Na superfusion and those data sets were aligned accordingly. For 100Na and 0Na superfusion, no I^– quenching was observed at the depolarizing extreme and each data set was then aligned to this common reference (blue traces). (B) Voltage dependence of I^– quenching for labeling at position 104 (single mutant A104C (upper) and double mutant A104C-R182A (lower)) is revealed in ΔF-V data for superfusion with 0Na (circles) and 100Na (squares). Data were pooled from individual cells by first fitting to the data set for 100Na superfusion to estimate ΔF_max (Eq. 1). Voltage-independent background quenching was eliminated by shifting the normalized data sets with and without quencher relative to one another to give consistent quenching, independent of I^–. (C) Complementary voltage dependence of I^– quenching for labeling at position 116; single mutant A116C (upper) and S155C (lower)) is revealed in ΔF-V data for superfusion with 0Na (circles) and 100Na (squares). For S155C, the 100Na and 0Na data were superimposed at the depolarizing limit and the 0Na and 0Na+I^– data were superimposed at the hyperpolarizing limit; for A116C, all data sets were superimposed at the depolarizing limit. (D) Quenching as a function of V for A116C (upper) and S155C (lower) shown for three superfusion conditions. ΔF₀-ΔF_I is the difference between normalized, control ΔF and that in the presence of I^– (n > 4 cells for each condition). To see this figure in color, go online.

To characterize the I^–-quenching, we acquired ΔF–V data over a wide range of membrane potentials and then examined how the fluorescence quenching at each Cys position was affected by voltage and the presence of sodium, which are reflective of different conformational states in the cycle (Fig. 1 A). For A104C, the normally bimodal voltage-dependent fluorescence of the probe was significantly altered in the presence of I^– under both superfusion conditions (Fig. 7 B, upper). With 100Na superfusion, we observed some quenching at hyperpolarizing potentials. However, the effect of I^– was most apparent for depolarizing potentials at which ΔF became less voltage-dependent, which suggested that ΔF was almost completely quenched, and thus the fluorophore is likely to be fully exposed to aqueous solution under those conditions. In the absence of external sodium, we observed similar behavior at depolarizing potentials, whereas at hyperpolarizing potentials the data with and without I^– superimposed well: this lack of quenching suggested that the fluorophore at Cys-104 was not exposed to the external solution under these conditions, in contrast to the results in the presence of external sodium. After incorporating a further mutation that exhibits perturbed voltage dependence (A104C-R182A) (Fig. 7 B, lower), the ΔF–V data were left-shifted by ∼100 mV relative to Cys-104 alone (see also Fig. 5, B and C) so that the slight quenching seen for superfusing in 100Na at hyperpolarizing potentials for A104C was now less evident, whereas quenching in the depolarizing range became more apparent. Therefore, the results for the double mutant further support the possibility that Cys-104 is 1) solvent-exposed at depolarizing potentials regardless of the presence of external sodium; 2) more buried by protein at hyperpolarizing potentials and in the presence of sodium; and 3) least accessible at intermediate potentials.

When considering the effect of I^– on positions 116 and 155, the complementary nature of their ΔF-V behavior was further underscored. In particular, the probe at A116C (Fig. 7 C, upper) displayed significant quenching at hyperpolarizing potentials, whereas for S155C (Fig. 7 C, lower), quenching occurred in the depolarizing range, which suggested that Cys-116 is exposed to solution only when the protein is outward-facing (states 1–3; Fig. 1 A), whereas Cys-155 is exposed only when the protein is inward-facing (states 0 and 6; Fig. 1 A). To investigate how quenching depends on the state of the protein with respect to the occupancy of Na1 and Na2, we quantified the relative amount of I^–-induced quenching at each test potential for A116C and S155C under three superfusion conditions (100, 0, and 100Li). Specifically, we determined ΔF₀-ΔF_I, where ΔF₀ and ΔF_I are the normalized ΔF in the absence and presence of 50 mM I^–, respectively (Fig. 7 D), and therefore larger values of ΔF₀-ΔF_I signify greater amounts of I^– quenching. For A116C, ΔF₀ -ΔF_I progressively increased as V became more negative for all three superfusing conditions, with the largest effect occurring for 100Na and intermediate quenching with 100Li. This result was consistent with the probe at Cys-116 only being exposed to solution when the protein is outward-facing (states 1–3; Fig. 1 A), with incremental increases in the degree of accessibility relative to the empty carrier (state 1) as Na1 (state 2) and Na2 (state 3) become occupied (Fig. 1 A). For S155C, I^–-dependent quenching increased with depolarization, whereas the data suggested that the amount of quenching was comparable under all superfusion conditions at the hyperpolarizing extreme. Superfusion in 100Na also increased the quenching with a peak close to 0 mV, whereas for superfusion with 100Li or 0Na, the I^–-dependent quenching was similar over the test potential range investigated. These results suggested that the probe at Cys-155 is exposed to solution mainly in inward-facing states (0, 6), and that while occupancy of Na1 (state 6; Fig. 1 A) does not alter the accessibility of the probe, binding of sodium to Na2 may increase its exposure further.

Discussion

We recently proposed a three-dimensional structure of hNaPi-IIa based on a homology model of the bacterial dicarboxylate transporter, VcINDY (11), which we used to predict positions in its first Na⁺ binding site (Na1) (12). In general, mutations in this region altered the voltage dependence of the transport cycle, and influenced cation interactions, including the ability of Li⁺ ions to substitute for the Na⁺ ions at Na1 and initiate subsequent steps in the cotransport cycle. We reasoned that such kinetic alterations should also result in changes to the distribution of conformational states that occur in response to altered membrane potential and binding/unbinding of cations. We previously investigated this effect using two types of real-time functional assays in which a change of state is provoked by rapid changes in membrane potential: 1) presteady-state charge relaxations and 2) VCF (3). Although the charge relaxation approach has revealed changes in the voltage-dependent kinetics caused by these perturbations, it cannot provide direct evidence that transport-specific molecular rearrangements actually occur as a result of the measured charge displacement. Moreover, the charge movement could arise from a single discrete charge or a distributed population of charges and must therefore be taken as a global measure of the system response. In contrast, VCF focuses on local conformational changes, whereby changes in fluorescence emission arise from alterations in the microenvironments of a population of fluorophores covalently linked to the same cysteine placed in or near functionally important regions of the protein. VCF can therefore potentially yield more direct evidence of local conformational changes.

Altered voltage dependence caused by Na1 mutations recapitulated in flNaPi-IIb

As most of our previous VCF studies were performed using the flNaPi-IIb isoform, we made substitutions in flNaPi-IIb at two of the sites identified in the hNaPi-IIa study (12): 1) the Q→N substitution at position 178 (206 in hNaPi-IIa), predicted to be close to Na1 and shown to directly influence cation interactions; and 2) the R→A substitution at position 182 (210 in hNaPi-IIa), which was proposed to exert its influence on Na1 interactions, as well as subsequent steps in the transport cycle, indirectly by modifying the kinetics of the empty carrier transition (0↔1; Fig. 1 A) in hNaPi-IIa (12). Introduction of these mutations into flNaPi-IIb shifted the voltage dependence toward hyperpolarizing potentials, recapitulating the hNaPi-IIa mutant behavior (12), and thereby underscored our view that this region serves a common structure-function role in all electrogenic isoforms, namely, binding of the first Na⁺ ion. However, we also observed differences in voltage dependence and cation specificity under the same experimental conditions (Fig. S2 B) that can be attributed to the features of the respective WT proteins, as previously reported (e.g., Forster et al. (1, 24), Andrini et al. (21), and Virkki et al. (25)). In particular, unlike the hNaPi-IIa mutants, where we showed that Li⁺ ions could substantially substitute for Na⁺ ions to drive electrogenic transport, the Li⁺-effect was much less evident for the equivalent mutants in the flounder (12). Given the high similarity in the proposed Na1 site regions among NaPi-II isoforms, these isoform-specific differences suggested that other, yet to be identified residues, presumably in the second shell around the substrates, also influence the kinetics of the complete transport cycle. Their identification would require more detailed investigation beyond the scope of this study.

The improved resolution of presteady-state relaxations recorded from oocytes expressing the flounder constructs led to further insights into effects of the mutations on their kinetics. The presteady-state behavior of the Na1 mutants included a hyperpolarizing shift of the Q-V data relative to WT (Figs. 3 B and 4, B and C), consistent with the steady-state behavior (Fig. 2). Moreover, both Na1 mutants showed a hyperpolarizing shift in the peaks of the respective relaxation time constants (τ^Q) in the presence and absence of external Na⁺ ions (Fig. 3 C). Thus, one might expect that the ratio of the rate constants associated with the apparent partial reactions (0↔1, empty carrier) and (1↔2, first Na⁺ interaction) (Fig. 1 A) should be affected similarly in all mutants. However, the Q→N substitution at position 178 resulted in a significantly increased τ_ON^Q only in the presence of external Na⁺ ions (Fig. 3 C), consistent with the residue at this position being directly involved in Na⁺ ion coordination. In contrast, the R→A substitution at position 182 affected the magnitude of τ_ON^Q in the absence of external Na⁺ ions (Fig. 3 C), consistent with its proposed role as a determinant of the voltage dependence of the state occupancy of the empty carrier (inward or outward facing, 0↔1) (12). Our presteady-state analysis also revealed that the positive charge at position 182 also contributed to the apparent valence of the transporter, as evidenced by the reduced slope of the Q-V data (Fig. 3 B). In contrast, this parameter did not change for Q178N (Fig. 3 B) relative to the WT, indicating that the valence associated with each voltage-dependent partial reaction was similar to that of WT. In summary, although the overall effect of these mutations on the steady-state kinetics was qualitatively similar, the underlying mechanisms were unique to each site.

Correlations between presteady-state behavior and changes in fluorescence intensity

A critical assumption concerning the applicability of VCF is that neither the Cys-substitution nor the subsequent labeling should significantly alter the underlying transport kinetics so that the implied conformational changes can be related to WT-like behavior. We previously identified three candidate reporter sites that satisfied these criteria, albeit with small deviations from WT behavior (3). Importantly, labeling each of these sites had yielded unique changes in fluorescence intensity that could be correlated with different state occupancies. However, investigation of the Na1 site required particular steady-state and presteady-state analysis to characterize the Na1-region perturbing mutations. In this study, we therefore also carried out these steady-state and presteady-state analyses for the single Cys mutants (at positions 104, 116, and 155). These data established that although minor shifts in the steady-state transport voltage dependence were observed (Fig. S2) for the double mutants, the dominant effects on the steady-state and presteady-state (Fig. 4) kinetics were attributable to the Na1 substitutions and therefore validated the use of these reporter sites for our VCF assays.

As mentioned above, we previously showed that labeling each reporter site resulted in a unique fluorometric response that reflects specific state occupancies depending on the conditions applied (3), according to our simple kinetic scheme (Fig. 1 A). For a given labeling position, we had assigned an apparent fluorescence intensity to each allowed state, which was weighted by the corresponding state occupancy probability (dependent on the cation concentration and membrane potential) to give the fractional contribution to the total fluorescence. We could thereby satisfactorily account for the time course and magnitude of ΔF reported by the respective fluorophores when a population of transporters is distributed over a set of conformationally distinct states (3). The ΔF-V data were interpreted as follows: labeling Cys-104 resulted in fluorescence emission mainly from occupancy of states 6, 1, and 3, thus both inward- and outward-facing orientations of the protein result in increased fluorescence intensity, corresponding to the hyperpolarizing and depolarizing potential extremes, respectively, but not at intermediate potentials (3). In contrast, labeling at positions 116 and 155 resulted in complementary voltage-dependent changes in ΔF, with maximum quenching occurring at either the positive or negative potential extremes, respectively. Thus, the fluorescence emission obtained by labeling Cys-116 is postulated to arise when states 1 and 2 or 3 are occupied, whereas when labeling Cys-155, the increased fluorescence emission resulted from occupancy of states 0 and 1 (3). If a Na1 mutation were to alter the state occupancy at a given membrane potential, this should also be reflected in the corresponding changes in fluorescence intensity under the assumption that changes in the microenvironment of the fluorophore truly correlate with predicted state occupancy. Indeed, we found that voltage-dependent shifts in the presteady-state kinetics induced by the mutations were also reflected in concomitant shifts of the voltage dependence of ΔF.

Further correlation between presteady-state charge movement and ΔF was obtained by comparing the respective ON-transition time constants (τ_ON^Q, τ_ON^F). We have previously reported a strong agreement between τ_ON^Q and τ_ON^F for the single mutants A116C and S155C (3). This agreement was recapitulated for the double mutants also when τ_ON^Q and τ_ON^F were significantly slower for the Q→N substitution at 178. In summary, the similarity of the presteady-state and fluorometry kinetics indicates that the same underlying molecular events are faithfully reported by the two assays.

Iodide quenching confirms that changes in the fluorophore microenvironment are associated with specific state transitions of NaPi-IIb

By using the collisional quencher iodide, we gained further insight into the nature of the changes to the fluorophore microenvironment and, by implication, into the accompanying localized molecular rearrangements. We reasoned that if the fluorophore were to become more exposed to the external solvent as a result of a conformational change, increased quenching in the presence of I^– should be observed (e.g., Cha and Bezanilla (26) and Mannuzzu et al. (27)).

We previously reported the effects of I^– on ΔF emitted from a fluorophore linked to 155, but those data suggested that I^– had only a marginal effect on the fluorescence emission (8). By extending the voltage range, we now unequivocally demonstrate significant quenching of ΔF for a label linked to Cys-155 (Fig. 7 D). Importantly, the increased quenching at positive potentials was observed even in the absence of external cations (0Na solution), which indicated that the membrane depolarization caused a significant conformational change corresponding to the empty carrier reorientation (i.e., changing from state 1 to state 0, Fig. 1 A) (3, 8). Thus, the quenching behavior reported here established that Cys-155 became progressively more exposed to the external solvent when the protein favored an inward-facing conformation in the absence of external cations. In the presence of Li⁺ ions (100Li solution), which are only able to bind at Na1 (21), I^–-dependent quenching of the fluorophore at Cys-155 was indistinguishable from that in the absence of cations (Fig. 7 D). At the depolarizing extreme, this insensitivity to Li⁺ may simply reflect the fact that all transporters are inwardly oriented so the Na1 site is presumably inaccessible from the external medium (21). However, at hyperpolarizing potentials, where external Li⁺ results in occupancy of state 2 (Li⁺ bound, Fig. 1 A), the similarity of the I^– quenching behavior indicated that the solvent accessibility of this fluorophore is unchanged relative to state 1 (the empty transporter), at least within the limits of detection.

Surprisingly, the addition of external sodium only affected the solvent accessibility of the fluorophore at Cys-155 at depolarizing potentials. This result was unexpected because most transporters should be inward facing at these potentials and yet the presence of Na⁺ ions in the external medium was able to cause an increase in solvent accessibility of the fluorophore at the extracellular surface. Determining the origins of this effect will require additional experiments in the future.

For the fluorophore at Cys-116, I^– quenching effects in the absence of external cations (0 Na) mirrored the findings for Cys-155 (Fig. 7 D). The greatest quenching occurred at hyperpolarizing potentials when the protein is predicted to be outwardly oriented (state 1, or states 2 or 3) and therefore, the fluorophore must be exposed to the external solvent in those states. Interestingly, the progressive increase in I^–-dependent quenching in the presence of Li⁺ ions and then Na⁺ ions (Fig. 3 D), demonstrates that the Cys-116 fluorophore becomes increasingly solvent accessible as the transporters shift from state 1 to state 2 (with Na1 occupied by Li⁺) and thence to state 3, when both Na1 and Na2 are occupied (100Na; Fig. 1 A).

Finally, I^– results for A104C were consistent with the fluorophore being exposed to the external solvent when the protein is either inwardly or outwardly orientated. These findings also argue against the I^– effect being an electrostatic phenomenon, as the membrane potential can be either negative or positive and produce the same effect. Nevertheless, quenching was strongest under conditions that favored inwardly oriented states (positive potentials; states 0 or 6), establishing that this site became strongly exposed to the solvent in that conformation. Furthermore, our finding that the A104C-R182A double mutant exhibited similar quenching behavior to the single Cys-104 mutant, but with a hyperpolarizing shift similar to the effect of the R→A substitution on presteady-state currents (Fig. 7 B), provided further evidence that ΔF is a direct measure of conformational changes of the protein.

Can our experimental data be reconciled with a structural model for NaPi-IIb?

The VCF data clearly demonstrate position-specific changes in the environments of each position during voltage-induced transitions and cation interactions, and with similar kinetics. However, as mentioned above, all three reporter positions are all expected to lie outside the transmembrane electric field, in addition to being >25 Å from the Na1 site (Fig. 1 C). Consequently, the observed changes in the fluorophore microenvironments most likely result from a relative movement of the substituted Cys with respect to neighboring structural elements, during the transition between inward- and outward-facing states.

To test these predictions at the structural level, knowledge of both outward and inward conformations would be required. Recently, Mulligan et al. (15) used a computational technique known as repeat-swap modeling (e.g., Vergara-Jaque et al. (28)) to predict an alternate conformation for VcINDY. Cross-linking data confirmed that VcINDY undergoes a significant conformational change, known as an elevator-like mechanism, in which the substrate-binding transport domain moves relative to the oligomeric interface domain (28). Having used the known structure of VcINDY as the basis for generating a structural model of hNaPi-IIa and flNaPi-IIb in the outward-facing conformation (10, 12) (Fig. 1 C), we extended the analogy and used the published repeat-swapped model of VcINDY as a template to predict the structure of flNaPi-IIb in an inward-facing conformation. As expected, comparison of the two flNaPi-IIb models suggested a significant vertical (∼15 Å) and rotational (∼37°) movement of the transport domain relative to the scaffold (Fig. 8; Movie S1 in the Supporting Material). Such a large conformational change is consistent with the observation of changes in fluorescence at positions far from the substrate-binding site.

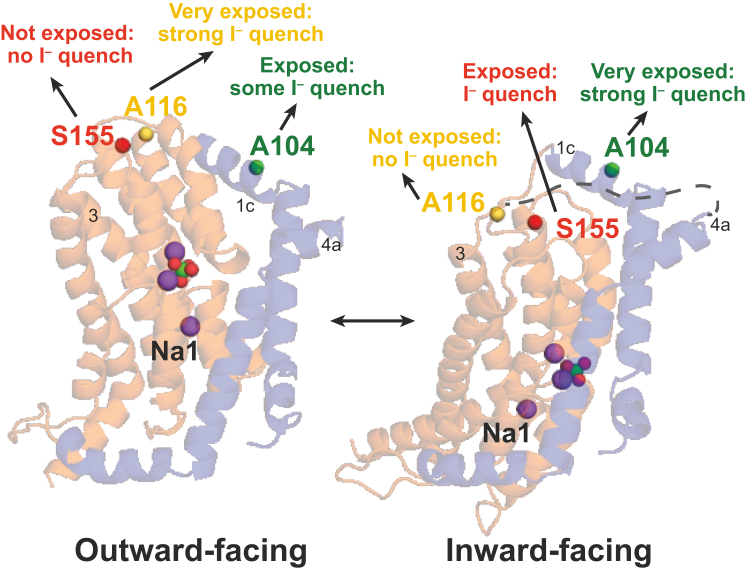
Figure 8.

Models of flNaPi-IIb in outward- and inward-facing open conformations. The protein is represented in cartoon; and the Na⁺ atoms, i.e., the P_i and Cα atoms of residues Ala-104, Ala-116, and Ser-155, are shown in purple, green/red, green, yellow, and red spheres, respectively. Domains were assigned according to the VcINDY template, and depicted with the transport domain colored orange, and the scaffold (or oligomerization domain in blue). The exposure and I^– quenching of fluorophores at Ala-104, Ala-116, and Ser-155 is indicated for each of the conformations. To see this figure in color, go online.

Having access to two structural models, we attempted to relate the changes in accessibility to the differences in the two conformations. Indeed, the environmental changes observed experimentally at two of the reporter sites (positions 104 and 116) appeared to be broadly consistent with the structural predictions. Specifically, when flNaPi-IIb is in the outward-facing conformation (corresponding to membrane hyperpolarization), positions 104 and 116 are exposed to the external medium and therefore probes at those positions would be amenable to I^– quenching, consistent with the experimental observations. When the transport domain moves inward, position 104, which is located on the scaffold domain, is predicted to remain exposed, explaining the strong I^– quenching observed.

On the other hand, the outward-facing model (corresponding to depolarizing potentials) predicts that position 155 would be exposed to the external solution, which is not in accord with our experimental data. Moreover, the inward-facing model suggests that both A116 and S155 remain exposed, which is also not in agreement with the S155C data. It is likely that this discrepancy arises from the limited structural resolution in this region, especially for the inward-facing model. In particular, these structural models necessarily excluded the large extracellular loop that links the top of TM3 to the start of TM4a (Fig. 1 B), which may be important in defining the environment of these fluorophores in one or both of the extreme states. In summary, the reported findings suggest concerted movements of entire protein domains, rather than reorientation of individual amino acid side chains; however, the limited number of investigated sites, in combination with the low resolution of the models, preclude the prediction of a defined transport model at this time.

Conclusions

We have combined conventional electrophysiology and voltage-clamp fluorometry to investigate voltage-induced conformational changes in real-time in a Na⁺-driven carrier system, NaPi-IIb. Our findings underscore the utility of this experimental technique to quantitate carrier protein dynamics under physiological conditions and, importantly, reveal the large-scale nature of the molecular rearrangements that occur during the transport cycle of a secondary active transporter.

Author Contributions

I.C.F. designed and performed experiments, analyzed and interpreted data; M.P. performed experiments and analyzed data; C.F.-F. performed computational modeling; and I.C.F., C.F.-F., L.R.F., and A.W. wrote the article.

Editor: Michael Pusch.

Supporting Material

Movie S1. Structural Models of flNaPi-IIb in Outward-Facing and Inward-Facing Conformations

These models were constructed based on their homology with VcINDY. Note that the expected accuracy of the outward-facing model is likely to be higher than that of the inward-facing model. Outward facing (also available at PMDB, with code PM0080462): flNaPi-IIb-OFC_on_4F35.pdb. Inward facing: flNaPi-IIb-IFC_on_4F35-RSM-PM0080216.pdb.