Abstract
Chromosome segregation during mitosis hinges on proper assembly of the microtubule spindle that establishes bipolar attachment to each chromosome. Experiments demonstrate allometry of mitotic spindles and a universal scaling relationship between spindle size and cell size across metazoans, which indicates a conserved principle of spindle assembly at play during evolution. However, the nature of this principle is currently unknown. Researchers have focused on deriving the mechanistic underpinning of the size scaling from the mechanical aspects of the spindle assembly process. In this work we take a different standpoint and ask: What is the size scaling for? We address this question from the functional perspectives of spindle assembly checkpoint (SAC). SAC is the critical surveillance mechanism that prevents premature chromosome segregation in the presence of unattached or misattached chromosomes. The SAC signal gets silenced after and only after the last chromosome-spindle attachment in mitosis. We previously established a model that explains the robustness of SAC silencing based on spindle-mediated spatiotemporal regulation of SAC proteins. Here, we refine the previous model, and find that robust and timely SAC silencing entails proper size scaling of mitotic spindle. This finding provides, to our knowledge, a novel, function-oriented angle toward understanding the observed spindle allometry, and the universal scaling relationship between spindle size and cell size in metazoans. In a broad sense, the functional requirement of robust SAC silencing could have helped shape the spindle assembly mechanism in evolution.
Introduction
Accurate chromosome segregation in the eukaryotic cell division, or mitosis, relies on the mitotic spindle (1), a fusiform structure consisting of microtubules, motor proteins, and other structural and regulatory components (1, 2). To segregate chromosomes, during early mitosis the microtubule spindle gradually forms and establishes a stable, bioriented connection with each chromosome at the chromosome’s outer centromere regions called “kinetochores”. Eventually, the spindle aligns all the chromosomes at its equator. Afterwards, chromosome segregation occurs and the spindle pulls the sister chromatids into two daughter cells (1). Accurate chromosome segregation is contingent upon stable connection of each chromosomal kinetochore to the microtubule spindle before chromosome segregation happens. Unattached or misattached kinetochores during chromosome segregation could cause lagging or loss of the associated chromosomes and consequently incorrect chromosome inheritance in daughter cells. To prevent such errors, the spindle assembly process is monitored by a stringent surveillance mechanism, the spindle assembly checkpoint (SAC) (3, 4). The SAC is activated at the unattached/misattached kinetochores. Active SAC signal prevents chromosome segregation and mitotic progression. The SAC is silenced when all the kinetochores are stably attached by spindle microtubules. Consequently, timing of SAC silencing after, and only after the last kinetochore-spindle attachment, dictates the accuracy of chromosome segregation.
While the basic molecular mechanism of spindle assembly is largely conserved in eukaryotes (3, 4), it is fundamentally challenging for such a complex mechanism to work consistently across tremendous size differences manifested across species, or among different cell types and developmental stages within the same organism. The mitotic spindle can vary from submicron in yeast to ∼60 μm in Xenopus eggs, whereas the cells that house these spindles may range from a few microns up to ∼1 mm (5). Recent experiments reveal a striking relationship between the spindle size and cell size (5, 6, 7, 8, 9, 10, 11), as well as between various dimensions of the spindle (e.g., spindle width, spindle length, spindle pole size) (7, 11, 12, 13, 14). Most intriguingly, the spindle size scales linearly with the cell size up to a certain limit; and such a biphasic scaling relationship, as well as the critical cell size and spindle size for the biphasic transition, appear surprisingly consistent across metazoan species (5, 8, 10). Such size scaling is also partially reproduced in in vitro spindle reconstitution experiments (15, 16). From the physics point of view, such universal size-scaling phenomena are highly significant, as they suggest intrinsic principles in the spatial organization of the mitotic spindle.
The most critical questions related to the size-scaling phenomenon lie in how it happens and what it is for. Great efforts have been devoted to understanding the mechanics of spindle assembly pertaining to the first question—in particular, how different molecules modulate the size and shape of mitotic spindle (17, 18, 19, 20, 21, 22). It is not clear, however, whether the size scaling simply reflects the natural consequences of the mechanical process or additionally fulfills any functional roles in mitosis. Such functional roles could have shaped the spindle assembly mechanism by evolutionary pressure. In this work we address the second question and initiate a theoretical investigation on the potential functional role of spindle size scaling, particularly from the perspective of SAC signaling.
Previously, we built a theoretical model (23), which explains for the first time, to our knowledge, how the SAC silencing process may achieve signal robustness—in other words, how the cell works against inevitable fluctuating noise and distinguishes the last kinetochore attachment out of many to determine the right timing for SAC silencing. The model attributes the robustness of SAC silencing to the spatiotemporal regulation observed in SAC components. Synthesizing the experimental observations, the model proposes a coherent picture in which the entire spindle acts as a transport system that regulates the spatiotemporal pattern of SAC via convection and diffusion. The spatiotemporal pattern of SAC gives rise to a robust signal for SAC silencing at the spindle pole. In this paradigm, the kinetochores send out the signal, the spindle transmits the signal, and the spindle poles process the signal and trigger SAC silencing. The transport system essentially encodes the stepwise kinetochore-spindle attachments into a nonlinear signal at the spindle pole such that the final kinetochore attachment induces a much larger signal change than previous attachments do. The significant signal jump guarantees signal robustness against noise.
We hypothesize that the dimensions of any part of this transport system could affect the outcome spindle pole signal for SAC silencing. In this article, we refine our established model and use it to explore the possible connection between the size scaling in mitotic spindles and the SAC silencing signal. The model results show that robust and timely SAC silencing requires a relationship between spindle length and spindle width similar to that observed in experiments (11, 12). More importantly, the same functional requirements for SAC impose constraints on the spindle size given the cell size, which remarkably recapitulates the observed universal scaling relationship between the spindle and cell sizes across the Metazoa (5). According to the model, the accumulation of SAC components at spindle pole critically depends on two processes: 1) convection along the spindle microtubules and 2) diffusion into the spindle from the cytoplasm. Because the characteristic times of these two processes scale with spindle and cell sizes differently, in small cells convection is the rate-limiting step for accumulating SAC components at the spindle pole, whereas diffusion takes over as the rate-limiting step as the cell size grows. Consequently, proper concentration of SAC components at spindle pole—that serves as the signal for SAC silencing—distinctly relies on spindle size as cell size increases. This study provides an explanation for the observed biphasic scaling relationship between spindle and cell sizes across metazoans (5). Our finding thus reveals a fundamental functional requirement that could have imposed significant evolutionary pressure on mitosis.
Materials and Methods
Detailed setup and equations of the SAC model are included in the Appendix.
Results
Model setup
In this section, we first summarize our established spatiotemporal model for SAC silencing (Fig. 1; see Materials and Methods for detailed formulation, and Chen and Liu (23)), and then refine the model to specifically address the size scaling of spindle.
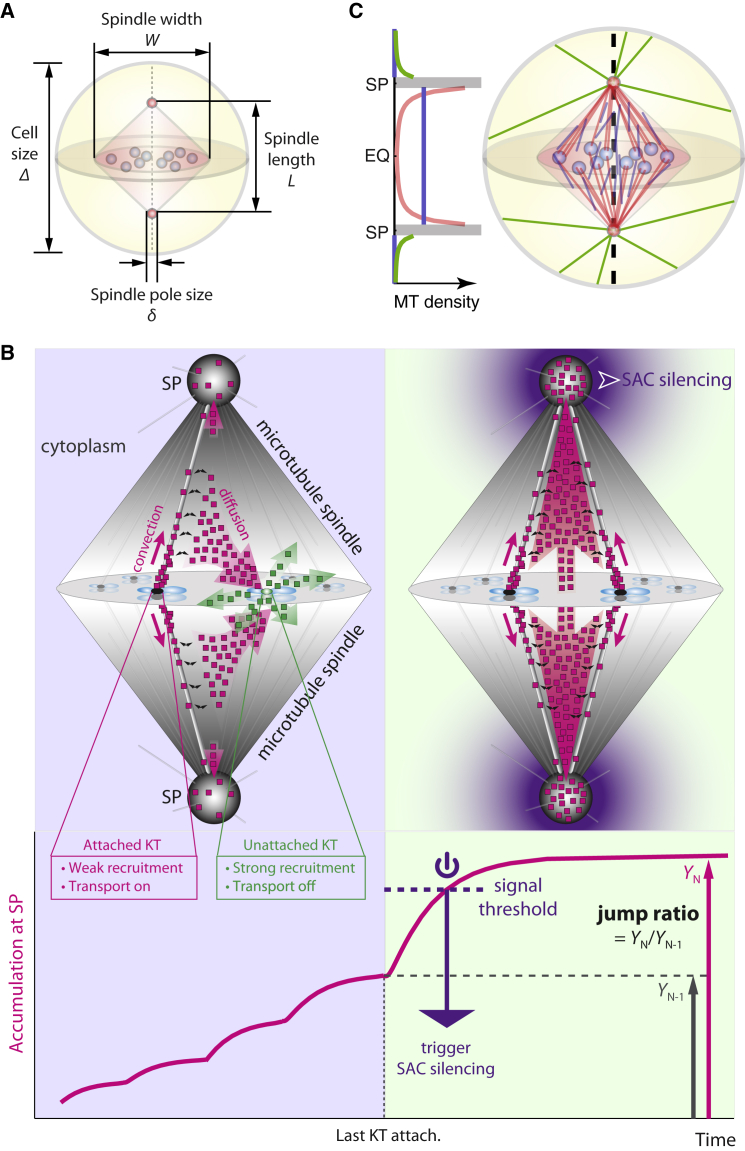
Figure 1.
Summary of model. (A) Notations for relevant geometric dimensions of the cell and the mitotic spindle. (B) Illustrative summary of the spatiotemporal model for SAC silencing. (Upper left panel) Poleward stream of SAC components (magenta squares) that emanated from attached kinetochores (black oval) is strongly diverted by unattached kinetochores (green oval). Unattached kinetochores convert proteins from streaming (magenta squares) to diffusive state (green squares). (Upper right panel) Once all kinetochores are attached, poleward stream becomes free of diversion, leading to significant increase of SAC accumulation at the spindle pole. The signal makes a robust trigger for SAC silencing that propagates throughout the cell. For clarity, fluxes of SAC components are only shown for two pairs of kinetochores in the foreground. Distribution of the squares does not reflect spatial distribution of SAC components. (Translucent magenta arrows) Flux of streaming proteins. (Translucent green arrows) Flux of diffusive proteins. (Solid magenta arrows) Proteins streaming poleward along microtubules. (Black curly arrows) Streaming proteins binding/unbinding with microtubules. (Lower panel) Spindle pole signal (accumulation of SAC components) with successive kinetochore-spindle attachments (magenta solid line). The last kinetochore attachment elevates the signal above the threshold and triggers SAC silencing. The jump ratio is defined as the ratio between the steady-state spindle pole signals after and before the last kinetochore attachment. (C) Illustration of microtubule distribution depicted by the current, improved model. (Red) Spindle microtubules in Group 1 characterized by N1. (Blue) Spindle microtubules in Group 2 characterized by ρ2. (Green) Astral microtubules outside spindle.
Our original model posits the following key assumptions about the spatiotemporal regulation on well-established experimental evidence:
-
(1)
Attachment of a kinetochore to the spindle microtubules induces a major change in the biochemical environment of the kinetochore and consequently a drastic shift in the protein dynamics at the kinetochore (Fig. 1 B). On an attached kinetochore the microtubules pulls the kinetochore away from the kinase-enriched inner centromere region and lowers the kinase activity at the kinetochore (24, 25, 26). These mitotic kinases regulate the protein dynamics at the kinetochore. On the one hand, high kinase activity promotes recruitment of SAC components onto the kinetochore (25, 27, 28). In the model, therefore, we assume a significant lower recruitment rate on attached kinetochores. On the other hand, high kinase activity inhibits dynein-mediated poleward streaming of the SAC components (29). Although SAC components continuously turn over from the unattached kinetochores (30, 31, 32), they do not form poleward streams, i.e., are not activated for poleward transport until the kinetochore is attached (33, 34, 35). Based on this observation, we assume in the model that SAC components that emanated from the attached kinetochores assume the streaming state, capable of traveling along the spindle microtubules toward the pole, while those that emanated from the unattached kinetochores assume the purely diffusive state, without binding affinity to the microtubule. The unattached and attached kinetochores essentially convert the SAC components in opposite directions between the streaming and diffusive states.
-
(2)
Binding to and traveling along the microtubules impose on the streaming SAC components a spatial regulation effect determined by the microtubule network in the cell (36, 37). In mitosis, the microtubule network is characterized by high microtubule density within the spindle structure, with minus-ends of the microtubules pointing toward the spindle poles (38). Such microtubule organization funnels the SAC components toward the spindle poles (36, 37), upon which the proteins are partially sequestered by the poles (Fig. 1 B).
The model predicts a nonlinear change in SAC concentration at the spindle pole in response to successive kinetochore-spindle attachments (23). The nonlinear response arises from a diversion effect on the poleward stream of SAC proteins by unattached kinetochores (Fig. 1 B). The streaming protein assumed in the model corresponds to a complex of dynein motor and cargo SAC components. Due to limited processivity of dynein, most streaming dynein-cargo complexes can temporarily fall off the microtubule before they reach the spindle pole (Fig. 1 B, black bent arrows) (39, 40). While not associated with the microtubule, the proteins have the chance to diffuse back to the kinetochores; most end up onto unattached kinetochores due to their higher recruitment rate (Fig. 1 B, magenta translucent arrow pointing toward the unattached kinetochore). The unattached kinetochores then convert the proteins back to the diffusive state, and thus effectively divert the poleward stream (Fig. 1 B, green translucent arrow). The diversion effect vanishes upon the final kinetochore attachment, causing a great boost in the protein flux toward the spindle pole (Fig. 1 B, right panel). The concentration of SAC components thus jumps at the spindle pole. From a broader perspective, kinetochores can be regarded as catalysis centers that interconvert the transport states of the SAC components in accordance to the status of kinetochore-spindle attachment. Upon the state conversion, the microtubule network shapes the spatial pattern of streaming SAC components through convection and diffusion. The spindle pole then leverages the concentration signal to control SAC silencing. Whether SAC silencing robustly occurs after the final kinetochore attachment depends both on the final signal level at the spindle pole and the jump ratio of the signal upon the final attachment (Fig. 1, A and B) (23, 24).
In this article, we focus on how robust and timely SAC silencing entails constraints on the dimensions of the mitotic spindle, and on the scaling relationship between spindle and cell sizes. Because microtubules serve as tracks for poleward convection, microtubule density directly regulates the signal level at the spindle pole and hence SAC silencing. Precisely addressing the effect of spindle size on SAC silencing thus warrants a model refinement in terms of how microtubule density redistributes in the cell as spindle size changes. Microtubules in a mitotic cell consist of two major populations: the spindle microtubules and the astral microtubules outside the spindle. Density of the astral microtubules is much lower than that of the spindle microtubules. In fact, the astral microtubules do not significantly affect the results (Fig. S1 in the Supporting Material). We thereby focus on the spindle microtubules in the model refinement.
Changing the spindle sizes inevitably affects the spatial profile of microtubule density in the spindle. Regardless of how microtubules are mechanistically organized, one can mathematically decompose the spindle microtubules into two groups: one with fixed number of microtubules and the other with fixed density of microtubules upon changes in spindle sizes (see Materials and Methods). The first group features a gradient of microtubule density that increases toward the spindle pole, whereas the second group supplies an even, base-level microtubule density in the spindle (Fig. 1 C). Linear combination of the two groups gives rise to a microtubule density profile in the spindle that increases from about the base level at the equator to a much higher level around the spindle pole. One might relate the two groups of microtubules to the kinetochore versus non-kinetochore microtubules (Fig. 1 C). Kinetochore microtubules (kMT) refer to those that form stable attachment with the kinetochores, and thus span the entire length of the half spindle between the kinetochore and spindle pole. As long as kinetochore-spindle attachments remain unchanged, the total number of microtubules in this group is conserved regardless of the spindle size. Nonkinetochore microtubules (non-kMT) are the highly dynamical microtubules that seed throughout the spindle (41, 42, 43, 44). Non-kMTs likely assume largely an even density profile, similar to that observed in bipolar spindle self-assembled in Xenopus egg extract without centrosomes (17). While different interpretations are possible and not necessarily exclude each other, for brevity, we will call the two groups of microtubules kMT and non-kMT in the rest of the article. The improved model setup does not alter the essence of robust SAC silencing (Fig. S2); but it characterizes the effects of size variations more accurately, and hence allows more realistic investigation of the principle of size scaling.
Allometric relationship between spindle length and width
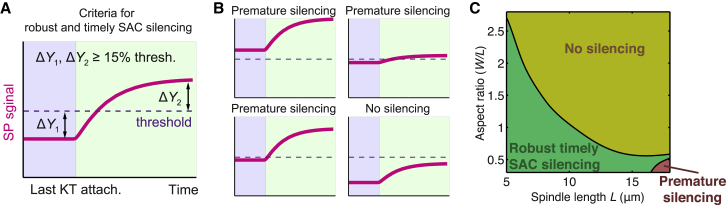
With the improved model, we first explore how length and width of the spindle affect the spindle pole signal for SAC silencing. Throughout the article we will characterize the effects on SAC silencing signal using the final steady-state signal at the spindle pole and the jump ratio of the signal upon the last kinetochore attachment. In particular, robust and timely SAC silencing requires the final signal level to exceed the threshold signal level, and robust SAC silencing additionally requires sufficient jump ratio (Fig. 2, A and B). For a chosen signal threshold (400 times bulk concentration in the cell) for triggering SAC silencing at the spindle pole, a case is defined as a “mitotic arrest” if the final steady-state spindle pole signal falls <115% of the threshold (Fig. 2 B), and “premature anaphase” if the steady-state spindle pole signal with one unattached kinetochore rises >85% of the threshold (Fig. 2 B). “Timely and robust SAC silencing” represents the cases in which the final signal is >115% threshold and the penultimate signal is <85% threshold (Fig. 2 A), a condition entailing a minimum jump ratio of 1.35. The criteria for timely and robust SAC silencing stem from our previous simulation results (23, 24). Having the penultimate signal >15% below the threshold ensures robust signaling against fluctuating noise; and having the final signal >15% above the threshold allows the signal to hit the threshold within reasonable time.
Figure 2.
Proper SAC silencing requires inverse correlation between spindle length and aspect ratio. (A) Criteria for robust and timely SAC silencing in model results. For the given threshold signal (400 times bulk concentration), the final steady-state signal has to be at least 15% above threshold and the penultimate steady-state signal at least 15% below threshold. (B) Examples of aberrancies in SAC silencing. Premature SAC silencing may result either from signals being too high (left panels) or insufficient jump ratio (upper-right panel). SAC silencing is inhibited if the signal is too low (lower-right panel). (C) Phase diagram of the SAC silencing behavior given spindle length and aspect ratio (i.e., spindle width/spindle length). Categorization of the simulation results follows the rules illustrated in (A) and (B).
We simulate the model with different lengths and widths of the spindle with the cell diameter fixed at 20 μm, and the spindle pole diameter fixed at 1 μm as normal somatic cell mitosis entails (Fig. 1 A). We summarize the simulation results in a phase diagram showing the predicted mitotic fate as a function of spindle dimensions (Fig. 2 C). The phase diagram shows that robust and timely SAC silencing requires an allometric relationship between spindle length and spindle width (Fig. 2 C). On average, longer spindle sets stronger constraint on the spindle width, and requires particularly low aspect ratio in the spindle for proper SAC silencing (Fig. 2 C). Deviations from the preferred allometry could cause aberrancy in SAC silencing. Specifically, a spindle too wide tends to incur mitotic arrest, and a spindle too narrow tends to incur premature anaphase onset (Fig. 2 C). In other words, conditions for proper SAC silencing could constrain the relationship between spindle length and spindle width. The findings suggest that the observed allometric scaling between spindle length and spindle width (11, 12) might be shaped by the functional requirement for proper SAC signaling.
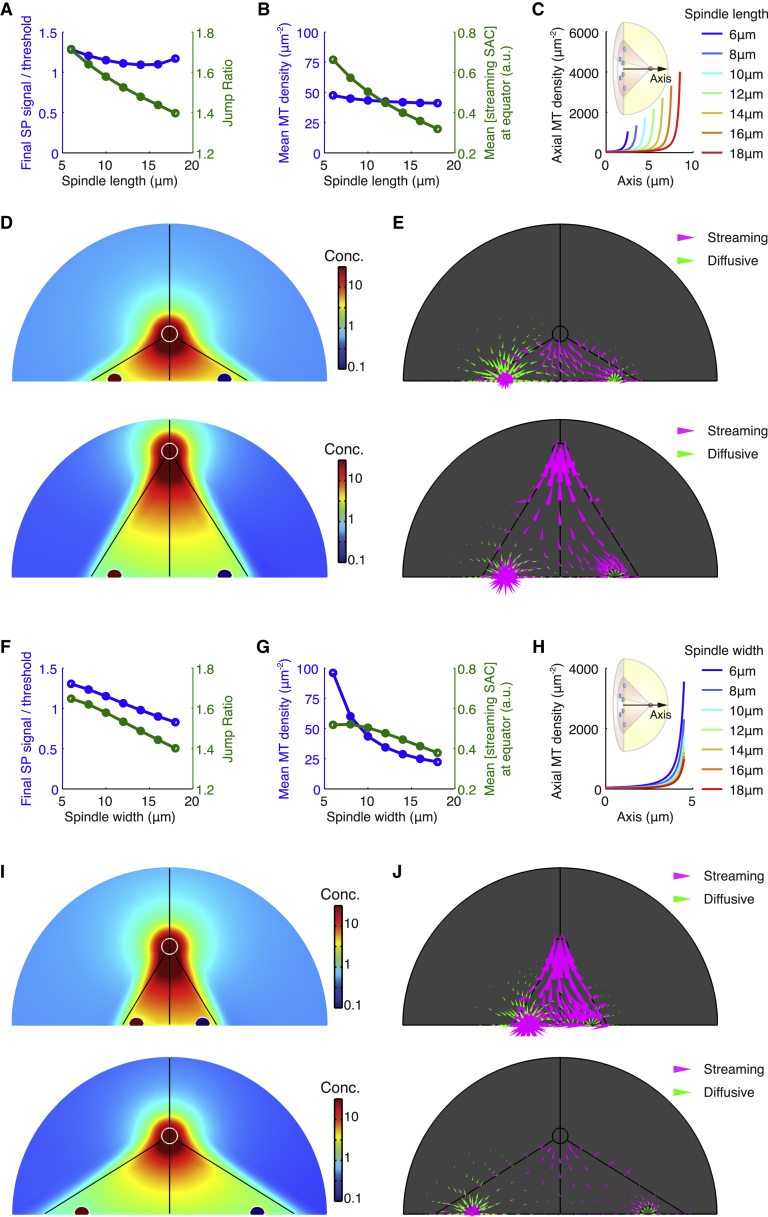
To better understand the predicted allometric relationship, we next investigate the effects of spindle length and spindle width separately. With fixed spindle width at 10 μm, the model results show that increasing the spindle length reduces the jump ratio (Fig. 3 A, green line), but barely affects the final spindle pole signal (Fig. 3 A, blue line). Noticeably, the mean density of microtubules in the spindle stays nearly unchanged as spindle length varies (Fig. 3 B, blue line). Conserved mean microtubule density in the spindle contributes to similar overall poleward flux and similar protein concentration at the spindle pole after the last kinetochore-spindle attachment. Nevertheless, the jump ratio drops in longer spindles, due to an effective inhibition of the diversion effect by the spindle pole. Just as the unattached kinetochore diverts the streaming proteins from entering the spindle pole, the spindle pole, from the opposite point of view, competes with the unattached kinetochore for streaming proteins and curbs the diversion effect. For this reason, increasing microtubule density without changes in spindle sizes lowers the jump ratio while boosting the spindle pole signal (Fig. S3). Strength of the competition by spindle pole reflects how hard the streaming proteins could escape from the spindle pole and diffuse back to the kinetochores. Due to extremely high microtubule density surrounding the spindle pole, a streaming protein released from the spindle pole tends to quickly reassociate with microtubules and return to the spindle pole. Therefore, higher microtubule density around the spindle pole in longer spindles (Fig. 3 C) promotes the competition. Meanwhile, a longer spindle gives longer distance between the spindle pole and the kinetochores, which makes it harder for streaming proteins to escape from poleward streaming and reach the kinetochores through diffusion. Accordingly, the proteins form a steeper concentration gradient in a longer spindle (Fig. 3 D), leaving a relatively smaller amount of streaming proteins accessible for the unattached kinetochores (Fig. 3 B, green line; Fig. 3 D). This effect ultimately compromises the flux diversion (Fig. 3 E) and hence reduces the jump ratio (Fig. 3 A). The low jump ratio particularly narrows down the admissible zone for proper SAC silencing in very long spindles (Fig. 2 C).
Figure 3.
Analysis for dependence of signal on spindle sizes. (A–E) Analysis for results with fixed spindle width and varying spindle lengths. (F–J) Analysis for results with fixed spindle length and varying spindle widths. (A and F) Final steady-state signal relative to the given threshold and jump ratio. (B and G) Mean microtubule density in the spindle and mean concentration of streaming SAC proteins at the equator (accessible for recruitment by kinetochores). (C and H) Microtubule density profiles along the spindle axis. (D and I) Concentration of SAC proteins inside the cell. (E and J) Flux map of streaming versus diffusive SAC proteins inside the cell. Arrow size is proportional to logarithm of flux intensity. (D and E, upper panels) Spindle width = 10 μm; spindle length = 6 μm. (D and E, lower panels) Spindle width = 10 μm; spindle length = 18 μm. (I and J, upper panels) Spindle length = 10 μm; spindle width = 6 μm. (I and J, lower panels) Spindle length = 10 μm; spindle width = 18 μm.
In comparison, increase in spindle width with spindle length fixed at 10 μm (Fig. 3 F, green line) affects the jump ratio less strongly than increase in spindle length does (Fig. 3 A, green line); but it causes a sizeable decrease in the final spindle pole signal (Fig. 3 F, blue line). In contrast to lengthening the spindle, widening the spindle significantly reduces microtubule density in the spindle (Fig. 3 G, blue line). Low microtubule density accordingly decreases the poleward flux and spindle pole signal after the last kinetochore-spindle attachment. Regarding the jump ratio, although lower microtubule density in wider spindles (Fig. 3, G and H) weakens the competition by spindle pole and thus promotes the jump ratio, the effect is outcompeted by the effect of another factor: dilution of protein concentration in wider spindles with larger volumes (Fig. 3 I). Overall, a smaller amount of streaming proteins can be recruited and diverted by the unattached kinetochores (Fig. 3 G, green line; Fig. 3 J), leading to a lower jump ratio. In other words, increasing spindle width results in two opposing effects, and hence keeps the jump ratio relatively insensitive to changes in spindle width (Fig. 3 F). We note that lengthening the spindle also increases the spindle volume (Fig. 3 D) and yields the dilution effect. But the dilution effect cooperates with higher microtubule density near the spindle pole (Fig. 3 C) to suppress the protein concentration near the equator (Fig. 3 B, green line) and reduce the jump ratio, instead of counteracting each other.
In sum, the spindle pole signal largely depends on the overall microtubule density in the spindle, but the jump ratio, which relies on the concentration of streaming proteins available to the unattached kinetochores, is regulated by the size-dependent changes in the microtubule density profile in the spindle. Altogether, robust, timely SAC silencing might have functionally shaped the observed allometric relationship between spindle length and width (11, 12).
Scaling between spindle size and cell size
We next examine how the scaling between spindle size and cell size affects the spindle pole-mediated SAC silencing. This is motivated by the observed universal scaling law between spindle size and cell size across the Metazoa (5), and the critical cell size at ∼100 μm, beyond which the spindle size remains relatively fixed as the cell size further increases.
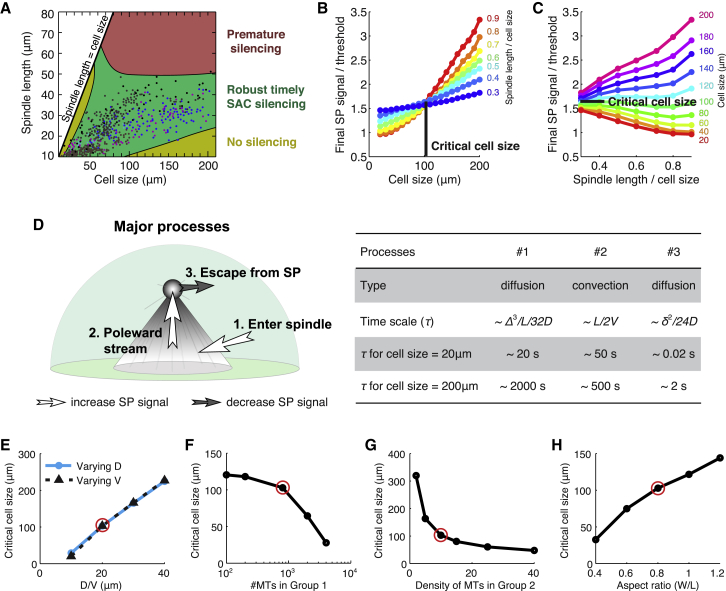
To address the above question, we simulate the model with different cell sizes and spindle sizes. We fix the ratio between cell size and spindle pole size, as suggested by experiments (10, 13). For simplicity, we also fix the aspect ratio between the spindle length and width for now. We obtain a phase diagram of mitotic fates following the same criteria as those given in Fig. 2 A. The admissible zone of cell size and spindle size required for robust, timely SAC silencing (Fig. 4 A) indeed shows strong correlation between cell size and spindle size up to a critical cell size at ∼100 μm. The admissible spindle size appears bounded by some maximum value as the cell size increases beyond the critical size (Fig. 4 A). The predicted biphasic relationship between spindle size and cell size is consistent with the experimental data (5) (Fig. 4 A, colored dots). Notice that the predicted functional requirements for robust SAC silencing entail necessary, but not sufficient conditions for spindle size scaling. The mechanistic process of spindle assembly likely introduces additional constraints on sizing of the spindle, e.g., force balance between molecular motors. Therefore, it is reasonable that the predicted zone is broader than the observed size scaling (Fig. 4 A). Nevertheless, it is deeply interesting to see the general biphasic behavior and maximum spindle size emerging from the model.
Figure 4.
Proper SAC silencing requires biphasic scaling law between spindle size and cell size. (A) Phase diagram of SAC silencing behavior given cell size and spindle length. The aspect ratio is fixed at 0.8. The experimental data (colored dots) are adapted from Crowder et al. (5). (B and C) Final signal at the spindle pole as function of cell size and spindle size. The spindle size is normalized against cell size to demonstrate relative size. The final signal is expressed in relative level to the threshold value. A critical cell size exists upon which the dependence of the spindle pole signal on spindle size switches direction. (D) Major processes that determine the spindle pole signal, along with estimated timescales for each process in small and large cells (Table S1). (E–H) Dependence of critical cell size on various model parameters. In (D–H), D ∼ diffusion coefficient of streaming proteins; V ∼ convection speed of streaming proteins; Δ ∼ cell diameter; L ∼ spindle length; and δ ∼ diameter of spindle pole (compare to Fig. 1A). Red circles: nominal parameter values (Table S1).
The predicted biphasic relationship stems from a reverse of correlation between spindle pole signal and spindle size around the critical cell size (Fig. 4, B and C). On the one hand, in small cells, increasing the spindle size reduces the spindle pole signal (echoing the results in the previous section); the opposite happens when the cell size becomes sufficiently large (Fig. 4, B and C). On the other hand, for a fixed ratio between cell size and spindle size, increasing the cell size almost always promotes spindle pole signal (Fig. 4 B). Therefore, in small cells, the effect of increasing cell size on the spindle pole signal is compensated by the effect of increasing spindle size, setting a positive correlation between cell size and spindle size under the requirement of timely SAC silencing. In large cells, however, the reversed dependence of spindle pole signal on the spindle size entails a significant change in the admissible correlation between spindle size and cell size.
While in the above simulations we have fixed the aspect ratio between the spindle length and width, as well as the ratio between cell size and spindle pole size, biphasic scaling between cell size and spindle size arises from the reverse of spindle size-spindle pole signal relationship as a general result for different spindle aspect ratios (Fig. S4), different relationships between cell size and spindle pole size (Fig. S5), and different spatial profiles of spindle microtubule density (Fig. S6). This universal behavior can be understood in light of a dimension analysis of the spatiotemporal regulation mechanism. For a compartmentalized spatial regulation mechanism like that modeled here, the partitioning of spatially regulated molecules into a particular compartment depends on the balance of material fluxes in and out of the compartment. Different fluxes reflect processes associated with different timescales; the ratio between the timescales for influx and efflux generally determines the steady-state level of molecule concentration in the compartment of interest. In the spatiotemporal regulation of SAC, the concentration at spindle pole largely comprises streaming proteins. Most streaming proteins accumulating at the spindle pole reach the pole through the following processes (Fig. 4 D): they first enter the microtubule-dense spindle from the microtubule-scarce cytoplasm, and then travel to the spindle pole via microtubule-mediated transport. Finally, the constant turnover of proteins from the spindle pole into the spindle and cytoplasm balances the influx to set the outcome concentration of proteins at the spindle pole. In this regard, the spindle pole signal critically depends on how fast the streaming proteins reach the spindle via diffusion and how fast they reach the spindle pole via convection. These two processes assume the longest timescales among various processes that promote the spindle pole signal (Figs. 5 A and S7), and thus become the rate-limiting steps that determine the final outcome. An increase in the spindle size (L) facilitates entrance into the spindle via diffusion, but delays poleward convection into the spindle pole (Fig. 4 D; Table S1). In small cells, diffusion is relatively fast compared to convection, making poleward convection the rate-limiting step (Fig. 4 D; Table S1). Thus, slower poleward convection caused by larger spindle size manifestly reduces the spindle pole signal (Fig. 5 B). In larger cells, contrarily, diffusion into the spindle is slow and rate-limiting (Fig. 5 B); hence increasing spindle size promotes the spindle pole signal by enhancing the resource of poleward streaming in the spindle (Fig. 5 B). To some extent, in a sufficiently large cell, diffusion becomes so slow that the spindle essentially loses sight of the cell boundary (Fig. 5 C): high concentration of streaming proteins inside the spindle mediates a local concentration gradient around the spindle that fades before the cell boundary is reached (Fig. S8). With the spindle size fixed as is, further increase in the cell size does not affect the spindle pole signal (Fig. S8). In this regime, therefore, spindle size is no longer correlated with cell size to ensure proper SAC silencing.
Figure 5.
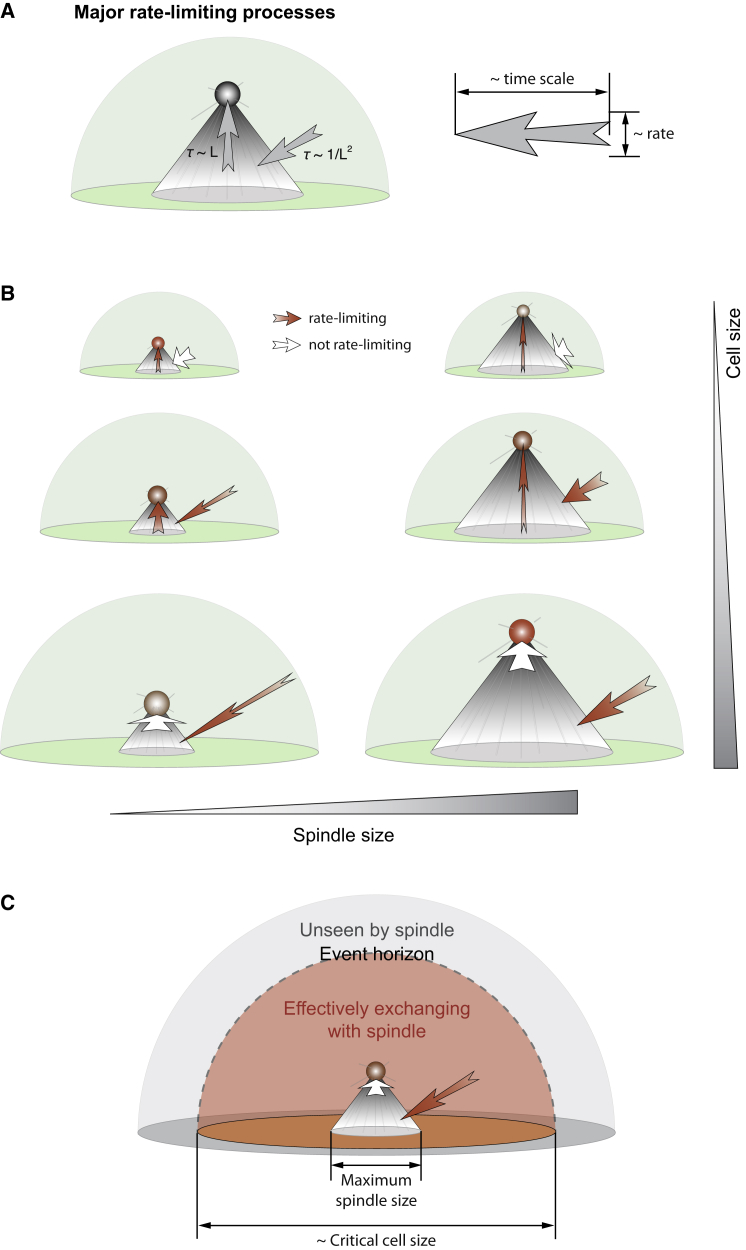
Illustrative summary of theory on spindle-cell size scaling. (A) Recapitulation of major rate-limiting processes related to the spatiotemporal regulation of SAC proteins: 1) diffusion into spindle and 2) poleward convection inside the spindle. The two processes scale with spindle size with opposite trends. (B) Illustration of how the rate-limiting step affects the spindle pole signal. The rate-limiting step changes from poleward convection to diffusion into spindle as the cell size increases. Hence, in small cells, a large spindle slows down convection and reduces spindle pole signal. In large cells, however, a large spindle facilitates diffusion into spindle and enhances spindle pole signal. (C) Event horizon for spindle-cytoplasm exchange. In large cells where diffusion into spindle is rate-limiting, the diffusion process imposes a gradient with a characteristic length scale. The length scale corresponds to the critical cell size. Above the critical cell size, extra cytoplasm outside the event horizon (dashed outline of the orange area) cannot exchange proteins effectively with the spindle, and is thus effectually unseen by the spindle.
Because competition between convection and diffusion timescales gives rise to the biphasic scaling law, one would expect the transitional cell size to rely on the diffusion coefficient and convection speed. Indeed, model simulations show that the critical cell size correlates linearly with the ratio between the diffusion coefficient and convection speed (Fig. 4 E). Furthermore, the critical cell size decreases as the number of kMTs or density of non-kMTs increase in the spindle (Fig. 4, F and G). This is because higher microtubule density in the spindle promotes poleward convection, and hence makes convection less likely to be the rate-limiting step. Finally, increasing the aspect ratio of the spindle shifts the critical cell size to higher value (Fig. 4 H). This is because given a specific spindle length, wider spindles are easier to target through diffusion, and thereby make diffusion less likely to be rate-limiting. Albeit affecting the critical cell size, most of these various factors represent the basic biophysical properties of the dynein motors and spindle assembly. Central and conserved as mitosis is for life, these factors are likely highly consistent throughout a wide array of organisms, leading to a universal scaling law between cell size and spindle size as observed (5).
Overall, our finding suggests a common origin of the size scaling that is relatively independent of system specifics, and provides an explanation for the observed scaling law across metazoan species from a functional perspective (5).
Discussion
Size scaling is a fascinating topic in biology that bears significant implications in evolution, and has been addressed and reviewed in many seminal works, e.g., Marshall et al. (45). In this work, we leverage our previously established spatiotemporal model framework for SAC silencing to deduce functional requirements for sizing of the mitotic spindle. The model results explain the observed allometric relationship between spindle length and width. Most strikingly, the model explains the observed universal scaling law between the cell size and spindle size. The biphasic scaling law emerges because increasing the cell size causes a transition of the rate-limiting step from poleward convection to diffusional targeting of the spindle. Because the rates of the two processes depend on the spindle size in opposite manners, the relationship between the spindle pole signal and spindle size relies on which step is rate-limiting. At the transitional cell size, the two processes tie—above the size diffusion limits the outcome; and below the size convection limits.
Allometry has been observed and studied in many fields. Allometric size relationship often roots in differential size dependences of interacting processes, very much like what we find here in the spatiotemporal mechanism for SAC silencing. In biomechanics, for example, it is well known that structures of wings and operational modes of flying differ dramatically in flying organisms of different sizes (46). This is because in large objects with high absolute speed, inertial force dominates over viscous force, and vice versa in microscopic objects with low speed. Therefore, large birds can take advantage of inertia to glide and save energy, whereas tiny birds and insects resort to high-frequency wing flapping. In the study of flying mechanisms people usually use the dimensionless Reynolds number to characterize the ratio between inertial force and viscous force (46).
In our case, it is the competition between diffusion and convection that lies in the core. This competition can be depicted by another dimensionless number, the Péclet number, Pe = LV/D, where L is the characteristic length, V is poleward convection speed, and D is diffusion coefficient. When the cell size changes, the system shifts from low to high Péclet number, i.e., from convection-limited to diffusion-limited. Variations in spindle size impose opposite effects on the spindle pole signal depending on the magnitude of the Péclet number. In this sense, this work reveals a universal organizational principle underlying the size scaling law in the mitotic process.
This work presents the simplest investigation into how proper functioning of SAC silencing constrains scaling of the spindle size. Only the roles of spindle dimensions and cell size on SAC silencing are tested by simulations, while all the other factors in the spindle configuration are kept fixed, e.g., microtubule density profile, spindle aspect ratio, and the ratio between spindle pole size and the cell size. In reality, these other factors may well vary across the metazoan kingdom. As exemplified in Figs. S4–S6, however, changes in any of these factors alone do not affect the qualitative essence of biphasic size scaling in the model prediction. This work represents a starting point for theorizing spindle size scaling. Further refinement of the model calls for future experiments that accurately characterize the spindle geometry and its relationship with SAC silencing—particularly how various factors in the spindle configuration correlate with each other in vivo.
In addition to keeping many factors of spindle configuration constant, we predict the spindle-cell size scaling relation (Fig. 4 A) by fixing both the number of chromosomes and the protein dynamics at the kinetochores. Yet the number of chromosomes varies greatly among animal cells, and the protein dynamics may also quantitatively differ in different species. Model results show that changes in the number of chromosomes alone do not affect the final signal level at the spindle pole (Fig. S9 A). Therefore, all the reasoning about timescale balancing (Figs. 4 D and 5) persists, and the biphasic transition on the phase plot should still hold at the same critical cell size. Instead of affecting the signal level, increasing the number of chromosomes significantly lowers the jump ratio and signal robustness (Fig. S9 B). This is because a single unattached kinetochore fails to divert the poleward streaming activated from too many attached kinetochores. However, this negative effect on signal robustness can be rescued by adjusting the protein dynamics at the kinetochores. Particularly, increasing the contrast between the recruitment rates of SAC components onto the unattached versus attached kinetochores significantly improves the jump ratio of the signal (Fig. S9, B–D). This result suggests that different species might adapt the contrast of recruitment between two types of kinetochore to the number of chromosomes, to achieve robust SAC silencing and maintain viable cell divisions. On the other hand, more chromosomes might entail additional changes in spindle geometry, such as a wider spindle to align all chromosomes at the equator in metaphase. Such induced geometric variation might influence the size scaling between cell and spindle. If the protein dynamics at kinetochores is uncorrelated with the spindle geometry, then its adaption to the number of chromosomes is independent of the size scaling. Under this context, we only need to consider the effect of change in spindle geometry that is associated with the number of chromosomes. For example, a wider spindle for accommodating more chromosomes introduces variations in the aspect ratio of the spindle; and the aspect ratio was kept fixed when predicting the scaling between spindle size and cell size (Fig. 4, A and G). However, changing the aspect ratio either by using another constant value, or by making the value dependent on the spindle size or cell size, does not alter the qualitative prediction of biphasic size scaling (Fig. S4). Currently, it is unclear whether and how protein dynamics at kinetochores depends on the number of chromosomes and the spindle dimensions. It is an interesting and open question how such dependence, if existing, modulates the size scaling in spindle. We will address this topic in future work.
Moreover, there are many additional variations in different species or cell types that our model has not yet characterized. For instance, the microtubule distribution in the model remains highly simplified even though we have improved it by incorporating the number-conserved and density-conserved groups. Real mitoses likely involve complicated variations of different microtubule organization mechanisms and interdependence between mechanisms. As another example, cell-specific signaling pathway might impose different threshold signal levels for silencing SAC in different cells or different species. If the threshold value could change with the cell size or spindle size, the model might not predict a universal scaling law. Besides SAC silencing, the effectiveness of SAC activation may also depend on the spindle and cell sizes. We will leave further improvement of the model and analysis of size scaling to the future when more experimental data in these aspects become available.
Furthermore, this work focuses on the effect of spindle sizes in diploid animal cells. Could a similar sizing effect apply to other eukaryotic cell types such as plant cells? Interestingly, plant cells generally tolerate polyploidy much better than animal cells. As discussed above, a higher chromosome number alone could incur higher chance of premature SAC silencing and chromosome mis-segregation (Fig. S9). By incorporating salient features in plant mitosis, our preliminary results show that neither plant-specific features in the mitotic spindle geometry (e.g., centrosome-less spindle assembly and wide spindle poles), nor polyploidy-associated size changes (e.g., wider spindle and larger cell) are likely to compensate for loss of signal robustness due to higher kinetochore counts (Fig. S10, A–E). But again, a higher contrast in SAC recruitment between unattached and attached kinetochores could improve signal robustness and make plant cells more tolerant against polyploidy (Fig. S10, B and C). After all, we would like to further note that spatiotemporal patterns of SAC in plants are slightly different from those in animals (47). In the future, we will further investigate exactly how such differences affect SAC silencing and size scaling of spindles in plants.
In sum, the very fact that our model results recapitulate the observed universal scaling law without further assumptions suggests strong conservation of many features of the spindle and the underlying spindle assembly process. This finding sheds some light on the functional constraints on mitotic spindle assembly, which shapes spindle size scaling during evolution of animal cells.
Author Contributions
J.L. developed the concept; J.C. and J.L. designed the models; J.C. implemented the simulations and performed data analysis; J.C. and J.L. interpreted the data; and J.C. and J.L. wrote the article.
Acknowledgments
This work is supported by the intramural research program at the National Heart, Lung, and Blood Institute of the National Institutes of Health, Bethesda, MD.
Editor: Charles Wolgemuth.
Footnotes
Ten figures and one table are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(16)30619-1.
Appendix
The spatiotemporal model for SAC silencing is expressed as compartmentalized convection-diffusion-reaction equations (23). The SAC components diffuse in the cytoplasm and undergo dynein-mediated convection along the microtubules. The binding/unbinding of SAC components with microtubules and spindle poles are described by reaction terms. The system includes NKT kinetochore domains, two spindle pole domains, and two associated cytoplasm domains (Figure 1A). To minimize computation load, the simulations are carried out on a quarter geometry reduced by the vertical cross plane and the equatorial plane of the spindle.
As summarized in the main text, a SAC component assumes either the streaming or diffusive state in the cytoplasm. The streaming state is further broken down into two sub-states, one for proteins associated with the microtubule and actively traveling towards the spindle pole (Y1), and the other for molecules temporarily dissociated from the microtubule and diffusing (Y0). Inter-conversion between the two sub-states, Y0 and Y1, depicts the binding/unbinding between the streaming proteins and the microtubules. In addition, proteins in the diffusive state (Y00) diffuse without microtubule binding affinity. Note that Y0 can bind with microtubule, but Y00 cannot. The overall spatiotemporal dynamics in the cytoplasm reads as Eqs. 1–3. Reflective boundary condition applies at the cell boundary.
In cytoplasm:
| (1) |
| (2) |
| (3) |
Meanings and values of the parameters in Eqs. 1–3 are given in Table S1. Specifically, the streaming velocity points toward the nearest spindle pole, as indicated by the unit vector at any given location in the cell, . The binding rate of streaming proteins to microtubules, konMT, is proportional to the local microtubule density ρMT (Eq. 4). Uext denotes the sequestration potential imposed by the spindle on the streaming proteins; it phenomenologically integrates all sequestrating factors that tend to retain SAC components within the spindle apparatus, e.g., association with spindle matrix (48, 49, 50), peri-spindle membranous networks (49, 51). kB is the Boltzmann constant, and T is temperature.
The microtubule network is treated as a mean density field that includes both the spindle and astral microtubules (Eq. 4). As mentioned in the main text, the microtubules in the spindle are decomposed into a group with fixed number (N1) and another group with fixed density (ρ2) upon changes in spindle sizes.
| (4) |
where is the distance toward the nearest spindle pole. N1 is the number of microtubules in Group 1. ρ2 is the microtubule density in Group 2. Nast denotes the number of astral microtubules outside the spindle. The astral microtubules are organized by the centrosome and hence the density should increase toward the spindle pole. For simplicity, density of the astral microtubules assumes the same form as Group 1 inside the spindle. α is half the vertex angle of the half spindle, i.e., . The denominators in Eq. 4 correspond to the in-spindle and out-of-spindle areas of the spherical surface with distance to the spindle pole. In reality, the microtubules undergo fast dynamics. But since the time scale associated with microtubule dynamics (∼30 s or less) is much shorter than the time scale associated with the change in spindle pole signal (∼10 min in typical somatic cell mitosis and much longer in larger cells (23, 52)), the microtubule dynamics are essentially averaged out and lumped into the binding/unbinding dynamics of the streaming proteins to the microtubules.
The model further assumes specific binding/unbinding of SAC components with the spindle pole. The spindle pole domain thus supports an additional state for the spindle-pole bound proteins (YP). YP lives exclusively on the spindle pole domain, and assumes the reflective boundary condition at the spindle pole boundary. The model sets the spindle pole as virtual domain for the other state variables, Y1, Y0 and Y00; therefore, Y1, Y0 and Y00 assume continuity conditions at the spindle pole boundary. Overall, Eqs. 5–8 depicts the spatiotemporal dynamics in the spindle pole domain.
At spindle pole:
| (5) |
| (6) |
| (7) |
| (8) |
The model assumes that the streaming proteins immediately fall off the microtubules upon entering the spindle pole ( = 40s−1 and = 0), bind with the spindle pole with rate konSP, and dissociate from the spindle pole with rate koffSP. Without detailed knowledge of the spindle pole-binding dynamics, this assumption characterizes partial sequestration of the streaming proteins at the spindle pole without loss of generality.
Finally, the kinetochore domains are separated from the cytoplasm. Each domain only accommodates the kinetochore-bound proteins (Eq. 9).
At the n-th kinetochore
| (9) |
The binding/unbinding dynamics to the kinetochore is characterized by the flux boundary conditions at the kinetochore boundaries.
At the boundary of unattached kinetochores, the boundary condition characterizes the strong recruitment and turnover as diffusive proteins:
| (10) |
| (11) |
| (12) |
| (13) |
At the boundary of attached kinetochores, the boundary condition characterizes the weak recruitment and issuance of streaming proteins:
| (14) |
| (15) |
| (16) |
| (17) |
In the above boundary conditions, n refers to the unit vector normal to the kinetochore boundary. Γ’s denote the fluxes of proteins across the kinetochore boundary; the subscripts indicate the proteins species associated with the specific flux. The saturating limit of kinetochore-bound proteins is set by the term . konKTu and konKTt are the recruitment rates of SAC components onto the unattached and the attached kinetochores, respectively. koffKT is the basic turnover rate of SAC components into the cytoplasm in the diffusive state; it applies to both types of kinetochores. kDoffKT is the transport activation rate of SAC components at the attached kinetochore.
In Eqs. 8–9, simple diffusion is applied to the spindle pole-bound (YP) and kinetochore-bound (YKn) species to homogenize the concentration of proteins in the spindle pole and kinetochore domain. This treatment takes place because our model concerns the average dynamics in these compartmentalized domains. With homogenization, the spindle pole signal and the flux across kinetochore boundaries depend on the average concentration of SAC components in the corresponding domains.
Supporting Citations
References (53, 54, 55, 56, 57, 58) appear in the Supporting Material.
Supporting Material
References
- 1.Morgan D.O. New Science Press; London, UK: 2007. The Cell Cycle—Principles of Control. [Google Scholar]
- 2.Walczak C.E., Heald R. Mechanisms of mitotic spindle assembly and function. Int. Rev. Cytol. 2008;265:111–158. doi: 10.1016/S0074-7696(07)65003-7. [DOI] [PubMed] [Google Scholar]
- 3.Musacchio A. Spindle assembly checkpoint: the third decade. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2011;366:3595–3604. doi: 10.1098/rstb.2011.0072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Musacchio A., Salmon E.D. The spindle-assembly checkpoint in space and time. Nat. Rev. Mol. Cell Biol. 2007;8:379–393. doi: 10.1038/nrm2163. [DOI] [PubMed] [Google Scholar]
- 5.Crowder M.E., Strzelecka M., Heald R. A comparative analysis of spindle morphometrics across metazoans. Curr. Biol. 2015;25:1542–1550. doi: 10.1016/j.cub.2015.04.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yamagata K., FitzHarris G. 4D imaging reveals a shift in chromosome segregation dynamics during mouse pre-implantation development. Cell Cycle. 2013;12:157–165. doi: 10.4161/cc.23052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hara Y., Kimura A. Cell-size-dependent spindle elongation in the Caenorhabditis elegans early embryo. Curr. Biol. 2009;19:1549–1554. doi: 10.1016/j.cub.2009.07.050. [DOI] [PubMed] [Google Scholar]
- 8.Wühr M., Chen Y., Mitchison T.J. Evidence for an upper limit to mitotic spindle length. Curr. Biol. 2008;18:1256–1261. doi: 10.1016/j.cub.2008.07.092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Farhadifar R., Baer C.F., Needleman D.J. Scaling, selection, and evolutionary dynamics of the mitotic spindle. Curr. Biol. 2015;25:732–740. doi: 10.1016/j.cub.2014.12.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Courtois A., Schuh M., Hiiragi T. The transition from meiotic to mitotic spindle assembly is gradual during early mammalian development. J. Cell Biol. 2012;198:357–370. doi: 10.1083/jcb.201202135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hara Y., Kimura A. An allometric relationship between mitotic spindle width, spindle length, and ploidy in Caenorhabditis elegans embryos. Mol. Biol. Cell. 2013;24:1411–1419. doi: 10.1091/mbc.E12-07-0528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Young S., Besson S., Welburn J.P. Length-dependent anisotropic scaling of spindle shape. Biol. Open. 2014;3:1217–1223. doi: 10.1242/bio.201410363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Decker M., Jaensch S., Hyman A.A. Limiting amounts of centrosome material set centrosome size in C. elegans embryos. Curr. Biol. 2011;21:1259–1267. doi: 10.1016/j.cub.2011.06.002. [DOI] [PubMed] [Google Scholar]
- 14.Greenan G., Brangwynne C.P., Hyman A.A. Centrosome size sets mitotic spindle length in Caenorhabditis elegans embryos. Curr. Biol. 2010;20:353–358. doi: 10.1016/j.cub.2009.12.050. [DOI] [PubMed] [Google Scholar]
- 15.Good M.C., Vahey M.D., Heald R. Cytoplasmic volume modulates spindle size during embryogenesis. Science. 2013;342:856–860. doi: 10.1126/science.1243147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hazel J., Krutkramelis K., Gatlin J.C. Changes in cytoplasmic volume are sufficient to drive spindle scaling. Science. 2013;342:853–856. doi: 10.1126/science.1243110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Reber S.B., Baumgart J., Jülicher F. XMAP215 activity sets spindle length by controlling the total mass of spindle microtubules. Nat. Cell Biol. 2013;15:1116–1122. doi: 10.1038/ncb2834. [DOI] [PubMed] [Google Scholar]
- 18.Ganem N.J., Compton D.A. The KinI kinesin Kif2a is required for bipolar spindle assembly through a functional relationship with MCAK. J. Cell Biol. 2004;166:473–478. doi: 10.1083/jcb.200404012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Loughlin R., Wilbur J.D., Heald R. Katanin contributes to interspecies spindle length scaling in Xenopus. Cell. 2011;147:1397–1407. doi: 10.1016/j.cell.2011.11.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wilbur J.D., Heald R. Mitotic spindle scaling during Xenopus development by Kif2a and importin alpha. eLife Sci. 2013;2:e00290. doi: 10.7554/eLife.00290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Brown K.S., Blower M.D., Heald R. Xenopus tropicalis egg extracts provide insight into scaling of the mitotic spindle. J. Cell Biol. 2007;176:765–770. doi: 10.1083/jcb.200610043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Conduit P.T., Raff J.W. CNN dynamics drive centrosome size asymmetry to ensure daughter centriole retention in Drosophila neuroblasts. Curr. Biol. 2010;20:2187–2192. doi: 10.1016/j.cub.2010.11.055. [DOI] [PubMed] [Google Scholar]
- 23.Chen J., Liu J. Spatial-temporal model for silencing of the mitotic spindle assembly checkpoint. Nat. Commun. 2014;5:4795. doi: 10.1038/ncomms5795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Liu D., Vader G., Lens S.M. Sensing chromosome bi-orientation by spatial separation of Aurora B kinase from kinetochore substrates. Science. 2009;323:1350–1353. doi: 10.1126/science.1167000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Welburn J.P., Vleugel M., Cheeseman I.M. Aurora B phosphorylates spatially distinct targets to differentially regulate the kinetochore-microtubule interface. Mol. Cell. 2010;38:383–392. doi: 10.1016/j.molcel.2010.02.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Maresca T.J., Salmon E.D. Intrakinetochore stretch is associated with changes in kinetochore phosphorylation and spindle assembly checkpoint activity. J. Cell Biol. 2009;184:373–381. doi: 10.1083/jcb.200808130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Famulski J.K., Chan G.K. Aurora B kinase-dependent recruitment of hZW10 and hROD to tensionless kinetochores. Curr. Biol. 2007;17:2143–2149. doi: 10.1016/j.cub.2007.11.037. [DOI] [PubMed] [Google Scholar]
- 28.Ditchfield C., Johnson V.L., Taylor S.S. Aurora B couples chromosome alignment with anaphase by targeting BubR1, Mad2, and Cenp-E to kinetochores. J. Cell Biol. 2003;161:267–280. doi: 10.1083/jcb.200208091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Whyte J., Bader J.R., Vaughan K.T. Phosphorylation regulates targeting of cytoplasmic dynein to kinetochores during mitosis. J. Cell Biol. 2008;183:819–834. doi: 10.1083/jcb.200804114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kallio M.J., Beardmore V.A., Gorbsky G.J. Rapid microtubule-independent dynamics of Cdc20 at kinetochores and centrosomes in mammalian cells. J. Cell Biol. 2002;158:841–847. doi: 10.1083/jcb.200201135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Howell B.J., Moree B., Salmon E.D. Spindle checkpoint protein dynamics at kinetochores in living cells. Curr. Biol. 2004;14:953–964. doi: 10.1016/j.cub.2004.05.053. [DOI] [PubMed] [Google Scholar]
- 32.Shah J.V., Botvinick E., Cleveland D.W. Dynamics of centromere and kinetochore proteins; implications for checkpoint signaling and silencing. Curr. Biol. 2004;14:942–952. doi: 10.1016/j.cub.2004.05.046. [DOI] [PubMed] [Google Scholar]
- 33.Basto R., Scaerou F., Karess R. In vivo dynamics of the rough deal checkpoint protein during Drosophila mitosis. Curr. Biol. 2004;14:56–61. doi: 10.1016/j.cub.2003.12.025. [DOI] [PubMed] [Google Scholar]
- 34.Famulski J.K., Vos L.J., Chan G.K. Dynein/dynactin-mediated transport of kinetochore components off kinetochores and onto spindle poles induced by nordihydroguaiaretic acid. PLoS One. 2011;6:e16494. doi: 10.1371/journal.pone.0016494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Buffin E., Lefebvre C., Karess R.E. Recruitment of Mad2 to the kinetochore requires the Rod/Zw10 complex. Curr. Biol. 2005;15:856–861. doi: 10.1016/j.cub.2005.03.052. [DOI] [PubMed] [Google Scholar]
- 36.Nédélec F., Surrey T., Maggs A.C. Dynamic concentration of motors in microtubule arrays. Phys. Rev. Lett. 2001;86:3192–3195. doi: 10.1103/PhysRevLett.86.3192. [DOI] [PubMed] [Google Scholar]
- 37.Chen J., Lippincott-Schwartz J., Liu J. Intracellular spatial localization regulated by the microtubule network. PLoS One. 2012;7:e34919. doi: 10.1371/journal.pone.0034919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Sharp D.J., Rogers G.C., Scholey J.M. Microtubule motors in mitosis. Nature. 2000;407:41–47. doi: 10.1038/35024000. [DOI] [PubMed] [Google Scholar]
- 39.King S.J., Schroer T.A. Dynactin increases the processivity of the cytoplasmic dynein motor. Nat. Cell Biol. 2000;2:20–24. doi: 10.1038/71338. [DOI] [PubMed] [Google Scholar]
- 40.Reck-Peterson S.L., Yildiz A., Vale R.D. Single-molecule analysis of dynein processivity and stepping behavior. Cell. 2006;126:335–348. doi: 10.1016/j.cell.2006.05.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Meunier S., Vernos I. Microtubule assembly during mitosis - from distinct origins to distinct functions? J. Cell Sci. 2012;125:2805–2814. doi: 10.1242/jcs.092429. [DOI] [PubMed] [Google Scholar]
- 42.Petry S., Groen A.C., Vale R.D. Branching microtubule nucleation in Xenopus egg extracts mediated by augmin and TPX2. Cell. 2013;152:768–777. doi: 10.1016/j.cell.2012.12.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Goshima G., Mayer M., Vale R.D. Augmin: a protein complex required for centrosome-independent microtubule generation within the spindle. J. Cell Biol. 2008;181:421–429. doi: 10.1083/jcb.200711053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Colombié N., Głuszek A.A., Ohkura H. Meiosis-specific stable binding of augmin to acentrosomal spindle poles promotes biased microtubule assembly in oocytes. PLoS Genet. 2013;9:e1003562. doi: 10.1371/journal.pgen.1003562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Marshall W.F., Young K.D., Roeder A.H.K. What determines cell size? BMC Biol. 2012;10:101. doi: 10.1186/1741-7007-10-101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Azuma A. 2nd Ed. AIAA Education; Reston, VA: 2006. The Biokinetics of Flying and Swimming. [Google Scholar]
- 47.Caillaud M.C., Paganelli L., Favery B. Spindle assembly checkpoint protein dynamics reveal conserved and unsuspected roles in plant cell division. PLoS One. 2009;4:e6757. doi: 10.1371/journal.pone.0006757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Zheng Y. A membranous spindle matrix orchestrates cell division. Nat. Rev. Mol. Cell Biol. 2010;11:529–535. doi: 10.1038/nrm2919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Johansen K.M., Forer A., Johansen J. Do nuclear envelope and intranuclear proteins reorganize during mitosis to form an elastic, hydrogel-like spindle matrix? Chromosome Res. 2011;19:345–365. doi: 10.1007/s10577-011-9187-6. [DOI] [PubMed] [Google Scholar]
- 50.Lince-Faria M., Maffini S., Maiato H. Spatiotemporal control of mitosis by the conserved spindle matrix protein Megator. J. Cell Biol. 2009;184:647–657. doi: 10.1083/jcb.200811012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Wolf K.W. Mitotic and meiotic spindles from two insect orders, Lepidoptera and Diptera, differ in terms of microtubule and membrane content. J. Cell Sci. 1990;97:91–100. [Google Scholar]
- 52.Chen J., Liu J. Erroneous silencing of the mitotic checkpoint by aberrant spindle pole-kinetochore coordination. Biophys. J. 2015;109:2418–2435. doi: 10.1016/j.bpj.2015.10.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Wang Z., Shah J.V., Cleveland D.W. In vivo quantitative studies of dynamic intracellular processes using fluorescence correlation spectroscopy. Biophys. J. 2006;91:343–351. doi: 10.1529/biophysj.105.077891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Wang Z., Sheetz M.P. One-dimensional diffusion on microtubules of particles coated with cytoplasmic dynein and immunoglobulins. Cell Struct. Funct. 1999;24:373–383. doi: 10.1247/csf.24.373. [DOI] [PubMed] [Google Scholar]
- 55.Ross J.L., Wallace K., Holzbaur E.L.F. Processive bidirectional motion of dynein-dynactin complexes in vitro. Nat. Cell Biol. 2006;8:562–570. doi: 10.1038/ncb1421. [DOI] [PubMed] [Google Scholar]
- 56.Needleman D.J., Groen A., Mitchison T. Fast microtubule dynamics in meiotic spindles measured by single molecule imaging: evidence that the spindle environment does not stabilize microtubules. Mol. Biol. Cell. 2010;21:323–333. doi: 10.1091/mbc.E09-09-0816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Heald R., Tournebize R., Hyman A. Spindle assembly in Xenopus egg extracts: respective roles of centrosomes and microtubule self-organization. J. Cell Biol. 1997;138:615–628. doi: 10.1083/jcb.138.3.615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Famulski J.K., Vos L., Chan G. Stable hZW10 kinetochore residency, mediated by hZwint-1 interaction, is essential for the mitotic checkpoint. J. Cell Biol. 2008;180:507–520. doi: 10.1083/jcb.200708021. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.