pong: fast analysis and visualization of latent clusters in population genetic data

Abstract

Motivation: A series of methods in population genetics use multilocus genotype data to assign individuals membership in latent clusters. These methods belong to a broad class of mixed-membership models, such as latent Dirichlet allocation used to analyze text corpora. Inference from mixed-membership models can produce different output matrices when repeatedly applied to the same inputs, and the number of latent clusters is a parameter that is often varied in the analysis pipeline. For these reasons, quantifying, visualizing, and annotating the output from mixed-membership models are bottlenecks for investigators across multiple disciplines from ecology to text data mining.

Results: We introduce pong, a network-graphical approach for analyzing and visualizing membership in latent clusters with a native interactive D3.js visualization. pong leverages efficient algorithms for solving the Assignment Problem to dramatically reduce runtime while increasing accuracy compared with other methods that process output from mixed-membership models. We apply pong to 225 705 unlinked genome-wide single-nucleotide variants from 2426 unrelated individuals in the 1000 Genomes Project, and identify previously overlooked aspects of global human population structure. We show that pong outpaces current solutions by more than an order of magnitude in runtime while providing a customizable and interactive visualization of population structure that is more accurate than those produced by current tools.

Availability and Implementation: pong is freely available and can be installed using the Python package management system pip. pong’s source code is available at https://github.com/abehr/pong.

Contact: aaron_behr@alumni.brown.edu or sramachandran@brown.edu

Supplementary Information: Supplementary data are available at Bioinformatics online.

1 Introduction

A series of generative models known as mixed-membership models have been developed that model grouped data, where each group is characterized by a mixture of latent components. One well-known example of a mixed-membership model is latent Dirichlet allocation (Blei et al., 2003), in which documents are modeled as a mixture of latent topics. Another widely used example is the model implemented in the population-genetic program Structure (Falush et al., 2003; Hubisz et al., 2009; Pritchard et al., 2000; Raj et al., 2014), where individuals are assigned to a mixture of latent clusters, or populations, based on multilocus genotype data.

In this article, we focus on the population-genetic application of mixed-membership models, and refer to this application as clustering inference; see Novembre (2014) for a review of multiple population-genetic clustering inference methods, including Structure. In Structure’s Bayesian Markov chain Monte Carlo algorithm, individuals are modeled as deriving ancestry from K clusters, where the value of K is user-specified. Each cluster is constrained to be in Hardy-Weinberg equilibrium, and clusters vary in their characteristic allele frequencies at each locus. Clustering inference using genetic data is a crucial step in many ecological and evolutionary studies. For example, identifying genetic subpopulations provides key insight into a sample’s ecology and evolution (Bryc et al., 2010; Glover et al., 2012; Moore et al., 2014), reveals ethnic variation in disease phenotypes (Moreno-Estrada et al., 2014), and reduces spurious correlations in genome-wide association studies (Price et al., 2006; Patterson et al., 2006; Galanter et al., 2012).

For a given multilocus genotype dataset with N individuals and K clusters, the output of a single algorithmic run of clustering inference is an N × K matrix, denoted as Q, of membership coefficients; these coefficients can be learned using a supervised or unsupervised approach. Membership coefficient $q_{ij}$ is the inferred proportion of individual i’s alleles inherited from cluster j. The row vector ${\vec{q}}_{i·}$ is interpreted as the genome-wide ancestry of individual i, and the K elements of ${\vec{q}}_{i·}$ sum to 1. Each column vector ${\vec{q}}_{·j}$ represents membership in the jth cluster across individuals.

Although covariates—such as population labels, geographic origin, language spoken or method of subsistence—are not used to infer membership coefficients, these covariates are essential for interpreting Q matrices. Given that over 16 000 studies have cited Structure to date, and 100 or more Q matrices are routinely produced in a single study, investigators need efficient algorithms that enable accurate processing and interpretation of output from clustering inference.

Algorithms designed to process Q matrices face three challenges. First, a given run, which yields a single Q matrix, is equally likely to reach any of K! column-permutations of the same collection of estimated membership coefficients due to the stochastic nature of clustering inference. This is known as label switching: for a fixed value of K and identical genetic input, column ${\vec{q}}_{·j}$ in the Q matrix produced by one run may not correspond to column ${\vec{q}}_{·j}$ in the Q matrix produced by another run (Jakobsson and Rosenberg, 2007; Jasra et al., 2005; Stephens, 2000). In our analyses of the 1000 Genomes (phase 3; Consortium, 2015), label switching occurred in 62.64% of pairwise comparisons among runs; that is, many matrices of membership coefficients were identical once columns were permuted to match, and rapidly finding permutations that maximize similarity between Q matrices is computationally expensive as K increases.

Second, even after adjusting for label switching, Q matrices with the same input genotype data and the same value of K may differ non-trivially. This is known as multimodality (Jakobsson and Rosenberg, 2007), and occurs when multiple sets of membership coefficients can be inferred from the data. We refer to runs that, despite identical inputs, differ non-trivially as belonging to different modes. For a fixed value of K, a set of runs grouped into the same mode based on some measure of similarity can be represented by a single Q matrix in that mode. Many studies using the maximum-likelihood approach for clustering inference implemented in ADMIXTURE (Alexander et al., 2009) ignore manifestations of multimodality (Consortium, 2015; Homburger et al., 2015; Moreno-Estrada et al., 2013), despite the fact that ADMIXTURE can identify different local maxima across different runs for a given value of K (e.g. Verdu et al., 2014). The complete characterization of modes present in clustering inference output gives unique insight into genetic differentiation within a sample.

A third complication arises for interpreting clustering inference output when the input parameter K is varied (all other inputs being equal): there is no column-permutation of a $Q_{N\times K}$ matrix that exactly corresponds to any $Q_{N\times (K+1)}$ matrix. We refer to this as the alignment-across-K problem. A common pipeline when applying clustering inference methods to genotype data is to increment K from 2 to some user-defined maximum value K _max, although some clustering inference methods also assist with choosing the value of K that best explains the data (Huelsenbeck et al., 2011; Raj et al., 2014). K _max can vary a great deal across studies [e.g., K _max = 5 in Glover et al. (2012); K _max = 20 in Moreno-Estrada et al. (2014)]. Accurate and automated analysis of clustering inference output across values of K is essential both for understanding a sample’s evolutionary history and for model selection.

The label-switching, multimodality, and alignment-across-K challenges must all be resolved in order to fully and accurately characterize genetic differentiation and shared ancestry in a dataset of interest. Here, we present pong, a new algorithm for fast post-hoc analysis of clustering inference output from population genetic data combined with an interactive JavaScript visualization using Data-Driven Documents (D3.js; https://github.com/mbostock/d3). Our package accounts for label switching, characterizes modes, and aligns Q matrices across values of K by constructing weighted bipartite graphs for each pair of Q matrices based on similarity in membership coefficients between clusters. Our construction of these graphs draws on efficient algorithms for solving the combinatorial optimization problem known as the Assignment Problem, thereby allowing pong to process hundreds of Q matrices in seconds. pong displays a representative Q matrix for each mode for each value of K, and identifies differences among modes that are easily missed during visual inspection. We compare pong against current solutions [CLUMPP by Jakobsson and Rosenberg (2007); augmented as Clumpak by Kopelman et al. (2015)], and find our approach reduces runtime by more than an order of magnitude. We also apply pong to clustering inference output from the 1000 Genomes (phase 3) and present the most comprehensive depiction of global human population structure in this dataset to date. pong has the potential to be applied broadly to identify modes, align output, and visualize output from inference based on mixed-membership models.

2 Algorithm

2.1 Overview

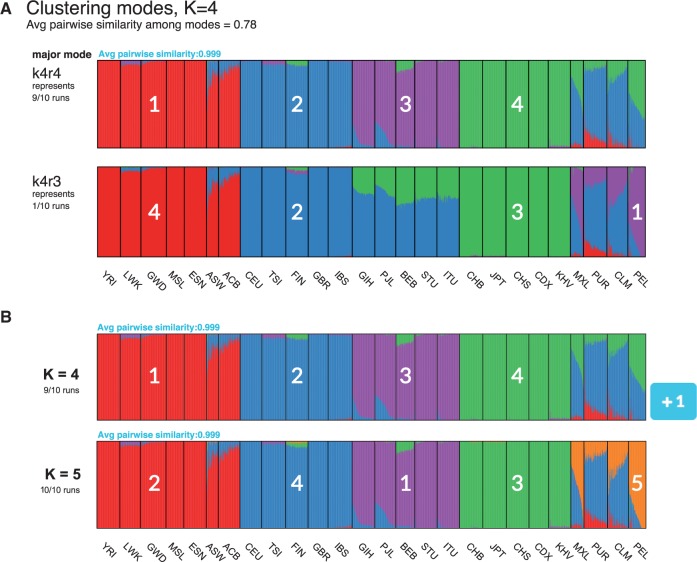
Figure 1 displays a screenshot of pong’s visualization of population structure in the 1000 Genomes data (phase 3; Consortium, 2015); final variant set released on November 6, 2014) based a set of 20 runs (K = 4, 5) from clustering inference with ADMIXTURE (Alexander et al., 2009). In order to generate visualizations highlighting similarities and differences among Q matrices, pong generates weighted bipartite graphs connecting clusters between runs within and across values of K (Sections 2.2, 2.3). Our goal of matching clusters across runs is analogous to the combinatorial optimization problem known as the Assignment Problem (Manber, 1989), for which numerous efficient algorithms exist (Kuhn, 1955, 1956; Munkres, 1957). pong’s novel approach of comparing clusters—column vectors of Q matrices—dramatically reduces runtime relative to existing methods that rely on permuting entire matrices.

Fig. 1.

pong’s front end produces a D3.js visualization of maximum-weight alignments between runs, shown here for 20 Q matrices produced from clustering inference with ADMIXTURE (Alexander et al., 2009) applied to 1000 Genomes data (phase 3; Consortium, 2015). Each individual’s genome-wide ancestry within a barplot is depicted by K stacked colored lines. The left-to-right order of individuals is the same in each barplot. The barplots here are annotated with numbers (white) indicating which column of the underlying Q matrix is represented by a given cluster. (A) Characterizing modes at K = 4 by displaying the representative run of the major mode (here, k4r4) and the representative run of each minor mode. Three-letter population codes are shown at the bottom. (B) The maximum-weight alignment for the representative run for the major mode at K = 4 (k4r4, panel A) to that at K = 5. Membership in cluster 4 at K = 4 represents shared ancestry in East Asian and admixed American populations, and has been partitioned into Clusters 3 and 5 (representing East Asian and Native American ancestry, respectively) in the representative run of the major mode at K = 5

Consider two Q matrices, $\mathcal{Q}=[q_{ij}]$ and $\mathcal{R}=[r_{ij}]$. Each weighted bipartite graph $G(\mathcal{Q},\mathcal{R})=(\{{\vec{q}}_{·j}\}\cup \{{\vec{r}}_{·k}\},E)$ encodes pairwise similarities between clusters in $\mathcal{Q}$ and clusters in $\mathcal{R}$. Edges in G are weighted according to a similarity metric computed between clusters (detailed in Supplementary Information); pong’s default similarity metric is derived from the Jaccard index used in set comparison, and emphasizes overlap in membership coefficients without incorporating individuals who have no membership in the clusters under comparison.

We define an alignment of $\mathcal{Q}$ and $\mathcal{R}$ as a bipartite perfect matching of their column vectors. pong’s first objective is to find the maximum-weight alignment for each pair of runs for a fixed value of K (Section 2.2). This information is used to identify modes within K, and we randomly choose a representative run (Q matrix) for each mode found in clustering inference. We call the mode containing the most runs within each value of K the major mode for that K value (Fig. 1A; ties are decided uniformly at random). pong’s second objective is to find the maximum-weight alignment between the representative run of each major mode across values of K (Section 2.3; Fig. 1B, Supplementary Figure S1). Identifying the maximum-weight alignment within and across K inherently solves the label switching problem without performing the computationally costly task of comparing whole-matrix permutations. Last, pong colors the visualization and highlights differences among modes based on these maximum-weight alignments.

2.2 Aligning runs for a fixed value of K and characterizing modes

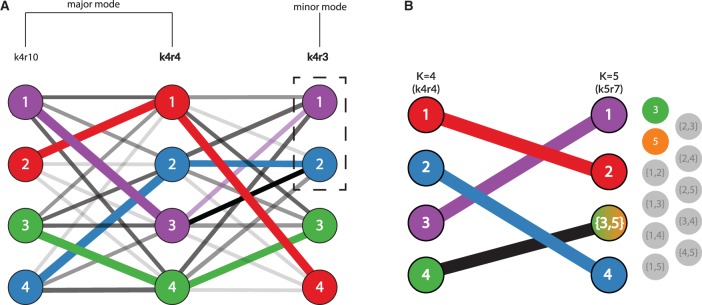
In order to identify modes in clustering inference for a fixed value of K = k, pong first uses the Munkres algorithm (Munkres, 1957) to find the maximum-weight alignment between each pair of runs at K = k (Fig. 2A). Next, for each value k, pong constructs another graph $G_k=(\{Q_{N\times k}\},E)$, where each edge connects a pair of runs, and the weight of a given edge is the average edge weight in the maximum-weight alignment for the pair of runs that edge connects. (The edge weight between a run and itself is 1.) The edge weight for a pair of runs in G_k encodes the similarity of the runs, and we define pairwise similarity for a pair of runs as the average edge weight in the maximum-weight alignment across all clusters for that pair. We use the average edge weight to compute pairwise similarity instead of the sum of edge weights so that edges in G_k are comparable across values of K.

Fig. 2.

pong’s back-end model for the alignment of Q matrices, shown here from clustering inference with ADMIXTURE (Alexander et al., 2009) applied to 1000 Genomes data (phase 3; Consortium, 2015). Panel labels correspond to panels in Figure 1, and numbers in graph vertices correspond to the clusters labeled in Figure 1. (A) Characterizing modes from three runs of clustering inference at K = 4, the smallest K value with multiple modes for this dataset. Edge thickness corresponds to the value of pong’s default cluster similarity metric $\mathcal{J}$ (derived from Jaccard’s index; see Supplementary Materials), while edge opacity ranks connections for a cluster in run k4r4 to a cluster in run k4r3 (or in run k4r10). Note that both cluster 2 and 3 in k4r4 are most similar based on metric $\mathcal{J}$ to cluster 2 in k4r3; in order to find the maximum-weight perfect matching between the runs, pong matches cluster 3 in k4r4 with cluster 1 in k4r3. Bold labels indicate representative runs for the two modes. Seven other runs (not displayed for ease of visualization) are grouped in the same mode as k4r4 and k4r10; these nine runs comprise the major mode at K = 4 (Fig. 1A). k4r3 is the only run in the minor mode (Fig. 1A). (B) Alignment of representative runs for the major modes at K = 4 to K = 5. $\left(\begin{array}{c}5\\ 2\end{array}\right)=10$ alignments are constructed between k4r4 and k5r7 (the representative run of the major mode at K = 5), constrained by the use of exactly one union node at K = 5. Of these 10 alignments, the alignment with maximum edge weight is shown and matches cluster 4 in k4r4 to the sum of clusters 3 and 5 in k5r7. The best matching for all other clusters are shown and informs the coloring of pong’s visualization (see Fig. 1B)

If a pair of runs has pairwise similarity less than 0.97 (by default; this threshold can be varied), the edge connecting that pair of runs is not added to G_k; this imposes a lower bound on the pairwise similarity between two runs in the same mode. pong defines modes as disjoint cliques in G_k, thereby solving the multimodality problem. Our approach is informed by the fact that modes differ in only a subset of membership coefficients, eliminating the need for permuting whole matrices to align runs. Once cliques are identified, a run is chosen at random to be the representative run for each mode at K = k, which enables consistent visualization of clustering inference output within each value of K.

2.3 Aligning a Q_N×K matrix to a Q_{N× (K+1)} matrix

Consider two Q matrices ${\mathcal{T}}_{N\times k}$ and ${\mathcal{U}}_{N\times (k+1)}$ where $\mathcal{T}$ and $\mathcal{U}$ represent the major modes at K = k and $K=(k+1)$, respectively. No perfect matching can be found between the clusters in $\mathcal{T}$ and the clusters in $\mathcal{U}$ because these matrices have different dimensions. In order to align these matrices, pong leverages the fact that column vectors of membership coefficients are partitioned as K increases and summed as K decreases (Fig. 1B).

For the pair of clusters ${\vec{u}}_{·a}$ and ${\vec{u}}_{·b}$ in $\mathcal{U}$, we define the union node ${\vec{u}}_{·\{a,b\}}={\sum }_{i=1}^N{u}_{ia}+u_{ib}$. pong then constructs the matrix $\mathcal{U}(a\cup b)$, which contains the clusters ${\vec{u}}_{·i}$ for $i\ne a,b$ and the union node ${\vec{u}}_{·\{a,b\}}$. Therefore, the dimension of $\mathcal{U}(a\cup b)$ is N × K, which is the same as the dimension of $\mathcal{T}$ (Fig. 2B). pong then finds the maximum-weight alignment between $\mathcal{T}$ and $\mathcal{U}(a\cup b)$ using the Munkres algorithm (Munkres, 1957). After finding the maximum-weight alignment for each pair of matrices $\mathcal{T}$ and $\mathcal{U}(i\cup j:i\ne j)$, the alignment that has the greatest average edge weight across all these $\left(\begin{array}{c}k+1\\ 2\end{array}\right)$ alignments is then used to solve the alignment-across-K problem. pong begins alignment across K between the representative runs of the major modes at K = 2 and K = 3 and proceeds through aligning $K=K_{\text{max}}-1$ and $K=K_{\max }$.

3 Implementation

pong’s back end is written in Python. Although providing covariates is strongly advised so visualizations can be annotated with relevant metadata, pong only requires one tab-delimited file containing: (i) a user-provided identification code for each run (e.g. k4r4 in Fig. 1A), (ii) the K-value for each run and (iii) the relative path to each Q matrix. pong is executed with a one-line command in the terminal, which can contain a series of flags to customize certain algorithmic and visualization parameters. pong’s back end then generates results from its characterization of modes and alignment procedures that are printed to a series of output files.

After characterizing modes and aligning runs, pong initializes a local web server instance to host its visualization. pong is packaged with all its dependencies, such that it can be run without an Internet connection. The user is prompted to open a web browser and navigate to a specified port, and the user’s actions in the browser window lead to the exchange of data, such as Q matrices, via web sockets. These data are bound to and used to render the visualization.

pong’s front-end visualization is implemented in D3.js. pong’s main visualization displays the representative Q matrix for the major mode for each value of K as a Scalable Vector Graphic (SVG), where each individual’s genome-wide ancestry is depicted by K stacked colored lines. Each SVG is annotated with its value of K, the number of runs grouped into the major mode, and the average pairwise similarity across all pairs of runs in the major mode (Fig. 1B).

For each value of K, a button is displayed to the right of the main visualization indicating the number of minor modes, if any exist (Fig. 1B). Clicking on the button opens a pop-up dialog box consisting of barplots for the representative run of each mode within the K value, and each plot is annotated with the representative run’s user-provided identification code and the number of runs in each mode (Fig. 1A). A dialog header reports the average pairwise similarity among pairs of representative runs for each mode, if there is more than one mode. Users can print or download any barplot in pong’s visualization in Portable Document Format (PDF) from the browser window.

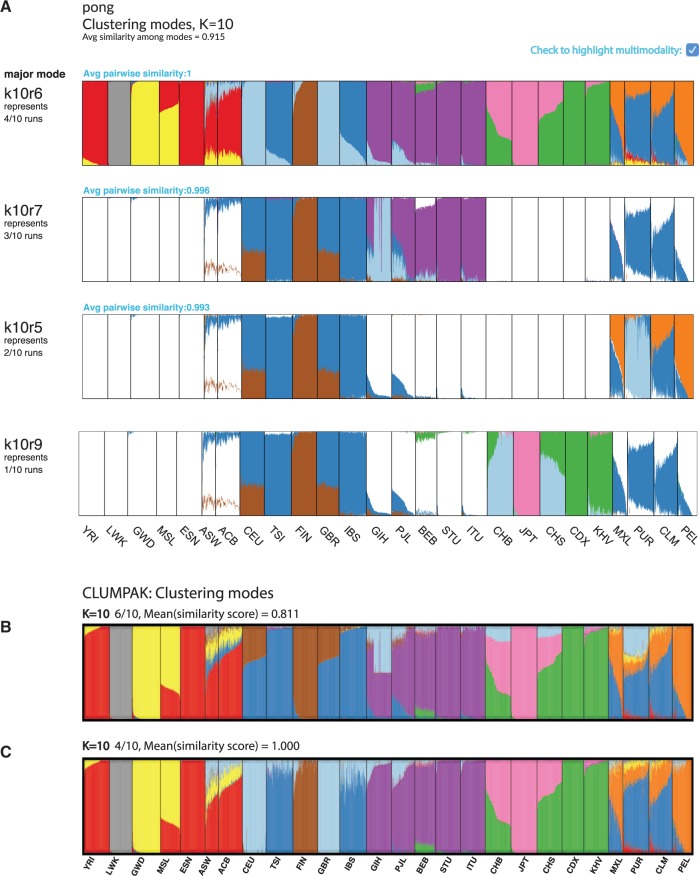
What truly sets pong’s visualization apart from existing methods for the graphical display of population structure is a series of interactive features, which we now detail. In the browser’s main visualization, the user may click on any population—or set of populations, by holding SHIFT—to highlight the selected group’s genome-wide ancestry across values of K. When mousing over a population, the population’s average membership (as a percentage) in each cluster is displayed in a tooltip. Within each dialog box characterizing modes, selecting a checkbox on the top right allows the user to highlight differences between the major mode’s representative plot and each minor mode’s representative plot (Fig. 3A). Clusters that do not differ beyond a threshold between a given major and minor mode are then shown as white in the minor mode, while the remaining clusters are shown at full opacity (Fig. 3A; see also edge weights in Fig. 2A).

Fig. 3.

Visualizations of modes in population structure identified by pong and Clumpak at K = 10 for clustering inference with ADMIXTURE (Alexander et al., 2009) applied to 1000 Genomes data (phase 3; Consortium, 2015). The new cluster of membership coefficients first identified at K = 10 is denoted by light blue in each barplot. (A) pong’s dialog box of modes at K = 10, with multimodality highlighted. (B) Clumpak’s major mode at K = 10 averages over six runs of clustering inference output; the reported mean similarity score among these six runs is 0.811. South Asian (GIH), Han Chinese (CHB and CHS), and Puerto Rican (PUR) individuals all have ancestry depicted by the light blue cluster in this plot. The six runs averaged here are instead partitioned into three minor modes by pong in panel A. (C) Clumpak’s minor mode at K = 10 averages over four identical runs (mean similarity score is 1.000). This barplot contains the same information as the barplot of k4r10, representing pong’s major mode in panel A

4 Results

We ran ADMIXTURE (Alexander et al., 2009) on 225 705 unlinked genome-wide single-nucleotide variants from 2426 unrelated individuals in the 1000 Genomes Project (phase 3; Consortium, 2015; see Supplementary Materials) to characterize population structure among globally distributed human populations. ADMIXTURE was run with K ranging from 2 to 10, and 10 runs were generated per value of K. Thus, a total of 90 Q matrices were produced; Figures 1 and 2 depict pong’s analysis of 20 of these runs. We also applied Clumpak (Kopelman et al., 2015), the state-of-the-art method for automated post-processing and visualization of clustering inference output, to these 90 runs (partial results shown in Figures 3B and C; see also Supplementary Figure S2).

Clumpak automatically runs CLUMPP (Jakobsson and Rosenberg, 2007) for each value of K as part of its pipeline, and produces visualizations within and across values of K using Distruct (Rosenberg, 2004), displaying one barplot per mode. Figure 3B shows Clumpak’s reported major mode in the 1000 Genomes dataset at K = 10, which averages over six runs; all major modes reported by Clumpak can be viewed in Supplementary Figure S2. Using Clumpak’s web server (http://clumpak.tau.ac.il/) with its default settings (including using CLUMP ’s fastest algorithm, LargeKGreedy, for aligning Q matrices for a fixed value of K) took 58 min and 18 s for post-processing of these 90 runs. We could not apply other CLUMPP algorithms to the 1000 Genomes dataset using Clumpak’s web server due to the server’s restrictions against exhaustive running times (Kopelman et al., 2015). We also installed Clumpak locally on Linux machines running Debian GNU/Linux 8 with 8 GB of RAM. Processing these 90 Q matrices took 74.275 hours using CLUMPP’s LargeKGreedy algorithm; using CLUMPP’s Greedy algorithm, which has increased accuracy over LargeKGreedy, Clumpak did not complete processing these Q matrices after four days. We also applied CLUMPP’s FullSearch algorithm, its most accurate algorithm, to the 10 Q matrices where K = 10; after 6.78 days, the job had still not completed.

Under its default settings, pong parsed input, characterized modes and aligned Q matrices within each value of K, and aligned Q matrices across K in 17.5 seconds on a Mid-2012 MacBook Pro with 8 GB RAM. After opening a web browser, pong’s interactive visualization loaded in an additional 3.2 s (Supplementary Figure S1 shows the main visualization).

In Figure 3A, pong identifies four modes at K = 10 in the 1000 Genomes dataset (phase 3). Light blue represents the cluster of membership coefficients first identified at K = 10 (see also Supplementary Figures S1 and S2). In run k10r4 (representing 4 out of 10 runs), light blue represents British/Central European ancestry in the major mode (CEU and GBR). However, light blue represents South Asian ancestry (GIH) in 3 out of 10 runs (e.g. run k10r7), Puerto Rican ancestry (PUR) in 2 out of 10 runs (e.g., run k10r3), and Han Chinese ancestry in run k10r9. pong’s display of representative runs for each mode allows the user to observe and interpret multiple sets of membership coefficients inferred from the data at a given value of K.

In contrast, the minor mode Clumpak outputs (Fig. 3C) is the same as pong’s major mode (Fig. 3A), while Clumpak’s major mode reported at K = 10 (Fig. 3B) averages over all minor modes identified by pong. The light blue in Clumpak’s reported major mode could be easily misinterpreted as shared ancestry among South Asian, East Asian, and Puerto Rican individuals, when in actuality these are distinct modes. We note that the highest-likelihood value of K for the 1000 Genomes data we analyzed is K = 8; at that value of K, we also see that Clumpak’s major mode suggests shared ancestry among individuals that are actually identified as having non-overlapping membership coefficients when individual runs are examined (Supplementary Figures S1 and S2).

Figure 3A is the first visualization of some of the modes observed in population structure of 1000 Genomes phase 3 data, as Consortium (2015) ran ADMIXTURE exactly once per K value [see Extended Data Figure 5 and Supplementary Materials of Consortium (2015)]. Supplementary Figure S3 shows pong’s visualization with consistent colors of all Q matrices released by Consortium (2015), K = 5 through 25; pong was able to process these Q matrices and render its visualization in 67.06 s. The modes identified in Figures 1, 3 and Supplementary Figure S1 differ substantially from the results reported by Consortium (2015). For example, in Figure 3A, pong depicts substructure in Puerto Rico and in China that is not observed in Extended Data Figure 5 by Consortium (2015). This could be due to different filters applied to the input SNP data (e.g. we removed relatives from data but did not filter based on minor allele frequency; see Supplementary Information), and we further note that these contrasting results indicate the need for efficient and accurate methods for processing and visualizing Q matrices.

5 Discussion

Here we introduce pong, a freely available user-friendly network-graphical method for post-processing output from clustering inference using population genetic data. We demonstrate that pong accurately aligns Q matrices orders of magnitude more quickly than do existing methods; it also provides a detailed characterization of modes among runs and produces a customizable, interactive D3.js visualization securely displayed using any modern web browser without requiring an internet connection. pong’s algorithm deviates from existing approaches by finding the maximum-weight perfect matching between column vectors of membership coefficients for pairs of Q matrices, and leverages the Hungarian algorithm to efficiently solve this series of optimization problems (Kuhn, 1955, 1956; Munkres, 1957).

Interpreting the results from multiple runs of clustering inference is a difficult process. Investigators often choose a single Q matrix at each value of K to display or discuss, overlooking complex signals present in their data because the process of producing the necessary visualizations is too time-consuming. pong’s speed allows the investigator to focus instead on conducting more runs of clustering inference in order to fully interpret the clustering in her sample of interest. Currently, many population-genetic studies only carry out one run of clustering inference per value of K (Consortium, 2015; Hallast et al., 2016; Homburger et al., 2015; Jeffares et al., 2015; Lorenzi et al., 2016; Mathieson et al., 2015; Moreno-Estrada et al., 2013), particularly when using ADMIXTURE’s maximum-likelihood approach (Alexander et al., 2009) to the inferential framework implemented in Structure (Pritchard et al., 2000). The likelihood landscape of the input genotype data is complex, and can hold different local maxima for a given value of K (see Verdu et al., 2014). Combining pong’s rapid algorithm and detailed, interactive visualization with posterior probabilities for K reported by clustering inference methods will allow investigators to accurately interpret results from clustering inference, thereby advancing our knowledge of the genetic structure of natural populations for a wide range of organisms. We further plan to extend pong to visualize results from other applications of mixed-membership models and to leverage the dynamic nature of bound data to increase the information provided by pong’s visualization.

Funding

This work was supported by a Brown University Undergraduate Teaching and Research Award (UTRA) to A.A.B., and a Research Experiences for Undergraduates Supplement to a National Science Foundation Faculty Early Career Development Award (DBI-1452622 to S.R.). S.R. is a Pew Scholar in the Biomedical Sciences supported by The Pew Charitable Trusts, and an Alfred P. Sloan Research Fellow.

Conflict of Interest: none declared.