Abstract
Otitis media (OM) is an inflammatory or infectious disease of the middle ear. Acute otitis media (AOM) and otitis media with effusion (OME) are the two major types of OM. However, the tympanic membrane (TM) motion differences induced by AOM and OME have not been quantified in animal models in the literature. In this study, the guinea pig AOM and OME models were created by transbullar injection of Streptococcus pneumoniae type 3 and lipopolysaccharide, respectively. To explore the effects of OM on the entire TM vibration, the measurements of full-field TM motions were performed in the AOM, OME and untreated control ears by using scanning laser Doppler vibrometry (SLDV). The results showed that both AOM and OME generally reduced the displacement peak and produced the traveling-wave-like motions at relatively low frequencies. Compared with the normal ear, OME resulted in a significant change of the TM displacement mainly in the inferior portion of the TM, and AOM significantly affected the surface motion across four quadrants. The SLDV measurements provide more insight into sound-induced TM vibration in diseased ears.
Keywords: Tympanic membrane, Acute otitis media, Otitis media with effusion, Middle ear
1. INTRODUCTION
Otitis media (OM) is an inflammatory or infectious disease of the middle ear with a variety of subtypes. Acute otitis media (AOM) and otitis media with effusion (OME) are the two main subtypes of OM. AOM is an acute infection of the middle ear caused by bacterial or viral invasion. OME is an inflammation of the middle ear with a collection of liquid in the middle ear cavity without signs or symptoms of an acute infection (Bluestone and Klein, 2007). Both disorders result in negative pressure and effusion in the middle ear. The inflammatory responses also lead to morphological changes and biomechanical variations of the middle ear soft tissues (Von Unge et al., 1997; Guan et al., 2013).
The biomechanical mechanisms of OM induced hearing loss are a continuing point of investigation by measurements and models (Grote and van Blitterswijk, 1984; Von Unge et al. 1997; Ravicz, et al., 2004; Gan et al., 2006; Gan and Wang 2007; Guan and Gan, 2013; Zhang et al. 2014). Recently, Guan et al. (2013) reported a comparison of TM mobility loss in AOM and OME models of guinea pig measured by single beam laser Doppler vibrometry (LDV). Data from that study showed that loss of umbo mobility can be attributed to a number of factors including the changes of middle ear pressure, effusion volume, and structural changes of the ossicular chain. However, the entire tympanic membrane (TM) motion change in OM ears has remained unclear despite the fact that the umbo displacement alteration were identified in previous studies.
Measurements of full-field TM surface vibration are valuable for understanding the sound transmission from the TM to the ossicular chain in normal and diseased ears (Tonndorf and Khanna, 1972; Von Unge et al., 1997; Wada et al., 2002; Rosowski et al., 2011). Several optical techniques have been used to measure the TM surface motion introduced by acoustic pressure (e.g. Moire interferometry: Decraemer et al., 1991; stroboscopic holographic interferometry: Aarnisalo et al. 2010; Cheng et al., 2010, 2013; optical coherence tomography: Djalilian et al., 2008; scanning laser Doppler vibrometry: Huber et al., 2001; de La Rochefoucauld and Olson, 2010). The movement of the TM in response to sound stimulation is sensitive to middle ear condition. Pathological changes in OM ears may result in different TM vibration patterns, which provide insight for the mechanism of hearing loss induced by OM.
This paper reports an investigation of the guinea pig TM motion in normal, AOM, and OME ears using scanning laser Doppler vibrometry (SLDV) techniques. The aim of this study is to explore the effects of different OMs on the motion of the entire TM. At first, sound induced TM motions in normal, AOM, and OME ears were measured as the maps of the displacement magnitude and phase on the TM surface. Then, the measurement results were compared between the normal, AOM, and OME ears with statistical analysis, and the difference of TM vibration pattern caused by AOM and OME was evaluated.
2. METHODS
2.1 Animal models
Eight Hartley guinea pigs, weighing between 250–340 g, were included in this study. The experimental protocol was approved by the Institutional Animal Care and Use Committee of the University of Oklahoma and met the guidelines of the National Institutes of Health.
The animals were free from middle ear disease as evaluated by otoscopic examination and divided into three groups: Control, AOM and OME. The control group included three animals without any treatment in both ears. The AOM group and OME group included three and two animals, respectively. Following the procedure reported by Guan et al. (2013), the AOM model was produced by transbullar injection of Streptococcus pneumoniae type 3 (0.1 ml at 1.3–2.4 × 106 CFU/ml, ATTC 6303) suspension bilaterally (N=6), and OME model was produced by transbullar injection of lipopolysaccharide (LPS, 0.1 ml, 100 μg/ml, of Klebsiella pneumoniae, Sigma) bilaterally (N=4).
On the third day post-inoculation, the animals were anesthetized with ketamine (40 mg/kg) and xylazine (10 mg/kg). Additional anesthesia was administered, as required, to maintain areflexia. The bony external auditory meatus of the guinea pig was surgically removed to expose about 80–90% of the lateral surface of the TM under the microscope. Because of the curved shape of the ear canal, the very inferior portion of the TM was not visible. The lateral surface of the TM was painted with a suspension of 3 % TiO2 powder (Acros Organics, NJ, USA) in saline to increase the amount of backscattered light from the translucent TM surface (Cheng et al. 2010). The effect of the TiO2 powder on the vibration of the TM can be neglected according to a study reported by Rosowski et al. (2009).
2.2 Scanning laser Doppler vibrometry measurement
The schematic diagram of the experimental set-up with the SLDV to measure the motion of the TM surface is shown in Fig. 1. A function generator (HP 35670A, Hewlett-Packard, Palo Alto, CA) and an amplifier (RCA SA-155, Radio Shack, Fort Worth, TX) provided excitation signals for a speaker (CF1, Tucker-Davis Technologies, Alachua, FL). A chirp stimulus at 80 dB SPL with the frequency range from 0.1 to 40 kHz was delivered onto the TM through a sound delivery tube. The sound pressure level was monitored by a probe microphone (Model 4938 B&K, Denmark), which was placed within 1–2 mm of the edge of the TM.
Figure 1.
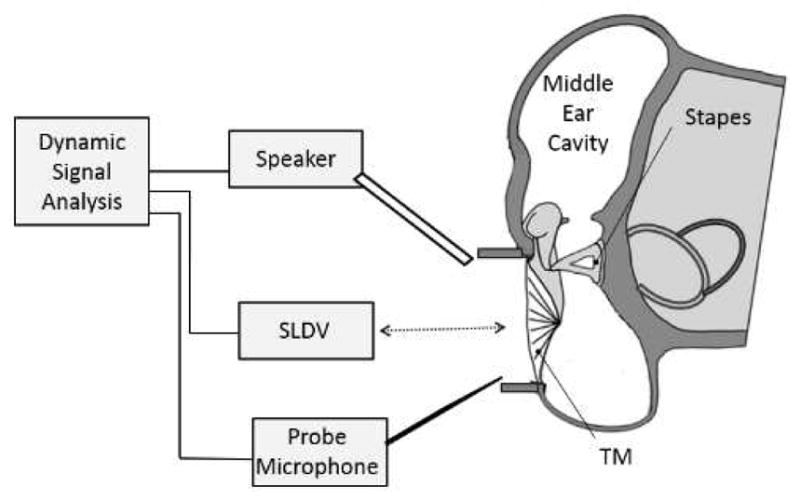
Schematic of the experimental setup with a scanning laser Doppler vibrometer (SLDV) for measuring full-field TM motion in guinea pig ear.
An SLDV (PSV-400, Polytec Inc., Irvine, CA) with a software package (PSV 8.8, Polytec Inc., Irvine, CA) was used to measure the full-field motion of the TM. The SLDV technology consists of an LDV sensor head with two moving mirrors having orthogonal axes, driven by galvanometetric actuators and control unit. The sensor head performs the velocity measurement, and two galvanometer scanners aim the laser beam at the pre-defined measurement point in two-dimensional space. During the scan, the laser beam moves point-by-point in a grid of discrete points recording the velocity of the point. After completion of the measurement of one acquisition point, the galvanometer-driven mirrors are then automatically repositioned and the data for the next measurement point are acquired. The acquired responses are post-processed at all the grid points by PSV software, and the velocity or displacement distribution on the surface is drawn by a linear interpolation of the values at neighboring grid points. Moreover, the system is equipped with a video camera inside the sensor head to acquire images of the measuring surface and monitor the location of the laser beam on the test surface.
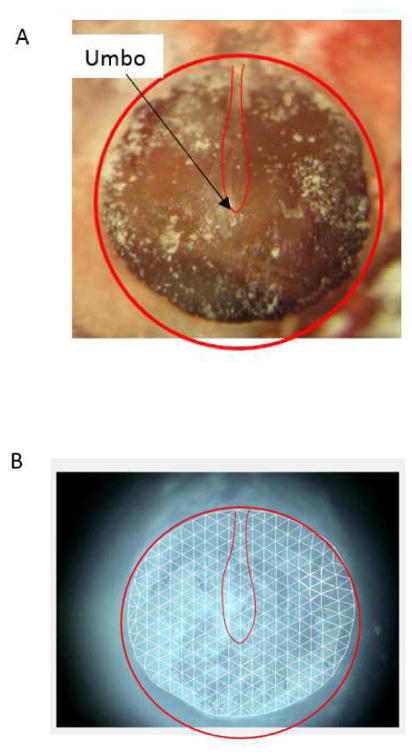
Figure 2A shows a photograph of an exposed TM surface, the laser beam was set perpendicular to the plane of the tympanic annulus. Figure 2B shows the scanning grids of measurement points which were set and aligned on the TM live video image in the PSV 8.8 software. The number of measurement points slightly varied with ears and was generally in the range of 260 to 300 points, which covered the exposed TM surface. Given the TM diameter of 5.2 mm (Wada et al. 1998) and 20 measurement points along the diameter perpendicular to the manubrium, this setup was capable of determining the displacement of the entire TM with a spatial resolution of about 0.28 mm. The vibration velocity and phase of each point was recorded sequentially by PSV-400, and the displacement results were further computed and analyzed with PSV 8.8 software. The scanning process took typically about 15–20 min, which was dependent on parameters such as the number of scanning points, the laser reflection signal level, and the sampling rate.
Figure 2.
(color online) (A) Picture of the exposed TM sample painted with a suspension of TiO2 powder. (B) The typical scanning points assigned on the TM surface. The thin red outline shows the connection of the TM to the manubrium of the malleus. The thick red outline indicates roughly the edge of the TM.
The PSV system incorporates a “signal enhancement (SE)” mode to improve the signal-to-noise ratio (SNR) of the measurement. The SE algorithm automatically increases the number of averages up to five times the manually set number of averages for points with low SNR. In this measurement, the manually set number of averages was three. Moreover, if the SNR is below a certain threshold level, the laser beam is moved slightly from its position, typically 50 μm at 1 m stand-off distance, and the measurement is taken again. The measurement procedure can be repeated up to seven times at different points around the measurement point chosen within the grid. By performing a weighted average of the measured data at different positions, the acquired signal quality is optimized. If a scanned point does not reach the acceptable SNR, the scanned point on the grid is marked, and the data at that point would be rejected. At the end of this procedure a scan point with a relatively low noise level was marked as optimal, while other scan points with acceptable SNR were marked as valid. This algorithm is incorporated in the Polytec PSV software. In this study, the data quality was checked for each point, and no rejected point was found for all samples at the frequency range from 0.5 to 20 kHz. Note that this procedure of SE increased the measurement time. Background noise measurements were performed in the absence of an excitation source, SNRs were calculated and, typically, values of 16 to 50 dB were found over the frequency range from 0.5 to 20 kHz.
Statistical analysis was performed on three groups of experimental data measured from the umbo and specified points at four quadrants. A student’s t-test was conducted, assuming two-sample unequal variances, to analyze the differences of displacements between three experimental groups: Control, OME and AOM. In all tests, p < 0.05 was considered statistically significant.
3. RESULTS
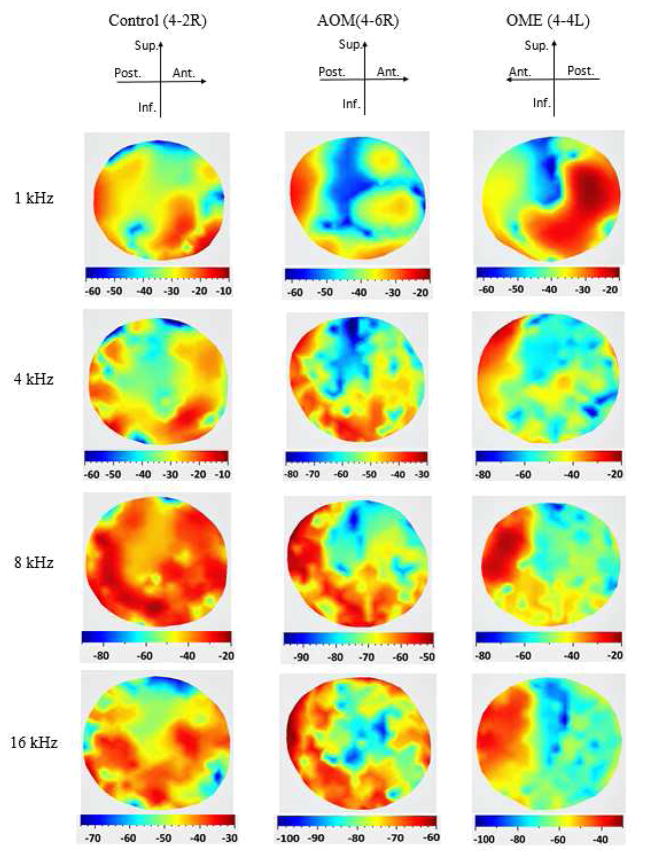
Figure 3 shows the typical deflection contours of TM motion measured by the SLDV on three ears: a control ear (No. 4-2R), an AOM ear (No. 4-6R) and an OME ear (No. 4-4L). The displacements were normalized by the input sound pressure, which was monitored at the edge of TM with the probe microphone. The color bar in the bottom of each image represents the displacement magnitude in a logarithmic scale relative to 1μm/Pa (unit: decibels, dB). The orientation of the TM is displayed in the top row of the figure.
Figure 3.
(color online) Typical displacement magnitude distributions of the TM lateral surface measured by SLDV on three ears: a control ear (4-2R), an AOM ear (4–6R), and an OME ear (4-4L) at four frequencies 1, 4, 8 and 16 kHz. The displacement is normalized by the input sound pressure and represented as a logarithmic scale in decibels (dB) relative to 1 μm/Pa.
For the non-infected control ear 4-2R, the deflection contours of the TM motion looked relatively simple with a major vibration peak region located at the inferior-anterior quadrant of the TM at 1 kHz. The maximal displacement magnitude was close to −11 dB (200 nm/Pa). When the frequency increased to 2 kHz, the general deflection pattern exhibited some changes, and the location of maximal displacement magnitude shifted to the posterior side (see Fig. S1 in Supplementary Material). At the frequency of 4 kHz, multiple displacement peak regions emerged at the posterior quadrants of the TM, and the area of each magnitude peak was decreased. At 8 kHz, the displacement pattern became more complicated and the maximal displacement regions were in the middle of the posterior-inferior portion, and the other peak regions were in the anterior portion. The peak displacement of the TM decreased with a maximal value of about −22 dB (80 nm/Pa). At the high frequency of 16 kHz, three main peak regions can be observed around the inferior portion of the TM, and the peak displacement of the entire TM decreased to −34 dB (20 nm/Pa).
For the AOM ear 4–6R, the deflection patterns of the TM motion had a few differences compared to the control ear. At 1 kHz, the maximal displacement was located at the posterior portion of the TM. A larger reduction in the overall displacement was observed, particularly in the posterior-inferior portion of the TM. At 4 kHz, the displacement contour of the TM became more complex and the peak regions were located at the posterior portion. The overall displacement level was further reduced with a maximal value of about −30 dB (30 μm/Pa). At 8 and 16 kHz, the maximal displacement decreased tremendously, about −50 dB (3 nm/Pa) at 8 kHz and −60 dB (1 nm/Pa) at 16 kHz. It can be observed that there are multiple small peaks scattered in the posterior portion of the TM at the high frequencies. The deflection contours in other frequencies were provided in Fig. S2 of the Supplementary Material.
For the OME ear 4-4L, the overall displacement level was low compared to the control ear at 1 kHz, and the displacement magnitude showed a peak region at the posterior portion of the TM. However, in the frequency range between 1 and 2 kHz, the number of local magnitude peaks on the surface increased steadily (see Fig. S3 of the Supplementary Material). For example, at 1.1 kHz, two displacement peaks emerged at the TM surface. At 1.5 Hz, two pairs of displacement peaks appeared in the surface, and when the frequency increased to 2 kHz, three pairs of peaks can be observed on the surface. At 4 kHz, as shown in Fig. 3 the displacement contour of the TM became more complex at the inferior portion of the TM, and the peak displacement decreased to −20 dB (100 nm/Pa). At high frequencies of 8 and 16 kHz, the peak regions were located at the anterior-superior quadrant with maximal displacements of −22 dB (80 nm/Pa) at 8 kHz and −35 dB (18 nm/Pa) at 16 kHz.
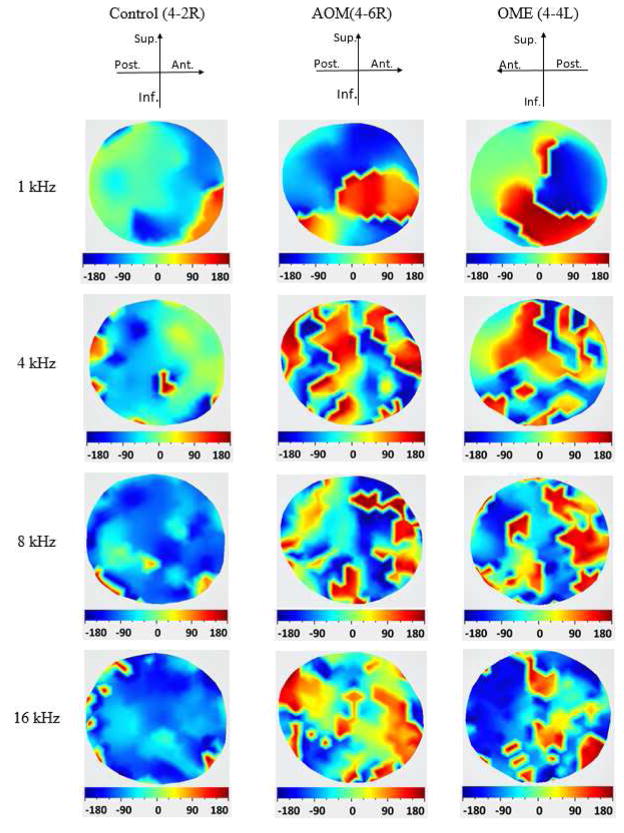
Figure 4 displays the phase contours of TM displacement in control ear (No. 4-2R), AOM ear (No. 4–6R), and OME ear (No. 4-4L). The displacement phase was described relative to the input sound pressure monitored at the edge of the TM. In the control 4-2R, the most posterior portion was moving in phase while the two regions of anterior portion were vibrating out of phase with each other at 1 kHz. However, it should be noted that in three of six control ears the TM vibrated in phase at 1 kHz. When the frequency increased to 4 kHz, the phase map became more complicated in the posterior portion: four small areas along the edge moved out of phase with the other region. The phase variation in the superior-anterior quadrant was more gradual than those in the anterior-inferior quadrant. At frequencies of 8 and 16 kHz, most areas of the TM generally moved in phase except for several small regions. In AOM 4-6R and OME 4-4L ears, the phase maps had similarities: The TM surface was not vibrating in phase and had relatively sudden half-cycle phase changes of the adjacent regions. At the frequency of 1 kHz the spatial variation of phase distribution was relatively simple, and there were two bigger regions moving half a cycle out of phase with each other. With 4, 8, and 16 kHz stimuli, the patterns of phase contours became more complicated. Multiple regions of the TM vibrated at the opposite phase to one another. The spatial variations of phase maps showed that the areas moving in phase were smaller in size compared to those at 1 kHz, indicating a rapid phase shift across the entire TM at high frequencies.
Figure 4.
(color online) Displacement phase distributions of the TM surface measured by SLDV on three ears: the control ear (4-2R), the AOM ear (4-6R), and the OME ear (4-4L) at four frequencies 1, 4, 8 and 16 kHz. The displacement phase relative to the input sound pressure.
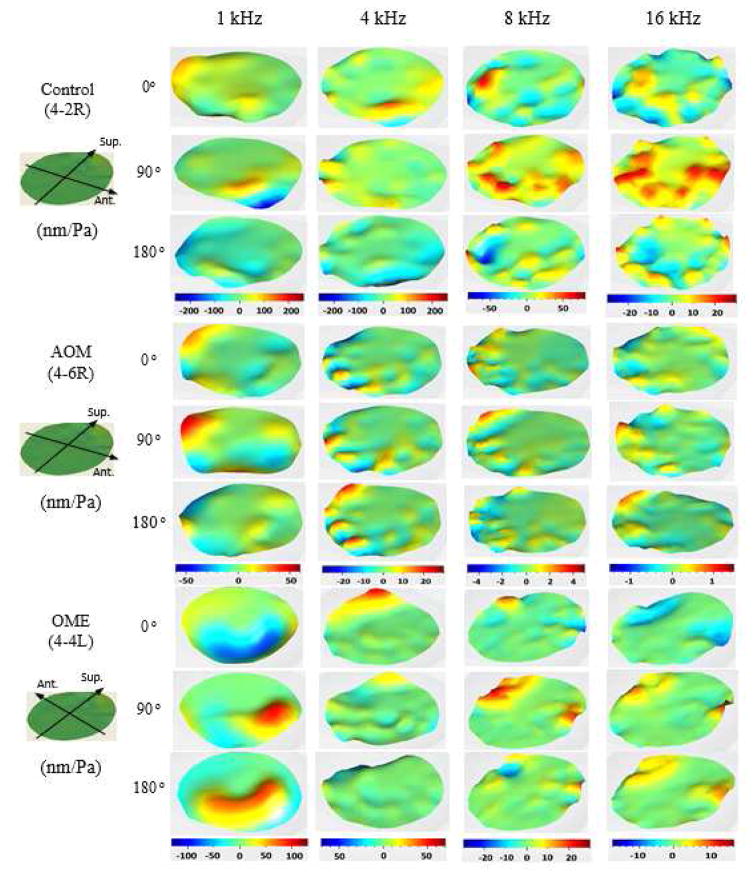
An alternative method for describing the TM motion is to exhibit the TM displacement pattern at different phases in a complete cycle. Figure 5 shows the instantaneous displacement pattern of the TM surface measured at three different phase angles (0, 1/4, and 1/2 cycles or 0, 90° and 180°) in the control ear 4-2R, the AOM ear 4-6R, and the OME ear 4-4L. This figure illustrates the displacement magnitude and relative phase change at different points on the TM surface at selected frequencies from 1 kHz to 16 kHz. In the control ear (4-2R), the largest deflection on the TM surface was in the anterior-inferior quadrant, and the local peaks in the inferior region were moving out of phase at the frequency of 1 kHz. When the frequency increased to 4 kHz, the local magnitude peaks on the TM surface increased to at least 6, and the peak displacements in the anterior-inferior quadrant occurred at a different phase from those major peaks in the posterior-inferior quadrant. At the high frequencies of 8 and 16 kHz, the multiple displacement peaks resulted in a more complex pattern exhibiting more phase variations. Moreover, at about 2.4 kHz, an apparent traveling-wave-like motion on the TM surface was observed in this control ear. With respect to the traveling waves of TM displacement in other control ears, the traveling waves appeared at a frequency varying from 2.2 kHz to 3.5 kHz for different ears. In general, the TM motion of normal ears contained both standing-wave-like modal patterns and traveling waves of displacement in high frequencies.
Figure 5.
(color online) Typical TM deflection pattern of three ears at three different phases in one cycle measured by SLDV in the control (4-2R), the AOM (4-6R) and the OME (4-4L) ears for selected frequencies of 1, 4, 8 and 16 kHz. The displacement is normalized by the input sound pressure.
In the AOM ear 4–6R, the instantaneous displacement pattern at 1 kHz shows the location of the displacement peak changing with phase angle. When the phase angle varied from 0° to 180°, the displacement peak moved from the posterior-superior quadrant to the posterior-inferior quadrant along the circumferential direction. This suggested the presence of a traveling-wave displacement component in the AOM ear at 1 kHz. When the frequency increased to higher than 1 kHz, the number of local magnitude peaks on the surface increased rapidly, and multiple local peaks vibrated in opposite directions. At the frequencies above 4 kHz, several alternative peaks and valleys appeared over the entire TM. Moreover, a traveling-wave component of the displacement could also be observed at 4 kHz.
In the OME ear 4-4L, there was a major displacement peak at 1 kHz, but the TM surface did not move in phase. A traveling-wave-like motion of the displacement could also be observed from the alteration of the peak location with phase angle. From phase angles of 90° to 180°, the location of the peak displacement moved from the posterior-superior quadrant to the posterior-inferior quadrant along the circumferential direction. Regarding the variation of phase difference with frequency (see Fig. S4 of the Supplementary Material), at the frequency of 1.1 kHz, the two peaks were moving half a cycle out of phase. At 1.5 and 2 kHz, the displacement peak regions could be divided into two sets according to their vibrating directions. The two sets of peaks vibrated at the opposite phase with each other. When frequency increased to higher than 3 kHz, the peak in one area had an opposite phase motion to that in the next area. Furthermore, in other OME ears, two or more local magnitude peaks were observed on the TM surface at 1 kHz, and the TM surface did not vibrate in phase. As frequency increased, there was a continued increase in spatial complexity of the TM motion.
Having examined the TM motion modes across all AOM and OME ears, a traveling wave motion of the TM could be typically observed at 0.7 kHz or below. The traveling wave at the low frequencies propagated along the circumferential direction of the TM, and the magnitude of the wave was the same level as the maximum displacement of the TM. As shown in the AOM and OME ears of Fig. 5, at 1 kHz, the location of maximal displacement magnitude on the TM shifted with phase angle. These results demonstrated that the primary motion pattern of the TM in AOM and OME ears was traveling wave mode at low frequencies. Additionally, when the frequency increased to about 1.4 kHz, both radial and circumferential traveling waves appeared on the TM surfaces.
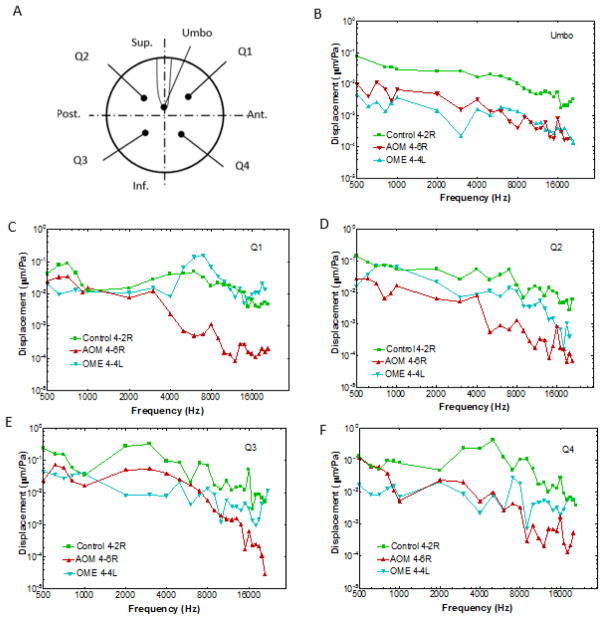
The sound-induced motions at the umbo and four specific locations were extracted from the whole surface motion as shown in Fig. 6. Figure 6A is a schematic of the selected nodal locations on the TM. The umbo was selected at the tip of the TM manubrium, and Q1 was the location at the center of the anterior-superior quadrant. The angle between the umbo-Q1 line and horizontal chord is about 45°. Similarly, Q2, Q3, and Q4 were selected at the angular central position of the posterior-superior quadrant, posterior-inferior quadrant, and anterior-inferior quadrant, respectively. The umbo and each defined quadrant location was positioned through a corresponding grid point. The measured results at the grid points were extracted to represent the responses at the umbo and four quadrant locations, respectively.
Figure 6.
The normalized displacement-frequency curves of the umbo and four quadrants in the control ear (4-2R), the AOM ear (4-6R), and the OME ear (4-4L).
Figures 6B–6F show the typical displacement-frequency curves obtained from the three ears: control ear 4-2R, AOM ear 4-6R and OME ear 4-4L at the umbo, Q1, Q2, Q3, and Q4 locations, respectively. The displacement magnitude was normalized with respect to the input sound pressure. At the umbo, the displacements of AOM and OME ears were lower than that of the control ear over frequencies of 0.5 to 20 kHz. The displacements at the four quadrant nodes of the AOM and OME ears were lower than that of the control ear except for the OME ear at the Q1 location. In general, the AOM affected the motion of the TM more than the OME at the high frequency range.
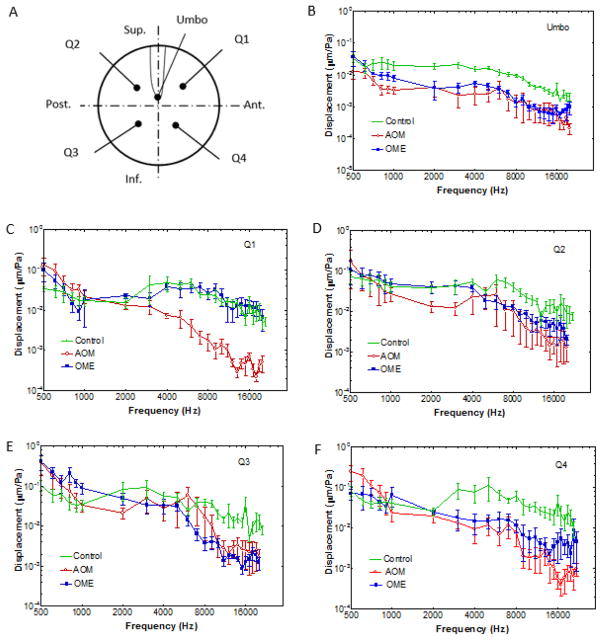
Figure 7 shows the mean normalized displacement-frequency curves with the standard errors at the umbo, Q1, Q2, Q3, and Q4 locations, respectively. Each panel includes the curves measured from the control (N=6), AOM (N=6), and OME (N=4) ears.
Figure 7.
(color online) The normalized displacement-frequency curves of the umbo and four quadrants in the control, AOM and OME ears. The error bars indicate the standard error of mean.
Comparing the mean displacements of control ears with those of AOM and OME ears in Fig. 7B, both AOM and OME significantly reduced the umbo movement over a broad frequency range. The umbo displacement curve of AOM ears was generally similar to that of OME ears except at low frequencies. In Fig. 7C, the mean displacement of OME ears at Q1 was similar to that of control ears, but the displacement curve of AOM was reduced considerably at high frequencies. The low frequency displacements in AOM and OME ears were greater than the control ears. It should be noted that one of OME ears (4-4R) had an obviously lower displacement (not shown in the figure) than other OME ears at the Q1 location, the individual displacement of 4-4R was close to AOM ears. The mean displacement curve of OME ears at Q2 (Fig. 7D) was similar to that of control at the frequencies below 3 kHz, and decreased at high frequencies. In AOM ears, the mean displacement at Q2 was lower than that of control ears at frequencies above 0.8 kHz. In the inferior quadrants (Q3 and Q4), the mean curves of AOM and OME ears were generally lower than that of control above 2 kHz. In contrast, at low frequencies, the displacement magnitudes in AOM and OME were slightly greater than those of the control ears. The reason for displacement increase at the low frequencies may be due to fluid in the middle ear. The fluid mass added to the TM shifted the system resonance frequency to a lower range, resulting in TM displacement increase in the OM ears at low frequencies.
Statistical analyses of the TM displacement magnitude data in Fig. 7 are listed in Table 1. The p-values were calculated by student’s t-test between the control and OME ears (I), control and AOM ears (II), and OME and AOM ears (III). For the umbo displacement, there was a significant difference (p<0.05) between control and OME ears at frequencies from 2 to 15 kHz (the 1st row of I in Table 1). Similarly, the difference between control and AOM ears was statically significant at the frequencies from 1 to 20 kHz (the 2nd row of II in Table 1). However, the umbo displacements between OME and AOM ears had no significant differences over all frequencies (the 3rd row of III in Table 1). In the superior quadrants (Q1 and Q2), there were no significant differences between the control and OME (Rows I) except for Q2 at 8 kHz, and in the inferior quadrants (Q3 and Q4), there were significant differences around 8 to 10 kHz. Those results indicated that significant displacement variations of OME ears occurred in the inferior region of the TM. Further comparison of the displacements in control and AOM ears (Rows II) suggested that significant differences existed in all quadrants, especially at the high frequency range. In addition, Table 1 demonstrated that there were no significant differences in displacements between the OME and AOM ears at the Q2, Q3 and Q4 locations (Rows III). The displacement at the Q1 location of OME was significantly different from AOM at the frequencies between 2 and 8 kHz.
Table 1.
Statistical analyses for the control, OME and AOM groups using the experimental data at the umbo and four quadrant locations in Fig 6. The p values were calculated by student t-test between the control and OME ears (I), control and AOM ears (II), and OME and AOM ears (III).
| Location | Frequency (Hz)
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 500 | 1000 | 2000 | 4000 | 6000 | 8000 | 10000 | 15000 | 20000 | ||
| Umbo | I | 0.873 | 0.109 | 0.036* | 0.013* | 0.022* | 0.000* | 0.001* | 0.002* | 0.189 |
| II | 0.098 | 0.045* | 0.001* | 0.003* | 0.040* | 0.000* | 0.001* | 0.009* | 0.033* | |
| III | 0.290 | 0.063 | 0.959 | 0.146 | 0.885 | 0.966 | 0.977 | 0.769 | 0.186 | |
| Q1 | I | 0.264 | 0.932 | 0.220 | 0.671 | 0.380 | 0.775 | 0.557 | 0.299 | 0.697 |
| II | 0.160 | 0.595 | 0.617 | 0.091 | 0.016* | 0.000* | 0.006* | 0.027* | 0.042* | |
| III | 0.612 | 0.835 | 0.039* | 0.017* | 0.034* | 0.057* | 0.139 | 0.101 | 0.186 | |
| Q2 | I | 0.589 | 0.799 | 0.887 | 0.219 | 0.099 | 0.034* | 0.060 | 0.124 | 0.238 |
| II | 0.490 | 0.432 | 0.027* | 0.105 | 0.269 | 0.034* | 0.019* | 0.062* | 0.196 | |
| III | 0.679 | 0.387 | 0.113 | 0.367 | 0.750 | 0.771 | 0.193 | 0.240 | 0.405 | |
| Q3 | I | 0.166 | 0.130 | 0.501 | 0.258 | 0.161 | 0.004* | 0.026* | 0.018* | 0.079 |
| II | 0.223 | 0.950 | 0.202 | 0.202 | 0.361 | 0.134 | 0.024* | 0.036* | 0.091 | |
| III | 0.882 | 0.134 | 0.192 | 0.823 | 0.259 | 0.345 | 0.958 | 0.323 | 0.658 | |
| Q4 | I | 0.715 | 0.507 | 0.844 | 0.152 | 0.036* | 0.024* | 0.006* | 0.086 | 0.110 |
| II | 0.195 | 0.281 | 0.531 | 0.121 | 0.019* | 0.018* | 0.005* | 0.006* | 0.006* | |
| III | 0.170 | 0.291 | 0.555 | 0.593 | 0.356 | 0.537 | 0.319 | 0.305 | 0.333 | |
Note:
indicates that the difference was significant (p<0.05).
The TM displacements in both AOM and OME ears showed quite variable from ear to ear, but the trends of AOM and OME effects on TM motion across the frequency range were generally consistent between the individual and mean results. Unlike the individual results, the statistical analyses were performed to determine the statistical significance based on all measured data. Not surprisingly, we see also the discrepancy of umbo displacement between the individual AOM and OME ears in Fig. 6 and that from the mean result in Fig. 7. The inconsistency between the individual results and the statistical data reflected the individual variations in the AOM and OME groups that were studied.
4. DISCUSSION
4.1 Comparison with published studies in guinea pig displacement measurement
In this study, the TM motion was measured in normal, AOM, and OME guinea pig ears using SLDV. For the untreated normal ears, three basic trends of TM motion over the frequency range were observed: (1) the deflection shape became more complicated with multiple peak regions when the frequency increased; (2) the local deflection peaks were circumferentially arranged around the manubrium at high frequencies; and (3) the traveling-wave-like motions occurred in both AOM and OME ears at relatively low frequencies.
The umbo displacement in normal guinea pig ears has been reported using a single beam LDV measurement (Dai et al., 2008; Guan et al., 2013; Guan and Gan, 2013). In this study, the umbo displacement extracted from the TM surface motion of 6 control ears (shown in Fig. 7B) are generally consistent with those reported by Guan et al. (2013) and Guan and Gan (2013). Note that their results were presented as the peak-peak displacement induced by 80 dB SPL and need to be normalized by sound pressure for a comparison with the present results.
Wada et al. (2002) reported the guinea pig TM surface motion of one normal ear measured by the time-averaged speckle pattern interferometry. A simple motion pattern of the TM surface was observed at 1 kHz, and the whole TM vibrated in phase. At 2.5 kHz, the TM had two local maxima in the posterior and inferior regions, and the phase difference between the two peak regions was about 180° under the condition of the closed bulla. In contrast, after modifying the bulla impedance with a ventilation tube, the TM vibration pattern retained the two local peaks in the posterior and inferior portions, but there was no phase difference between the two peaks. While frequency was increased to 4 kHz, a complicated motion pattern with multiple displacement peaks was observed. In this study, the motion pattern of the TM surface in normal ears was relatively simple with one or two local peaks, and three of six control ears vibrated in phase at 1 kHz. At 2.5 kHz, the TM displacement of ear 4-2R had two peak regions in the posterior and inferior portions (see Fig. S3 in the Supplementary Material), and the two peaks was in phase. The locations of local maxima were close to Wada et al.’s measurements, but the phase difference was similar to the result with a ventilation tube. At 4 kHz, both this study and Wada’s results showed that the peak number around the manubrium increased and the vibration pattern became more complicated.
Guan et al. (2013) reported the umbo displacement difference between control, AOM and OME ears, and their data showed that both AOM and OME resulted in the reduction of umbo displacement across all frequencies. In this SLDV measurement, the mean umbo displacement of AOM ears was lower than that of control ears as shown in Fig. 7B, but the mean umbo displacement of the OME ears was not obviously reduced at frequencies below 0.6 kHz. Furthermore, Guan et al. (2013) reported that the mean umbo displacement of AOM ears was significantly lower than that of OME at frequencies from 0.2 to 4 kHz. However, in the present SLDV measurement, the AOM and OME models did not exhibit significantly different umbo displacements across all frequencies as shown in Fig. 7B and Table 1. The differences in umbo displacements of OM ears between the previous study and this study may be attributed to the measuring equipment, experimental setup, sample size, and middle ear effusion level.
In addition to fluid level variation, the TM orientation may have a significant effect on the umbo vibration at the presence of middle ear fluid (Ravicz et al., 2004). The orientation difference resulted in variable TM area in contact with fluid, causing large changes in the measured umbo displacement. In Guan’s study, a single beam laser measurement was performed to characterize the motion of the umbo, and the direction of the laser beam was aimed at the umbo. In contrast, the SLDV measured the entire TM displacement along one direction normal to the tympanic ring. Due to the different experimental setups, it is possible that the TM oblique was inconsistent between the two studies, affecting the consistency of umbo displacements of the two measurements (SLDV and single LDV). Furthermore, the middle ear fluid may also cause the umbo displacement to be larger than the normal at low frequencies. The measured results of umbo velocity (Ravicz et al., 2004) and TM power reflectance (Voss et al. 2012) showed some of the TM displacements in the middle ear fluid conditions were larger than the normal from temporal bone measurements with saline. Those observations were similar to the results in Fig. 7.
It should also be noted that the inconsistency between the present results and previous data by Guan et al. (2013) may be a reflection of a large amount of individual variation within the AOM or OME group. The other reason causing the inconsistency may be due to small sample size (n=4 for OME and n=6 for AOM) in this study. Larger sample size will be needed to better define and delineate differences between normal and OM ears as well as between AOM and OME ears, as the probable individual variation in responses between ears would become less relevant in a large sample group.
4.2 Comparison of TM displacements in AOM and OME ears
Comparing the TM displacements of the AOM and OME ears, the greatest difference occurred in the anterior-superior quadrant (Q1), where a significant reduction of the displacement in AOM ears was observed (Fig. 7C). In the posterior quadrants (Q2 and Q3), the AOM and OME curves exhibited a complicated relationship: the mean displacement of AOM ears was generally lower than that of OME ears at frequencies below 2.5 kHz. In the higher frequency range, the AOM displacement curve remained generally lower than the OME at Q2 except for 5–6 kHz, but higher than the OME at Q3. At location Q4, there was a general trend for the AOM displacement to be lower than that of OME except at low frequencies.
In OME ears, the middle ear effusion adds mass to the TM and results in a reduction of TM displacement at high frequencies. Table 1 shows that there was no significant difference in Q1 and Q2 between the control and OME, but significant difference in Q3 and Q4 at high frequencies, which indicated the effusion was primarily in the inferior region of the TM. The volume of middle ear effusion in 3-day OME ears of guinea pig was approximately 0.10 to 0.13 ml (Guan et al. 2013). Such fluid volume can only cover the inferior portion of the TM. These results suggest that the middle ear fluid added more mass to the inferior portion of the TM, which reduced the motion at high frequencies.
In AOM ears, in addition to the effusion and the negative pressure in the middle ear cavity, middle ear structural changes have been observed in AOM models of guinea pigs (von Unge et al. 1997; Guan et al. 2013). As illustrated in Fig. 7 and Table 1, there were significant differences in TM displacements between the AOM and normal ears not only in the inferior portion of the TM, but also in the superior portion. The present protocol to create OME and AOM models was the same as the previous study of Guan et al. (2013). Measured from a portion of the samples, the volume of middle ear effusion in AOM and OME ears approximately ranged from 0.06 to 0.09 ml, and 0.08 to 0.10 ml, respectively. Those amounts of effusion were not much different from the previous study (Guan et al. 2013). Despite the fact that the middle ear pressure was not measured in this study, Guan et al. (2013) reported that no statistical difference was found in volume of middle ear effusion and middle ear pressure between the 3-day AOM and OME models of guinea pig. Consequently, the TM displacement difference between AOM and OME ears in the superior portion suggests that there exist additional mechanisms more than middle ear and effusion, resulting in the TM motion alteration in AOM ears.
4.3 Significance of full-field TM motion measurement in OM ears
In addition to the high frequency effect of middle ear fluid, the present results also demonstrated that the middle ear fluid changed TM motion modes at low frequencies. In normal middle ear, the sound-induced TM surface vibration appears as standing-wave-like motion (modal motion) at low frequencies, and the traveling-wave-like motion occurs at frequencies above 2.2 kHz. Rosowski et al. (2011) described that the traveling wave of normal ears propagates from the membrane’s rim to the umbo at 2–8 kHz. In this study, the measured results from both AOM and OME ears showed that the traveling-wave-like motions occurred at frequencies below 1 kHz, and the traveling wave at low frequencies did not progress from the tympanic rim toward the umbo, instead, along the circumferential direction of TM. Additionally, the magnitude of the traveling wave component at low frequencies was the same level with the maximum displacement. Thus, the traveling waves on the TM surface of AOM and OME ears observed at low frequencies differed from those of normal TM reported by Rosowski et al. (2011). Such traveling waves on the TM of AOM and OME ears are mainly due to the coupled fluid-structure interaction between the TM and middle ear fluid, rather than the TM material property changes induced by infection. Thus, the occurrence of traveling-wave-like motions in the OM ears at lower frequencies provides an additional indicator of the presence of middle ear effusion. In other words, the traveling waves of the TM occurring at low frequencies provide a mechanical feature to assess the effects of middle ear fluid.
The individual TM displacement curve in AOM or OME ears exhibited more oscillations at low frequencies compared to the normal ears (Fig. 4 in Guan et al. 2013). From the present measurements of full-field TM motions, we could see the superposition of the modal motion and travelling wave in the umbo vibration, and the traveling wave caused an additional oscillation imposed on the displacement of modal patterns. This can be an explanation of more fluctuations in the frequency-displacement response curves of the TM measured in AOM and OME conditions.
From the clinical point of view, the low frequency traveling waves induced by OM also have the mechanical effects on placement of tympanostomy tubes. The ventilation tube may interact with the propagation of traveling waves in OM ears and cause a local change in the mechanical stress generated in the TM. Such stress of the TM can affect the occurrence of different histological changes, including local atrophy, otorrhoea, and myringosclerosis. Vard et al. (2008) investigated the biomechanical consequences of ventilation tubes on the stress within the tympanic membrane using the finite element model, but the potential influence of the residual fluid in the middle ear cavity was ignored. To optimize performance of the ventilation tube, a refined analysis with the traveling wave effects should be conducted to further examine the interaction between the tubes and TM tissue.
The umbo vibration is commonly used to assess the TM mobility difference between two OM diseases, AOM and OME. In this study, measurements on the full-field TM motion were carried out. As shown in Fig. 7, the entire TM vibration information in OME and AOM ears may also have significant implications for the differentiation of AOM and OME from a mechanical viewpoint.
5. CONCLUSION
The measurements of full-field TM motion were performed by using SLDV in normal, AOM and OME ears of guinea pigs. The TM surface motion of normal ears showed relatively simple deflection patterns at low frequencies, while more complex patterns appeared at higher frequencies. The middle ear infection generally reduced the displacement peak and resulted in more complicated TM vibration patterns at low frequencies. Compared with the normal ear, OME resulted in a significant change of TM displacement mainly in the inferior portion, and AOM significantly affected the surface vibration across all four quadrants. In both OME and AOM ears, a traveling-wave component of the TM displacement was observed at lower frequencies than that in normal ears.
Supplementary Material
Research Highlights.
Measurement of full-field motion of TM was performed in AOM and OME models.
OM reduced TM displacement with complicated TM vibration pattern.
AOM and OME caused traveling-wave-like motion on the TM at low frequencies.
Difference of TM motion in AOM and OME ears was in the superior-anterior quadrant.
Acknowledgments
The authors thank Dr. Xiangming Zhang, former graduate student in the Biomedical Engineering Lab at the University of Oklahoma, for participating in SLDV measurement. This work was supported by NIH R01DC011585.
Abbreviations
- AOM
acute otitis media
- LDV
laser Doppler vibrometry
- OM
otitis media
- OME
otitis media with effusion
- SLDV
scanning laser Doppler vibrometry
- SNR
signal-to-noise ratio
- TM
tympanic membrane
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Aarnisalo AA, Cheng JT, Ravicz ME, Furlong C, Merchant SN, Rosowski JJ. Motion of the tympanic membrane after cartilage tympanoplasty determined by stroboscopic holography. Hear Res. 2010;263:78–84. doi: 10.1016/j.heares.2009.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bluestone CD, Klein JO. Otitis media in infants and children. 4. BC, Decker, Inc; Hamilton: 2007. [Google Scholar]
- Cheng JT, Aarnisalo AA, Harrington E, Hernandez-Montes MS, Furlong C, Merchant SN, Rosowski JJ. Motion of the surface of the human tympanic membrane measured with stroboscopic holography. Hear Res. 2010;263:66–77. doi: 10.1016/j.heares.2009.12.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dai C, Gan RZ. Change of middle ear transfer function in otitis media with effusion model of guinea pigs. Hear Res. 2008;243:78–86. doi: 10.1016/j.heares.2008.05.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de La Rochefoucauld O, Olson ES. A sum of simple and complex motions on the eardrum and manubrium in gerbil. Hear Res. 2010;263:9–15. doi: 10.1016/j.heares.2009.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Decraemer WF, Dirckx JJJ, Funnell WRJ. Shape and derived geometrical parameters of the adult, human tympanic membrane measured with a phase-shift moire interferometer. Hear Res. 1991;51:107–122. doi: 10.1016/0378-5955(91)90010-7. [DOI] [PubMed] [Google Scholar]
- Djalilian HR, Ridgway J, Tam M, Sepehr A, Chen Z, Wong BJ. Imaging the human tympanic membrane using optical coherence tomography in vivo. Otol Neurotol. 2008;29(8):1091–1094. doi: 10.1097/MAO.0b013e31818a08ce. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gan RZ, Dai C, Wood MW. Laser interferometry measurements of middle ear fluid and pressure effects on sound transmission. J Acoust Soc Am. 2006;120(6):3799–3810. doi: 10.1121/1.2372454. [DOI] [PubMed] [Google Scholar]
- Gan RZ, Wang X. Multifield coupled finite element analysis for sound transmission in otitis media with effusion. J Acoust Soc Am. 2007;122(6):3527–3538. doi: 10.1121/1.2793699. [DOI] [PubMed] [Google Scholar]
- Grote JJ, van Blitterswijk CA. Acute otitis media. An animal experimental study. Acta Otolaryngol. 1984;98(3–4):239–49. doi: 10.3109/00016488409107560. [DOI] [PubMed] [Google Scholar]
- Guan X, Li W, Gan RZ. Comparison of eardrum mobility in acute otitis media and otitis media with effusion models. Otol Neurotol. 2013;34(7):1316–1320. doi: 10.1097/MAO.0b013e3182941a95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guan X, Gan RZ. Mechanisms of tympanic membrane and incus mobility loss in acute otitis media model of guinea pig. J Assoc Res Otolaryngol. 2013;14(3):295–307. doi: 10.1007/s10162-013-0379-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huber AM, Schwab C, Linder T, Stoeckli SJ, Ferrazzini M, Dillier N, Fisch U. Evaluation of eardrum laser doppler interferometry as a diagnostic tool. Laryngoscope. 2001;111(3):501–507. doi: 10.1097/00005537-200103000-00022. [DOI] [PubMed] [Google Scholar]
- Ravicz ME, Rosowski JJ, Merchant SN. Mechanisms of hearing loss resulting from middle-ear fluid. Hear Res. 2004;195(1–2):103–130. doi: 10.1016/j.heares.2004.05.010. [DOI] [PubMed] [Google Scholar]
- Rosowski JJ, Cheng JT, Ravicz ME, Hulli N, Hernandez-Montes M, Harrington E, Furlong C. Computer-assisted time-averaged holograms of the motion of the surface of the mammalian tympanic membrane with sound stimuli of 0.4–25 kHz. Hear Res. 2009;253:83–96. doi: 10.1016/j.heares.2009.03.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosowski JJ, Cheng JT, Merchant SN, Harrington E, Furlong C. New data on the motion of the normal and reconstructed tympanic membrane. Otol Neurotol. 2011;32(9):1559–1567. doi: 10.1097/MAO.0b013e31822e94f3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tonndorf J, Khanna SM. Tympanic-membrane vibrations in human cadaver ears studied by time averaged holography. J Acoust Soc Am. 1972;52(4):1221–1233. doi: 10.1121/1.1913236. [DOI] [PubMed] [Google Scholar]
- Vard JP, Kelly DJ, Blayney AW, Prendergast PJ. The influence of ventilation tube design on the magnitude of stress imposed at the implant/tympanic membrane interface. Med Eng & Phys. 2008;30(2):154–163. doi: 10.1016/j.medengphy.2007.03.005. [DOI] [PubMed] [Google Scholar]
- Von Unge M, Decraemer WF, Bagger-Sjoback D, Van Den Berghe D. Tympanic membrane changes in experimental purulent otitis media. Hear Res. 1997;106:123–36. doi: 10.1016/s0378-5955(97)00008-7. [DOI] [PubMed] [Google Scholar]
- Voss SE, Merchant GR, Horton NJ. Effects of middle ear disorders on power reflectance measured in cadaveric ear canals. Ear Hear. 2012;32(2):195–208. doi: 10.1097/AUD.0b013e31823235b5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wada H, Momose K, Sugawara M, Hozawa K, Takasaka T. Measurement of guinea pig middle ear using computer-aided three-dimensional reconstruction system. Otology Japan. 1998;8(5):511–515. doi: 10.1016/s0378-5955(98)00007-0. [DOI] [PubMed] [Google Scholar]
- Wada H, Ando M, Takeuchi M, Sugawara H, Koike T, Kobayashi T, Hozawa K, Gemma T, Nara M. Vibration measurement of the tympanic membrane of guinea pig temporal bones using time-averaged speckle pattern interferometry. J Acoust Soc Am. 2002;111(5):2189–2199. doi: 10.1121/1.1467671. [DOI] [PubMed] [Google Scholar]
- Zhang X, Guan X, Nakmali D, Palan V, Pineda M, Gan RZ. Experimental and modeling study of human tympanic membrane motion in the presence of middle ear liquid. J Assoc Res Otolaryngol. 2014;15(6):867–881. doi: 10.1007/s10162-014-0482-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.