Abstract
MMPBSA methods have become widely adopted in estimating protein-ligand binding affinities due to their efficiency and high correlation with experiment. Here we investigated different computational alternatives on their impact to the agreement of MMPBSA calculations with experiment. Seven receptor families with both high-quality crystal structures and binding affinities were selected. We first studied the performance of nonpolar solvation models and found that the modern approach that separately models hydrophobic and dispersion interactions dramatically reduces RMSD’s of computed relative binding affinities. The numerical setup of the Poisson-Boltzmann methods was analyzed next. Our data shows that the impact of grid spacing to the quality of MMPBSA calculations is small: the numerical error at the grid spacing of 0.5 Angstrom is already small enough to be negligible. We further analyzed the impact of different atomic radius sets and different molecular surface definitions and found weak influences on the agreement with experiment. The influence of solute dielectric constant was also analyzed: a higher dielectric constant generally improves the overall agreement with experiment, especially for highly charged binding pockets. Our data also show that the converged simulations cause slight reduction in the agreement with experiment. Finally we briefly explored the direction of estimating absolute binding free energies. Upon correction of the binding-induced rearrangement free energy and the binding entropy lost, the errors in absolute binding affinities are also reduced dramatically when the modern nonpolar solvent model was used, though further developments are apparently necessary to further improve the MMPBSA methods.
Graphical abstract
The modern nonpolar solvent model that separately models solvation hydrophobic and dispersion interactions dramatically reduces RMSDs of computed relative binding affinities in Molecular Mechanics Poisson-Boltzmann Surface Area (MMPBSA) methods.
Introduction
It is widely accepted that high-level quantum approaches provide the most detailed and accurate description of molecular structures, dynamics, and functions. However, for many biochemical systems that are often too large and/or processes that are too long, classical approaches have proven to be sufficiently accurate and are now more commonly applied due to their efficiency. To model biochemical systems classically, both long-range polar and short-range non-polar interactions are important for accurate and transferrable models1–3.
Most biomolecules exist and function in aqueous environments. Interactions between biomolecules and their surrounding play important roles in the structures, dynamics, and functions of biomolecular systems, so that molecular models and simulations must account relevant solute-solvent interactions. To mimic the solvent-solute interactions, explicit and implicit models are both applicable. In explicit solvent models, all atoms are treated explicitly in a pair-wise fashion. These models need a large amount of computational resource to compute and sample the interactions of individual atoms of both solute and water molecules. Implicit solvation models attempt to model the solute and solvent interactions in a mean-field fashion, saving the computational and sampling time in simulating water explicitly. Although the implicit models are less accurate, their performance in many biological applications is remarkably good and reproducible.
Many widely used implicit models are based on the Poisson-Boltzmann (PB) equation2–18, which models the polar solvation interactions as classical electrostatic interactions19–40. In this method the water is set as a high dielectric region and the solute is set as a low dielectric region19. Most biological applications of the PB equation rely on numerical solutions of the underlining partial differential equation, which can now be obtained routinely for biomolecules and their complexes. Among the numerical methods, finite-difference method24, 33, 34, 41–50, finite-element method51–59 and boundary-element method60–75 are mostly used. The PB-based solvent models have widely biological applications. For example, they have been applied to prediction of pKa values for ionizable groups in biomolecules76–80, solvation free energies81, 82, binding free energies83–87, and protein folding and design88–96. The nonpolar solvation is typically estimated by the surface area (SA) method. Recently, deficiencies of the classical surface area-dependent models to estimate the total nonpolar solvation contribution in the case of macromolecules have been discussed97–116. These deficiencies mainly arise due to overlooking solvation contributions of interior (buried) atoms. Modern nonpolar solvation models rely on separate terms to model cavity and van der Waals contributions to overcome these limitations97–116. However, it is yet to be widely adopted for practical biomolecular applications.
In this study, we focus on the applications of PB-based solvent models to the protein ligand binding interactions, particularly via coupling with explicit solvent molecular dynamics simulations, in the Molecular Mechanics Poisson-Boltzmann Surface Area (MMPBSA) approach117–121. The MMPBSA approach allows addressing contributions from electrostatic and van der Waals interactions and changes in solvation to binding affinities. If conformational entropy can be estimated, its contribution to binding can also be included following standard thermodynamics principle. Of course, computation of solvation contributions to binding affinity, both polar and nonpolar components, are not as straightforward as the intramolecular electrostatic and van der Waals interactions. In addition estimation of entropic contributions to binding affinity is equally challenging if not more than the estimation of solvation contributions.
Here we investigated different existing computational alternatives to estimate protein-ligand binding affinities within the MMPBSA framework117–121. Specifically we focused our discussion on the performance of nonpolar solvation models, the numerical PB setup (particularly the grid spacing effect). Other related issues, such as the atomic radius definitions, molecular surface definitions, solute dielectrics, and simulation length, were also analyzed in the context of the modern nonpolar solvent model. Both relative and absolute binding affinities were analyzed following the single-trajectory MMPBSA approach, or a revised MMPBSA approach to properly model the entropic contribution to absolute binding affinities.
Materials and Method
System Selection
The complexes of proteins and ligands were selected from the PDBBind database122. Experimental crystal structures and binding affinities were reported for all seven selected systems, including trypsin β, thrombin α, cyclin-dependent kinase (CDK), cAMP-dependent kinase (PKA), urokinase-type plasminogen activator, β-glucosidase A, and coagulation factor Xa, with numbers of complexes of 57, 25, 11, 8, 19, 18 and 15, respectively. Here complexes of cyclin-dependent kinase and cAMP-dependent kinase were combined into one group “CDK+PKA” due to their similar structures, so final data analyses were reported for six groups. For each receptor, the complexes were selected based on the following rules: (a) the number of heavy atoms of a ligand is < 50; (b) the number of rings in a ligand is < 5; (c) the maximum number of atoms in a ring in a ligand is < 30; and (d) the number of rotatable bonds in a ligand is < 10.
Molecular Dynamics Simulation
Crystal structures were downloaded from the RCSB protein databank. For each crystal structure of the complex, only the single protein chain and the ligand for the complex, and structural waters close to the chosen ligand or protein chain (less than 4 Å) were used in subsequent simulations. Structural ions were also retained if needed. Missing residues were modeled with Modeller123 version 9.11 with sequences given in the PDB file. The Amber FF14SB force field was used for the proteins and the Amber GAFF parameters were employed for the ligands124, 125. Hydrogen atoms of ligand were modeled by the REDUCE program in Amber 14125. The ligand atomic partial charges were then generated by the empirical charge model - AM1-BCC126 by using the ANTECHAMBER program of Amber 14127. Each complex was solvated in a TIP3P water box with a minimum distance 8.0 from the surface of the complex to the edge of the simulation box. Each system was neutralized by adding Na+ or Cl− ions.
The solvated complexes undergo two stages of energy minimization: first with the backbones of proteins restrained and followed with a completely free minimization with no restraint. Each minimization stage consisted of 2500-step steepest descent minimization first and then another 2500-step conjugated gradient. Subsequently a 100-ps MD simulation was conducted to heat the system from 0 to 300K in the NVT ensemble. This was followed with a 100-ps simulation equilibrate the density to 1g/cc at 300 K and 1 bar. Finally production MD was run for 10-ns and atomic coordinates were saved as snapshots every 10-ps.
MM-PBSA Calculation
After molecular dynamics simulations, the snapshots were utilized to post-process binding free energies by the single-trajectory MMPBSA method117–121. Specifically, for a non-covalent binding reaction in the aqueous phase
| (1) |
where R, L, and R:L represent receptor, ligand, and complex, respectively, the binding free energy, ΔGbind,aqu, can be computed as
| (2) |
where ΔGbind,vac is the binding free energy in the vacuum phase, and ΔGbind,solv is the solvation free energy change upon binding
| (3) |
where ΔGR:L,solv, ΔGR,solv and ΔGL,solv are solvation free energies of complex, receptor and ligand, respectively.
Here the solvation free energies were computed by calculating two different components separately, polar and non-polar, both within the implicit solvation framework
| (4) |
The polar part, ΔGsolv,polar, can be calculated by solving the Poisson-Boltzmann (PB) equation. In cases where both the ionic strength and solvent potential are low, and when symmetric electrolytes are considered, the PB equation can be linearized to:
| (5) |
where . Here ν denotes the solvent, I represents the ionic strength of the solution, and is defined as I = z2c. After solving potential ϕ, ΔGsolv,polar can be computed as
| (6) |
The non-polar part, ΔGsolv,non−polar, is typically estimated by the surface area (SA) method. Modern nonpolar solvation models use separate terms to model cavity and van der Waals dispersion contributions to overcome the reported limitations of the classical approach. Both the classical (INP=1) and the modern nonpolar solvent model (INP=2) have been implemented in Amber. This gives us an opportunity to assess the performance of both nonpolar solvent models in this analysis. The INP=1 option uses the solvent accessible surface area (SAS) to correlate the total nonpolar solvation free energy as
| (7) |
The INP=2 option only uses the solvent accessible surface area/or its enclosed volume (SAV) to correlate the repulsive (hydrophobic/cavity) term, and applies a surface-integration approach to compute the attractive (dispersion) term as97
| (8) |
Absolute Binding Free Energy Calculation
The standard free energy change, ΔG0, for binding can be expressed as128–130
| (9) |
where R is the gas constant, T is the temperature, C0 is the standard state concentration (1M). ZR:L, ZR, and ZL are the configuration integrals of the complex, receptor, and ligand, respectively. Here the first term of Eqn (9), in theory, accounts for full energetic and configurational changes of all involved molecules upon binding.
The configurational integrals are apparently very difficult to compute for typical proteins or protein complexes due to the extremely high dimensionalities of the integrals. In this study, it is approximated by the sum of the free energy change given the assumption of no configurational rearrangement and the free energy change upon configurational rearrangement, ΔGConf. The free energy change without configurational rearrangement is approximated by the single-trajectory MMPBSA method, ΔGmmpbsa. The free energy change upon configurational rearrangement, ΔGConf, is taken from a previous analysis by Gao et al.131. Therefore Eqn (9) can be approximated as
| (10) |
where is a constant, with a value of 7.0 kcal/mol at the standard condition128–130.
Results and Discussion
Influence of Nonpolar Solvent Modeling
As reviewed in Introduction, deficiencies of the classical solvent-accessible surface area-dependent models lie in their negligence of solvation contributions of interior (buried) atoms97–116. Modern nonpolar solvent models addressing the overlook exist, but they are yet to be widely adopted for practical biomolecular applications. Here we intend to study the effect of these newer nonpolar solvent models in the context of protein ligand binding affinity modeling.
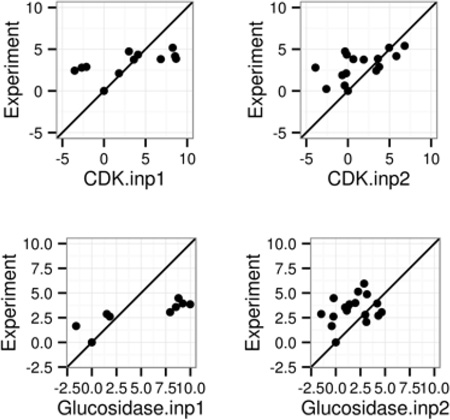
Table 1 and Figure 1 summarize the performance analytics of both classical (INP=1) and modern methods (INP=2) in reproducing the relative binding free energies for the six tested receptor groups. Our initial attention to relative binding free energies is mainly due to the widely used assumptions in the MMPBSA approach that often ignores conformational rearrangement upon binding. Figure 1 plots the correlations of ΔΔG between experimental data versus simulation data for both INP=1 and INP=2. The detailed data of RMSD, R (Pearson product-moment correlation coefficient) and linear regression slope are listed in Table 1. Overall, all simulation data display visible correlations with the experimental data for both INP =1 and 2.
Table 1.
Effects of nonpolar solvent modeling (inp) upon the performance of MMPBSA to predict relative binding affinities. All calculations were conducted with the default SES surface (sasopt=0), the default solvent probe (dprob=1.4), the default atomic radius option (radiopt=0), and the default grid spacing of 0.50 Angstrom (space=0.50). The RMSD’s of ΔΔG are in kcal/mol.
| Systems | INP=1 | INP=2 | ||||
|---|---|---|---|---|---|---|
| RMSD | R | Slope | RMSD | R | Slope | |
| CDK+PKA | 5.81 | 0.81 | 0.18 | 3.42 | 0.71 | 0.29 |
| glucosidase | 4.43 | 0.57 | 0.16 | 1.94 | 0.30 | 0.23 |
| thrombin | 11.02 | 0.87 | 0.23 | 4.26 | 0.86 | 0.42 |
| trypsin | 9.89 | 0.74 | 0.18 | 3.30 | 0.53 | 0.32 |
| urokinase | 7.19 | 0.73 | 0.22 | 2.61 | 0.53 | 0.33 |
| Factor Xa | 5.99 | 0.75 | 0.23 | 3.26 | 0.67 | 0.27 |
Figure 1.
Correlation between MMPBSA predicted and experimental relative binding affinities (kcal/mol). Left and right columns are for INP=1 and INP=2, respectively. See Table 1 for more details. A through F refer to the following protein targets, respectively: CDK+PKA, β-glucosidase A, thrombin α, trypsin, urokinase-type plasminogen activator, and coagulation factor Xa.
However it is also apparent that the INP=2 data are closer to the perfect agreements, i.e. the diagonal line, even if the correlation measures are quite similar between the two. The better correlation is reflected in the higher slopes of linear regression: the slope ranges from 0.18 to 0.23 for INP=1, and they ranges from 0.23 to 0.33 for INP=2. The RMSD’s of ΔΔG are 1.94–4.26 kcal/mol for INP=2, also smaller than those with INP=1: 4.43–11.02 kcal/mol as shown in Table 1. It is worth noting that Pearson correlation coefficients (R in Table 1) are higher with INP=1. This is mainly due to the fact that the ranges of data are larger in INP=1, which tend to lead to better looking correlation, a trick that was often exploited in choosing binding test cases.
Influence of numerical PB methods
In the MMPBSA calculations, the finite-difference Poisson-Boltzmann (FDPB) methods are often employed. Overall finer grid spacing always lead more accurate calculations. However, finer grid spacing or higher accuracy also asks for higher memory and longer CPU time. Indeed, straightforward estimation shows that the memory scales as the number of the grid nodes that is proportional to (1/h)3. Basically 8 times more memory would be needed when the grid spacing is halved. Even if the convergence rate remains the same (i.e. iteration number is independent of the number of grid nodes), the CPU time would also be 8 times longer.
Prior studies by the community have shown that a grid spacing of 0.50 Å is a good compromise for modern FDPB solvers. Here we want to demonstrate that the effect of grid spacing on the quality of the MMPBSA performance with the testing data of the INP=2 runs as examples. For easy comparison, three sets of calculations, with spacing of 0.25, 0.50, and 1.00 Å, were used in the otherwise same calculations for the same tested target groups and are summarized in Table 2. The detailed correlation measures are reported in Table S1 and Figure S1 & S2 in Supplementary Materials. Overall the simulation agrees with experiment quite similarly regardless of the three tested grid spacings. Inspect of the correlation plots for the 0.25 Å and 1.00 Å calculations (Figure S1 & S2) shows that their overall trends are quite similar to those in Figure 1, conducted at 0.50 Å. This confirms the community default spacing that was often used in prior studies, 0.50 Å, is a very good choice, at lest for the tested FDPB solvers implemented in Amber/PBSA.
Table 2.
Effects of grid spacing (space) upon the performance of MMPBSA. The testing conditions are the same as those in Table 1 but with all three tested grid spacings of 1.00, 0.50, and 0.25 Angstrom. All calculations were conducted with the new nonpolar solvent model (inp=2), the default SES surface (sasopt=0), the default solvent probe (dprob=1.4), and the default atomic radius option (radiopt=0) as in Table 1. The spacings are in Angstrom (Å). The RMSD’s of ΔΔG are in kcal/mol.
| Spacing | RMSD | R | Slope | |||
|---|---|---|---|---|---|---|
| Median | Range | Median | Range | Median | Range | |
| 0.25 | 3.26 | 1.89–4.25 | 0.61 | 0.30–0.86 | 0.30 | 0.23–0.42 |
| 0.50 | 3.28 | 1.94–4.26 | 0.60 | 0.30–0.86 | 0.31 | 0.23–0.42 |
| 1.00 | 3.38 | 1.98–4.23 | 0.59 | 0.29–0.86 | 0.30 | 0.21–0.42 |
It is worth pointing out that the conclusion above does not rule out numerical differences when different grid spacing is used. Table 3 summarizes the numerical differences for selected complex in each group by listing detailed EPB energies of ΔG, Gcomplex, Greceptor and Gligand. Here ΔG = Gcomplex − Greceptor − Gligand. Every complex has the same converged trend that ΔG becomes more positive when grid spacing is reduced from 1.00 to 0.25 Å. This trend is same as observed in our previous studies on model molecules tested with the same FDPB method37, 39. Overall, Gcomplex and Greceptor differ by 1% between the 0.25 and 0.50 Å calculations and around 2% between the 0.50 and 1.00 Å calculations. The Gligand converges better with around 0.5% differences between the 0.25 and 0.50 Å calculations and around 1% differences between the 0.50 to 1.00 Å calculations. In summary, the numerical convergence errors do exist in FDPB calculations at the commonly used grid spacing, but are far less than other errors in MMPBSA calculations and their influence on the MMPBSA quality is not significant as demonstrated by the highly consistent correlation plots in Figures 1, S1, and S2.
Table 3.
The detailed EPB energy changes for six selected complexes for the calculations reported in Table 2. Grid spacings are in Angstrom, and the free energies are in kcal/mol.
| Spacing | 0.25 | 0.50 | 1.00 | |
|---|---|---|---|---|
| CDK+PKA (1Q8W) ΔG=−8.22 |
ΔGpb | 38.22 | 38.05 | 37.66 |
| Gcomplex | −1015.08 | −1009.11 | −989.98 | |
| Greceptor | −1037.07 | −1030.98 | −1011.63 | |
| Gligand | −16.23 | −16.18 | −16.01 | |
| Glucosidase (2J75) ΔG=−10.01 |
ΔGpb | 18.45 | 18.16 | 17.15 |
| Gcomplex | −1155.17 | −1148.50 | −1127.40 | |
| Greceptor | −1164.35 | −1157.53 | −1136.03 | |
| Gligand | −9.26 | −9.13 | −8.52 | |
| Thrombin (1VZQ) ΔG=−17.52 |
ΔGpb | 3.75 | 3.36 | 2.26 |
| Gcomplex | −1013.07 | −1008.16 | −992.10 | |
| Greceptor | −998.43 | −993.21 | −976.32 | |
| Gligand | −18.39 | −18.31 | −18.03 | |
| Trypsin (1O2Q) ΔG=−18.87 |
ΔGpb | 19.87 | 19.67 | 18.94 |
| Gcomplex | −531.31 | −527.06 | −513.28 | |
| Greceptor | −540.93 | −536.51 | −522.09 | |
| Gligand | −10.26 | −10.22 | −10.13 | |
| Urokinase (1C5Z) ΔG=−13.23 |
ΔGpb | 38.41 | 38.32 | 37.97 |
| Gcomplex | −660.30 | −655.93 | −641.54 | |
| Greceptor | −684.76 | −680.31 | −665.62 | |
| Gligand | −13.96 | −13.94 | −13.89 | |
| Factor Xa (1LPZ) ΔG=−20.19 |
ΔGpb | 12.93 | 12.77 | 12.31 |
| Gcomplex | −687.45 | −682.79 | −668.09 | |
| Greceptor | −683.83 | −679.08 | −664.12 | |
| Gligand | −16.55 | −16.48 | −16.28 |
Influence to molecular surface definitions
Influence of Atomic Radius Set and Solvent Probe Radius
In this analysis, we first addressed the most apparent choice in the construction of molecular surface, i.e. the choices of atomic radii and solvent probe radius. Here we tested two atomic sets as provided in Amber, that of default mbondi radius set125 and those optimized by Tan and Luo with respect to TIP3P electrostatic free energy simulations26. Tan and Luo also pointed out that electrostatic interaction free energy profiles depend on solvent probe radius and 0.6 Å was found to better reproduce molecular interaction energies of tested dimers in the TIP3P explicit solvent model, so this was also tested here and compared with the default 1.4 Å value widely used in the literature. All together four combinations were tested and summarized in Table 4. The detailed performance for each receptor with each combination of setups is shown in Table S2. Table 4 shows that all these reasonable radius choices lead to overall comparable performance with respect to experiment. However, the use of 0.6 Å for the solvent probe (dprob=0.6) does lead a consistently better agreement (albeit a small improvement) with experiment. As shown by Tan and Luo, the issue with the default solvent probe of 1.4 Å is its overestimation of energy barrier upon formation of dimers26. This appears to play some role in the protein-ligand complexes even if the crystal structures, i.e. tightly bound structures, were used in simulations. Of course, not every ligand atoms are in tight contact with protein atoms upon binding, which may explain the benefit with the optimized solvent probe value.
Table 4.
The effects of atomic radius option (radiopt) and solvent probe radius (dprob) upon the performance of MMPBSA. All calculations were conducted with the new nonpolar solvent model (inp=2) and the default SES surface (sasopt=0) as in Table 1, but with all four tested combinations of radius and probe options. The probe radii are in Angstrom. RMSD’s of ΔΔG are in kcal/mol.
| Setting | RMSD | R | Slope | |||
|---|---|---|---|---|---|---|
| Median | Range | Median | Range | Median | Range | |
| radiopt=0/dprob=0.6 | 3.05 | 1.54–4.39 | 0.66 | 0.47–0.86 | 0.38 | 0.26–0.42 |
| radiopt=0/dprob=1.4 | 3.28 | 1.94–4.26 | 0.60 | 0.30–0.86 | 0.31 | 0.23–0.42 |
| radiopt=1/dprob=0.6 | 3.11 | 1.77–4.89 | 0.70 | 0.59–0.87 | 0.37 | 0.27–0.41 |
| radiopt=1/dprob=1.4 | 3.33 | 1.93–4.81 | 0.62 | 0.39–0.87 | 0.30 | 0.25–0.39 |
On the other hand, the optimized protein radii do not seem to help too much. One reason is that the ligand atoms were always set to use the same mbondi radii since the optimized radius set only covers naturally occurring protein and nucleic acid residues26. Further parameterization studies are apparently needed to fully address this issue in a more consistent manner.
Influence of Molecular Surface Definition
Next we intend to go beyond the classical SES definition that has become the default molecular surface definition since the early days of FDPB methods. Numerous computational studies with this definition have been shown to be consistent with experiment for a wide range of calculations. Nevertheless, there are also suggestions that van der Waals surface may present partial solvation reality especially when static structures were used132. In addition, modern surface definitions that intend to improve the electrostatic modeling using pseudo density functions also become readily available30, 133.
In MMPBSA calculations, the surface definition directly influences the dielectric distribution, so that the electrostatic binding free energies are directly impacted by the choice of the surface definitions. Here we compared three available surface definitions in Amber/PBSA (Table 5/S3): solvent excluded surface (SES), van der Waals surface (VDW), and a recently proposed smoothed revised density surface (DEN). To simplify the comparison, all surfaces were constructed with the optimized solvent probe radius (dprob=0.6) as in the previous subsection26. Furthermore, we tested these surfaces with both available atomic radius sets and found all of them perform rather similarly. Indeed there are minor numerical differences in all three quality measurements deployed, but the changes are rather minute. This is an interesting observation since both VDW and DEN surfaces are much faster to compute than the classical SES surface, whose usage is virtually 30% of the FDPB calculations, almost the same as the CPU time of high-performance iterative solvers. This is consistent with prior studies as conducted by Zhou and coworkers, who showed that the VDW surface delivers quite impressive agreement with experiment for their tested systems132.
Table 5.
The effects of molecular surface definitions (sasopt) upon the performance of MMPBSA. Both the default Amber atomic radius definition (radiopt=0) and optimized atomic radius (radiopt=1) were used in the analysis. The testing conditions are otherwise the same as those in Table 1 but with all six tested combinations of surface and radius options. Here the solvent probe is set to the optimized value (dprob=0.6) in SES and DEN as reported in our previous studies26, 30. For VDW dprob=0.0 by definition. The RMSD’s of ΔΔG are in kcal/mol.
| Setting | RMSD | R | Slope | |||
|---|---|---|---|---|---|---|
| Median | Range | Median | Range | Median | Range | |
| SES, radiopt=0 | 3.05 | 1.54–4.39 | 0.66 | 0.47–0.86 | 0.38 | 0.26–0.42 |
| VDW, radiopt=0 | 3.22 | 1.67–4.88 | 0.69 | 0.54–0.87 | 0.34 | 0.25–0.40 |
| DEN, radiopt=0 | 2.94 | 1.65–3.99 | 0.66 | 0.40–0.87 | 0.35 | 0.26–0.44 |
| SES, radiopt=1 | 3.11 | 1.77–4.89 | 0.70 | 0.59–0.87 | 0.37 | 0.27–0.41 |
| VDW, radiopt=1 | 3.30 | 1.73–5.05 | 0.69 | 0.53–0.86 | 0.35 | 0.24–0.41 |
| DEN, radiopt=1 | 3.05 | 1.70–4.46 | 0.69 | 0.43–0.88 | 0.35 | 0.29–0.43 |
Sensitivity to Solute Dielectric Constant
The effects of solute dielectric constant in MMPBSA calculations and pure PBSA calculations have been analyzed before120, 134, 135. It was shown that a solute dielectric constant higher than that used in molecular dynamics (i.e. 4 instead of 1) often leads to better agreement with experiment. Here we intend to analyze whether a similar strategy can be adopted when the modern nonpolar solvent treatment (INP=2) is used. Table 6 summarizes the performance measures by using dielectric constant 4 as in Table 1, the default molecular mechanics dielectric constant 1, as well as the “high” dielectric constant of 20 that was often used in pKa predictions by the PB models. Similar to previous analyses, the performance of dielectric constant 4 is apparently better than 1 when the modern nonpolar solvent model is used, consistent with previous findings with classical nonpolar solvent models120, 134. As shown in Table S4, the linear regression slopes are around 0 when dielectric constant 1 was used for 4 out of 6 receptors. The positive correlations are also lost. In addition, relative free energy RMSDs are around 2 or 3 times larger than those with dielectric constant 4, showing significantly larger disagreement with experiment. For the two remaining receptors CDK+PKA and thrombin α, the ε = 1 performance measures are also worse than those of ε = 4, though the slopes are still positive. When the dielectric constant is increased to 20, the performance measures are quite similar to those of calculations with dielectric of 4, with only one dramatic improvement for receptor β-glucosidase A.
Table 6.
The effects of solute dielectric constant (epsin) upon the performance of MMPBSA. All calculations were conducted with the new nonpolar solvent model (inp=2) and the default SES surface (sasopt=0) as in Table 1, but with all three tested dielectric constant options. The RMSD’s of ΔΔG are in kcal/mol.
| Dielectric constant |
RMSD | R | Slope | |||
|---|---|---|---|---|---|---|
| Median | Range | Median | Range | Median | Range | |
| 1 | 5.82 | 4.28–7.78 | 0.20 | 0.18–0.86 | 0.05 | −0.16–0.34 |
| 4 | 3.28 | 1.94–4.26 | 0.60 | 0.30–0.86 | 0.31 | 0.23–0.42 |
| 20 | 3.46 | 1.79–4.88 | 0.66 | 0.46–0.86 | 0.32 | 0.27–0.39 |
The results of β-glucosidase A complexes are interesting due to their distinctive sensitiveness to dielectric constant: for both INP=1120 and INP=2 the correlations with experiment are significantly higher with ε = 20. This, in part, can be explained by the charge state of the binding pocket, where there are two GLU residues (GLU166 and GLU351) with their carboxyl groups pointing to each other. The contribution of these acidic groups to electrostatic potential is apparently sensitive to the solute dielectric constant as well as the protonation states. In this study one GLU (166) is protonated but the other GLU (351) is charged as in other catalytic dyads136. Still the electrostatic polarization effects (both electronic and others) in binding interactions cannot be fully accounted for until the dielectric constant is raised to a value much higher than 4.
The introduction of a higher solute dielectric constant is a reasonable but crude treatment to account for the screening of electrostatic interactions due to polarization of electronic, orientational, and solvent-exchange origins. Since our method has explicitly sampled protein-ligand motion, the use of high dielectric constant is arguably unnecessary. However the electronic polarization does contributes to binding affinity. In addition, typical short MD simulations utilized for MMPBSA calculations are probably insufficient for sampling all the orientational and solvent-exchange effects. Thus, the use of a high dielectric constant is still a reasonable practice for rapid assessment of protein-ligand binding interactions in MMPBSA calculations. Nevertheless, the use of a polarizable force field57, 137–139 would arguably offer a more self-consistent treatment of electronic polarization effects for MMPBSA, at least for protein-ligand binding systems involving charges in the binding sites.
Convergence of Free Energy Simulation versus Accuracy
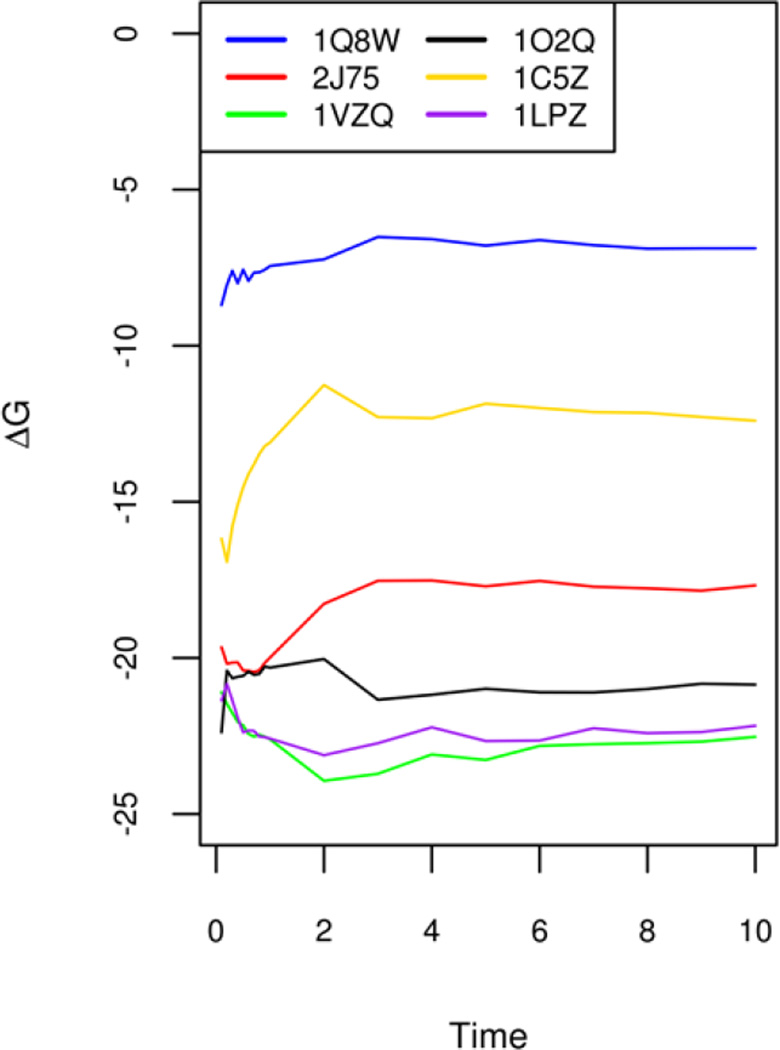
There are reports in the literature indicating that longer MD simulations tend to cause reduced agreement between MMPBSA calculations and experiment120. However, even with the relatively straightforward single-trajectory method analyzed here, nontrivial MD simulations appear to be necessary so that average values are converged in MMPBSA calculations. Figure 2 shows the convergence of binding free energies (ΔG) of six selected complexes chosen from the six groups. It is clear that the short 1ns MD simulation is not enough to reach convergence in average binding affinities. Thus all simulations for all six groups were extended up to 10ns and the MMPBSA analysis was rerun to see the impact of long MD simulations upon the agreements with experiment. The comparison of the “converged” MMPBSA results and those with just the first 1ns is shown in Table 7. It is clear that the agreements with experiment do appear to be slightly reduced, especially in relative free energy RMSD’s, though not that dramatic. On the other hand, the correlation coefficients and slopes are not uniformly reduced: sometimes higher when convergence is achieved. Overall correlation coefficients and the linear regression slopes remain in the highly similar ranges.
Figure 2.
Convergence of simulated binding free energies of selected complexes from 0ns to 10ns. The six complexes with PDB IDs 1Q8W, 2J75, 1VZQ, 1O2Q, 1C5,Z and 1LPZ are chosen from each of the six targets, respectively: CDK+PKA, β-glucosidase A, thrombin α, trypsin, urokinase-type plasminogen activator, and coagulation factor Xa.
Table 7.
Convergence of simulated free energy versus accuracy: comparison of MMPBSA results using converged free energies versus those using just the first nanosecond. All calculations were conducted with the DEN surface (sasopt=2) and optimized radius set (radiopt=1) as in Table 5 for efficiency. The RMSD’s of ΔΔG are in kcal/mol. See Figure 3 for the free energy convergence analysis.
| Systems | 10ns | 1ns | ||||
|---|---|---|---|---|---|---|
| RMSD | R | Slope | RMSD | R | Slope | |
| CDK+PKA | 3.65 | 0.72 | 0.30 | 3.51 | 0.73 | 0.29 |
| glucosidase | 1.77 | 0.47 | 0.38 | 1.70 | 0.43 | 0.34 |
| thrombin | 4.58 | 0.86 | 0.40 | 4.46 | 0.88 | 0.41 |
| trypsin | 3.10 | 0.67 | 0.37 | 3.25 | 0.66 | 0.36 |
| urokinase | 2.23 | 0.67 | 0.47 | 2.17 | 0.60 | 0.43 |
| Factor Xa | 3.00 | 0.70 | 0.30 | 2.85 | 0.71 | 0.31 |
Of course, all the tested complexes are with good crystal structures. This is probably why the differences between the two sets are so small because the structures are quite stable throughout the 10ns simulations. This in part supports the initial structural model setups in the calculations. However, it is unclear the difference would remain this small if docked complexes were utilized in these types of simulations. It is possible that much longer simulations would be necessary to fully observe “convergence” or to fully relax/optimize the docked complex structures.
Influence of Nonpolar Solvent Modeling on Absolute Binding Free Energies
In the single trajectory approach utilized in the above analyses, the entropic term was assumed to remain constant throughout a wide range of ligands for the same receptor. This is apparently an approximation, but without it, significantly more computation is needed. Nevertheless, we have investigated the possibility of augmenting the single-trajectory MMPBSA results by calculating the entropic contributions explicitly. Since our previous analysis shows that the normal mode approximation does not benefit too much to the quality of the MMPBSA calculations120, we resorted to the analysis by Gao et al.131, who developed a sophisticated method to account for the both the entropic and enthalpic effects of ligand conformational restriction to protein-ligand binding free energy, ΔGconf. In their method, multiple conformational energy wells were sampled, followed by the calculation of configuration integral based on the quasi-harmonic approximation of each well131.
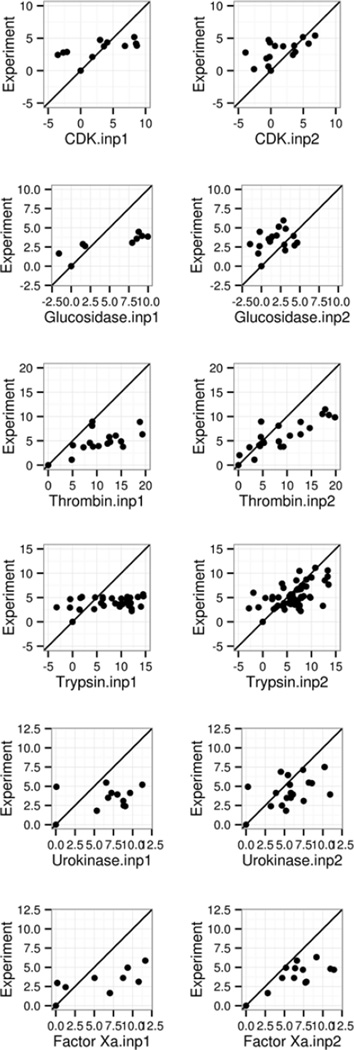
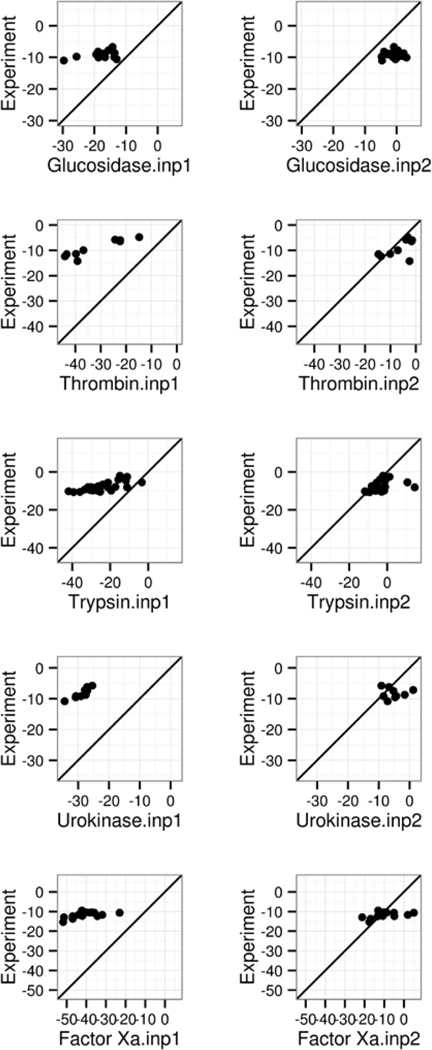
The ΔGconf from Gao et al.’s work was employed in this study as in our previous analysis of the classical method (INP=1)120, to augment the MMPBSA analysis presented here for the modern method (INP=2). Note that the data by Gao et al. do not cover every complex that was analyzed here. For those covered by both studies, we estimated the absolute binding free energies as outlined in Eqn (10) (Table 8/Figure 3). The comparison of the classical and modern nonpolar models in Table 8 show that the RMSD’s of absolute binding free energies are clearly smaller by INP=2 for all five groups of receptors analyzed. The modern nonpolar solvent model improves the MMPBSA performance for Thrombin α, trypsin β, urokinase-type plasminogen activator, and coagulation factor Xa dramatically, with RMSD’s reduced by around 3–4 times over those by the classical model. The improvement is more apparent in the correlation plots in Figure 3, supporting the use of the modern nonpolar solvent model in protein ligand binding calculations. Of course errors are still quite large, indicating further developments are needed o improve the MMPBSA method.
Table 8.
Effects of nonpolar solvent modeling (inp) upon the performance of MMPBSA in prediction of absolute binding affinities: The RMSD’s of absolute binding free energies (kcal/mol) between simulation and experiment for inp=1 and 2, respectively. The absolute binding free energies were estimated as outlined in Eqn (10) for those complexes with pre-computed configurational arrangement free energies (in parentheses) from Ref131. See Figure 3 for the scatter plots for both sets of data.
| Systems | INP=1 | INP=2 |
|---|---|---|
| Glucosidase (14) | 9.73 | 8.55 |
| Thrombin (9) | 23.90 | 4.85 |
| Trypsin (30) | 18.50 | 6.16 |
| Urokinase (9) | 20.70 | 4.70 |
| Factor Xa (14) | 29.48 | 6.69 |
Figure 3.
Correlation between MMPBSA predicted and experimental absolute binding affinities (kcal/mol). The absolute binding affinities by MM-PBSA were computed as described in text. Left and right columns are for INP=1 and INP=2, respectively. A through F refer to the following protein targets, respectively: β-glucosidase A, thrombin α, trypsin, urokinase-type plasminogen activator, and coagulation factor Xa.
Conclusion
In this study we first investigated how well the different nonpolar solvation models behave in protein-ligand binding affinity modeling by the MMPBSA methods. For both the classical and the modern methods, all simulation data display visible correlations with the experimental relative binding affinities. It is clear that the RMSD’s of relative binding affinities can be improved dramatically when the modern nonpolar solvent model is used. Visual inspection of the correlation plots also show that the relative affinities by the modern method agree with experiment better in that the scatter plots are closer to the diagonal line even if the correlation coefficients are quite similar between the two. Of course it is worth pointing out that the tested modern nonpolar solvent model was optimized for small molecules or protein side chains, where a single scaling constant was found to best reproduce the correlation of hydrophobic cavity free energy and molecular surface or volume97. Its handling of larger “ligands” as in protein-protein or protein-nucleic acid complexes remains to be investigated and improved. Further development is apparently necessary in this area.
An often-raised concern in MMPBSA calculations is the numerical accuracy in the numerical FDPB methods. Our testing of different grid spacings of 0.25, 0.50, and 1.00 Angstrom show that the agreement with experiment is quite similar regardless of the grid spacing used. This confirms the community-wide practice of using 0.50 Angstrom spacing in many prior studies. Detailed PB energetic analysis shows that electrostatic binding free energies do depend on the grid spacing used. However, the numerical convergence errors observed in the numerical FDPB calculations are far less than other errors in MMPBSA and the influence on the MMPBSA quality is not significant as demonstrated by the virtually identical correlation scatter plots with different grid spacings tested.
We further analyzed the impact of molecular surface upon the MMPBSA performance via two different perspectives. First we investigated the choices of atomic and solvent probe radii. Our comparison shows that all reasonable radius choices lead to overall comparable performance with respect to experiment. Nevertheless our data does show a consistent, albeit small, improvement when previously optimized solvent probe of 0.6 Angstrom was used in PB calculations. As shown by Tan and Luo, the limitation with the default 1.4 Angstrom is its overestimation of free energy barrier upon formation of dimers26. However the optimized protein radii do not seem to help too much. One reason is that the ligand atoms were always set to use the same mbondi radii since the optimized radius set only covers naturally occurring protein and nucleic acid residues. We next investigated the impact of molecular surface definitions by comparing the SES definition with the VDW and DEN definitions. Our data show that all of them perform rather similarly. Indeed there are only minor numerical differences in all the quality measures deployed. This is interesting because both VDW and DEN surfaces are much faster to compute than the classical SES surface. Their usage would potentially improve the efficiency of the MMPBSA methods.
The choice of solute dielectric is also surveyed and its impact on MMPBSA calculations is investigated when the modern nonpolar solvent model is used. Consistent with the findings for the classical nonpolar solvent model, the use of dielectric constant of 4 is better than the default molecular mechanics value of 1. Worth noting is the significant improvement in the RMSDs of relative binding affinities, which are 2 to 3 times smaller times than those with the vacuum dielectric constant. When the dielectric constant is increased to 20, the performance measures remain quite similar to those of calculations with the dielectric constant of 4, with only one dramatic improvement observed in β-glucosidase A due to its highly charged binding pocket.
Our convergence analysis shows that 1ns MD trajectory is apparently not enough to reach convergence in the averaged binding free energies. The comparison of the “converged” MMPBSA results and those with just the first 1ns trajectory shows that the agreements with experiment do appear to be slightly reduced, especially in relative binding free energy RMSD’s, though not that dramatic. On the other hand, correlation coefficients and the linear regression slopes remain in the highly similar ranges.
Finally we touched the issue of estimating absolute binding free energies via the MMPBSA methods. We estimated absolute binding affinities upon correction of binding-induced configurational arrangement, ΔGconf, and also the entropy lost upon binding. The comparison with experiment shows that the errors in absolute binding affinities can be reduced dramatically when the modern nonpolar solvent model was used. The improvement shows that it is promising to further explore the feasibility to use the MMPBSA methods to estimate absolute binding affinities of protein-ligand systems given the initial success of incorporating binding entropy lost, configurational rearrangement, electronic polarization, and long-range effect in nonpolar solvation. Of course the disagreement is still noticeable, indicating further rooms for improvement. We are working actively to address alternatives to further improve the MMPBSA methods.
Supplementary Material
Acknowledgments
This work was supported by National Institute of Health/NIGMS (GM093040 & GM079383 to RL and GM114237 to PR).
References
- 1.Perutz MF. Science. 1978;201:1187. doi: 10.1126/science.694508. [DOI] [PubMed] [Google Scholar]
- 2.Davis ME, Mccammon JA. Chem Rev. 1990;90:509. [Google Scholar]
- 3.Honig B, Nicholls A. Science. 1995;268:1144. doi: 10.1126/science.7761829. [DOI] [PubMed] [Google Scholar]
- 4.Honig B, Sharp K, Yang AS. J. Phys. Chem. 1993;97:1101. [Google Scholar]
- 5.Beglov D, Roux B. Journal of Chemical Physics. 1996;104:8678. [Google Scholar]
- 6.Cramer CJ, Truhlar DG. Chemical Reviews. 1999;99:2161. doi: 10.1021/cr960149m. [DOI] [PubMed] [Google Scholar]
- 7.Bashford D, Case DA. Annual Review Of Physical Chemistry. 2000;51:129. doi: 10.1146/annurev.physchem.51.1.129. [DOI] [PubMed] [Google Scholar]
- 8.Baker NA. Curr. Opin. Struct. Biol. 2005;15:137. doi: 10.1016/j.sbi.2005.02.001. [DOI] [PubMed] [Google Scholar]
- 9.Chen JH, Im WP, Brooks CL. Journal of the American Chemical Society. 2006;128:3728. doi: 10.1021/ja057216r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Feig M, Chocholousova J, Tanizaki S. Theoretical Chemistry Accounts. 2006;116:194. [Google Scholar]
- 11.Koehl P. Curr. Opin. Struct. Biol. 2006;16:142. doi: 10.1016/j.sbi.2006.03.001. [DOI] [PubMed] [Google Scholar]
- 12.Im W, Chen JH, Brooks CL. Peptide Solvation and H-Bonds. 2006;72:173. [Google Scholar]
- 13.Lu BZ, Zhou YC, Holst MJ, McCammon JA. Communications in Computational Physics. 2008;3:973. doi: 10.4208/cicp.081009.130611a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wang J, Tan CH, Tan YH, Lu Q, Luo R. Communications in Computational Physics. 2008;3:1010. [Google Scholar]
- 15.Altman MD, Bardhan JP, White JK, Tidor B. Journal of Computational Chemistry. 2009;30:132. doi: 10.1002/jcc.21027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cai Q, Wang J, Hsieh M-J, Ye X, Luo R. In: Annual Reports in Computational Chemistry. Ralph AW, editor. Vol. 8. Elsevier; 2012. p. 149. [Google Scholar]
- 17.Xiao L, Wang C, Luo R. Journal of Theoretical and Computational Chemistry. 2014;13:1430001. [Google Scholar]
- 18.Botello-Smith WM, Cai Q, Luo R. Journal of Theoretical and Computational Chemistry. 2014;13:1440008. [Google Scholar]
- 19.Warwicker J, Watson HC. J Mol Biol. 1982;157:671. doi: 10.1016/0022-2836(82)90505-8. [DOI] [PubMed] [Google Scholar]
- 20.Bashford D, Karplus M. Biochemistry. 1990;29:10219. doi: 10.1021/bi00496a010. [DOI] [PubMed] [Google Scholar]
- 21.Jeancharles A, Nicholls A, Sharp K, Honig B, Tempczyk A, Hendrickson TF, Still WC. Journal of the American Chemical Society. 1991;113:1454. [Google Scholar]
- 22.Gilson MK. Curr. Opin. Struct. Biol. 1995;5:216. doi: 10.1016/0959-440x(95)80079-4. [DOI] [PubMed] [Google Scholar]
- 23.Edinger SR, Cortis C, Shenkin PS, Friesner RA. J. Phys. Chem. B. 1997;101:1190. [Google Scholar]
- 24.Luo R, David L, Gilson MK. Journal of Computational Chemistry. 2002;23:1244. doi: 10.1002/jcc.10120. [DOI] [PubMed] [Google Scholar]
- 25.Lu Q, Luo R. Journal of Chemical Physics. 2003;119:11035. [Google Scholar]
- 26.Tan C, Yang L, Luo R. Journal of Physical Chemistry B. 2006;110:18680. doi: 10.1021/jp063479b. [DOI] [PubMed] [Google Scholar]
- 27.Cai Q, Wang J, Zhao H-K, Luo R. Journal of Chemical Physics. 2009:130. doi: 10.1063/1.3099708. [DOI] [PubMed] [Google Scholar]
- 28.Wang J, Cai Q, Li Z-L, Zhao H-K, Luo R. Chemical Physics Letters. 2009;468:112. doi: 10.1016/j.cplett.2008.12.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ye X, Cai Q, Yang W, Luo R. Biophysical Journal. 2009;97:554. doi: 10.1016/j.bpj.2009.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ye X, Wang J, Luo R. Journal of Chemical Theory and Computation. 2010;6:1157. doi: 10.1021/ct900318u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Luo R, Moult J, Gilson MK. Journal of Physical Chemistry B. 1997;101:11226. [Google Scholar]
- 32.Wang J, Tan C, Chanco E, Luo R. Physical Chemistry Chemical Physics. 2010;12:1194. doi: 10.1039/b917775b. [DOI] [PubMed] [Google Scholar]
- 33.Wang J, Luo R. Journal of Computational Chemistry. 2010;31:1689. doi: 10.1002/jcc.21456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Cai Q, Hsieh M-J, Wang J, Luo R. Journal of Chemical Theory and Computation. 2010;6:203. doi: 10.1021/ct900381r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hsieh MJ, Luo R. Journal of Molecular Modeling. 2011;17:1985. doi: 10.1007/s00894-010-0904-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Cai Q, Ye X, Wang J, Luo R. Journal of Chemical Theory and Computation. 2011;7:3608. doi: 10.1021/ct200389p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Wang J, Cai Q, Xiang Y, Luo R. Journal of Chemical Theory and Computation. 2012;8:2741. doi: 10.1021/ct300341d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Botello-Smith WM, Liu X, Cai Q, Li Z, Zhao H, Luo R. Chemical Physics Letters. 2012 doi: 10.1016/j.cplett.2012.10.081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Liu X, Wang C, Wang J, Li Z, Zhao H, Luo R. Physical Chemistry Chemical Physics. 2013 doi: 10.1039/c2cp41894k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Wang C, Wang J, Cai Q, Li ZL, Zhao H, Luo R. Computational and Theoretical Chemistry. 2013;1024:34. doi: 10.1016/j.comptc.2013.09.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Klapper I, Hagstrom R, Fine R, Sharp K, Honig B. Proteins Structure Function and Genetics. 1986;1:47. doi: 10.1002/prot.340010109. [DOI] [PubMed] [Google Scholar]
- 42.Davis ME, McCammon JA. Journal of Computational Chemistry. 1989;10:386. [Google Scholar]
- 43.Nicholls A, Honig B. Journal of Computational Chemistry. 1991;12:435. doi: 10.1002/jcc.1161. [DOI] [PubMed] [Google Scholar]
- 44.Luty BA, Davis ME, McCammon JA. Journal of Computational Chemistry. 1992;13:1114. [Google Scholar]
- 45.Holst M, Saied F. Journal of Computational Chemistry. 1993;14:105. [Google Scholar]
- 46.Forsten KE, Kozack RE, Lauffenburger DA, Subramaniam S. J. Phys. Chem. 1994;98:5580. [Google Scholar]
- 47.Holst MJ, Saied F. Journal of Computational Chemistry. 1995;16:337. [Google Scholar]
- 48.Bashford D. Lecture Notes in Computer Science. 1997;1343:233. [Google Scholar]
- 49.Im W, Beglov D, Roux B. Comput. Phys. Commun. 1998;111:59. [Google Scholar]
- 50.Rocchia W, Alexov E, Honig B. J. Phys. Chem. B. 2001;105:6507. [Google Scholar]
- 51.Cortis CM, Friesner RA. Journal of Computational Chemistry. 1997;18:1591. [Google Scholar]
- 52.Holst M, Baker N, Wang F. Journal of Computational Chemistry. 2000;21:1319. [Google Scholar]
- 53.Baker N, Holst M, Wang F. Journal of Computational Chemistry. 2000;21:1343. [Google Scholar]
- 54.Shestakov AI, Milovich JL, Noy A. Journal of Colloid and Interface Science. 2002;247:62. doi: 10.1006/jcis.2001.8033. [DOI] [PubMed] [Google Scholar]
- 55.Chen L, Holst MJ, Xu JC. Siam Journal on Numerical Analysis. 2007;45:2298. [Google Scholar]
- 56.Xie D, Zhou S. BIT Numerical Mathematics. 2007;47:853. [Google Scholar]
- 57.Wang J, Cieplak P, Li J, Wang J, Cai Q, Hsieh M, Lei H, Luo R, Duan Y. Journal of Physical Chemistry B. 2011;115:3100. doi: 10.1021/jp1121382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Lu B, Holst MJ, McCammon JA, Zhou YC. J Comput Phys. 2010;229:6979. doi: 10.1016/j.jcp.2010.05.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Bond SD, Chaudhry JH, Cyr EC, Olson LN. Journal of Computational Chemistry. 2010;31:1625. doi: 10.1002/jcc.21446. [DOI] [PubMed] [Google Scholar]
- 60.Miertus S, Scrocco E, Tomasi J. Chemical Physics. 1981;55:117. [Google Scholar]
- 61.Hoshi H, Sakurai M, Inoue Y, Chujo R. Journal of Chemical Physics. 1987;87:1107. [Google Scholar]
- 62.Zauhar RJ, Morgan RS. Journal of Computational Chemistry. 1988;9:171. [Google Scholar]
- 63.Rashin AA. J. Phys. Chem. 1990;94:1725. [Google Scholar]
- 64.Yoon BJ, Lenhoff AM. Journal of Computational Chemistry. 1990;11:1080. [Google Scholar]
- 65.Juffer AH, Botta EFF, Vankeulen BAM, Vanderploeg A, Berendsen HJC. J Comput Phys. 1991;97:144. [Google Scholar]
- 66.Zhou HX. Biophys J. 1993;65:955. doi: 10.1016/S0006-3495(93)81094-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Bharadwaj R, Windemuth A, Sridharan S, Honig B, Nicholls A. Journal of Computational Chemistry. 1995;16:898. [Google Scholar]
- 68.Purisima EO, Nilar SH. Journal of Computational Chemistry. 1995;16:681. [Google Scholar]
- 69.Liang J, Subramaniam S. Biophysical Journal. 1997;73:1830. doi: 10.1016/S0006-3495(97)78213-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Vorobjev YN, Scheraga HA. Journal of Computational Chemistry. 1997;18:569. [Google Scholar]
- 71.Totrov M, Abagyan R. Biopolymers. 2001;60:124. doi: 10.1002/1097-0282(2001)60:2<124::AID-BIP1008>3.0.CO;2-S. [DOI] [PubMed] [Google Scholar]
- 72.Boschitsch AH, Fenley MO, Zhou HX. J. Phys. Chem. B. 2002;106:2741. [Google Scholar]
- 73.Lu BZ, Cheng XL, Huang JF, McCammon JA. Proceedings of the National Academy of Sciences of the United States of America. 2006;103:19314. doi: 10.1073/pnas.0605166103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Lu B, Cheng X, Huang J, McCammon JA. Journal of Chemical Theory and Computation. 2009;5:1692. doi: 10.1021/ct900083k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Bajaj C, Chen S-C, Rand A. Siam Journal on Scientific Computing. 2011;33:826. doi: 10.1137/090764645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Georgescu RE, Alexov EG, Gunner MR. Biophys J. 2002;83:1731. doi: 10.1016/S0006-3495(02)73940-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Nielsen JE, McCammon JA. Protein Sci. 2003;12:313. doi: 10.1110/ps.0229903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Warwicker J. Protein Sci. 2004;13:2793. doi: 10.1110/ps.04785604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Tang CL, Alexov E, Pyle AM, Honig B. J Mol Biol. 2007;366:1475. doi: 10.1016/j.jmb.2006.12.001. [DOI] [PubMed] [Google Scholar]
- 80.Wang L, Li L, Alexov E. Proteins: Structure, Function, and Bioinformatics. 2015;83:2186. doi: 10.1002/prot.24935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Shivakumar D, Deng YQ, Roux B. J Chem Theory Comput. 2009;5:919. doi: 10.1021/ct800445x. [DOI] [PubMed] [Google Scholar]
- 82.Nicholls A, Mobley DL, Guthrie JP, Chodera JD, Bayly CI, Cooper MD, Pande VS. J Med Chem. 2008;51:769. doi: 10.1021/jm070549+. [DOI] [PubMed] [Google Scholar]
- 83.Swanson JMJ, Henchman RH, McCammon JA. Biophys J. 2004;86:67. doi: 10.1016/S0006-3495(04)74084-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Bertonati C, Honig B, Alexov E. Biophys J. 2007;92:1891. doi: 10.1529/biophysj.106.092122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Brice AR, Dominy BN. J Comput Chem. 2011;32:1431. doi: 10.1002/jcc.21727. [DOI] [PubMed] [Google Scholar]
- 86.Luo R, Gilson HSR, Potter MJ, Gilson MK. Biophysical Journal. 2001;80:140. doi: 10.1016/S0006-3495(01)76001-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.David L, Luo R, Head MS, Gilson MK. Journal of Physical Chemistry B. 1999;103:1031. [Google Scholar]
- 88.Marshall SA, Vizcarra CL, Mayo SL. Protein Sci. 2005;14:1293. doi: 10.1110/ps.041259105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Hsieh MJ, Luo R. Proteins-Structure Function and Bioinformatics. 2004;56:475. doi: 10.1002/prot.20133. [DOI] [PubMed] [Google Scholar]
- 90.Wen EZ, Luo R. Journal of Chemical Physics. 2004;121:2412. doi: 10.1063/1.1768151. [DOI] [PubMed] [Google Scholar]
- 91.Wen EZ, Hsieh MJ, Kollman PA, Luo R. Journal of Molecular Graphics & Modelling. 2004;22:415. doi: 10.1016/j.jmgm.2003.12.008. [DOI] [PubMed] [Google Scholar]
- 92.Lwin TZ, Luo R. Journal of Chemical Physics. 2005:123. doi: 10.1063/1.2102871. [DOI] [PubMed] [Google Scholar]
- 93.Lwin TZ, Zhou RH, Luo R. Journal of Chemical Physics. 2006:124. doi: 10.1063/1.2161202. [DOI] [PubMed] [Google Scholar]
- 94.Lwin TZ, Luo R. Protein Science. 2006;15:2642. doi: 10.1110/ps.062438006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Tan Y-H, Luo R. Journal of Physical Chemistry B. 2008;112:1875. doi: 10.1021/jp709660v. [DOI] [PubMed] [Google Scholar]
- 96.Tan Y, Luo R. BMC Biophysics. 2009;2:5. doi: 10.1186/1757-5036-2-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Tan C, Tan YH, Luo R. J Phys Chem B. 2007;111:12263. doi: 10.1021/jp073399n. [DOI] [PubMed] [Google Scholar]
- 98.Gallicchio E, Kubo MM, Levy RM. J Phys Chem B. 2000;104:6271. [Google Scholar]
- 99.Gallicchio E, Zhang LY, Levy RM. J Comput Chem. 2002;23:517. doi: 10.1002/jcc.10045. [DOI] [PubMed] [Google Scholar]
- 100.Levy RM, Zhang LY, Gallicchio E, Felts AK. J Am Chem Soc. 2003;125:9523. doi: 10.1021/ja029833a. [DOI] [PubMed] [Google Scholar]
- 101.Gallicchio E, Levy RM. J Comput Chem. 2004;25:479. doi: 10.1002/jcc.10400. [DOI] [PubMed] [Google Scholar]
- 102.Su Y, Gallicchio E. Biophys Chem. 2004;109:251. doi: 10.1016/j.bpc.2003.11.007. [DOI] [PubMed] [Google Scholar]
- 103.Weeks JD, Chandler D, Andersen HC. J Chem Phys. 1971;54:5237. [Google Scholar]
- 104.Floris F, Tomasi J. J Comput Chem. 1989;10:616. [Google Scholar]
- 105.Floris FM, Tomasi J, Ahuir JLP. J Comput Chem. 1991;12:784. [Google Scholar]
- 106.Zacharias M. J Phys Chem A. 2003;107:3000. [Google Scholar]
- 107.Widom B. J Phys Chem-Us. 1982;86:869. [Google Scholar]
- 108.Pratt LR, Chandler D. J Chem Phys. 1977;67:3683. [Google Scholar]
- 109.Ashbaugh HS, Kaler EW, Paulaitis ME. J Am Chem Soc. 1999;121:9243. [Google Scholar]
- 110.Smith R, Tanford C. Proceedings of the National Academy of Sciences of the United States of America. 1973;70:289. doi: 10.1073/pnas.70.2.289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Kang YK, Nemethy G, Scheraga HA. J Phys Chem-Us. 1987;91:4105. [Google Scholar]
- 112.Lum K, Chandler D, Weeks JD. J Phys Chem B. 1999;103:4570. [Google Scholar]
- 113.Hummer G. J Am Chem Soc. 1999;121:6299. [Google Scholar]
- 114.Dzubiella J, Swanson JMJ, McCammon JA. J Chem Phys. 2006:124. doi: 10.1063/1.2171192. [DOI] [PubMed] [Google Scholar]
- 115.Wagoner JA, Baker NA. Proceedings of the National Academy of Sciences of the United States of America. 2006;103:8331. doi: 10.1073/pnas.0600118103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Pratt LR, Chandler D. J Chem Phys. 1980;73:3434. [Google Scholar]
- 117.Kollman PA, Massova I, Reyes C, Kuhn B, Huo SH, Chong L, Lee M, Lee T, Duan Y, Wang W, Donini O, Cieplak P, Srinivasan J, Case DA, Cheatham TE. Accounts Chem Res. 2000;33:889. doi: 10.1021/ar000033j. [DOI] [PubMed] [Google Scholar]
- 118.Srinivasan J, Cheatham TE, Cieplak P, Kollman PA, Case DA. J Am Chem Soc. 1998;120:9401. [Google Scholar]
- 119.Gohlke H, Case DA. J Comput Chem. 2004;25:238. doi: 10.1002/jcc.10379. [DOI] [PubMed] [Google Scholar]
- 120.Yang TY, Wu JC, Yan CL, Wang YF, Luo R, Gonzales MB, Dalby KN, Ren PY. Proteins-Structure Function and Bioinformatics. 2011;79:1940. doi: 10.1002/prot.23018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Miller BR, McGee TD, Swails JM, Homeyer N, Gohlke H, Roitberg AE. J Chem Theory Comput. 2012;8:3314. doi: 10.1021/ct300418h. [DOI] [PubMed] [Google Scholar]
- 122.Wang RX, Fang XL, Lu YP, Yang CY, Wang SM. J Med Chem. 2005;48:4111. doi: 10.1021/jm048957q. [DOI] [PubMed] [Google Scholar]
- 123.Fiser A, Sali A. Method Enzymol. 2003;374:461. doi: 10.1016/S0076-6879(03)74020-8. [DOI] [PubMed] [Google Scholar]
- 124.Wang JM, Wolf RM, Caldwell JW, Kollman PA, Case DA. J Comput Chem. 2004;25:1157. doi: 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- 125.Case DA, Cheatham TE, Darden T, Gohlke H, Luo R, Merz KM, Onufriev A, Simmerling C, Wang B, Woods RJ. Journal of Computational Chemistry. 2005;26:1668. doi: 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Jakalian A, Jack DB, Bayly CI. J Comput Chem. 2002;23:1623. doi: 10.1002/jcc.10128. [DOI] [PubMed] [Google Scholar]
- 127.Wang JM, Wang W, Kollman PA, Case DA. J Mol Graph Model. 2006;25:247. doi: 10.1016/j.jmgm.2005.12.005. [DOI] [PubMed] [Google Scholar]
- 128.Gilson MK, Given JA, Bush BL, McCammon JA. Biophys J. 1997;72:1047. doi: 10.1016/S0006-3495(97)78756-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Luo R, Head MS, Given JA, Gilson MK. Biophysical Chemistry. 1999;78:183. doi: 10.1016/s0301-4622(98)00229-4. [DOI] [PubMed] [Google Scholar]
- 130.Luo R, Gilson MK. Journal of the American Chemical Society. 2000;122:2934. [Google Scholar]
- 131.Gao C, Park MS, Stern HA. Biophys J. 2010;98:901. doi: 10.1016/j.bpj.2009.11.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Pang X, Zhou H-X. Communications in computational physics. 2013;13:1. doi: 10.4208/cicp.270711.140911s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Grant JA, Pickup BT. The Journal of Physical Chemistry. 1995;99:3503. [Google Scholar]
- 134.Hou T, Wang J, Li Y, Wang W. Journal of Chemical Information and Modeling. 2011;51:69. doi: 10.1021/ci100275a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Talley K, Ng C, Shoppell M, Kundrotas P, Alexov E. PMC Biophysics. 2008;1:1. doi: 10.1186/1757-5036-1-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Luo R, Head MS, Moult J, Gilson MK. Journal of the American Chemical Society. 1998;120:6138. [Google Scholar]
- 137.Wang J, Cieplak P, Li J, Hou T, Luo R, Duan Y. Journal of Physical Chemistry B. 2011;115:3091. doi: 10.1021/jp112133g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 138.Wang J, Cieplak P, Cai Q, Hsieh MJ, Wang JM, Duan Y, Luo R. Journal of Physical Chemistry B. 2012;116:7999. doi: 10.1021/jp212117d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139.Wang JM, Cieplak P, Li J, Cai Q, Hsieh MJ, Luo R, Duan Y. Journal of Physical Chemistry B. 2012;116:7088. doi: 10.1021/jp3019759. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.