Coherent control of long-range photoinduced electron transfer by stimulated X-ray Raman processes

Significance

Electron transfer is ubiquitous in chemical reactions and many biophysical processes such as respiration and photosynthesis. In this work, we show how broadband X-ray pulses can be used to change the local electronic structures of donor–bridge–acceptor (DBA) molecular systems, thus enabling and controlling electron transfer between designated sites in the molecule. An X-ray–stimulated Raman process can control electron transfer with atomic specificity and ultrafast timescale. With an appropriate X-ray pulse setting, electron pathways can be selectively enhanced. The control can be implemented at the donor, bridge, or acceptor sites in a DBA system.

Abstract

We show that X-ray pulses resonant with selected core transitions can manipulate electron transfer (ET) in molecules with ultrafast and atomic selectivity. We present possible protocols for coherently controlling ET dynamics in donor–bridge–acceptor (DBA) systems by stimulated X-ray resonant Raman processes involving various transitions between the D, B, and A sites. Simulations presented for a Ru(II)–Co(III) model complex demonstrate how the shapes, phases and amplitudes of the X-ray pulses can be optimized to create charge on demand at selected atoms, by opening up otherwise blocked ET pathways.

Long-range electron transfer (ET) over tens of angstroms in molecular assemblies plays an essential role in many biological processes, artificial light-harvesting schemes, and sensor applications (1–7). Using lasers to precisely control ET pathways and rates has been a long-term goal of chemists (8). The manner in which infrared light can excite molecular vibrations to affect ET in donor–bridge–acceptor (DBA) systems has been studied theoretically (9, 10) and experimentally (11–14).

The rapid development of bright X-ray lasers and high harmonic sources has opened up new opportunities for X-ray spectroscopy (15). We have recently demonstrated that stimulated X-ray Raman spectroscopy (16, 17) with broadband X-ray pulses can reveal the time-evolving oxidation states of various species in the long-range ET process of the protein azurin (18). Here we show that by coupling to core-excited states, resonant X-ray pulses can precisely target either the donor, bridge, or the acceptor site in an ET process by altering the valence electronic states in its vicinity by triggering the bridge-to-acceptor (BA), the donor-to-bridge (DB), or the bridge-to-bridge (BB) ET transfer. We show how the ET pathways in a model DBA system ([(CN)₄Ru^II(tpphz)Co^III(CN)₄]³⁻) can be coherently manipulated by X-ray pulses resonant with the acceptor.

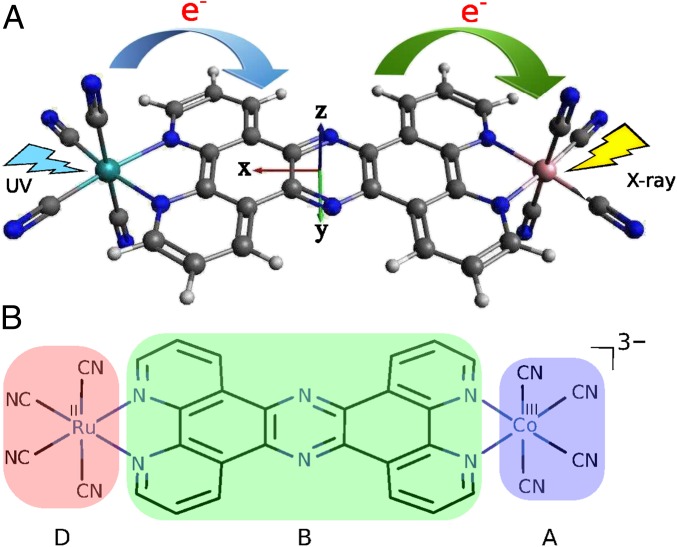
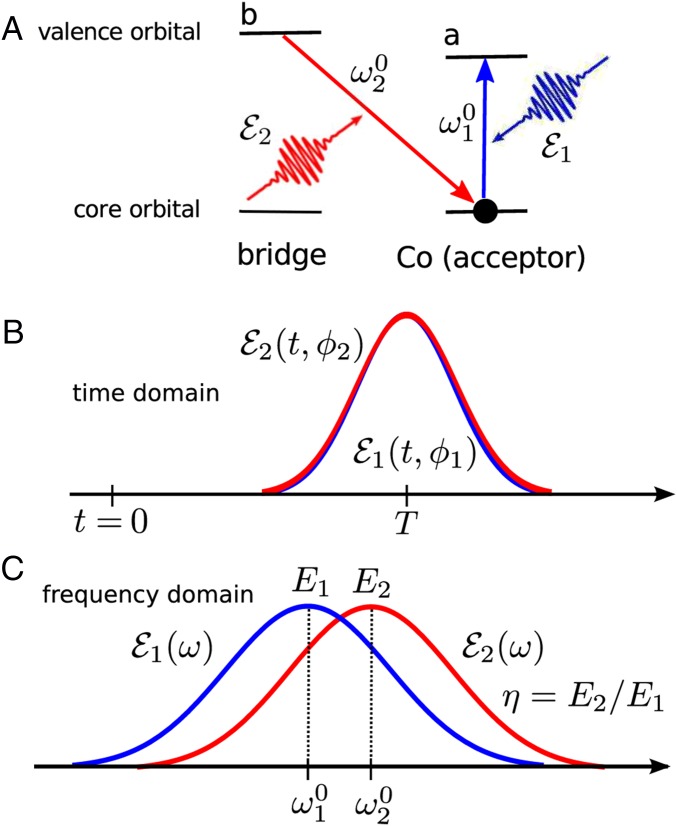
Application is made to a Ru–Co light-harvesting complex (shown in Fig. 1 A and B) where an electron is transferred from the donor Ru^II to the acceptor Co^III to create Ru^III/Co^II. X-ray pulses can create valence excitations via a Raman process (19), thus altering the occupied molecular orbitals (MOs). We shall focus on the BA ET coherent control scheme illustrated in Fig. 2A. In a stimulated Raman process a core hole created by the X-ray pulse on the acceptor is instantaneously filled by a valence electron on the bridge, resulting in a B→A ET. Such an ET process is analogous to the valence-to-core X-ray spontaneous emission observed in transition metal complexes with ligand-to-metal charge transfer (20).

Fig. 1.

(A) Three-dimensional molecular structure of the Ru–Co complex [(CN)₄ Ru^II(tpphz)Co^III(CN)₄]³⁻, which is a simplified model of that studied in refs. 21–23. The D→B and B→A ET steps are represented by the blue and green arrows, respectively. The B→A ET step is aided by an X-ray pulse shot at the Co center. The coordinate axes are also shown. Color code: Ru, light blue; Co, pink; N, deep blue; C, black; H, light gray. (B) Chemical structure of the Ru–Co complex. The donor, bridge, and acceptor fragments are labeled and shaded with different colors.

Fig. 2.

(A) The acceptor control stimulated X-ray Raman process invoked by two X-ray pulses, of which the carrier frequencies ${\omega }_1^0$ are resonant with the cobalt (acceptor) local core excitation and ${\omega }_2^0$ is resonant with the bridge to cobalt emission transition, respectively. (B) The two pulses ${\mathrm{ℰ}}_1$ (blue) and ${\mathrm{ℰ}}_2$ (red) in the time domain with their phases ${\varphi }_1$ and ${\varphi }_2$, respectively. See SI Appendix, Eq. S14 for detailed expressions. (C) The two pulses in the frequency domain with the carrier frequencies ${\omega }_1^0=\mathrm{7,720.65}$ eV and ${\omega }_2^0=\mathrm{7,721.53}$ eV, bandwidths ${\sigma }_1={\sigma }_2=3$ eV, and the maximum field intensities $E_1=E_2=5\times {10}^{11}$ V/cm. The amplitude ratio η is defined as $E_2/E_1$. See SI Appendix, Eq. S15 for expressions.

Effective Model Hamiltonian for the Ru–Co Complex

Long-range ET in the bimetallic Ru–Co complex [(bpy)₂¹Ru^II (tpphz)¹Co^III(bpy)₂]⁵⁺ (low spin in the ground state) was investigated recently by transient optical absorption, X-ray absorption, X-ray diffuse scattering, and X-ray emission (21–23). This complex has been proposed for artificial light-harvesting applications. The DB ET step is very fast ($<50$ fs) but the BA ET is much slower (picoseconds). The system ends up in a [(bpy)₂²Ru^III(tpphz)⁴Co^II(bpy)₂]⁵⁺ high-spin charge-separated state. Our goal is to accelerate the BA step by a stimulated X-ray Raman process. To reduce the computational cost while keeping the essential ET physics of the original complex, we have studied the simplified model complex [(CN)₄ Ru^II(tpphz)Co^III(CN)₄]³⁻ (Fig. 1 A and B) where the bpy ligands are replaced with (CN)⁻. This eliminates the complicated spin crossover transition at the Co center (23), because the strong ligands (CN)⁻ favor the low-spin state.

The relevant ET parameters were obtained from electronic structure calculations. Because the Ru and Co centers are far apart, electronic structure calculations can be carried out for smaller fragments [(CN)₄ Ru^II(tpphz)]²⁻ and [⁻(tpphz)Co^III(CN)₄]²⁻ (the tpphz ligand is negatively charged). Computational details are given in Materials and Methods.

We model the ET in this complex using two frontier orbitals on each of the donor, the bridge, and the acceptor site; these are the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO). Neglecting spin, each site has four possible states: the ground state $|0\rangle$, where the HOMO is occupied and LUMO is not; the negatively charged state $c_m^{†}|0\rangle$ (both orbitals are occupied); the positive charged hole state $v_m^{†}|0\rangle$ (both orbitals are unoccupied); and a single electron–hole pair (Frenkel exciton) state $c_m^{†}{v}_m^{†}|0\rangle$, where the HOMO electron is moved to the LUMO. The operators $c_m^{†}$ ($c_m$) and $v_n^{†}$ ($v_n$) create (annihilate) an electron on site m and a hole on site n, respectively. They satisfy the Fermi commutation relations $\left\{c_m,c_n^{†}\right\}={\delta }_{mn}$, $\left\{v_m,v_n^{†}\right\}={\delta }_{mn}$. Out of all of the orbitals only three states D, B, and A are relevant to the ET process and are described below. Whereas the DB coupling is strong and the BA coupling is weak, we neglect the direct donor–acceptor coupling.

Initial photoexcitation creates an electron–hole pair on the donor $|D\rangle =c_d^{†}{v}_d^{†}|0\rangle$. We assume that there are no electronic coherences and only donor population is generated. This can be achieved by, e.g., resonant optical or X-ray Raman pulse that is tuned to the vicinity of the Ru atom in the donor molecule. The electron then hops from orbital d to orbital b due to the strong $D/B$ coupling, thereby creating state $|B\rangle =c_d{c}_b^{†}|D\rangle \equiv c_b^{†}{v}_d^{†}|0\rangle$. The ET is completed when an electron hops from the bridge to acceptor due to the weak $B/A$ coupling creating the final state: $|A\rangle =c_b{c}_a^{†}|B\rangle \equiv c_a^{†}{v}_d^{†}|0\rangle$. We had calculated the matrix elements of the Hamiltonian in SI Appendix, Eq. S1 in this diabatic basis $|D\rangle$,$|B\rangle$,$|A\rangle$.

Enabling Electron Transfer Pathways by an X-Ray Raman Process

In the absence of the X-ray pulse the ET process is described by a generalized Redfield master equation:

$$\dot{\rho }=-\mathrm{ℒ}\left[\rho \right],$$ [1]

where the Liouvillian $\mathrm{ℒ}\left[\rho \right]=i/\hslash \left[H_s,\rho \right]-K\rho$ is a rank 9 tensor in the space of D, B, A states (three populations and six coherences). Here $H_s=H_{DBA}+H_{hop}$ is a $3\times 3$ Hamiltonian matrix which includes the DBA diagonal part $H_{DBA}$ (SI Appendix, Eq. S3) plus the electron hopping off-diagonal part $H_{hop}$ (SI Appendix, Eq. S4), and K denotes $9\times 9$ Redfield ET rate matrix (SI Appendix, Eqs. S6–S8). The ET includes several pathways that involve both population hopping (sequential) as well as electronic coherences between adiabatic states (superexchange) (24).

The time evolution of the acceptor population can be observed by various spectroscopic measurements including fluorescence and transient absorption. Using Eq. 1 we had calculated acceptor population. After photoexcitation of the excited state population of the donor state D at time $t=0$ in the diabatic basis, the electron wave packet goes through various states including the population and coherences between states D, B, A, and finally populates the acceptor state A at time t given by

$$P_A^{\left(0\right)}\left(t\right)=i\hslash {\mathcal{G}}_{AA,DD}\left(t\right),$$ [2]

where the zero superscript indicates that this is a reference calculation in the absence of the X-ray. ${\mathcal{G}}_{AA,DD}\left(t\right)={\left[e^{-\mathrm{ℒ}t}\right]}_{AA,DD}$ is the Liouville space Green’s function matrix element that represents electron transfer dynamics between donor and acceptor populations and is given by SI Appendix, Eq. S10.

We now introduce an X-ray pulse at time $t_1$ after the photoexcitation. This pulse can promote an electron from the core orbital to the valence orbital of the acceptor, and the core hole is simultaneously filled by an electron from the bridge valence orbital. In this X-ray Raman process shown in Fig. 2A, the electron is transferred from orbital b to a via an inelastic process or from a to a and b to b via an elastic process. The ET can be controlled by an X-ray Raman excitation as long as the lifetime of the valence excited state created by the X-ray Raman process is comparable to or longer than the ET timescale. Interaction of the molecule with light is described by a dipole matter–field coupling in SI Appendix, Eq. S13. By placing a core electron on a valence orbital of the acceptor (orbital a) and filling this core hole with the valence electron from the bridge (orbital b), the pulse enables electrons to tunnel through the bridge and reach the acceptor. We had calculated the acceptor population induced by the X-ray pulse and its variation with $t_2$ (the time delay between the X-ray pulse arrival and observation time) and $t_1$ (the X-ray pulse delay relative to the initial photoexcitation). The ET dynamics consists of three steps (see the diagram in SI Appendix, Fig. S1). During $t_1$ (before the X-ray pulse) the system evolves according to the Redfield master equation (Eq. 1) and is promoted from population ${\rho }_{DD}$ to some superposition of bridge and acceptor states ${\rho }_{mn}$, $m,n=A,B,D$. The second step is the evolution during the X-ray pulse. We use perturbation theory in the X-ray field–matter interaction with the diagram in SI Appendix, Fig. S1. In the first-order perturbation theory with respect to X-ray intensity the density matrix of the system is changed from ${\rho }_{mn}$ to ${\rho }_{qn}$, $q=A,B,D$. We consider two X-ray pulses (Fig. 2 B and C): ${\mathrm{ℰ}}_1$ with phase ${\varphi }_1$ and central frequency ${\omega }_1^0$ resonant with adiabatic transition $A\prime \to x$, and ${\mathrm{ℰ}}_2$ with phase ${\varphi }_2$ and central frequency ${\omega }_2^0$ resonant with transition $B\prime \to x$, where $A\prime$, $B\prime$, and x correspond to the acceptor, bridge adiabatic states, and the intermediate core excited state on the acceptor, respectively. The adiabatic delocalized basis is used for calculating the relevant dipole moments because the Hamiltonian in this basis is diagonal (SI Appendix). In the localized (diabatic basis) one can therefore select pulses for the elastic $m\to x\to m$ and inelastic $m\to x\to q\ne m$, $m,q=A,B,D$ Raman processes. Therefore, when $q=m$ the X-ray interacts twice with the same state (if $q=m=A$ via $E_1$ and if $q=m=B$ via $E_2$). Similarly, if $q=A$, $m=B$, or $q=B$, $m=A$ interaction with X-ray occurs with both $E_1$ and $E_2$ pulses. Finally, during the third ET step which occurs during the remaining time interval $t_2$ electron again evolves according to Eq. 1 from the state ${\rho }_{qn}$ to its final state ${\rho }_{AA}$. Assuming well-separated pulses, the incremental acceptor population linear in X-ray intensity is given by (see SI Appendix, Eqs. S6–S18 and SI Appendix, Fig. S1 for details)

$$\mathrm{\Delta }{P}_A\left(t_1,t_2\right)=2\mathrm{ℛ}{\displaystyle \sum _{i,j=\mathrm{1,2}}\hspace{0.17em}{\displaystyle \sum _{m,n,q=A,B}\hspace{0.17em}{\mathcal{G}}_{AA,qn}\left(t_2\right){\alpha }_{qm}^{\left(ij\right)}{\mathcal{G}}_{mn,DD}\left(t_1\right)}},$$ [3]

where $\mathrm{ℛ}$ denotes the real part, and generalized polarizability tensor ${\alpha }_{qm}^{\left(ij\right)}$ is defined by

$$\begin{array}{c}{\alpha }_{mn}^{\left(ij\right)}=-i{\displaystyle \int \frac{d\omega }{2\pi }\left({\mathbf{e}}_i\cdot {\mathit{\mu }}_{xm}\right)\left({\mathbf{e}}_j\cdot {\mathit{\mu }}_{nx}^{\text{*}}\right)}\\ \times \frac{{\mathrm{ℰ}}_i^{\text{*}}\left(\omega \right){\mathrm{ℰ}}_j\left(\omega +{\omega }_i^0-{\omega }_j^0+{\omega }_m-{\omega }_n\right)e^{i\left({\varphi }_i-{\varphi }_j\right)}}{\omega +{\omega }_i^0-{\omega }_{xm}+i{\mathrm{\Gamma }}_x}.\end{array}$$ [4]

Here $i=1$ if $q=A$, $i=2$ if $q=B$, $j=1$ if $m=A$, and $j=2$ if $m=B$. SI Appendix, Eq. S3 contains both elastic and inelastic components of the ET pathways. The elastic components involve $q=m=A,B$ and consequently $i=j$, which are independent of the phase of the field, whereas inelastic components $i\ne j$ depend upon phase difference between the field $E_1$ and $E_2$: $\varphi ={\varphi }_1-{\varphi }_2$. Note that ${\alpha }_{qm}^{\left(ij\right)}$ also depends on the amplitude ratio $\eta =E_2/E_1$. Zero-, first-, and second-order terms in η correspond to elastic process $q=m=A$, inelastic process $q\ne m$, and elastic $q=m=B$, respectively. Therefore, the effects of the amplitude ratio η and phase ϕ on ET control will be demonstrated below.

Results and Discussion

The following parameters were used in our simulations: donor energy $E_D=0$ eV, bridge $E_B=2.8$ eV, acceptor energy $E_A=5.4$ eV, and hopping couplings are $t_{DB}=0.6$ eV, $t_{BA}=0.008$ eV. The corresponding electron transfer times are $k_{DB}^{-1}=20$ fs and $k_{BA}^{-1}=2$ ps. The acceptor has a single core state with energy ${\omega }_x=\mathrm{7,725.3}$ eV (to resemble the Co K-edge excitation energy) and linewidth ${\mathrm{\Gamma }}_x=1.5$ eV. The dipole moments in the adiabatic basis (SI Appendix) are taken to be ${\mu }_{A\prime x}=-0.00086$ a.u. and ${\mu }_{B\prime x}=0.00033$ a.u.. These values are rationalized in SI Appendix. We further assume Gaussian pulse envelopes ${\mathrm{ℰ}}_j\left(\omega \right)=\sqrt{2\pi }{\sigma }_j{E}_j{e}^{-(1/2){\sigma }_j^2{\omega }^2-i{\varphi }_j}$, with the carrier frequency ${\omega }_1^0=\mathrm{7,720.65}$ eV, ${\omega }_2^0=\mathrm{7,721.53}$ eV, bandwidth ${\sigma }_1={\sigma }_2=3$ eV, and maximum field intensity $E_1=E_2=5\times {10}^{11}$ V/cm. Due to the weak dipole transitions this strong electric field can still be treated within perturbation theory. Ionization cross-section is suppressed for Co when the pulse is resonant to a core excitation.

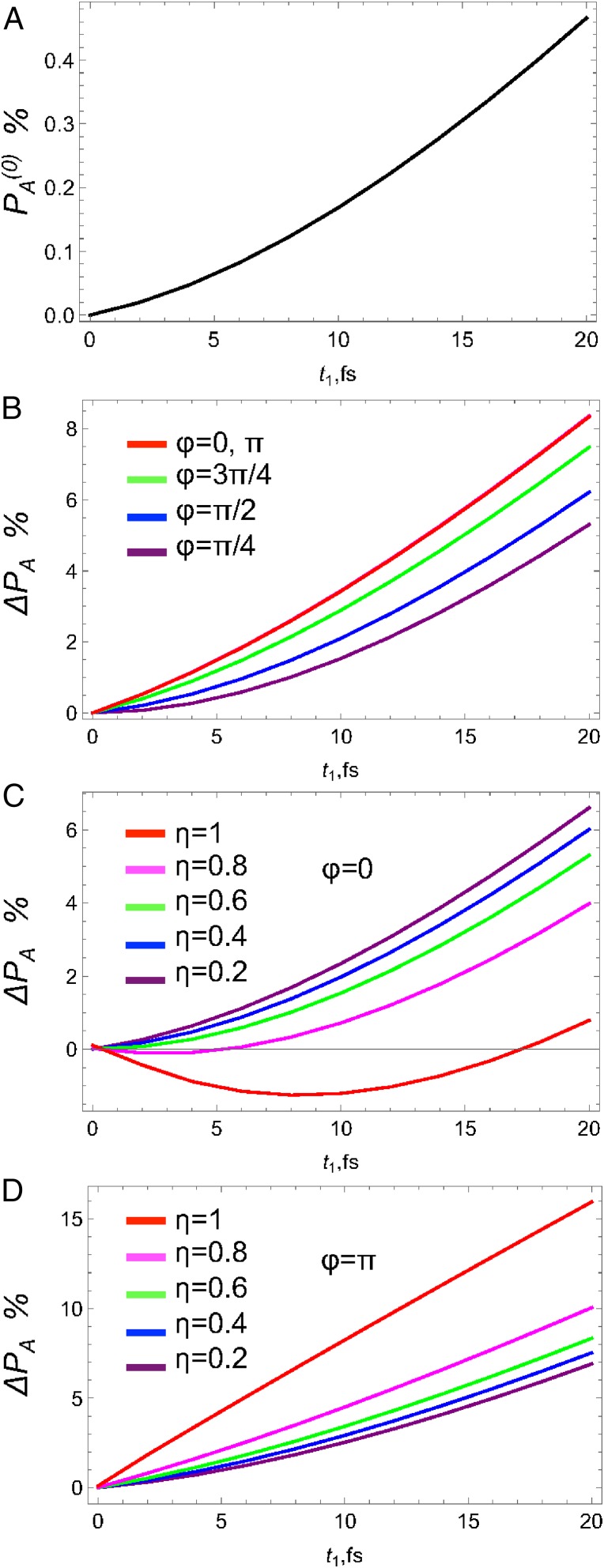
We first study the variation with $t_1$ for $t_2=3$ fs. The time growth of the acceptor population $P_A^{\left(0\right)}\left(t_1\right)$ in the absence of the X-ray pulse shown in Fig. 3A is limited by the slow BA ET rate reaching 0.5% at $t_1=20$ fs. The incremental acceptor population $\mathrm{\Delta }{P}_A\left(t_1\right)$ caused by the X-ray pulse is governed by ${\mathcal{G}}_{AA,qn}\left(t_2\right)$ as shown in Fig. 3B. This large population increase (up to 8% at 20 fs) may be used for transistor or gating applications (25). One can see that coherent control is possible and $\mathrm{\Delta }{P}_A$ can change from 5% to 8.5% by varying ϕ from $\pi /4$ to π. Fig. 3C shows the variation of $\mathrm{\Delta }{P}_A$ with η at $\varphi =0$. Note that increasing η from 0.2 to 1 decreases the acceptor population from 6% down to 1%. Fig. 3D shows that for $\varphi =\pi$ the acceptor population increases from 5% to 15%. This is due to the interference in various pathways that involve different powers of η from zeroth power (elastic $A\to x\to A$) to first (inelastic $B\to x\to A$) to quadratic (elastic $B\to x\to B$).

Fig. 3.

Acceptor population vs. $t_1$ at $t_2=3$ fs (right after the X-ray pulse) in the Ru–Co model complex. (A) Population without the X-ray pulse $P_A^{\left(0\right)}\left(t_1\right)$. (B) Incremental population due to X-ray $\mathrm{\Delta }{P}_A$ for different phases ϕ; (C) for different amplitude ratio η and $\varphi =0$; (D) Same as in C but for $\varphi =\pi$.

We next turn to the variation of the acceptor population after the X-ray pulse has passed. In Fig. 4A we show the unperturbed population $P_A^{\left(0\right)}$ vs. $t_2$ at different $t_1$. It shows the gradual increase in population with increase of the pulse delay due to more population transferred to acceptor at later times via the ET kinetics. The corresponding population changes from 0% to 0.4% at $t_2=0$ to 0.6% to 1.1% at $t_2=20$ fs. Similar increase can be observed for the incremental population $\mathrm{\Delta }{P}_A$ as shown in Fig. 4B. However, in this case population reaches 4.5%, which is much larger than the unperturbed value. The phase control is depicted in Fig. 4C. The maximum population change occurs at $t_2=0$ from $\varphi =0$ reaching 8% down to 5% at $\varphi =\pi /4$ and intermediate values at $\varphi =\pi /2$ and $\varphi =3\pi /4$. At $t_2=20$ fs the population changes from 9% at $\varphi =0,\pi$ down to 6.7% at $\varphi =\pi /4$. Finally, the field amplitude ratio η can also control the population. In this case, independently of the value of ϕ the population always increases with increase of the strength of inelastic component at $t_2=0$ from 7% at $\eta =0.2$ to 8.2% at $\eta =1$ and at $t_2=20$ fs from 7.2% at $\eta =0.2$ to 9.5% at $\eta =1$.

Fig. 4.

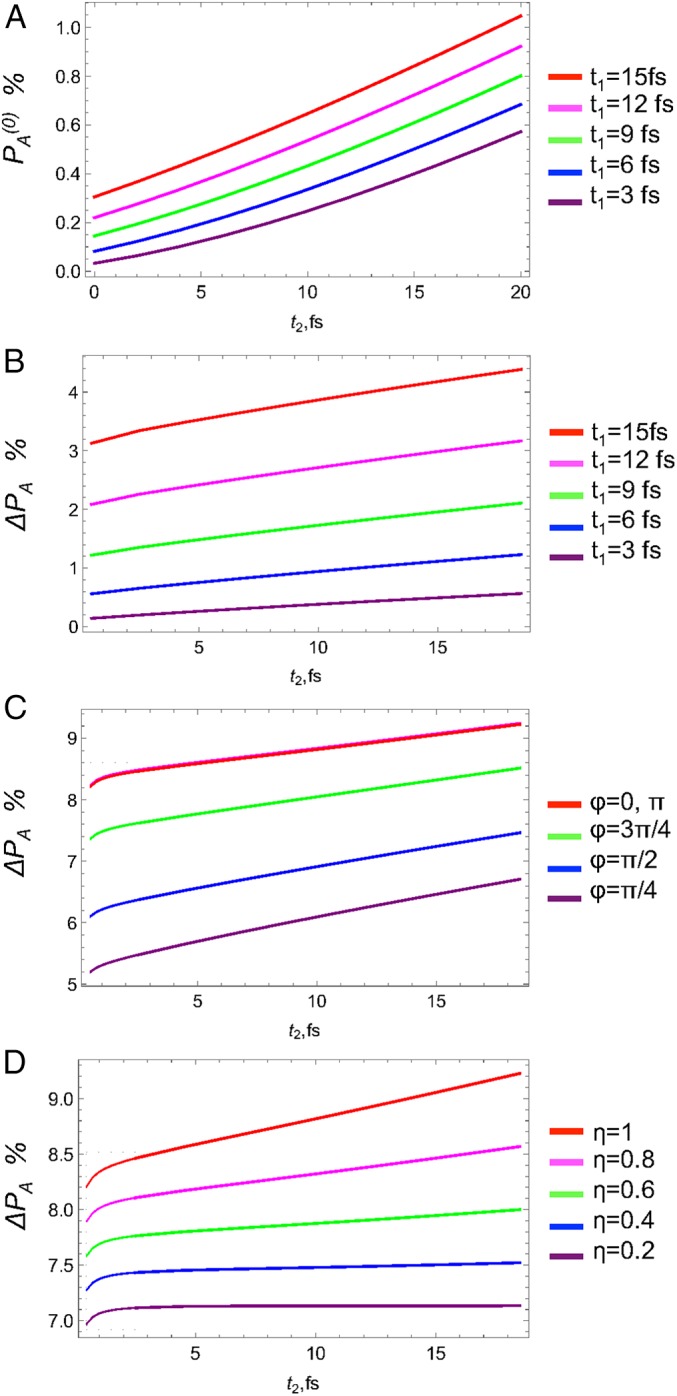
Incremental acceptor population without the X-ray pulse $\mathrm{\Delta }{P}_A^{\left(0\right)}$ vs. $t_2$ for different $t_1$ (A), with the X-ray pulse $\mathrm{\Delta }{P}_A$ vs. $t_2$ for different $t_1$ (B), phase ϕ (C), amplitude ratio η at $\varphi =0$ (D).

The X-ray pulse can significantly affect the acceptor population in a limited parameter regime (e.g., appropriate dipole moments for the core transitions ${\mu }_B$, ${\mu }_A$, electron transfer rates $K_{BA}$ and $K_{DB}$, as well as electric field intensities $I_j={\left|{\mathrm{ℰ}}_j\right|}^2$). We use a weak X-ray pulse, so that $\mathrm{\Delta }{P}_A$ is less than 10%. Assuming ultrashort δ pulses ${\mathrm{ℰ}}_j\left(t-t_1\right)=I_j^{1/2}\delta \left(t-t_1\right)$ for equal parameters of both pulses $I_1=I_2$, ${\sigma }_1={\sigma }_2$, we obtain that the ratio of the inelastic component (that involved $B\to x\to A$ transition) to elastic ($A\to x\to A$) (SI Appendix, Eq. S19) should obey

$$\frac{\left|{\mu }_{Bx}\right|}{\left|{\mu }_{Ax}\right|}>\frac{K_{BA}}{K_{DB}}.$$ [5]

Eq. 5 provides an important restriction on the pulse and matter parameters suitable for ET coherent control where inelastic component of the stimulated Raman process contributes substantially to the acceptor population.

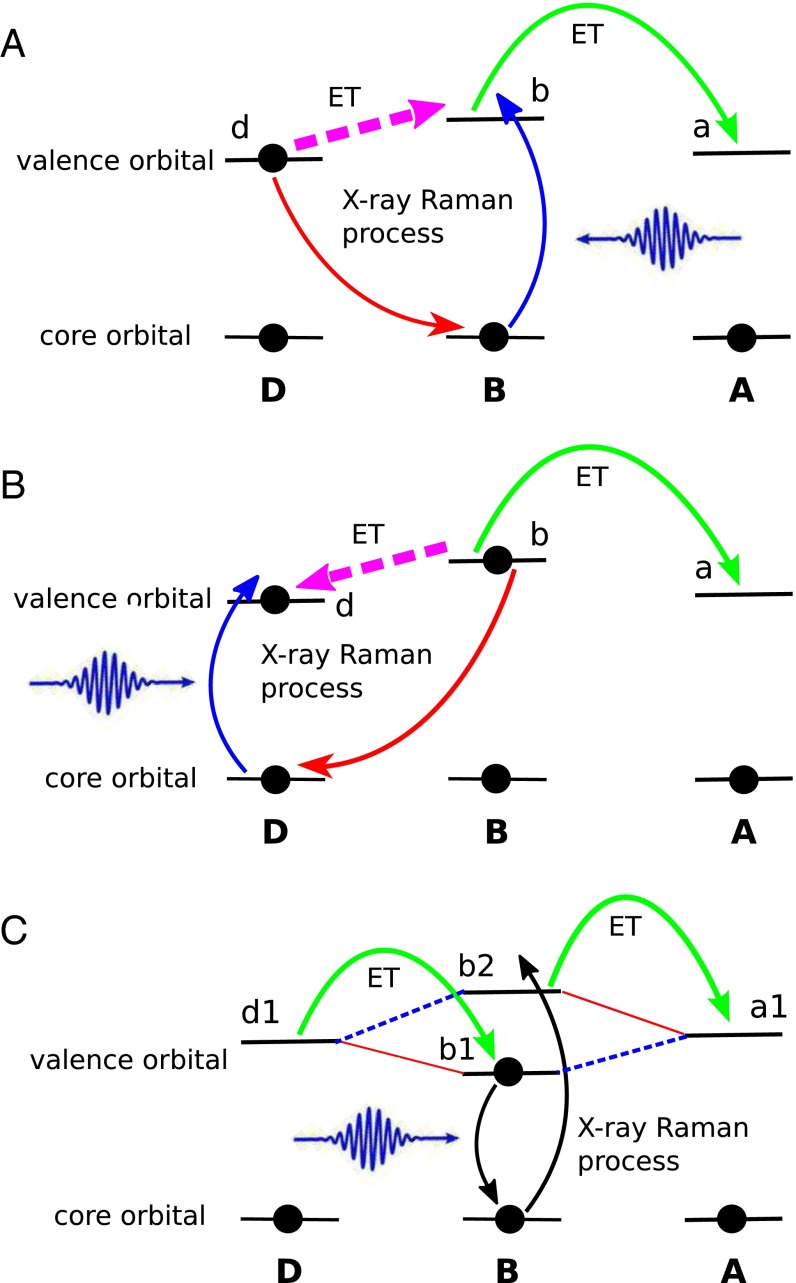
Other ET control schemes are possible. The present scheme shown in Fig. 2A is based on control of the core hole on acceptor. However, if the core hole is on the bridge, the X-ray Raman process may induce A→B ET and the D→B→A ET process is hindered. Another control scenario may arise in DB and BB coherent control schemes. As sketched in Fig. 5 A–C, one can either use X-rays to induce electronic transitions between donor and bridge MOs (Fig. 5 A and B), or move electrons between MOs on the same or different bridges (Fig. 5C), thus enabling or blocking ET pathways. The DB control scheme is analogous to the BA discussed above. The only difference is the ET process manipulated by the X-ray pulse is the D→B step. In Fig. 5C strong and weak interactions between orbitals on different sites are represented by red solid and blue dashed lines, respectively. The donor orbital has strong coupling to the bridge orbital $b1$ but weak coupling to $b2$; whereas the acceptor orbital has strong coupling to $b2$ but weak coupling to $b1$. The ET process is thus hindered by the weak couplings. To overcome this, the bridge orbital occupations are altered by an X-ray Raman process (see the black arrows in Fig. 5C), so that both D/B and B/A interactions become strong. The superexchange and sequential mechanisms are two limiting cases of ET (26). This BB control scheme can represent both sequential ET in which the transferred electron actually populates the bridge, and a superexchange ET mechanism in which the transferred electron does not populate the bridge and the X-ray pulse simply paves the pathway for the electron. The orbitals involved in the X-ray Raman process are not necessarily localized on the same bridge site if the DBA system contains more than one bridge site. In this case the X-ray pulse controls the electron flow between bridges.

Fig. 5.

The DB and BB coherent control schemes. ET processes with X-ray control are represented by magenta dashed arrows. (A) The DB control scheme which facilitates the D→B→A ET process (core excitation on the bridge). (B) The DB control scheme which hinders the D→B→A ET process (core excitation on the donor). (C) The BB control scheme. The red solid lines represent the strong interactions between orbitals, and blue dashed lines represent weak interactions. Relevant molecular orbitals are also labeled. Orbitals $b1$ and $b2$ can be on the same or different bridges.

Conclusions

We have demonstrated how a stimulated X-ray Raman process can induce the B→A transition, thus enabling the D→B→A ET process. An X-ray pulse resonant with a core transition interacting with a pair of bridge and acceptor electronic states may be used to coherently control the ET process in a DBA system. Alternatively, one can induce ET by an ionization with an off-resonant X-ray pulse. However, this may cause the system to decay through multiple channels, which complicates the process. Pulse delays, shapes, phases, and intensities can be tuned to enhance the ET. This coherent control tool for ET processes can be used for processing of functional electronic materials (27), disease diagnostics (28), and X-ray sterilization (29).

Infrared (IR) pulses have been used recently to excite selected vibrational modes after triggering ET by UV pulses (11, 12). In the superexchange ET mechanism, vibrations can affect the interferences between various ET pathways, so that some ET pathways could be totally switched off (9). Similar experimental observations have been reported, but for the sequential ET mechanisms (12). IR pulses only weakly perturb the electronic structure and the molecular geometry, which facilitates their application for biomolecular ET coherent control.

The X-ray pulses used here can substantially alter the electronic structure of the bridge, whereas vibrations generated by IR pulses only change phases of different ET pathways and therefore affect their interferences (9–12, 30, 31). UV-vis pulses may access the same valence excited states prepared by an X-ray Raman process. However, UV-vis excitations lack the site selectivity of X-rays. In addition, short X-ray pulses can capture ultrafast ET dynamics that goes beyond the reach of UV pulses.

Coherent control has been successfully used to manipulate the relative strength of competing optical processes (32) but the major goal has always been the steering of chemical reactions in desired directions by properly shaped and timed optical pulses (33–39). The X-ray control schemes presented here offer opportunities for manipulating and monitoring chemical reactions which involve an electron transfer step. These could provide new synthetic routes for molecules and materials. X-ray pulses allow for a molecular level control with atomic selectivity and high temporal resolution which is not possible by optical techniques (40). Our earlier studies had demonstrated that stimulated X-ray Raman spectroscopy can be used to elucidate the catalytic reaction mechanism of the cytochrome P450 complex (41) by probing the oxidation state history of reactants, products, and various intermediates. By combining narrowband and broadband pulses, the hybrid X-ray Raman technique (42) [previously denoted as attosecond stimulated X-ray Raman spectroscopy (43)] offers a unique combination of spectral and temporal resolution, making it possible to take snapshots of ultrafast chemical reaction dynamics, which is not possible by conventional IR and optical techniques. Raman lineshapes are not affected by the core lifetime and are thus much narrower than those of X-ray absorption, which significantly enhances their resolution and selectivity. Going beyond the detection of reaction intermediates, with the control schemes proposed here one can selectively enhance or suppress ET steps, thereby facilitating or hindering selected chemical reaction steps, and then probe the reacting system by additional sequences of X-ray pulses (18). These offer a class of applications to X-ray free-electron laser and high harmonic light sources.

Finally, we note that competing decay channels with the resonant X-ray Raman of a core-hole state, such as Auger electron emission, must be taken into account. Auger processes are dominant in the core-hole decay processes of light atoms, but are less important for heavy atoms. For Co, the atomic spontaneous K-edge X-ray fluorescence and Auger yields are 0.373 and 0.627, respectively (44). However, unlike the abovementioned spontaneous processes, in stimulated X-ray Raman processes intense pulses can be used to enhance the Raman cross-section and suppress the Auger decay channels. For example, it was observed that the charge-transfer excitations in NiO were enhanced by resonant X-ray Raman scattering (45). In this study we focused on the acceptor control scheme. However, we can also use the same strategy to control the electron transfer via the donor, Ru atom. For Ru, the spontaneous K-edge Auger decay yield is only 0.206 (44). Considering many heavy metal complexes used as photosensitizers in solar cell applications, it is safe to neglect the effect of Auger decay when applying our proposed X-ray electron transfer control scheme to these systems. For example, in solid-state systems, the saturation of the stimulated emission on the Si (100) surfaces with X-ray free-electron laser was observed (46), which indicates the Auger decay channels have been suppressed. It was demonstrated that the stimulated X-ray Raman in CO molecules can compete well with the Auger processes (47, 48).

Materials and Methods

The geometry of the Ru–Co model complex was optimized using the Becke three-parameter and Lee–Yang–Parr hybrid (B3LYP) exchange-correlation energy functional (49, 50). The Ru atom was decribed by the Stuttgart/Dresden relativistic pseudopotential and its corresponding basis set (51). The Co atom was described by the improved default triple-zeta valence basis set with small polarization (def2-TZVP) (52), and the 6–31G* basis set (53) was used for other light atoms. Solvation effect was considered by using the polarized continuum model (54–56) with the solvent acetonitrile. Valence excited-state calculations were done at the time-dependent density functional theory (TDDFT) level of theory using the Coulomb-attenuating method version of the B3LYP functional (CAM-B3LYP) (57). All geometry optimization and valence excitation calculations were done with the quantum chemistry program package Gaussian (58). To compare the transition dipoles of charge transfer and localized core excitation around the Co center, the Co 1s core excitation calculations were done with the quantum chemistry program package NWChem (59) at the TDDFT/Tamm–Dancoff approximation (60) level of theory using the exchange-correlation functional CAM-B3LYP. The def2-TZVP basis set was used for Co and N, and the 6–31G* basis set was used for other atoms.