Significance
Species colonizations frequently occur in regions already occupied by other species of the same genus, or by other genotypes of the same species. When hybrid genotypes become more invasive than their parents, improved local adaptation is inevitably assumed. Here, we show that there is another way that hybridization could facilitate invasions, by temporarily overcoming pollen limitation when populations are small. We verify this conclusion using two contemporary sequential invaders, a plant analog of the Neanderthal–modern human system. Our findings indicate that it may be misleading to assume that all cases of invasive hybrids result from enhanced phenotypic suitability. Our hypothesis may be even more relevant to animal species because, unlike plants, animals can rarely escape mate limitation by self-fertilization.
Keywords: species colonization, mating system, model, Cakile, sea-rockets
Abstract
The founding population in most new species introductions, or at the leading edge of an ongoing invasion, is likely to be small. Severe Allee effects—reductions in individual fitness at low population density—may then result in a failure of the species to colonize, even if the habitat could support a much larger population. Using a simulation model for plant populations that incorporates demography, mating systems, quantitative genetics, and pollinators, we show that Allee effects can potentially be overcome by transient hybridization with a resident species or an earlier colonizer. This mechanism does not require the invocation of adaptive changes usually attributed to invasions following hybridization. We verify our result in a case study of sequential invasions by two plant species where the outcrosser Cakile maritima has replaced an earlier, inbreeding, colonizer Cakile edentula (Brassicaceae). Observed historical rates of replacement are consistent with model predictions from hybrid-alleviated Allee effects in outcrossers, although other causes cannot be ruled out.
Colonizing species rarely encounter empty environments and may, as a result, come into contact with close relatives. The most intensively discussed case of related colonizer–resident interactions, although by no means the only example, is the entry of modern humans into regions occupied by Neanderthals (1), eventually replacing them. Colonizing and resident species can interact in various ways, with consequences for their population dynamics. Competition, for example, is likely to impede successful establishment and population growth of newcomers; in contrast, resident species may facilitate new colonizers through hybridization or by shared interactions with organisms from other trophic levels. Although some interactions have been identified and are widely considered to predominate, there may be other interactions whose significance is yet to be explored. These interactions may be important in some or many cases, and a better knowledge of them might alter our interpretations of empirical observations. Here, we will investigate one such potential interaction, arising from hybridization between plant species sharing animal pollinators.
Hybridization can introduce adaptive alleles that contribute to expansion into new habitats (2, 3) and may result in new taxa. Local adaptation, resulting from changes in fitness, is the only positive role for species hybridization considered in the invasion literature; the same is true for admixtures of species genotypes from multiple sources. However, is it possible that there could be other benefits from hybridization, purely demographic ones? Furthermore, are these additional benefits capable of altering invasion dynamics over similar timescales and magnitudes? If so, such interactions would need to be excluded before adaptation can merely be assumed.
Many colonizing populations are susceptible to the demographic challenge of Allee dynamics, either because the initial founding population is small (4, 5) or because rare, long distance dispersers, beyond the present range, will initiate low-density satellite populations (6). Allee effects could slow range expansion or even halt it completely (7). In plants, a small founding population can experience Allee effects because of a scarcity of compatible mates, low pollinator visitation, or both (8, 9); the term “pollen limitation” is often used as a generic term when the exact mechanism is unclear. In the extreme case of a single arriving adult, population persistence would normally be impossible unless the species is capable of asexual reproduction or self-fertilization [“Baker’s Law” (10)]. Here, we propose a positive role for hybridization in species invasions and range expansion, a purely demographic mechanism without the requirement for any new adaptation to result.
If a mate-limited colonizing species is capable of hybridizing with a species already present, the colonizing species could overcome the otherwise insurmountable limitations imposed by Allee effects. Early-generation interspecific crosses (i.e., hybrids) could enable the colonizer genes to establish. Pure colonizer-type individuals can subsequently arise through crossing among hybrid lineages (11) or repeated backcrossing with the colonizer parents. We further hypothesize that this hybridization-rescue effect is more likely to eventuate if the new species and hybrids are more attractive to pollinators or when the hybrids are more compatible (i.e., more likely to produce viable offspring) with the newcomer than with the established species. That is, after sufficient generations of asymmetric breeding (backcrossing to the new colonizer), plants will increasingly come to resemble the original newcomers. The arriving species will essentially have been reconstituted, at least in its nuclear genome, and its population can increase now that it has escaped the critical effects of Allee dynamics. In effect, resident populations of a cross-compatible species, which may otherwise negatively affect the newly colonizing species through competition, become stepping stones through the landscape for a self-incompatible species via hybridization.
We develop a model that confirms that transient hybridization can overcome Allee effects under a wide range of ecological settings in relation to breeding system, pollinator behavior, and life history traits. Moreover, we show in a case study using a simplified version of the model that the parameter values required for the demographic mechanism to be as effective as genetic changes in fitness are fulfilled by the sequential invaders Cakile edentula and Cakile maritima. Our hypothesis therefore provides a possible explanation for the rapid replacement of C. edentula over a large part of its invasive range by C. maritima in the west of North America, New Zealand, and Australia (12–15).
Results
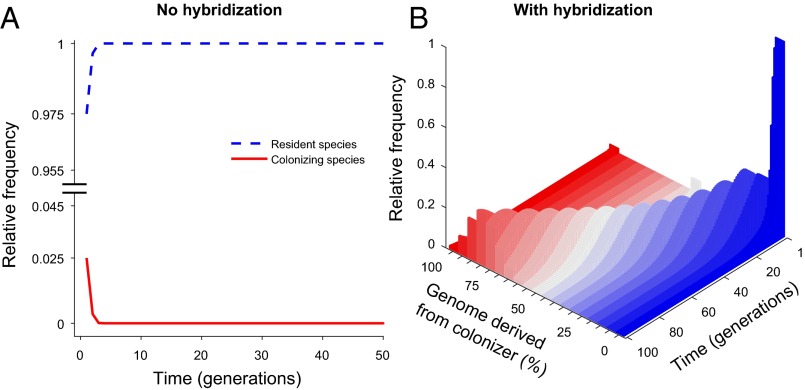
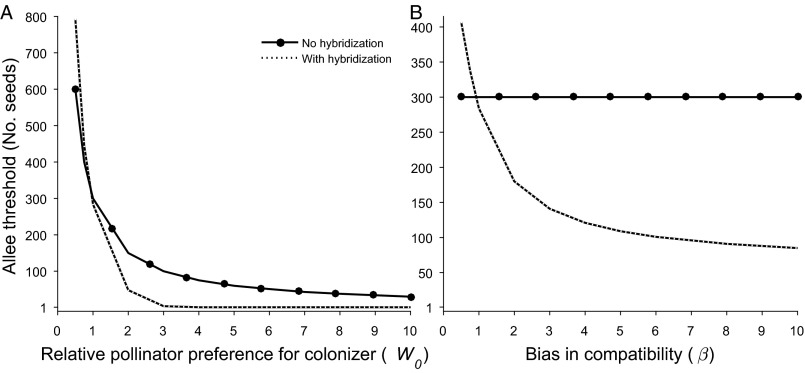
Our hypothesis is clearly supported by the model results. In the absence of hybridization, when we introduce a small number of seeds, the incoming species population declines rapidly to extinction (Fig. 1A). The same propagule pressure but with hybridization transforms the population from one dominated by resident species and resident-like genotypes (blue in Fig. 1B) to one dominated by colonizer and colonizer-like genotypes (red in Fig. 1B). Over time, the colonizer genotype is reconstituted and the resident species is eventually replaced by the new colonizer. Allee population thresholds are always smaller with hybridization than without it, proving that introgression is asymmetric in favor of the colonizer [i.e., when (Fig. 2A) or (Fig. 2B)]. Even with no bias in pollinator behavior () or compatibility (), hybridization still reduces the Allee threshold slightly (Fig. 2) because some of the otherwise wasted pollen results in seed production via the resident species, thus contributing positively to the dynamics of colonizer genes.
Fig. 1.
Dynamics predicted by the generic model when a small number of a colonizing species arrives at a new location currently occupied by a resident species: no hybridization (A) and hybridization (B). Although in both A and B, pollinator preference parameter is set to favor more backcrossing to the incoming genotype than to the resident species, the incoming genotype fails to establish when it does not hybridize with the resident species (A). However, when there is hybridization (B), the population steadily accumulates a higher proportion of individuals similar to the colonizer, whereas the resident genotypes decline in abundance and are finally replaced by the colonizer. Dark red indicates individuals whose genome is indistinguishable from the colonizer, dark blue indicates genomes indistinguishable from the resident species, and gray represents hybrid genotypes comprising 50% of each parental species’ genome. See Tables S1 and S2 for lists of parameters and their values.
Fig. 2.
The critical number of propagules for the establishment of a colonizing species, the predicted Allee threshold, as a function of either pollinator behavior (assuming equal compatibility, β = 1) (A) or reproductive compatibility of hybrids with the parental genotypes (assuming equal pollinator preference, W0 = 1) (B). Note that B would also indicate the results expected from passive pollination, such as by wind. Compatibility, , has no effect on the dynamics of either species when they do not hybridize: the Allee threshold is therefore constant for the no-hybridization scenario (solid line in B). When W0 = 1 and β = 1, backcrossing is symmetric, but when β is larger than 1, F1 and later generation hybrids are more compatible with the colonizing-type individuals. In our simulations, the criterion for the Allee threshold was that the population size (seed number) after 100 generations was the same as the initial population size. See Tables S1 and S2 for lists of parameters and their values.
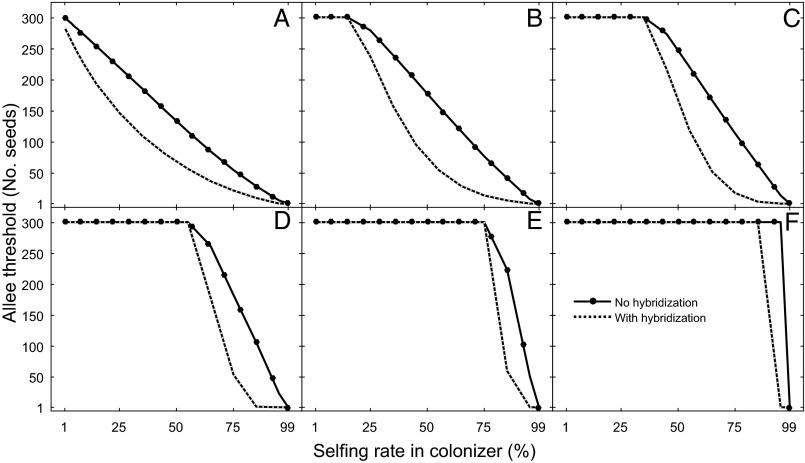
Consistent with the established theory that selfing provides reproductive assurance (16), the Allee threshold for establishment of colonizing species decreases with its selfing rate for both hybridization and no-hybridization scenarios. However, Allee thresholds were always smaller for a hybridizing colonizer than the nonhybridizing one over a wider range of simulated breeding systems of both species (Fig. 3). Because the resident species adopts a more autogamous breeding system, Allee thresholds become larger in the colonizing species, but with hybridization, the incoming species could still invade the resident population (Fig. 3).
Fig. 3.
Predicted Allee thresholds for the establishment of a colonizing species as a function of its self-fertilization rate, assuming that the resident species has a self-fertilization rate of 1% (A), 20% (B), 40% (C), 60% (D), 80% (E), or 99% (F). The minimum number of seeds necessary for the establishment of the colonizer, its Allee threshold, is never larger with hybridization than without. See Tables S1 and S2 for lists of parameters and their values.
To test our predictions in a contemporary invasion, we parameterized a simplified version of our model with a single hybrid category (F1 hybrids), using empirical data from Cakile maritima [self-compatible (SC) (17)] and C. edentula [self-incompatible (SI) (17, 18)]. Why and how the established invader (C. edentula) has been replaced by a newly arrived species (C. maritima) in three parts of the world has remained a mystery over the 40 y since the replacement was first reported (13). Could hybridization with the prior SC invading plant have increased the probability of subsequent establishment of an SI species? Hybrids between the two species can be produced easily by hand (17). We have also confirmed, using genetic markers, that individuals with intermediate morphology near the leading edge of the C. maritima invasion in Tasmania are the results of hybridization (19).
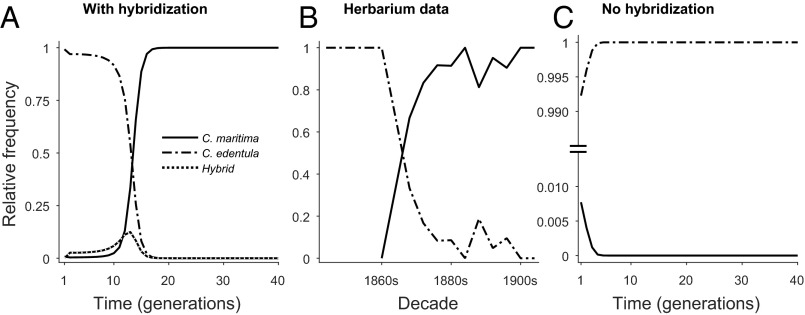
We simulated the dynamics of C. maritima with and without hybridization with C. edentula. The results indicate that hybridization could facilitate the establishment of a small (otherwise sub-Allee threshold) population of the primarily self-incompatible C. maritima (Fig. 4), with a strong correspondence between the timescales for species replacement predicted by the model simulation (Fig. 4A) and the frequency of C. maritima relative to C. edentula in herbarium specimens (Fig. 4B) (20). Without hybridization, small initial populations of C. maritima were predicted to fail to establish (Fig. 4C). A note of caution is required for this comparison: our model simulates the population dynamics within a single location (with no account of subsequent spread), whereas herbarium data give a (very crude) representation of invasion dynamics over a wider geographic scale (21). Our simulation results are, however, also in good agreement with the replacement time-scale observed on Lord Howe Island, where C. maritima replaced C. edentula in perhaps 20–30 y (14).
Fig. 4.
Population dynamics of Cakile predicted by the simplified model (A and C) and evidence from herbarium samples (B). Whereas hybrid presence is predicted to be ephemeral, the predicted dynamics of C. maritima and C. edentula (A) corresponds to the pattern and time scale of change in their representation in herbarium specimens (B) collected from Victoria and South Australia. Adapted from ref. 20. C shows what would happen without hybridization. Parameters and their values are given in Table S3.
Our simulation model and the Cakile system provide support for our hypothesis of an overlooked, purely demographic, role for hybridization in both establishment and spread. A robust test of the hypothesis would require deliberate introductions into regions lacking one or other species, which would probably be unethical or unwise. However, in the case of SI and SC Cakile species in Australia, there is now clear evidence that interspecific hybridization has occurred during the establishment and expansion of C. maritima (19). Genetic and morphological evidence across the current C. maritima invasion wave-front in Tasmania (19) match what would be expected if species replacement by this mechanism had occurred. Specifically, in places where C. edentula has a very high relative frequency, hybrids are common and even plants that are morphologically indistinguishable from one parent often have the chloroplast genotypes of the other (19). In regions where C. edentula has long since disappeared and there is now little evidence of nuclear introgression, C. edentula chloroplasts may still be common in C. maritima, indicating extensive past hybridization and reconstitution of parental phenotypes. Although our artificial intercrossing provided no evidence for bias in cross-compatibility of hybrids with the two parental species (Fig. S3), pollinators clearly preferred to visit C. maritima-like individuals over C. edentula when both were present (SI Text, Simplified Model for C. maritima and C. edentula, Sources of data for parameterization). We note that introgression has been proposed before for these species (22) but based on less convincing data and without any mechanism being proposed (19).
Fig. S3.
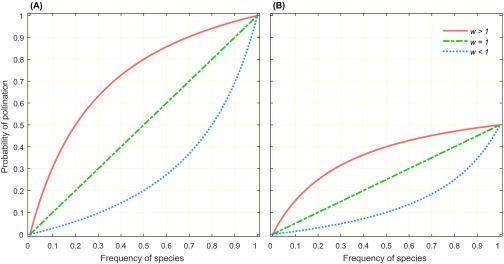
Fraction of pollinator visits to a given species, as a function of its relative abundance and attractiveness () in a mixed population of two species which share pollinator services. The likelihood of a visit to the mixed population is initially determined by the total size of the mixed population using Eq. S6, whereas the proportion of visits (of the total probable visits) to a given species is then determined by the attractiveness of that species, using Eqs. S10 and S11. For example, in A, because the total size of population was large (500 individuals), the likelihood of a visit was ∼1, whereas in B, with 50 plants, the maximum likelihood of a visit was 0.5 (these probabilities were calculated using Eq. S6 with and ). When both species are equally preferred by pollinators (), the proportion of visits to any species is equal to their frequency (green line), whereas if the species is either more attractive or less attractive, the visitation probability exhibits a convex (; red line) or concave (; blue line) relationship, respectively.
If this demographic phenomenon does occur in nature, is it idiosyncratic—a unique combination of species sharing pollinators and invading the same habitat in the same sequence—and of little relevance to ecology and evolution in general, or is it more common? We believe that the latter may be true. First, both hybridization (3) and Allee effects are common in biological invasions (7). Evidence is mounting for the importance of hybridization as one of the processes driving invasions, although so far, the explanations have relied solely upon genetic consequences of hybridization endowing adaptive benefits (refs. 2 and 3 but see ref. 11). Indeed, the risks of extinction and genetic swamping of native species have been raised as dire consequences of hybridization (2). Allee effects or, more specifically, pollen-limited seed production, are expected to be common, because more than 80% of plants rely on pollen transfer for reproduction (23) and ∼50% of plant species are obligate outcrossers (24). Pollen limitation, resulting from low availability of both compatible mates and pollinators, seems to be more common in introduced species than their native counterparts (25, 26). First, our model shows that the presence of another species can alleviate such pollen limitation and reduce Allee effects through hybridization with related species. Second, our model shows that the rescue effect of hybridization will be stronger when there is an asymmetry in the direction of introgression (backcrossing): this phenomenon seems to be common in both natural and artificial hybridizations. Pollinators rarely commit to random foraging bouts but rather discriminate among plant types (27); such behavior can result in assortative mating and produce the required asymmetry. Intercrossing success (i.e., the production of viable seeds) is also known to be affected by the direction of crossing (28, 29). The interplay between these pre- and/or postzygotic processes can result in unequal transfer of parental genetic material into the genome of hybrid progeny (28, 29). Whereas the short-term demographic consequence of this asymmetry is facilitation of establishment, the long-term outcome can be species replacement as we see in Cakile species.
SI Text
Generic Model to Simulate the Dynamics of Hybridizing Annual Species.
Generic model formulation.
We first construct a deterministic population model for a single annual species, of a single genotype, and then show how it can be extended to two species, to include more cooccurring genotypes that arise because of hybridization and later-generation backcrossing. Throughout we use population density and population size (or number) interchangeably, assuming that for a fixed area, changes in density are equal to changes in number.
Single species.
Suppose that a population consists of N diploid seeds at time t, . Seeds germinate and are recruited into the population as seedlings and assumed to be spread evenly within the receiving patch of habitat. The proportion surviving to maturity is a function of both density-dependent and density-independent factors, collectively represented by . Each surviving plant has the potential to produce ovules in the absence of competition from other plants, but its per capita ovule production decreases with population density, following a negative density-dependent function , where indicates number of adult plants: . Each plant can self-fertilize a fraction s of its ovules, whereas the remaining (1 − s) fraction is available for outcrossing. Because of pollinator or mate limitations, however, not all 1 − s will be outcrossed and some will be aborted. We assume that the probability of successful pollination is positively related to the population density (i.e., there is an Allee effect) following . A positive correlation between population density and pollinator visitation rate has been observed in many studies and has been implemented in population dynamics models (35). The difference equation with both negative (ovule production and survival) and positive (pollination success) density regulation for a single species’ population dynamics is therefore given by
| [S1] |
For density-dependent and density-independent recruitment of seeds into the population, we use a Beverton–Holt type model:
| [S2] |
where L denotes the proportion of seeds recruited independent of population density, whereas b is the rate of decrease in survivorship of a plant as density increases. We used a rectangular hyperbola to describe ovule reduction as related to density of mature plants, :
| [S3] |
where d is a coefficient: the larger the value of d, the stronger the negative effect of density on reproduction. Given that M = NS(N), Eq. S3 can be written as a function of :
| [S4] |
which can be simplified to
| [S5] |
For pollination probability, or “pollinator foraging choice” (30), we used Holling type III functional response to relate the probability of pollination to population size:
| [S6] |
and, again,
| [S7] |
This type of functional response is expected for generalists that frequently switch between flower types (35) or if pollinators engage in an area-restricted search strategy (36). The reciprocal of gives the population size at which 50% of plants will be visited (and pollinated) by pollinators. The parameter determines the shape of the curve: when is large, there is little change in probability of pollination at low densities compared with a small , which gives a higher pollination rate at the same low densities. When , the model reduces to a type II or saturating functional response. Eq. S7 can be simplified to , and Eq. S1 becomes
| [S8] |
This model results in component Allee dynamics (37) by negatively relating recruitment and per capita fecundity to population density, while positively scaling pollination probability.
Two species.
Now suppose that an equally competitive congeneric species already occurs in the habitat (we will call this a resident, which could be either a native or a previously established invader) and can interact with the above species in both positive and negative ways. The assumption is made that both species are homogenously distributed across space. A negative interaction occurs because of competition between the two species for limited abiotic resources and is reflected in their reproduction, , and survival, , functions. The intensity of competition, embedded within and , is assumed to depend on the total number of both species regardless of the species identity. This equality in competitiveness of species is required to ensure that any difference between hybridization and nonhybridization scenarios is solely attributable to hybridization and not to an a priori fitness differential. However, the model can accommodate species inequality in any traits, as shown in Eq. S16. A positive interaction can occur when there is a positive relationship between the chance of pollination and the total population size, such that on the right hand side of Eq. S6 is replaced by the combined number of individuals from the two species. However, the two species may also compete for pollinators and, depending on their relative attractiveness to pollinators, may experience differential outcrossing success, accounted for by the function (see below). Using subscript , where = 0 denotes the invader and = 1 indicates the resident species, the difference equation for two interacting species is given by
| [S9] |
where is the total density summed across all genotypes; with k = 0 (invader) and k = 1 (resident). is the proportion of pollinator visits to species . If both species are equally preferred by pollinators (i.e., visited randomly) then the likelihood of a visit to any given species is proportional to its frequency in the population, i.e., , where is the relative frequency of adult plants. However, the two species may differ in their attractiveness such that pollinators visit plants of the invasive species for every one plant of the resident species. Then the proportion of visits to the invasive species is
| [S10] |
and to the resident is
| [S11] |
where and are the relative frequencies of invader and resident plants in the mixed population (, whereas and are adjusted frequencies after accounting for the bias in pollinator preference (see Fig. S1 for a graphical explanation of the pollination submodel). When the two species hybridize and produce viable offspring, the population will consist of three genotypes in the next generation: two parental pure species plus the F1 hybrid, so . We use = 0.5 to indicate that the hybrid genotype is intermediate relative to its parents. In the later generations, more intermediate genotypes will be produced through backcrossing and segregation (accounted for in Eq. S12), so can then take any values between 0 and 1. However, as a workable assumption, we consider variable as a discrete variable with G genotypic classes. We use the number of chromosomes as a proxy for determining G (the total number of genotype classes) and the chromosome combination of the two parental species to characterize . That is, suppose that species A (e.g., invasive) and B (resident) both have 2n = 18 chromosomes and can freely cross with each other. Individuals from this mixed population can then be categorized in 19 genotype classes based on the number of chromosomes that they receive from the two species [i.e., (18,0), (17,1),… (1,17), (0,18)]. The first element in (•,•) indicates the number of chromosomes from species A, , whereas the second element is the number of chromosomes from species B, . An individual with an (18,0) chromosome combination is regarded as a pure individual of species A, whereas (0,18) denotes a pure individual of species B. We map chromosome combinations to variable using , which gives = 1 for species A and = 0 for species B (the use of in the numerator is arbitrary). In this paper, we assign = 0 to the incoming species and = 1 to the resident species. Crossing-over can result in more intermediate genotypes, where a single chromosome can comprise various proportions of the genome from the two species, but for simplicity, we do not consider this possibility in our model. It should not affect our qualitative conclusions.
Fig. S1.
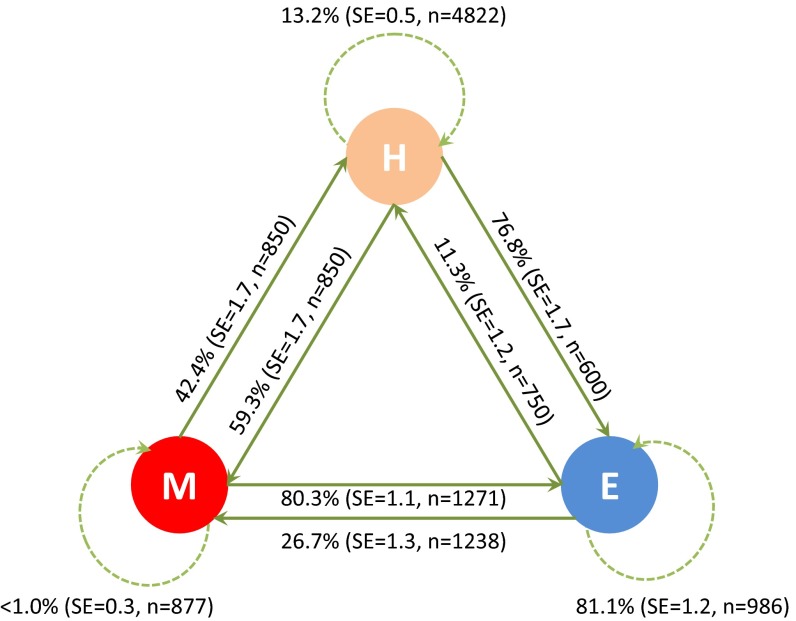
Probability of successful crossing (i.e., viable seed production) for different directions of hand-crossing. The arrow shows the direction of pollen transfer from a donor to a recipient plant: C. maritima (M), C. edentula (E), and F1 hybrids (H). Spontaneous self-fertilization rates are shown as dashed lines. n indicates number of crosses.
A diploid genotype with a total of alien chromosomes ( and ) undergoing gametogenesis can produce haploid gametes (an F1 hybrid which has n alien chromosomes can produce the maximum number of gamete types, which is n + 1). A gamete can possess alien chromosomes where range from 0 up to (i.e., ) with probability given by
| [S12] |
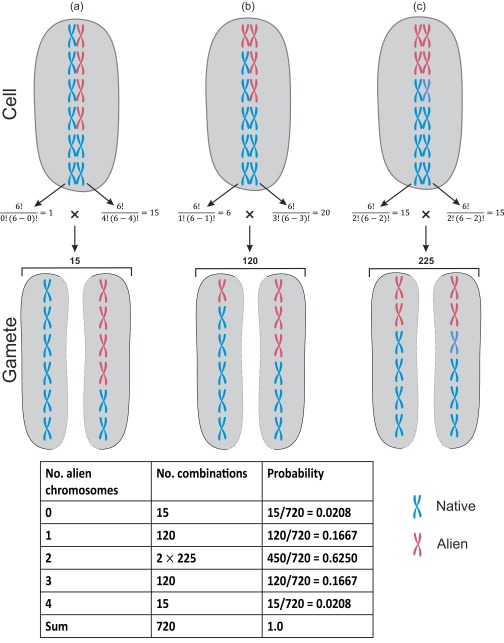
This formula is based on the number of ways that chromosomes can line up at the cell equator during the metaphase of the first meiotic division. As shown in Fig. S2, with , various arrangements are possible: (i) all alien chromosomes (red) can occur on the same strand, (ii) one alien chromosome on the left strand and three on the right, and (iii) two alien chromosomes on either side. Within each of these arrangements, many different combinations (i.e., positioning of aliens along the native strand) can take place. Indeed, in the numerator of Eq. S12 gives the number of possible ways that alien chromosomes (out of ) can be positioned on the left strand, whereas gives the number of positions for the remaining alien chromosomes (i.e., ) on the right strand. Note that when the number of alien chromosomes on the left and right strands are the same (i.e., ), the number of combinations for that gamete type doubles. The denominator in Eq. S12 simply gives the total number of all possible combinations.
Fig. S2.
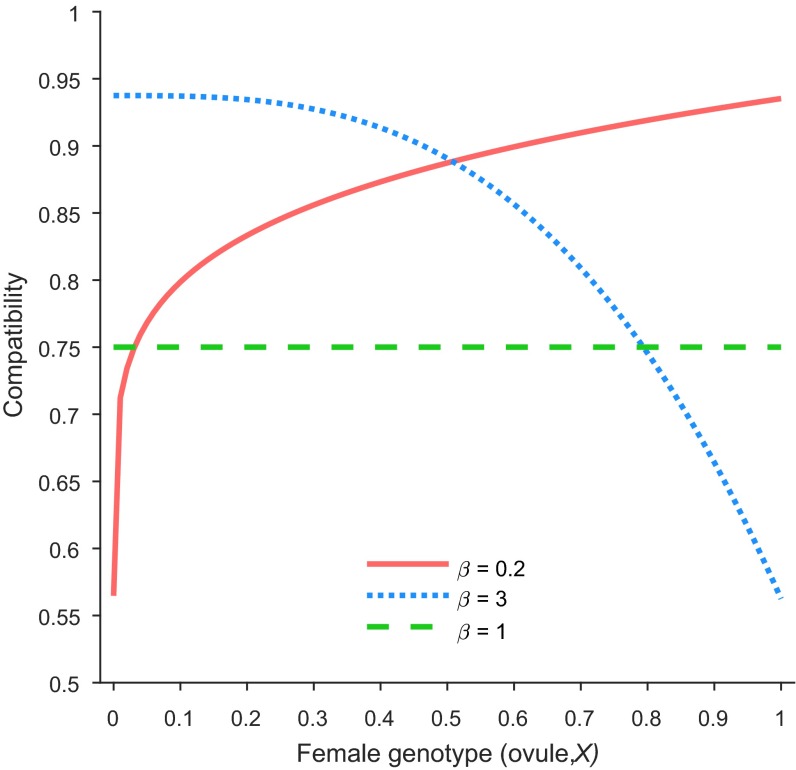
Compatibility of F1 hybrid pollen (i.e., = 0.5) with the ovules of various genotypes as predicted by Eq. S15 for three values. When is larger than 1 (here, = 3; blue), the hybrid is more compatible (i.e., more likely to produce viable offspring) with the incoming genotype, whereas it has lower compatibility with the resident genotype. When is smaller than 1 (here, = 0.2, red), the opposite is true, whereas for = 1 (green), all genotypes exhibit the same level of compatibility with the hybrid. In this example, the compatibility of the two pure parental genotypes, , was set at 0.5.
Now, suppose that a female genotype with alien chromosomes is crossed with a male genotype with alien chromosomes. We obtained the probability of producing offspring x (with , where ) from parents with genotypes and using a discrete convolution:
| [S13] |
In this formula, and are two vectors containing the probabilities for gamete types that can be produced by parents and , respectively, following Eq. S12, and h ranges over all legal subscripts for and , specifically, . Note that we transform to using , which represents the proportion of alien chromosomes within the genome ranging from 0 (pure invasive species) to 1 (pure resident species). Our genetic model gives rise to similar qualitative outcomes as the hypergeometric phenotypic model (31, 32). The difference equation model that allows for hybridization then takes the form:
| [S14] |
where indicates the total number of genotypes in the population. The function in Eq. S14 indicates the compatibility (i.e., the likelihood of producing viable offspring once pollinated) of female genotype y with the male genotype z and is calculated using
| [S15] |
where parameter indicates the compatibility between the two parental species, whereas introduces asymmetry in the direction of backcrossing (asymmetric compatibility). The model (Eq. S15) assumes that the compatibility between two genotypes increases as these two genotypes come to share more genome from the same species. For the specific cases of (cross between two pure individuals of the incoming species) and (cross between two pure individuals of the established species), the model gives but if . Note that always holds if or . When , F1 and later generation hybrids are more compatible with the incoming-type individuals, whereas for compatibility is biased toward the resident species and for introgression is symmetric (Fig. S3). Studies with both natural and artificial crossing have shown that the intercrossing success rate can be affected by the direction of crossing (38), and our model accounts for such an asymmetry by incorporating the bias parameter .
To relate genotype to a phenotypic character (any model parameter), we assumed that trait values (e.g., selfing rate) are normally distributed among genotypes, following Hall et al. (39) with minor modifications:
| [S16] |
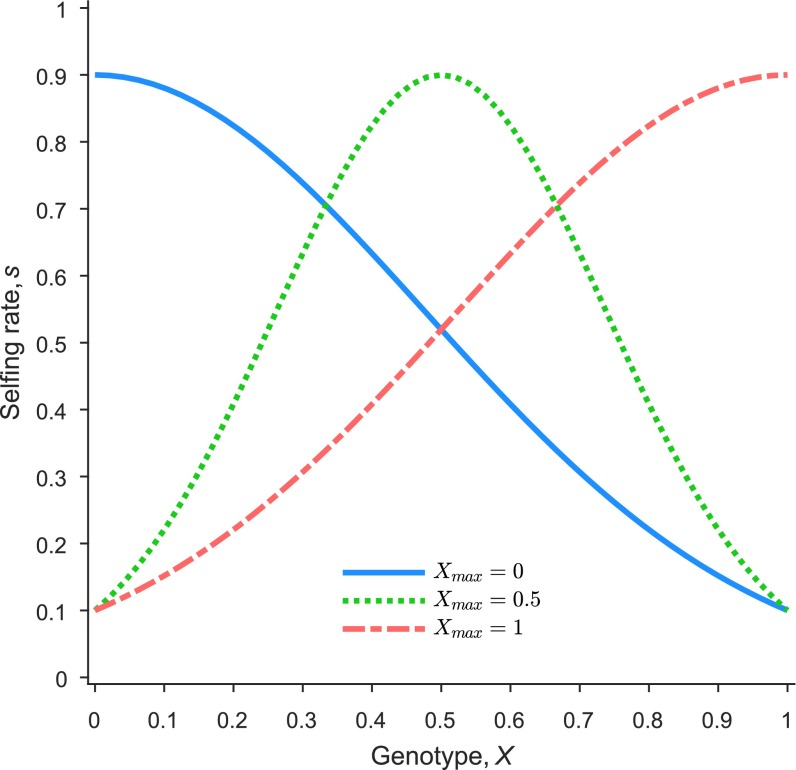
where is the maximum value of a given trait, whereas is the genotype which acquires that maximum trait value. The parameter represents the variance, which can be solved to give the minimum value of for a specific genotype. For example, we may choose to assign the highest selfing rate to genotype (newcomer species) and then calculate such that the genotype (resident species) obtains the lowest selfing rate among all genotypes (Fig. S4).
Fig. S4.
Some chromosome arrangements for a hypothetical diploid genotype with 2n = 12 where eight chromosomes descend from the resident species (blue) and four () from the alien species (red). All alien chromosomes may be located on a single strand (A) or occur on the two strands (B and C). The number of ways that alien chromosomes can be positioned within each strand is given by and for left and right strands, respectively (Eq. S12), and the total number of combinations is the product of these two values. For example, there are 15 different ways to position 4 alien chromosomes on the right strand while having no alien chromosome on the left strand. This arrangement will result in two gamete types (one with no alien chromosomes and one with four) with the equal probability of 0.0208. The inset table provides the probability values for each of the five gamete types (i.e., ) that can be produced by a diploid genotype with n = 6 and .
A list of model parameters is given in Table S1. To summarize, some of the assumptions of our model are as follows:
-
i)
There is no persistent seedbank.
-
ii)
Both density-dependent and density-independent factors act at the same time to determine the survival rate. For example, if disturbance occurs first whereby many seedlings die, then the density-dependent mortality would be minimal.
-
iii)
Self-fertilization occurs first, and the remaining flowers then out-cross.
-
iv)
Pollination success is only determined by population size and attractiveness of genotypes (the frequency of pollen from any genotype in the pollen pool is proportional to the relative abundance of adult plants of that genotype in the mixed population and the per capita pollen production is therefore the same for all genotypes).
-
v)
There is no difference between chromosomes when mapping genotype to phenotype (i.e., it is the number of chromosomes that matters, not their type)
-
vi)
There is no crossing over.
-
vii)
Self-fertilization incurs no inbreeding depression. Inbreeding depression could easily be incorporated into the model as another multiplier (for example, of selfing rate s) in Eq. S1 and its multigenotype derivation (Eq. S14), but the results would not change qualitatively.
Table S1.
List of parameters used in the generic model
| Parameter | Definition | Range |
| Density-independent survival (i.e., fraction of seeds that germinate and survive to maturity) | ||
| Density-dependent coefficients for seedling survivorship to maturity | ||
| Per capita flower production | ||
| Density-dependent coefficients for flower production reduction | ||
| Selfing rate (i.e., proportion of flowers that produce seeds through self-fertilization) | ||
| Pollination switching density parameter: 1/ gives the population size at which the chance of pollination is 50% | ||
| Switching exponent parameter in pollination equation (shape parameter): when , the Eq. S6 will collapse to type II functional response | ||
| Compatibility of the two parental species when they intercross | ||
| Compatibility bias parameter | ||
| No. of chromosomes in haploid | ||
| Total no. of alien chromosomes in a diploid genotype | ||
| No. of alien chromosomes in a haploid gamete | ||
| Index variable indicating the identity of a genotype (e.g., represents the newcomer species, whereas denotes the resident species). Total no. of elements (genotypes) in is . | ||
| Relative frequency of a given genotype in the population | ||
| Relative frequency of a given genotype in the population after adjustment for pollinator preference | ||
| A weight parameter that adjusts the relative frequency of genotype according to its degree of attractiveness to pollinators | ||
| An index variable indicating the identity of a female genotype (i.e., pollen recipient) | As | |
| An index variable indicating the identity of a male genotype (i.e., pollen donor) | As | |
| Maximum value of a given trait (model parameter) | Variable | |
| The genotype to which the maximum value of a trait () is assigned | As | |
| Variance of a phenotypic trait across genotypes |
Simulations.
We simulated the population dynamics of 19 genotypic classes corresponding to a diploid species with 2n = 18 over 100 generations. All simulations were run using Matlab (version 2014a); code is given in SI Appendix. Table S2 provides details of parameter values (and range) used for various simulations related to the effect of pollinator behavior, mating system, compatibility between genotypes under hybridization, and no-hybridization scenarios.
Table S2.
Parameter values (and ranges) used for simulations of the generic model
| Parameter | Value/range | |||
| Invasion dynamics* | Pollinator preference† | Bias in compatibility† | Mating system‡ | |
| 0.1 | 0.1 | 0.1 | 0.1 | |
| 0.0001 | 0.0001 | 0.0001 | 0.0001 | |
| 1,000 | 1,000 | 1,000 | 1,000 | |
| 0.1 | 0.1 | 0.1 | 0.1 | |
| 0.01 | 0.01 | 0.01 | = [1...99%] | |
| = [1, 20, 40, 60, 80, 99%] | ||||
| 0.035 | 0.035 | 0.035 | 0.035 | |
| 3.5 | 3.5 | 3.5 | 3.5 | |
| 0 and 0.5 | 0 and 0.5 | 0 and 0.5 | 0 and 0.5 | |
| 1 | 1 | [1…10] | 1 | |
| 18 | 18 | 18 | 18 | |
| 5 | [1…10] | 1 | 1 | |
| 50 | [1…300] | [1…300] | [1…300] | |
| 1,950 | 300 | 300 | 300 | |
Simplified Model for C. maritima and C. edentula.
Model assumptions.
To test the hypothesis that hybridization could have facilitated the invasion of C. maritima without enhancing fitness, we used a reduced version of the generic model. This simplified model simulates the invasion dynamics of only three genotype classes (34): C. maritima, C. edentula, and their F1 hybrid. The variable thus takes three values: 0 for C. maritima, 1 for C. edentula, and 0.5 for hybrids. The main reason for reducing the number of genotypes is that there is no information on the demography and biology of intermediate genotypes (later generation hybrids). Furthermore, this simplification makes the model more tractable without affecting the qualitative conclusions. We used intercrossing compatibility rates obtained from artificial hybridization experiments rather than using Eq. S15.
The model was parameterized using both the literature and our own experimental or observational data; for a few parameters, for which there were no estimates, we evaluated a range of plausible parameter values to test whether their precise values affect the qualitative results. If no parameter estimate was available for the hybrid genotype, we used the average of the two parental species, because hybrids tend to be intermediate in most characters relative to their parents (17). See Table S3 for a list of parameter values and their sources: although some parameters are in favor of C. maritima (e.g., higher fecundity and survival) compared with C. edentula, this inherent fitness advantage alone is insufficient for C. maritima to drive a well-established C. edentula population to extinction (Fig. 4).
Table S3.
Parameters of the simplified model and their values (range) used in the simulations
| Genotype | * | † | ‡ | § | ¶ | # | || | ** |
| C. maritima | 0.08 | 0.0001 | 1,195 | 0.1 | 0.01 | 7.5 | ||
| C. edentula | 0.03 | 0.0001 | 906 | 0.1 | 0.8 | 4.25 | ||
| Hybrid | 0.055 | 0.0001 | 1,486 | 0.1 | 0.2 | 1 |
is the fraction of the seedbank that results in mature plants. The average survival to flowering (across a foredune and open beach habitats) was ∼8 and 3% for C. maritima and C. edentula, respectively, in California (15). For hybrids, we assumed the average of the two parental species.
is the density-dependent mortality parameter, assumed to be constant across the three genotypes. A value of 0.0001 would result in a carrying capacity ∼500 adult plants (regardless of the genotype).
is the number of flowers produced by a single plant in the absence of competition and was obtained from our common garden experiment of five, six, and two populations of C. maritima, C. edentula, and putative hybrids.
indicates the proportional reduction in the number of flowers as the population density increases. This coefficient was estimated from the data of Keddy (40) for C. edentula. There are no similar data for C. maritima or hybrids, so we assumed that the three genotypes exhibit the same response to density.
is the fraction of flowers that produce seeds through selfing. Selfing rates for the three genotypes were obtained from our hand-crossing experiment.
is a coefficient in the pollination foraging submodel (Eq. S6): the coefficient’s reciprocal is the population size at which the probability of pollination is 50%. Because there are no empirical data, a range of values was tested for this parameter. For the simulation presented in Fig. 4 and Fig. S5, we used a value of 0.035 corresponding to a population size of ∼30 plants for 50% pollination. The results of simulations using the given range in the Table S3 is shown in Fig. S7.
is a shape parameter in the pollination foraging model (Eq. S6). Because there are no empirical data, a range of values was tested. For the simulation presented in Fig. 4 and Fig. S5, we used a value of 3.5, which results in a sigmoid response [type III functional response (30, 41)]. The results of simulations using the given range in the Table S3 is shown in Fig. S7.
is a weighting parameter that adjusts the relative frequency of genotypes according to their attractiveness to pollinators. These values were obtained from our field observations in a mixed population. For hybrid genotypes, we assumed the average of the two parental species.
Initial population sizes.
Almost no data exist on the number of arriving propagules in accidental introductions (4); clearly, the number could be as few as one or it could be several orders of magnitude greater, depending on the dispersal vector and chance. We have no information on the founding population sizes (number of seeds arrived) of C. maritima when the species was first introduced to Australia, or even for its dispersal from one beach to the next during subsequent spread. However, we know that C. edentula had time to saturate most of its preferred habitats by the time C. maritima arrived as the second invader. The number of Cakile adult plants that can be found on a beach is highly variable, so it is equally hard to say what a plausible carrying capacity would be. Highly disturbed beaches may function as sink populations and never support more than a few individuals, whereas a sheltered beach may be a source population of many thousands of plants and a net exporter of seeds. In our simulations, we fixed the carrying capacity of a beach at 500 adult plants (regardless of the species: this value is within the range of our field observations for small beaches) and then introduced 1–600 seeds of C. maritima (with unit increment).
We simulated the dynamics of the three genotypes over 40 generations. To estimate the Allee threshold for C. maritima, we compared the number of C. maritima seeds after 40 generations with the initial size of the founding population: the minimum initial seed number that resulted in a positive population growth was taken to be the Allee threshold. When C. edentula was present on the beach, its population size was set at the carrying capacity (i.e., ∼500 individuals). However, we tested situations other than an equilibrium state, wherein C. edentula occurred with a lower number of individuals as if its habitat had recently been disturbed (Fig. S5). The results indicate that hybridization could facilitate the establishment of a small (otherwise sub-Allee threshold) population of the primarily self-incompatible C. maritima (Fig. S5).
Fig. S5.
An example of mapping genotype to a phenotypic character (e.g., selfing rate, ) using Eq. S16. determines the location (i.e., genotype) at which the maximum value of a trait, , occurs (here a selfing rate of 0.9).
Sources of data for parameterization.
The number of flowers () produced by each species and their hybrids was obtained from a common garden experiment in pots containing a sandy soil. Plants were derived from seeds of C. maritima and C. edentula and the progeny of putative hybrids (later confirmed as hybrids by simple sequence repeat markers) collected from five, six, and two locations, respectively, across their invaded ranges in Australia. The number of flowers produced by each plant over its lifetime was determined when plants were no longer flowering, by counting the number of scars and pedicels left on the racemes. Cakile maritima, C. edentula, and putative hybrids produced an average of 1,195 (SE = 72; n = 54), 906 (SE = 59; n = 63), and 1,486 (SE = 128; n = 38) flowers, respectively. These numbers are within the ranges estimated in beach populations in Tasmania.
Data on intercrossing compatibility were determined in two glasshouse experiments, where we first produced F1 hybrids and then established a series of reciprocal crosses between the F1 hybrids and their parental species. The probability of producing viable offspring when crossed was calculated from the number of viable (germinable) seeds divided by the total number of crosses made between genotypes. Selfing rates were determined by excluding pollinators. No viable seeds were produced when C. maritima was selfed by hand, although a very small number of putative spontaneous selfs occurred on caged plants; it was therefore not possible to measure inbreeding depression. Fig. S6 shows the average compatibility for the various conspecific crossings implemented in these experiments; as can be seen, backcrosses are almost equally compatible in either direction. However, hybrids are more likely to backcross with C. maritima than with C. edentula because they have larger flowers than C. edentula: in our common garden experiment, mean petal dimensions (displayed section of petal only) were 5.42 × 2.01 mm for putative hybrids, 6.19 × 2.45 mm for C. maritima, but only 4.35 × 1.19 mm for the inbreeder C. edentula, which, on some occasions, may not even produce all four petals (17).
Fig. S6.
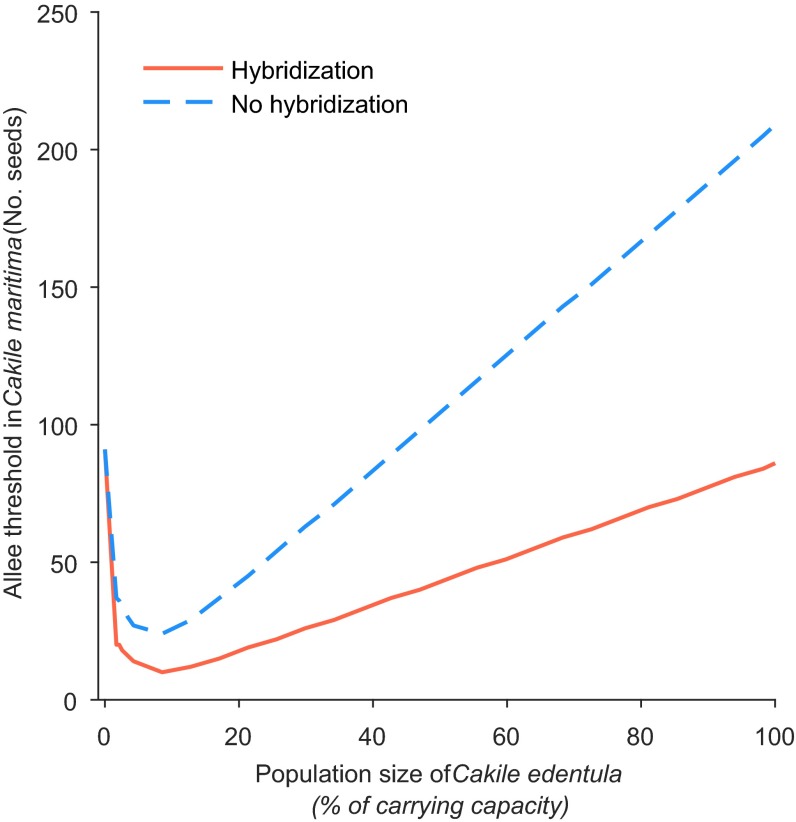
Predicted Allee thresholds for the establishment of C. maritima. The critical number of arriving seeds, estimated for two invasion scenarios of C. maritima at various initial plant densities of C. edentula (relative to the combined carrying capacity). The minimum number of seeds necessary for C. maritima establishment is always smaller with (solid line) than without (dashed line) hybridization and is more than halved by hybridization. See Table S3 for parameter values used in above simulations.
We monitored pollinator visits to 47 C. maritima and 37 C. edentula plants on a beach in Tasmania where both species were approximately in equal abundance. C. maritima has a more conspicuous display, with more open flowers per raceme and larger flowers (see above). Both species were mainly visited by honey bees (Apis mellifera); other common visitors were European bumblebees (Bombus terrestris) and cabbage white butterflies (Pieris brassicae). Although hybrids and their back-crosses may have been present, we chose plants that had all of the characteristics of their assumed parent species. We recorded the time from the start of recording until the first visitor and the number of flowers subsequently visited on that plant. We analyzed these time-to-event data with the Proc Reliability procedure of SAS to fit a lognormal distribution (version 9.3; SAS Institute). The mean times to first visit were 110 s for C. maritima and 830 s for C. edentula, implying that C. maritima was visited by pollinators 7.5 times as frequently as C. edentula. Pollinators also visited more flowers per visit on C. maritima than C. edentula: using a Poisson distribution, the average number of flowers visited per pollinator was 11.7 for C. maritima and 6.2 for C. edentula.
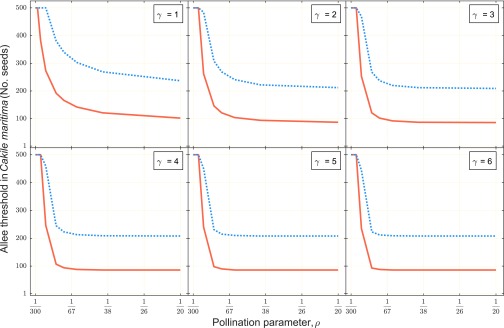
All details of experiments outlined above can be obtained from R.D.C. For and , parameters that describe the relationship between population density and probability of pollinator visit, we investigated the sensitivity of the model predictions over a wide range of parameter values (Table S3), because we had no empirical estimates for these two parameters. As shown in Fig. S7, a model with hybridization always gave smaller Allee thresholds over all tested ranges of these two parameters (Fig. S7).
Fig. S7.
Predicted Allee thresholds for the establishment of C. maritima, as a function of pollination parameters and . The reciprocal of is the population size at which the probability of pollination is 50%, whereas is a shape parameter. The minimum number of seeds necessary for C. maritima establishment is smaller with (solid line) than without hybridization (dotted line). See Table S3 for other parameter values used in above simulations.
Materials and Methods
We developed a density-dependent, time-discrete, deterministic model based on the life cycle of an annual plant with no persistent seedbank and occurring in a small, isolated patch of suitable habitat. The model incorporates demography, mating systems, pollinators, and quantitative genetics through the following recurrence difference equation:
where is the number of seeds from genotype in generation , and denotes the total number of female adults with genotype y, surviving from total seeds according to a Beverton–Holt type recruitment function, (Eq. S1). is the per capita ovule production of female genotype in the absence of neighboring plants, which decreases with total adult population size according to a rectangular hyperbolic function (Eq. S3) because of resource competition and other negative interactions between plants. A fraction of flowers produces seeds through selfing, whereas the nonselfed proportion relies on pollinators for seed production. Not all pollen from other genotypes will result in viable offspring; hence the compatibility of genotype with genotype is given by (Fig. S2). The relative frequency of genotype y, adjusted for pollinator preference (Fig. S3), is , whereas the probability of pollination is related to the total adult population size following a Holling type III functional response, (30).
We used the number of chromosomes as a proxy for determining the total number of genotype classes (which is ) and the chromosome combination of the two parental species to characterize (Fig. S4). That is, a pure individual of the incoming species, denoted by , has no alien chromosome from the resident species whereas the karyotype of an F1 hybrid embodies an equal number of chromosomes from the two parental species, so it is shown as . The proportion of ancestry from the incoming species decreases as approaches 1, whereas that of the resident species increases, with indicating a pure individual of the resident species with no alien chromosome from the incoming species. A diploid individual then undergoes gametogenesis following the principle of independent assortment of chromosomes, assuming no crossing over, where a haploid gamete randomly receives a mixture of chromosomes from the two parental species. By taking the convolution over the gamete types that can be produced by two crossing diploid individuals, we obtained the probability of two parents with genotype and producing an offspring with genotype . In essence, our quantitative genetic model is similar to the hypergeometric phenotypic model used previously to study sympatric speciation (31, 32) and risk of extinction by hybridization (33). We mapped genotypic class to a phenotypic character using a Gaussian model (30) (Fig. S5). We simulated the population dynamics of 19 genotypic classes corresponding to a diploid species with over 100 generations. This value was chosen to correspond to Cakile spp. (2n = 18) which we consider later. A smaller or larger number of chromosomes will respectively either increase or decrease the speed at which species replacement will occur but without altering the qualitative dynamics. Full details of the model and simulations are provided in SI Text, Generic Model to Simulate the Dynamics of Hybridizing Annual Species, Generic model formulation and SI Appendix.
We compared the population dynamics of the newcomer under two scenarios: (i) hybridization with an established species; and (ii) an established relative present but no hybridization. Fecundity and survival parameters were chosen to be constant and equal for the two species and for all hybrids to ensure no fitness advantage or disadvantage from hybridization. These assumptions can be altered according to the question being investigated. As a measure of establishment success, we estimated “Allee thresholds” as the minimum number of colonizing individuals required to ensure positive population growth for each scenario. A facilitation effect for hybridization would be apparent as a smaller Allee threshold than that observed for the no-hybridization scenario. We investigated the sensitivity of the model predictions over a wide range of parameter values related to initial population size, mating systems of the interacting genotypes, intercrossability, pollinator behavior, and pollination-plant density relationship (Table S2).
To verify the findings of the above theoretical model, a reduced version including only three genotypes, the two parental species, and a single hybrid class (34), was parameterized using empirical data from Cakile maritima and C. edentula (see Fig. S6 for example simulation). Parameter values related to fecundity were obtained from a common garden experiment. The selfing rates and cross-compatibility of the genotypes were quantified in two artificial crossing experiments (Fig. S1). Pollinator visitation rates were obtained by monitoring a population where the two species had similar relative frequencies. For hybrids, we used the average phenotypic values of the two parental species when no data existed. For all other parameters, we used published data and if no data were available, we ran the model over a wide range of parameter values to ensure consistent outcomes (e.g., Fig. S7). See SI Text, Simplified Model for C. maritima and C. edentula for detailed descriptions of the estimation of parameters.
Supplementary Material
Acknowledgments
We thank Juliette Bouhours for advice on the development of the model and Sally Otto for comments on an earlier draft. Funding was from Australian Research Council Discovery Grant DP140100608 (to R.D.C., M.A.L., and K.D.). S.O. received a Victorian International Research Scholarship. C.L. was funded by the China Scholarship Council. M.A.L. acknowledges funding from the Natural Sciences and Engineering Research Council and a Canada Research Chair.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
See Commentary on page 9963.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1605626113/-/DCSupplemental.
References
- 1.Papagianni D, Morse MA. The Neanderthal Story: How Modern Science is Rewriting Their Story. Thames & Hudson; London: 2015. [Google Scholar]
- 2.Ellstrand NC, Schierenbeck KA. Hybridization as a stimulus for the evolution of invasiveness in plants? Proc Natl Acad Sci USA. 2000;97(13):7043–7050. doi: 10.1073/pnas.97.13.7043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hovick SM, Whitney KD. Hybridisation is associated with increased fecundity and size in invasive taxa: Meta-analytic support for the hybridisation-invasion hypothesis. Ecol Lett. 2014;17(11):1464–1477. doi: 10.1111/ele.12355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Simberloff D. The role of propagule pressure in biological invasions. Annu Rev Ecol Evol Syst. 2009;40:81–102. [Google Scholar]
- 5.Dlugosch KM, Parker IM. Founding events in species invasions: Genetic variation, adaptive evolution, and the role of multiple introductions. Mol Ecol. 2008;17(1):431–449. doi: 10.1111/j.1365-294X.2007.03538.x. [DOI] [PubMed] [Google Scholar]
- 6.Taylor CM, Hastings A. Allee effects in biological invasions. Ecol Lett. 2005;8:895–908. [Google Scholar]
- 7.Keitt TH, Lewis MA, Holt RD. Allee effects, invasion pinning, and species’ borders. Am Nat. 2001;157(2):203–216. doi: 10.1086/318633. [DOI] [PubMed] [Google Scholar]
- 8.Elam DR, Ridley CE, Goodell K, Ellstrand NC. Population size and relatedness affect fitness of a self-incompatible invasive plant. Proc Natl Acad Sci USA. 2007;104(2):549–552. doi: 10.1073/pnas.0607306104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Elliott SE, Irwin RE. Effects of flowering plant density on pollinator visitation, pollen receipt, and seed production in Delphinium barbeyi (Ranunculaceae) Am J Bot. 2009;96(5):912–919. doi: 10.3732/ajb.0800260. [DOI] [PubMed] [Google Scholar]
- 10.Cheptou P-O. Clarifying Baker’s Law. Ann Bot (Lond) 2012;109(3):633–641. doi: 10.1093/aob/mcr127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Huxel GR. Rapid displacement of native species by invasive species: Effects of hybridization. Biol Conserv. 1999;89(2):143–152. [Google Scholar]
- 12.Cousens RD, Ades PK, Mesgaran MB, Ohadi S. Reassessment of the invasion history of two species of Cakile (Brassicaceae) in Australia. Cunninghamia. 2013;13:275–290. [Google Scholar]
- 13.Barbour MG, Rodman JE. Saga of the West Coast sea-rockets: Cakile edentula ssp. californica and C. maritima. Rhodora. 1970;72(791):370–386. [Google Scholar]
- 14.Mills K. Replacement of Cakile edentula with Cakile maritima in New South Wales and on Lord Howe Island. Cunninghamia. 2013;13:291–294. [Google Scholar]
- 15.Boyd RS, Barbour MG. Replacement of Cakile edentula by C. maritima in the strand habitat of California. Am Midl Nat. 1993;130(2):209–228. [Google Scholar]
- 16.Busch JW, Delph LF. The relative importance of reproductive assurance and automatic selection as hypotheses for the evolution of self-fertilization. Ann Bot (Lond) 2012;109(3):553–562. doi: 10.1093/aob/mcr219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Rodman JE. Systematics and evolution of the genus Cakile (Cruciferae) Contrib Gray Herb Harvard Uni. 1974;205:3–146. [Google Scholar]
- 18.Thrall PH, Young AG, Burdon JJ. An analysis of mating structure in populations of the annual sea rocket, Cakile maritima (Brassicaceae) Aust J Bot. 2000;48(6):731–738. [Google Scholar]
- 19.Ohadi S, et al. Genetic structure along the strandline: Unravelling invasion history in a one-dimensional system. J Biogeogr. 2015;43(3):451–460. [Google Scholar]
- 20.Rodman JE. Introduction, establishment and replacement of sea-rockets (Cakile, Cruciferae) in Australia. J Biogeogr. 1986;13(2):159–171. [Google Scholar]
- 21.Hyndman RJ, Mesgaran MB, Cousens RD. Statistical issues with using herbarium data for the estimation of invasion lag-phases. Biol Invasions. 2015;17(12):3371–3381. [Google Scholar]
- 22.Cody ML, Cody TWD. Morphology and spatial distribution of alien sea-rockets (Cakile spp.) on South Australian and western Canadian beaches. Aust J Bot. 2004;52(2):175–183. [Google Scholar]
- 23.Ollerton J, Winfree R, Tarrant S. How many flowering plants are pollinated by animals? Oikos. 2011;120(3):321–326. [Google Scholar]
- 24.Igic B, Kohn JR. The distribution of plant mating systems: Study bias against obligately outcrossing species. Evolution. 2006;60(5):1098–1103. [PubMed] [Google Scholar]
- 25.Burns JH, Ashman T-L, Steets JA, Harmon-Threatt A, Knight TM. A phylogenetically controlled analysis of the roles of reproductive traits in plant invasions. Oecologia. 2011;166(4):1009–1017. doi: 10.1007/s00442-011-1929-9. [DOI] [PubMed] [Google Scholar]
- 26.Bufford JL, Daehler CC. Sterility and lack of pollinator services explain reproductive failure in non-invasive ornamental plants. Divers Distrib. 2014;20(8):975–985. [Google Scholar]
- 27.Jones KN. Analysis of pollinator foraging: Tests for non‐random behaviour. Funct Ecol. 1997;11(2):255–259. [Google Scholar]
- 28.Ruhsam M, Hollingsworth PM, Ennos RA. Early evolution in a hybrid swarm between outcrossing and selfing lineages in Geum. Heredity (Edinb) 2011;107(3):246–255. doi: 10.1038/hdy.2011.9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sweigart AL, Willis JH. Patterns of nucleotide diversity in two species of Mimulus are affected by mating system and asymmetric introgression. Evolution. 2003;57(11):2490–2506. doi: 10.1111/j.0014-3820.2003.tb01494.x. [DOI] [PubMed] [Google Scholar]
- 30.Morgan MT, Wilson WG, Knight TM. Plant population dynamics, pollinator foraging, and the selection of self-fertilization. Am Nat. 2005;166(2):169–183. doi: 10.1086/431317. [DOI] [PubMed] [Google Scholar]
- 31.Doebeli M. A quantitative genetic competition model for sympatric speciation. J Evol Biol. 1996;9(6):893–909. [Google Scholar]
- 32.Barton NH. On the spread of new gene combinations in the third phase of Wright’s shifting-balance. Evolution. 1992;46(2):551–557. doi: 10.1111/j.1558-5646.1992.tb02058.x. [DOI] [PubMed] [Google Scholar]
- 33.Ferdy JB, Austerlitz F. Extinction and introgression in a community of partially cross-fertile plant species. Am Nat. 2002;160(1):74–86. doi: 10.1086/340606. [DOI] [PubMed] [Google Scholar]
- 34.Wolf DE, Takebayashi N, Rieseberg LH. Predicting the risk of extinction through hybridization. Conserv Biol. 2001;15(4):1039–1053. [Google Scholar]
- 35.Willmer P. Pollination and Floral Ecology. Princeton Univ Press; Princeton: 2011. [Google Scholar]
- 36.Tinbergen N, Impekoven M, Franck D. An experiment on spacing-out as a defence against predation. Behaviour. 1967;28(3/4):307–320. [Google Scholar]
- 37.Stephens PA, Sutherland WJ, Freckleton RP. What is the Allee effect? Oikos. 1999;87(1):185–190. [Google Scholar]
- 38.Goodwillie C, Ness JM. Interactions of hybridization and mating systems: A case study in Leptosiphon (Polemoniaceae) Am J Bot. 2013;100(6):1002–1013. doi: 10.3732/ajb.1200616. [DOI] [PubMed] [Google Scholar]
- 39.Hall RJ, Hastings A, Ayres DR. Explaining the explosion: Modelling hybrid invasions. Proc Biol Sci. 2006;273(1592):1385–1389. doi: 10.1098/rspb.2006.3473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Keddy PA. Experimental demography of the sand-dune annual, Cakile edentula, growing along an environmental gradient in Nova Scotia. J Ecol. 1981;69(2):615–630. [Google Scholar]
- 41.Feldman T, Morris WF, Wilson WG. When can two plant species facilitate each other’s pollination? Oikos. 2004;105(1):197–207. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.