pH determines the energetic efficiency of the cyanobacterial CO₂ concentrating mechanism

Significance

Cyanobacteria are responsible for roughly 10% of global photosynthetic primary production of reduced carbon. Although cyanobacteria are incredibly diverse, all known species contain a complex protein system called the CO₂ concentrating mechanism (CCM), which enables rapid growth even in environments with extremely limited CO₂. The CCM enables cyanobacteria to accumulate HCO₃⁻ and convert this inorganic carbon pool to utilizable CO₂. We demonstrate here that a quantitative description of the CCM must include the effect of pH on the abundance of HCO₃⁻ and H₂CO₃. This pH-dependent description is consistent with cyanobacterial physiology. Furthermore, the model predicts that alkaline cytosolic pH reduces the energetic cost of the CCM, consistent with pH measurements of photosynthesizing cyanobacteria.

Abstract

Many carbon-fixing bacteria rely on a CO₂ concentrating mechanism (CCM) to elevate the CO₂ concentration around the carboxylating enzyme ribulose bisphosphate carboxylase/oxygenase (RuBisCO). The CCM is postulated to simultaneously enhance the rate of carboxylation and minimize oxygenation, a competitive reaction with O₂ also catalyzed by RuBisCO. To achieve this effect, the CCM combines two features: active transport of inorganic carbon into the cell and colocalization of carbonic anhydrase and RuBisCO inside proteinaceous microcompartments called carboxysomes. Understanding the significance of the various CCM components requires reconciling biochemical intuition with a quantitative description of the system. To this end, we have developed a mathematical model of the CCM to analyze its energetic costs and the inherent intertwining of physiology and pH. We find that intracellular pH greatly affects the cost of inorganic carbon accumulation. At low pH the inorganic carbon pool contains more of the highly cell-permeable H₂CO₃, necessitating a substantial expenditure of energy on transport to maintain internal inorganic carbon levels. An intracellular pH ≈8 reduces leakage, making the CCM significantly more energetically efficient. This pH prediction coincides well with our measurement of intracellular pH in a model cyanobacterium. We also demonstrate that CO₂ retention in the carboxysome is necessary, whereas selective uptake of HCO₃⁻ into the carboxysome would not appreciably enhance energetic efficiency. Altogether, integration of pH produces a model that is quantitatively consistent with cyanobacterial physiology, emphasizing that pH cannot be neglected when describing biological systems interacting with inorganic carbon pools.

Cyanobacteria and many other autotrophs use a CO₂ concentrating mechanism (CCM) to increase the cellular pool of inorganic carbon and facilitate the Calvin–Benson–Bassham (CBB) cycle (1). Specifically, the CCM functions to supply CO₂ to ribulose bisphosphate carboxylase/oxygenase (RuBisCO), the primary carboxylating enzyme of the CBB cycle. High levels of CO₂ are essential to cyanobacterial metabolism because RuBisCO has relatively slow carboxylation kinetics and is promiscuous, catalyzing an off-pathway reaction with O₂ called oxygenation (2–4).

RuBisCO oxygenation produces 2-phosphoglycolate (2PG), which is not part of the CBB cycle and must be recycled. Recycling 2PG through photorespiratory pathways is costly, consuming reduced carbon and energy resources (5, 6). The problem of RuBisCO’s limited specificity is all the more pronounced because there is $\approx 20$ times more O₂ than CO₂ in aqueous solutions equilibrated with present-day atmosphere (SI Appendix, Fig. S1). CCMs overcome these problems by concentrating CO₂ near RuBisCO, favorably increasing the ratio of CO₂ to O₂. High concentrations of CO₂ maximize the rate of carboxylation and competitively inhibit oxygenation. Indeed, it is widely thought that the evolution of CCMs served to ameliorate energetic costs associated with large photorespiratory fluxes in the present-day atmosphere (7).

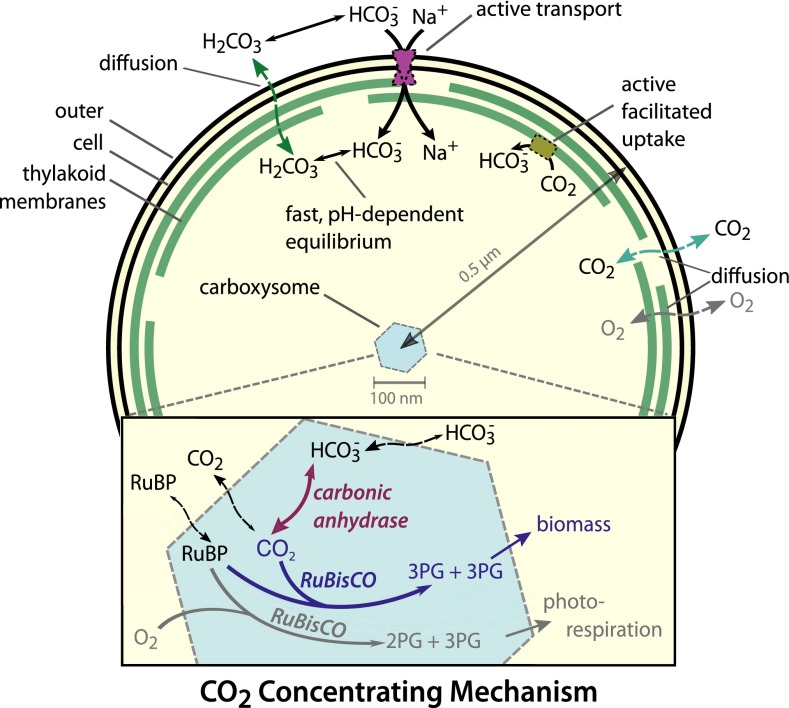
Based on diverse experimental studies, a convincing model of the bacterial CCM has emerged (Fig. 1) wherein the CCM has two primary components: active accumulation of inorganic carbon (Ci) in the cytosol and organization of RuBisCO with carbonic anhydrase (CA) inside proteinaceous organelles called carboxysomes (8). Perturbations to either component disrupt the CCM and produce mutants that require elevated CO₂ for growth (9, 10). Two energetically activated transport mechanisms—HCO₃⁻ transport and facilitated uptake of CO₂—enable accumulation of bicarbonate (HCO₃⁻) in the cytosol (8). HCO₃⁻ transport is generally coupled to Na⁺ gradients or ATP hydrolysis and facilitated uptake is hypothesized to couple oxidation of NAD(P)H to unidirectional hydration of CO₂ (Fig. 1) (8). Accumulation of charged HCO₃⁻ is preferable to accumulation of CO₂ because HCO₃⁻ escapes much less readily through the cell membrane, as we discuss below. Together, these uptake systems generate a cytosolic HCO₃⁻ concentration >10 mM, which is $\approx 30$ times the equilibrium concentration of HCO₃⁻ in water at neutral pH at 25 °C (SI Appendix, Fig. S1) (11).

Fig. 1.

Schematic of the generally accepted model of the cyanobacterial CCM. The cyanobacterial CCM concentrates HCO₃⁻ in the cytosol via two classes of uptake systems: transporters and facilitated uptake systems. We focus on Na⁺-activated transporters, which transport one Na⁺ with each HCO₃⁻. Facilitated uptake of CO₂ is catalyzed by proteins on the thylakoid membrane and is thought to couple NAD(P)H oxidation to the vectorial conversion of CO₂ into HCO₃⁻. Roughly 250 RuBisCOs (2,000 active sites) and 100 CAs are localized to the carboxysome. HCO₃⁻ concentrated in the cytosol enters the carboxysome, where it is converted to a high CO₂ concentration by CA activity. This elevated CO₂ concentration increases the rate of RuBisCO carboxylation and competitively inhibits oxygenation, increasing the overall efficiency of carbon fixation. For parameter values and model details see SI Appendix. References for each model component are given in the main text. 3PG, 3-phosphoglycerate.

Carboxysomes are icosahedral compartments approximately 100 nm in diameter and composed of a protein shell surrounding an enzyme-filled lumen (12). The carboxysome lumen is densely packed (>400 mg protein/mL) with about 2,000 RuBisCO and 100 CA active sites (12). Because CA activity is absent from the cytosol and the spontaneous dehydration of HCO₃⁻ to CO₂ is relatively slow (13), HCO₃⁻ does not equilibrate with CO₂ in the cytosol (10). Rather, HCO₃⁻ enters the carboxysome where CA activity readily equilibrates it with CO₂ (10). Crucially, the carboxysome shell must slow the diffusive loss of CO₂ so that CA activity produces a locally elevated carboxysomal CO₂ concentration (9). At sufficiently high CO₂ concentrations, RuBisCO is saturated, oxygenation is inhibited, and carboxylation proceeds at the maximum rate (1).

To define the regimes wherein the cyanobacterial CCM leads to efficient carbon fixation, we previously developed a reaction-diffusion model of the CCM (14). Even when presented with very low extracellular CO₂ concentrations (i.e., very high relative O₂ concentrations), the modeled CCM can saturate RuBisCO and drastically reduce oxygenation (14). Surprisingly, the model suggested that the CCM does not require selective uptake of HCO₃⁻ into the carboxysome, selective retention of CO₂ inside the compartment, or exclusion of O₂. Rather, a nonspecific permeability barrier at the carboxysome shell could give rise to CO₂-concentrating activity. These results built upon previous models (7, 15–17) and further explained how CCM activity, which makes cyanobacterial growth largely insensitive to the environmental concentration of Ci, could arise from its known protein components.

An unexplained observation of our previous work was substantial leakage of HCO₃⁻ across the cell membrane, with >99% of carbon import leaking out of the cell as HCO₃⁻ (14). Because HCO₃⁻ accumulation is energetically driven, large leakage fluxes consume substantial energy and require an implausible fraction (>50%) of the membrane surface for transporters (SI Appendix). Here, we identify the cell membrane permeability to HCO₃⁻ as a key parameter determining leakage. All previous models of the CCM tracked only HCO₃⁻, implicitly ignoring other species of hydrated Ci (H₂CO₃, HCO₃⁻, and CO₃²⁻, which we collectively term H_total) and their contribution to cell permeability (14–19). This implicit assumption is at odds with biochemical intuition that charge is a major determinant of membrane permeability (20). Indeed, the often-cited permeability coefficient of $\approx 3\times {10}^{-4}$ cm/s is representative of the uncharged H₂CO₃ but three to four orders of magnitude too high for HCO₃⁻ and CO₃²⁻ (SI Appendix) (21, 22). A recent model of the minimal CCM of Prochlorococcus MED4 made the inverse assumption: that the cell membrane is negligibly permeable to HCO₃⁻, implicitly ignoring the rapid interconversion of HCO₃⁻ with the uncharged and highly permeable H₂CO₃ (23).

To reconcile these varying treatments and conduct a careful accounting of Ci species, we take advantage of pH as a key physiological parameter governing the composition of the Ci pool. The relative concentration of species in H_total (H₂CO₃, HCO₃⁻, and CO₃²⁻) depends strongly on pH (SI Appendix, Fig. S1). Because these species differ in their net charge, pH will influence the rate of Ci leakage from the cell and the energetic costs associated with carbon accumulation. Because RuBisCO and CA activities are pH-dependent, the pH will also affect enzymatic rates inside the carboxysome. We have integrated these effects into our previous analytical and numerical models of the CCM (14) to produce a “pH-aware” model of the CCM, which is described in mathematical detail in SI Appendix.

The pH-aware model is now consistent with cyanobacterial physiology in a number of important ways. In optimal conditions, the model produces absolute fluxes that are similar to measured values and consistent with cyanobacterial growth rates. Unlike in previous models, these fluxes can be supported by transporters occupying a very small fraction of membrane surface area (<1%), leaving space for the essential biochemistry of transport, photosynthesis, and chemiosmosis (SI Appendix). Finally, characteristic differences in the Ci transport modalities used by oceanic and freshwater cyanobacteria can be explained through the pH-aware model by the characteristic pH and salinity differences between ocean and freshwater (SI Appendix). Given this broad consistency with cyanobacterial physiology and genetics, the pH-aware model can also be used to examine open questions related to the CCM.

Our updated, pH-aware model also enables us to test the hypothesis that the CCM reduces the energetic costs associated with fixing carbon. We calculate the effect of pH on the energetic cost of carbon fixation, carbon concentration, and photorespiration. According to our calculation, the CCM requires considerably less energy than implied by our previous model (SI Appendix). We further demonstrate that a selective carboxysome that prefers to take up HCO₃⁻ and retain CO₂ is not required to produce an energy-efficient CCM. Rather, a low absolute permeability to CO₂ is the crucial characteristic of an energy-efficient carboxysome. Moreover, the pH-aware model predicts an intracellular pH range that optimizes CCM efficiency in cyanobacteria actively fixing carbon. We validate this prediction by measuring the intracellular pH in live cyanobacterial cells (Synechococcus elongatus PCC 7942). Thus, the CCM offers another example where the properties of complex systems central to bacterial growth are well-explained by the principle of energetic cost minimization (24–26), in this case explaining the remodeling of cytosolic pH and transport modalities to minimize the cost of Ci accumulation for the CCM.

Results

The Effect of pH on the Permeability of Ci to the Cell Membrane.

All cells regulate their cytosolic pH due to the inherent pH dependence of biochemical reactions (27). However, cytosolic pH varies substantially between organisms and growth conditions (28, 29). Here, we use a mathematical model to examine how the cyanobacterial CCM functions over a range of cytosolic pH values. We include the effect of pH on the permeability of the cell membrane to constituents of the Ci pool and on the enzymatic activities located within the carboxysome.

The equilibrium composition of the Ci pool (CO₂, H₂CO₃, HCO₃⁻, and CO₃²⁻) is highly pH-dependent (SI Appendix, Fig. S1). Whether these species reach equilibrium with each other, however, depends on how the rate of uncatalyzed interconversion compares to the rates of other processes (e.g., transport and enzymatic catalysis) that produce and consume specific species. The spontaneous dehydration of H_total to CO₂ [$T_{1/2}>10$ s (13)] is much slower than diffusion and transport, and so the CCM can maintain H_total out of equilibrium with CO₂ in the cytosol (10). Equilibration between HCO₃⁻, H₂CO₃, and CO₃²⁻ within the H_total pool is, however, extremely fast [$T_{1/2}<1\hspace{0.17em}\hspace{0.5em}\text{μs}$ (30)]. As such, the dominant species among HCO₃⁻, H₂CO₃, and CO₃²⁻ will be determined by the pH, and so the contribution of each species to the cell permeability of H_total must be examined individually.

Due to the energetic penalty associated with the passage of charge into the membrane, small, charged molecules typically have membrane permeability coefficients 10⁴ to 10⁵ times smaller than uncharged molecules of comparable size (20). Consequently, HCO₃⁻ and CO₃²⁻ are dramatically less cell-permeable than the uncharged H₂CO₃. In addition to having a low membrane permeability, CO₃²⁻ contributes negligibly (<5%) to the H_total pool below pH 9 and can be neglected (SI Appendix). As such, H₂CO₃ can be treated as a monoprotic acid equilibrating quickly with HCO₃⁻. The primary literature on the permeability of small molecules gives permeability coefficients of ≈10⁻³ cm/s for H₂CO₃ and ≈10⁻⁷ cm/s for HCO₃⁻ (21, 22).

Given these values, we assume $k_m^{H_{2}C{O}_3}\ll k_m^{HC{O}_3^{-}}$ and derive that the rate of H_total diffusion across the membrane is dominated by the diffusion of uncharged H₂CO₃

$$\text{diffusive}\hspace{0.17em}{H}_{total}\hspace{0.17em}\text{flux}=k_m^{H_{2}C{O}_3}\mathrm{\Delta }{H}_{2}C{O}_3+k_m^{HC{O}_3^{-}}\mathrm{\Delta }HC{O}_3^{-}\approx k_m^{H_{2}C{O}_3}\mathrm{\Delta }{H}_{2}C{O}_3.$$

Here, $\mathrm{\Delta }{H}_{2}C{O}_3$ and $\mathrm{\Delta }HC{O}_3^{-}$ are the concentration differences of $H_{2}C{O}_3$ and $HC{O}_3^{-}$ across the cell membrane (see SI Appendix for derivation). To a first approximation, H₂CO₃ is the only species of H_total that will cross the cell membrane diffusively at an appreciable rate, regardless of the relative concentrations of H₂CO₃ and HCO₃⁻.

The above equation describes the diffusion of H_total into the cell as a function of the H₂CO₃ concentration gradient. However, the CCM model tracks HCO₃⁻ and not H₂CO₃ because HCO₃⁻ is the substrate of CA. To integrate this equation into the CCM model, therefore, we assume fast equilibrium of the H_total pool and calculate the equilibrium ratio $\left[HC{O}_3^{-}\right]/\left[H_{2}C{O}_3\right]={10}^{pH-p{K}_1}$ to determine $\mathrm{\Delta }{H}_{2}C{O}_3$ across the cell membrane. Because the concentration and composition of H_total may differ markedly across the cell membrane (due to differences in pH, ionic strength, and the action of Ci transporters), this substitution yields separate terms for the inward (first term) and outward (second term) diffusional velocities

$$\text{diffusive}\hspace{0.17em}HC{O}_3^{-}\hspace{0.17em}\text{flux}\hspace{0.17em}=\hspace{0.17em}\left({\left[HC{O}_3^{-}\right]}_{out}\hspace{0.17em}{k}_m^{H_{2}C{O}_3}\hspace{0.17em}{10}^{\left(p{K}_1-p{H}_{out}\right)}-{\left[HC{O}_3^{-}\right]}_{cytosol}\hspace{0.17em}{k}_m^{H_{2}C{O}_3}\hspace{0.17em}{10}^{\left(p{K}_1-p{H}_{cytosol}\right)}\right).$$

Here, $k_m^{H_{2}C{O}_3}=3\times {10}^{-3}$ cm/s is the velocity of H₂CO₃ permeation and ${10}^{(p{K}_1-pH)}$ is the ratio of H₂CO₃ to HCO₃⁻ as a function of the pH and the first pK_a of H₂CO₃ ($p{K}_1\approx 3.2)$ (22, 31). This equation holds across the entire pH range considered here ($6.5\le \text{pH}\le 9$; see SI Appendix for full derivation). If the cytosolic and extracellular pH are equal, the pH-dependent velocity of HCO₃⁻ membrane permeation equals $k_m^{H_{2}C{O}_3}\hspace{0.17em}{10}^{(p{K}_1-pH)}$, recovering a functional form equivalent to the previous model. At pH 7, this equation yields a velocity of $\approx 5\times {10}^{-7}$ cm/s, 1,000-fold smaller than the commonly used value of $3\times {10}^{-4}$ cm/s (32, 33). Indeed, this higher effective velocity implies an implausible cytosolic pH of about 4 (SI Appendix).

Functional Form of the pH-Aware CCM Model.

The pH-aware CCM model is a system of coupled reaction-diffusion differential equations in spherical coordinates. The equations describe the entry of Ci into the cell and the carboxysome as well as diffusion and the chemical reactions within the carboxysome. This system can be solved both numerically and analytically at steady state (14). We write the fluxes for CO₂, C, and HCO₃⁻, H, at the cell membrane, $r=R_b$, as

$$D\frac{\partial C}{\partial r}=-\hspace{0.17em}\alpha C_{cytosol}+k_m^C\left(C_{out}-C_{cytosol}\right)$$

$$D\frac{\partial H}{\partial r}=j_c{H}_{out}+\hspace{0.17em}\alpha C_{cytosol}+\left({\left[HC{O}_3^{-}\right]}_{out}\hspace{0.17em}{k}_m^{H_{2}C{O}_3}\hspace{0.17em}{10}^{\left(p{K}_1-p{H}_{out}\right)}-{\left[HC{O}_3^{-}\right]}_{cytosol}\hspace{0.17em}{k}_m^{H_{2}C{O}_3}\hspace{0.17em}{10}^{\left(p{K}_1-p{H}_{cytosol}\right)}\right).$$

Here D is the diffusion constant for small molecules in water (10⁻⁵ cm²/s), $j_c$ is the velocity of active HCO₃⁻ transport, $\alpha$ is the velocity of CO₂ to HCO₃⁻ conversion, and $k_m^C$ and $k_m^{H_{2}C{O}_3}$ are the permeability of the cell membrane to CO₂ and H₂CO₃, respectively. $k_m^C$ is set to 0.3 cm/s and $k_m^{H_{2}C{O}_3}=$ $3\times {10}^{-3}$ cm/s as described above.

As previously discussed, the spontaneous dehydration of HCO₃⁻ is slow, so we assume no relevant chemical reactions in the cytosol (Fig. 1). We evaluate this assumption through a consistency check on the resulting model concentrations and fluxes and find it to be reasonable (SI Appendix). Therefore, diffusion sets the steady-state concentrations of CO₂ and HCO₃⁻ in the cytosol via ${\nabla }^{2}C=0$, ${\nabla }^{2}H=0$, where ${\nabla }^2$ is the second derivative in spherical coordinates. Assuming the same carboxysome permeability, $k_c$, for both CO₂ and HCO₃⁻, diffusive leakage at the carboxysome shell is expressed as

$$D\frac{\partial C}{\partial r}=k_c\left(C_{cytosol}-C_{carboxysome}\right)$$

$$D\frac{\partial H}{\partial r}=k_c(H_{cytosol}-H_{carboxysome})$$

at r = R_c, the boundary of the carboxysome. The pH-aware model can also be used to consider differential carboxysome permeability to CO₂ and HCO₃⁻, as described in Discussion and SI Appendix. Inside the carboxysome, the model considers diffusion of substrates as well as CA ($R_{CA}$) and RuBisCO ($R_{Rub}$) activities. The balance of enzymatic and diffusive rates set the steady-state concentrations of CO₂ and HCO₃⁻ in the carboxysome as

$$\text{D}{\nabla }^{2}C+R_{CA}-\hspace{0.17em}{R}_{Rub}=0$$

$$\text{D}{\nabla }^{2}H-R_{CA}=0,$$

where the enzymatic rates $R_{CA}$ and $R_{Rub}$ are depend on pH in the manner described below.

The Effect of pH on Enzymatic Activity in the Carboxysome.

The enzymatic mechanisms of RuBisCO and CA are inherently pH-dependent (34), and so it is critical to include the pH dependence of these enzymes in describing the pH dependence of the CCM. The carboxysomal CA is an efficient enzyme, well described by reversible Michaelis–Menten kinetics, with a dehydration $k_{cat}\approx 5\times {10}^5\hspace{0.17em}{\text{s}}^{-1}$ (35). When the intrashellular CA is saturated, increased HCO₃⁻ transport has no effect on the carboxysomal CO₂ concentration. As a result, saturated CA implies that HCO₃⁻ uptake could be lower without affecting the carboxylation rate (14). Therefore, efficient CCM function occurs, in part, when CA is not saturated. Because CA is a fast enzyme with ≈100 active sites in the carboxysome, CO₂ and HCO₃⁻ are held in equilibrium within the carboxysome when CA is not saturated (SI Appendix). In this pseudoequilibrium condition, the ratio of CO₂ to HCO₃⁻ in the carboxysome is determined by the pH dependence of the reaction equilibrium constant $K_{eq}^{\text{'}}\left(pH\right)=\left[HC{O}_3^{-}\right]/\left[C{O}_2\right]$. We calculate the pH dependence of $K_{eq}^{\text{'}}$ from the Gibbs formation energies of the relevant species (27, 36). For reversible reactions such as the dehydration of bicarbonate, a modest change in the pH can have a large effect on $K_{eq}^{\text{'}}$—about 10-fold between pH 7 and 8 (SI Appendix).

RuBisCO activity also varies with pH, with the carboxylation k_cat reaching maximum near pH 7.5 (34). We describe the RuBisCO reaction with irreversible Michaelis–Menten kinetics and assume RuBisCO kinetic parameters measured at pH 7.8 for the S. elongatus PCC 6301 RuBisCO. The pH dependence of RuBisCO kinetics was modeled by rescaling the Michaelis–Menten kinetic constants by the pH dependence observed for the cyanobacterial RuBisCO from Anabaena variabilis (SI Appendix, Fig. S4).

A pH-Aware CCM Model.

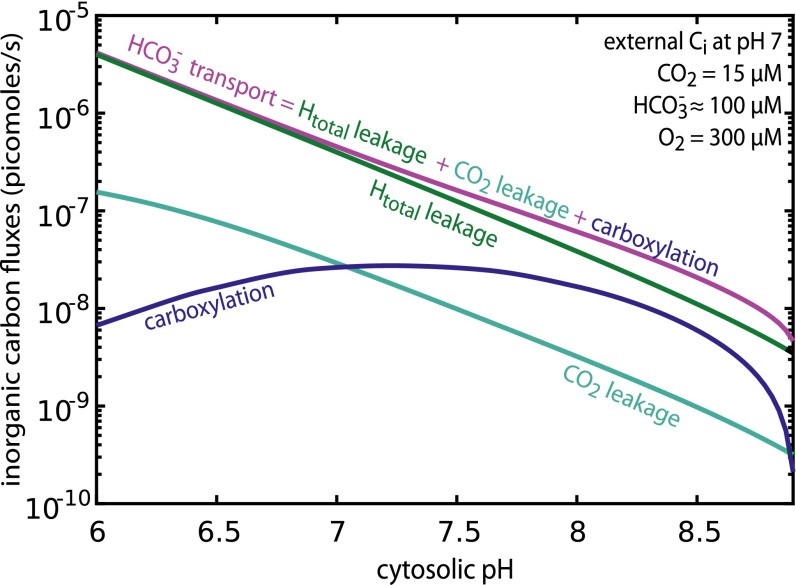
With the pH dependence of permeability and enzymatic activity integrated into the model, we asked a simple question: What is the role of cytosolic pH in shaping the flow of carbon through the CCM? To answer this question, we calculated the HCO₃⁻ transport flux required to achieve the measured $\approx 30\hspace{0.17em}\hspace{0.5em}\text{mM}$ cytosolic HCO₃⁻ concentration (37–39) across a range of cytosolic pH values (Fig. 2). For this calculation, the carboxysome permeability was set to 3 × 10⁻⁵ cm/s (optimum for cytosolic pH 8; SI Appendix) and facilitated CO₂ uptake was set to zero for simplicity. The carboxysome permeability represents the velocity at which CO₂ and HCO₃⁻ traverse the carboxysome shell, including both transit of pores found in shell proteins and any “leakiness” of the shell itself. Carbon is conserved and so fluxes importing Ci into the cell (active HCO₃⁻ transport) must equal the sum of fluxes consuming Ci within the cell: H_total leakage, CO₂ leakage, and carboxylation. This conservation law is captured by the equation shown in Fig. 2.

Fig. 2.

Increased cytosolic pH reduces Ci fluxes required to achieve efficient CO₂ fixation. Ci fluxes are plotted as a function of pH. As carbon is conserved, the HCO₃⁻ transport flux (purple) equals the sum of H_total leakage (green), CO₂ leakage (teal), and carboxylation (blue). RuBisCO achieves a maximum carboxylation rate near pH 7.5. Carboxysome permeability was set to 3 × 10⁻⁵ cm/s and HCO₃⁻ transport rate was set to yield 30 mM cytosolic HCO₃⁻ at each pH. The extracellular Ci pool was assumed to be in equilibrium with the external pH, which was fixed at 7 for this analysis. These fluxes neglect the uncatalyzed dehydration of HCO₃⁻, which would act to increase CO₂ leakage. Compensating for increased leakage would require a small increase in HCO₃⁻ transport (SI Appendix).

Analyzing the pH dependence of carbon fluxes shows that CCM performance is expected to improve dramatically with increasing cytosolic pH (Fig. 2). Indeed, the amount of active transport required to maintain 30 mM cytosolic HCO₃⁻ decreases exponentially with increasing pH (i.e., linearly on a log scale). At pH 7 and below, more than 85% of the HCO₃⁻ influx leaks out of the cell. Above pH 7, CO₂ leakage and carboxylation fluxes contribute more prominently to the flux balance, with leakage representing $\approx 65\%$ at pH 8. The log-linear relationship between pH and H_total leakage arises from the exponential (power-law) dependence of H_total permeability on pH described above. HCO₃⁻ transport fluxes also display a log-linear relationship with cytosolic pH (Fig. 2) and absolute transport rates at pH 8 are on the order of 10⁻⁷ pmol per cell per s, approaching the ≈10⁻⁸ pmol per cell per s uptake flux measured in the marine cyanobacterium Prochlorococcus MED4 (23).

In Fig. 2, the carboxylation rate declines above pH 7.5 because RuBisCO achieves maximal catalytic rate at that pH (34). At a cytosolic pH of 8 ≈30% of Ci uptake is ultimately fixed by RuBisCO, compared with ≈1% in the previous model. Economic operation of the CCM is strongly dependent on the cytosolic pH, with pH $\cong 8$ curtailing diffusive loss of H_total. Although greatly reduced, loss of HCO₃⁻ (through H₂CO₃ leakage) remains a substantial flux and cannot be neglected even above pH 8. A full description of the model, including all kinetic parameters and pH dependencies, is given in SI Appendix.

The Energetic Cost of CO₂ Fixation.

The pH-aware model can also be used to calculate the energetic cost of fixing carbon through the CCM. This cost is composed of three components: the cost of transport, the cost of the CBB cycle, and the cost of photorespiratory pathways recycling 2PG (Fig. 3). The per-fixation cost of the CBB cycle is approximately constant, but the costs of transport and photorespiration depend on the pH and the efficacy of the CCM (i.e., how much carboxylation and oxygenation take place). Here, we express the cost of fixation in units of H⁺ gradient dissipation— the number of H⁺ transported along the concentration gradient (i.e., the fundamental currency of the electrochemical potential). Cyanobacteria convert a proton gradient into ATP by means of the F₁F_o ATP synthase, which synthesizes one ATP for every four H⁺ translocated (40, 41).

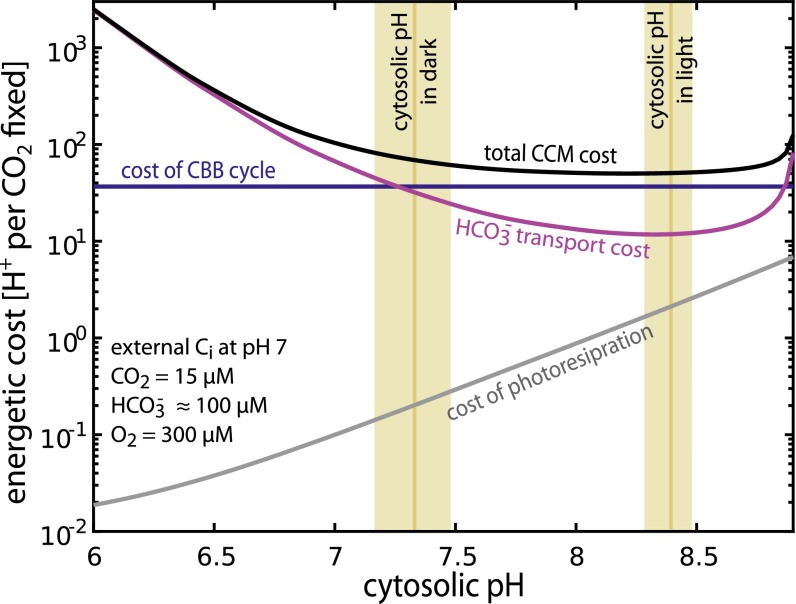
Fig. 3.

Energetic costs associated with the CCM depend strongly on the cytosolic pH. The total energetic cost of concentrating CO₂ per CO₂ fixation (black) is plotted for cytosolic pH ranging from 6 to 9. The purple line denotes the cost of HCO₃⁻ transport and the blue line gives the per-fixation cost of the CBB cycle, which is assumed to be independent of pH. The gray line gives the cost of recycling 2PG through the C₂ photorespiratory pathway. The measured cytosolic pH of S. elongatus 7942 is shown as gold bars with bar width denoting the SE (Methods). The extracellular Ci pool was assumed to be in equilibrium with the external pH, which was fixed at 7 for this analysis.

Active transport of Ci is the chief energetic cost associated with the CCM. The biochemical mechanism of facilitated CO₂ uptake is not known and so we focus on the primary cyanobacterial HCO₃⁻ transporters, Na⁺ symporters, which import one Na⁺ with each HCO₃⁻. In model cyanobacteria like S. elongatus, antiporters exchange Na⁺ and H⁺, and so sodium and proton gradients are interchangeable (7, 42). This allows HCO₃⁻ transport cost to be expressed in units of H⁺ transported across the membrane per CO₂ fixed. We assume a cost of four H⁺ per HCO₃⁻ transported (SI Appendix) to calculate the per-fixation cost of HCO₃⁻ transport shown in Fig. 2.

The cost of the CBB cycle and the C₂ photorespiratory pathway can be estimated from their known stoichiometry. We calculate the cost of the CBB cycle as ≈37 H⁺ per CO₂ fixed and the cost of the C₂ pathway ≈26 H⁺ per 2PG recycled (SI Appendix). The total cost of CO₂ fixation and 2PG recovery will depend on the relative amount of oxygenation according to the formula

$$\text{fixation}\hspace{0.17em}\text{and}\hspace{0.17em}\text{recovery}\hspace{0.17em}\text{cost}=\hspace{0.17em}\frac{\left(37+26\hspace{0.17em}{R}_O\right)}{1-\frac{R_O}{2}},$$

where R_O is the ratio of oxygenation to carboxylation rates ($R_o=V_o/V_c$), $37\hspace{0.17em}\hspace{0.5em}{\text{H}}^{+}$ is the per-carboxylation cost of the CBB cycle, and $26\hspace{0.17em}\hspace{0.5em}{\text{H}}^{+}$ is the per-oxygenation cost of C₂ photorespiration. The cost has units of H⁺ per carboxylation. This formula accounts for the fact that each turn of the C₂ cycle releases one CO₂, which must be fixed again to maintain carbon balance (SI Appendix). In the limit of low photorespiration, $R_o$ approaches zero and the above formula converges to ≈37 H⁺ per CO₂, the calculated cost of fixation through the CCB cycle. As the modeled CCM strongly limits oxygenation, the “fixation and recovery cost” is dominated by the cost of the CBB cycle, which is roughly constant (blue line in Fig. 3). The rate and cost of photorespiration, in contrast, is tied to the ratio of CO₂ to O₂ in the carboxysome (i.e., CCM efficacy) and so depends on pH (gray line in Fig. 3).

The projected cost of transport (purple line) falls beneath that of the CBB cycle (Fig. 3) as the cytosolic pH surpasses 7. The modeled cyanobacterial CCM approaches a total cost of ≈50 H⁺ per fixation near pH 8. At pH ≈8, active transport costs about 10-fold less than the CBB cycle and, we calculate, requires <1% of cell surface area (SI Appendix). Notably, photorespiratory costs increase at elevated pH (Fig. 3) and oxygenation could account for as many as 2% of RuBisCO turnovers near pH 8. This might explain the absolute requirement for photorespiratory pathways in model cyanobacteria (43). Increased photorespiration can be understood as follows: CA equilibrates CO₂ with HCO₃⁻ in the carboxysome and increased pH favors HCO₃⁻ over CO₂ (SI Appendix, Fig. S1). As such, the carboxysomal CO₂ concentration decreases as the pH increases, increasing the O₂:CO₂ ratio and, consequently, photorespiration. So long as the pH remains beneath 8.5, the cost of photorespiration never exceeds 3% of total. Taken together, these cost calculations suggest that a cytosolic 7.5 < pH < 8.5 minimizes total energetic costs without requiring substantial photorespiratory flux. At a cytosolic pH <6.2 transport is prohibitively costly, at least an order of magnitude more so that carbon fixation itself.

S. elongatus Cyotosolic pH is Within the Optimal Range for CCM Operation.

Increased cytosolic pH decreases the permeability of the bicarbonate pool to the cell membrane, reduces the amount of HCO₃⁻ transport required per CO₂ fixation, and decreases the total cost of CO₂ fixation through the CCM. Our model predicts an optimal cytosolic pH range of 7.5–8.5 to minimize the total energetic cost of fixing carbon through the CCM. To test the prediction of an optimal cytosolic pH range, we measured the cytosolic pH of light- and dark-acclimated cyanobacteria (S. elongatus PCC 7942) using the ratiometric pH-sensitive dye BCECF-AM (Methods). As shown in Fig. 3, cytosolic pH differs between dark-acclimated cells, which do not grow or fix CO₂ appreciably, and light-acclimated cells, which fix carbon and grow. Strikingly, the cytosolic pH of S. elongatus increases from $7.3\pm 0.2$ in the dark to $8.4\pm 0.1$ in the light (Fig. 3 and SI Appendix, Fig. S8). This is expected because the photosynthetic light reactions pump H⁺ from the cytosol into the thylakoid lumen (44) and the pH values are consistent with previous measurements of cytosolic pH in cyanobacteria (45–48). The pH in the light coincides well with our prediction of an optimal cytosolic pH range for carbon-fixing cyanobacteria.

Discussion

Here, we demonstrate that CCM function is strongly dependent on pH. Most importantly, we show that Ci leakage is dominated by H₂CO₃ within the physiological pH range (SI Appendix). Elevated cytosolic pH increases the relative abundance of charged HCO₃⁻ and so reduces leakage and the energetic cost of maintaining a high cytosolic concentration of H_total. This mirrors heterotrophic transport strategies such as the phosphorylation of glucose after uptake, which serves to “trap” glucose in the cell. We predict an optimal cytosolic pH range of 7.5–8.5 for carbon-fixing cyanobacteria. At pH 7.7 the total energetic cost of fixing carbon through the CCM is minimized, with higher pH offering diminishing returns (Fig. 3). We experimentally verified that cyanobacteria (S. elongatus 7942) achieve a cytosolic pH in this range while fixing carbon (Fig. 3). Moreover, S. elongatus cytosolic pH in the light (during carbon fixation) is ≈8.4 and differs markedly from the pH ≈7.3 measured in dark-acclimated cells (Fig. 3).

Notably, efficient operation of the CCM depends on two crucial unknown parameters: the velocity of active HCO₃⁻ transport and the permeability of the carboxysome to CO₂ and HCO₃⁻ (14). These parameters are interdependent: Changing the carboxysome permeability alters the HCO₃⁻ transport flux required to concentrate CO₂ in the carboxysome, as shown in SI Appendix, Fig. S6. Integrating pH into the model does not qualitatively change the interdependence of carboxysome permeability and active HCO₃⁻ transport. However, at pH 8, the pH-aware CCM model demands 10² to 10⁴ times less active HCO₃⁻ transport than our previous model to achieve efficient CO₂ fixation (Fig. 2). We defined the optimum permeability as the value that minimizes the active HCO₃⁻ transport flux required to saturate RuBisCO. The optimal carboxysome permeability at pH 8 is also 30-fold lower than previously reported (3 × 10⁻⁵ instead of 10⁻³ cm/s), but carboxysome permeabilities as high as 10⁻² cm/s can support CO₂-concentrating activity (SI Appendix, Fig. S6).

This updated, pH-aware model now agrees with cyanobacterial physiology in several ways. In optimal pH conditions the predicted fluxes for HCO₃⁻ transport, leakage, and carboxylation are all within an order of magnitude of measured values (23). In contrast to earlier models, which required >50% of the cell membrane surface for Ci transport, these fluxes demand less than 1% of cell membrane surface area (SI Appendix). The pH-aware model also helps rationalize the distribution of Ci transport systems among cyanobacteria. Freshwater cyanobacteria, which live near neutral pH, typically have genes coding for both facilitated CO₂ uptake and energetically activated HCO₃⁻ transport systems. Oceanic cyanobacteria, which live at pH ≈8, typically encode only HCO₃⁻ transporters (23, 32). Based on our analysis of the pH-aware model, a sizable fraction of Ci can be taken up as CO₂ in a near-neutral pH environment like freshwater, whereas in an environment at pH 8 CO₂ uptake would contribute negligibly to the overall Ci uptake rate (SI Appendix, Fig. S9).

Selectivity at the Carboxysome Shell.

Throughout the text, we assumed that the carboxysome is equally permeable to CO₂ and HCO₃⁻. However, recent structures of carboxysome shell proteins offer a potential mechanism for differential permeability of CO₂ and HCO₃⁻: The pores of shell proteins typically carry positive charge, which might increase the rate of HCO₃⁻ transit relative to CO₂ (12, 49). Indeed, recent experimental evidence suggests that protein compartments can be selectively permeable (50, 51). Intuitively, it seems that a very high HCO₃⁻ permeability and a very low CO₂ permeability would be best for the efficient operation of the CCM. Such permeabilities would maximize HCO₃⁻ uptake and minimize loss of CO₂, ensuring that every carbon entering the carboxysome is ultimately fixed.

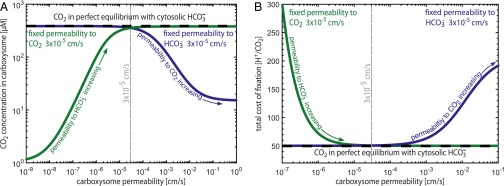
We used the pH-aware model to examine this intuition. As shown in Fig. 4, selectivity does not substantially improve the performance of the CCM. Rather, we find that a low permeability for CO₂ ($\mathrm{<}{10}^{-4}$ cm/s) is a critical requirement for CCM function. To explain this nonintuitive result, note that the best possible case for the CCM is that the carboxysomal CA brings the cytosolic HCO₃⁻ pool into perfect equilibrium with CO₂ inside the carboxysome (i.e., with negligible leakage of carboxysomal CO₂; dashed black line in Fig. 4A). Because no energetic coupling is known or hypothesized to exist inside the carboxysome, equilibration of cytosolic HCO₃⁻ with carboxysomal CO₂ would maximize the carboxysomal CO₂ concentration. Indeed, the optimal single carboxysome permeability $k_c=3\times {10}^{-5}$ cm/s very nearly achieves this equilibrium CO₂ concentration (within 5%; gray dashed line in Fig. 4A).

Fig. 4.

A selective carboxysome would not substantially improve CCM efficiency. The CO₂ concentration in the carboxysome is maximized when it is brought into equilibrium with the cytosolic HCO₃⁻ pool, shown as the black dashed line in A and B. A CCM using the single optimal permeability computed through the pH-aware model (dashed gray line) achieves a carboxysomal CO₂ concentration within 5% of this maximum. Selectivity at the carboxyome shell is thought to increase HCO₃⁻ permeability relative to CO₂ by means of charge interactions in the pores of the carboxysome shell. Selectivity might intuitively result in greater trapping of CO₂ (tracing the purple curve toward lower permeabilities) or faster uptake of HCO₃⁻ (tracing the green curve toward higher permeabilities), but neither of these strategies can increase the carboxysomal CO₂ concentration above equilibrium. As shown in B, selectivity would not substantially reduce the total cost of fixing carbon through the CCM, which is already nearly minimized at the single optimal permeability of 3 × 10⁻⁵ cm/s. Increasing the CO₂ permeability beyond 10⁻⁴ cm/s, however, exponentially increases the cost of fixation due to leakage of CO₂ from the carboxysome to the cytosol.

Whereas a selective system could reduce the amount of active HCO₃⁻ transport required per fixation (SI Appendix), transport costs represent ∼20% of the total cost at a cytosolic pH of 8 (Fig. 3) and so selectivity would have only a very small effect on the total cost of fixation in these conditions (<2%; gray dashed line in Fig. 4B). Increasing the permeability of the carboxysome to CO₂ beyond ${10}^{-4}$ cm/s, however, exponentially increases the cost of fixation irrespective of the HCO₃⁻ permeability (Fig. 4B and SI Appendix). As a result, we find that selectivity is not necessary to produce a functional and energetically efficient CCM and suggest that future research should focus on understanding how the carboxysome maintains a permeability barrier to CO₂ (SI Appendix).

A Relatively Acidic Carboxysome Would Benefit the CCM.

It has been suggested that the carboxysome might maintain a pH gradient, with the cytosolic and carboxysomal pHs differing (37, 52). Altering the pH in the carboxysome would influence CCM efficiency in two ways. pH affects the equilibrium composition of Ci and the kinetics of the carboxysomal enzymes. A more acidic pH <8 would increase the equilibrium CO₂ concentration relative to the cytosol (SI Appendix, Fig. S1) and increase RuBisCO’s maximum carboxylation rate (SI Appendix, Fig. S4). Indeed, because the combined action of CA and RuBisCO produces a net H⁺, it may be possible for the cell to maintain a steady state where the carboxysomal pH differs from the cytosol (SI Appendix).

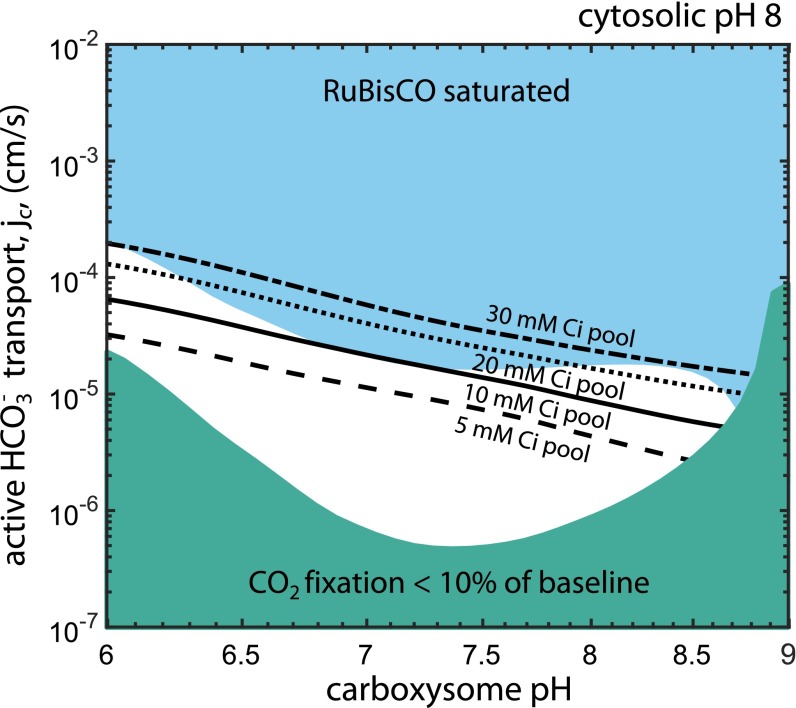
Fig. 5 shows that, within limits, a relatively acidic carboxysome would result in a higher degree of RuBisCO saturation at the same rate of cellular HCO₃⁻ uptake, with a carboxysomal pH ≈7 minimizing the amount of HCO₃⁻ uptake required to saturate RuBisCO (blue region). If the carboxysome is too acidic, however, it can deleteriously affect RuBisCO kinetics (SI Appendix, Fig. S4). An alkaline carboxysomal pH >8.5 would encumber the CCM on two fronts: As the pH increases, the equilibrium CO₂ concentration decreases exponentially and RuBisCO’s maximum carboxylation rate vanishes (34). Furthermore, we find that a cytosolic HCO₃⁻ concentration beneath ≈10 mM is insufficient to saturate the carboxysomal RuBisCO (Fig. 5 and SI Appendix). This can be seen by calculating the CO₂ concentration that would be achieved by equilibrating 5 mM HCO₃⁻, $\left[C{O}_2\right]=\left[HC{O}_3^{-}\right]{10}^{\left(p{K}_{eff}-pH\right)}\approx 5\hspace{0.17em}\hspace{0.5em}\text{mM}\times {10}^{6.1-7}\approx 600\hspace{0.5em}\hspace{0.17em}\text{μM}$, where pK_eff = 6.1 is the effective pK_a, between aqueous CO₂ and HCO₃⁻ (SI Appendix). The modeled RuBisCO, by contrast, has a carboxylation K_m that increases with decreasing pH, reaching ∼1 mM at pH 7 (SI Appendix, Fig. S4), and so cannot be saturated by 5 mM cytosolic HCO₃⁻. Although the absolute carboxylation K_m varies between RuBisCO forms (2), the plant enzyme displays a similar pH dependence, with pH 7 resulting in at least twofold reduced CO₂ affinity (34, 53, 54).

Fig. 5.

A relatively acidic carboxysome would improve CCM performance. The phase space depicts the effect of varying carboxysomal pH and HCO₃⁻ transport on the degree of RuBisCO saturation in the carboxysome. The cytosolic pH was set to 8. The blue region denotes the portion of phase space wherein RuBisCO is saturated with CO₂. When the carboxysomal pH is relatively acidic (roughly pH 7) less HCO₃⁻ uptake is required to saturate RuBisCO because the equilibrium between CO₂ and HCO₃⁻ favors CO₂ more than at pH 8 (SI Appendix). Moreover, RuBisCO has an increased carboxylation k_cat at this pH. The minimum cytosolic HCO₃⁻ concentration (black lines) that allows for saturation of the carboxysomal RuBisCO is 10–20 mM, depending on RuBisCOs CO₂ affinity, which also varies with pH (SI Appendix). The teal region denotes the portion of phase space where the total CO₂ fixation flux is less than 10% of the flux in reference conditions (pH 8 in the cytosol and carboxysome). This region is labeled to emphasize that the fixation flux collapses at basic pH because the carboxylation k_cat is projected to vanish in this regime (SI Appendix, Fig. S4A).

Model Assumptions and Future Directions.

The major insight of the pH-aware model is that the effective permeability of the membrane to H_total depends on the relative abundance of the species comprising H_total (HCO₃⁻, H₂CO₃, and CO₃²⁻) and hence on the pH and ionic strength (SI Appendix). The model ignores the effect of H₂CO₃ and CO₃²⁻ on all other CCM fluxes. HCO₃⁻ is the true substrate of CA, so it is reasonable to ignore the enzyme’s interaction with other species (55). However, it is not known whether HCO₃⁻, H₂CO₃, and CO₃²⁻ are equally permeable to the carboxysome. As mentioned above, pores on the carboxysome shell often carry positive charge, so it is plausible that charge would affect the rate substrates enter the carboxysome (12, 49). Direct measurement of the permeability characteristics of the carboxysome would be of great help in understanding the CCM.

We further assume throughout this work that CO₂ is the limiting substrate for RuBisCO carboxylation, that is, that the carboxylation rate does not depend on the concentration of the five-carbon carboxylation substrate ribulose-1,5-bisphosphate (RuBP). This assumption is supported by measurements of millimolar RuBP in S. elongatus (37), but it remains unclear how RuBP enters the carboxysome (49, 56). Similarly, we assume that O₂ enters the carboxysome quickly enough to equalize concentrations across the carboxysome shell (SI Appendix), that is, that the CCM is not an “oxygen-blocking mechanism.”

In our analysis of the membrane permeability of H_total, we assumed that the permeability of H₂CO₃ is well-approximated by those of formic and acetic acids (H₂CO₂ and H₄C₂O₂, respectively; SI Appendix). Model results are particularly sensitive to our assumptions about membrane and carboxysome permeabilities (SI Appendix, Fig. S11), emphasizing that quantitation of these permeability values is vital to understanding the cyanobacterial CCM. We further assume the cytosolic and carboxysomal pH are equal based on the observation of fast pH equilibration across the α-carboxysome shell (52). However, it may be possible for the CCM to maintain a ∆pH across the carboxysome shell (SI Appendix). Although the pH-aware model suggests that a relatively acidic carboxysomal pH ≈7 would enhance CCM efficiency (Fig. 5), it is difficult to imagine how the carboxysomal pH might be measured in vivo. Finally, we assume a 30 mM concentration of cytosolic HCO₃⁻ based on a number of measurements (37–39), and we ignored the effect of uncatalyzed dehydration on the cytosolic HCO₃⁻ concentration. In the SI Appendix we show that the spontaneous interconversion of HCO₃⁻ and CO₂ has the same pH dependence as H_total permeability and including this reaction would result in a 15% increase in the HCO₃⁻ transport rate at most. As discussed above, ≈10 mM is the lowest cytosolic HCO₃⁻ concentration that would saturate the modeled carboxysomal RuBisCO with CO₂ (Fig. 5 and SI Appendix).

A long history of research into photosynthetic physiology has shown that diverse phototrophs maintain a basic pH near 8 around RuBisCO while fixing carbon. Spinach chloroplasts, which contain no CCM, maintain a pH near 7 in the dark and shift to pH ≈8 in the light (57). As such, it is unclear whether the prevailing pH is an adaptation to the CCM or the CCM adapted to the pH. Indeed, active photosynthesis requires pumping of protons into the thylakoid and so it is sensible that the pH should increase in the stroma/cytoplasm (45, 58). We simply note that these explanations are not mutually exclusive (i.e., that it is possible that a pH ≈8 results from photosynthetic proton pumping and also optimizes CCM efficiency). Many eukaryotic algae have a CCM based on a structure called the pyrenoid that is evolutionarily distinct from, but physiologically similar to, the cyanobacterial CCM (7). Similar coordinated pH shifts are also known to occur in algal chloroplasts (59). Perhaps a shift from pH ≈7 in the dark to pH ≈8 in the light reflects a coordination of chloroplast pH with the algal CCM. We hope that future investigations into pH homeostasis and intracellular fluxes of carbon-fixing organisms help refine our understanding of the inner workings of CCMs.

Methods

Modeling.

The analytic equations of our previous model (14) were updated to account for the effect of pH on the composition of H_total, H_total membrane permeability, and RuBisCO and CA activity. The pH-dependent composition of H_total was calculated using thermodynamic potentials derived by Noor et al. (36). Permeability coefficients for CO₂, H₂CO₃, and HCO₃⁻ and were derived from literature values for those and similar molecules. The pH dependence of RuBisCO and CA kinetics were extracted from biochemical studies and scaled to match the carboxysomal enzymes. We further developed a mathematical framework to integrate the pH dependence of H_total permeability and selectivity at the carboxysome shell while preserving our capacity to solve the model analytically. In addition to the integration of detailed pH dependence, we described a carbon flux balance relation and model the energetic cost of all fluxes in the model except for facilitated CO₂ uptake. To verify the accuracy of our analytic solutions, we compared them to results produced by simulating a numerical model. The updated model is described in detail in SI Appendix, implemented in MATLAB and freely available at https://github.com/SavageLab/ccm/.

S. elongatus pH Measurement.

The intracellular pH of S. elongatus 7942 was measured using the ratiometric pH dye 2′,7′-bis(2-carboxyethyl)-5 (6)-carboxyfluorescein acetoxymethyl ester (BCECF-AM). The calibration curve was generated as follows. S. elongatus 7942 was grown to midlog phase, washed, and resuspended in BG11 media with 20 μM BCECF-AM. Cells were incubated with BCECF-AM for 30 min in the light at 30 °C and then resuspended in BG11 of defined pH containing 20 μM of the ionophore nigericin. After a 10-min incubation, four replicates of each pH condition were quickly loaded onto a 96-well plate and fluorescence was measured in a Tecan M1000 plate reader with excitation/emission pairs 440/535 and 490/535. The 490:440 emission ratio was fit to a Boltzmann sigmoid to generate the calibration curve in SI Appendix, Fig. S8.

S. elongatus 7942 in midlog phase was preincubated in light or in the dark for 9 h. These cultures were washed and resuspended in their spent growth media with 20 μM BCECF-AM and incubated for 30 min at 30 °C in the light or dark as appropriate. For dark-treated cultures, all pipetting steps were carried out in a dark room with a low-intensity green LED light. Fluorescence was measured as above. Fluorescence ratios were calculated for each replicated and converted to pH values by inverting the calibration curve.