EEG functional connectivity, axon delays and white matter disease

Abstract

Objective

Both structural and functional brain connectivities are closely linked to white matter disease. We discuss several such links of potential interest to neurologists, neurosurgeons, radiologists, and non-clinical neuroscientists.

Methods

Treatment of brains as genuine complex systems suggests major emphasis on the multi-scale nature of brain connectivity and dynamic behavior. Cross-scale interactions of local, regional, and global networks are apparently responsible for much of EEG's oscillatory behaviors. Finite axon propagation speed, often assumed to be infinite in local network models, is central to our conceptual framework.

Results

Myelin controls axon speed, and the synchrony of impulse traffic between distant cortical regions appears to be critical for optimal mental performance and learning.

Results

Several experiments suggest that axon conduction speed is plastic, thereby altering the regional and global white matter connections that facilitate binding of remote local networks.

Conclusions

Combined EEG and high resolution EEG can provide distinct multi-scale estimates of functional connectivity in both healthy and diseased brains with measures like frequency and phase spectra, covariance, and coherence.

Significance

White matter disease may profoundly disrupt normal EEG coherence patterns, but currently these kinds of studies are rare in scientific labs and essentially missing from clinical environments.

1. Introduction

1.1. Multi-scale structural connectivity

Radiologists use several imaging technologies to diagnose and treat diseases or support basic science. Brain imaging can reveal both structure and function; however, so-called “structural” measures like computed tomography (CT) and magnetic resonance imaging (MRI) may also be viewed as dynamic imaging, that is, imaging on very long time scales–yearly scales in maturating brains and weeks or months in the case of growing tumors. By contrast, intermediate time-scale methods like functional magnetic resonance imaging (fMRI) and positron emission tomography (PET) track brain changes over seconds or minutes. Electroencephalography (EEG) provides complementary information on much faster time scales (milliseconds). In this paper we outline several potential new relationships between large scale structural and functional imaging, the former focused on white matter and the latter employing EEG.

EEG functional connectivity at large scales is believed to be strongly influenced by white matter axons, especially the cortico-cortical axons, which outnumber thalamo-cortical and callosal axons by perhaps 50–1 in humans (Braitenberg, 1978; Katznelson, 1981; Nunez, 1995; Braitenberg and Schüz, 1991); our anatomical focus here is on these cortico-cortical axons. Axon connectivity may be estimated from the injection of tracers transported along cell projections in the living brains of animals (Braitenberg and Schüz, 1991; Kotter, 2007). In humans, structural connectivity is accessible by postmortem examination of dissected tissue (Krieg, 1963, 1973) or noninvasive brain imaging methods like diffusion tensor imaging (DTI). In DTI, MRI is used to measure the preferred direction of water diffusion in each brain voxel, thereby providing estimates of major white matter tracks at the 1 mm scale (Sporns, 2011). This approach is based on the idea that the direction of fastest diffusion indicates voxel fiber orientation, where here the label “fiber” suggests bundles of multiple parallel axons.

While DTI demonstrates impressive technology, it currently falls far short of the resolution required to view most individual axons. Diameter histograms of human white matter axons are peaked in the 1 μm range (Tomasch, 1954; Bishop and Smith, 1964; Blinkov and Glezer, 1968); that is, about 1000 times smaller than the 1 mm resolution of DTI. Human white matter actually contains about 10¹⁰ cortico-cortical axons, that is, one axon for each cortical pyramidal cell (Braitenberg, 1978), far more than the number of tracts revealed by DTI images. Thus comprehensive maps of axon connectivity at multiple mesoscopic and macroscopic scales may be “years away” as argued by Sporns (2011).

1.2. Multi-scale functional connectivity

Measures with much higher temporal resolution than fMRI and PET are obtained with EEG, which operates on millisecond time scales, providing dynamic images faster than the speed of thought. By “images,” we mean multiple spatial–temporal dynamic scalp patterns, including frequency and phase spectra, topographic maps, traveling and standing waves, covariance, and coherence structure, all potentially important brain state-dependent measures of neocortical dynamics, including functional connectivity (Thatcher et al., 1987; Gevins et al., 1994, 1997; Nunez, 1995; Nunez et al., 1997, 1999; Srinivasan, 1999; Barry et al., 2004; Nunez and Srinivasan, 2006a,b; Murias et al., 2007; Jirsa and McIntosh, 2007).

The price paid for EEG's excellent temporal resolution is poor spatial resolution. While MRI and PET provide excellent mm scale spatial resolution, unprocessed scalp potentials (EEG) provide very coarse (e.g., 5–10 cm) spatial resolution. Thus, each scalp electrode records neural source activity averaged over tissue containing something like 100 million neurons. Despite this extreme space averaging, EEG has revealed many robust relationships to behavioral, cognitive, and clinical states in thousands of studies published since Hans Berger's original paper in 1929. Thus far, most of the clinically useful relationships have involved distinct EEG frequency spectra observed in different brain states, the delta, theta, alpha, beta, and gamma oscillations. Here we propose multi-scale coherence structure as a potentially viable new clinical measure.

The broad field of electrophysiology spans about five orders of magnitude of spatial scale as summarized in Table 1, indicating recording of local field potentials (LFP), electrocorticography (ECoG), low (spatial) resolution EEG, and high resolution EEG (HR-EEG) (Nunez et al., 1994; Srinivasan et al., 1998). Also included is magnetoencephalography (MEG), which provides spatial and temporal resolution similar to EEG, but is mainly sensitive to cortical dipole axes parallel to MEG coils, typically sources in cortical folds (Salmelin and Hari, 1994; Srinivasan et al., 2007). The theoretical and experimental bases for the estimated resolutions in Table 1 are reviewed in (Nunez, 1995; Nunez and Srinivasan, 2006a).

Table 1.

Estimated spatial resolution of recorded potentials or magnetic fields generated by cortical sources.

Recording method	Typical spatial resolution (mm)
Microelectrode of radius ξ	⩾ξ
LFP	0.1–1
ECoG	2–5
Intra-skull recording	5–10
Untransformed EEG	50–70
Untransformed MEG	50–70
High resolution EEG	20–30
High resolution MEG	Unknown

HR-EEG methods employ computer algorithms (e.g., Laplacian or dura image) to provide estimates of brain or dura surface potentials at roughly the 2–3 cm scale by employing dense scalp electrode recordings (e.g., 64–256 electrodes) processed with estimated geometric and electrical properties of head tissue. Thus, the effective scale of HR-EEG is intermediate between ECoG and EEG. Since the classical inverse problem, i.e., locating brain sources based only on surface measurements, suffers from notorious (and often understated) non-uniqueness (Nunez and Srinivasan, 2006a), we avoid such methods here. By contrast, the inward continuation solutions of HR-EEG provide “unique” estimates of dura potential distributions, which are independent of assumptions about sources, although accuracy is limited by head model uncertainty, noise, and scalp electrode density.

Fundamental questions about relationships between anatomical and functional connectivity involve the spatial and temporal scales at which such measures are obtained. Here we promote the idea that brains are genuine complex systems; this view, if actually taken seriously, demands a strong emphasis on the multi-scale nature of brain tissue, which is believed responsible for much of its dynamic behavior: spatial–temporal patterns of synaptic action, action potential firing rates, cell assembly formation, dominant frequency bands, coherence structures and so forth, recorded at various spatial scales of electrophysiology summarized in Table 1. Our focus on multiscale neocortical dynamics motivates a close look at ECoG/EEG relationships as well as multiscale scalp measures of functional connectivity estimated with EEG and HR-EEG coherence. Freeman (2003) suggests a colorful metaphor for this complex multimodal, multiscale information transport: the wave packet: an action potential for the 21st century. Traveling wave packets in numerous scientific fields are generally composed of multiple components with a broad range of wavelengths and phase velocities, all contributing to information and/or energy transport.

2. White matter matters

Here we propose close relationships between EEG or HR-EEG functional connectivity measures like narrow band (e.g., 1 Hz) alpha and theta coherence to cortico-cortical axon propagation; such relations may have important implications for diagnosis and treatment of brain diseases. While scalp coherence patterns must be partly determined by the (mostly) myelinated cortico-cortical axons, this does not imply that pairs of cortical locations with high coherence need be directly connected. Rather, cortical coherence structure is part and parcel of the global dynamic system, and changes robustly with behavioral or cognitive tasks. While EEG coherence is not wholly determined by white matter myelination and connection structure, it is expected to be strongly constrained by such properties.

Myelin controls action potential speed, and the synchrony of impulse traffic between distant cortical regions may be critical for optimal mental performance and learning. A broad range of psychiatric disorders, including schizophrenia, chronic depression, bipolar disorder, obsessive–compulsive disorder and posttraumatic stress disorder, has recently been associated with white matter defects, as have neurodevelopmental cognitive and emotional disorders including autism, dyslexia and attention-deficit hyperactivity disorder. The evidence for white matter involvement consists of gene expression studies, several different kinds of brain imaging methods and histological analysis of post mortem tissue.

One of us, Fields (2005, 2008a,b, 2013), has long discussed the possible role of myelin in brain information processing. Myelin insulation in the central nervous system is provided by a class of glial cells called oligodendroglials, which provide a similar function to Schwann cells in the peripheral nervous system. A central dogma of synaptic plasticity during learning is the importance of temporal coincidence of firing among multiple synaptic inputs to any neuron with respect to firing of that postsynaptic neuron. It is generally expected that inputs coincidently active with postsynaptic neuronal firing will form functionally strengthened connections, but inputs that fire non-coincidently will tend to be eliminated. The molecular mechanisms for synaptic plasticity according to coincident firing have been studied extensively; however, the conduction time through axons from presynaptic neurons is rarely considered.

If two presynaptic neurons are located at different distances from the postsynaptic neuron, the synaptic signals will not arrive simultaneously if propagating at the same axon speeds; a similar argument applies to widely separated local networks as in Fig 1. To arrive simultaneously, axon propagation speed must be delayed from the proximal neuron and/or increased in axons from the more distant neuron. If the signals successfully arrive simultaneously, the voltage changes produced by each input will add, creating a larger transmembrane voltage response. A response reaching critical threshold voltage triggers the recipient neuron to fire impulses and initiate molecular events to reinforce those synapses. Millisecond precision is apparently required for the coincident arrival and summation of synaptic signals, because the voltage change produced when a synapse fires lasts only about 2–4 ms. Thus, axonal propagation time appears to be a critical variable in information processing and synaptic function. Considering the many variables affecting propagation delays, genetic instruction alone would seem inadequate to specify the optimal propagation speed in every axon.

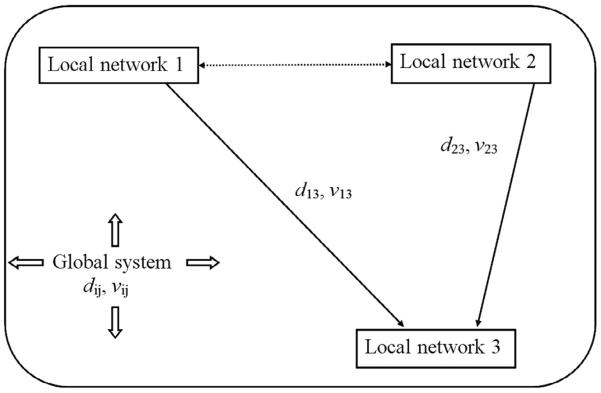
Fig. 1.

Three semi-autonomous local networks are shown here as embedded in a global system of synaptic and action potential fields. “Semi-autonomous” indicates that, to first approximation, each local network is unconnected or only very weakly connected to other networks so as to produce truly “local” oscillation frequencies. By contrast, any introduction of strong functional connections (e.g., the dashed arrow between networks 1 and 2), results in larger scale (regional) networks with new oscillation frequencies. The inputs from networks 1 and 2 to network 3 arrive at approximately the same time only if axon speeds v₁₃, v₂₃ are adjusted to account for different separation distances d₁₃, d₂₃. The global system of white matter axons involves a broad range of interaction distances d_ij and axon speeds v_ij between pairs of cortical locations ij, resulting in global oscillation (resonant) frequencies that can act top-down on local networks, modulating or facilitating local oscillations and providing a global binding mechanism in addition to local/regional binding.

Propagation speed varies widely among different axons, and many axons are slowly conducting and unmyelinated. The human corpus callosum is unmyelinated at birth; about 30% of the fibers remain unmyelinated in adults. The propagation time between hemispheres is about 30 ms through myelinated callosal fibers and 150–300 ms through unmyelinated fibers. Synaptic integration can be expected to be strongly influenced by whether or not intercallosal axons become myelinated. In certain studied neural circuits, transmission speed is adjusted to produce synchronous arrival of synaptic inputs from multiple axons that must travel over different distances to reach the same target (Fields, 2008a,b). Synaptic signals must arrive simultaneously through axons of widely varying path lengths to fire the electric organ of electric fish, for example. This is achieved by higher propagation speeds in axons from motor neurons located farther from the organ, and slower speeds through shorter axons innervating the organ (Fields, 2008a). Similarly, axons from peripheral retinal regions conduct faster than axons from neurons at the center of the retina to assure simultaneous arrival of impulses in the brain (Stanford, 1987). In still another example, experiments in myelin-deficient rats show that myelination is the primary factor producing uniform propagation latency between inferior olive and cerebellar cortex, despite wide variation in axon length (Lang and Rosenbluth, 2003).

3. Local, regional and global networks

Here we adopt a conceptual framework in which brain dynamic behaviors (e.g., EEG oscillations) are generated at multiple spatial scales. We conjecture that large, small, and intermediate (regional) scale “networks” (or more accurately, cell assemblies) continuously form and dissolve on millisecond or so time scales according to the instantaneous strengths of functional connections between subsystems, resulting in a productive synthesis of functional specialization and functional integration. In simple language, different brain areas and different neurons do different things; they are differentiated. At the same time they interact to give rise to a unified consciousness so they are also integrated (Edelman and Tononi, 2000).

To demonstrate this general idea, Fig. 1 shows three semi-autonomous local networks embedded in a global system of synaptic and action potentials, somewhat analogous to social networks embedded in a culture (Nunez and Srinivasan, 2006b). In this case the label “semi-autonomous” indicates that, to first approximation, each local network is disconnected or only weakly connected to other networks so as to produce truly “local” oscillation frequencies. By contrast, strong interactions between local networks result in new, larger scale networks with oscillation frequencies that are generally much different than the original smaller scale frequencies. For example, such generation of new frequencies is expected if the connection between networks 1 and 2 (dashed double arrow) becomes sufficiently strong (Nunez 1995, 2010; Izhikevich, 1999).

The inputs from networks 1 and 2 to network 3 will be “synchronous” (arrive at approximately the same time) only if the separation distances d₁₃, d₂₃ and axon speeds v₁₃, v₂₃ yield nearly identical time delays between local systems, satisfying the condition (Pajevic et al., 2013)

$$\frac{d_{13}}{v_{13}}\approx \frac{d_{23}}{v_{23}}$$ (1)

Thus, synchronous arrival from unequal distances requires modified axon speeds, apparently by myelin plasticity (Fields, 2008a,b, 2013). By contrast, connections in the global system may have arbitrary strengths and a broad range of distances d_ij and axon speeds v_ij between pairs of cortical locations ij. The resulting global oscillation (resonant) frequencies, due mainly to axon delays, can act top-down on local networks (Nunez, 1989, 1995, 2010; Srinivasan et al., 2013; Nunez et al., 2013; Nunez and Srinivasan, 2014), providing a global binding mechanism in addition to local/regional binding. The critical role of myelin in local, regional, and global systems is discussed further in the following sections.

4. Brains exhibit state-dependent functional connections

Human brains are typically viewed as the pre-eminent complex systems with cognition believed to emerge from dynamic interactions within and between brain sub-systems (Ingber, 1982, 1995; Freeman, 1992,a,b, 2003; Ingber and Nunez, 1995; Friston et al., 1995; Haken, 1996, 1999; Tononi and Edelman, 1998; Edelman and Tononi, 2000; Robinson et al., 2004; Buzsaki, 2006; Sporns, 2011; Bassett and Gazzaniga, 2011; Uhlhaas and Singer, 2012). Here we cite two salient anatomical and physiological features that contribute to brain complexity and, by implication, the conditions apparently required for healthy cognition. These features give rise to multi-scale spatial–temporal patterns of brain activity, revealed with imaging techniques like EEG, which are strongly correlated with mental states.

One such salient feature is anatomical and physiological nested hierarchy; cortical anatomy and physiology consist of neurons within minicolumns within modules within macrocolumns (Szentagothai, 1978; Ingber, 1982; Nunez, 1995, 2010; Jirsa and Haken, 1997; Feinberg, 2009, 2012; Fingelkurts et al., 2013). Emergence and complexity generally occur in hierarchically nested physical and biological systems where each higher level of complexity displays novel emergent features based on the levels below it, their interactions, and their interactions with higher levels. Such systems may follow general principles that underlie many complex systems, including anthropology, artificial intelligence, chemistry, economics, meteorology, molecular biology, neuroscience, physics, psychology, and sociology (Ingber, 1985; Scott, 1995; Gell-Mann and Lloyd, 1996; Nunez and Srinivasan, 2006a,b; Edelman and Tononi, 2000; Ingber and Nunez, 2010; Sporns, 2011; Bassett and Gazzaniga, 2011; Pesenson, 2013). While cross-scale interactions are essential to complex system behavior, experimental data are typically limited to relatively narrow (and mostly non-overlapping) ranges of spatial–temporal scales as in the examples of LFP, ECoG, EEG, and HR-EEG summarized in Table 1.

A second salient feature of many complex systems is non-local interactions in which dynamic activity at one location influences distant locations without affecting intermediate regions, as enabled in human brains by long (up to 15–20 cm) cortico-cortical fibers (Krieg, 1963, 1973; Braitenberg, 1978; Braitenberg and Schüz, 1991; Nunez, 1995, 2010, 2011) and in human social systems by modern long distant communications facilitating small world behavior (Bassett and Bullmore, 2009). The label “small world” originates from the purported maximum six steps separating any two persons in the world; small worlds are widely studied in graph theory. “Graph” is mathematician's abstract jargon for network (Watts, 1999); graph theory has found numerous applications in both scientific and non-scientific areas. Roughly speaking, a typical small world graph exhibits high local clustering combined with a much smaller number (but above some critical minimum) of long distant connections.

The high density of short-range (mm scale) intra-cortical connections coupled with an admixture of cortico-cortical axons favors small world behavior. For example, the path length between any pair of neocortical neurons is estimated to be no more than 2 or 3 synaptic connections (Braitenberg, 1978). Small worlds often promote high complexity; they also appear to be abundant in brain structural networks, across systems, scales and species (Sporns, 2011; Bassett and Gazzaniga, 2011). The issue of propagation delays in affecting the timing of synaptic inputs, phase synchrony of local oscillations, and so forth demands study in context cortical information processing (Fields, 2005, 2008a,b, 2013).

5. Synchronized source regions and multi-scale recordings

Our emphasis on the inherent multi-scale nature of complex brains motivates discussion of several experimental implications of this paradigm. In particular, EEG, HR-EEG, and ECoG are selectively sensitive to cortical source regions of different sizes. EEG (scalp) provides “smeared out” (space averaged) representations of ECoG (cortical or dura surface potentials), which enjoys unquestioned ability to provide local detail. Thus, many neuroscientists view ECoG as a “gold standard,” by which to judge EEG accuracy as in the common example of epilepsy patients evaluated for resection surgery.

We mostly agree with this general view when dealing only with localized sources like seizure foci (Niedermeyer and Lopes da Silva, 2005). However, if one actually accepts brains as genuine complex systems, rather than just paying lip service to the idea, a much more nuanced picture emerges, especially in cognitive neuroscience studies and potential new clinical studies in which widely distributed sources could provide essential information. In such cases ECoG can be complementary to EEG, provided such data are accurately interpreted, but it cannot be the final judge of global accuracy.

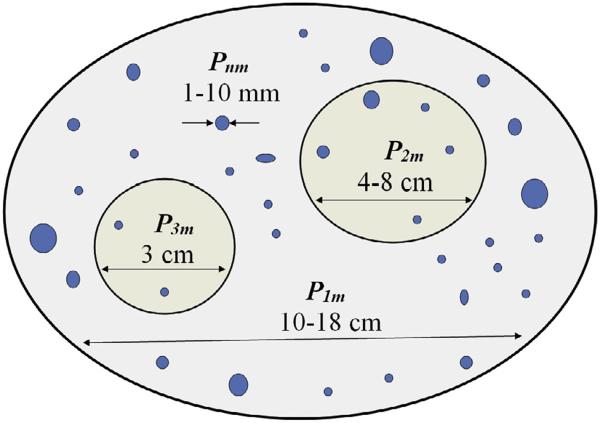
Fig. 2 represents several internally synchronous source regions on an idealized smooth cortical surface. The symbol P_nm(r, t) represents mesoscopic (mm) scale sources, that is, current dipole per unit volume at cortical location and time (r, t); here we include only the surface normal component of this vector. The n subscript indicates source region; the m subscript indicates the individual mm scale sources within that region. The choice of the mm scale to define P_nm(r, t), involving integration over smaller scales, is partly arbitrary, but conveniently related to cortical column depth and macrocolumn scale (Nunez and Srinivasan, 2006a).

Fig. 2.

Internally synchronized cortical source regions are shown for an idealized (unfolded) cortical surface. The P symbols represent meso-scale sources, that is, current dipoles per unit volume (μA/cm²) defined at the mm scale of cortical macrocolumns by integrating over 10¹¹ or so micro-scale synaptic sources in each column (Nunez and Srinivasan, 2006). Meso-scale sources within each region are assumed to oscillate approximately in phase. Source regions may or may not be active at the same time, and they generally oscillate at different frequencies. The illustrated diameters of the synchronous source regions (dipole layers) have the following significance: Region P_1m represents the approximate size of maximum sensitivity of an unprocessed scalp recording. Scalp potentials due to constant magnitude oscillations P will progressively increase with synchronized region size up to this maximum; still larger size increases result in lower scalp potentials. P_2m represents the size of maximum sensitivity of high resolution EEG (Laplacian or dura image). P_3m represents the approximate minimum sized synchronized region that can be recorded on the scalp without averaging (the neurologist's rule of thumb is 6 cm²). In addition the multiple mm scale synchronous regions P_nm shown in blue represent cortical sources that are invisible at the scalp without averaging. Such small scale sources (e.g., local alpha or gamma oscillations) could easily dominate ECoG recordings such that the large scale source regions recorded at the scalp (e.g., global alpha) are strongly suppressed in the ECoG.

Each P_nm(r, t) is generated by 10¹⁰ or so microscopic synaptic current sources active at membrane surfaces together with passive membrane return current. P_nm(r, t) may also be viewed as a kind of “effective” mesoscale transcortical current density, expressed in micro amps/mm². The P_nm(r, t) depend on synaptic strengths, their distribution across cortical depth and internal (e.g., within each macrocolumn) synchrony. In the simple example of Fig. 2, the 3 cm diameter region may then be represented by about 707 meso-scale sources, each occupying 1 mm², that is, P_3m(r, t), m = 1707.

Sources within each synchronized region are assumed in this example to oscillate approximately in phase, but generally with different magnitudes. Different source regions may or may not be active at the same time, and they generally oscillate at different frequencies. We also allow for small source regions embedded in larger regions consistent with the conceptual framework of Fig. 1 and the alpha rhythm studies described in Section 7. The particular synchronous source regions (dipole layers) illustrated in Fig. 2 has the following significance: The large region P_1m(r, t) represents the approximate size of maximum sensitivity of an unprocessed scalp recording. This implies that scalp potentials due to constant magnitude oscillations P_1m(r, t) will progressively increase with synchronized region size up to this maximum (if such region actually forms), but still larger size increases result in lower scalp potentials.

Similarly, P_2m(r, t) represents the size of maximum sensitivity of HR-EEG (Laplacian or dura image). P_3m(r, t) represents the approximate minimum sized synchronized region that can be recorded on the scalp without averaging, consistent with the neurologist's rule of thumb of 6 cm² (Cooper et al., 1965; Delucchi et al., 1975; Pfurtscheller and Cooper, 1975; Nunez, 1995; Ebersole, 1997; Nunez and Srinivasan, 2006a). The close relationship of source synchrony to EEG amplitudes is widely accepted; thus, amplitude reductions are often labeled “desynchronization” (Pfurtscheller and Lopes da Silva, 1999). This can occur because of substantial frequency-specific reductions in synchronized region sizes, or alternately, by synchrony reduction within regions.

The multiple sub-cm scale synchronous regions P_nm(r, t) shown in blue represent cortical sources that remain invisible at the scalp, at least without averaging. Such small scale sources (e.g., local alpha or gamma oscillations) could easily dominate ECoG recordings such that the large scale source regions recorded at the scalp (e.g., global alpha) are not observed in the ECoG. The approximate ratios of cortical to scalp potential magnitude estimated from source models consisting of dipole layers (e.g., spherical caps) in head volume conductor models are P_1m(r, t) (2–5), P_2m(r, t) (5–15), P_3m(r, t) (10–20), P_nm(r, t) (>50–100) (Nunez and Srinivasan, 2006a, see Figs. 1–20, 8–7 and 8–8). These crude estimates assume perfect synchrony within each region; the ratios increase for cases of partial internal synchrony. For example, if only some of the sources P_3m(r, t) in region 3 are synchronous, the resulting ratio of cortical to scalp potential could easily be greater than 50–100.

Our estimated ratios also ignore reference electrode effects, moderate uncertainty in volume conductor models and sources in cortical folds, but the general picture and magnitude estimates outlined here are essentially unaltered by such details. Region 1 with the estimated 2–5 ratio is consistent with typical reports of observed ECoG/EEG amplitude ratios suggesting that scalp EEG is normally generated by very large synchronous dipole layers, often with only minimal or even negligible contributions from small and intermediate sized regions. MEG, on the other hand, largely ignores global activity, focusing on more isolated source regions often in cortical folds (Nunez, 1995; Nunez and Srinivasan, 2006a; Srinivasan et al., 2007). HR-EEG is also able to pick out smaller scale sources by essentially “ignoring” (filtering) the largest scale sources. ECoG is very good at recording mm scale source regions, but may fail to observe very large scale rhythms, at least in the absence of directed attempts to look specifically for global rhythms.

6. Alpha rhythms, local and global

Alpha rhythms (8–13 Hz) provide an appropriate starting point for clinical EEG exams (Klass and Daly, 1979; Niedermeyer and Lopes da Silva, 2005). Some clinical questions are: Does the patient show alpha rhythms with eyes closed, especially over posterior scalp? Are its spatial–temporal characteristics appropriate for the patient's age? How does it react to eyes opening, hyperventilation, drowsiness and so forth? Pathology is often associated with pronounced differences recorded over contralateral hemispheres or with very low alpha frequencies. While some modern neuroscientists have tended to trivialize alpha rhythms as discussed in Nunez and Srinivasan (2006a), extensive ECoG/ EEG studies by pioneers Grey Walter, Wilder Penfield, and Herbert Jasper (circa 1940–1970) showed that the so-called human “alpha rhythm” is actually a very complex process consisting of multiple rhythms, generated at different cortical locations and in different sized synchronized cortical areas, and exhibiting different reactivity to eyes open/closed, motor, and mental activity. Alpha rhythms recorded on the scalp represent only the most synchronized processes over the largest cortical areas, consistent with our analyses of Figs. 2–4 (Jasper and Penfield, 1949; Penfield and Jasper, 1954; Cooper et al., 1965; Delucchi et al., 1975; Nunez, 1995, 2010, 2011; Basar et al., 1997; Ebersole, 1997).

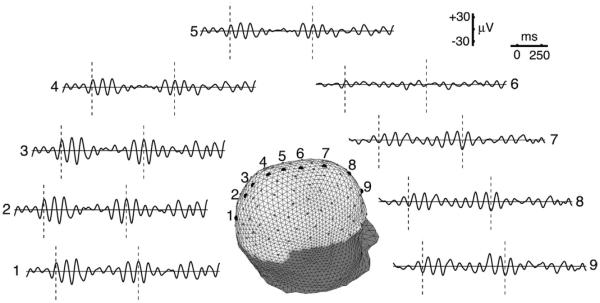
Fig. 4.

High resolution estimates (HR-EEG) of the same EEG data shown in Fig. 3 are obtained by passing the recorded waveforms from 111 sensors (excluding 17 lower edge sites for technical reasons) to the New Orleans spline-Laplacian algorithm that “knows” the basic physics of current spread through brain, skull, and scalp tissue. Nearly identical results are obtained from the independent Melbourne dura imaging algorithm, which unlike the Laplacian, is based on a 3-sphere head model. These two algorithms essentially filter out the very large scale (low spatial frequency) scalp potentials, which consist of some unknown combination of passive current spread and genuine large scale cortical source activity. The largest high resolution signals occur at middle sites 5 and 6 where the unprocessed potentials are smallest. The apparent explanation follows from Fig. 2; high resolution estimates are more sensitive to sources in smaller patches (dipole layers) of cortex. The alpha rhythms apparently have multiple contributions, including a global process (e.g., standing wave) and a local source region near the middle of the electrode array. This local oscillation, called the mu rhythm, is blocked by movement or planned movement because of its proximity to motor cortex. A second local alpha process, blocked by eye opening, was found in occipital cortex (not shown). Reproduced with permission from (Nunez and Srinivasan, 2006).

One human alpha band oscillation, localized in motor cortex and labeled the mu rhythm, is blocked by movement or planned movement (Jasper and Penfield, 1949; Pfurtscheller and Lopes da Silva, 1999). An investigation of inter-hemispheric scalp coherence between the left and right sensorimotor hand areas using HR-EEG (local Laplacian) revealed a superposition of both bilaterally coherent and incoherent rhythmic activities within the alpha band in 10 of 12 subjects (Andrew and Pfurtscheller, 1997; Andrew, 2000). In 3 subjects, the rhythms were clearly separated in frequency. In the remaining 7 subjects, coherent and incoherent frequencies overlapped; however, the two kinds of rhythm were clearly distinguished functionally by their reactivity or non-reactivity to movement and by their inter-hemispheric coherence. Thus, both local and more global alpha rhythms were shown to coexist within the same cortical tissue, consistent with the overlapping source regions shown in Fig. 2. Such distinct alpha rhythms may or may not have overlapping frequency spectra in experimental practice, depending partly on signal stationarity and frequency resolution.

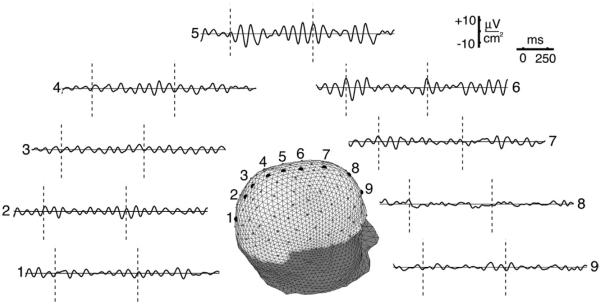
Here we illustrate the local–global alpha distinction with a modern study employing 111 active electrodes out of 128; the lower row of scalp signals was excluded for technical reasons. This subject was very relaxed with closed eyes, a condition that encourages global alpha. The small dots in Fig. 3 show sensor locations on our subject's scalp, and the large dots indicate nine locations along the midline where two seconds of alpha rhythms are displayed (Nunez and Srinivasan, 2006a). We note several classic features this alpha signal: amplitude variations over the two-second period and oscillations with frequency near 10 Hz. Alpha rhythms are clearly evident at all midline sensor locations and nearly all other sensor locations (not shown), suggesting that the alpha sources originate from widespread locations in the cerebral cortex. That is, this alpha appears from this view to be much more of a global than local phenomenon. The dashed vertical lines indicate fixed time slices in Fig. 3, showing that waveforms in anterior (7–9) and posterior (1–3) regions tend to be 180° out of phase. Amplitudes are largest at these same locations and smaller in central sites (4–6). The spatial distribution of alpha rhythm is roughly consistent with a standing wave with a node (point of zero amplitude) near the center of the array, with 1/2 of the wave appearing on the scalp and 1/2 postulated to occupy the mesial cortex.

Fig. 3.

Two seconds of alpha rhythm(s) recorded from 128 electrodes (small dots) is shown at 9 midline locations (large dots). The subject has closed eyes and is very relaxed to enhance global alpha. Potentials were recorded with respect to a fixed reference; then transformed to the common average reference. These rhythms are evident at all mid line sensor locations and nearly all other sensor locations (not shown), suggesting that the alpha sources originate from widespread locations in the cerebral cortex. The dashed vertical lines indicate fixed time slices, showing that waveforms in the front (7–9) and back (1–3) of the head tend to be 180° out of phase. Amplitudes are largest at these same locations and smaller in middle sites (4–6). The spatial distribution of alpha rhythm is approximately that of a standing wave with a node (point of zero amplitude) near the center of the array, with 1/2 of the wave appearing on the scalp and 1/2 postulated to occupy the underside (mesial surface) of cortex. Reproduced with permission from (Nunez and Srinivasan, 2006).

This general picture of global cortical sources is, however, complicated by spatially non-periodic amplitude differences between waveforms recorded at different scalp locations, which do not appear to fit the global standing wave picture. In order to shed more light on the origins, we constructed high resolution estimates (HR-EEG) of this same EEG data. To accomplish this, we passed the recorded waveforms from all 111 chosen electrodes to our high resolution computer algorithm (spline Laplacian) that “knows” much of the physics of current spread through brain, skull, and scalp tissue. The computer algorithm filters out the very large scale (low spatial frequency) scalp potentials, which consist of some (generally) unknown combination of passive current spread and genuine large scale cortical source activity.

The “New Orleans spline Laplacian,” employed here, has been checked with more than a thousand simulations using many localized and distributed source distributions placed in volume conductor models (Nunez et al., 1994, 2001; Srinivasan, 1998). With 131 electrodes, point by point comparison of Laplacian-estimated to calculated dura potential (due to known model sources) typically yields correlation coefficients in the 0.95 range (Wingeier, 2004; Nunez and Srinivasan, 2006a).

This spline Laplacian has also been compared directly to an alternate HR-EEG method called “Melbourne dura imaging,” developed in Australia in the early 1990s by Richard Silberstein and Peter Cadusch. In hundreds of simulations, correlations between these two independent estimates of dura surface potential are also in the 0.95 range when more than about 120 electrodes are employed (Nunez et al., 1994, 2001; Wingeier, 2004; Nunez and Srinivasan, 2006a). The basic independence of these two HR-EEG methods is revealed when fewer electrodes are used; e.g., with 64 electrodes, correlations typically fall into the 0.8–0.85 range.

The HR-EEG obtained from the Fig. 3 data set is shown in Fig. 4. Notably, the largest HR-EEG signals occur at central sites 5 and 6 where the unprocessed potentials are smallest. The apparent explanation is that HR-EEG estimates are more sensitive to sources in smaller patches (dipole layers) of cortex as in the discussion of Fig. 2. The subject's alpha rhythms have multiple contributions, including a global alpha (e.g., standing wave) and a local source region (mu rhythm) near the middle of the electrode array. A similar procedure revealed a local occipital alpha superimposed on the global alpha (Nunez and Srinivasan, 2006a). MEG studies have identified local alpha sources in motor, occipital and parieto-occipital cortex (Salmelin and Hari, 1994), but MEG is insensitive to global fields (Nunez, 1995; Srinivasan et al., 2007). Studies of steady state visually evoked potentials (SSVEP) reveal both local and global alpha resonances in frontal cortex that may be separated in frequency by 1–3 Hz (Srinivasan et al., 2006).

In another study revealing clear distinctions between local and global alpha rhythms, EEG was recorded with 128 electrodes in children aged 6–11 and young adults (Srinivasan, 1999). A high resolution (spline-Laplacian) algorithm was employed to obtain power and coherence estimates at a second scale smaller than the raw EEG, essentially applying a high pass spatial filter to the same data. Power and coherence characterized the spatial structures of the alpha rhythm at the two distinct spatial scales of raw EEG and HR-EEG. In adults, the alpha rhythm was characterized by high coherence between distant electrodes in both measures, that is, a clear indication of global alpha. The children had reduced anterior power and reduced coherence of raw EEG between anterior and posterior electrodes at the peak alpha frequency in comparison to adults. Also, the children's HR-EEG alpha rhythm showed much higher power than adults at both anterior and posterior electrodes, but was weakly correlated across the scalp. In other words, children produced strong local alpha at multiple locations and, at the same time, weak global alpha compared to adults, apparently due to immature cortico-cortical axon myelination.

7. Network oscillations and myelin plasticity

Myelin is critical for sustaining oscillatory neural activity and entrainment between “generators” (e.g., cell assemblies or networks at multiple scales) in brain regions separated by substantial conduction delays. Much brain activity is rhythmic, and interactions between different oscillators appear to be critical for complex information processing. Coordination of electrical activity among large assemblies of widely distributed neurons provides context-dependent binding of neurons into functionally coherent assemblies and selective gating of signals. Over large distances, reciprocal coupling of oscillatory networks requires significant conduction times as indicated in Fig. 1.

Variations in conduction velocity can be detrimental, since the temporal precision needed for the oscillatory coupling and phase-locking increases with oscillation frequency. Recent modeling shows that relatively small changes in conduction delays can have significant effects on the temporal and spatial aspects of neuronal oscillations (Pajevic et al., 2013). Indeed, this modeling suggests that mechanisms to adjust conduction delays seem necessary to prevent destructive interference resulting from changes in frequency or coupling strength between oscillators that are coupled by conduction delays.

Myelin has the largest effect on conduction velocity; thus myelination can also have a strong effect on these oscillatory processes. Changes in myelination during development, as well as research indicating that functional activity can influence myelination, suggest the possibility of conduction velocity plasticity. Evidence for activity-dependent regulation of myelination is rapidly accumulating from cellular, organismal, and human brain imaging studies. Functional activity and action potentials can influence development of myelin sheaths (Fields, 2013 for review) and control of the local synthesis of myelin in distal processes of oligodendrocytes. Activity-dependent glutamate release from axons promotes the formation of a transmembrane signaling complex between oligodendrocytes in contact with axons and stimulates local synthesis of myelin basic protein (Wake et al., 2011). This mechanism is expected to promote preferential myelination of electrically active axons. Human brain imaging shows structural differences in white matter regions after learning (Zatorre et al., 2012), and social isolation in mice can alter myelination of prefrontal cortex with behavioral consequences (Makinodan et al., 2012; Liu et al., 2012).

Postnatal development of coordinated oscillatory activity between prefrontal cortex and hippocampus parallels the postnatal myelination of hippocampus. In humans, myelination of hippocampus begins prenatally, but continues through childhood, based on histological analysis (Abraham et al., 2010), and extends into adulthood as evidenced by MRI (Giedd et al., 1996). The first axons to be myelinated in the hippocampal circuit are the large hippocampal pyramidal cells that project to their respective subcortical and cortical fields. Myelination of the alveus in the human hippocampus is active during the third postnatal month, but the first oligodendrogial cells are not detected in the dentate gyrus until the fifth month of age. GABAergic neurons in the medial septum are putative pacemaker neurons that drive hippocampal network activity. These axons are myelinated, suggesting that appropriate conduction velocity, achieved through myelination, is required for adult-like function of septo-hipppocampal circuitry (Abraham et al., 2010).

Disruption in brain synchronization contributes to dysfunction, for example in autism, by destroying the coherence of brain rhythms and slowing overall cognitive processing speed (Welsh et al., 2005). Thalamocortical dysrhythmia is associated with schizophrenia, obsessive–compulsive disorder, and depressive disorder (Schulman et al., 2011), and the natural oscillation frequencies in prefrontal cortex are slower in individuals with schizophrenia (Ferrarelli et al., 2012). In one recent study, patients with schizophrenia could be discriminated from controls with 90% prediction accuracy by abnormal neural oscillation patterns (Xu et al., 2012) related to lexical processing (Xu et al., 2013). Dyslexic children reportedly show significantly lower power 40 Hz oscillations in processing non-verbal sounds (Ucles et al., 2009). All of these examples demonstrate the importance of synchrony and oscillations in normal brain function.

8. Axon delays predict several large-scale EEG properties

A voluminous EEG literature has long demonstrated robust correlations between the very large scale slow oscillations of EEG and cognitive functions or disease states. Many mathematical models have been advanced over the past 40+ years to explain limited aspects of EEG dynamics, e.g., oscillation frequencies observed at different experimental scales (Nunez, 1995; Nunez and Srinivasan, 2006a,b). Local models (see Fig. 1) treat cortical or thalamo-cortical interactions in which axon propagation speeds are assumed to be infinite as in the classic local model of Wilson and Cowan (1972, 1973) and many more recent variations. The underlying time scales in such models are often PSP rise and decay times, predicting self-sustained (limit cycle) oscillations in local cell assemblies (Srinivasan et al., 2013).

By contrast, global models based on delays in the cortico-cortical axons provide the underlying time scales for dynamic behaviors. The models predict a human global alpha rhythm environment in which many kinds of independent local alpha and other oscillations may be embedded in motor, occipital and other cortical regions, consistent with EEG, HR-EEG, and ECoG data (see Fig. 1). The basic idea behind global models is simple; action potentials at each cortical location generate synaptic action at distant locations after time delays that depend on axon propagation speed and separation distance. These very approximate models, based on integral or integro-differential equations, employ enough genuine physiology and anatomy to provide several qualitative and semi-quantitative connections to (cm scale) EEG, but they cannot predict smaller scale phenomena unless coupled with local theories. (Nunez, 1974, 1989, 1995, 1981, 2000; Katznelson, 1981, 1982; Srinivasan, 1995; Jirsa and Haken, 1997; Nunez et al., 2001; Wingeier, 2004; Nunez and Srinivasan, 2006a,b, 2014; Jirsa, 2009). In one simple one-dimensional model, standing waves of synaptic action density are predicted with resonant frequencies given by

$$f_n=\frac{v}{L}\sqrt{n^2-{\left(\frac{\beta \lambda L}{2\pi }\right)}^2}n=2,3,4,\dots$$ (2)

An apparently realistic example of cortico-cortical parameters is thus: Histograms of white matter axons diameters peak in the 1–1.5 μm range (Tomasch, 1954; Bishop and Smith, 1964; Blinkov and Glezer, 1968), suggesting a range of propagation speeds (Waxman and Bennett, 1972; Swadlow et al., 1978; Nunez, 1995) v ~ 600–900 cm/s. The idealized (exponential) rate of axon number fall-off with cortical separation is assumed to be something like λ ~ 0.1–0.3 cm⁻¹. The chosen neocortical tissue parameters are the anterior–posterior neocortical “circumference” after smoothing out cortical folds L ~ 60–70 cm and the (non dimensional) background “excitability” of neocortex β ~ 1, controlled by neuromodulators on long time scales.

These example parameter values are not known accurately, but appear realistic. Predicted lowest modes are typically in the beta and alpha bands in states with small β; but frequencies are reduced to alpha, theta and delta bands for larger β (Nunez and Srinivasan, 2014). That is, as β increases lower mode frequencies become slower and new higher modes are predicted to appear as in some sleep and anesthesia states. Experimental connections to a dozen or so kinds of EEG experiments include maturation of global alpha due to axon myelination, which increases the propagation speed v in Eq. (2), resulting in higher global frequencies. Other experimental connections are: traveling and standing waves, brain state tuning in sleep and anesthesia, amplitude/frequency relations, brain size relations, and spatial/temporal frequency relations (Nunez, 1995, 2000; Nunez and Srinivasan, 2006a,b, 2014). We do not, however, claim that this global theory based on cortico-cortical axon delays can explain local dynamics (e.g., local alpha, gamma) that may be generated in thalamo-cortical or other local networks (Nunez, 1989; Robinson et al., 2004; Valdés-Hernández et al., 2009; Nunez and Srinivasan, 2014).

When author PLN first proposed this global traveling/standing wave model based on axon propagation delays over 40 years ago (Nunez, 1974, 1989, 1995), all existing neocortical dynamic models were strictly local. In order to keep the mathematics tractable, the model assumes exponential fall-off in the number of cortico-cortical fibers with cortical separation distance, thereby neglecting specificity of connections, e.g., heterogeneous white matter distributions. The model predicts the global oscillations of Eq. (2), where the parameter λ determines the fall-off rate. More recently we have made some initial progress in generalizing this approach to include specific point-to-point connections as shown in Fig. 1 (Nunez and Srinivasan, 2013). Since any distribution of cortico-cortical axons can be expressed as a superposition of point-to-point connections, further generalizations to more realistic distributions can be anticipated, as demonstrated by others (Jirsa, 2009; Pinotsis et al., 2013).

9. Multi-scale EEG coherence

The standard, Fourier transform-based multi-channel signal measure coherence is a squared correlation coefficient expressed as a function of frequency; it can provide robust measures of cognitive state and white matter maturation or disease (Thatcher et al., 1987; Nunez, 1995; Nunez et al., 1997, 1999; Srinivasan et al., 1998; Srinivasan, 1999; Murias et al., 2007). Synchrony (or phase synchrony) of two signals occurs when they retain equal or near equal phases at some frequency over an extended time interval. Coherence is a measure of phase consistency; thus two signals that remain in phase over time (synchronous) must be coherent (coherence equal to one). However, the opposite case need not be true, that is, out-of-phase signals (asynchronous) may or may not maintain a fixed phase relationship; coherence can then be anything between zero and one. Since EEG is generally composed of multiple frequency components, any pair of signals can be synchronous or coherent in some frequency bands and asynchronous or incoherent at other frequencies.

Before the 1990s some EEG scientists and animal physiologists suspected that the observed high alpha scalp coherence (e.g., 0.6–0.9) over large distances (>10–20 cm) did not reflect cortical source coherence, but resulted only from passive current spread (volume conduction). This view was based partly on the fast fall off of coherence (typically over less than 1 cm) recorded from animal cortex with mm scale electrodes (Nunez, 1995). But, this volume conduction interpretation ignores the fact that high human scalp coherence over large distances is mostly confined to narrow frequency bands (often the lower range of alpha frequencies), and volume conduction is essentially independent of EEG frequency. Furthermore, alpha coherence is easily manipulated by eye opening or cognitive tasks having no connection to volume conduction.

This misunderstanding of scalp coherence also involved a failure to appreciate that the dynamic variables that characterize complex systems are generally expected to be scale-sensitive (Ingber, 1982, 1985, 1995; Nunez, 1995, 2010; Nunez et al., 1997, 2001, 2013; Nunez and Srinivasan, 2010, 2013; Sporns, 2011). Thus, cortical coherence patterns estimated with mm scale (mesoscopic) cortical electrodes are not generally expected to mirror (macroscopic) scalp coherence between the same cortical regions as implied by Fig. 2, for example. It has been shown that HR-EEG coherence estimates are typically conservative; that is, they tend to underestimate cortical source coherence by filtering out the very low spatial frequencies, which generally occur from a combination of volume conduction and genuine large scale synchronous source regions (Nunez et al., 1997, 1999; Srinivasan et al., 1998; Nunez and Srinivasan, 2006a). Thus, for example, high EEG coherence over region 1 of Fig. 2 might not be observed with HR-EEG, which is much more effective than EEG at finding coherence relations between region sizes closer to regions 2 and 3. In summary, multi-scale EEG coherence patterns provide distinct and complementary information about functional connectivity.

10. Discussion

If EEG were composed of only globally dominant systems (e.g., linear standing waves) with no active local networks as predicted by basic global models based only on axon delays, coherence between all pairs of cortical locations could be close to one, determined partly by spatial–temporal thalamo-cortical input properties. At the other extreme, a cortex dominated by uncorrelated local networks would exhibit scalp coherence close to zero provided reference and volume conduction distortions were removed. Given that brains are complex systems, we expect that EEG dynamic behavior can approach either of these limiting cases and most everything in between depending on brain state.

We here promote a conceptual framework in which local networks are generally embedded in global fields or “global networks” with state-dependent inter-correlations as depicted in Fig. 1. The local networks can facilitate detailed, state-dependent scalp coherence patterns, revealed at the large, but somewhat distinct scales of EEG and HR-EEG. Thus, for example, EEG or HR-EEG coherence between multiple pairs of scalp locations may increase with cognitive task (mental calculations) in the theta and upper alpha bands while simultaneously falling in the lower alpha band (Wingeier, 2004; Nunez and Srinivasan, 2006a). This outcome is consistent with formation of local theta and alpha “calculation” networks, along with a reduction in global alpha coherence that may or may not occur with amplitude reduction. In other studies, steady state visually evoked potentials (SSVEP) and evoked magnetic fields have been employed to reduce signal to noise ratios and follow narrow band scalp coherence patterns. SSVEP coherence structure has been shown to be reliably correlated with several kinds of mental activity (Silberstein, 1995a,b; Srinivasan et al., 1999, 2007; Silberstein et al., 2003, 2004).

We have proposed several relationships between large (cm) scale structural and functional imaging with implications for new kinds of cognitive and clinical studies. The general importance of white matter to brain science, and cortico-cortical axons in particular, is emphasized in the context of disease states as well as making critical contributions to EEG dynamic properties, especially scalp coherence patterns. The observation that local networks, global systems and intermediate scale (regional) systems exhibit distinct properties emphasizes the importance of multi-scale coherence measures. To approach this goal, we suggest that combined EEG and HR-EEG can provide complementary coherence estimates that are maximally sensitive to large (~5–10 cm) and intermediate (~2–3 cm) spatial scale source regions, respectively. Such two-scale coherence patterns can then provide distinct estimates of global versus more local processes. It is to be expected that white matter disease profoundly disrupts such coherence patterns, but thus far these kinds of studies are rare in the scientific world, and essentially non-existent in clinical environments. Perhaps this may change in the not too distant future.

We conclude with a general speculation concerning evolutionary influences on brain dynamic behaviors that lead to healthy consciousness. Our conceptual framework embraces the idea of local and regional networks embedded in global brain environments of synaptic and action potentials. We have also argued that synchrony of impulse traffic between distant cortical regions is required for optimal mental performance. If these two ideas are conjoined, we are motivated to speculate on the role of natural selection in shaping modern brains. Healthy brains seem to require that local, regional, and global time scales evolve to become “compatible,” in the sense of satisfying the basic synchrony requirement. The apparent implication is that boundary conditions (e.g., brain size and other large scale properties) provide critical influences on small scales, e.g., neuron thresholds, columnar connection patterns, myelination, and so forth. We might label this evolutionary process, “top-down, multi-scale neocortical dynamic plasticity driven by natural selection.” In simpler language, a healthy consciousness seems to require matching dynamical properties across spatial scales; failure to maintain such match may result in mental illness or even the entire absence of conscious awareness. Additional discussions of closely related issues include (Silberstein, 1995b; Nunez, 2010; Feinberg, 2012; Uhlhaas and Singer, 2012; Nunez et al., 2013; Fingelkurts et al., 2013; Buzsáki et al., 2013).

HIGHLIGHTS.

• Many brain diseases are associated with white matter defects.

• Axon conduction speed is plastic, determined largely by myelination.

• EEG and high resolution EEG provide complementary measures of functional connectivity.