Analysis of recurrent events with an associated informative dropout time: Application of the joint frailty model

Abstract

This paper considers the analysis of a repeat event outcome in clinical trials of chronic diseases in the context of dependent censoring (e.g. mortality). It has particular application in the context of recurrent heart failure hospitalisations in trials of heart failure. Semi‐parametric joint frailty models (JFMs) simultaneously analyse recurrent heart failure hospitalisations and time to cardiovascular death, estimating distinct hazard ratios whilst individual‐specific latent variables induce associations between the two processes. A simulation study was carried out to assess the suitability of the JFM versus marginal analyses of recurrent events and cardiovascular death using standard methods. Hazard ratios were consistently overestimated when marginal models were used, whilst the JFM produced good, well‐estimated results. An application to the Candesartan in Heart failure: Assessment of Reduction in Mortality and morbidity programme was considered. The JFM gave unbiased estimates of treatment effects in the presence of dependent censoring. We advocate the use of the JFM for future trials that consider recurrent events as the primary outcome. © 2016 The Authors. Statistics in Medicine Published by John Wiley & Sons Ltd.

1. Introduction

This work is motivated by the need for more appropriate methods of statistical analysis in clinical trials with recurrent event data such as asthma attacks, cancer recurrences and heart failure hospitalisations, which we will consider here. Typically, in clinical trials for heart failure, composite outcomes (e.g. heart failure hospitalisation or cardiovascular (CV) death) are adopted as the primary endpoint as they combine fatal and non‐fatal events, which increases the event rate and avoids multiplicity issues 1. However, composite endpoints that only consider the first event are suboptimal for a chronic disease such as heart failure, which is characterised by recurrent heart failure hospitalisations, because repeat events within individuals are ignored in analyses 2. Recurrent hospitalisations are also an indication of worsening condition, and so by ignoring these repeat events, we do not assess the true burden of the disease.

Methods for the analysis of recurrent events include the Poisson, negative binomial, Andersen–Gill and Wei‐Lin‐Weissfeld (WLW) approaches 3, 4, 5. The Poisson model is a commonly misused approach to determine if rates of an event differ between two treatment groups 6. The Poisson distribution assumes that the underlying event rate is the same in all subjects (and follows a Poisson process). This does not hold in the case of heart failure hospitalisations, where the observed distribution of the number of events is markedly more skew than the Poisson distribution. In heart failure, some patients are inherently more/less frail than others, subsequently presenting with increased/fewer hospitalisations, respectively. If this overdispersion is ignored, standard errors are likely to be too small resulting in confidence intervals that are too narrow and an increase in the type I error rate. An alternative approach is to use the negative binomial distribution, which induces an association between repeat events within individuals through a random effect term, which is assumed to follow a gamma distribution 7. The negative binomial assumes individual‐specific Poisson event rates conditional on a random effect for each patient's true underlying rate. Alternatively, the Andersen–Gill model analyses gap times (i.e. the times between consecutive events) and is an extension of the Cox proportional‐hazards model 8. In the Cox proportional‐hazards model, each individual's time to event contributes to the partial likelihood, but in the Andersen‐Gill model, each gap time contributes independently. The WLW method, in contrast, considers each ordered event in turn as the outcome in a sequence of applications of the Cox proportional‐hazards model 9. The distinctive feature of the WLW model is that each individual's time at risk for each event (i.e. first, second, third event etc.) is considered to start at randomisation, so full randomised treatment groups are compared. So in the case of heart failure hospitalisations, time to first hospitalisation would be analysed, and then total time to second hospitalisation would be analysed separately, including everyone randomised, even if they hadn't yet had a first hospitalisation. Analysis continues in this manner giving distinct estimated hazard ratios for each ordered hospitalisation. Both the Andersen–Gill and WLW methods assume independence of events, but hospitalisations within individuals are likely to be related to each other, and so robust standard errors can be used to accommodate heterogeneity 10.

A key characteristic of heart failure is that an increase in hospitalisations for worsening condition is associated with an increased risk of CV death, and so any censoring due to CV death is not independent of the recurrent event process 11. It is important that any analyses focussing on recurrent heart failure hospitalisations account for the competing risk of CV death. Methods for handling competing risks in the analysis of time‐to‐event data are well established 12, but these methods do not take into account recurrent events of the same type within individuals. The Poisson, negative binomial, Andersen–Gill and WLW methods do not, in general, incorporate competing risks into the analysis of recurrent events. One simple strategy for incorporating CV death into analyses of recurrent heart failure hospitalisations is to consider this outcome as an additional event in the recurrent event process 4. That is, one considers a composite of recurrent heart failure hospitalisations and CV death. This updated recurrent event process can then be analysed using the Poisson, negative binomial, Andersen–Gill and WLW models as before. Alternatively, the Ghosh and Lin non‐parametric method analyses recurrent events whilst allowing for mortality as informative censoring 13. This method allows non‐parametric inferences for a mean function in one‐sample and two‐sample settings, producing only log‐rank P‐values and not estimating the treatment effect. Alternatively, the Ghosh and Lin semi‐parametric method considers regression models, which specify multiplicative covariate effects on the mean function allowing for an estimated treatment effect in analyses 14.

A joint frailty model (JFM) simultaneously analyses recurrent events and an associated time to event whilst taking into account the relationship between the two processes and is the focus of this article 15. In the analysis of heart failure hospitalisations and CV death, this method allows simultaneous estimation of the effect of treatment on both recurrent heart failure hospitalisations and mortality, under the assumption that the two processes are independent of one another after conditioning on an individual specific random effect term.

This paper specifically examines the use of the JFM in the analysis of recurrent heart failure hospitalisations in the presence of the competing risk of CV death. A simulation study assesses its suitability as compared with the marginal analysis of time to CV death using the Cox proportional‐hazards model and the WLW and Ghosh and Lin semi‐parametric models for the marginal analyses of the recurrent events, ignoring and incorporating competing risks, respectively. Following this, the methods are applied to two clinical trials in heart failure: Candesartan in Heart failure: Assessment of Reduction in Mortality and morbidity (CHARM)‐Added and CHARM‐Alternative.

2. Data

The CHARM programme comprised three component arms, each considering distinct but complementary populations 16. Here, we study two such components, CHARM‐Added and CHARM‐Alternative trials, which randomised patients with reduced ejection fraction on or not on angiotensin‐converting enzyme (ACE) inhibitors, respectively, to candesartan versus placebo 17, 18. CHARM‐Preserved is not considered here as this trial considered patients presenting with milder heart failure. Table 1 summarises the key outcomes for the CHARM‐Added and CHARM‐Alternative trials. CHARM‐Added followed 2548 patients for a median follow‐up of 41 months, and CHARM‐Alternative enrolled 2028 patients followed for a median of 33.7 months. There were 649 and 471 CV deaths in CHARM‐Added and in CHARM‐Alternative, respectively. In CHARM‐Added, 703 patients presented with a total of 1402 heart failure hospitalisations, of which 699 (49.9%) were repeats. There were 500 patients in CHARM‐Alternative with at least one heart failure hospitalisation, and there were 1001 hospitalisations in total, with 501 (50.0%) being repeats.

Table 1.

Summary of key outcomes for CHARM‐Added and CHARM‐Alternative.^∗Composite of first investigator reported HF hospitalisation or CV death.

	CHARM‐Added		CHARM‐Alternative
	Placebo	Candesartan	Placebo	Candesartan
Randomised	1272	1276	1015	1013
Total follow‐up (years)	3713	3848	2584	2660
All cause deaths	412	377	296	265
CV deaths	347	302	252	219
Unadjudicated composite∗	561	497	412	340
$\ge$ 1 HFH	380	323	289	211
$\ge$ 2 HFH	187	131	126	94
Number of HFHs:
1	193	192	163	117
2	91	74	58	45
3	37	24	29	21
4	21	14	16	9
5	19	8	8	10
6	6	4	7	3
7	5	3	2	2
8	3	2	3	3
9	1	0	1	0
10	1	2	2	1
11	2	0	0	0
12	1	0	0	0
Total HFH	813	589	579	422

CHARM: Candesartan in Heart failure: Assessment of Reduction in Mortality and morbidity.

The pre‐defined primary endpoint for both trials was the composite of first heart failure hospitalisation and CV death. This composite endpoint was analysed as time to first event using the Cox proportional‐hazards model. As this primary analysis considered only the first hospitalisation for worsening heart failure, only first hospitalisations were adjudicated by an independent clinical‐event committee, and any repeats within individuals remained unadjudicated. Hence, to ensure a fair comparison between methodologies, the primary analysis was repeated using the investigator reported first heart failure hospitalisations for each patient.

3. Modelling strategies

3.1. Marginal models for recurrent and terminal events

We began the simulation study by considering the composite endpoint of first heart failure hospitalisation and CV death as this remains a common practice in the analysis of heart failure trials. We analysed the time to the composite endpoint using the Cox proportional‐hazards model 19. This model was also used to marginally analyse time to CV death. Under this model, the hazard function for individual i = 1,…,n is given, in general, by the following:

$${\lambda }_i\left(t\right)=\exp \left\{\beta z_i\right\}{\lambda }_0\left(t\right),$$

where λ ₀(t) is the baseline hazard function, z _i denotes treatment allocation (z _i=1 for active treatment and z _i=0 for control) and β is the associated regression coefficient. The associated hazard ratios are given by H R _COMP= exp{β _COMP} and H R _CPH= exp{β _CPH} for the composite endpoint and CV death, respectively.

The composite of recurrent heart failure hospitalisations and CV death was analysed using the WLW model, and the Ghosh and Lin semi‐parametric model was used to analyse the recurrent heart failure hospitalisations adjusted for mortality. The WLW model is an elaboration of the Cox proportional‐hazards model that allows recurrent time to event outcomes to be analysed 9. This model limits analysis to the first K events (either heart failure hospitalisations or CV death) within each patient, and each event is used as the outcome in a distinct application of the Cox proportional‐hazards model:

$${\lambda }_{\mathrm{ik}}\left(t\right)=\exp \left\{{\beta }_k{z}_i\right\}{\lambda }_{0k}\left(t\right),k=1,\dots ,K.$$

The hazard for individual i allocated to treatment z _i of event k at time t is given by λ _ik(t). The total number of events per person that are included in the analyses, K, is typically chosen such that β _k can be estimated with a useful degree of precision. The WLW model also estimates the ‘average effect’ of treatment on recurrent heart failure hospitalisations and CV death, β which can be calculated as a weighted average of ${\widehat{\beta }}_k$, the weighting aimed at ensuring the minimum variance for the estimate. This method assumes that all heart failure hospitalisations are independent, which is unrealistic as hospitalisations within the same individual are likely to be related to each other. Furthermore, data of this sort are likely to be heterogeneous, with some patients being inherently more/less frail than others, subsequently presenting with increased/fewer hospitalisations, respectively. Robust standard errors are used to allow for this dependency and heterogeneity. The average hazard ratio is then given by H R _WLW= exp{β _WLW}. The unique feature of the WLW model is that for each of the K heart failure hospitalisations, each individual's time at risk for that particular hospitalisation is assumed to commence at the time of randomisation for that patient. So this means that as soon as a patient is randomised, they are included in the risk sets for all hospitalisations.

The Ghosh and Lin semi‐parametric method considers the marginal expected number of recurrent heart failure hospitalisations up to some particular time, t, acknowledging the fact that death is a terminal event after which no further recurrent hospitalisations can be experienced 14. This means that although a patient stays in the risk set beyond time to death, their associated recurrent hospitalisation count stays constant, fixed at whatever value it was just prior to death. Let $N_i^{\ast }\left(t\right)$ be the number of heart failure hospitalisations over the time interval [0,t] for individual i and let D _i be the time of death, so that $N_i^{\ast }\left(t\right)$ does not jump after D _i. Treatment is assumed to have a multiplicative effect on the baseline mean function, whilst the stochastic structure of the recurrent hospitalisations process is left completely unspecified. This means that there are no restrictions on the nature of dependence amongst repeat heart failure hospitalisations within an individual or between hospitalisations and death. Define the marginal expected number of recurrent heart failure hospitalisations for person i up to t, associated with z _i and which acknowledges that no further recurrences occur after death as ${\mu }_i\left(t\right)=\mathbb{E}\left\{N_i^{\ast }\right(t)\mid z_i\}$, which can be formulated through the semi‐parametric model:

$${\mu }_i\left(t\right)=\exp \left\{\beta z_i\right\}{\mu }_0\left(t\right),$$

where μ ₀(t) is an unspecified continuous function. This model assumes time‐invariance of the treatment effect, and the hazard ratio is given by H R _GL= exp{β _GL}.

3.2. Joint frailty model

The JFM is a semi‐parametric model that accounts for the dependence between recurrent heart failure hospitalisations and death through a patient‐specific frailty term 15. This analyses the recurrent heart failure hospitalisations and times to CV death simultaneously with a latent variable (frailty) inducing an association between the two event processes. Recall that the Ghosh and Lin approach treats death as a terminating event, meaning that patients who have died remain in the risk set for future heart failure hospitalisations with their count remaining constant. Care needs to be taken with this method therefore, as an increase in the mortality rate will consequently result in a decrease in the expected number of heart failure hospitalisations for an individual. This model reflects the fact that one way in which treatment may reduce the number of hospitalisations is by increasing the mortality rate. Thus, if a treatment decreases both the heart failure hospitalisation rate and the mortality rate, estimated treatment effects for the hospitalisation rates may be attenuated under the Ghosh and Lin model. Conversely, the JFM treats CV death as a competing risk with patients then being censored from further repeat heart failure hospitalisations. Hospitalisations that patients would have experienced had they not died are treated as missing data, and the JFM captures this ‘lost information’ in the estimation of underlying event rates and treatment effects. The JFM takes into account the increased risk of CV death because of recurrent heart failure hospitalisations and also takes into account the competing risk of death when considering the recurrent event process, but assumes that the two outcomes are independent of each other conditional on the frailty term. Any non‐CV deaths are handled as non‐informative censoring.

Define T _i0=0 and let $T_{i1},T_{i2},\dots ,T_{i{N}_i}$ be the recurrent event times for person i, where N _i is the number of recurrent events before X _i=min(C _i,D _i), the minimum of an independent censoring time C _i and a dependent CV death time D _i. The JFM is defined through the hazard functions for the recurrent event process and CV death:

$$\begin{array}{cc}{r}_i(t\mid {\omega }_i)& ={\omega }_i\exp \left\{{\beta }_1{z}_i\right\}{r}_0\left(t\right)={\omega }_i{r}_i\left(t\right)\\ {\lambda }_i(t\mid {\omega }_i)& ={\omega }_i^{\alpha }\exp \left\{{\beta }_2{z}_i\right\}{\lambda }_0\left(t\right)={\omega }_i^{\alpha }{\lambda }_i\left(t\right).\end{array}$$

The recurrent heart failure hospitalisations hazard function for the ith patient conditional on the patient‐specific random frailty, ω _i, is given by r _i and is proportional to the baseline intensity function, r ₀. The conditional hazard function for time to CV death for patient i is given by, λ _i, with the baseline hazard given by λ ₀, and β ₁, β ₂ are the regression coefficients associated with treatment covariate z _i. Patient‐specific independent random effects are denoted by ω _i and are most commonly and conveniently assumed to follow a gamma distribution with mean 1 and variance θ. The correlation of the recurrent events is quantified by θ, with higher values corresponding to greater within‐patient correlation and also greater between‐patient variability. The parameter α determines the relationship between the recurrent heart failure hospitalisations and time to CV death. When α < 0, higher frailty will result in a greater risk of recurrence and lower risk of terminal event (i.e. a negative correlation between the frailties), and when α > 0, higher frailty will result in a greater risk of recurrence and is associated with a higher risk of CV death (i.e. a positive correlation between the frailties). When α = 1, the impact of frailty is identical on recurrent and terminating events, and α = 0 means that the recurrent event process is independent of CV death, and the two outcomes can be analysed separately.

Let t _ij and x _i be the observed recurrent event times and follow‐up, respectively. Denote by δ _ij and Δ_i, the indicator of the recurrent event at time t _ij and the indicator of CV death at time x _i, respectively. The likelihood for person i is then given by the following:

$$L_i=\underset{{\omega }_i}{\int }\prod _{j=1}^{N_i}{\left[{\omega }_i{r}_i\left(t_{\mathrm{ij}}\right)\right]}^{{\delta }_{\mathrm{ij}}}\exp \left\{\underset{0}{\overset{x_i}{\int }}{\omega }_i{r}_i\left(t\right)\mathrm{dt}\right\}{\left[\underset{i}{\overset{\alpha }{\omega }}{\lambda }_i\left(x_i\right)\right]}^{{\mathrm{\Delta }}_i}\exp \left\{\underset{0}{\overset{x_i}{\int }}\underset{i}{\overset{\alpha }{\omega }}{\lambda }_i\left(t\right)\mathrm{dt}\right\}{f}_{\theta }\left({\omega }_i\right)d{\omega }_i.$$

Adopting piecewise constant hazards for the recurrent events and CV death allows estimation of the likelihood by Gaussian quadrature 20. The implementation of Gaussian quadrature techniques is incorporated into Proc NLMIXED of SAS 9.1 21. The joint model gives two distinct hazard ratios: H R _JFM1= exp{β ₁} is the hazard ratio associated with the effect of treatment on the recurrent event rate, and H R _JFM2= exp{β ₂} is the terminal event hazard ratio.

4. Simulation study

Various data scenarios were used to evaluate the power and estimated treatment effects using the modelling strategies described in the previous section. Heart failure hospitalisation rates and CV death rates for a simulated cohort were generated with parameters comparable with those observed in the COMPANION and CUPID Phase II heart failure studies 22, 23. Data sets were simulated with 300 subjects in each group and varied frailty variance, θ, (1–3.5), frailty exponent, α(0–3), recurrent (0.9–1.2) and terminal (25–31%) annual event rates around expected values, as well as sensible treatment effect sizes (0.67–0.75). The rate of independent censoring, θ _C, was set at 5%. Greater frailty variance, θ, corresponds to stronger correlation between recurrent event gap times and larger between subjects variation with respect to event recurrences and terminal events. Zero variance corresponds to independent recurrent events.

Subjects assigned to treatment group with probability 0.5 and different distributions for ω _i were considered: ω _i∼gamma(θ, θ) and log(ω _i)∼Normal(0, θ). Time to independent censoring, time to terminal event and recurrent event gap times were generated using an exponential distribution with rate parameters 1/λ _C, 1/λ _i(t∣ω _i) and 1/r _i(t∣ω _i), respectively, where the parameter λ _C was assumed to be independent of the recurrent heart failure hospitalisations. The parameter λ _i(t∣ω _i) was based on the simulation parameters: λ ₀(t), H R _λ (terminal event hazard ratio), generated frailty, ω _i, and frailty exponent, α. If either the censoring or terminal time was greater than some specified maximum follow‐up time, t _MAX, the subject was considered censored at t _MAX.

The parameter r _i(t∣ω _i) was based on the simulation parameters: r ₀(t), H R _r (recurrent event hazard ratio) and generated frailty, ω _i. Recurrent event gap times were added to the previous event time (or 0 if no previous event) to arrive at the current event time. Generation of recurrent event times for a given subject continued until the time of censoring, or time of CV death (whichever is sooner) was exceeded. If a recurrent event time was equal to the CV death time, the time was assigned to CV death. For each simulation run, defined by a unique combination of parameter values, there were 500 simulated data sets. Mean estimated hazard ratios were calculated over all 500 runs, and power was calculated as the proportion of runs for which the estimated hazard ratio significantly differed from 1 with significance level 0.05.

Table 2 presents the treatment effect estimates (hazard ratios) for the composite endpoint, heart failure hospitalisations and CV death using simulation run data generated with a gamma frailty. For recurrent hospitalisations, marginal (WLW and Ghosh and Lin semi‐parametric) and JFMs are compared, which are in turn compared with the results arising from the analysis of the composite of first heart failure hospitalisation and CV death. While for CV death, the JFM is compared with the traditional Cox proportional‐hazards model. When α = 0 (indicating that recurrent and terminal events are independent), the Cox model and JFM produced identical estimates as expected, and so results for this data scenario are not presented in Table 2. The difference in hazard ratios for CV death, estimated under the different modelling strategies, increased substantially with α becoming larger. When α = 3(meaning that the two frailties are positively correlated) and the hazard ratio for CV death was H R _λ=0.67, we see that the hazard ratio estimates from the traditional Cox proportional hazards model were in the range 0.84–0.91, whereas for the JFM, the estimates remained within 0.66–0.69. When the correlation between recurrent and terminal events was strong, the proportional hazards assumption in the traditional Cox model was substantially violated, and the respective estimated hazard ratios were biased. When α = 0.5, however, the correlation between recurrent and terminal events was much weaker, and the bias in the estimates obtained from the Cox proportional‐hazards model decreased substantially.

Table 2.

Simulation results, values are estimated hazard ratio (percentage power). H R _COMP: hazard ratio from the Cox proportional‐hazards model for the composite of first heart failure hospitalisation and cardiovascular death. H R _WLW, H R _GL, H R _JFM1: hazard ratios from WLW, Ghosh and Lin and joint frailty models respectively for recurrent heart failure hospitalisations. H R _CPH, H R _JFM2: hazard ratios from Cox proportional‐hazards and joint frailty models respectively for time to cardiovascular death. θ, α, r ₀, λ ₀, λ _C: frailty variance, frailty exponent, baseline annual recurrent event rate, baseline annual terminal event rate and annual independent censoring rate respectively.

Simulation parameters							Composite	Recurrent events			Terminal event
θ	α	r 0	λ 0	λ C	H R r	H R λ	H R COMP	H R WLW	H R GL	HRJFM1	H R CPH	HRJFM2
3.5	3	0.9	31%	5%	0.67	0.67	0.87 (23)	0.87 (35)	0.76 (49)	0.68 (53)	0.91 (8)	0.68 (12)
3.5	3	1.2	31%	5%	0.67	0.67	0.87 (26)	0.87 (38)	0.76 (53)	0.70 (48)	0.91 (8)	0.69 (10)
3.5	1	0.9	31%	5%	0.67	0.67	0.84 (29)	0.83 (46)	0.81 (28)	0.69 (54)	0.79 (36)	0.66 (44)
3.5	1	1.2	31%	5%	0.67	0.67	0.84 (33)	0.83 (50)	0.81 (32)	0.69 (55)	0.77 (37)	0.65 (39)
3.5	0.5	0.9	31%	5%	0.67	0.67	0.81 (40)	0.80 (62)	0.79 (35)	0.71 (52)	0.72 (54)	0.67 (57)
3.5	0.5	1.2	31%	5%	0.67	0.67	0.82 (40)	0.80 (67)	0.79 (37)	0.71 (53)	0.71 (55)	0.67 (58)
1.45	3	0.9	25%	5%	0.67	0.67	0.80 (52)	0.83 (62)	0.72 (73)	0.68 (77)	0.86 (15)	0.67 (16)
1.45	3	1.2	31%	5%	0.67	0.67	0.82 (48)	0.85 (62)	0.73 (81)	0.67 (83)	0.86 (15)	0.66 (17)
1.45	1	0.9	25%	5%	0.67	0.67	0.77 (66)	0.77 (80)	0.72 (69)	0.68 (80)	0.71 (50)	0.66 (50)
1.45	1	1.2	31%	5%	0.67	0.67	0.80 (63)	0.82 (85)	0.76 (77)	0.70 (87)	0.72 (54)	0.65 (56)
1.45	0.5	0.9	25%	5%	0.67	0.67	0.76 (68)	0.76 (88)	0.71 (72)	0.69 (77)	0.68 (57)	0.67 (58)
1.45	0.5	1.2	31%	5%	0.67	0.67	0.77 (72)	0.80 (92)	0.72 (75)	0.69 (84)	0.68 (66)	0.67 (67)
1	3	1.2	31%	5%	0.67	0.67	0.79 (69)	0.83 (74)	0.72 (88)	0.67 (91)	0.84 (23)	0.66 (23)
1	3	1.2	31%	5%	0.67	0.75	0.79 (64)	0.83 (74)	0.70 (91)	0.67 (91)	0.88 (14)	0.75 (14)
1	1	1.2	31%	5%	0.67	0.67	0.76 (77)	0.78 (93)	0.72 (85)	0.68 (91)	0.71 (58)	0.67 (57)
1	1	1.2	31%	5%	0.67	0.75	0.77 (70)	0.80 (90)	0.70 (89)	0.68 (90)	0.78 (37)	0.75 (35)
1	0.5	1.2	31%	5%	0.67	0.67	0.75 (83)	0.77 (95)	0.70 (88)	0.68 (93)	0.68 (67)	0.66 (68)
1	0.5	1.2	31%	5%	0.67	0.75	0.76 (77)	0.79 (92)	0.70 (88)	0.68 (92)	0.76 (42)	0.75 (42)

The hazard ratios for the recurrent heart failure hospitalisations were also very well estimated by the JFM, while they are notably overestimated (attenuated to the null) when marginal models were used. Each of the estimated treatment effects, however, did demonstrate a directionally similar effect, which would make them useful as sensitivity analyses. Looking at the marginal models for recurrent events, the Ghosh and Lin semi‐parametric model performed better than the WLW and composite endpoint analyses. Interestingly, the Cox proportional‐hazards model and the WLW performed very similarly in terms of bias but, unsurprisingly, the WLW displayed greater power. The impact of frailty on power can also be seen in Table 2. Larger values of frailty variance, θ, correspond to greater within‐patient correlation (and greater between‐patient variability) which resulted in lower power in all of the models considered. Strong correlations between recurrent hospitalisations within individuals meant that the amount of information contributed by an additional event for a particular patient was reduced, leading to lower power. Note that these scenarios were powered for recurrent events and not mortality.

The JFM was also found to be robust to mis‐specification of the frailty distribution, with good agreement between the simulation parameters and subsequent estimates when the data were generated with a log‐Normal frailty and analysed using a gamma distribution (results not shown).

5. Application

The primary endpoint in the CHARM‐Added and CHARM‐Alternative trials was the composite of first heart failure hospitalisation and CV death, analysed as time to first event using the Cox proportional‐hazards model 17, 18. Using the investigator reported heart failure hospitalisations, for CHARM‐Added, there were 561 and 497 patients with the primary endpoint in the placebo and candesartan groups respectively, yielding a hazard ratio of 0.833 (95% confidence interval (CI) 0.74‐0.94, P=0.003) and 412 versus 340 patients in the placebo and candesartan groups respectively in CHARM‐Alternative, with an estimated hazard ratio of 0.772 (95% CI 0.67‐0.89, P=0.0004).

The Ghosh and Lin non‐parametric estimates of the cumulative incidence of heart failure hospitalisations per 100 patients, allowing for mortality, for CHARM‐Added and CHARM‐Alternative are shown in Figure 1. Both plots show immediate separation of the two treatment group curves with the candesartan group having consistently fewer hospitalisations than the placebo group. For CHARM‐Added, there appears to be continuous divergence of the two curves whereas for CHARM‐Alternative, there appears to be more rapid divergence for the first year, which then slows beyond that. As the Ghosh and Lin semi‐parametric model was found to be less biased than the WLW in the simulation study, results from analyses of CHARM‐Added and CHARM‐Alternative using this model are in Table 3 alongside results from the JFM. Both analyses estimated a highly statistically significant reduction in the hazard for hospitalisation for worsening heart failure because of candesartan. A comparatively attenuated non‐significant reduction in the hazard for CV death was also observed.

Figure 1.

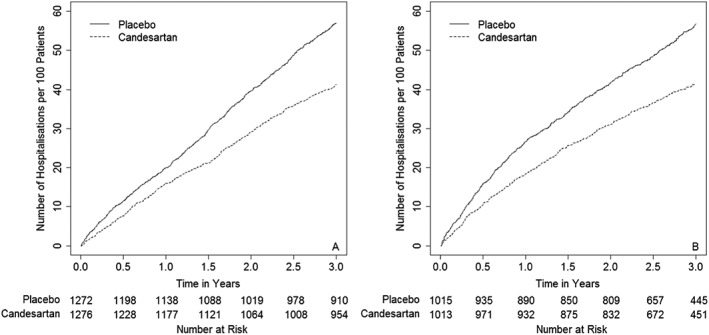
Ghosh and Lin cumulative incidence per 100 patients for recurrent heart failure hospitalisations for A: Candesartan in Heart failure: Assessment of Reduction in Mortality and morbidity (CHARM)‐Added and B: CHARM‐Alternative.

Table 3.

Results from application to CHARM‐Added and CHARM‐Alternative. H R _GL, H R _JFM1: hazard ratios from Ghosh and Lin and joint frailty models respectively for recurrent heart failure hospitalisations. H R _CPH, H R _JFM2: hazard ratios from Cox proportional‐hazards and joint frailty models respectively for time to CV death. θ, α: frailty variance and frailty exponent respectively.

	CHARM‐Added			CHARM‐Alternative
	Estimate	95% CI	P‐value	Estimate	95% CI	P‐value
H R GL	0.683	0.57‐0.82	<0.0001	0.687	0.55‐0.86	0.0008
H R JFM1	0.650	0.53‐0.80	<0.0001	0.608	0.49‐0.76	<0.0001
H R CPH	0.842	0.72‐0.98	0.029	0.847	0.71‐1.02	0.072
H R JFM2	0.839	0.70‐1.01	0.065	0.851	0.68‐1.07	0.172
θ (SE)	3.751 (0.208)			3.452 (0.207)
α (SE)	0.688 (0.054)			0.846 (0.069)

CHARM, Candesartan in Heart failure: Assessment of Reduction in Mortality and morbidity.

A small difference in estimates was observed when using the Ghosh and Lin semi‐parametric model as compared with the JFM. In this application, however, the observed bias in using the marginal model compared with the JFM was not so severe that conclusions about the treatment effects would be misleading. The marginal analysis of CV death using the Cox proportional‐hazards model gave estimates that were in line with the JFM. The Kaplan–Meier curves for time to CV death for CHARM‐Added and CHARM‐Alternative can be seen in Figure 2. Those treated with candesartan consistently have fewer CV deaths than those in the placebo group. For CHARM‐Added, the survival curves appear to be similar for the first 6 months with continued separation thereafter, and for CHARM‐Alternative, there is a more marked difference for the first 18 months, after which the curves converge slightly. The reason for this agreement could possibly be that there was only a modest, non‐significant treatment difference for CV death. Also, note the small estimated value of α, and recall that in the simulation study, it was observed that estimate hazard ratios were generally in agreement amongst the marginal and JFMs for α = 0.5.

Figure 2.

Kaplan–Meier curves for time to cardiovascular (CV)‐Death for A: Candesartan in Heart failure: Assessment of Reduction in Mortality and morbidity (CHARM)‐Added, and B: CHARM‐Alternative.

Overall, estimates of hazard ratios for recurrent heart failure hospitalisations and hazard ratios for CV death were very similar between CHARM‐Added and CHARM‐Alternative. For patients with reduced ejection fraction on or not on ACE inhibitors (CHARM‐Added and CHARM‐Alternative respectively), treatment with candesartan reduced the rate of recurrent hospitalisations by 35% and 39%, respectively, and reduced the hazard for CV death by 16% and 15%, respectively. Estimates of the frailty variance, θ, were large in each of the analyses, suggesting high levels of within‐subject correlation for recurrent events and substantial heterogeneity in between‐subject heart failure hospitalisation hazards.

6. Discussion

The JFM provides good reproducible treatment effect estimates for various data scenarios when recurrent and terminal events are correlated. Bias in estimated treatment effects through the use of marginal models in the presence of correlation between recurrent and terminal events have been clearly observed and was found to increase with stronger correlations.

The frailty model is different from the marginal models, and the proportionality assumption generally cannot hold for both frailty and marginal models at the same time. When recurrent and terminal events are not independent (i.e. α ≠ 0) and when between‐patient effects are accounted for by a multiplicative frailty, the proportional hazards assumption is violated and so hazard ratios from the marginal model may be substantially biased. The stronger the correlation between recurrent and terminal events, the larger the difference between estimated treatment effects from the marginal and frailty models. The interpretation of treatment effects under the marginal and frailty model are different, and so estimated regression coefficients may be substantially different too.

The estimated hazard ratios for recurrent events from the Ghosh and Lin semi‐parametric model, which accounted for the competing risk of CV death, agreed better with those from the JFM than estimates from the WLW approach. Overestimates of the treatment effect under this model were likely due to the differences in the model interpretations (marginal versus frailty models). In general, the Ghosh and Lin model provides a marginal estimate of the treatment effect for recurrent events that is adjusted by the presence of a terminal event, but does not explicitly estimate the effect of treatment on the hazard of the terminal event. If interest lies in the effect of treatment on both recurrent and terminal events, the JFM would clearly be more suitable.

Justification for the use of the WLW model in the analysis of recurrent events is driven by the fact that treatment effect estimates are based upon comparisons of the complete treatment groups for each ordered event in turn as all randomised patients are included in the risk set for each distinct event 24. Application of the WLW method is also recommended as the nature of the relationship between recurrent events needs not be known, but this failure to model within‐patient associations results in inefficiencies in estimates of treatment effects. Further criticisms of the WLW model are that this approach includes patients in the risk set for the kth event who might not necessarily have presented with the k − 1th event, thus ignoring the ordered nature of events. Additionally, the treatment effect of the kth event will carry through to subsequent events, thus influencing estimates of treatment effects on later events. Also, note that in order to obtain an overall estimate of treatment effect when using the WLW method, a weighted average of the individual estimated hazard ratios must be calculated, and it is unclear as to how this ‘average effect’ should be interpreted.

This article considered a derivation of the JFM that depended on a single covariate: treatment effect. This model can easily be extended to consider a vector of covariates by considering the following hazard functions for the recurrent event process and CV death:

$$\begin{array}{cc}{r}_i(t\mid {\omega }_i)& ={\omega }_i\exp \left\{\underset{1}{\overset{\prime }{\mathit{\beta }}}{\mathbf{Z}}_i\right\}{r}_0\left(t\right)={\omega }_i{r}_i\left(t\right)\\ {\lambda }_i(t\mid {\omega }_i)& ={\omega }_i^{\alpha }\exp \left\{\underset{2}{\overset{\prime }{\mathit{\beta }}}{\mathbf{Z}}_i\right\}{\lambda }_0\left(t\right)={\omega }_i^{\alpha }{\lambda }_i\left(t\right),\end{array}$$

where β ₁, β ₂ are p × 1 vectors of regression coefficients associated with vectors of covariates Z ₁ and Z ₂, respectively. Additionally, the formulation of the JFM presented in this article considered a single frailty term, θ, with the effect of this frailty on the two processes being allowed to differ through the use of α. Alternatively, each of the two event processes could be specified with their own random effects with a covariance allowed between the two. An example of a suitable distribution is the Wicksell–Kibble bivariate gamma, which allows specification of marginal gamma distributions which are correlated 25.

We note that although the JFM provides good reproducible estimates of the treatment effect, formal examination of the goodness of fit between expected and observed values has not been examined here. This would not be a straightforward task given the presence of dependent censoring and would be an interesting area for further research.

One of the treatment effects estimated in the semi‐parametric JFM is the hazard ratio for recurrent events. In the case of heart failure hospitalisations, this can be interpreted as an increase/decrease in the instantaneous probability of an event recurrence at a particular point in time, subject to a patient's past event history. Alternatively, parametric formulations of the JFM consider the effect of treatment on an individual's recurrent event rate, that is the ratio of rates of heart failure hospitalisations 4, 26. These rate ratios for recurrent events have a more clinically intuitive interpretation than a hazard ratio for a repeat event.

In conclusion, we intend that the analyses and results presented here indicate a way forward for trials of chronic diseases that are characterised by recurrent events in the presence of dependent censoring. We encourage further case studies considering the application of the JFM, so that in due course, these methods become a routinely accepted key component in the analysis and reporting of trials of chronic diseases. What matters is that trials of chronic diseases that are characterised by recurrent events stop giving priority to inefficient methods (composite endpoints that only consider time to first event) and make better use of the totality of evidence whilst accounting for competing risks that may also be present.

Rogers, J. K. , Yaroshinsky, A. , Pocock, S. J. , Stokar, D. , and Pogoda, J. (2016) Analysis of recurrent events with an associated informative dropout time: Application of the joint frailty model. Statist. Med., 35: 2195–2205. doi: 10.1002/sim.6853.