A K-fold Averaging Cross-validation Procedure

Abstract

Cross-validation type of methods have been widely used to facilitate model estimation and variable selection. In this work, we suggest a new K-fold cross validation procedure to select a candidate ‘optimal’ model from each hold-out fold and average the K candidate ‘optimal’ models to obtain the ultimate model. Due to the averaging effect, the variance of the proposed estimates can be significantly reduced. This new procedure results in more stable and efficient parameter estimation than the classical K-fold cross validation procedure. In addition, we show the asymptotic equivalence between the proposed and classical cross validation procedures in the linear regression setting. We also demonstrate the broad applicability of the proposed procedure via two examples of parameter sparsity regularization and quantile smoothing splines modeling. We illustrate the promise of the proposed method through simulations and a real data example.

1 Introduction

Cross-validation (CV) has been widely used for model selection in regression problems. Its theoretical properties and empirical performance have been extensively discussed in the literature including the pioneering work of Stone (1974, 1977) and Geisser (1975). Burman (1989) studied the properties of leave-one-out CV and K-fold CV procedures. Shao (1993) and Rao and Wu (2005) provided theoretical insights and asymptotic theories of model selection with a fixed number of variables for linear models. Wong (1983) examined consistency of CV in kernel nonparametric regression. Zhang (1993) showed superiority of leave-K-out CV over leave-one-out CV in linear regression. Kohavi (1995) assessed the performance in terms of model estimation and variable selection at various values of K₁ and K₂ respectively in K₁-fold CV and leave-K₂-out CV. For robust model selection, Ronchetti et al. (1997) suggested a robust loss function to measure the prediction error. Substantial practical and theoretical results of traditional and newer CV approaches were summarized in a review paper by Arlot and Celisse (2010).

In a typical K-fold CV procedure for a linear model, the data set is randomly and evenly split into K parts (if possible). A candidate model is built based on K − 1 parts of the data set, called a training set. Prediction accuracy of this candidate model is then evaluated on a test set containing the data in the hold-out part. By respectively using each of the K parts as the test set and repeating the model building and evaluation procedure, we choose the model with the smallest cross-validation score (typically, the mean squared prediction error MSPE) as the ‘optimal’ model. Given p independent variables, there are in total of 2^p − 1 possible models. In the K-fold CV procedure, each model is in fact evaluated K times. Therefore, a single ‘optimal’ model is selected via K(2^p − 1) times of model evaluation.

In this work, we propose a new cross-validation procedure with the core idea of first choosing K candidate ‘optimal’ models to build the ultimate model. On each training set, the 2^p − 1 models are fitted and the candidate ‘optimal’ model is selected with the smallest cross-validation score obtained from the corresponding test set. This procedure is repeated on K training and test sets to obtain K candidate ‘optimal’ models. At last, the ultimate model is obtained with its parameter estimates as the average values across K candidate ‘optimal’ models. Therefore, we call the proposed method K-fold averaging cross-validation (ACV). Due to the averaging effect, efficiency of the final parameter estimates obtained by ACV improves over that of the traditional K-fold CV. We note that parameter estimates of CV and ACV are identical when all the candidate ‘optimal’ models from ACV are identical to the model selected by the traditional CV.

The proposed ACV procedure is also applicable to high dimensional data to determine the amount of penalty imposed by a regularization method, e.g., LASSO (Tibshirani; 1996). In fact, the ACV procedure has broad applications as CV to problems wherein regularization parameters associated with a penalization method need to be determined. This will be demonstrated via an application to smoothing spline based nonparametric modeling (Nychka et al.; 1995).

The paper is organized as follows. We describe the explicit expression of the ACV estimator and its asymptotic property in linear regression models in Section 2. We discuss the connection and distinction between ACV and CV in the applications of LASSO and smoothing spline based modeling in Section 3. We illustrate the proposed method through simulation studies in Section 4 and through application to a real data set in Section 5. And we provide some concluding remarks in Section 6.

2 K-fold averaging cross-validation in a linear model

2.1 Basic setting

Consider a linear model

$$\mathbf{Y}=\mathbf{X}\beta +∊,$$

where Y = (y₁, …, y_n)′ is the response vector, X = {x_ij} is an n × p design matrix for the full model, and ∊ = (∊₁, …, ∊_n)′ is a vector of iid random variables with mean 0 and variance σ². We assume that p is fixed. All the observations are divided into K parts such that every part is mutually exclusive. Throughout this paper, we assume that K is finite and fixed. In this paper, we consider deterministic predictors, but when X is random, the results are valid almost surely if the two assumptions in Section 2.3 and the assumption on ∊ are satisfied almost surely for given X.

We use n_k to denote the sample size in the k^th fold, where ${\sum }_{k=1}^K{n}_k=n$. We define M_k as the selected model based on the k^th hold-out fold (test set), and let its corresponding design matrix be X_k with all observations. We further assume that X_k is full rank for any k.

When the k^th fold is a test set, a design matrix in the k^th fold is defined as X_nk, and the design matrix of the corresponding training set is denoted as X_−nk. Y_k and Y_−k are the response observations corresponding to X_nk and X_−nk, respectively.

The choice of a candidate ‘optimal’ model is made based on the mean squared prediction error in the hold-out fold. The M_k can be represented as a subset of {1, …, p}. Let |M_k| be the number of elements (or, equivalently the number of independent variables) in M_k. Further, let X_MK,−nk be the design matrix composed of variables of M_k in the training set which has a size of n − n_k by |M_k|. And we denote β˜_k as an estimator of β with M_k. For example, the β˜_k obtained from the least squares method can be expressed as ${({\mathbf{X}}_k^{\prime }{\mathbf{X}}_k)}^{-1}{\mathbf{X}}_k^{\prime }\mathbf{Y}$, which is a length-|M_k| vector.

Since the β˜_ks are averaged over k to obtain the ultimate parameter estimates, we need to ensure that each of them is of length p. For this purpose, we introduce the transformation matrix T_k, which is of size p × |M_k|. Each column vector of T_k is composed of a 1 and (p − 1) 0s. For example, if x₂ and x₄ are selected and p = 6, then M_k = {2,4}, and T_k contains two column vectors of (0, 1, 0, 0, 0, 0)′ and (0, 0, 0, 1, 0, 0)′, where the position of 1 in the i^th column is specified in the i^th element of M_k, and the variables not contained in M_k are indexed as 0. As a result, the size of β˜_k is changed to p via multiplying by T_k. Going back to the example, β˜_k = (1,2)′ yields T_kβ˜_k = (0, 1, 0, 2, 0, 0)′. And T_k also indicates the selected model with XT_k = X_k.

To measure the discrepancy between the observations and the predicted values, we use a squared error loss. The MSPE evaluated with the data Y_k can be written as

$${\mathit{\text{MSPE}}}_k=\frac{1}{n_k}{({\mathbf{Y}}_k-{\mathbf{X}}_{n_k}{\widehat{\beta }}_{-n_k})}^{\prime }({\mathbf{Y}}_k-{\mathbf{X}}_{n_k}{\widehat{\beta }}_{-n_k}),$$ (1)

where the least squares estimate ${\widehat{\beta }}_{-n_k}={\mathbf{T}}_k{({\mathbf{X}}_{M_k,-n_k}^{\prime }{\mathbf{X}}_{M_k,-n_k})}^{-1}{\mathbf{X}}_{M_k,-n_k}^{\prime }{\mathbf{Y}}_{-k}$. Note that β̂_−nk depends on the variables contained in M_k. Because β̂_−nk is not our final estimator, convergence of (1) to 0 does not necessarily deduce consistency of the estimator defined in (2); whereas it does in the method of leave-n_k-out cross-validation described in Zhang (1993) and Shao (1993). Rather, we choose M_k or equivalently X_k by minimizing (1), and use it to construct the ultimate estimator. The explicit form of the proposed parameter estimator based on the least squares method is provided below.

2.2 A new estimator

In the traditional K-fold CV, a selected model is what produces smallest prediction error where the number of predicted values is the same as sample size. That is, K-fold CV selects a model which minimizes ${\sum }_{k=1}^K{\mathit{\text{MSPE}}}_k/K$.

The fundamental distinction of our method is to choose a candidate ‘optimal’ model X_k based on the hold-out fold, and then iterate this procedure for k = 1, …, K. Note that the model selection at each iteration provides an opportunity to choose different (up to K) plausible models, which is not the case in K-fold CV. At last, the K candidate ‘optimal’ models are averaged to yield an ultimate model.

The regression coefficient estimator of the model optimally chosen by the k^th fold is

$${\widehat{\beta }}_k={\mathbf{T}}_k{({\mathbf{X}}_k^{\prime }{\mathbf{X}}_k)}^{-1}{\mathbf{X}}_k^{\prime }\mathbf{Y},$$

where X_k is an n × | M_k| design matrix containing all the n values of the explanatory variables in M_k selected by the k^th fold according to (1). Note again that T_k is the transformation matrix to ensure the length of β̂_k to be p. Then, the ultimate estimator of the regression coefficients in the K-fold ACV procedure is defined as

$${\widehat{\beta }}_{\mathit{\text{ACV}}}=\frac{1}{K}\sum _{k=1}^K{\widehat{\beta }}_k=\frac{1}{K}\sum _{k=1}^K{\mathbf{T}}_k{({\mathbf{X}}_k^{\prime }{\mathbf{X}}_k)}^{-1}{\mathbf{X}}_k^{\prime }\mathbf{Y},$$ (2)

Accordingly, the fitted value of Y by ACV is

$${\widehat{\mathbf{Y}}}_{\mathit{\text{ACV}}}=\mathbf{X}{\widehat{\beta }}_{\mathit{\text{ACV}}}=\frac{1}{K}\sum _{k=1}^K{\mathbf{X}}_k{({\mathbf{X}}_k^{\prime }{\mathbf{X}}_k)}^{-1}{\mathbf{X}}_k^{\prime }\mathbf{Y}={\mathbf{H}}_{\mathit{\text{ACV}}}\mathbf{Y}.$$

Let ${\mathbf{P}}_k={\mathbf{X}}_k{({\mathbf{X}}_k^{\prime }{\mathbf{X}}_k)}^{-1}{\mathbf{X}}_k^{\prime }$, then ${\mathbf{H}}_{\mathit{\text{ACV}}}={\sum }_{k=1}^K{\mathbf{P}}_k/K$. Since X is deterministic predictors, we have,

$$\begin{array}{c}E(\mathbf{X}{\widehat{\beta }}_{\mathit{\text{ACV}}})={\mathbf{H}}_{\mathit{\text{ACV}}}E(\mathbf{Y})={\mathbf{H}}_{\mathit{\text{ACV}}}\mathbf{X}\beta ,\hfill \\ \mathit{Var}(\mathbf{X}{\widehat{\beta }}_{\mathit{\text{ACV}}})=\mathit{Var}({\mathbf{H}}_{\mathit{\text{ACV}}}\mathbf{Y})={\mathbf{H}}_{\mathit{\text{ACV}}}^{\prime }{\mathbf{H}}_{\mathit{\text{ACV}}}{\sigma }^2.\hfill \end{array}$$ (3)

Although each P_k is a projection matrix, H_ACV is not a projection matrix in general. This implies that β̂_ACV is likely a biased estimator (Hoaglin and Welsch; 1978). However, efficiency of the estimator can be substantially gained from averaging. To account for variability induced by randomly splitting the data, we repeat the splitting step several times in both CV and ACV procedures. Alternatively, we can use a balanced split. Note that there are n!/(n₁!n₂!⋯n_K!) different ways of splitting data. Then, all observations have equal probability of being included in the training set and in the test set, thus there is no random variation arises from the splitting. In practice, the random variation from the split is ignorable, and only a few times of splitting observed to be enough in the simulation studies.

Connection with Bagging

The bootstrap aggregating approach (Bagging) suggested by Breiman (1996) is similar to our proposed method in terms of the repeated parameter estimation and variable selection steps. The Bagging procedure first generates a sample of size n. Based on the generated sample, it performs model selection according to a criterion such as K-fold CV and obtains the least squares estimator, ${\widehat{\beta }}_1^{\mathit{\text{Bagging}}}$. After repeating this process B times, $({\widehat{\beta }}_1^{\mathit{\text{Bagging}}},\dots ,{\widehat{\beta }}_B^{\mathit{\text{Bagging}}})$ are obtained and averaged to form a final estimate. The distinction is that Bagging procedure requires generating bootstrap samples from the original data set, while the proposed ACV always use original data set and average only ‘optimal’ models obtained from each hold-out fold to form a final model.

Connection with BMA

The ACV method also shares some similarity with Bayesian model averaging (BMA) (Raftery et al.; 1997) where the posterior distribution of β given data D is

$$\mathit{\text{Pr}}(\beta |D)=\sum _{\upsilon =1}^V\mathit{\text{Pr}}(\beta |M_{\upsilon },D)\mathit{\text{Pr}}(M_{\upsilon }|D),$$

where V = 2^p − 1. This is a weighted average of the posterior distribution of β, wherein the weight corresponds to the posterior model probabilities. Based on this formulation, we can view ACV as a special case of BMA by setting Pr(M_υ|D) = 1/K if M_υ ∈{M₁, …, M_K} and Pr(M_υ|D) = 0 otherwise. Thus, we average those ‘optimally’ selected models based on the MSPE_k defined in (1) with the equal weight, instead of averaging across all 2^p − 1 possible models as in BMA. In fact, ACV can be modified to obtain the similar form of BMA. We define ${\widehat{\beta }}_k^{\mathit{\text{FMA}}}={\sum }_{\upsilon =1}^V{w}_{k,\upsilon }{\widehat{\beta }}_{k,\upsilon }$, where β̂_k,υ is the estimate of the υ^th model and its corresponding weight is w_k,υ. Because we concern finding the smallest MSPE_k among 2^p − 1 possible ones using data in the k^th hold-out fold, we use the MSPE_k values from the υ^th model, MSPE_k,υ, to estimate w_k,υ. For example, we can use $w_{k,\upsilon }=1/\sqrt{{\mathit{\text{MSPE}}}_{k,\upsilon }}$ that is normalized to sum up to 1. Hence, we can build a new version of model averaging as $1/K{\sum }_{k=1}^K{\widehat{\beta }}_k^{\mathit{\text{FMA}}}$. The properties of this model averaging method will not be pursued in this work.

Remark: The ACV procedure can be integrated with robust model estimation. For example, instead of the mean one may consider using a component-wise median estimation among the candidate models. M-estimator (Huber and Ronchetti; 2009) or other types of robust estimators can also be used.

2.3 Theoretical Properties

We denote the true model as M_*. A model M can be classified into two categories (Shao; 1993):

• Category I: M ⊇ M_*

• Category II: At least one component of M_* is not contained in M.

Now, we introduce the following assumptions:

Assumption A. n/n_k → K for all k = 1, …, K.

Assumption B. For M_k in Category II,

$$\underset{n\to \infty }{lim\; inf}{n}^{-1}{\beta }^{\prime }{\mathbf{X}}^{\prime }({\mathbf{I}}_n-{\mathbf{P}}_k)\mathbf{X}\beta =b_k>0,\text{and}{n}^{-1}{\beta }^{\prime }{\mathbf{X}}^{\prime }{\mathbf{P}}_k\mathbf{X}\beta \to 0.$$

Assumption B is adopted from Zhang (1993). Notice that b_k is non-zero when M_k is in Category II, but becomes zero when M_k is in category I.

We define the mean squared error (MSE) of ACV as

$${\mathit{\text{MSE}}}_{\mathit{\text{ACV}}}=\frac{1}{n}E({(\mathbf{X}\beta -\mathbf{X}{\widehat{\beta }}_{\mathit{\text{ACV}}})}^{\prime }(\mathbf{X}\beta -\mathbf{X}{\widehat{\beta }}_{\mathit{\text{ACV}}})).$$ (4)

Note that MSE_ACV is defined based on the ultimate parameter estimates and uses all the explanatory variables, which is different from MSPE_k used to select the candidate ‘optimal’ model in the hold-out fold k. Using (3), (4) is expressed as

$${\mathit{\text{MSE}}}_{\mathit{\text{ACV}}}=\frac{1}{n}\mathit{\text{tr}}(\mathit{Var}(\mathbf{X}{\widehat{\beta }}_{\mathit{\text{ACV}}}))+\frac{1}{n}{\Vert E(\mathbf{X}{\widehat{\beta }}_{\mathit{\text{ACV}}}-\mathbf{X}\beta )\Vert }^2=\frac{1}{n}\mathit{\text{tr}}({\mathbf{H}}_{\mathit{\text{ACV}}}^{\prime }{\mathbf{H}}_{\mathit{\text{ACV}}}){\sigma }^2+\frac{1}{n}{\beta }^{\prime }{\mathbf{X}}^{\prime }{({\mathbf{I}}_n-{\mathbf{H}}_{\mathit{\text{ACV}}})}^{\prime }({\mathbf{I}}_n-{\mathbf{H}}_{\mathit{\text{ACV}}})\mathbf{X}\beta ,$$ (5)

where I_n is an identity matrix of size n, and tr(·) is a trace.

Now, let the model chosen by the traditional K-fold CV as X_o. Then, the MSE of the traditional K-fold CV (MSE_CV) is obtained by replacing H_ACV with the projection matrix of X_o.

$${\mathit{\text{MSE}}}_{\mathit{\text{CV}}}=\frac{d}{n}{\sigma }^2+\frac{1}{n}{\beta }^{\prime }{\mathbf{X}}^{\prime }({\mathbf{I}}_n-{\mathbf{P}}_{\mathit{\text{CV}}})\mathbf{X}\beta ,$$ (6)

where d = tr(P_CV) ≤ p and ${\mathbf{P}}_{\mathit{\text{CV}}}={\mathbf{X}}_o{({\mathbf{X}}_o^{\prime }{\mathbf{X}}_o)}^{-1}{\mathbf{X}}_o^{\prime }$. Then, it is readily seen that ${\mathit{\text{MSE}}}_{\mathit{\text{CV}}}=\frac{d}{n}{\sigma }^2=O(n^{-1})$ when X_o is in Category I, since the second term on the right-hand side (RHS) of equation (6) is 0. When X_o is in Category II, MSE_CV is dominated by $\frac{1}{n}{\beta }^{\prime }{\mathbf{X}}^{\prime }({\mathbf{I}}_n-{\mathbf{P}}_{\mathit{\text{CV}}})\mathbf{X}\beta$, which is greater than 0 by Assumption B.

In Theorem 1, we show that the two estimates chosen by CV and ACV are asymptotically equivalent as the sample size increases.

Theorem 1

Let $M_f={\cup }_{k=1}^K{M}_k$ be a union of M_k for k = 1, …, K. Under Assumptions A and B,

1. MSE_ACV = MSE_CV + O(n⁻¹) if M_f and X_o are in Category I.

2. MSE_ACV = MSE_CV + o(1) if M_f and X₀ are in Category II.

Note that the rate of decrease in both MSE_ACV and MSE_CV is subject to inclusion of the true model. This implies that inclusion of the true model will determine the asymptotic behavior of ACV and CV, even though the two sets of parameter estimates are asymptotically equivalent.

Remark: Some existing work use a slightly different but more realistic definition of MSE, since β is unknown in practice, which can be written as ${\mathit{\text{MSE}}}_{\mathit{\text{ACV}}}=\frac{1}{n}E({(\mathbf{Y}-\mathbf{X}{\widehat{\beta }}_{\mathit{\text{ACV}}})}^{\prime }(\mathbf{Y}-\mathbf{X}{\widehat{\beta }}_{\mathit{\text{ACV}}}))$ and ${\mathit{\text{MSE}}}_{\mathit{\text{CV}}}=\frac{1}{n}E({(\mathbf{Y}-\mathbf{X}{\widehat{\beta }}_{\mathit{\text{CV}}})}^{\prime }(\mathbf{Y}-\mathbf{X}{\widehat{\beta }}_{\mathit{\text{CV}}}))$ Using this definition, we can derive the same asymptotic equivalence of β̂_ACV and β̂_CV.

Now, we show the reduced variance of β̂_ACV under the finite sample.

Lemma 1

Under the setting in Section 2.1, we have

$$det(\mathit{var}({\widehat{\beta }}_{\mathit{\text{ACV}}}))=det(\mathit{var}(\frac{1}{K}\sum _{k=1}^K{\widehat{\beta }}_k))\le det(\mathit{var}({\widehat{\beta }}_{\mathit{\text{CV}}})).$$

The inequality holds when β̂_ks are all identical.

This implies that the variance of β̂_ACV is smaller than β̂_CV (as $\sqrt{det(A_k)}$ measures the volume of A_k) due to the averaging effect except for the case when β̂_ks are all identical. Under our empirical experiments in Section 4, the magnitude of the reduced variance tends to be larger than the allowed bias, thus results in more accurate model selection by ACV. This indicates the proposed method could take advantage of bias-variance tradeoff.

3 Integration of ACV with other methods

Lasso penalization

we introduce some applications of ACV beyond the traditional linear regression problem with a fairly small p as discussed in Section 2. When the number of variables p is large, it is impractical to fit all 2^p − 1 models. Rather, we use a penalization method such as LASSO (Tibshirani; 1996), which is widely used for handling high-dimensional data. Such penalization methods convert a model selection problem to controlling the amount of regularization applied to the parameter estimates. Specifically, LASSO is defined as

$${\widehat{\beta }}^{\mathit{\text{LASSO}}}(\lambda )=arg\underset{\beta \in {\mathbb{R}}^p}{min}({\Vert \mathbf{Y}-\mathbf{X}\beta \Vert }^2+\lambda \sum _{j=1}^p|{\beta }_j|).$$

Because λ takes a real number in [0, ∞), we cannot consider all the possible models. We examine some candidate values of λ in a reasonable range. With K-fold CV, a λ̂_CV that produces the smallest cross validated score is claimed as ‘optimal.’

In this case, ACV intends to select K candidate ‘optimal’ values of λ̂_k based on the cross-validated score from hold-out fold k = 1, …, K. Let ${\widehat{\beta }}_{-n_k}^{\mathit{\text{LASSO}}}(\lambda )$ be a LASSO estimate that is obtained based on all the samples excluding the ones in the k^th fold. The ultimate estimate of λ follows as ${\widehat{\lambda }}_{\mathit{\text{ACV}}}=\frac{1}{K}{\sum }_{k=1}^K{\widehat{\lambda }}_k$, where

$${\widehat{\lambda }}_k=arg\underset{\lambda \in [0,\infty )}{min}(\frac{1}{n_k}{\Vert {\mathbf{Y}}_k-{\mathbf{X}}_{n_k}{\widehat{\beta }}_{-n_k}^{\mathit{\text{LASSO}}}(\lambda )\Vert }^2).$$

Such way of averaging enables obtaining a more stable estimate of the penalization parameter. Because the possible number of λ values is infinite, a manageable solution is to use several values of λ on a discrete grid for assessment. Note that λ̂_ACV is likely to be more accurate than the estimate of CV using the same grid, due to the averaging effect of ACV.

Moreover, the computational efficiency of ACV is similar to CV. In both the methods, the major computation comes from estimating model with the (K − 1) folds of training data and from evaluating the performance with the hold-out fold. For ACV, the additional steps of choosing K candidate ‘optimal’ values and averaging could significantly improve the performance at trivial additional computation cost. We make comparisons between β̂^LASSO(λ̂_CV) and β̂^LASSC(λ̂_ACV) via simulation studies that will be described later.

Quantile smoothing splines

The cross-validation method is also frequently used in many different versions of smoothing splines to control the amount of roughness of the fitted function. Quantile smoothing splines are developed for targeting conditional quantiles in a nonparametric fashion. There are several different definitions of such smoothing splines; we use the method proposed by Bloomfield and Steiger (1983) and Nychka et al. (1995). Basically, a quantile smoothing spline is taken as the minimizer of

$$\frac{1}{n}\sum _{i=1}^n{\rho }_q(y_i-g(x_i))+\lambda \int {\{g^{″}(x)\}}^2\mathit{\text{dx}},$$

where ρ_q(u) = u{q − I(u < 0)} is the check function of Koenker and Bassett (1978) and 0 < q < 1. With a conditional probability density of f_Y|X(Y|X), the q^th conditional quantile function g_q(x) is a function of x such that $q={\int }_{-\infty }^{g_q(x)}{f}_{Y|X}(y|x)\mathit{\text{dy}}$. Here, the roughness of the fitted curves is determined by the value of λ. We define ${\widehat{\lambda }}_{\mathit{\text{CV}}}^q$ as the minimizer of the cross-validated score where the check loss function is used for validation. Similar to the procedure of conducting ACV under LASSO, we can obtain the ACV version of ${\widehat{\lambda }}_{\mathit{\text{ACV}}}^q$ for quantile smoothing splines. We use simulations to investigate the empirical properties of ${\widehat{\lambda }}_{\mathit{\text{CV}}}^q$ and ${\widehat{\lambda }}_{\mathit{\text{ACV}}}^q$.

4 Simulations

In empirical studies, it is desirable for K, the number of folds, to be reasonably large in order to receive the benefit of averaging. We consider K = 5 and 10 throughout the simulation studies. We investigate the performance of CV and ACV in three scenarios: the traditional linear regression model, LASSO regularization method, and quantile smoothing splines. For these scenarios, the corresponding ACV methods described in Section 2 and Section 3 are used. The classical CV procedure is described as follows.

The CV Procedure

1. Randomly and evenly split the data set into K folds.

2. Use K −1 folds of data as a training data set to fit the linear model (or, LASSO, and quantile smoothing splines).

3. With the fitted models in (2), predict the value of the response variable in the hold-out fold.

4. From the response variable in hold-out fold (say, k^th fold), calculate mean squared prediction error by ${\mathit{\text{MSPE}}}_k={\sum }_{i∊{\aleph }_k}{(y_i-{\widehat{y}}_i^{\mathit{\text{pred}}})}^2/n_k$, where ${\widehat{y}}_i^{\mathit{\text{pred}}}$ is the predicted value for y_i and ℵ_k is the data set in k^th fold.

5. Repeat (2) through (4) for K times so that each of K fold is used as a hold-out fold from which we obtain MSPE₁, …, MSPE_K.

6. Each candidate model obtains a prediction performance measure ${\sum }_{k=1}^K{\mathit{\text{MSPE}}}_k/K$. The ‘optimal’ model which minimizes ${\sum }_{k=1}^K{\mathit{\text{MSPE}}}_k/K$ will be selected.

4.1 Linear model

Assume a linear model Y = Xβ + ∊ as described in Section 2.1 with ∊_is following an iid standard normal distribution. We consider the number of samples n = 200. The X is generated from a multivariate normal distribution with mean 0 and the correlation between the i^th and j^th covariates ρ = 0.5^|i−j|. We consider three cases of the true values of β: (i) β = (3, 0, 0, 0, 0, 0, 0, 0)′; (ii) β = (3, 1.5, 0, 0, 2, 0, 0, 0)′; and (iii) β = (2, 2, 2, 2, 2, 2, 2, 2)′ that represent sparse, intermediate, and dense parameter space, respectively.

To measure accuracy of the estimates, we use the mean squared error (MSE) defined as

$$\mathit{\text{MSE}}=E_{\widehat{\beta }}{\Vert \mathbf{X}\widehat{\beta }-\mathbf{X}\beta \Vert }^2=E_{\widehat{\beta }}\{{(\widehat{\beta }-\beta )}^{\prime }{\mathbf{X}}^{\prime }\mathbf{X}(\widehat{\beta }-\beta )\}.$$ (7)

With L Monte Carlo (MC) samples (L = 1000), the estimate $\widehat{\mathit{\text{MSE}}}$ can be computed as $1/L{\sum }_{l=1}^L\{{({\widehat{\beta }}^l-\beta )}^{\prime }{\mathbf{X}}_l^{\prime }{\mathbf{X}}_l({\widehat{\beta }}^l-\beta )\}$ where β̂^l is the estimate of β for the l^th MC sample.

In addition, Bagging procedure is applied to the same MC samples. Since CV and ACV choose a model from 2⁸ −1 = 255 possible models, we let Bagging procedure to select from 255 re-sampled (with replacement) data sets from one MC sample. The size of re-sampled data set is 200. The results of both CV and ACV are reported in Table 1. In Table 1, “reduction(%)” denotes the reduction of MSE achieved by ACV in comparison to CV. We see that the largest reduction is attained in case (i) which is the sparse scenario, while no reduction is made in the dense case (iii). In the dense case (iii), ACV is able to select the true model K times which leads to the accurate ultimate model via averaging, and thus results in the identical values of MSE as CV. Performance of Bagging is consistent over the three cases, and thus relatively works fine in the dense case, but is outperformed by CV and ACV.

Table 1.

Estimate of MSE (multiplied by 10²) and its standard error (in parentheses, multiplied by 10²) based on 1000 MC samples for CV, ACV and Bagging.

	β=(3,0,0,0,0,0,0,0)′	β=(3,1.5,0,0,2,0,0,0)′	β=(2,2,2,2,2,2,2,2)′
CV, K = 5	516.4 (13.6)	593.1 (13.3)	806.3 (13.0)
ACV, K = 5	405.8 (8.7)	521.1 (5.8)	806.3 (13.0)
reduction(%)	21.43	12.15	0
CV, K = 10	509.3 (13.7)	590.9 (13.3)	806.3 (13.0)
ACV, K = 10	370.1 (7.6)	553.4 (5.8)	806.3 (13.0)
reduction(%)	27.34	6.35	0
Bagging	811.4(13.1)	808.3(13.1)	810.6(13.0)

4.2 Lasso penalization

We also investigate the performance of CV and ACV in the case of large p with the usage of sparsity penalization. We use the similar simulation set-up with n = 200 in the previous section, but increase p to 1000 and set ρ = 0. The β is set to have 50 non-zero values and 950 zeros. Two different sets of non-zero values are considered as follows: (i) 25 values are randomly generated from Unif(1, 2), and the other 25 from Unif(−2, −1); and (ii) 25 values are taken to be 1 and the others are with values of −1. We interrogate 200 equally spaced values of λ in (0.001, 0.4) with K = 10.

We compare CV and ACV in terms of parameter estimation and identification of true non-zero parameters. We again use MSE in (7) to measure the estimation accuracy. The mean and its standard error of 1000 MSE values, respectively, obtained from 1000 MC samples in each case are reported in Table 2. We see that ACV reduces MSE by about 30% comparing to CV in each case. To investigate accuracy of detecting the 50 true non-zero parameters, we focus on the 50 variables with the largest absolute values of the parameter estimates, and record the number of detected true non-zero ones among them. In Table 3, we report the distribution of the number of detected true non-zero βs of CV subtracted from that of ACV. In case (i), ACV and CV show the identical detection accuracy for 352 times out of 1000 runs. Note that ACV performs better than CV for 426 times, while CV outperforms ACV for 222 times. In case (ii), ACV detects more true non-zero βs than CV for 466 times, but fewer for 228 times. It is also noticeable that ACV outperforms CV with the number of accurate detection as high as 15, while CV outperforms ACV with no more than 6 accurate detection.

Table 2.

Estimates of MSE and its standard error (in parentheses) based on 1000 MC samples for CV and ACV.

	CV	ACV	reduction(%)
case (i)	573.2 (17.8)	381.3 (6.3)	33.5
case (ii)	487.4 (13.3)	342.8 (5.6)	29.7

Table 3.

The distribution of the number of detected true non-zero βs of CV subtracted from that of ACV, based on 1000 MC samples.

	−6 to −4	−3	−2	−1	0	1	2	3	4	5 to 7	8 to 15
case (i)	14	17	51	140	352	170	108	62	31	39	16
case (ii)	14	15	61	138	306	181	112	58	46	48	21

4.3 Quantile smoothing splines

In this section, we investigate applicability of the proposed method ACV in the problem of quantile smoothing splines. We consider the mean of the observations from a sinusoid curve with period 1, which is expressed as

$$y_i=sin(2\pi x_i)+{∊}_i,i=1,\dots ,n,$$

where x_is are iid from the standard uniform distribution with n = 200. We consider two distribution settings for the iid ∊_i's: (i) N(0,0.2²); and (ii) shifted exponential distribution with the median 0 and the standard deviation 0.2. A fine grid search of the smoothing parameter is conducted to select the ‘optimal’ value by CV and ACV with L MC samples (L = 1000) and K = 5. We adopt the empirical estimate of MSE by MC samples as,

$$\mathit{\text{MSE}}=\frac{1}{L}\sum _{l=1}^L\frac{1}{n}\sum _{i=1}^n{(g(x_i)-{\widehat{g}}^l(x_i))}^2,$$

where g(x_i) is the true underlying function, and ĝ^l(x_i) indicates the fitted value at x_i from the l^th MC sample. The results at several quantiles are shown in Table 4, where reduction(%) stands for the percentage of reduction in the average value of MSE achieved by ACV comparing to CV. Under the normal error distribution in case (i), the result for q > 0.5 is not reported because of the similarity to q < 0.5. The considerable reductions achieved by ACV indicate that its averaging strategy results in better selection of the penalization parameter. For both the cases, quantiles in the region of high conditional density of the errors lead to greater reduction (%) in MSE, comparing to the low density regions. The rationale is that fewer observations are available to estimate the targeted quantile in the low density regions, and thus the advantage of ACV is not as prominent. This can be seen at q = 0.9 in case (ii) that the performances of these two methods are very similar with n = 200. To verify this finding, we increase the sample size to 400 and observe 5% reduction in MSE by using ACV. Thus, it is important to keep a sufficient number of observations in the hold-out fold to take advantage of ACV.

Table 4.

Estimate of MSE and its standard error (in parentheses) based on 1000 MC samples for CV and ACV. All numbers are multiplied by 10⁴.

case (i)	q=0.1	q=0.2	q=0.3	q=0.4	q=0.5
CV	84.25(1.8)	63.39(1.2)	55.72(1.1)	51.63(1.0)	50.92(1.0)
ACV	83.13(1.8)	58.83(1.2)	50.55(1.0)	46.78(0.9)	45.10(0.8)
reduction(%)	1.32	7.21	9.28	9.4	11.42
case (ii)	q=0.1	q=0.25	q=0.5	q=0.75	q=0.9
CV	2.21(0.06)	5.02(0.12)	13.14(0.28)	35.84(0.08)	89.67(2.0)
ACV	1.81(0.04)	4.28(0.09)	11.81(0.23)	33.68(0.07)	90.41(2.3)
reduction(%)	18.28	14.75	10.08	6.03	−0.82

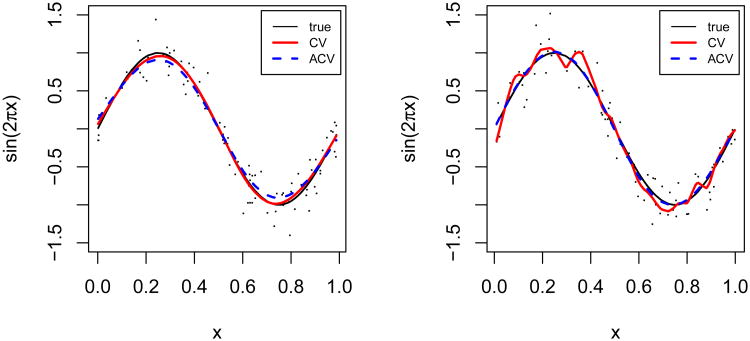
Another phenomenon often observed is data over-fitting by CV. In Figure 1, we demonstrate this point by two plots of the fitted curves that produce the maximum (left panel) and minimum (right panel) values of MSE_ACV/MSE_CV among 1000 MC samples, respectively. In the left panel, ACV in fact performs similarly to CV. In contrast, the right panel shows the obvious over-fitting by CV, manifested by its jagged curve.

Figure 1.

Under a normal error distribution, the fitted model selected by ACV performs relatively ‘worst’ compared to that selected by CV (left), and ACV performs relatively ‘best’ compared to CV (right) among 1000 simulated data sets.

5 A real example

Isaacs et al. (1983) established the reference percentiles of children for the serum concentrations of immunoglobulin-G (IgG) in grams per liter, based on 298 children of ages 6 months to 6 years. They considered various polynomial regressions treating IgG as the response and age (in month) as an explanatory variable. The best-fit model provided by Isaacs et al. (1983) is ${\mathit{\text{IgG}}}^{\frac{1}{2}}=1.16+0.2715\ast {\mathit{\text{age}}}^{\frac{1}{2}}-0.01195\ast \mathit{\text{age}}$ for the 50^th percentile, which is drawn as a dashed line in Figure 2. Royston and Altman (1994) revisited this data and used additive polynomial regressions with smoother fitted lines to eliminate the jaggedness near the boundary ages of 6 months and 6 years. Herein, we target selecting an appropriate smoothing penalty parameter for quantile smoothing splines to obtain well-behaved reference percentiles.

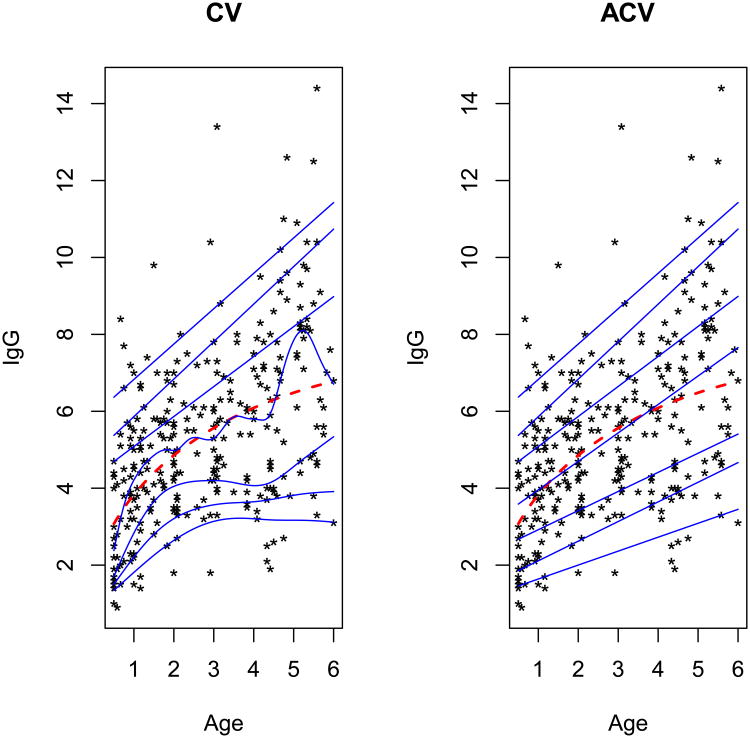
Figure 2.

Fitted quantile smoothing splines at q=0.05, 0.1, 0.25, 0.5, 0.75, 0.9, and 0.95, highlighted in blue from the bottom to the top, in the immunoglobulin-G data set. The dashed fitting line is obtained from the model given by Isaacs et al. (1983). The results of CV and ACV are shown in the left and right panels, respectively.

To find the ‘optimal’ λ̂, we examined 2000 log(λ) values within (−35, −0.2). First, the data is randomly divided into 5 (nearly) equal parts, among which one contains 58 observations and each other part contains 60 observations. To account for the variability due to random split, we iterate the procedure 200 times for both ACV and CV. The penalization parameter values, denoted by λ̂_ACV and λ̂_CV, are obtained by averaging their respective 200 estimates of λ. The fitted conditional quantile lines of the IgG data at q = 0.05, 0.1, 0.25, 0.5, 0.75, 0.9, and 0.95 are plotted in blue from the bottom to the top in Figure 2.

In the data set, we find mild heteroscedasticity of increasing variance as Age increases. It is reflected by the fit from both CV and ACV. It is clear that the fitted line at q = 0.5 provided by CV appears to be less smooth than ACV. We notice that ACV shares more similarity with the model given by Isaacs et al. (1983) which is the dashed line. At q = 0.25, the non-monotonic fitting line of CV implies that the IgG level of 3-year-old children is higher than that of 4-year-old children, which seems insensible from the perspective of biology. Overall, ACV provides smoother fit to data than CV. We also summarize the logarithm-transformed λ̂_CV and λ̂_ACV at various quantiles in Table 5. We can see that λ̂_CV changes considerably across the quantiles, whereas λ̂_ACV is stable (around −1.5) due to the averaging effect.

Table 5.

Average values of log(λ̂_CV) and log(λ̂_ACV) at various quantiles over 200 different random splits.

	q=0.05	q=0.1	q=0.25	q=0.5	q=0.75	q=0.9	q=0.95
CV	−15.49	−15.59	−16.73	−19.86	−4.02	−3.85	−3.84
ACV	−1.58	−1.62	−1.7	−1.64	−1.42	−1.5	−1.52

6 Conclusion

In this work, we propose a K-fold averaging cross-validation procedure for model selection and parameter estimation. We establish its theoretical property and show its promise via empirical investigation. Since cross-validation is actively employed in many areas of statistics, ACV can also be applied to a broad range of modeling procedures. For example, ACV can be easily used with penalized model selection method, for which selection of penalty parameters is of interest. Demonstrated through simulations with usage of LASSO, the ACV method outperforms the CV method in terms of mean squared error and selection accuracy. We also investigate its applicability in quantile smoothing splines, and demonstrate its capability of providing more smooth data fit than the traditional CV method.

One shall pay attention to the size of the test set and selection of K when implementing ACV. A large value of K combined with a small sample size may cause insufficient fit of the data since K-fold ACV performs model selection based on 1/K of the data. We recommend including a sufficient number of observations in a test set. Note that the desirable size of the test set also depends on complexity of the underlying true model.

Appendix

Proof of Theorem 1

Proof

$$\mathit{\text{tr}}({\mathbf{H}}_{\mathit{\text{ACV}}}^{\prime }{\mathbf{H}}_{\mathit{\text{ACV}}})=\frac{1}{K^2}\mathit{\text{tr}}({(\sum _{k=1}^K{\mathbf{P}}_k)}^{\prime }(\sum _{k=1}^K{\mathbf{P}}_k))\le \frac{1}{K}\mathit{\text{tr}}(\sum _{k=1}^K{\mathbf{P}}_k^{\prime }{\mathbf{P}}_k)$$ (8)

Since ${\mathbf{P}}_k^{\prime }{\mathbf{P}}_k={\mathbf{P}}_k$ and tr(P_k) = | M_k|, we have,

$$\frac{{\sigma }^2}{n}\mathit{\text{tr}}({\mathbf{H}}_{\mathit{\text{ACV}}}^{\prime }{\mathbf{H}}_{\mathit{\text{ACV}}})\le \frac{{\sigma }^2}{n}\frac{1}{K}\sum _{k=1}^K|M_k|,$$ (9)

where $\frac{1}{K}{\sum }_{k=1}^K|M_k|\equiv d\ast$ is the mean number of selected variables from ACV. Thus, |d − d*| ≤ p, which leads to $|d-d\ast |\frac{{\sigma }^2}{n}=O(n^{-1})$. The second term on the RHS of (5) will disappear when M_f is in Category I, which completes the proof of (a).

When M_f is in Category II, the second term on the RHS of (5) will be

$$\frac{1}{n}{\beta }^{\prime }{\mathbf{X}}^{\prime }{({\mathbf{I}}_n-{\mathbf{H}}_{\mathit{\text{ACV}}})}^{\prime }({\mathbf{I}}_n-{\mathbf{H}}_{\mathit{\text{ACV}}})\mathbf{X}\beta \le \underset{1\le k\le K}{max}\frac{1}{n}{\beta }^{\prime }{\mathbf{X}}^{\prime }({\mathbf{I}}_n-{\mathbf{P}}_k)X\beta .$$ (10)

When it is subtracted by the second term on the RHS of equation (6), we have

$$\frac{1}{n}{\beta }^{\prime }{\mathbf{X}}^{\prime }{({\mathbf{I}}_n-{\mathbf{H}}_{\mathit{\text{ACV}}})}^{\prime }({\mathbf{I}}_n-{\mathbf{H}}_{\mathit{\text{ACV}}})\mathbf{X}\beta -\frac{1}{n}{\beta }^{\prime }{\mathbf{X}}^{\prime }({\mathbf{I}}_n-{\mathbf{P}}_{\mathit{\text{CV}}})\mathbf{X}\beta \le \underset{1\le k\le K}{max}\frac{1}{n}{\beta }^{\prime }{\mathbf{X}}^{\prime }({\mathbf{P}}_{\mathit{\text{CV}}}-{\mathbf{P}}_k)\mathbf{X}\beta .$$ (11)

By Assumption B, the RHS of equation (11) is o(1), which completes the proof of (b).

Proof of Lemma 1

Proof

First, define max_1≤k≤KA_k to be A_k with maximum determinant for k = 1, …, K, where A_k is a positive definite matrix. Note that det(A_k) > 0 as a property of positive definite matrix, and this is the case here since we assume X_k is full column rank. From the facts that the value of correlation is always between −1 and 1, and det(A_kA_k′) = det(A_k)det(A_k′), we have

$$det(cov({\widehat{\beta }}_k,{\widehat{\beta }}_{k^{\prime }}))\le det\left(\sqrt{\mathit{var}({\widehat{\beta }}_k)}\sqrt{\mathit{var}({\widehat{\beta }}_{k^{\prime }})}\right)=det\left(\sqrt{\mathit{var}({\widehat{\beta }}_k)}\right)det\left(\sqrt{\mathit{var}({\widehat{\beta }}_{k^{\prime }})}\right)\le det(\underset{1\le k\le K}{max}\mathit{var}({\widehat{\beta }}_k)),$$

where the last inequality directly comes from the definition. Therefore, we have,

$$det(\mathit{var}(\frac{1}{K}\sum _{k=1}^K{\widehat{\beta }}_k))=det(\frac{1}{K^2}\sum _{k=1}^K\mathit{var}({\widehat{\beta }}_k)+\frac{2}{K^2}\sum _{1\le k\le k^{\prime }\le K}\mathit{cov}({\widehat{\beta }}_k,{\widehat{\beta }}_{k^{\prime }}))\le det(\frac{1}{K}\underset{1\le k\le K}{max}\mathit{var}({\widehat{\beta }}_k)+\frac{K(K-1)}{K^2}\underset{1\le k\le K}{max}\mathit{var}({\widehat{\beta }}_k))=det(\underset{1\le k\le K}{max}\mathit{var}({\widehat{\beta }}_k))=det(\mathit{var}({\widehat{\beta }}_{\mathit{\text{CV}}}))$$

When β̂_ks are identical for k = 1, …, K, the above inequality becomes equality. Further, when the selected models from all the folds {β̂_k} are identical, it is in fact the same as a selected model by the traditional K-fold CV. Thus, we have β̂_ACV = β̂_CV, which confirms the last equality.