Abstract
Aims
We aimed to use longitudinal data from an established screening programme with good quality assurance and quality control procedures and a stable well‐trained workforce to determine the accuracy of grading in diabetic retinopathy screening.
Methods
We used a continuous time‐hidden Markov model with five states to estimate the probability of true progression or regression of retinopathy and the conditional probability of an observed grade given the true grade (misclassification). The true stage of retinopathy was modelled as a function of the duration of diabetes and HbA1c.
Results
The modelling dataset consisted of 65 839 grades from 14 187 people. The median number [interquartile range (IQR)] of examinations was 5 (3, 6) and the median (IQR) interval between examinations was 1.04 (0.99, 1.17) years. In total, 14 227 grades (21.6%) were estimated as being misclassified, 10 592 (16.1%) represented over‐grading and 3635 (5.5%) represented under‐grading. There were 1935 (2.9%) misclassified referrals, 1305 were false‐positive results (2.2%) and 630 were false‐negative results (11.0%). Misclassification of background diabetic retinopathy as no detectable retinopathy was common (3.4% of all grades) but rarely preceded referable maculopathy or retinopathy.
Conclusion
Misclassification between lower grades of retinopathy is not uncommon but is unlikely to lead to significant delays in referring people for sight‐threatening retinopathy.
What's new?
A statistical modelling approach can be used to retrospectively evaluate the accuracy of screening programmes for diabetic retinopathy.
Our model predicts that misclassification of background retinopathy as no detectable retinopathy is unlikely to lead to clinically significant delays in referring people with sight‐threatening retinopathy.
This study adds to a growing body of evidence that suggests screening intervals for people graded as no background retinopathy could be safely extended to 2 or 3 years.
What's new?
A statistical modelling approach can be used to retrospectively evaluate the accuracy of screening programmes for diabetic retinopathy.
Our model predicts that misclassification of background retinopathy as no detectable retinopathy is unlikely to lead to clinically significant delays in referring people with sight‐threatening retinopathy.
This study adds to a growing body of evidence that suggests screening intervals for people graded as no background retinopathy could be safely extended to 2 or 3 years.
Introduction
Annual screening for diabetic retinopathy (DR) is recommended for people with diabetes, with referral to ophthalmology clinics for people with sight‐threatening retinopathy. It has been put forward that screening intervals may be extended using risk stratification 1. One method for this would be to use the results of two screening episodes to stratify people by risk level and for those at lower risk, the screening interval may be extended beyond a year. As part of the screening process, digital photographs of the retina are graded according to the degree of retinopathy from R0 to R3 and the presence of maculopathy (M0 or M1). Grading is not a deterministic process and there is variation between graders 2 and within graders 3. Hence, screening can lead to misclassification of the true level of retinopathy. Under‐grading can occur because subtle abnormalities such as small microaneurysms or intraretinal microvascular abnormalities are missed or graders may downgrade or miss abnormalities. Over‐grading may occur because dust spots or pigment spots are graded as microaneurysms or minor abnormalities are mistaken for more serious lesions.
Grading output can give the impression of change over time (progression or deterioration) when the condition is actually stable. This may have implications for screening intervals, as people might have their screening interval extended after apparently negative results when they should have been screened more often or be screened annually when they should have their screening interval extended. The effectiveness of retinopathy screening programmes is affected by the precision and accuracy of grading of photographs, but direct estimation of misclassification rates has never been attempted, and accuracy of screening is only usually reported in terms of referable disease.
The aim of this study was to quantify the level of misclassification in an established screening programme for retinopathy with established quality control procedures and a stable well‐trained workforce using statistical methodology, and to assess what effect misclassification will have for screening programmes that plan to extend the screening interval in people with no evidence of retinopathy.
Subjects and Methods
We obtained longitudinal data on retinal photographs from 2005 to 2012 from the Gloucestershire Diabetic Eye Screening Programme. Clinical risk factor data including duration of diabetes, HbA1c and cholesterol, as well as the gender and age of each subject were also obtained. The screening programmes invites people for annual screening but some people may attend less frequently. At each screening episode, visual acuity was assessed using logMAR charts and colour digital retinal photographs were taken of two standard 45° fields (macula and disc centred) per eye after dilation of the pupils. Photographs were then graded by trained assessors in a central location for the presence of maculopathy and retinopathy and the severity of retinopathy. The criteria for grading has been described in detail elsewhere 1, but images were graded by a primary grader and images with any level of retinopathy were then graded by a second grader; 10% of all images without retinopathy were second graded and arbitrated by a third grader.
In the absence of a reference test or gold‐standard measure to represent the underlying true state of retinopathy at each screening occasion, we used statistical models to estimate the reference or true state using only the observed sequences of screening grade and risk‐factor data. The statistical model builds on the results determined by screeners and graders and attempts to gain an advantage over decisions made in real time by considering all of the data across the whole cohort over the whole period. To illustrate how it may be possible to estimate the true grade in the absence of a gold‐standard test, imagine if we had a dataset of only one patient, graded many times. If a patient is graded with high retinopathy at one visit, no retinopathy at the next, then high retinopathy and then no retinopathy and so on – we would suspect that the grading process was inaccurate, even without having access to a gold standard at any of these time points. In practice, we have a dataset of many patients. The more patients there are with apparent inconsistencies, the higher the estimated misclassification rate in the screening and grading. The model is a mathematical ‘algorithm’ that, at its heart, does nothing more than apply – and quantify – the above reasoning. In order to operationalize the model, we defined a univariate five‐level outcome to represent five states in a model: (1) no detectable retinopathy and no evidence of maculopathy in either eye; (2) background retinopathy in one eye, no detectable retinopathy in the other eye and no maculopathy in either eye; (3) background retinopathy in both eyes both without maculopathy; (4) maculopathy in at least one eye and any retinopathy; and (5) pre‐proliferative or proliferative retinopathy in one or both eyes in the absence of maculopathy (Fig. 1).
Figure 1.
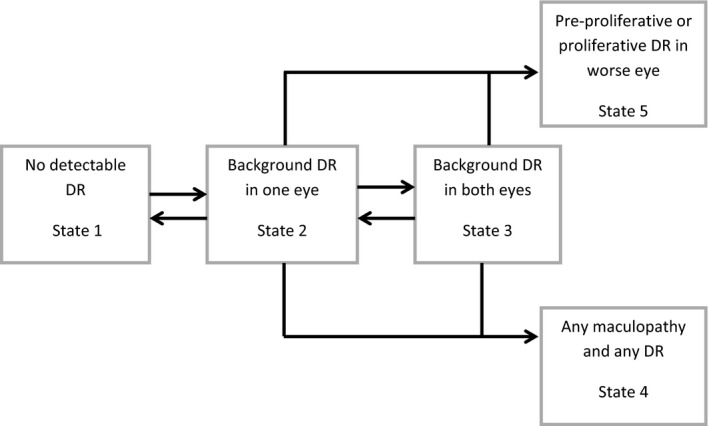
Graphical representation of the transition model. Arrows from one state to another represent instantaneous transitions to be estimated. Absence of arrows indicates instantaneous progression is not possible.
We treated these five levels of retinopathy and maculopathy as states in a Markov model. Markov models have been used extensively to model disease progression and to evaluate cancer screenings strategies 4, 5. A hidden Markov model (HMM) consists of a matrix representing the true disease process as transition rates and a second matrix, the misclassification matrix, representing the distinction between true retinopathy state and retinopathy grade recorded by an imperfect grading process; thus an HMM accounts for the fact that the true disease state is not always reflected by the test and may be misclassified 6. We used a continuous‐time HMM to simultaneously estimate the transition rates (intensities) between states and the probabilities of misclassification 5. We then used the model to retrospectively estimate the true grade for each of the observed screening grades.
The following modelling assumptions about the natural progression of disease were made:
as there is evidence to suggest that background retinopathy can develop and subsequently disappear 7, movement back and forth was permitted between states 1, 2 and 3;
we assumed that eyes develop referable retinopathy or maculopathy having developed background retinopathy, hence there is no direct link from state 1 to the referable states (4 and 5); and
once disease has progressed to true referable retinopathy or maculopathy, remission back to background retinopathy (without treatment) is assumed impossible, hence the referable states are absorbing states.
We did not constrain any misclassification probabilities. The model therefore estimates a 5 × 5 matrix of instantaneous transition probabilities with forced zero entries representing the modelling assumptions listed above and an unrestricted 5 × 5 matrix representing misclassification probabilities.
The model was fitted using the msm function 8 in R 3.0.2 9. Observations were excluded if retinopathy or maculopathy grade were missing from either eye or were obviously duplicate entries, and people were excluded if they only had one useable observation or did not have a baseline HbA1c, serum cholesterol or duration of diabetes recorded. A number of different versions of the HMM were assessed, adjusting transition rates for the duration of diabetes, baseline HbA1c, age, gender and cholesterol. We considered only the variables identified as important predictors in a risk stratification model in a previous study 10. The parameter estimates relating to each of these covariates are equivalent to hazard ratios for the risk of moving between states and are constant over time. The final model was selected by starting with one that included all available covariates and then removing non‐significant parameters. The fitted model was then used to estimate the true grade of retinopathy for each of the observed grades in the data. We used the Viterbi algorithm 11 to calculate the true grade of retinopathy for each person and each observation. The Viterbi algorithm is an example of a dynamic programming method that aims to find the most probable sequence of true states for any given observation sequence 12. How the Viterbi algorithm estimates the most probable or estimated true sequence of states or grades is best illustrated using a hypothetical example. For an observed sequence of five screening images say; O = {no DR, no DR, no DR, background DR in both eyes, no DR}, the algorithm calculates a ‘score’ or probability based on the observed sequence and one of many possible true sequence (Q1, Q2, Q3 … Qk) using probabilities of disease progression and misclassification informed by the whole cohort. The algorithm then selects the true sequence with the highest score or probability. In this hypothetical example, if the version of the true sequence in which there was no change, i.e. Q1 = {no DR, no DR, no DR, no DR, no DR} had higher probability than any other sequence, including the one that mirrors the observed set of results, i.e. Q2 = {no DR, no DR, no DR, background DR in both eyes, no DR}, then it would be selected over all other explanations for the observed sequence. In this example, the fourth observation of the sequence would be counted as misclassified. We used this approach to estimate the misclassification rate for the entire cohort (see Appendix Table A1).
We then identified people for whom the model algorithm predicted background retinopathy in one eye (state 2) or background retinopathy in both eyes (state 3) but were observed as no detectable retinopathy (misclassified). We then calculated the interval between the misclassified screen and an observed referral level grade of either maculopathy or retinopathy (state 4 or 5) if one occurred. We then repeated this, counting people for whom both the observed grade and estimated true grade were a level that warranted referral.
Results
The results of 68 992 examinations for 14 810 people were extracted from the screening service database. We excluded 623 people and 3153 observations because they had incomplete or unusable data. The remaining 14 187 people (65 839 observations and 59 949 person‐years of follow‐up) constituted the modelling cohort. The median number [interquartile range (IQR)] of examinations in the modelling cohort was 5 (3, 6). There were 8412 (57%) men, median (IQR) HbA1c at baseline was 51 mmol/l (44–61 mmol/l) equivalent to 6.8% (6.2% to 7.7%), median (IQR) age was 64 (55–72) years and median (IQR) duration of diabetes at baseline was 2.5 (0.8–7.3) years. Median (IQR) interval between examinations was 1.04 (0.99, 1.17) years.
Table 1 shows the counts of transitions across all individuals in the cohort. These are the number of times one grade has been followed by another and does not take into account misclassification or elapsed time. Row percentages are also given and can be interpreted roughly as empirical probabilities of observing changes in consecutive examinations.
Table 1.
Frequencies of successive states observed in the screening data
| State | To | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| No detectable retinopathy | Background retinopathy in one eye | Background retinopathy in both eyes | Referable maculopathy | Referable retinopathy (pre‐proliferative or proliferative) | ||
| From | 1 | 21 127 (76%) | 4 694 (17%) | 1 723 (6%) | 191 (1%) | 19 (0%) |
| 2 | 4 630 (45%) | 3 466 (34%) | 1 854 (18%) | 219 (2%) | 44 (0%) | |
| 3 | 1 446 (16%) | 1 608 (18%) | 4 660 (53%) | 784 (9%) | 285 (3%) | |
| 4 | 162 (5%) | 179 (5%) | 582 (16%) | 2 309 (64%) | 349 (10%) | |
| 5 | 19 (1%) | 18 (1%) | 192 (15%) | 357 (27%) | 735 (56%) | |
From = previously observed grade. To = next observed grade.
The final model adjusted transition rates for duration of diabetes and HbA1c. Cholesterol level, age and gender did not independently affect transition rates (had non‐significant hazard ratios) and were dropped from the final model. Table 2 shows the matrix of estimated transition intensities or rates with their 95% confidence intervals. Diagonal elements represent (minus) the rate or potential for leaving the current state 13. Off‐diagonal elements are proportional to the probabilities governing the next state. The misclassification matrix of estimated error probabilities is given in Table 3; here, off‐diagonal elements represent probabilities of grading errors, and diagonal elements probabilities of correct grading.
Table 2.
Fitted transition intensities matrix. Cells represent transition rates (95% CI)
| States | To | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| No detectable retinopathy | Background retinopathy in one eye | Background retinopathy in both eyes | Referable maculopathy | Referable retinopathy (pre‐proliferative or proliferative) | ||
| From | 1 | −0.11 (−0.12 to −0.10) | 0.11 (0.10 to 0.12) | – | – | – |
| 2 | 0.12 (0.10 to 0.14) | −0.22 (−0.25 to −0.19) | 0.10 (0.09 to 0.11) | 0.004 (0.002 to 0.007 | 0.00004 (0 to 0.007) | |
| 3 | – | 0.12 (0.10 to 0.14) | −0.16 (−0.18 to −0.13) | 0.02 (0.02 to 0.03) | 0.02 (0.01 to 0.02) | |
| 4 | – | – | – | 0 | – | |
| 5 | – | – | – | – | 0 | |
Diagonal cells are minus the instantaneous rate of exiting the current state, off‐diagonals are proportional to the probability of moving to that state. Hence, −0.22 is the rate that people exit from the state 2 is 0.22 and the proportion leaving the current state in one year is 1 − exp(−0.22) = 0.2. From leaving state 2, the next state would be background retinopathy in both eyes with probability 0.10/0.22 = 0.45 and no retinopathy with probability 0.12/0.22 = 0.55
Table 3.
Estimated error matrix
| States | Observed grade | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| No detectable retinopathy | Background retinopathy in one eye | Background retinopathy in both eyes | Referable maculopathy | Referable retinopathy (pre‐proliferative or proliferative) | ||
| Estimated true grade | 1 | 0.87 | 0.11 | 0.02 | 0.003 | 0.0001 |
| 2 | 0.21 | 0.55 | 0.22 | 0.02 | 0.002 | |
| 3 | 0.006 | 0.03 | 0.84 | 0.10 | 0.02 | |
| 4 | 0.002 | 0.007 | 0.06 | 0.85 | 0.08 | |
| 5 | 0.002 | 0.005 | 0.10 | 0.23 | 0.67 | |
We used the model to estimate the true state for each observed grade in the data in order to assess the overall accuracy of the screening program. In total, 14 227 grades (21.6%) were estimated to be misclassified. Most of these, 10 592 (16.1% of the total), represented over‐grading (observed grade more severe than estimated true grade) and 3635 (5.5% of the total) represented under‐grading (observed grade less severe than estimated true grade). We found 1305 (2%) grades equivalent to false‐positive referrals, i.e. the observed grade was sufficient for referral when the true grade was not, and 630 (1%) were false negatives, i.e. the observed grade was non‐referral but the estimated true grade was referral level.
We then calculated the number of times background retinopathy was under‐graded as no detectable retinopathy. We estimated that on 1997 occasions, people were observed and graded as no detectable retinopathy (state 1) when their true grade was most probably background retinopathy in one eye (state 2), and on 245 occasions no detectable retinopathy was observed when the model estimated that the true grade was background retinopathy in both eyes (state 3). In all, under‐grading background retinopathy as no detectable retinopathy represented 3.4% of all screening episodes.
Because there is a possibility that people being screened in the future may have their screening interval extended when no retinopathy has been detected (observed state 1), we looked to see how many of the people under‐graded in this way went on to have referable retinopathy or referable maculopathy and calculated the time between the misclassified grade and the referable grade. Of 1770 people who were misclassified as no detectable retinopathy at least once, 151 were later observed as having referable maculopathy and 23 as having referable retinopathy. Of the 151 with referable maculopathy, 40 (26%) were observed with maculopathy within 2 years and 80 (53%) within 3 years of their initial no detectable retinopathy grade. Of the 23 referrals for retinopathy, 7 (30%) were observed within 2 years and 11 (48%) were observed within 3 years. Because misclassification is also possible with referable disease, we repeated this calculation taking into account the estimated true grade at the time of the observed referral grade. Of the 151 with observed referable maculopathy, only 31 (21%) also had estimated true referable disease. Of the 23 with observed referable retinopathy, 7 (30%) had estimated true referable disease. This shows that for this particular subset of people (observed with no detectable retinopathy and misclassified) a referral grade within 3 years is more likely to be a false positive than a true positive.
If we do not take into account possible misclassification of the referral grade, 47 people would have experienced a delay in referral (for either maculopathy or retinopathy) if their screening interval had been extended to 2 years and this figure would rise to 91 if the interval was extended to 3 years. If we take into account potential misclassification of the referral grade, the number of people experiencing a delay drops to 5 within 2 years and 20 within 3 years. Therefore, 42/47 (89%) and 71/91 (78%) represented false‐positive referrals. As a total of the entire follow‐up of the study, extending the screening interval to 2 years for people with no detectable retinopathy would mean 8 per 1000 people screened for 10 years experiencing a delay in referral due to misclassification, and 15 per 1000 people screened for 10 years for a 3‐year interval. Taking into account misclassification, we estimate the number of delayed referrals decreases to < 1 per 1000 people screened for 10 years for 2‐year intervals and 3 per 1000 people screened for 10 years for 3‐year intervals.
Discussion
Our results show that misclassification of retinopathy in this programme in this period may happen frequently (21.6%), but occurs mostly between background (R1) in one or both eyes and no detectable retinopathy. This screening programme appeared to over‐grade more than under‐grade (16.1% vs. 5.5%), and tended to over‐refer (2%) rather than under‐refer (1%). This is of course a pragmatic and clinically safe approach. Because under‐grading may mean that some people will have their next screening interval extended, we looked to see how many would incur a delay in their referral to specialist eye services. Although misclassification of background retinopathy as no detectable retinopathy happens frequently, the nature of the progression of retinopathy means that very few go onto true referable disease within 2 or 3 years. Our results suggest that extending the screening interval for people with no detectable retinopathy at the last screen to 2 years would result in very few delays in referral. Delays in referral are likely to be very rare if the screening interval is extended based on two consecutive screens with no detectable retinopathy.
The significant advantage of this modelling approach to evaluating the accuracy of a screening programme is in its efficiency. Re‐grading images as part of a quality control approach is extremely valuable, but is expensive and time‐consuming and may not overcome the issues of between grader variability or changes in staffing or grading protocols (arbitration on R1/R0, for example). A modelling‐based evaluation approach could be applied to any screening programme at minimal cost. The specific method we have used (hidden Markov model) is able to take into account that different screening programmes will have people with different risk profiles and as a result it will be possible to compare different screening programmes and identify programmes with higher proportions of under‐ and over‐grading both at the level of background and referable disease.
All models make assumptions and there are a number of limitations to this approach. Significant violations to the key assumptions of the model, namely, that sequences of screening results and subsequently the progression of retinopathy can be described as a Markov process would probably invalidate our results. As by the definition of the model, the Markov process itself is hidden and not directly observable, this means that it is not easy to check whether this assumption holds true 14. In addition, in order to obtain working estimates, certain simplifications need to be made; for example, we cannot estimate the likelihood of screening missing or over‐referring in the presence of both referable retinopathy and maculopathy. We can, however, assess whether predictions made by the model are reasonable and in line with other estimates. We are also mindful that models such as these can have alternative parameter estimates that equally explain the observed data and that these could yield significantly different estimates. However, we managed to obtain estimates that are ‘maximum likelihood’, which avoided having to arbitrarily choose between one of many potential sets of estimates.
There also limitations that are not due to the approach itself, and would be common to any method of evaluation. A screening programme may not have access to all the relevant patient clinical data or it may be too sparse. In our analysis, we could not adjust for type of diabetes because there were not enough people with Type 1 diabetes to obtain reasonable estimates. However, in this case, diabetes type does not seem to independently affect the risk of progression over and above duration, HbA1c and status of retinopathy 1. Finally, any screening programme will have incomplete attendance and this could, in theory, affect the evaluation of the programme, especially if non‐attendance is associated with grades of retinopathy that are more prone to misclassification.
We compared 6‐year progression rates predicted by our model with those reported in the UKPDS 50 15. Our model predicts that for those observed as no detectable retinopathy at baseline, 37.8% will develop background retinopathy in one or both eyes within 6 years, compared with 37.9% who had no detectable retinopathy (10 10 using the ETDRS classification) at baseline and ETDRS 20–35 retinopathy 6 years on in the UKPDS. Six‐year progression rates from no detectable retinopathy to referable retinopathy (ETDRS > 43) were 2.77 (2.2% maculopathy) using our model and 1.5% in the UKPDS.
A direct comparison of our estimated misclassification rates with external and independent estimates from the literature is compromised by a lack of uniformity in grading systems, differences in screening methods and the varying case‐mixes of people included in such studies. Estimates of specificity and sensitivity from diagnostic accuracy studies provide a useful, if somewhat limited, comparison with our estimates because they only report misclassification of referable disease. False‐positive rates reported from studies comparing mydriatic digital retinal photography with a reference of either slit‐lamp biomicroscopy or seven‐field stereo‐photography varied considerably from as low as 1% 16 to as high as 16% 17. We estimated the percentage of false‐positive rates (1 – specificity) in this screening data to be 2.2%. These estimates are similar to the false‐positive rates reported previously Scanlon et al. 18 and Stellingwerf et al. 16 but much lower than in some other reports 17, 19, 20. There is also considerable variation in the false‐negative rates reported in the literature, ranging from 7% 19 to 20% 18. The false‐negative rate predicted by our model is 11.0%, which is towards the middle of the range of false‐negative rates reported in the literature 16, 17, 18, 19, 20.
More direct comparisons are possible with estimates of misclassification derived directly from screening programmes. However, such reports are few and far between. Healy et al. 21 compared retinopathy screening grading and hospital eye services from the same screening programme and reported that the screening service grades were in agreement with hospital eye services in 76.9% of eyes. This figure is close to the overall error rate (21.6%) estimated by our model, but is only an approximation because the hospital eye service does not necessarily represent a gold standard. A more independent comparison can be made between our estimates and those reported from regrading images from other screening programmes. Manjunatha et al. 22 reported that of the 2716 images initially graded as no detectable retinopathy that they re‐examined, 367 (13.5%) were considered to have background retinopathy after arbitration.
Looker et al. 23 previously used the same methodology to model the potential impact of extending screening intervals for retinopathy. The focus of their study was different to ours, but they did publish their estimated misclassification probabilities as supplementary web material (ESM, table 6; available from http://link.springer.com/content/esm/art:10.1007/s00125-013-2928-7/file/MediaObjects/125_2013_2928_MOESM7_ESM.pdf). Their error matrix suggests that under‐grading is more common than over‐grading in their screening programme, but to be sure of this, one would need to know case‐mix of retinopathy for the people being screened. For example, Looker et al. estimate that nearly half (49.2%) of all the people with observable retinopathy or maculopathy are under‐graded as having mild background retinopathy in that screening programme.
Our modelling‐based evaluation gives valuable insights into the chance of correct or incorrect assignments (misclassifications) from a screening programme for retinopathy and shows that this approach could be used to evaluate and compare other screening programmes. In these data, misclassification between lower grades of retinopathy is not uncommon, but under the current recommendations for annual screening, or if screening is extended to 2 or 3 years for those with no retinopathy, it is unlikely to have a significant effect on patient outcomes. Misclassification of referable retinopathy into a lower grade is more of a concern as this means that opportunities to intervene are inevitably delayed, which may be potentially harmful. Our findings suggest that the false‐negative rate is not insignificant and could be as high as 11%; more work may need to be done reduce this.
We have shown that it is feasible to use a model‐based approach to estimate the accuracy of a diabetic retinopathy screening programme at an aggregate level. We believe this method to be widely applicable and can be replicated quickly, easily and at minimal cost. The model‐based evaluation could inform organizers of screening programmes to identify problem areas and potential weaknesses in the delivery of retinopathy screening.
Funding sources
JLO's time working on this project was funded by the National Institute for Health Researchers' School for Primary Care Research (NIHR SPCR). The views expressed are those of the authors and not necessarily those of the NHS, the NIHR or the Department of Health. This research was supported from the NIHR Health Technology Assessment grant 10/66/01.
Competing interests
Professor Peter Scanlon is the Clinical Director for the English NHS Diabetic Eye Screening Programme.
Acknowledgements
We would like to acknowledge Professor Andrew Farmer, Dr Jose Leal and Dr Ramon Luengo‐Fernandez for their input in the early stages of this project.
Table A1.
Actual number of misclassifications resulting from the Viterbi algorithm
| States | Observed grade | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| No detectable retinopathy | Background retinopathy in one eye | Background retinopathy in both eyes | Referable maculopathy | Referable retinopathy (pre‐proliferative or proliferative) | ||
| Estimated true grade | 1 | 33 668 | 5 098 | 1 113 | 187 | 24 |
| 2 | 1 997 | 7 082 | 2 781 | 238 | 26 | |
| 3 | 245 | 388 | 6 430 | 687 | 143 | |
| 4 | 36 | 48 | 315 | 3 195 | 295 | |
| 5 | 9 | 15 | 207 | 375 | 1 237 | |
Diabet. Med. 33, 896–903 (2016)
[The copyright line for this article was changed on 23 February 2016 after original online publication]
References
- 1. Stratton IM, Aldington SJ, Taylor DJ, Adler AI, Scanlon PH. A simple risk stratification for time to development of sight‐threatening diabetic retinopathy. Diabetes Care 2013; 36: 580–585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Ruamviboonsuk P, Teerasuwanajak K, Tiensuwan M, Yuttitham K. Interobserver agreement in the interpretation of single‐field digital fundus images for diabetic retinopathy screening. Ophthalmology 2006; 113: 826–832. [DOI] [PubMed] [Google Scholar]
- 3. Milton RC, Ganley JP, Lynk RH. Variability in grading diabetic retinopathy from stereo fundus photographs: comparison of physician and lay readers. Br J Ophthalmol 1977; 61: 192–201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Uhry Z, Hédelin G, Colonna M, Asselain B, Arveux P, Rogel A et al Multi‐state Markov models in cancer screening evaluation: a brief review and case study. Stat Methods Med Res 2010; 19: 463–486. [DOI] [PubMed] [Google Scholar]
- 5. Jackson CH, Sharples LD, Thompson SG, Duffy SW, Couto E. Multistate Markov Models for disease progression with classification error. J R Stat Soc Ser D (The Stat) 2003; 52: 193–209. [Google Scholar]
- 6. Bureau A, Shiboski S, Hughes JP. Applications of continuous time hidden Markov models to the study of misclassified disease outcomes. Stat Med 2003; 22: 441–462. [DOI] [PubMed] [Google Scholar]
- 7. Kohner EM, Stratton IM, Aldington SJ, Turner RC, Matthews DR. Microaneurysms in the development of diabetic retinopathy (UKPDS 42). UK Prospective Diabetes Study Group. Diabetologia 1999; 42: 1107–1112. [DOI] [PubMed] [Google Scholar]
- 8. Jackson C. Multi‐state modelling with R: the msm package. 2007. Available at http://www.leg.ufpr.br/lib/exe/fetch.php/projetos:msc:msm-manual.pdf Last accessed 21 December 2011.
- 9. R Core Team . R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria, 2015.
- 10. Scanlon PH, Aldington SJ, Leal J, Luengo‐Fernandez R, Oke J, Sivaprasad S et al Development of a cost‐effectiveness model for optimisation of the screening interval in diabetic retinopathy screening. Health Technol Assess 2015; 19: 1–116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Zucchini W, MacDonald IL. Hidden Markov Models for Time Series. Boca Raton, FL: CRC Press, 2009. [Google Scholar]
- 12. Rabiner LR. A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition. Available at http://citeseer.ist.psu.edu/viewdoc/summary?doi=10.1.1.131.2084 Last accessed 7 September 2015.
- 13. Miller DK, Homan SM. Determining transition probabilities: confusion and suggestions. Med Decis Mak 1994; 14: 52–58. [DOI] [PubMed] [Google Scholar]
- 14. Titman AC. Model diagnostics in multi‐state models of biological systems. PhD thesis, University of Cambridge, 2007. Available at http://www.maths.lancs.ac.uk/~titman/thesis.pdf Last accessed 7 September 2015. [Google Scholar]
- 15. Stratton IM, Kohner EM, Aldington SJ, Turner RC, Holman RR, Manley SE et al UKPDS 50: risk factors for incidence and progression of retinopathy in Type II diabetes over 6 years from diagnosis. Diabetologia 2001; 44: 156–163. [DOI] [PubMed] [Google Scholar]
- 16. Stellingwerf C, Hardus PLLJ, Hooymans JMM. Two‐field photography can identify patients with vision‐threatening diabetic retinopathy: a screening approach in the primary care setting. Diabetes Care 2001; 24: 2086–2090. [DOI] [PubMed] [Google Scholar]
- 17. Harding SP, Broadbent DM, Neoh C, White MC, Vora J. Sensitivity and specificity of photography and direct ophthalmoscopy in screening for sight threatening eye disease: the Liverpool Diabetic Eye Study. BMJ 1995. Oct 28; 7013: 1131–1135. Available at http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=2551056&tool=pmcentrez&rendertype=abstract [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Scanlon PH, Malhotra R, Greenwood RH, Aldington SJ, Foy C, Flatman M et al Comparison of two reference standards in validating two field mydriatic digital photography as a method of screening for diabetic retinopathy. Br J Ophthalmol 2003; 87: 1258–1263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Olson JA, Strachan FM, Hipwell JH, Goatman KA, McHardy KC, Forrester JV et al A comparative evaluation of digital imaging, retinal photography and optometrist examination in screening for diabetic retinopathy. Diabet Med 2003; 20: 528–534. [DOI] [PubMed] [Google Scholar]
- 20. Scanlon PH, Malhotra R, Thomas G, Foy C, Kirkpatrick JN, Lewis‐Barned N et al The effectiveness of screening for diabetic retinopathy by digital imaging photography and technician ophthalmoscopy. Diabet Med 2003; 20: 467–474. [DOI] [PubMed] [Google Scholar]
- 21. Healy R, Sallam A, Jones V, Donachie PHJ, Scanlon PH, Stratton IM et al Agreement between photographic screening and hospital biomicroscopy grading of diabetic retinopathy and maculopathy. Eur J Ophthalmol 2014; 24: 550–558. [DOI] [PubMed] [Google Scholar]
- 22. Manjunatha RS, Manjunatha NP, Baskar V, Headon MP, Singh BM, Viswanath a K. Quality assurance in the diabetic retinopathy screening programme: evaluating the benefit of universal regrading of the normal primary grade. Diabet Med; 29: 287–288. [DOI] [PubMed] [Google Scholar]
- 23. Looker HC, Nyangoma SO, Cromie DT, Olson JA, Leese GP, Philip S et al Predicted impact of extending the screening interval for diabetic retinopathy: the Scottish Diabetic Retinopathy Screening programme. Diabetologia 2013; 56: 1716–1725. [DOI] [PMC free article] [PubMed] [Google Scholar]


