Abstract
A now common goal in medical research is to investigate the inter‐relationships between a repeatedly measured biomarker, measured with error, and the time to an event of interest. This form of question can be tackled with a joint longitudinal‐survival model, with the most common approach combining a longitudinal mixed effects model with a proportional hazards survival model, where the models are linked through shared random effects. In this article, we look at incorporating delayed entry (left truncation), which has received relatively little attention. The extension to delayed entry requires a second set of numerical integration, beyond that required in a standard joint model. We therefore implement two sets of fully adaptive Gauss–Hermite quadrature with nested Gauss–Kronrod quadrature (to allow time‐dependent association structures), conducted simultaneously, to evaluate the likelihood. We evaluate fully adaptive quadrature compared with previously proposed non‐adaptive quadrature through a simulation study, showing substantial improvements, both in terms of minimising bias and reducing computation time. We further investigate, through simulation, the consequences of misspecifying the longitudinal trajectory and its impact on estimates of association. Our scenarios showed the current value association structure to be very robust, compared with the rate of change that we found to be highly sensitive showing that assuming a simpler trend when the truth is more complex can lead to substantial bias. With emphasis on flexible parametric approaches, we generalise previous models by proposing the use of polynomials or splines to capture the longitudinal trend and restricted cubic splines to model the baseline log hazard function. The methods are illustrated on a dataset of breast cancer patients, modelling mammographic density jointly with survival, where we show how to incorporate density measurements prior to the at‐risk period, to make use of all the available information. User‐friendly Stata software is provided. © 2015 The Authors. Statistics in Medicine Published by John Wiley & Sons Ltd.
Keywords: joint modelling, delayed entry, left truncation, survival analysis, mixed effects, adaptive Gauss–Hermite quadrature
1. Introduction
Joint modelling of longitudinal and survival data has been extensively studied in the methodological literature, as it provides an efficient method to not only account for measurement error in a longitudinal biomarker included in a survival analysis but also alternatively account for informative dropout when the longitudinal process is of primary interest 1, 2. It has been shown through simulation that simply including the observed longitudinal outcome as a time‐varying covariate in a survival analysis can severely underestimate the true association 3. The most common form of joint model uses shared parameters, which links the longitudinal and survival components through random effects. With the increasing availability of user‐friendly software 4, 5, 6, 7, this form of joint model is beginning to find its place in applied clinical research 2, 8, 9. However, there is a multitude of further research needed, in particular, to utilise joint models fully in application to registry‐based datasets.
In this article, we incorporate delayed entry (left truncation) into the standard joint model framework, an aspect that has received relatively limited attention. Delayed entry occurs when a patient is not at risk of the event of interest until a time t > 0. Within a survival analysis setting, this occurs, for example, when using age as the timescale, which can be an improved way of controlling for the effect of age 10. Here, we can draw parallels with the challenges that arise when incorporating random effects into a delayed entry survival model 11, 12. Not only do we have the ‘weeding out’ process induced by the frailties, where patients with smaller frailties are more likely to have longer survival times, but the delayed entry causes a second selection issue, where patients with smaller frailties are more likely to reach the threshold set by an entry time.
Standard shared frailty survival models allowing delayed entry have received limited attention, which is particularly highlighted by the limited availability of software. The extensive frailtypack 13 in R allows left truncation with clustered survival times, in particular, a shared frailty model 14, an additive frailty model with two correlated random effects (intercept and slope) 15 and a nested frailty model with two levels of clustering allowing for independent gamma distributed random effects 16.
Incorporating delayed entry into the framework of joint longitudinal‐survival models has also received limited attention. Dantan et al. developed a joint model for longitudinal data and an illness–death process in cognitive ageing 17. They also allowed for an intermediate pre‐diagnosis state through a random change point. Estimation was conducted through maximum likelihood, using non‐adaptive Gauss–Hermite quadrature to evaluate analytically intractable integrals, using 20‐point quadrature in their simulation study, and state that use of fewer points leads to bias. Piccorelli and Schluchter 18 developed an expectation–maximization algorithm to jointly model repeatedly measured pulmonary function (FEV1% predicted) and survival in cystic fibrosis patients using registry data. Not all patients were followed from birth, which subsequently results in left truncation when using age as the timescale. They assumed a linear mixed effects model for the longitudinal outcome, with random intercept and slope, which, along with a transformation of age at death, were assumed to follow a trivariate normal distribution. Van den Hout and Muniz‐Terrera 19 developed a joint model for repeatedly measured discrete data, arising from tests of cognitive function, and survival in the analysis of an older population. They allowed for a random intercept and linear slope in the longitudinal submodel, assessing a binomial or beta‐binomial formulation, and a Weibull or Gompertz survival model. As interest was in prediction, they emphasised the benefits of adopting a parametric survival submodel. They looked at specific association structures to ensure that the cumulative hazard function could be calculated analytically and used 13‐point non‐adaptive Gauss–Hermite quadrature to integrate out the random effects. Within the alternative joint latent class modelling framework, Proust‐Lima et al. incorporated delayed entry into a joint model of multivariate longitudinal outcomes and a time to event 20.
The previous approaches described earlier can be considered limited to a random intercept and single random linear slope in the longitudinal submodel and standard parametric choices such as the Weibull or Gompertz for the survival submodel. Limited association structures, describing how the longitudinal and survival components are linked, were also implemented. Furthermore, the choice of non‐adaptive quadrature can be highly computationally intensive, particularly as a large number of quadrature points have been shown to be required to obtain appropriate standard errors 21. In this article, we emphasise the use of flexible parametric approaches, where in particular, we propose to incorporate fixed and random effect polynomials of time into the longitudinal submodel. This generalises previous approaches, allowing a highly flexible way of capturing nonlinear trajectories of the longitudinal outcome over time. Furthermore, to allow flexibility in parametric survival submodel formulations, we propose to model the baseline log hazard function using restricted cubic splines, which can capture multiple turning points/more complex shapes in the underlying event rate 22, 23. The extension to delayed entry requires a second set of numerical integration, beyond that required in a standard joint model, to evaluate the likelihood, which we propose to evaluate using fully adaptive Gauss–Hermite quadrature.
The clinical example that we use to illustrate this work comes from a study in breast cancer 24, where interest is in investigating the association between changes in mammographic density after diagnosis, and the time to death due to breast cancer. Mammographic density, which reflects the amount of fibroglandular tissue in the breast, is one of the strongest risk factors for breast cancer 25. It has also been suggested that, in women diagnosed with breast cancer, change in mammography density over time may be associated with prognosis/response to treatment 24, 26. The original study of Li et al. considered only the first two measurements/mammograms (diagnosis and follow‐up) to focus on the relationship between early response to treatment (in terms of mammography density change) and survival. We now re‐analyse the data and include information on all available measurements during follow‐up. Given that all patients have at least two measurements, by definition they cannot experience the event of interest until after the time of second measurement. Therefore, analysis requires delayed entry to be accounted for; however, we can still incorporate the baseline mammographic density measurement prior to entry within the longitudinal submodel.
In Section 2, we derive a joint model, incorporating delayed entry and flexible parametric formulations for the longitudinal trajectory, and baseline hazard function. In Section 3, we describe the estimation approach using adaptive Gauss–Hermite quadrature. In Section 4, we conduct a simulation study to (i) evaluate the performance of fully adaptive Gauss–Hermite quadrature, comparing with previously proposed non‐adaptive quadrature, and (ii) investigate the impact of misspecification of the longitudinal trajectory on estimates of association. In Section 5, we illustrate the methods in application to the breast cancer dataset, investigating the association between change in mammographic density over time and breast cancer survival. We describe user‐friendly Stata software, written by the first author, which was used to fit all the models in this paper, and describe a variety of other models available in the Supporting Information. We conclude the paper in Section 6 with a discussion.
2. Model framework and likelihood
We begin with some notation. Let T i be the observed survival time of the ith patient, where i = 1,…,n, with T i=min(S i,C i), the minimum of the true survival time, S i, and C i the censoring time. We define an event indicator d i, which takes the value of 1 if S i≤C i and 0 otherwise. We also have T 0i, the time at which a patient becomes at risk of the event, with T 0i<T i. Let y ij={y i(t ij),j = 1,…,n i} denote the observed longitudinal responses, with y i(t ij) the jth observed longitudinal response of a continuous biomarker for the ith patient taken at time t ij. Each patient has n i repeated measures. We further define a vector of time‐independent baseline covariates, Ui. To maintain flexibility, different subsets of Ui can be included in either the longitudinal or survival submodels. We define a vector of patient‐specific random effects, b i, which serve to capture the correlation between measurements of the same patient and the association between the longitudinal and survival outcomes.
2.1. Model framework
2.1.1. Longitudinal submodel
We assume a linear mixed effects model for the continuous longitudinal outcome, with
| (1) |
| (2) |
where X i and Z i are design matrices for the fixed (β) and random effects (b i), respectively. Baseline covariates can be included, represented by u i, with a vector of corresponding regression coefficients, δ. Measurement error is incorporated through ε ij, which we assume is independent to the random effects. We also assume that cov(ε ij,ε ik) = 0 (where j ≠ k).
Previously joint models with delayed entry have assumed a linear growth curve (random intercept and random linear slope); however, here, we wish to generalise to allow for the possibility of nonlinear trajectories by allowing both X i and Z i to contain (fractional) polynomial functions of time 27. Alternatively, we could use restricted cubic splines; however, in this article, we concentrate on the use of polynomials, but splines may be used in the associated Stata software (Supporting Information).
2.1.2. Survival submodel
We define the proportional hazards survival submodel
| (3) |
where s(log(t)|γ,k 0) is a restricted cubic spline function of log(t), that is, the log baseline hazard function with knot vector k 0 and coefficient vector γ. Using splines to model the baseline log hazard function can provide a very flexible framework to capture turning points in the underlying hazard function, while the restricted nature ensures a sensible form in the tails, that is, linearity is imposed beyond the boundary knots that are placed at the minimum and maximum event times. Further details on this form of survival model can be found elsewhere 22, 23. A recent extensive simulation study showed that the AIC and BIC can be used to guide knot selection effectively 28. We also have v i∈U i, which is a set of baseline covariates with associated vector of log hazard ratios, ψ, and α 1 is termed the association parameter, representing a log hazard ratio for a one‐unit increase in the longitudinal outcome at time t. This association is termed the current value association structure, which is one of the many ways to link the longitudinal and survival components. In the illustrative breast cancer example, we study how the rate of change of mammographic density is associated with survival, which can be investigated using the following association structure:
| (4) |
where
The interpretation of α 2 under the slope association is the log hazard ratio for a one‐unit increase in the rate of change of the longitudinal outcome at time t. Both the current value and slope associations can be considered time‐dependent association structures, and therefore, it is of direct interest to investigate the impact of model misspecification in terms of capturing the longitudinal trajectory and how it impacts on the estimates of association, our α parameters. Other association structures have been studied, for example, time‐independent structures, linking say the random intercept; however, we refer the reader elsewhere for further details 29, 30.
2.2. Likelihood
We define the parameter vector to be θ={θ t,θ y,θ b}. The likelihood for the ith patient, L i, conditional on entry time T 0i, can be written as
| (5) |
where
| (6) |
The numerator in Equation (5) is the likelihood under a standard joint model, with the addition being the denominator due to the delayed entry aspect.
Assuming a continuous normally distributed longitudinal outcome, we have
| (7) |
and assuming normally distributed random effects gives
| (8) |
with variance–covariance matrix, Σ, where Q is the dimension of the random effects. Under a proportional hazards survival model, we have
| (9) |
with h() defined in Equation (3) or (4). Maximising the likelihood in Equation (5) is a computationally challenging task, as integrating out the random effects, in both the numerator and denominator, requires separate numerical integration. Furthermore, each set of numerical integration has a nested integral required to calculate the cumulative hazard function and subsequently the survival function, because of the use of splines to model the log baseline hazard function. However, this is also often required when using time‐dependent association structures combined with standard parametric choices for the baseline hazard, such as the Weibull 6.
3. Estimation
The overall log likelihood, L, is given by
| (10) |
and can be maximised using the Newton–Raphson technique in the ml engine in Stata, with derivatives calculated using finite differences. However, we must employ numerical integration techniques to calculate the joint likelihood. The implementation of adaptive quadrature has been shown to be far superior to non‐adaptive within a standard joint model context 21. With the extension to delayed entry, this requires a second set of numerical integration, to be conducted simultaneously, in order to calculate the denominator in Equation (5).
We briefly describe our implementation of adaptive quadrature to evaluate the joint likelihood 31, 32, 33. Beginning with the numerator in Equation (5), which is equivalent to the joint likelihood when delayed entry is not present, the integrals can be evaluated employing adaptive Gauss–Hermite quadrature. Following 32, consider the kernel normal distribution of , multiplying and dividing the numerator of Equation (5) by the kernel give
| (11) |
with subject‐specific random effect posterior means and variance–covariance matrices, and . Equation (11) can then be evaluated using Gauss–Hermite quadrature using this alternative normal kernel density, with the nodes appropriately transformed using , where are the vector of nodes based on the multivariate standard normal kernel, which is pre‐multiplied by the Cholesky decomposition of the estimated subject‐specific variance–covariance matrix of the random effects, .
This gives
| (12) |
where are the quadrature weights from the standard normal kernel. Similarly, the denominator in Equation (5) can be evaluated using a separate set of adaptive Gauss–Hermite quadrature as follows, where
| (13) |
where .
We implement the following algorithm:
Obtain starting values for θ 0. These are obtained by fitting a separate linear mixed effects model, obtaining patient‐specific predictions from the mixed effects model and including them as a time‐varying covariate within a standard survival model (this assumes the current value association but is appropriately altered under different association structures). This is a computationally efficient way of obtaining excellent starting values for the full joint model. We also obtain initial values for the quadrature node locations, and using empirical Bayes predictions of the random effects from the same separate linear mixed effects model, and use a default of 0 and 1 for and .
- Repeat for k = 1,2,… until Newton–Raphson iterations have converged.
- Predict the subject‐specific posterior means and standard deviations, and :
- Predict the subject‐specific posterior means and standard deviations, and using adaptive quadrature based on previous estimates, and .
- Repeat for j = 1,2,… until convergence:
- Predict the subject‐specific posterior means and standard deviations, and using adaptive quadrature based on previous estimates, and .
- Update the parameter estimates to θ k using adaptive quadrature using and .
We use a tolerance of 1.0E − 08 for the convergence of the quadrature node locations in the j iterations and standard convergence criteria for the k iterations, that is, the full Newton–Raphson iterations.
4. Simulation study
In this section, we conduct a simulation study with two primary aims: (i) to investigate the performance of fully adaptive Gauss–Hermite quadrature in calculating the joint likelihood with delayed entry, comparing with previously proposed non‐adaptive quadrature, and (ii) to investigate the impact of misspecification of the longitudinal trajectory on estimates of association.
We assume the following longitudinal trajectory:
| (14) |
where
| (15) |
that is, a random intercept and random linear slope with fixed squared and cubic powers of time. To investigate the impact of misspecifying the longitudinal submodel on estimates of association, we simulate scenarios using either the current value structure shown in Equation (3) or the rate of change structure shown in Equation (4). This allows us to directly compare their robustness. Therefore, we simulate under the following survival submodel, with a Weibull baseline hazard function and current value structure,
| (16) |
or the rate of change structure,
| (17) |
Parameter values are given as follows: β 0=4.348, β 1=−0.239, β 2=0.0264, β 3=−0.00108, σ 0=1.143, σ 1=0.0704, ρ =− 0.0923, λ = 0.00574 and γ = 1.197. These were based on fitting separate survival and longitudinal models to the breast cancer dataset to provide plausible functions from which to simulate. The assumed true underlying baseline hazard function, longitudinal trajectory and rate of change of the longitudinal trajectory are shown in Figure 1.
Figure 1.
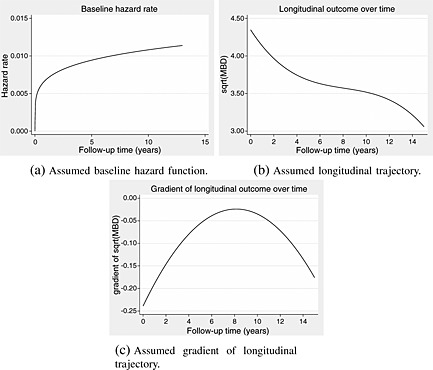
Assumed functions based on models applied to the breast cancer data to inform the simulation study.
In scenarios that assume the current value structure, we vary α 1={0.1,0.25,0.5}, and in scenarios that assume the rate of change structure, we vary α 2={1,2,3}. Survival times are simulated using the general survival simulation algorithm of Crowther and Lambert 34. In each simulation, 1000 patient survival times are generated using Equation (16) or (17), with accompanying entry times generated from a uniform distribution U(0,3). Any patients whose survival time is less than their entry time are deleted. Observed longitudinal measurements are then simulated at a patient's entry time and annually thereafter, with up to 10 measurements per patient, from , where σ e=0.591. Finally, administrative censoring is applied at 15 years. Any measurements simulated after the patients survival/censoring time are deleted.
To each simulated dataset under each set of parameter values, we apply both the joint model defined by Equations (14)–(16) or (17), that is, the true model (either current value or rate of change structure, as appropriate) and a joint model assuming just a random intercept and random linear slope in the longitudinal submodel, with no squared or cubic fixed effect time terms to assess the impact of misspecifying the trajectory. Each model is applied using 5‐point adaptive Gauss–Hermite and 5‐point and 15‐point non‐adaptive quadrature. We conduct 200 repetitions of each simulation scenario and present results in Tables 1 and 2. Bias, percentage bias and coverage are calculated on the parametrised scales, for example, standard deviations and the shape and scale parameters are on the log scale, and the correlation between the random intercept and slope is parametrised using the inverse hyperbolic tangent transformation (this is the standard parametrisation used in Stata for correlation parameters 35).
Table 1.
Simulation results of bias, percentage bias, coverage and mean square error of all parameters from current value association structure scenarios.
| Scenario | Parameter | Truth | 5‐point adaptive quadrature | 5‐point non‐adaptive quadrature | 15‐point non‐adaptive quadrature | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Polynomial | Linear | Polynomial | Linear | Polynomial | Linear | |||||||||||||||||||||
| Bias | % bias | CP | MSE | Bias | % bias | CP | MSE | Bias | % bias | CP | MSE | Bias | % bias | CP | MSE | Bias | % bias | CP | MSE | Bias | % bias | CP | MSE | |||
| 1 | β 0 | 4.348 | −0.002 | −0.04 | 95.0 | 0.002 | −0.308 | −7.08 | 0.0 | 0.096 | −0.004 | −0.10 | 66.0 | 0.009 | −0.312 | −7.18 | 1.0 | 0.105 | −0.002 | −0.04 | 90.0 | 0.003 | −0.308 | −7.08 | 0.0 | 0.097 |
| β 1 | −0.239 | 0.000 | −0.02 | 93.0 | 0.001 | 0.180 | −75.22 | 0.0 | 0.032 | 0.000 | −0.04 | 93.0 | 0.001 | 0.180 | −75.33 | 0.0 | 0.032 | 0.000 | −0.03 | 92.0 | 0.001 | 0.180 | −75.27 | 0.0 | 0.032 | |
| log(σ 0) | 0.133 | −0.002 | 0.08 | 94.0 | 0.002 | 0.008 | −0.32 | 94.5 | 0.002 | −0.371 | 13.96 | 0.0 | 0.142 | −0.358 | 13.49 | 0.0 | 0.133 | −0.031 | 1.17 | 89.5 | 0.003 | −0.021 | 0.78 | 93.5 | 0.003 | |
| log(σ 1) | −2.654 | −0.002 | −1.30 | 95.0 | 0.001 | 0.001 | 0.53 | 94.5 | 0.001 | −0.147 | −110.18 | 0.5 | 0.023 | −0.146 | −109.33 | 0.5 | 0.023 | −0.038 | −28.57 | 62.5 | 0.002 | −0.038 | −28.54 | 60.0 | 0.002 | |
| atanh(ρ) | −0.093 | 0.004 | −4.60 | 96.0 | 0.002 | −0.005 | 5.77 | 96.5 | 0.002 | 0.307 | −331.48 | 0.0 | 0.095 | 0.302 | −326.01 | 0.0 | 0.092 | 0.138 | −148.65 | 0.0 | 0.020 | 0.131 | −142.09 | 0.0 | 0.018 | |
| log(σ e) | −0.526 | 0.000 | −0.01 | 93.0 | 0.000 | 0.006 | −1.12 | 87.0 | 0.000 | 0.040 | −7.57 | 0.0 | 0.002 | 0.046 | −8.66 | 0.0 | 0.002 | 0.004 | −0.72 | 91.5 | 0.000 | 0.010 | −1.86 | 75.0 | 0.000 | |
| log(λ) | −5.160 | −0.021 | 0.41 | 94.0 | 0.230 | −0.025 | 0.48 | 95.0 | 0.227 | −0.020 | 0.39 | 94.0 | 0.231 | −0.029 | 0.56 | 94.0 | 0.228 | −0.021 | 0.41 | 94.5 | 0.229 | −0.025 | 0.48 | 95.0 | 0.227 | |
| log(γ) | 0.180 | −0.005 | −2.78 | 94.5 | 0.011 | −0.004 | −2.22 | 95.5 | 0.011 | −0.004 | −2.22 | 95.0 | 0.011 | −0.004 | −2.22 | 95.0 | 0.011 | −0.005 | −2.78 | 95.0 | 0.011 | −0.004 | −2.22 | 95.5 | 0.011 | |
| α | 0.100 | 0.008 | 8.00 | 95.5 | 0.004 | 0.009 | 9.00 | 95.5 | 0.004 | 0.008 | 8.00 | 96.5 | 0.004 | 0.010 | 10.00 | 96.0 | 0.004 | 0.008 | 8.00 | 95.0 | 0.004 | 0.009 | 9.00 | 95.5 | 0.004 | |
| 2 | β 0 | 4.348 | −0.008 | −0.18 | 90.5 | 0.003 | −0.311 | −7.16 | 0.0 | 0.099 | −0.001 | −0.03 | 61.5 | 0.009 | −0.307 | −7.07 | 0.0 | 0.102 | −0.008 | −0.18 | 87.0 | 0.004 | −0.312 | −7.17 | 0.0 | 0.100 |
| β 1 | −0.239 | −0.000 | 0.08 | 92.0 | 0.001 | 0.179 | −75.06 | 0.0 | 0.032 | −0.001 | 0.25 | 93.0 | 0.001 | 0.180 | −75.34 | 0.0 | 0.032 | −0.000 | 0.13 | 92.0 | 0.001 | 0.180 | −75.25 | 0.0 | 0.032 | |
| log(σ 0) | 0.133 | −0.002 | 0.06 | 93.5 | 0.002 | 0.009 | −0.32 | 93.0 | 0.002 | −0.378 | 14.25 | 0.0 | 0.148 | −0.370 | 13.94 | 0.0 | 0.142 | −0.032 | 1.20 | 91.0 | 0.004 | −0.024 | 0.89 | 91.5 | 0.003 | |
| log(σ 1) | −2.654 | −0.002 | −1.13 | 95.0 | 0.001 | 0.004 | 2.83 | 93.5 | 0.001 | −0.151 | −113.54 | 0.0 | 0.024 | −0.149 | −111.90 | 0.0 | 0.024 | −0.039 | −29.34 | 58.0 | 0.002 | −0.037 | −27.46 | 62.5 | 0.002 | |
| atanh(ρ) | −0.093 | 0.001 | −0.70 | 95.0 | 0.003 | −0.016 | 17.07 | 93.5 | 0.003 | 0.309 | −334.51 | 0.0 | 0.097 | 0.307 | −331.72 | 0.0 | 0.095 | 0.138 | −149.17 | 0.0 | 0.020 | 0.132 | −142.21 | 1.0 | 0.018 | |
| log(σ e) | −0.526 | 0.001 | −0.10 | 95.0 | 0.000 | 0.006 | −1.23 | 88.0 | 0.000 | 0.039 | −7.50 | 0.0 | 0.002 | 0.046 | −8.67 | 0.0 | 0.002 | 0.004 | −0.83 | 93.5 | 0.000 | 0.011 | −2.02 | 74.5 | 0.000 | |
| log(λ) | −5.160 | 0.004 | −0.08 | 97.5 | 0.105 | −0.005 | 0.10 | 97.0 | 0.107 | 0.017 | −0.33 | 97.5 | 0.111 | 0.001 | −0.02 | 96.5 | 0.113 | 0.006 | −0.12 | 97.5 | 0.105 | −0.003 | 0.06 | 97.0 | 0.106 | |
| log(γ) | 0.180 | −0.008 | −4.45 | 96.5 | 0.006 | −0.007 | −3.89 | 96.5 | 0.006 | −0.008 | −4.45 | 96.0 | 0.006 | −0.006 | −3.33 | 96.5 | 0.006 | −0.009 | −5.00 | 96.5 | 0.006 | −0.008 | −4.45 | 96.5 | 0.006 | |
| α | 0.250 | 0.003 | 1.20 | 95.0 | 0.002 | 0.004 | 1.60 | 95.0 | 0.003 | −0.000 | 0.00 | 95.5 | 0.003 | 0.002 | 0.80 | 95.5 | 0.003 | 0.003 | 1.20 | 94.5 | 0.002 | 0.004 | 1.60 | 94.0 | 0.003 | |
| 3 | β 0 | 4.348 | −0.003 | −0.06 | 93.0 | 0.003 | −0.286 | −6.59 | 0.0 | 0.084 | −0.029 | −0.67 | 65.5 | 0.011 | −0.320 | −7.36 | 0.0 | 0.110 | −0.006 | −0.15 | 90.5 | 0.004 | −0.295 | −6.79 | 0.0 | 0.090 |
| β 1 | −0.239 | −0.000 | 0.16 | 96.5 | 0.001 | 0.176 | −73.50 | 0.0 | 0.031 | −0.004 | 1.49 | 95.5 | 0.001 | 0.178 | −74.48 | 0.0 | 0.032 | −0.001 | 0.38 | 95.5 | 0.001 | 0.178 | −74.65 | 0.0 | 0.032 | |
| log(σ 0) | 0.133 | 0.007 | −0.25 | 95.0 | 0.003 | 0.007 | −0.26 | 93.5 | 0.003 | −0.397 | 14.95 | 0.0 | 0.165 | −0.409 | 15.42 | 0.0 | 0.176 | −0.026 | 0.96 | 91.0 | 0.004 | −0.034 | 1.28 | 91.5 | 0.005 | |
| log(σ 1) | −2.654 | −0.001 | −0.84 | 97.0 | 0.001 | 0.016 | 11.67 | 93.0 | 0.001 | −0.137 | −102.91 | 1.0 | 0.020 | −0.129 | −96.65 | 2.0 | 0.018 | −0.035 | −26.32 | 68.0 | 0.002 | −0.026 | −19.82 | 75.0 | 0.002 | |
| atanh(ρ) | −0.093 | −0.005 | 5.55 | 95.0 | 0.004 | −0.051 | 55.62 | 85.0 | 0.007 | 0.329 | −355.80 | 0.0 | 0.110 | 0.328 | −354.57 | 0.0 | 0.113 | 0.141 | −152.17 | 1.5 | 0.023 | 0.129 | −139.19 | 3.5 | 0.022 | |
| log(σ e) | −0.526 | −0.000 | 0.02 | 96.0 | 0.000 | 0.006 | −1.16 | 91.5 | 0.000 | 0.038 | −7.31 | 2.0 | 0.002 | 0.045 | −8.64 | 0.0 | 0.002 | 0.004 | −0.74 | 94.5 | 0.000 | 0.011 | −2.09 | 81.5 | 0.000 | |
| log(λ) | −5.160 | −0.058 | 1.12 | 95.0 | 0.086 | −0.084 | 1.63 | 95.0 | 0.089 | −0.037 | 0.72 | 94.0 | 0.084 | −0.078 | 1.51 | 95.0 | 0.090 | −0.061 | 1.18 | 95.5 | 0.085 | −0.089 | 1.72 | 95.0 | 0.089 | |
| log(γ) | 0.180 | 0.010 | 5.56 | 94.0 | 0.003 | 0.014 | 7.78 | 94.0 | 0.004 | 0.016 | 8.89 | 92.0 | 0.004 | 0.020 | 11.11 | 92.0 | 0.004 | 0.009 | 5.00 | 95.5 | 0.003 | 0.012 | 6.67 | 94.5 | 0.003 | |
| α | 0.500 | 0.005 | 1.00 | 94.0 | 0.002 | 0.010 | 2.00 | 94.0 | 0.002 | −0.004 | −0.80 | 93.0 | 0.002 | 0.004 | 0.80 | 92.5 | 0.002 | 0.007 | 1.40 | 93.5 | 0.002 | 0.012 | 2.40 | 93.5 | 0.002 | |
CP, coverage probability; MSE, mean square error; atanh, inverse hyperbolic tangent.
Table 2.
Simulation results of bias, percentage bias, coverage and mean square error of all parameters from rate of change association structure scenarios.
| Scenario | Parameter | Truth | 5‐point adaptive quadrature | 5‐point non‐adaptive quadrature | 15‐point non‐adaptive quadrature | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Polynomial | Linear | Polynomial | Linear | Polynomial | Linear | |||||||||||||||||||||
| Bias | % bias | CP | MSE | Bias | % bias | CP | MSE | Bias | % bias | CP | MSE | Bias | % bias | CP | MSE | Bias | % bias | CP | MSE | Bias | % bias | CP | MSE | |||
| 1 | β 0 | 4.348 | −0.003 | −0.06 | 98.0 | 0.002 | −0.312 | −7.18 | 0.0 | 0.099 | −0.012 | −0.27 | 68.8 | 0.012 | −0.318 | −7.31 | 0.0 | 0.107 | −0.005 | −0.11 | 90.9 | 0.004 | −0.312 | −7.17 | 0.0 | 0.100 |
| β 1 | −0.239 | 0.000 | −0.07 | 96.0 | 0.001 | 0.180 | −75.33 | 0.0 | 0.032 | 0.001 | −0.32 | 96.0 | 0.001 | 0.180 | −75.46 | 0.0 | 0.033 | −0.000 | 0.02 | 95.5 | 0.001 | 0.180 | −75.32 | 0.0 | 0.032 | |
| log(σ 0) | 0.133 | 0.002 | −0.07 | 95.0 | 0.002 | 0.012 | −0.47 | 94.0 | 0.002 | −0.366 | 13.79 | 0.0 | 0.139 | −0.355 | 13.37 | 0.0 | 0.130 | −0.026 | 0.99 | 91.9 | 0.003 | −0.017 | 0.62 | 94.0 | 0.002 | |
| log(σ 1) | −2.654 | 0.000 | 0.17 | 96.0 | 0.001 | 0.002 | 1.37 | 95.0 | 0.001 | −0.150 | −112.72 | 0.5 | 0.024 | −0.149 | −111.93 | 0.5 | 0.024 | −0.037 | −27.43 | 63.6 | 0.002 | −0.036 | −26.95 | 62.0 | 0.002 | |
| atanh(ρ) | −0.093 | −0.000 | 0.46 | 95.0 | 0.003 | −0.008 | 8.50 | 93.5 | 0.003 | 0.305 | −329.61 | 0.0 | 0.094 | 0.302 | −326.27 | 0.0 | 0.092 | 0.133 | −144.25 | 1.0 | 0.019 | 0.128 | −138.35 | 0.0 | 0.017 | |
| log(σ e) | −0.526 | −0.000 | 0.06 | 93.5 | 0.000 | 0.006 | −1.08 | 88.0 | 0.000 | 0.040 | −7.52 | 1.0 | 0.002 | 0.045 | −8.64 | 0.5 | 0.002 | 0.003 | −0.65 | 92.4 | 0.000 | 0.010 | −1.83 | 77.5 | 0.000 | |
| log(λ) | −5.160 | 0.012 | −0.23 | 97.0 | 0.284 | −0.160 | 3.10 | 98.0 | 0.232 | −0.002 | 0.04 | 98.0 | 0.525 | −0.117 | 2.27 | 97.0 | 0.225 | 0.002 | −0.04 | 97.0 | 0.298 | −0.152 | 2.95 | 98.0 | 0.231 | |
| log(γ) | 0.180 | −0.013 | −7.22 | 99.0 | 0.020 | 0.005 | 2.78 | 95.5 | 0.016 | −0.009 | −5.00 | 98.5 | 0.070 | 0.005 | 2.78 | 95.5 | 0.016 | −0.010 | −5.56 | 99.0 | 0.023 | 0.005 | 2.78 | 95.5 | 0.016 | |
| α | 1.000 | 0.129 | 12.90 | 96.0 | 3.373 | −1.577 | −157.70 | 87.5 | 8.427 | 0.025 | 2.50 | 96.0 | 6.612 | −0.942 | −94.20 | 94.5 | 7.940 | 0.086 | 8.60 | 97.0 | 3.415 | −1.461 | −146.10 | 88.0 | 8.283 | |
| 2 | β 0 | 4.348 | 0.001 | 0.03 | 94.0 | 0.003 | −0.308 | −7.09 | 0.0 | 0.096 | −0.002 | −0.03 | 62.5 | 0.009 | −0.308 | −7.08 | 0.0 | 0.102 | −0.001 | −0.02 | 90.5 | 0.003 | −0.310 | −7.12 | 0.0 | 0.098 |
| β 1 | −0.239 | −0.000 | 0.14 | 92.0 | 0.001 | 0.180 | −75.22 | 0.0 | 0.032 | −0.000 | 0.19 | 90.5 | 0.001 | 0.180 | −75.22 | 0.0 | 0.032 | −0.000 | 0.14 | 91.0 | 0.001 | 0.180 | −75.22 | 0.0 | 0.032 | |
| log(σ 0) | 0.133 | −0.006 | 0.24 | 93.5 | 0.002 | 0.003 | −0.10 | 91.5 | 0.002 | −0.367 | 13.84 | 0.0 | 0.139 | −0.357 | 13.46 | 0.0 | 0.132 | −0.037 | 1.40 | 86.4 | 0.004 | −0.028 | 1.06 | 88.0 | 0.003 | |
| log(σ 1) | −2.654 | 0.001 | 0.49 | 96.5 | 0.001 | 0.002 | 1.65 | 96.0 | 0.001 | −0.154 | −115.22 | 1.0 | 0.025 | −0.152 | −114.28 | 0.0 | 0.025 | −0.038 | −28.23 | 59.8 | 0.002 | −0.037 | −27.41 | 60.5 | 0.002 | |
| atanh(ρ) | −0.093 | 0.004 | −4.69 | 96.0 | 0.002 | −0.003 | 3.37 | 95.0 | 0.002 | 0.301 | −325.19 | 0.0 | 0.092 | 0.298 | −322.48 | 0.0 | 0.090 | 0.139 | −150.38 | 0.5 | 0.020 | 0.134 | −145.32 | 0.0 | 0.019 | |
| log(σ e) | −0.526 | −0.000 | 0.01 | 96.0 | 0.000 | 0.006 | −1.12 | 89.5 | 0.000 | 0.039 | −7.39 | 0.0 | 0.002 | 0.045 | −8.51 | 0.0 | 0.002 | 0.004 | −0.77 | 92.0 | 0.000 | 0.010 | −1.90 | 78.5 | 0.000 | |
| log(λ) | −5.160 | −0.079 | 1.53 | 97.5 | 0.329 | −0.297 | 5.76 | 93.0 | 0.293 | −0.075 | 1.45 | 97.0 | 0.289 | −0.268 | 5.19 | 94.0 | 0.274 | −0.076 | 1.47 | 97.0 | 0.324 | −0.287 | 5.56 | 93.5 | 0.288 | |
| log(γ) | 0.180 | 0.007 | 3.89 | 96.5 | 0.026 | 0.035 | 19.45 | 95.0 | 0.015 | 0.007 | 3.89 | 97.5 | 0.021 | 0.035 | 19.45 | 94.5 | 0.015 | 0.007 | 3.89 | 97.5 | 0.025 | 0.035 | 19.45 | 95.0 | 0.015 | |
| α | 2.000 | 0.038 | 1.90 | 91.5 | 3.760 | −1.916 | −95.80 | 88.5 | 9.180 | −0.033 | −1.65 | 92.0 | 3.473 | −1.531 | −76.55 | 94.5 | 7.972 | 0.042 | 2.10 | 91.5 | 3.601 | −1.767 | −88.35 | 93.0 | 8.548 | |
| 3 | β 0 | 4.348 | −0.002 | −0.05 | 94.9 | 0.003 | −0.312 | −7.18 | 0.0 | 0.099 | 0.003 | 0.06 | 66.5 | 0.008 | −0.303 | −6.97 | 0.0 | 0.098 | −0.002 | −0.05 | 86.4 | 0.008 | −0.312 | −7.18 | 0.0 | 0.099 |
| β 1 | −0.239 | −0.000 | 0.13 | 95.4 | 0.001 | 0.180 | −75.39 | 0.0 | 0.032 | −0.001 | 0.61 | 93.9 | 0.001 | 0.180 | −75.40 | 0.0 | 0.032 | −0.000 | 0.15 | 93.9 | 0.001 | 0.180 | −75.39 | 0.0 | 0.032 | |
| log(σ 0) | 0.133 | −0.006 | 0.22 | 98.0 | 0.002 | 0.003 | −0.11 | 94.5 | 0.002 | −0.368 | 13.86 | 0.0 | 0.139 | −0.358 | 13.50 | 0.0 | 0.132 | −0.035 | 1.31 | 89.9 | 0.022 | −0.026 | 0.97 | 93.0 | 0.003 | |
| log(σ 1) | −2.654 | −0.002 | −1.13 | 96.4 | 0.001 | −0.000 | −0.21 | 95.0 | 0.001 | −0.157 | −118.09 | 0.0 | 0.026 | −0.155 | −116.40 | 0.0 | 0.025 | −0.039 | −29.37 | 56.1 | 0.003 | −0.039 | −29.36 | 55.5 | 0.002 | |
| atanh(ρ) | −0.093 | 0.006 | −6.44 | 98.0 | 0.002 | −0.001 | 1.42 | 96.5 | 0.002 | 0.301 | −325.44 | 0.0 | 0.092 | 0.299 | −323.11 | 0.0 | 0.090 | 0.138 | −148.75 | 0.5 | 0.020 | 0.133 | −143.67 | 0.5 | 0.019 | |
| log(σ e) | −0.526 | 0.001 | −0.11 | 95.9 | 0.000 | 0.006 | −1.21 | 86.5 | 0.000 | 0.039 | −7.50 | 0.0 | 0.002 | 0.045 | −8.59 | 0.0 | 0.002 | 0.004 | −0.84 | 89.9 | 0.001 | 0.010 | −1.95 | 76.0 | 0.000 | |
| log(λ) | −5.160 | −0.012 | 0.23 | 99.0 | 0.365 | −0.256 | 4.96 | 94.0 | 0.310 | −0.031 | 0.60 | 97.0 | 2.117 | −0.242 | 4.69 | 93.0 | 0.319 | −0.006 | 0.12 | 97.5 | 0.891 | −0.249 | 4.83 | 94.5 | 0.308 | |
| log(γ) | 0.180 | −0.010 | −5.56 | 98.0 | 0.030 | 0.025 | 13.89 | 95.0 | 0.019 | −0.005 | −2.78 | 96.4 | 0.537 | 0.025 | 13.89 | 95.0 | 0.019 | −0.012 | −6.67 | 96.5 | 0.153 | 0.025 | 13.89 | 94.5 | 0.019 | |
| α | 3.000 | 0.138 | 4.60 | 98.5 | 3.126 | −1.815 | −60.50 | 86.0 | 9.738 | −0.143 | −4.77 | 94.4 | 3.717 | −1.715 | −57.17 | 92.5 | 9.497 | 0.106 | 3.53 | 95.5 | 8.320 | −1.704 | −56.80 | 88.0 | 9.109 | |
CP, coverage probability; MSE, mean square error; atanh, inverse hyperbolic tangent.
4.1. Results – current value
Results for the current value simulation scenarios are presented in Table 1. When fitting the true model, we generally find unbiased results and coverage probabilities around the optimum 95% from 5‐point adaptive quadrature across all scenarios, compared with substantial bias in estimates of variance and correlation parameters in the longitudinal submodel from 5‐point and 15‐point non‐adaptive quadrature, in particular, underestimating random effect standard deviations. For example, in scenario 1 under 5‐point adaptive quadrature, we observe 0.08% bias and 94% coverage probability in estimates of the log standard deviation of the random intercept, compared with 13.96% bias and 0.0% coverage probability from 5‐point non‐adaptive quadrature. All numerical integration techniques provide generally unbiased estimates of the association parameter, with coverage probabilities close to 95%.
Looking specifically at the 5‐point adaptive quadrature results, comparing the true model with the linear misspecified joint model, survival parameters appear to be minimally effected by the misspecification. Estimates of the association parameter appear to be generally unbiased in both the true and misspecified models. All simulations for each scenario converged except one iteration in scenario 3, with 5‐point adaptive quadrature when fitting the true model.
4.2. Results – rate of change
Results from the rate of change simulation scenarios are presented in Table 2. When fitting the true model, 5‐point adaptive quadrature produces results with minimal bias and with coverage probabilities broadly close to the optimum 95%. Comparing this with moderate to high levels of bias under 5‐point non‐adaptive quadrature and sub‐optimum coverage probabilities, which are slightly alleviated by 15‐point non‐adaptive quadrature, both, however, do not approach the performance of adaptive quadrature.
Looking at estimates under 5‐point adaptive quadrature and comparing between the simpler linear model and the true polynomial model, we observe substantial bias in the estimates of the association parameter (α) in the linear model compared with the true model. For example, in scenario 2, we observe percentage biases in estimate of −95.80% and 1.90% under the linear and polynomial models, respectively. This is consistent across all three scenarios.
Finally, comparing computation time under scenario 3, when α = 3, the median computation time to convergence on a standard laptop with 4 GB of RAM and i5 processor, with 5‐point adaptive quadrature, was 30 s (range 26, 57), compared with 114 s (range 85, 205) with 15‐point non‐adaptive. Full computation times for each scenario are not shown as the simulations were not all run on the same computer. All simulations for each scenario with the linear model converged; however, one out of 200 simulations failed to converge in each of the true model fits, across numerical integration types. Results are presented for simulations that converged.
5. Joint modelling of repeatedly measured mammographic density and breast cancer survival
The clinical example that we use to illustrate this work comes from a population‐based, case–control study conducted in Sweden between 1993 and 1995 of patients diagnosed with breast cancer 24. The original study by Li et al. looked at change in mammographic density between baseline mammographic density measurement and first follow‐up measurement, as a prognostic marker. No modelling of mammographic density was carried out. Mammographic density, which reflects the amount of fibroglandular tissue in the breast, is one of the strongest risk factors for breast cancer 25. It has also been suggested that, in women diagnosed with breast cancer, change in mammography density over time may be associated with prognosis/response to treatment 24, 26. Joint modelling provides the possibility to use all available measurements during follow‐up and to learn about how mammography density changes through time as a function of treatment, accounting for dropout and measurement error, as well as providing a framework for formulating hypotheses relating to density change (as a marker of response to treatment) to survival. Because of patients having at least two measurements, they are not at risk of the event of interest until time of their second mammographic screening, and therefore, delayed entry is required. Primary interest is therefore in the rate of change association structure, shown in Equation (4); however, we also investigate the current value formulation shown in Equation (3), as it is the most commonly used association structure, and we can investigate whether the results shown in the simulation study are echoed in the applied analyses.
The dataset consists of 974 patients, of which 121 (12.4%) died during follow‐up. Maximum follow‐up is 15.45 years. A total of 6158 measurements of percentage mammographic density are available. The median number of mammograms per patient was 6, with a range of (2, 13). This dataset was used to inform the simulation study in the previous section. The following covariates were used in our analysis: age at diagnosis (years), body mass index (BMI) (kg/m2, measured at interview), tamoxifen treatment (yes/no), oestrogen receptor status (negative/positive/missing), tumour size (mm, range 1–80), number of metastatic nodes (range 0–38), grade (1 = well differentiated, 2 = moderately differentiated, 3 = poorly differentiated and 4 = missing), chemotherapy (yes/no), ever used hormone replacement therapy (yes/no) and radiotherapy (yes/no). Some missing data were present in oestrogen receptor status (27.4% missing) and grade (30.1% missing), which are included by using missing categories. In all analyses, we use the square root of percentage mammographic density to account for some right skewness, and consequently now all subsequent references to percentage mammographic density mean the square root of it. The Kaplan–Meier curve is shown in Figure 2.
Figure 2.
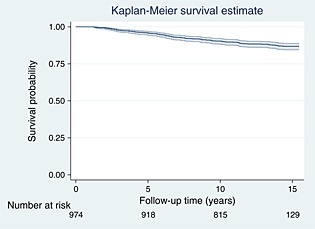
Kaplan–Meier survival curve of the breast cancer dataset, with 95% confidence interval.
We begin with preliminary modelling of the survival data only, investigating the shape of the baseline hazard function using restricted cubic splines on the log hazard scale 22, 23. We use the AIC and BIC to guide the selection of the number of spline terms to capture the baseline hazard function 28. Results are presented in Table 3, with up to 5 degrees of freedom (6 knots), plus an intercept for each baseline hazard function.
Table 3.
AIC and BIC for spline hazard models with varying degrees of freedom (d.f.).
| d.f. | AIC | BIC |
|---|---|---|
| 1 | 935.764 | 941.356 |
| 2 | 922.638 | 931.025 |
| 3 | 924.126 | 935.309 |
| 4 | 925.828 | 939.807 |
| 5 | 925.926 | 942.700 |
Table 3 indicates that both the AIC and BIC select 2 degrees of freedom (3 knots). We illustrate the fitted baseline hazard functions in Figure 3.
Figure 3.
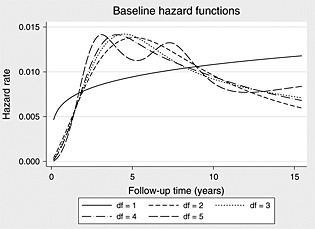
Predicted baseline hazard functions across differing degrees of freedom.
When d.f.=2, we can see from Figure 3 the presence of a turning point in the baseline hazard function, which would be missed if a simpler Weibull model would have been used.
We can also conduct preliminary separate modelling of the percentage mammographic density measurements to obtain an idea of the trend over time, to inform the full joint model. Beginning with a random intercept and random linear trend to allow for patient‐to‐patient variability, we can also investigate a more flexible trend by adding fixed polynomials of time. Results from adding a squared, cubic and quartic powers of time are shown in Table 4.
Table 4.
Longitudinal mixed effects model results for percentage mammographic density over time.
| Parameter | Estimate | Standard error | p‐value | 95% CI | |
|---|---|---|---|---|---|
| Time | −0.3513 | 0.0292 | <0.001 | −0.4086 | −0.2940 |
| Time2 | 0.0840 | 0.0128 | <0.001 | 0.0589 | 0.1091 |
| Time3 | −0.0103 | 0.0019 | <0.001 | −0.0141 | −0.0065 |
| Time4 | 0.0004 | 0.0001 | <0.001 | 0.0002 | 0.0006 |
| Intercept | 4.3744 | 0.0409 | <0.001 | 4.2942 | 4.4546 |
| Random effects | |||||
| sd(Time) | 0.0703 | 0.0042 | 0.0626 | 0.0789 | |
| sd(Intercept) | 1.1428 | 0.0290 | 1.0874 | 1.2009 | |
| corr(Time,Intercept) | −0.0918 | 0.0556 | −0.1993 | 0.0179 | |
| sd(Residual) | 0.5895 | 0.0063 | 0.5773 | 0.6020 | |
Now moving to the joint modelling framework, we apply the following joint model, based on the aforementioned separate modelling, and therefore assume that
| (18) |
modelling percentage density over time with a random intercept, random linear slope and fixed effects of time squared, cubed and to the fourth power. In the survival submodel, we use 2 degrees of freedom to model the baseline hazard function, and the rate of change (slope) association structure, as follows:
| (19) |
with h 0(t) the baseline spline function. We also fit a simpler joint model,
| (20) |
assuming a random intercept and random linear trend, and compare estimates of association. However, we have a variety of important covariates that could impact on the longitudinal and survival estimates. In the longitudinal submodel, we adjust for age at diagnosis (years), BMI (kg/m2), ever used hormone replacement therapy (yes/no) and tumour size (mm, range 1–80), and in the survival submodel, we also adjust for age, BMI, tamoxifen treatment, oestrogen receptor status (negative/positive/missing), tumour size, number of metastatic nodes (range 0–38), grade (1 = well differentiated, 2 = moderately differentiated, 3 = poorly differentiated and 4 = missing) and chemotherapy (yes/no). Results are presented in Table 5, comparing the linear and polynomial models.
Table 5.
Full joint model results applied to the breast cancer cohort, comparing estimates of the rate of change association between the simpler linear model and the informed polynomial trajectory model.
| Parameter | Linear | Polynomial | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Estimate | Standard error | p‐value | 95% CI | Estimate | Standard error | p‐value | 95% CI | |||
| Longitudinal | ||||||||||
| Time | −0.088 | 0.004 | 0.000 | −0.096 | −0.080 | −0.351 | 0.029 | 0.000 | −0.409 | −0.294 |
| Time2 | — | — | — | — | — | 0.084 | 0.013 | 0.000 | 0.058 | 0.109 |
| Time3 | — | — | — | — | — | −0.010 | 0.002 | 0.000 | −0.014 | −0.006 |
| Time4 | — | — | — | — | — | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 |
| Age (years) | −0.029 | 0.006 | 0.000 | −0.039 | −0.018 | −0.029 | 0.006 | 0.000 | −0.040 | −0.018 |
| BMI (kg/m2) | −0.110 | 0.009 | 0.000 | −0.129 | −0.092 | −0.111 | 0.009 | 0.000 | −0.129 | −0.093 |
| HR therapy | 0.003 | 0.071 | 0.972 | −0.136 | 0.141 | 0.002 | 0.070 | 0.975 | −0.136 | 0.140 |
| Tumour size (mm) | 0.006 | 0.004 | 0.107 | −0.001 | 0.013 | 0.005 | 0.004 | 0.128 | −0.002 | 0.012 |
| Intercept | 8.699 | 0.412 | 0.000 | 7.892 | 9.506 | 8.925 | 0.415 | 0.000 | 8.112 | 9.737 |
| Survival | ||||||||||
| Association | 4.756 | 4.518 | 0.293 | −4.100 | 13.612 | 0.192 | 0.607 | 0.752 | −0.998 | 1.382 |
| Age (years) | −0.024 | 0.017 | 0.159 | −0.058 | 0.010 | −0.017 | 0.015 | 0.264 | −0.046 | 0.013 |
| BMI (kg/m2) | 0.013 | 0.024 | 0.605 | −0.035 | 0.060 | 0.016 | 0.024 | 0.507 | −0.031 | 0.062 |
| Tamoxifen | 0.416 | 0.206 | 0.043 | 0.013 | 0.818 | 0.407 | 0.205 | 0.047 | 0.006 | 0.808 |
| ER status | −0.416 | 0.259 | 0.108 | −0.922 | 0.091 | −0.458 | 0.252 | 0.069 | −0.953 | 0.036 |
| Missing ER status | −0.382 | 0.313 | 0.223 | −0.996 | 0.232 | −0.443 | 0.304 | 0.145 | −1.039 | 0.153 |
| Tumour size (mm) | 0.026 | 0.008 | 0.001 | 0.011 | 0.041 | 0.024 | 0.007 | 0.001 | 0.010 | 0.039 |
| No. of metastatic nodes | 0.087 | 0.014 | 0.000 | 0.059 | 0.116 | 0.088 | 0.013 | 0.000 | 0.062 | 0.115 |
| Grade = 2 | 0.610 | 0.446 | 0.172 | −0.265 | 1.485 | 0.617 | 0.445 | 0.166 | −0.256 | 1.489 |
| Grade = 3 | 0.490 | 0.453 | 0.279 | −0.398 | 1.377 | 0.516 | 0.451 | 0.253 | −0.368 | 1.399 |
| Grade = Missing | 0.616 | 0.447 | 0.168 | −0.260 | 1.492 | 0.647 | 0.445 | 0.146 | −0.225 | 1.520 |
| Chemotherapy | 0.238 | 0.318 | 0.454 | −0.385 | 0.861 | 0.231 | 0.312 | 0.460 | −0.381 | 0.842 |
| Spline 1 | −0.028 | 0.136 | 0.836 | −0.294 | 0.238 | −0.064 | 0.156 | 0.682 | −0.371 | 0.242 |
| Spline 2 | 0.177 | 0.127 | 0.162 | −0.071 | 0.426 | 0.214 | 0.171 | 0.212 | −0.122 | 0.549 |
| Intercept | −4.035 | 1.414 | 0.004 | −6.806 | −1.264 | −4.910 | 1.126 | 0.000 | −7.117 | −2.703 |
| Random effects | ||||||||||
| sd(Time) | 0.069 | 0.004 | — | 0.061 | 0.078 | 0.070 | 0.004 | — | 0.063 | 0.079 |
| sd(Intercept) | 1.025 | 0.027 | — | 0.974 | 1.079 | 1.026 | 0.027 | — | 0.975 | 1.080 |
| corr(Time,Intercept) | −0.007 | 0.061 | — | −0.126 | 0.112 | −0.005 | 0.060 | — | −0.122 | 0.112 |
| sd(Residual) | 0.601 | 0.006 | — | 0.589 | 0.614 | 0.589 | 0.006 | — | 0.577 | 0.602 |
BMI, body mass index; ER, oestrogen receptor; HR, hormone replacement.
From Table 5, looking at the polynomial‐based model, we observe no statistically significant association between the rate of change of percentage mammographic density over time and breast cancer survival, with an association estimate of 0.192 (95% CI: −0.998, 1.382). We find a marked difference in the estimates of association when assuming a simpler longitudinal trajectory, with an estimated association of 4.756 (95% CI: −4.100, 13.612). We also note that as the association estimate is non‐statistically significant, we obtain identical estimates of the random effects, to 3 decimal places, to those from the separate longitudinal model shown in Table 4.
We now fit joint models with the current value association structure, comparing the polynomial longitudinal trajectory model,
| (21) |
with the simpler linear trajectory model,
| (22) |
and compare estimates of association. Results are presented in Table 6
Table 6.
Full joint model results applied to the breast cancer cohort, comparing estimates of the current value association between the simpler linear model and the informed polynomial trajectory model.
| Parameter | Linear | Polynomial | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Estimate | Standard error | p‐value | 95% CI | Estimate | Standard error | p‐value | 95% CI | |||
| Longitudinal | ||||||||||
| Time | −0.090 | 0.004 | 0.000 | −0.097 | −0.082 | −0.351 | 0.029 | 0.000 | −0.409 | −0.294 |
| Time2 | — | — | — | — | — | 0.084 | 0.013 | 0.000 | 0.059 | 0.109 |
| Time3 | — | — | — | — | — | −0.010 | 0.002 | 0.000 | −0.014 | −0.006 |
| Time4 | — | — | — | — | — | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 |
| Age (years) | −0.028 | 0.006 | 0.000 | −0.039 | −0.018 | −0.029 | 0.006 | 0.000 | −0.040 | −0.018 |
| BMI (kg/m2) | −0.110 | 0.009 | 0.000 | −0.129 | −0.092 | −0.111 | 0.009 | 0.000 | −0.129 | −0.092 |
| HR therapy | 0.000 | 0.071 | 1.000 | −0.138 | 0.138 | 0.002 | 0.070 | 0.982 | −0.137 | 0.140 |
| Tumour size (mm) | 0.006 | 0.004 | 0.110 | −0.001 | 0.013 | 0.006 | 0.004 | 0.121 | −0.001 | 0.013 |
| Intercept | 8.697 | 0.412 | 0.000 | 7.890 | 9.504 | 8.925 | 0.415 | 0.000 | 8.112 | 9.738 |
| Survival | ||||||||||
| Association | 0.105 | 0.087 | 0.226 | −0.065 | 0.275 | 0.106 | 0.083 | 0.202 | −0.057 | 0.268 |
| Age (years) | −0.015 | 0.015 | 0.307 | −0.045 | 0.014 | −0.015 | 0.015 | 0.305 | −0.045 | 0.014 |
| BMI (kg/m2) | 0.028 | 0.025 | 0.274 | −0.022 | 0.077 | 0.028 | 0.025 | 0.270 | −0.021 | 0.077 |
| Tamoxifen | 0.409 | 0.205 | 0.045 | 0.008 | 0.810 | 0.408 | 0.205 | 0.046 | 0.007 | 0.809 |
| ER status | −0.487 | 0.251 | 0.053 | −0.980 | 0.006 | −0.488 | 0.251 | 0.052 | −0.980 | 0.005 |
| Missing ER status | −0.457 | 0.303 | 0.132 | −1.051 | 0.138 | −0.458 | 0.303 | 0.131 | −1.052 | 0.137 |
| Tumour size (mm) | 0.024 | 0.007 | 0.001 | 0.010 | 0.038 | 0.024 | 0.007 | 0.001 | 0.010 | 0.038 |
| No. of metastatic nodes | 0.088 | 0.013 | 0.000 | 0.062 | 0.115 | 0.088 | 0.013 | 0.000 | 0.062 | 0.115 |
| Grade = 2 | 0.600 | 0.445 | 0.178 | −0.272 | 1.473 | 0.600 | 0.445 | 0.178 | −0.273 | 1.472 |
| Grade = 3 | 0.489 | 0.452 | 0.279 | −0.396 | 1.374 | 0.487 | 0.452 | 0.281 | −0.398 | 1.372 |
| Grade = Missing | 0.600 | 0.447 | 0.180 | −0.276 | 1.476 | 0.599 | 0.447 | 0.180 | −0.277 | 1.475 |
| Chemotherapy | 0.253 | 0.312 | 0.417 | −0.358 | 0.864 | 0.254 | 0.312 | 0.415 | −0.357 | 0.865 |
| Spline 1 | −0.006 | 0.138 | 0.964 | −0.276 | 0.264 | −0.030 | 0.136 | 0.827 | −0.297 | 0.237 |
| Spline 2 | 0.160 | 0.129 | 0.213 | −0.092 | 0.413 | 0.206 | 0.130 | 0.112 | −0.048 | 0.461 |
| Intercept | −5.636 | 1.269 | 0.000 | −8.125 | −3.148 | −5.654 | 1.262 | 0.000 | −8.128 | −3.181 |
| Random effects | ||||||||||
| sd(Time) | 0.069 | 0.004 | — | 0.061 | 0.078 | 0.070 | 0.004 | — | 0.063 | 0.079 |
| sd(Intercept) | 1.027 | 0.027 | — | 0.976 | 1.081 | 1.027 | 0.027 | — | 0.975 | 1.080 |
| corr(Time,Intercept) | −0.015 | 0.061 | — | −0.133 | 0.104 | −0.005 | 0.060 | — | −0.122 | 0.112 |
| sd(Residual) | 0.601 | 0.006 | — | 0.589 | 0.614 | 0.589 | 0.006 | — | 0.577 | 0.602 |
BMI, body mass index; ER, oestrogen receptor; HR, hormone replacement.
From Table 6, under the full joint model with polynomial trajectory, we find a non‐statistically significant association of 0.106 (95% CI: −0.057, 0.268). We observe a very similar association estimate from the simpler linear model, 0.105 (95% CI: −0.065, 0.275), in agreement with the findings of the simulation study, showing the robustness of the current value association.
All Stata do files used in the simulation study, and applied joint model analyses of the breast cancer data are included in the Supporting Information.
6. Discussion
In this article, we proposed a flexible joint model incorporating delayed entry (left truncation), using restricted cubic splines to model the baseline hazard function, and (fractional) polynomials in the longitudinal submodel to capture complex trajectories of biomarkers over time. The addition of delayed entry required a second set of numerical integration beyond that of the standard joint model. We proposed to use fully adaptive quadrature to evaluate the likelihood, as an alternative to previously proposed non‐adaptive quadrature.
Through simulation, we investigated the performance of fully adaptive Gauss–Hermite quadrature in calculating the joint likelihood, comparing it with non‐adaptive quadrature. Our results showed substantial improvement in terms of bias and coverage under the adaptive routines, particularly in estimates of longitudinal submodel parameters. In order to achieve similar performance as the adaptive routines, it is expected that a minimum of 30 quadrature points would be required, as has been found in standard joint models 21. In terms of computation time, this is an important issue. For example, comparing computation time under scenario 3 with the rate of change association structure, when α = 3, the median computation time to convergence on a standard laptop with 4 GB of RAM and an i5 processor, with 5‐point adaptive quadrature, was 30 s (range 26, 57), compared with 114 s (range 85, 205) with 15‐point non‐adaptive. If 30‐point non‐adaptive quadrature is required, then this difference will clearly grow further. This is an important consideration as joint models begin to be used on larger registry‐based datasets where the number of patients may be in the tens of thousands, not hundreds.
We also investigated the impact of misspecifying the longitudinal trajectory through simulation, an issue that we believe has not been investigated before. We used scenarios that were based on a cubic polynomial trajectory longitudinal submodel fitted to the breast cancer data, and subsequently fitted the true joint model, and a more simplistic random intercept and random linear slope longitudinal submodel. We assessed the impact of misspecifying the trajectory under both the current value association and the rate of change association structures. In our scenarios, we found the current value association structure to be quite robust to the misspecification. Conversely, we found the rate of change association structure to be very sensitive, with substantial bias present in estimates of the association parameter when the simpler linear trajectory was fitted. Given the assumed trajectory, shown in Figure 1b, it appears that under the current value association structure, the linear approximation to the more complex true cubic shape did not impact greatly. Conversely, assuming a constant rate of change when the truth is a more complex squared function impacted greatly. If a more complex shape had been chosen for the trajectory, for example, incorporating a turning point within the range of the data, we expect the current value to be as sensitive to misspecification. Another aspect of the longitudinal trajectory that we could have investigated is the assumption of normally distributed random effects; however, multiple authors have found joint models quite robust to deviations from this assumption 36, 37.
We illustrated the methodology with an example in breast cancer, where primary interest was in the association between change in mammographic density over time and breast cancer survival. It built on previous work that looked at change in mammographic density between the scan at diagnosis and the first follow‐up scan. In the joint model analysis, we were mainly interested in the current slope or current value association structures (Equation (4)) to link density change to survival. In a future study, we will use the joint modelling framework to explore other, perhaps more clinically relevant, association structures. Discrepancy between our results and those in Li et al. may be due to the fact that they focus on the impact of density change close to diagnosis. We have here focused on developing the joint modelling framework for this dataset with delayed entry that can incorporate all follow‐up density measurements/model density as a longitudinal outcome. In line with the simulation study, we also compared the robustness of the rate of change, and current value association structures to using a simpler longitudinal trajectory compared with the separate modelling‐informed polynomial trajectory. Results from the applied analyses indicated complete agreement to those found in the simulation study, showing robustness of the association parameter, compared with a substantial lack of robustness in the rate of change specification. An important limitation to note is that in our model framework, we do not consider time‐dependent feedback. This may occur, for example, if tamoxifen therapy affected mammographic density, which, subsequently, affected whether a patient was then asked to take or discontinue tamoxifen. However, we only had information on whether a patient was taking tamoxifen or not, at baseline, and had no information on adherence.
In our application, we used preliminary separate modelling, utilising the AIC and BIC to guide the selection of the functional form of both the longitudinal trajectory and the baseline hazard function. We did not include this approach within the simulation study where we fitted the true and a misspecified model, which is a limitation. In applied studies, we do not know the truth, and therefore, some form of model selection must be used. The optimal method to select both these functional forms is an area of further research 38.
For the time‐to‐event outcome, we used restricted cubic splines on the log hazard scale to model the baseline hazard function, with knot selection guided by the AIC and BIC, which has been shown to be an effective model‐building strategy 28. It must be noted that sensitivity analyses should be conducted to assess the impact of the number of degrees of freedom used to model both the baseline and indeed the longitudinal trajectory. Alternative flexible formulations could have been explored, for example, Proust‐Lima et al. used penalised cubic M‐splines on the hazard scale 20. We could have used age as the timescale in our illustrative example but in this case time because diagnosis can be considered the more appropriate timescale to use; however, in many examples, a delayed entry joint model will be required when using age as the timescale.
In our analyses, we used missing indicator variables for covariates with any missing data present, allowing us to use the full dataset. This is clearly not ideal, and therefore, incorporating a multiple imputation approach suitable for use in a joint modelling framework would be a very useful area of future research. A Bayesian approach may also be of use in this context. Extensions to the modelling framework also include incorporating multiple longitudinal outcomes, within a generalised linear mixed longitudinal submodel that would allow also binary and Poisson outcomes. Furthermore, the extension to a multi‐state survival submodel would allow event‐specific associations between complex longitudinal profiles and multiple events. Alternatives to the joint modelling framework could be investigated and compared, such as the use of inverse probability weights to account for dropout or regression calibration approaches; however, they give focus to either the longitudinal or survival components, whereas a joint model allows the elucidation of inferences to be drawn about both processes simultaneously.
Supporting information
Supporting info item
Acknowledgements
The authors would like to thank two anonymous reviewers and an associate editor for their comments that greatly improved the paper. Michael Crowther is 50% funded by the National Institute for Health Research (NIHR) Doctoral Research Fellowship (DRF‐2012‐05‐409). Keith Abrams is partially supported by NIHR as a Senior Investigator (NF‐SI‐0512‐10159).
Crowther, M. J. , Andersson, T. M.‐L. , Lambert, P. C. , Abrams, K. R. , and Humphreys, K. (2016) Joint modelling of longitudinal and survival data: incorporating delayed entry and an assessment of model misspecification. Statist. Med., 35: 1193–1209. doi: 10.1002/sim.6779.
References
- 1. Rizopoulos D. Joint Models for Longitudinal and Time‐to‐event Data with Applications in R. Chapman & Hall: London, 2012. [Google Scholar]
- 2. Gould AL, Boye ME, Crowther MJ, Ibrahim JG, Quartey G, Micallef S, Bois FY. Joint modeling of survival and longitudinal non‐survival data: current methods and issues. Report of the DIA Bayesian joint modeling working group. Statistics in Medicine 2015; 34(14):2181–2195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Sweeting MJ, Thompson SG. Joint modelling of longitudinal and time‐to‐event data with application to predicting abdominal aortic aneurysm growth and rupture. Biometrical Journal 2011; 53(5):750–763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Rizopoulos D. JM: an R package for the joint modelling of longitudinal and time‐to‐event data. Journal of Statistical Software 2010; 35(9):1–33.21603108 [Google Scholar]
- 5. Philipson P, Sousa I, Diggle P, Williamson P, Kolamunnage‐Dona R, Henderson R. joineR – joint modelling of repeated measurements and time‐to‐event data. 2012. https://cran.r-project.org/web/packages/joineR/vignettes/joineR.pdf.
- 6. Crowther MJ, Abrams KR, Lambert PC. Joint modeling of longitudinal and survival data. Stata Journa 2013; 13(1):165–184. [Google Scholar]
- 7. Zhang D, Chen MH, Ibrahim JG, Boye ME, Shen W. JMFit: a SAS macro for assessing model fit in joint models of longitudinal and survival data. 2015. Submitted. [DOI] [PMC free article] [PubMed]
- 8. Ekinci EI, Moran JL, Thomas MC, Cheong K, Clarke S, Chen A, Dobson M, Leong A, Macisaac RJ, Jerums G. Relationship between urinary sodium excretion over time and mortality in type 2 diabetes. Diabetes Care 2014; 37(4):e62–e63. [DOI] [PubMed] [Google Scholar]
- 9. Nuñez J, Nuñez E, Rizopoulos D, Miñana G, Bodí V, Bondanza L, Husser O, Merlos P, Santas E, Pascual‐Figal D, Chorro FJ, Sanchis J. Red blood cell distribution width is longitudinally associated with mortality and anemia in heart failure patients. Circulation Journal 2014; 78(2):410–418. [DOI] [PubMed] [Google Scholar]
- 10. Thiébaut ACM, Bénichou J. Choice of time‐scale in Cox's model analysis of epidemiologic cohort data: a simulation study. Statistics in Medicine 2004; 23(24):3803–3820. [DOI] [PubMed] [Google Scholar]
- 11. Jensen H, Brookmeyer R, Aaby P, Andersen PK. Shared frailty model for left‐truncated multivariate survival data. Technical Report, 2004.
- 12. van den Berg GJ, Drepper B. Inference for shared‐frailty survival models with left‐truncated data. Econometric Reviews 2014. DOI: 10.1080/07474938.2014.975640. [Google Scholar]
- 13. Rondeau V, Gonzalez JR. frailtypack: a computer program for the analysis of correlated failure time data using penalized likelihood estimation. Comput Methods Programs Biomed 2005; 80(2):154–164. [DOI] [PubMed] [Google Scholar]
- 14. Rondeau V, Commenges D, Joly P. Maximum penalized likelihood estimation in a gamma‐frailty model. Lifetime Data Analysis 2003; 9(2):139–153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Rondeau V, Michiels S, Liquet B, Pignon JP. Investigating trial and treatment heterogeneity in an individual patient data meta‐analysis of survival data by means of the penalized maximum likelihood approach. Statistics in Medicine 2008; 27(11):1894–1910. [DOI] [PubMed] [Google Scholar]
- 16. Rondeau V, Filleul L, Joly P. Nested frailty models using maximum penalized likelihood estimation. Statistics in Medicine 2006; 25(23):4036–4052. [DOI] [PubMed] [Google Scholar]
- 17. Dantan E, Joly P, Dartigues JF, Jacqmin‐Gadda H. Joint model with latent state for longitudinal and multistate data. Biostatistics 2011; 12(4):723–736. [DOI] [PubMed] [Google Scholar]
- 18. Piccorelli AV, Schluchter MD. Jointly modeling the relationship between longitudinal and survival data subject to left truncation with applications to cystic fibrosis. Statistics in Medicine 2012; 31(29):3931–3945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. van den Hout A, Muniz‐Terrera G. Joint models for discrete longitudinal outcomes in ageing research. Journal of the Royal Statistical Society. Series C (Applied Statistics) 2016; 65(1):167–186. [Google Scholar]
- 20. Proust‐Lima C, Joly P, Dartigues JF, Jacqmin‐Gadda H. Joint modelling of multivariate longitudinal outcomes and a time‐to‐event: a nonlinear latent class approach. Computational Statistics & Data Analysis 2009; 53(4):1142–1154. [Google Scholar]
- 21. Crowther MJ, Abrams KR, Lambert PC. Flexible parametric joint modelling of longitudinal and survival data. Statistics in Medicine 2012; 31(30):4456–4471. [DOI] [PubMed] [Google Scholar]
- 22. Crowther MJ, Lambert PC. stgenreg: a Stata package for the general parametric analysis of survival data. Journal of Statistical Software 2013; 53(12):1–17. [Google Scholar]
- 23. Crowther MJ, Lambert PC. A general framework for parametric survival analysis. Statistics in Medicine 2014; 33(30):5280–5297. [DOI] [PubMed] [Google Scholar]
- 24. Li J, Humphreys K, Eriksson L, Edgren G, Czene K, Hall P. Mammographic density reduction is a prognostic marker of response to adjuvant tamoxifen therapy in postmenopausal patients with breast cancer. Journal of Clinical Oncology 2013; 31(18):2249–2256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Boyd NF, Martin LJ, Yaffe MJ, Minkin S. Mammographic density and breast cancer risk: current understanding and future prospects. Breast Cancer Research 2011; 13(6):223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Kim J, Han W, Moon HG, Ahn S, Shin HC, You JM, Han SW, Im SA, Kim TY, Koo H. et al. Breast density change as a predictive surrogate for response to adjuvant endocrine therapy in hormone receptor positive breast cancer. Breast Cancer Research 2012; 14(4):R102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Royston P, Sauerbrei W. Multivariable Model‐building: A Pragmatic Approach to Regression Analysis Based on Fractional Polynomials for Modelling Continuous Variables. Wiley: Chichester, 2008. [Google Scholar]
- 28. Rutherford MJ, Crowther MJ, Lambert PC. The use of restricted cubic splines to approximate complex hazard functions in the analysis of time‐to‐event data: a simulation study. Journal of Statistical Computation and Simulation 2015; 85(4):777–793. [Google Scholar]
- 29. Rizopoulos D, Ghosh P. A Bayesian semiparametric multivariate joint model for multiple longitudinal outcomes and a time‐to‐event. Statistics in Medicine 2011; 30(12):1366–1380. [DOI] [PubMed] [Google Scholar]
- 30. Crowther MJ, Lambert PC, Abrams KR. Adjusting for measurement error in baseline prognostic biomarkers included in a time‐to‐event analysis: a joint modelling approach. BMC Medical Research Methodology 2013; 13(146). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Pinheiro JC, Bates DM. Approximations to the log‐likelihood function in the nonlinear mixed‐effects model. Journal of Computational and Graphical Statistics 1995; 4(1):12–35. [Google Scholar]
- 32. Tuerlinckx F, Rijmen F, Verbeke G, Boeck PD. Statistical inference in generalized linear mixed models: a review. British Journal of Mathematical and Statistical Psychology 2006; 59(Pt 2):225–255. [DOI] [PubMed] [Google Scholar]
- 33. Rabe‐Hesketh S, Skrondal A, Pickles A. Reliable estimation of generalized linear mixed models using adaptive quadrature. Stata Journal 2002; 2:1–21. [Google Scholar]
- 34. Crowther MJ, Lambert PC. Simulating biologically plausible complex survival data. Statistics in Medicine 2013; 32(23):4118–4134. [DOI] [PubMed] [Google Scholar]
- 35. StataCorp . Statistical software: release 12. College Station, TX: StataCorp LP 2011. [Google Scholar]
- 36. Rizopoulos D, Verbeke G, Molenberghs G. Shared parameter models under random effects misspecification. Biometrika 2008; 95(1):63–74. [Google Scholar]
- 37. Huang X, Stefanski LA, Davidian M. Latent‐model robustness in joint models for a primary endpoint and a longitudinal process. Biometrics 2009; 65(3):719–727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Zhang D, Chen MH, Ibrahim JG, Boye ME, Wang P, Shen W. Assessing model fit in joint models of longitudinal and survival data with applications to cancer clinical trials. Statistics in Medicine 2014; 33(27):4715–4733. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting info item


