Stable encoding of sounds over a broad range of statistical parameters in the auditory cortex

Abstract

Natural auditory scenes possess highly structured statistical regularities, which are dictated by the physics of sound production in nature, such as scale‐invariance. We recently identified that natural water sounds exhibit a particular type of scale invariance, in which the temporal modulation within spectral bands scales with the centre frequency of the band. Here, we tested how neurons in the mammalian primary auditory cortex encode sounds that exhibit this property, but differ in their statistical parameters. The stimuli varied in spectro‐temporal density and cyclo‐temporal statistics over several orders of magnitude, corresponding to a range of water‐like percepts, from pattering of rain to a slow stream. We recorded neuronal activity in the primary auditory cortex of awake rats presented with these stimuli. The responses of the majority of individual neurons were selective for a subset of stimuli with specific statistics. However, as a neuronal population, the responses were remarkably stable over large changes in stimulus statistics, exhibiting a similar range in firing rate, response strength, variability and information rate, and only minor variation in receptive field parameters. This pattern of neuronal responses suggests a potentially general principle for cortical encoding of complex acoustic scenes: while individual cortical neurons exhibit selectivity for specific statistical features, a neuronal population preserves a constant response structure across a broad range of statistical parameters.

Introduction

Natural environmental sounds span a broad range of frequencies, and possess characteristic spectro‐temporal statistical regularities in their structure (Voss & Clarke, 1975; Singh & Theunissen, 2003). Encoding information about these statistical regularities is an important processing step in the central auditory pathway, required for accurate analysis of an auditory scene (Bregman, 1990; Chandrasekaran et al., 2009). Spectro‐temporal statistical regularities in sounds can be used by the auditory system to recognize specific sounds and distinguish them from each other (Woolley et al., 2005; Geffen et al., 2011; McDermott & Simoncelli, 2011; McDermott et al., 2013; Gervain et al., 2014).

The power spectrum of natural sounds scales inversely with the frequency, following the 1/f statistics law (Voss & Clarke, 1975; Attias & Schreiner, 1997; Singh & Theunissen, 2003). Furthermore, the overall power spectrum and the temporal modulation spectrum also obey scale‐invariant statistics. Neurons in the central auditory pathway encode small variations in spectro‐temporally modulated stimuli (Elhilali et al., 2004) and respond preferentially to sounds exhibiting natural characteristics (Nelken et al., 1999; Woolley et al., 2005), and 1/f frequency spectrum in particular (Escabi & Read, 2005; Garcia‐Lazaro et al., 2006; Rodriguez et al., 2010). Changes in the statistical structure of stimuli, including the spectro‐temporal density, or the spectro‐temporal range, affect response properties of cortical neurons, leading to gain adaptation in their firing rate (Blake & Merzenich, 2002; Valentine & Eggermont, 2004; Asari & Zador, 2009; Pienkowski & Eggermont, 2009; Eggermont, 2011; Rabinowitz et al., 2011; Natan et al., 2015).

Recently, we identified an additional form of scale‐invariance in environmental sounds (Geffen et al., 2011; Gervain et al., 2014). In sounds of running water, a subset of environmental sounds, the temporal modulation spectrum across spectral bands scales with the centre frequency of the band (Geffen et al., 2011; Gervain et al., 2014). When the recording of running water was stretched or compressed temporally, it was still perceived as a natural, water‐like sound (Geffen et al., 2011). Such a relationship corresponds to the optimal representation of a sound waveform under sparse coding assumptions (Lewicki, 2002; Garcia‐Lazaro et al., 2006; Smith & Lewicki, 2006). Sounds that obeyed the invariant scaling relationship but which varied in cyclo‐temporal coefficients and spectro‐temporal sound density evoked different percepts, ranging from pattering of rain to sound of a waterfall to artificial ringing. In the present study, we adapted this set of stimuli to the hearing range of rats to examine how changing spectro‐temporal statistical properties affect responses of neurons in the primary auditory cortex (A1), an essential area for encoding complex and behaviourally meaningful sounds (Nelken, 2004; Aizenberg & Geffen, 2013; Carruthers et al., 2013, 2015; Mizrahi et al., 2014; Aizenberg et al., 2015).

We recorded the responses of neurons in A1 of awake rats to naturalistic, scale‐invariant sounds, designed to mimic the variety of natural water sounds, as their statistical structure was varied. We found that individual neurons exhibited tuning for a specific cyclo‐temporal coefficient and spectro‐temporal density of the stimulus, yet over the population of neurons, sounds with vastly different statistics evoked a similar range of response parameters.

Materials and methods

This study was performed in strict accordance with the recommendations in the Guide for the Care and Use of Laboratory Animals of the National Institutes of Health. The protocol was approved by the Institutional Animal Care and Use Committee of the University of Pennsylvania.

Animals

Subjects in all experiments were adult male rats. Rats were housed in a temperature‐ and humidity‐controlled vivarium on a reversed 24‐ light–dark cycle with food and water provided ad libiditum.

Surgery

Sprague Dawley or Long Evans adult male rats (n = 5) were anaesthetized with an intraperitoneal injection of a mixture of ketamine (60 mg per kg body weight) and dexmedetomidine (0.25 mg/kg). Buprenorphine (0.1 mg/kg) was administered as an operative analgesic with ketoprofen (5 mg/kg) as post‐operative analgesic. Rats were implanted with chronic custom‐built multi‐tetrode microdrives as previously described (Otazu et al., 2009). The animal's head was secured in a stereotactic frame (David Kopf Instruments, Tujunga, CA, USA). Following the recession of the temporal muscle, a craniotomy and durotomy were performed over the location of the primary auditory cortex. A microdrive housed eight tetrodes, of which two were used for reference and six for signal channels. Each tetrode consisted of four polyimide‐coated Nichrome wires (Kenthal‐PalmCoast, FL, USA; wire diameter of 12 μm) twisted together, and was controlled independently with a turn of a screw. Two screws (one reference and one ground) were inserted in the skull at locations distal from A1. The tetrodes were implanted 4.5–6.5 mm posterior to bregma and 6.0 mm left of the midline, covered with agar solution (3.5%) and secured to the skull with dental acrylic (Metabond) and dental cement. The location of the electrodes was verified based on the stereotaxic coordinates, the electrode position in relation to brain surface blood vessels, and through histological reconstruction of the electrode tracks post‐mortem. The electrodes were gradually advanced below the brain surface in daily increments of 40–50 μm. The location was also confirmed by identifying the frequency tuning curve of the recorded units. The recorded units’ best frequency, which elicited the highest firing rate, spanned the range of rat hearing and was consistent with previous studies (Sally & Kelly, 1988).

Stimulus construction

To generate scale‐invariant sounds, the sound waveform, y(t), was modelled as a sum of droplets, where each droplet, x _i(a _i, f _i, Q, τ _i; t) was modelled as a gammatone function (Geffen et al., 2011):

$$y(t)=\sum _i{x}_i(a_i,f_i,\mathrm{Q},{\mathit{\tau }}_i;t)=\sum _i{a}_i\frac{f_i}{\mathrm{Q}}(t-{\mathit{\tau }}_i)e^{-f(t-{\mathit{\tau }}_i)/Q_i}\text{sin}(2\mathit{\pi }{f}_i(t-{\mathit{\tau }}_i))$$

with parameters amplitude, a _i, frequency, f _i, onset time, τ _i, and cycle constant of decay, Q, drawn at random from distinct probability distributions. f _i was uniform random in log‐frequency space, between 400 and 80000 Hz; onset time was uniform random with mean rate r. Five distinct 7‐s stimuli were generated, each comprising a different set of values of Q and r (in units of droplets/octave/s), chosen from: Stimulus 1: Q = 2, r _med = 530; Stimulus 2: Q = 0.5, r _med = 530; Stimulus 3: Q = 8, r _med = 530; Stimulus 4: Q = 2, r _low = 53; Stimulus 5: Q = 2, r _high = 5300. The resulting waveforms were normalized for equal root‐mean‐square sound pressure level. Further, to make the signal punctate within each spectral band, the amplitude distribution of the droplets was drawn from an inverse square distribution, $p(z)\sim \frac{1}{z^2}$ (Geffen et al., 2011). The distributions of droplet amplitude and frequencies were exactly matched between the stimuli – all sounds generated at the same rate were produced with the same random seed.

Each stimulus was 7 s long, and repeated at least 40 times with an inter‐stimulus interval of 1 s.

Neural recordings

Neural signals were analysed as previously described (Carruthers et al., 2013, 2015; Aizenberg et al., 2015; Natan et al., 2015). Neuronal signals were acquired daily from 24 chronically implanted electrodes in awake, freely moving rats using a Neuralynx Cheetah system. The neuronal signal was filtered between 0.6 and 6.0 kHz, digitized and recorded at 32 kHz. Discharge waveforms were clustered into single‐unit and multi‐unit clusters using either Neuralynx Spike Sort 3D or Plexon Off‐line Spike Sorter software (Carruthers et al., 2013). Discharge waveforms had to form a visually identifiable distinct cluster in a projection onto a three‐dimensional subspace (Otazu et al., 2009; Bizley et al., 2010; Brasselet et al., 2012).

The acoustical stimulus was delivered via a magnetic speaker (MF‐1, Tucker‐Davis Technologies, Alachua, FL, USA) positioned above the recording chamber. The speaker output was calibrated using Bruel and Kjaer 1/4‐inch free‐field microphone type 4939, which was placed at the location that would normally be occupied by the animal's ear, by presenting a recording of repeated white noise bursts and tone pips between 400 and 80 000 Hz. From these measurements, the speaker transfer function and its inverse were computed. The input to the microphone was adjusted using the inverse of the transfer function such that the speaker output was 70 dB (sound pressure level relative to 20 μP, SPL) tones, within 3 dB, between 400 and 80 000 Hz. Spectral and temporal distortion products were measured in response to tone pips between 1 and 80 kHz, and were found to be >50 dB below the SPL of the fundamental (Carruthers et al., 2013). All stimuli were presented at 400 kHz sampling rate, using custom‐built software based on a commercially available data acquisition toolbox (Mathworks, Inc., Natick, MA, USA), and a high‐speed data acquisition card (National Instruments, Inc., Austin, TX, USA).

Frequency response analysis

We first presented a stimulus designed to map the frequency response function of the recorded units: consisting of 50 tones, each 50 ms long, between 400 and 80 000 Hz, logarithmically spaced, at 70 dB SPL, repeated five times. The response strength, which combined onset and offset responses, was computed as the mean firing rate of neurons during 0–80 ms after tone onset. The best frequency was computed as the frequency of the tone that evoked the maximum response strength (Brown & Harrison, 2009; Carruthers et al., 2013).

Droplet stimulus representation

The stimulus, s(f, t), was represented either as the spectrogram of the sound waveform (2048‐point spectrogram computed in Matlab) or as a matrix of droplet onset time/magnitude. The droplet onset matrix was computed from the stimulus design matrix, by binning the droplet onset time into 5‐ms bins, and droplet centre frequency into 0.0772‐octave windows. The value of each point of the matrix was the sum of magnitudes of all droplets originating in that bin.

Firing rate and response strength

The discharge times in each trial were histogrammed in 1‐ms bins after stimulus onset (0–8 s), averaged across trials, and smoothed with a Gaussian filter with 3‐ms standard deviation. Mean firing rate was computed as the response averaged across the first 7 s of stimulus presentation. The response strength was computed as the difference between the firing rate during the stimulus and that during the baseline, divided by the standard error of the mean of the firing rate at the baseline over trials. The response was considered significant if the response strength exceeded 6.

Selectivity index and sparseness

For each neuron, the selectivity index was computed as the difference between the strongest and the mean response strength to the five stimuli for each unit, normalized by the strongest response.

For each neuron, sparseness, S, was computed using the following formula (Weliky et al., 2003):

$$S=1-\frac{{\left({\sum }_i\frac{v}{N}\right)}^2}{{\sum }_i\frac{v_i^2}{N}},$$

where v _i is the firing rate (spikes/s) of a single neuron to the ith stimulus, and n is the total number of stimuli (n = 5). S takes a value between 0 and 1, where a higher value indicates that the neuron responds to a narrow range of stimuli and a lower value indicates that the neuron responds to a broad range of stimuli.

Linear‐non‐linear model fit

The response of each unit, r(t), was computed as the probability of emitting a discharge within a 5‐ms temporal bin relative to the onset of the stimulus. We fitted a linear – non‐linear model (LN model) computed using a standard reverse correlation technique (Theunissen et al., 2001; Baccus & Meister, 2002; Escabi & Read, 2003; Geffen et al., 2007), using a spectrogram or the droplet‐based representation as an input.

To determine the droplet‐temporal receptive field (DTRF), the stimulus was represented in terms of the onset time and maximum amplitude of each droplet within its frequency band. One hundred uniformly, logarithmically distributed frequency bands were used (range: 0.4–80 kHz). DTRF was computed as the normalized average of the stimulus preceding each discharge.

To determine the spectrogram‐based spectro‐temporal receptive field (STRF), the stimulus was represented as a spectrogram of the waveform. We used the Auditory Toolbox to compute a cochleagram‐based representation of the stimulus (Lyon, 1982; Meddis et al., 1990; Slaney, 1998) with sampling rate of 400 kHz and decimation factor 100. STRF and cochleagram‐based receptive fields were computed as reverse‐correlation between discharge times and the spectrogram or cochleagram of the stimulus, using ridge regression (Theunissen et al., 2001).

The linear prediction of the firing rate was computed as the convolution of the stimulus with DTRF, cochleagram‐based receptive field or STRF. The instantaneous non‐linearity was computed directly from firing rate vs. linear prediction plot (Baccus & Meister, 2002; Geffen et al., 2007).

The model parameters were fitted to the data over randomly selected 50% of trials. The remaining 50% of trials were used to test the prediction accuracy of the model (Ahn et al., 2014). The prediction accuracy of the LN model was assessed by computing the coefficient of correlation between the predicted and recorded firing rate. Only neurons with correlation coefficient above 0.13 for either droplet‐based or spectrogram‐based prediction for at least one stimulus were included in the comparisons for model prediction quality over different variants of the model (Figs 5 and 7). This value was chosen as the elbow in the histogram of model prediction correlation coefficients, followed by visual inspection of the predicted and actual firing rates for the cases close to the chosen threshold.

Figure 5.

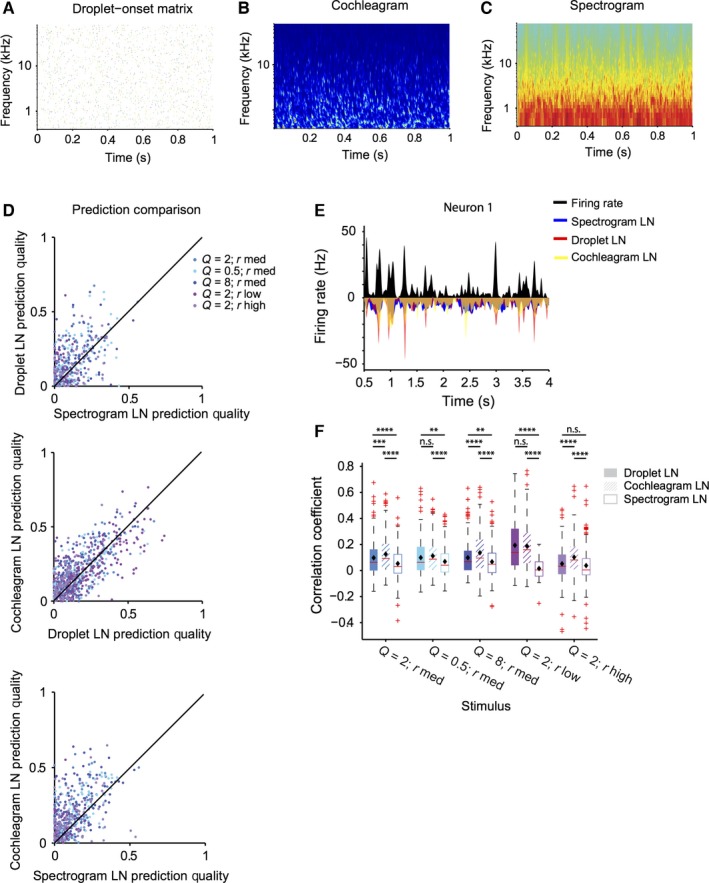
LN model based on droplet‐onset matrix predicts responses to the stimulus better than spectrogram‐based LN model. (A) Representation of the acoustic waveform of the droplet stimulus as a droplet‐onset matrix. (B) Representation of the acoustic waveform of the droplet stimulus as a spectrogram. (C) Representation of the acoustic waveform of the droplet stimulus as a cochleagram. (D) Prediction quality based on the droplet, spectrogram, or cochleagram‐based prediction. Prediction quality is significantly higher for droplet and cochleagram‐based prediction than spectrogram (for droplet: P (all stimuli) = 2.2e‐15; for cochleagram: P (all stimuli) = 5.8e‐43]. (E) LN prediction and recorded firing rate (black) for the spectrogram‐based (blue), droplet‐based (red) and cochleagram‐based (yellow) model for a representative neuron. (F) Quartile plot for the prediction quality for the droplet, spectrogram and cochleagram based prediction (filled bars: droplet‐temporal receptive field‐based prediction, open bars: spectro‐temporal receptive field‐based prediction, cross‐hatched bars: cochleagram‐based prediction). **P < 0.01, ***P < 0.001, ****P < 0.0001, Wilcoxon sign rank test, corrected for multiple comparisons.

Figure 7.

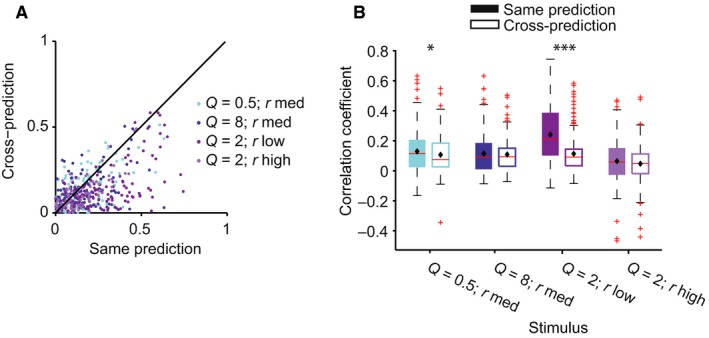
LN model fails in predicting the responses of neurons to stimulus with different statistical parameters. (A) Prediction quality of the LN model, for neuronal responses to four stimuli based on a model that was fitted based on the responses to ‘cross‐condition’ (baseline, Q = 2, r _med) vs. to the ‘same‐condition’. Prediction quality is significantly higher for responses to ‘same’ vs. ‘cross’ stimulus (P = 3.9e‐32 across all stimuli). (B) Quartile plot for the prediction quality of the model fitted to the ‘same’ (filled bars) vs. ‘baseline’ (open bars) stimulus. ***P < 0.001; *P < 0.05: paired t‐test.

Receptive field measurement

The spectral width, temporal width, time to peak and peak frequency of the positive lobe of the DTRF were computed using standard methods (Woolley et al., 2006; Shechter & Depireux, 2007; Schneider & Woolley, 2010). DTRF was denoised by setting all values outside of a significant positive cluster of pixels to 0. To determine the significance of the cluster, the z‐score of pixels was computed relative to the baseline values from a DTRF generated with scrambled spike trains, using the Stat4ci toolbox (Chauvin et al., 2005). To measure temporal parameters of the receptive field, the positive portion of the cluster‐corrected DTRF was averaged across frequencies, and fitted with a one‐dimensional gaussian filter. Delay to peak was defined as the centre of the gaussian fit. Temporal width was defined as twice the standard deviation of the gaussian fit. Likewise, to measure spectral parameters of the DTRF, the DTRF was averaged across time, and fitted with a one‐dimensional gaussian. Peak frequency and spectral width were defined as the centre and 2 ×  standard deviation of the gaussian fit, respectively. Only DTRFs that produced prediction accuracy of 0.13 or higher over the full set of trials for at least one of the stimuli were included in the analysis.

Fano factor

A Fano factor was computed as the mean of the variance of the firing rate over individual trials (in 50‐ms bins), divided by the mean firing rate in each bin. Because of the sparseness of responses, only ten bins with the highest firing rates were used for each neuron.

Information measured

Mutual information was computed between the response and the stimulus as previously described (Magri et al., 2009; Kayser et al., 2010). The mutual information between stimuli S and neural responses V is defined as:

$$I(S;V)=\sum _{v,s}P(s)P(v|s){\text{log}}_2\frac{P(v|s)}{P(v)}$$

where P(s) is the probability of presenting stimulus s, P(v|s) is the probability of observing response v when stimulus s is presented, and P(v) is the probability of observing response v across all trials to any stimulus. A value of zero would indicate that there is no relationship between the stimulus and the response.

The 7‐s stimulus was separated into seven ‘chunks’, each 1 s long. Mutual information was computed for 50 randomly selected responses to each of the stimulus ‘chunks’, and averaged. Each instance of the response was a randomly selected spike count in six consecutive 2‐ms bins to a stimulus chunk (Kayser et al., 2010). These parameters were selected following a pilot calculation of mutual information on a subset of data with variable timing and number of bins.

Statistical comparisons

Samples with n < 50 that did not pass the Shapiro–Wilk test for normality were compared using a Wilcoxon signed rank test. Measurements across different stimulus conditions with n > 50 were compared via paired Student's t‐test, with a post‐hoc Bonferroni multiple‐comparison correction when appropriate unless otherwise noted. P < 0.05 was considered significant, unless otherwise noted.

Results

We characterized the responses of neurons in the auditory cortex to acoustic stimuli designed to capture the statistical properties of natural water sounds. To construct these stimuli, we adapted the random droplet stimuli that were originally constructed to mimic the sound percept of water sounds (Geffen et al., 2011; Gervain et al., 2014), for presentation in the electrophysiological recordings to rats by expanding the frequency range and sample rate. The stimulus consisted of a superposition of gammatones, which can be thought of as individual droplet sounds, that are uniformly distributed in log‐frequency space, and in time (Fig. 1A). The amplitude of each droplet sound was drawn from a random probability distribution, as described in the Methods. The length of each droplet sound was scaled relative to its frequency, to mimic the statistical structure of environmental sounds (Fig. 1B) (Geffen et al., 2011).

Figure 1.

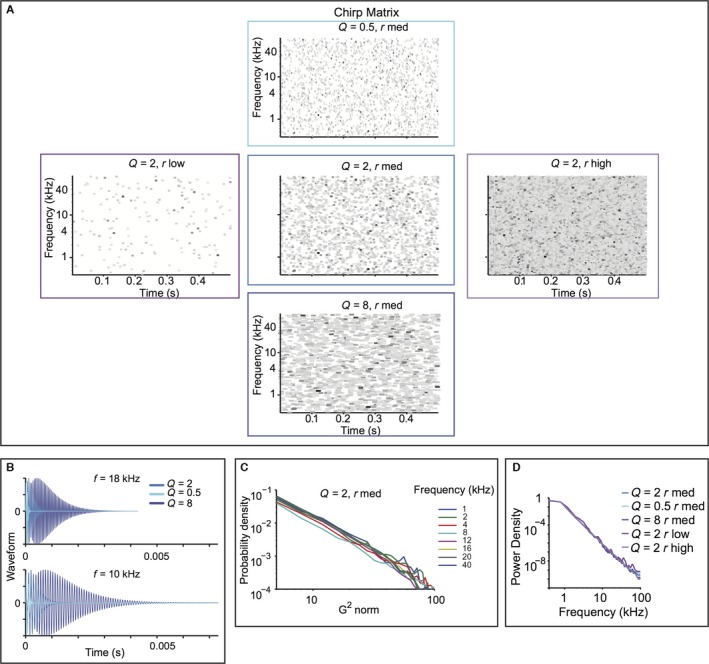
The random droplet stimulus mimics scale‐invariant structure of natural stimuli, while allowing spectro‐temporal constant (Q) and density (rate) to vary. (A) Droplet onset matrix for the five stimuli used in the study. Each line depicts an individual droplet, plotted according to its centre frequency and onset time. Colour depicts relative maximum amplitude, darker colours corresponding to higher amplitudes. Width corresponds to Q. (B) Time course of the waveform for individual droplets. Top: centre frequency of 18 kHz. Bottom: centre frequency of 10 kHz. Droplets are depicted for Q = 0.5, 2 and 8. (C) Histogram of the gammatone transform of the Q = 2, r _med stimulus. (D) Power spectrum density for each of the five stimuli in eight frequency bands.

We varied two stimulus parameters: the cyclo‐temporal coefficient, Q, and the droplet density, r (Geffen et al., 2011). Q denotes the ratio between the time constant of decay for the individual droplets, and their centre frequency. As such, it regulates how many cycles are contained within each droplet. Sounds with high Q have a sustained quality to them, sounding metallic. Sounds with Q = 2 sound natural, water‐like. Sounds with low Q sound like pattering of rain. For very low Q, sounds are static‐like, resembling fire crackling or similar fire‐like sounds. r specifies how many droplets per second are combined to generate the stimulus. Sounds with r _high and Q = 2 sound like a fast waterfall, and with r _low and Q = 2 sound like dripping water (Geffen et al., 2011).

To cover the range of variability expected from natural sounds, we selected three values of Q and r to construct five random droplet stimuli (Geffen et al., 2011) (Fig. 1A). The probability density of the stimulus gammatone transform exhibited a logarithmic relationship within distinct spectral bands. The density curves overlapped across a vast range of frequencies, demonstrating that the stimulus preserved the self‐similar scaling structure, from 1 to 40 kHz (Fig. 1C). Furthermore, these stimuli had a logarithmic power spectrum (Fig. 1D). This indicates that these sounds possessed scale‐invariance not just in the power spectrum, but also in temporal statistics across spectral channels. The random droplet stimulus allowed us to measure not only the response strength, but also the temporal and spectral time course of the dependency of the responses on the stimulus for the different statistical parameters.

The stimulus reliably drives auditory‐evoked responses in the primary auditory cortex

We recorded the activity of 654 units in the primary auditory cortex in awake rats, in response to the five variants of the random droplet stimulus. We used the stimulus with Q = 2, r _med, as the baseline stimulus, as this stimulus was perceived as most natural by human listeners (Geffen et al., 2011). Individual units reliably followed the stimulus, repeated 50 times, exhibiting a significantly modified level of activity during the stimulus presentation, as compared with baseline responses (n = 368 out of 654, response strength > 6, Fig. 2A–C).

Figure 2.

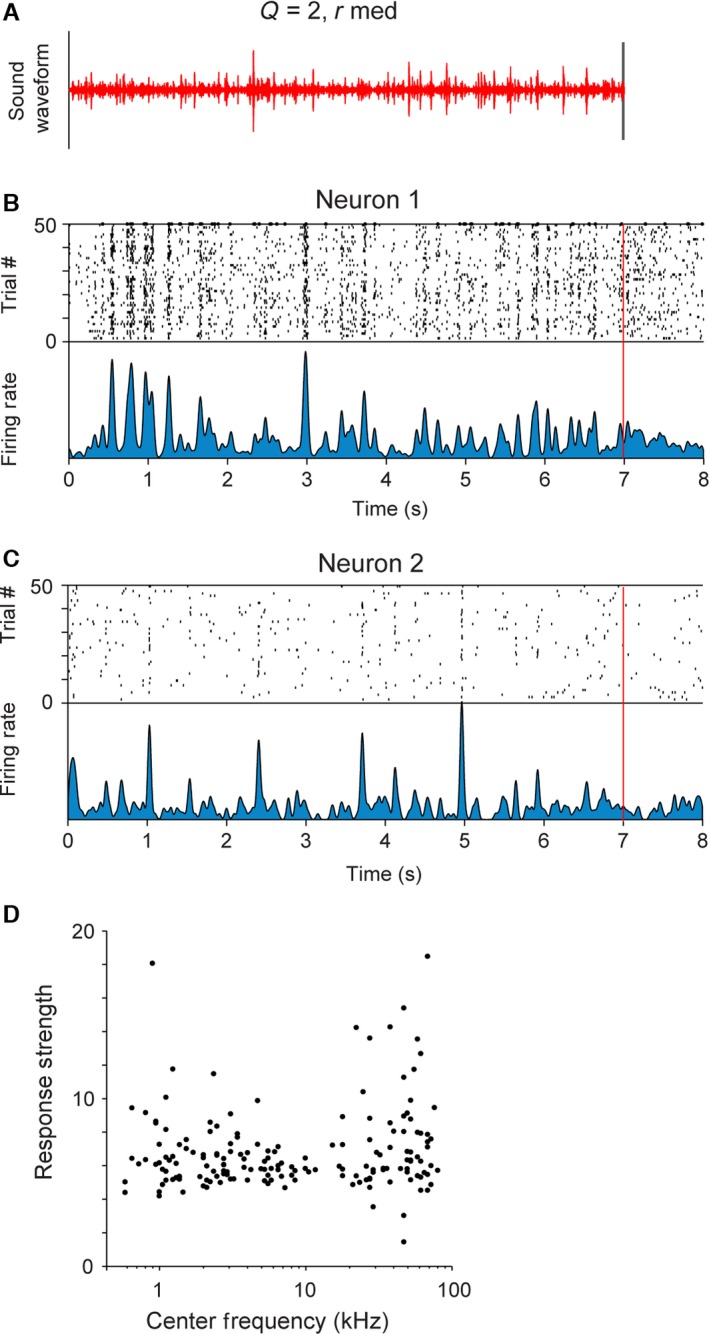
Neurons in primary auditory cortex exhibit reliable responses to the stimulus. (A) Stimulus waveform for the baseline stimulus (Q = 2, rmed). (B, C) Raster plot and firing rate of responses of a representative unit showing time‐locking responses to the stimulus. Top panel: raster plot – each black line denotes an action potential produced by the neuron at a particular delay from stimulus onset (x‐axis) in a particular trial (y‐axis). Bottom panel: mean firing rate of the neuron. (D) Mean response strength of recorded units to the stimulus vs. their centre frequency (n = 368).

The types of responses ranged from sparse, time‐locked responses to sustained responses (Fig. 2B and C). Two representative neuronal responses are depicted in Fig. 2B and C. Neuron 1 exhibited elevated responses throughout the stimulus presentation (Fig. 2B), whereas neuron 2 exhibited sparse responses (Fig. 2C).

The recorded units spanned a broad range of best frequencies, corresponding to the hearing range of rats. Neurons across the full range of best frequencies exhibited significant responses to the stimulus (Fig. 2D, n = 368), as expected for a broadband stimulus.

Selectivity of neuronal responses for specific stimulus statistics

We next tested whether and how changing the spectro‐temporal statistical structure of the stimulus affected neuronal response patterns. The responses of the same neuron to variants of the stimuli included time‐locked excitatory responses, elevated sustained responses or suppressed responses (Fig. 3).

Figure 3.

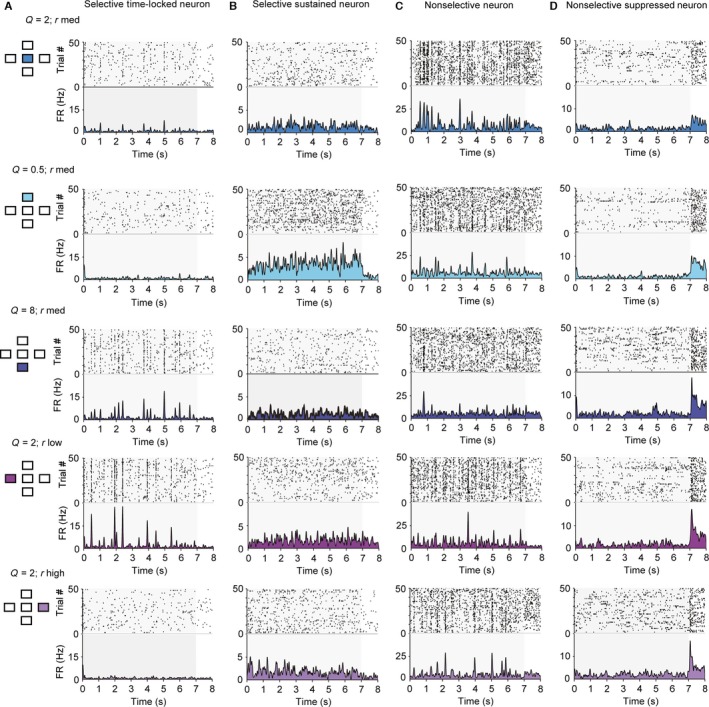
Neurons in primary auditory cortex exhibit diverse responses to the five stimuli used in the study. Responses of four sample units to the five stimuli used in the study. Each row depicts raster plot and firing rate of responses to one of the five stimuli. Left inset: diagram depicting which stimulus was used (compare with Fig. 1A). (A) Responses of a selective time‐locked neuron. (B) Responses of a selective sustained neuron. (C) Responses of a non‐selective neuron. (D) Responses of a non‐selective suppressed neuron.

The majority of recorded units exhibited selectivity for a subset of the stimuli. Time‐locked responses to a subset of stimuli were more common (Fig. 3A). Figure 3A depicts a neuron that exhibited time‐locked, sparse responses to stimuli of Q = 2, r _low or r _med, and Q = 8, rate r _high. The faster fluctuating (Q = 0.5) or more dense (r _high) stimuli were less efficient in driving this neuron. Some neurons exhibited sustained responses (Fig. 3B). The neuron whose response is depicted in Fig. 3B exhibited an elevated firing rate, but not precise time locking to the stimulus. It was most responsive for the stimulus with Q = 0.5, r _med. Some neurons responded significantly to all five stimuli (Fig. 3C and D). While elevated responses (Fig. 3C) were more common, some suppressed responses were also observed (Fig. 3D).

To assay selectivity in neuronal responses to different stimuli, we computed the selectivity index and the sparseness index. The selectivity index was measured as the difference between the strongest and the mean response strength to the five stimuli for each unit, normalized by the strongest response (Fig. 4A). This measure is 1 if the neuron responds to only one stimulus and 0 if it responds to all stimuli with equal strength. The sparseness index quantified how specific the neuronal responses were to a particular stimulus (Fig. 4B). We found that, typically, neurons were responsive to more than a single stimulus. Still, most neurons exhibited a non‐zero selectivity ratio (mean selectivity index = 0.24) and sparseness index (mean sparseness index = 0.069). These values were higher than when responses were randomly shuffled across stimuli (Fig. 4, selectivity: P = 1.9e‐9; sparseness, P = 4.1e‐57, Wilcoxon sign rank test), such that ~50% of neurons were above the 5% significance threshold for the shuffled data. These results indicate that most neurons exhibited higher selectivity for a subset of stimuli than would be expected by chance.

Figure 4.

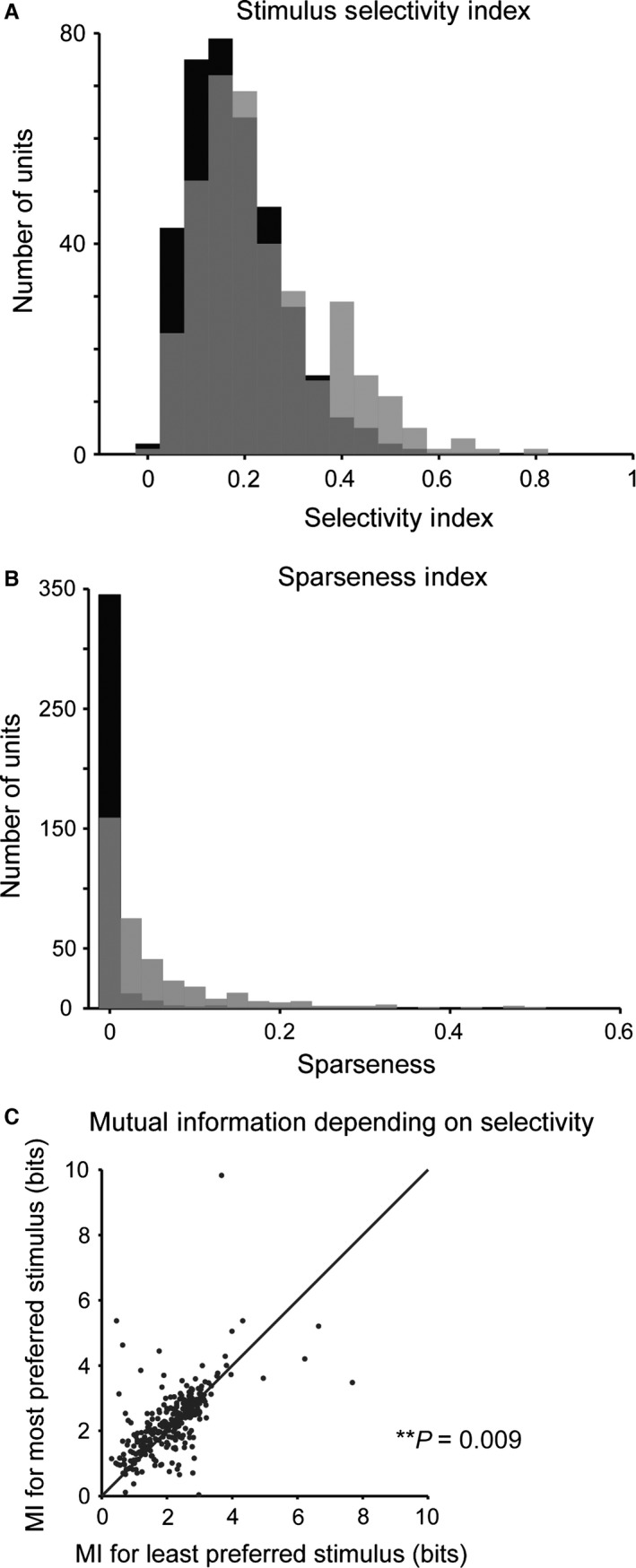
Neurons in primary auditory cortex exhibit selectivity for specific spectro‐temporal statistics. (A) Histogram of stimulus selectivity index across the recorded neuronal population (grey) and for randomly shuffled responses (black). Many units exhibit selective responses to a subset of stimuli. The selectivity index is higher for recorded than for shuffled responses. (B) Histogram of the sparseness of responses across the recorded neuronal population (grey) and for randomly shuffled responses (black). Sparseness is higher for the recorded population than for shuffled responses. (C) Mutual information between the responses and the stimulus is higher for the stimulus, for which the neuron exhibits high selectivity. P = 0.009, paired t‐test.

Did selectivity for a specific stimulus imply that a neuron encoded more information about its structure? We estimated the information conveyed about the stimulus by neuronal responses across different stimulus conditions. We applied an information‐theoretic calculation following a previously developed procedure (Magri et al., 2009; Kayser et al., 2010) by estimating the information (in bits) in six successive 2‐ms bins between the neuronal responses and the stimulus over seven 1‐s stimulus ‘chunks’. Neurons exhibited significantly higher mutual information for stimuli to which they responded most strongly as compared with those that they responded to least strongly (Fig. 4C, n = 304, P = 0.009).

Mutual information may be increased due to an increase in reliability of neuronal responses (Kayser et al., 2010). Consistently, we found a positive correlation between mutual information and the inverse of the Fano factor for responses of neurons to both most and least preferred stimuli (most preferred: correlation coefficient = 0.12, P = 0.04; least preferred: correlation coefficient = 0.31, P = 2.1e‐8). However, there was no difference in the Fano factor between responses to the most preferred and the least preferred stimulus (sign rank test, P > 0.05). Therefore, the increase in mutual information may be attributed to increased responses of individual neurons to the preferred stimuli.

Droplet onset and spectrogram fits of the linear/non‐linear model to neuronal responses

We next sought to characterize which parameters of neuronal responses change with the spectro‐temporal statistics of the stimuli. Responses of neurons in the auditory cortex to an acoustic stimulus have previously been successfully modelled through a linear/non‐linear (LN) model (Eggermont et al., 1983b; deCharms et al., 1998; Depireux et al., 2001; Escabi & Read, 2003; Linden et al., 2003; Gourevitch et al., 2009). This model is used to predict the firing rate of a neuron in response to a new stimulus by first convolving the stimulus with a linear filter, and then passing the linear prediction through an instantaneous non‐linearity (Geffen et al., 2007, 2009). The linear filter can be thought of as the receptive field of the neuron, and the instantaneous non‐linearity to represent the transformation from inputs that change membrane voltage to neuronal spiking.

We fitted the parameters of the linear and non‐linear components of the responses of each neuron to the stimulus. There was, however, an important problem in comparing these parameters. Typically, the receptive field of the neuron is computed as the reverse correlation of the firing rate of the neuron to the spectrogram of the stimulus. In the case of a white noise stimulus, this operation is equivalent to a spike‐triggered average of the stimulus. The changing cyclo‐temporal coefficient of the stimulus introduces dependencies across time within spectro‐temporal channels, resulting in temporal correlations. These correlations are further exaggerated in the spectrogram‐based representation of the stimulus due to binned sampling. To overcome this uneven sampling of the stimulus space, a standard approach is to use decorrelation, in which the linear prediction from the spike‐triggered average is divided by the auto‐correlation of the stimulus (Theunissen et al., 2001; Baccus & Meister, 2002). We applied this approach to the spectrogram‐based representation of the stimulus. However, the time scale of correlations would typically dominate over the time course of neuronal responses, effectively smoothing them and therefore precluding the analysis of the receptive field changes across different statistics of the stimulus.

The construction of the droplet‐based stimulus allowed us to innovatively extend an existing approach to estimate the linear filter (deCharms et al., 1998). Instead of the spectrogram‐based representation, the stimulus was represented by the droplet‐onset matrix. This matrix, by construction, does not contain any correlations, and therefore the optimal filter can be computed as the spike‐triggered average of the droplet‐onset matrix, normalized by mean amplitude of each spectral channel. The droplet‐onset matrix does not contain information about Q, so the matrix is the same for all stimuli at the same rate. Using this matrix as the stimulus representation allowed us to test the hypothesis that the neurons respond predominantly to the onsets of the droplets in the stimulus, rather than their sustained structure. In other words, the information about the sustained ‘ringing’ of droplets may prove less important to the majority of neurons than the timing of the droplet onsets. Such a response pattern would allow the neurons to create a sparse representation of the stimulus, and would be consistent with previous hypotheses on sparse representation of natural acoustic stimuli in the auditory cortex (Smith & Lewicki, 2006; Hromadka et al., 2008). An analogous representation is provided by the cochleagram, a standard method for representing acoustic stimuli (Lyon, 1982; Meddis et al., 1990; Slaney, 1998). In a cochleagram, the acoustic waveform is transformed across spectro‐temporally delimited channels using kernels that scale the bandwidth relative to the centre frequency (Smith & Lewicki, 2006; McDermott et al., 2013).

Therefore, we fitted the LN model to the responses of each neuron under three different representations of the stimulus. The stimulus was represented as either a spectrogram or a cochleagram, and the filter was computed as the spectro‐temporal receptive field; or in the droplet onset representation, in which only the information about the droplet onset time, amplitude and frequency was contained –DTRF (Fig. 5A–C).

We analysed the performance of the model by fitting it based on responses on a random subset of 50% of trials, and computing the correlation coefficient between the prediction for the firing rate and the measured firing rate for the remaining 50% of the trials (Carruthers et al., 2013; Ahn et al., 2014). We found that the droplet‐based and cochleagram‐based representation provided more accurate predictions of the neuronal responses than the spectrogram‐based model (Fig. 5D–F, n = 232). This relationship held when computed over all stimuli [Droplet: 45%, P (all stimuli) = 2.2e‐15, Cochleagram: 60%, P (all stimuli) = 5.8e‐43], but also for most individual stimuli [Droplet: P (Q = 2, r_med) = 2.7e‐6; P (Q = 0.5, r_med) = 0.0031; P (Q = 8, r_med) = 0.0026; P (Q = 2, r_low) = 2.8e‐8; P (Q = 2, r_high) > 0.05 ‐ not significant, Cochleagram: P (Q = 2, r_med) = 7.5e‐13; P (Q = 0.5, r_med) = 1.1e‐6; P (Q = 8, r_med) = 7.6e‐10; P (Q = 2, r_low) = 1.3e‐8; P (Q = 2, r_high) = 2.8e‐10], except Q = 2, r_high. Because this stimulus Q = 2, r_low corresponds to the highest r value (densest dynamics), the result is probably due to the spectrogram approximation being more similar to the droplet matrix under the fastest stimulus dynamics as compared to the other stimuli. The predictions based on the cochleagram‐based representations were more accurate than the droplet‐based representations over all stimuli, but the improvement was not as great as for droplet‐based prediction over the spectrogram‐based prediction [35%, P (all stimuli) = 7.7e‐12] and for stimuli 1, 3 and 5 [P (Q = 2, r_med) = 2.9e‐4; P (Q = 0.5, r_med) > 0.05, not significant; P (Q = 8, r_med) = 9.3e‐6; P (Q = 2, r_low) > 0.05, not significant; P (Q = 2, r_high) = 1.7e‐8]. In some studies, neurons in the auditory cortex have been shown to be more sensitive to stimulus onsets, rather than the prolonged ‘ringing’ of distinct spectral components. This observation may provide an explanation for the improved performance of the LN model when using droplet‐based representation of the stimulus, as this model is more sensitive to the stimulus onsets by design.

Response parameters of the receptive field of A1 neurons do not exhibit systematic change with changing cyclo‐temporal constant

We next examined whether there were any systematic changes in the time course and the spectral structure of the receptive field depending on the stimulus (Fig. 6). We measured the spectral width, temporal delay and temporal length of the positive lobes of the cyclo‐temporal receptive fields (the linear component of the model computed using the droplet‐onset matrix as the stimulus) of the recorded units (Woolley et al., 2006; Shechter & Depireux, 2007; Schneider & Woolley, 2010). Across the neuronal population, there were only modest changes in a small subset of DTRF parameters (Fig. 6C): for Q = 0.5, r _med stimulus, the peak frequency was slightly reduced (P = 0.008); for Q = 2, r _low stimulus, temporal width of DTRF increased (P = 0.004) whereas spectral width decreased (P = 0.011) as compared with the baseline Q = 2, r _med stimulus. This difference is attributed to the temporal delay between droplet onsets in the low‐droplet‐rate stimulus, which allows for more sustained neuronal responses. This suggests that rather than scaling the receptive field's temporal response with changing Q and droplet rate, over the population of neurons, the receptive fields cover the same range of parameters despite the change in the statistical structure of the stimulus.

Figure 6.

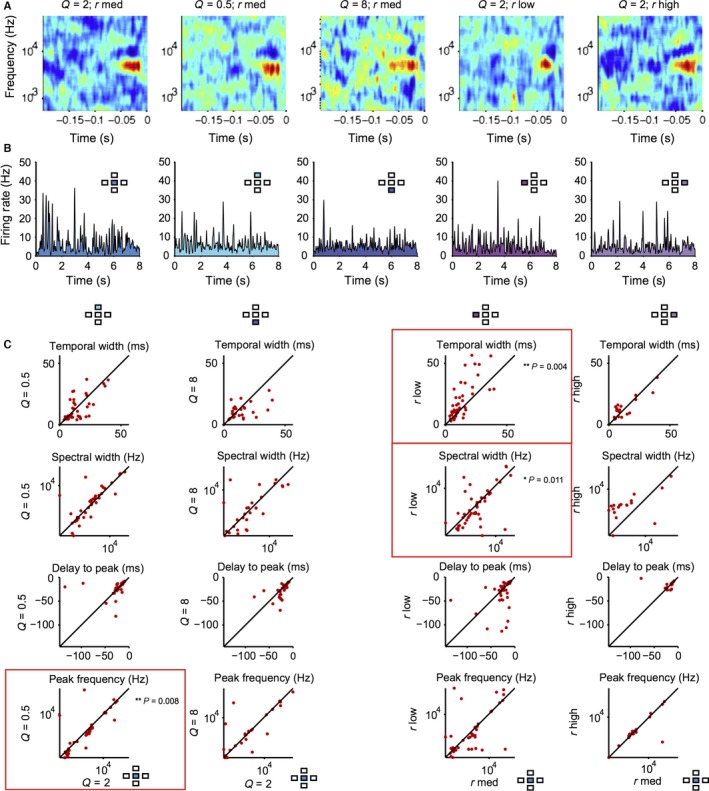
Spectro‐temporal receptive fields of neurons do not exhibit consistent changes with the stimulus statistics. (A) Droplet‐temporal receptive field of a representative neuron for the five stimuli. (B) Firing rate of the neuron to five stimuli. (C) Parameters of droplet‐temporal receptive field for each measured neuron for stimuli with different statistics vs. baseline (Q = 2, r _med) stimulus: temporal width, spectral width, delay to peak and peak frequency of the DTRF. *P < 0.05, **P < 0.01, Wilcoxon signed‐rank test.

We also tested whether over repeated presentations of the same stimulus there was adaptation in the receptive field parameters over time. We computed DRTFs separately for both the first and the last 20 trials and the first and last five trials of each stimulus repeat. We found no significant differences for any parameters for any stimulus over the first and last halves of stimulus blocks (P > 0.06 for all comparisons). These results demonstrate that there is no adaptation to stimulus repeats over time within presentation of the same stimulus.

Nonetheless, we found that the prediction accuracy for each neuron's response was significantly higher using the LN parameters from the corresponding stimulus (same condition) than from the baseline condition (cross‐prediction) (Fig. 7, n = 165, P = 4e‐12 over all five stimuli, P < 0.05 for stimuli 2 and 4). This analysis demonstrates that while there are no systematic changes over the neuronal population, at the level of individual units, the LN parameters differ between the stimuli.

Neuronal population maintains stable mean response profiles across varying stimulus statistics

Whereas for individual neurons there were large differences in response strength for different stimuli, across the population there were no significant differences in the response strength or mean firing rate between stimuli. Over the population of neurons, the mean response strength (Fig. 8A) did not change significantly with Q or rate as compared with the baseline stimulus (n = 368, P > 0.05 for each comparison, Stimulus 1: Q = 2, r _med; Stimulus 2: Q = 0.5, r_med; Stimulus 3: Q = 8, r_med; Stimulus 4: Q = 2, r_low; Stimulus 5: Q = 2, r_high). The mean firing rate was also remarkably stable: it did not differ from baseline for stimuli 2, 3 and 4 (Fig. 8B, n = 368), and was only marginally smaller for stimulus 5 (Q = 2, r _high: difference 8.8%, P = 0.0068).

Figure 8.

Neuronal population exhibits even responses to stimuli with different stimulus statistics. (A) Mean response strength over the population of neurons to the five stimuli. (B) Mean firing rate over the population of neurons to the five stimuli. (C) Mean Fano factor over the population of neurons to the five stimuli. (D) Mean mutual information between the response and the stimulus for the five stimuli. **P < 0.01; *P < 0.05: paired t‐test to responses to baseline stimulus.

We next assayed the variability of the firing rate of neuronal responses. We calculated the Fano factor, which indicates how variable the discharge count is over trials relative to the mean firing rate. For a Poisson neuron, the standard deviation of the response is equal to the mean, and Fano factor is 1. Typical Fano factors for neurons recorded in the awake mammalian cortex exceed 1. Indeed, our calculations of the Fano factor demonstrate that it exceeded 1 on average for all stimuli. The mean Fano factor did not differ from the baseline for stimuli 2, 3 and 4 (Fig. 8C, n = 368, P > 0.05), and was only marginally increased for stimulus 5 (Q = 2, r _high: difference 7.5%, P = 0.026). Importantly, the mutual information was not significantly different in a population pairwise comparison across all neurons tested (Fig. 8D, n = 304, P > 0.05) between the stimuli, further underlining the stability of the distribution of neuronal response parameters across different stimulus statistics.

Overall, our data demonstrate that stimuli with different cyclo‐temporal statistics or density are stable in their representation over the neuronal population.

Discussion

Natural water sounds exhibit spectro‐temporal regularities in their structure, which are characterized by scale‐invariant statistics. The goal of this study was to establish how populations of neurons in the auditory cortex respond to sounds across a wide range of spectro‐temporal parameters that correspond to a range of acoustic percepts (Geffen et al., 2011). We focused on two statistical quantities, which we had previously identified as perceptually relevant for distinguishing water‐like sounds. Cyclo‐temporal coefficient, Q, refers to the ratio of temporal change within a particular frequency band to its centre frequency. Droplet rate corresponds to the spectro‐temporal density of sounds. We found that most units recorded in A1 exhibited tuning for specific combinations of Q and droplet rate. However, over the neuronal population, the responses and response parameters were stable across the broad range of the spectro‐temporal statistics of the stimulus. These results suggest that tuning to spectro‐temporal statistics in neurons may be distributed in such a way as to preserve the mean responses over the population, rather than individual neurons.

Even population responses across changed stimulus statistics

Spectro‐temporal statistics vary greatly between different acoustic environments. Within different water sounds, the statistics can differ over several orders of magnitude, from a loud gurgling brook to rain pattering on the roof to droplets falling from a slowly melting icicle. Yet our auditory system needs to be able to represent the multitude of sounds with a limited set of resources. This limited set of resources is generally constrained by the range of the firing rate of neurons, as well as their noise level. Our results demonstrate that, for the group of water‐like sounds, the response properties are matched over the neuronal population across a large range of stimulus statistics. Conservation of the mean firing rate and other response characteristics of neurons is considered an important organizational principle for sensory systems. Neuronal selectivity can be thus thought of as a process that enables neurons to preserve mean response parameters in the context of stimuli with vastly different statistical structure. The specialization of response properties of individual neurons to specific subsets of spectro‐temporal stimulus statistics may arise from a combination of inputs tuned to relatively simple statistics of the stimulus (McDermott & Simoncelli, 2011), and facilitate perceptual discrimination of acoustic environmental sounds (McDermott et al., 2013).

Naturalistic stimulus to probe spectro‐temporal receptive field properties of auditory neurons under naturalistic conditions

Typically, responses of neurons in the auditory cortex to sounds are characterized by identifying their spectro‐temporal receptive fields (Depireux et al., 2001; Escabi & Schreiner, 2002; Theunissen et al., 2004). The stimuli that are used to map the spectro‐temporal receptive field include random pip and random chord sequences (Eggermont et al., 1983b; deCharms et al., 1998; Blake & Merzenich, 2002; Escabi & Read, 2003; Linden et al., 2003; Gourevitch & Eggermont, 2008). These stimuli differ from the scale‐invariant stimulus set because the temporal dynamics are at the same timescale within each spectral band. Similarly, white noise (Eggermont et al., 1983a) or dynamic ripple stimuli (Klein et al., 2000; Depireux et al., 2001; Elhilali et al., 2004), designed to measure the responses of neurons for sound with continuously changing temporal modulations, apply temporal modulations uniformly across all spectral channels. By contrast, the random droplet stimuli probe the auditory system within the statistical regime characteristic of water‐like sounds, in which the temporal modulation of the structure of sounds scales with the centre frequency of the droplet (Geffen et al., 2011; Gervain et al., 2014).

Numerous studies have shown that the response properties of neurons depend on the statistical make‐up of the stimuli with which they are probed. A receptive field measured with a white‐noise stimulus can differ from that measured with a stimulus with scale‐invariant statistics (Sharpee et al., 2004). Therefore, the use of the droplet stimulus is advantageous in measuring the receptive fields of neurons in that it reflects an important property of natural sounds. In estimating the linear receptive field of neurons, using a stimulus that follows a random distribution of parameters is furthermore of an advantage for practical reasons: as the stimulus space is sampled uniformly, the optimal filter can be constructed without a correction for stimulus auto‐correlation. The present stimulus provides such a representation in the droplet‐based matrix because the timing of the droplets as well as their amplitude are picked from a random distribution that does not have correlations in either time or frequency.

Changing Q modulates both the rise/fall time of the amplitude of each droplet as well as the bandwidth, and therefore can affect auditory responses through several mechanisms at different stages of auditory processing. Temporal envelope and modulation frequency are important parameters that have previously been shown to be important for psychoacoustic (Irino & Patterson, 1996) and physiological responses to sounds (Heil et al., 1992; Heil, 1997; Lu et al., 2001; Krebs et al., 2008; Lesica & Grothe, 2008; Zheng & Escabi, 2008; Lin & Liu, 2010). Therefore, the selective responses for different Q–r combinations may be a result of integration of changes in the auditory periphery (Lu et al., 2001; Lin & Liu, 2010; Heil & Peterson, 2015) as well as central processing (Blake & Merzenich, 2002; Valentine & Eggermont, 2004).

Variability of neuronal responses and time course of spectro‐temporal receptive fields

The temporal width of the receptive fields that we identified in the study is very tight – some of the receptive fields contained a positive lobe with a width of <10 ms (Fig. 6C). This is consistent with several previous studies that have demonstrated that neuronal responses in A1 provide important information about the stimulus at the time scale of 1–3 ms (Yang et al., 2008; Kayser et al., 2010). Remarkably, our analysis revealed that as the droplet presentation rate slowed, the temporal integration window of the receptive field became longer. This suggests that under the regime of slower modulations, the droplet onsets trigger more sustained responses than under the regime with fast scale of modulations. It is plausible that higher‐order statistics, which differ between stimuli with short and long Q parameters, may account for this change.

Non‐linear transformation of the stimulus

The droplet‐based LN model belongs to a greater family of non‐linear linear – non‐linear models as the droplet‐onset matrix can be thought of as a non‐linear transformation of the stimulus (Marmarelis & Marmarelis, 1978; Butts et al., 2011; McFarland et al., 2013). We note that this stimulus representation differs from the commonly used cochlear gammatone‐like filter bank, constructing a cochleagram (Klein et al., 2000; Elhilali et al., 2004) in that the gammatone onsets are specified during stimulus construction, and rather than being used as filters, are components of the stimulus. In a recent study, we found that for A1 responses to another class of stimuli, rat ultrasonic vocalizations, a non‐linear transformation of the stimulus into a dominant amplitude‐ and frequency‐modulated parametrized tone led to a more accurate prediction of the LN model (Carruthers et al., 2013). Similarly, in the present study, the representation of the stimulus as a droplet‐based matrix provides a more accurate prediction than a spectrogram‐based representation for all but the most sluggish stimulus. A similar stimulus was used to model the receptive fields of neurons in response to sounds with constant temporal statistics across different frequency bands (deCharms et al., 1998), but that approach did not extend to scale‐invariant sounds, in which the spectro‐temporal coefficient Q is presented across frequency bands. While our representation probably oversimplifies the operations that are performed within the auditory periphery, it is consistent with previous predictions and experimental observations for processing of acoustic stimuli by the cochlea and the auditory nerve (Robles & Ruggero, 2001).

Although LN models have been successfully used to study the linear components and receptive fields of neurons throughout the auditory pathway, these models carry significant limitations, which pose constraints on the interpretation of our results. In using a single‐stage model, it is difficult to pinpoint at which stage of the pathway the transformation takes place. On the other hand, more complex models that include several linear and non‐linear terms may preclude a summary of the effect of statistics of the stimulus on a subset of response parameters (Ahrens et al., 2008; Christianson et al., 2008). Adding the pre‐processing step for representing the stimulus as an ensemble of gammatones expands the ability of the LN model to predict the stimulus responses, while simplifying the representation of the stimulus.

Generalization of the random droplet stimulus to probe speech and other communication signals

An additional advantage of this stimulus is that the droplet‐like representation can be used to construct a representation of an arbitrary complex sound, and that such a representation is optimal for sparsely firing neurons (Smith & Lewicki, 2006; Carlson et al., 2012). It has been previously demonstrated that the optimal sparse code for representing natural sounds consists of unitary scale‐invariant impulses that correspond to the auditory revcorr filters (Smith & Lewicki, 2006). The random droplet stimulus can be modified to probe specificity of neuronal responses to speech and communication signals. To represent a speech signal, the acoustic waveform could be projected on the impulse functions, used as band‐passed filters, and represented as ‘spikes’. The droplets used in the present stimulus can be viewed as a simplified, generalizable version of such impulses, and would produce a similar representation of different environmental sounds, beyond the range of measured water sounds. Decomposing a speech acoustic waveform on spectro‐temporal channels will then allow us to compute the cross‐correlation functions across those channels. A random droplet signal can be constructed to match the cross‐correlation functions, and the responses across different statistical dependencies can be compared.

Speech contains important information at different time scales, which is relevant for different aspects of speech comprehension (Rosen, 1992; Poeppel, 2003). Introducing the dependencies at varying time scales into the random droplet stimulus would allow us to test neuronal responses to different aspects of speech and vocalization processing.