Development of Long-term Spatiotemporal Models for Ambient Ozone in Six Metropolitan regions of the United States: The MESA Air Study

Abstract

Background

Current epidemiologic studies rely on simple ozone metrics which may not appropriately capture population ozone exposure. For understanding health effects of long-term ozone exposure in population studies, it is advantageous for exposure estimation to incorporate the complex spatiotemporal pattern of ozone concentrations at fine scales.

Objective

To develop a geo-statistical exposure prediction model that predicts fine scale spatiotemporal variations of ambient ozone in six United States metropolitan regions.

Methods

We developed a modeling framework that estimates temporal trends from regulatory agency and cohort-specific monitoring data from MESA Air measurement campaigns and incorporates land use regression with universal kriging using predictor variables from a large geographic database. The cohort-specific data were measured at home and community locations. The framework was applied in estimating two-week average ozone concentrations from 1999 to 2013 in models of each of the six MESA Air metropolitan regions.

Results

Ozone models perform well in both spatial and temporal dimensions at the agency monitoring sites in terms of prediction accuracy. City-specific leave-one (site)-out cross-validation R² accounting for temporal and spatial variability ranged from 0.65 to 0.88 in the six regions. For predictions at the home sites, the R² is between 0.60 and 0.91 for cross-validation that left out 10% of home sites in turn. The predicted ozone concentrations vary substantially over space and time in all the metropolitan regions.

Conclusion

Using the available data, our spatiotemporal models are able to accurately predict long-term ozone concentrations at fine spatial scales in multiple regions. The model predictions will allow for investigation of the long-term health effects of ambient ozone concentrations in future epidemiological studies.

1. Introduction

Ground-level ozone is the classic indicator for the mixture of photochemical oxidants originating from anthropogenic and biogenic precursor emissions (EPA, 2006). Ozone itself is a potent oxidizing agent that has clear harmful effects on human health, as has been amply demonstrated in human chamber exposure studies (ISA, 2013). Observational associations between short-term exposure to ozone and respiratory morbidity and mortality have also been documented in the United States and Europe (ISA, 2013; WHO, 2013). Chronic effects of ozone exposure on lung function development, asthma incidence and pulmonary inflammation have been suggested (ISA, 2013). However, compared to the large body of evidence on long-term effects of traffic related pollutants (e.g. nitrogen dioxide and particulate matter), relatively little research has examined health effects related to long-term ozone exposure. In the United States, national-wide ozone levels have decreased steadily in the past decade, although with some heterogeneity between urban and rural areas (EPA, 2014; Chan et al. 2009; Cooper et al. 2012; Lefohn et al. 2010; Simon et al. 2015).

Attempts to estimate long-term ozone exposure in large populations are scarce and challenging, largely because of the complex spatiotemporal pattern of ozone concentrations at fine scales. Previous epidemiological studies on long-term ozone exposure generally relied on estimates from nearby monitoring sites (Jerrett et al., 2009) or simple spatial interpolation techniques such as inverse distance weighting (Bretton et al., 2012; Jerrett et al., 2013; Lipsett et al., 2011). More advanced exposure estimation techniques include chemical transport modeling (CTM) and land use regression (LUR) modeling: CTM approaches with resolution to grids measured in km²s are typically not spatially resolved enough to characterize exposures at very local scales (i.e., meters). Recent LUR models have utilized a large number of covariates, such as traffic characteristics and land use/land cover, to account for spatial distributions of air pollutants (Hoek et al., 2008; Malmqvist et al., 2014); hese models did not take temporal variations into account which is important for ozone, as varying spatiotemporal ozone patterns have been observed in the United States (ISA, 2013). Some spatiotemporal ozone modeling efforts were exclusively based on a limited amount of routinely collected monitoring data over large regions (Adam-Poupart et al., 2014; de Nazelle et al., 2010; Yu et al., 2009). However, routinely collected monitoring data from relatively few sites are unable to capture roadside decrements of ozone caused by scavenging by freshly emitted nitric oxide (NO) in urban areas, resulting in overestimation of ozone exposure for some segments of the population samples used in epidemiological studies.

The Multi-Ethnic Study of Atherosclerosis and Air Pollution (MESA Air) was designed to examine the effects of long-term air pollution exposure on cardiovascular health (Kaufman et al., 2012). Air pollution data including ozone were collected through an intensive measurement campaign in six metropolitan regions (Baltimore, Maryland; Chicago, Illinois; Los Angeles, California; New York, New York; St. Paul, Minnesota; Winston-Salem, North Carolina) in order to better represent spatial and temporal patterns of the air pollutants (Cohen et al., 2009). This paper describes the development and the performance of spatiotemporal models of long-term ozone concentrations in these six metropolitan regions.

2. Materials and Methods

Separate models were developed for each of the six MESA metropolitan regions because of the diversity of study areas and differences in available GIS predictor variables, although an identical procedure for estimating model parameters was employed for all regions. Briefly, the spatiotemporal model, which we describe in more detail below, decomposes space-time ozone concentrations into spatially varying long-term averages, spatially-varying seasonal and long-term trends, and spatially-correlated but temporally-independent residuals, and accommodates data from a complex and irregular monitoring design. Ozone predictions were made at the residential addresses of MESA Air study participants for use in future epidemiological analyses.

2.1 Monitoring data

Spatiotemporal models developed for ozone were based upon continuous long-term measurements from the Air Quality System (AQS) of the U.S. Environmental Protection Agency (EPA) (EPA, 2013) and the spatially dense supplementary data specific to the MESA Air study (Cohen et al., 2009; Zhang et al., 2014). Given the large regional scale of spatial variation in ozone concentrations and the typical seasonal monitoring schedules for AQS sites, we chose AQS monitoring sites within a wide buffer (75-200km) surrounding each metropolitan center (see Figure A.1 in Appendix A). In Los Angeles and New York, measurements were conducted in Los Angeles County and New York City, as well as in nearby Riverside County, CA and Rockland County, NY, as dictated by the locations of MESA Air participants. Therefore, two 75km buffers were generated in each of these two study regions. In Chicago, the modeling region was restricted to locations west of 87.5°W longitude due to incomplete covariate data. In Winston-Salem and St. Paul, buffers were expanded to 200 km in order to include AQS monitor sites with complete data throughout the whole period.

Hourly ozone AQS data were obtained from 1999 to 2013 to provide information on long-term temporal trends. Data were aggregated into daily means and then at a two-week time scale (centered on Wednesday) in order to mitigate the influence of daily meteorology, reduce temporal autocorrelation, and importantly to match the MESA Air sampling design. In most of the regions, ozone data were collected in warm seasons between April and September, but at least one AQS station operated continuously during the entire study period (for Winston-Salem and St. Paul starting from 2005). In Los Angeles, ozone data were continuously recorded throughout the entire study period at all monitoring sites. AQS stations that contained data for less than two years were excluded in order to get reliable estimate of main time trends by the spatiotemporal model. In total, 14-48 AQS stations were included for modeling, depending on the metropolitan region (Table 1).

Table 1.

Spatiotemporal model specifications for ozone in the six MESA regions.

								2Spatial Smoothing
City	Buffer (km)	No. of AQS Sites	No. of Fixed Sites	No. of Home Sites	No. of Predictor Variables	No. of Time Trends	1No. of PLS Scores	Long Term (β0)	Time Trend (βi)
3LA+RS	75	44	7	117	184	2	(3,2,2)	Yes	No
New York	75	27	2	90	222	2	(1,2,1)	Yes	No
Chicago	100	30	5	80	181	1	(2,1)	No	No
Baltimore	100	41	4	60	202	2	(2,2,1)	Yes	No
4W-S	200	48	4	100	204	2	(1,2,1)	Yes	No
St Paul	200	14	4	96	192	1	(1,1)	No	No

¹Number of PLS scores for (long-term mean, 1^st time trend, 2^nd time trend);

²Yes, exponential covariance structure. No, independent covariance structure

³Los Angeles and Riverside

⁴Winston-Salem

The core ozone measurements in MESA Air were conducted between 2005 and 2009 using Ogawa samplers. For all the measurements, only 3 out of the 1433 samples were below the limit of detection (LOD) and were replaced with the value LOD/2. More details of the MESA Air monitoring campaign, including data collection and site selection procedures, have been described previously (Cohen et al., 2009). Briefly, 60 to 117 sites were located at the participants' addresses (home sites) in each study region. At each home monitoring site, 1 to 3 two-week measurements in different seasons were made, with sites selected to represent various exposure settings (e.g., street, urban and regional background). In 2009, a supplementary measurement campaign was implemented in which simultaneous (“snapshot”) measurements were made at home addresses in three of the MESA Air regions (Chicago, Winston-Salem and St. Paul) (Zhang et al., 2014). In addition, 2 to 7 fixed sites were operated continuously for one year, with one of the fixed sites collocated with an AQS station in each region (Table 1).

2.2 Geographic covariates

More than 220 geographic covariates were used for model development. Variables covered a wide diversity of geographic features, such as traffic (e.g., distance to near major road and, within buffers, lengths of roads and truck routes, and counts of intersections), industrial and port emissions, population density, land use (e.g., commercial space), and land cover (e.g., green space). Moreover, we incorporated an annual average of specific emission sources for NOx, SO₂, CO, PM_2.5 and PM₁₀ from the U.S. EPA Emission Inventory Group and a long-term average of primary mobile source emissions estimated by the California Line-source (CALINE) dispersion model, as these are potentially related to ozone formation and destruction (Eckhoff and Braverman, 1995). Details of the geographic variables are described in Table A.1, Appendix A.

Geographic covariates with minimal variation or potentially highly influential values were excluded from the modeling process (Keller et al. 2015). Specifically, variables were removed if: (a) more than 80% of the monitoring sites had the same value, (b) more than 2% of the observations were more than five times the standard deviations away from the mean, (c) the standard deviation of the distribution of values at participant residences was more than five times the standard deviation of the distribution of values at monitoring locations, or (d) the maximum value was 10% among all monitoring sites (for land-use variables only). Variable screening procedures were implemented separately for each region.

2.3 Spatiotemporal Model Development

A hierarchical spatiotemporal model was developed to fully accommodate the unique features of our data, which contained a small number of sites providing information on temporal variation and a larger number of sites with short-term measurements providing broader spatial coverage. Technical details of implementation, including the model structures and principles (Lindström et al., 2012; Sampson et al., 2011; Szpiro et al., 2010), and a recent application of the model for NO₂, NOx, PM_2.5 and an indicator of black carbon (light absorption coefficient)., have been published (Keller et al. 2015). The model comprises a spatio-temporal trend model and spatio-temporal residuals, which can be written as:

$$C(s,t)=\mu (s,t)+\nu (s,t)$$ (1)

where C(s,t) denotes the two-week average concentration of ozone at location s and time t. The μ(s, t) represents the spatiotemporal mean surface, and ν(s, t) is the spatiotemporal residual variation. The μ(s, t) can be further decomposed into:

$$\mu (s,t)={\beta }_0(s)+{\sum }_{i=1}^m{\beta }_i(s)f_i(t)$$ (2)

where β₀(s) denotes the long-term mean at location s and β_i(s) are spatially-varying coefficients for smooth time trends f_i(t).

In general, we calculated the time trends f_i(t) from AQS and MESA Air fixed sites, which account for the temporal structure across an entire study region. We obtained the coefficients β₀(s) and β_i(s) according to the linear relationship between each time trend and the observations at each AQS/MESA Air fixed sites. We modelled the spatially varying coefficients based on GIS covariates via Partial Least Squares (PLS) and incorporated a large number of spatially dense monitoring data from MESA Air to allow specific trend and concentration level at the locations of interest.

We applied an iterative EM (Expectation-Maximization) procedure to fill in missing values in the time series and derived the trends from singular value decomposition (SVD) of the space-time data matrix (Fuentes et al. 2007; Sampson et al. 2011). An appropriate number of time trends m was determined by cross validation of low-rank SVD approximations of the space-time data matrix (SVDsmoothCV package) and the overall model performance. The long-term average β₀(s) and time trend coefficients β_i(s) are modeled as spatial random fields with a LUR mean in a universal kriging framework, distributed as:

$${\beta }_i~N[{\mathbf{X}}_i(s){\mathit{\alpha }}_i,{\sum }_i({\varphi }_i,{\sigma }_i,{\tau }_i)],i=0,1,\dots ,\mathrm{m}.$$ (3)

where X_i(s) are a group of reduced-dimension components (scores) from combinations of geographic covariates computed by PLS (Keller et al. 2015). Rather than use variable selection methods for geographic covariates, we reduced the dimensionality of the covariates using PLS. Similar to principal components analysis (PCA), PLS computes linear combinations, called scores, of the columns of a data matrix. Unlike PCA, the PLS procedure constructs scores that maximize the covariance between the scores and an outcome rather than the variance between the scores. The PLS scores were developed separately for the long-term average and time trend coefficients. The numbers of PLS scores were determined by cross-validation using the pls function (in the plsr package in R). α_i are vectors of estimated regression coefficients. The covariance structure for β_i, denoted by Σ_i, is either an independence model with variance τ_i or a spatial smoothing model with an exponential covariance function parameterized by range ϕ_i, partial sill σ_i, and nugget τ_i (Cressie, 1993).

The zero-mean spatiotemporal residual term ν(s, t) has a spatial correlation structure and is assumed independent at each time point. It includes a random effect for each time point to model short-term variations that affect an entire region, such as large-scale meteorological events.

The best models were selected based on CV R² to determine the number of time trends f_i(t) and the PLS scores X_i(s). Rather than the overall CV for the model performances as will be mentioned later, these particular CVs used the R package's built-in functionalities to select appropriate number of components for model development. Once the PLS scores X_i(s) and time trends f_i(t) were computed, the regression and covariance parameters were estimated via maximum likelihood, using the SpatioTemporal package (Lindström et al., 2012) in R 2.15.1 (R Core Team).

2.4 Model validation

We used k-fold cross validation (CV) to evaluate model performance. Monitoring sites were repeatedly separated into training and test data set. We re-estimated the regression and covariance parameter (maintaining the time trends and PLS scores) based on the training data set to predict ozone concentrations in the test data set. For each assessment of the model performance, we computed two measures of CV performance: 1) the traditional regression-based R² (CV_REG) which is derived from correlations between observed values and CV predictions, and 2) the mean square error (MSE)-based R² (CV_MSE), taking into account absolute values in terms of mean squared prediction error rather than merely correlation. This is defined as:

$${\text{CV}}_{\mathit{\text{MSE}}}{\mathrm{R}}^2=\mathit{max}(0,1-\frac{\mathit{\text{MSE}}}{\mathit{\text{Var}}(\mathit{\text{Obs}})})$$ (4)

where MSE can be written as:

$$\mathit{\text{MSE}}=\frac{{\sum }_{i=1}^n{({\mathit{\text{Obs}}}_i-{\mathit{\text{Pred}}}_i)}^2}{n}$$ (5)

The more commonly estimated CV_REG R² is higher than the CV_MSE R², but it does not measure accuracy of fit with respect to the reference line (the 1:1 diagonal), which is reflected by the CV_MSE R². Due to the different features of the monitor types, we evaluated the AQS (together with fixed) sites and the home sites separately. For AQS and fixed sites, we used leave-one (site)-out CV (LOOCV) due to the relatively small number of sites per metropolitan region. For the CV_REG and CV_MSE R², we computed the across-sites median R² between predictions and observations at two-week time points throughout the entire study period to evaluate the performance in representing temporal variability and the across-years median R² between annual averaged predictions and observations for the AQS and fixed sites to represent the performance of the model in representing spatial variability. For the data at the home sites, which were intended to reflect spatial contrasts of ozone at the places of most interest, we used ten-fold CV by successively leaving out one-tenth of the home-site data for validation. Since the home site data are temporally sparse but spatially rich, Lindström et al. (2014) proposed a temporally-adjusted adaptation of CV_MSE R², which we call spatial CV_MSE R², that calculated the variance from the average values at AQS and fixed sites as reference instead of the variance from the home sites observations in (4) in order to focus on spatial prediction accuracy. Since most of the AQS data were collected in warm seasons rather than in cold seasons, we also separately examined the prediction ability of the models (using the main models rather than developing seasonal models separately) in the separate seasons at the home and AQS/fixed sites.

Once the best models were successfully developed, we applied them to predict the ozone concentrations at cohort participant residences on a two-week scale from 1999 to 2013. Finally, we computed the correlations between the annual averaged ozone estimates and previously published NO₂, NOx, PM_2.5 and black carbon estimates at the same locations (Keller et al. 2015).

3. Results

3.1 Ozone Concentrations

Substantial variability of two-week average ozone concentrations measured at the AQS and participant home sites was observed in all six MESA regions (Figure 1). Observations at the AQS monitors, which captured regional spatial and long-term temporal characteristics of ozone, showed larger variability and higher median concentrations compared with project-specific measurements from home and fixed sites that were made locally within each city. The correlation coefficient between AQS monitor measurements and MESA Air campaign measurements at co-located sites, however, was 0.88, with almost no bias (see Figure A.2 in Appendix A). There was also variability in ozone concentrations across the study areas over the monitoring periods, with the lowest median values in New York (AQS: 26.2 ppb, fixed: 17.4 ppb, home: 19.2 ppb) and the highest median values in Winston-Salem (AQS: 32.9 ppb, fixed 27.7 ppb, home: 28.9 ppb). Ozone concentrations were consistently high in warm seasons (April to September) and low in cold seasons (October to March).

Figure 1.

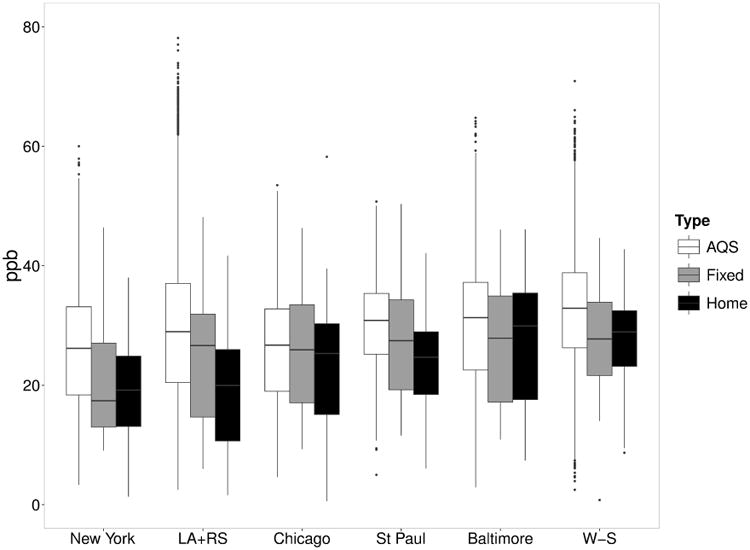
Boxplot of two-week average of ozone concentrations at AQS, Fixed and Home locations across the entire period in the six MESA regions. LA+RS: Los Angeles and Riverside in California. W-S: Winston-Salem in North Carolina. The upper, middle and lower lines in the box show the 75%, 50%(median) and 25% of the observations. The outliers are calculated as the observations higher or lower than 1.5 × IQR + median.

3.2 Model Structures

Table 1 describes an overview of the ozone model structures in the six MESA regions. Models varied across the study regions due to differences in ozone concentration variability, geography, meteorology, and local pollution sources/sinks. Most of the models selected two time trends, with two exceptions where a single time trend was selected (Chicago and St Paul). The first time trend showed clear seasonal variation of O₃ over the years. An example of the two smoothed trends for the ozone model and the plots of the fitted trends for a selected AQS and fixed site in Baltimore are shown in Figure A.3 in Appendix A. Good agreement between observations and the smoothed trend was observed, with the first time trend explaining most of the temporal variability of ozone. Regarding covariates, models typically contained 1 to 3 PLS scores for the long-term mean and the time trends. The GIS covariates explained long-term mean variation well in all six regions based on cross validation from PLS, but fitted the time trends relatively poorly in two regions: the Winston-Salem and New York City areas (data not shown). An illustration of the contributions of GIS covariates to the PLS scores (loadings) for the long-term mean is displayed in Figure A.4 in Appendix A for the six study regions. In general, the loadings of the PLS scores showed similar patterns for the geographical categories across the study regions though the magnitude varied individually. The long-term mean ozone was positively associated with elevation and urban green space (Dev Open, Grass, Shrub), and was negatively associated with the features indicating primary emissions (e.g., traffic and anthropogenic). In Los Angeles, New York, Baltimore and Winston-Salem, spatial smoothing (via universal kriging) was included in the long-term mean. No models included spatial smoothing in the time trend coefficients (β_i(s)) in any of the study regions.

3.3 Model Performances

Table 2 presents the cross validation results for the ozone models at the home sites and at the AQS/fixed monitoring locations, respectively. Overall, the model performed best in Baltimore, followed by St Paul, Chicago and the Los Angeles Basin. The home CV R²s, which indicate the performance in time and space combined, were moderate to high across the study areas (CV_MSE R²: 0.60-0.91; CV_REG R²: 0.62-0.90). The R² remained moderate to good after time adjustment (spatial CV_MSE R²: 0.47-0.88), suggesting good prediction ability in terms of spatial accuracy. For the AQS/fixed locations, the model performed better in term of precision (CV_REG R²) than accuracy (CV_MSE R²) in predicting both temporal (CV_REG R²: 0.88-0.91; CV_MSE R²: 0.59-0.88) and spatial patterns (CV_REG R²: 0.15-0.82; CV_MSE R²: 0.01-0.72). The CV R²s suggested moderately good to excellent agreement between the model and the AQS/fixed measurements, with one notable exception in Winston-Salem (spatial CV_MSE R²: 0.01; CV_REG R²: 0.15). Models predicted consistently better in cold seasons than in warm seasons (see Table A.2 in Appendix A).

Table 2.

Model performances using cross validations at the home and AQS+Fixed sites.

	1MESA Home Sites			2AQS and MESA Fixed Sites
City	Overall CVMSE R2	Overall CVREG R2	3Spatial CVMSE R2	Overall CVMSE R2	Overall CVREG R2	4Spatial CVMSE R2	4Spatial CVREG R2	5Temp CVMSE R2	5Temp CVREG R2
6LA	0.67	0.78	0.87	0.70	0.78	0.39	0.71	0.60	0.88
Baltimore	0.90	0.89	0.64	0.88	0.88	0.72	0.75	0.88	0.91
Chicago	0.71	0.72	0.47	0.82	0.84	0.32	0.44	0.83	0.89
New York	0.60	0.61	0.81	0.76	0.84	0.41	0.82	0.59	0.90
7W-S	0.66	0.76	0.60	0.65	0.73	0.01	0.15	0.69	0.89
St Paul	0.91	0.90	0.88	0.81	0.82	0.58	0.80	0.75	0.89

¹Ten-fold CV at home locations;

²Leave one out cross validation (LOOCV) at AQS and fixed locations;

³Time adjusted CV representing spatial accuracy at the home addresses;

⁴Median CV_MSE and CV_REG R² based on annual averages at each AQS and fixed location across years, which reflects spatial prediction ability of the models;

⁵Median CV_MSE and CV_REG R² between predictions and observations at two-week time points across the entire study period for individual sites.

⁶Los Angeles basin including Los Angeles and Riverside

⁷Winston-Salem

3.4 Model Predictions

Figure 2 is a map of predicted long-term mean ozone levels (1999 to 2013) across the greater Los Angeles Basin and demonstrates expected patterns: Ozone levels were higher in the rural and mountain areas compared with those of the downtown metropolitan areas. Concentrations were substantially higher in areas far from highways (Figure 2a), which was a common pattern in all the study regions. Moreover, the ozone concentrations were consistently low and had low variability along highways throughout the period, but varied greatly in the downtown metropolitan and the rural areas over time (Figure 2b). A cross sectional map of ozone levels shows a trend of increasing concentrations from downtown Los Angeles to the Riverside County area and a slow increasing trend between 1999 and 2013 (Figure 2c).

Figure 2.

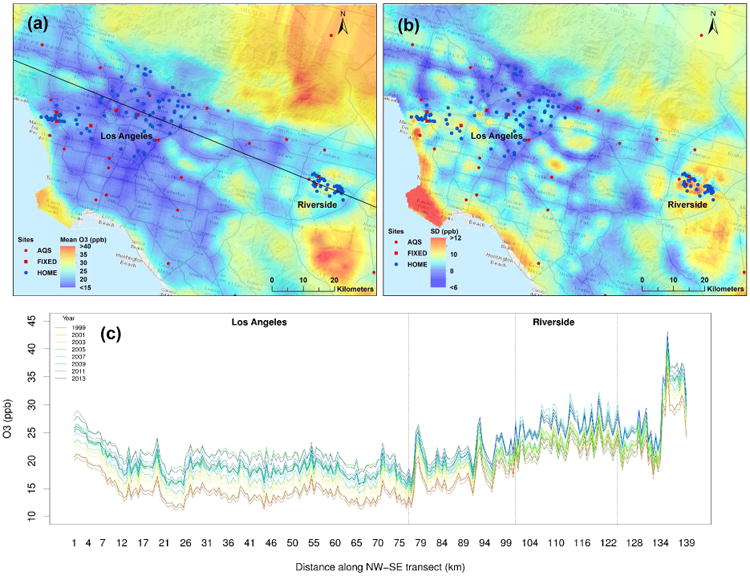
(a) Map of predicted long-term average and (b) map of standard deviation of ozone in Los Angeles and Riverside from 1999 to 2013. (c) Annual average predicted concentrations across the transect shown in Figure 2a (black line, NW to SE), though the counties of Los Angeles and Riverside from 1999 to 2013.

Figure 3 shows boxplots of long-term predictions of ozone concentrations at all the MESA participant residences. There is a clear difference in ozone levels between seasons. The mean concentrations tended to be higher in Winston-Salem and Baltimore and lower in New York. The correlations of ozone estimates with our NO₂, NOx, PM_2.5 and black carbon estimates were generally high in New York and Baltimore, but lower in the other study regions (see Table A. 3 in Appendix A). The correlation of ozone was generally highest with black carbon and lowest with PM_2.5.

Figure 3.

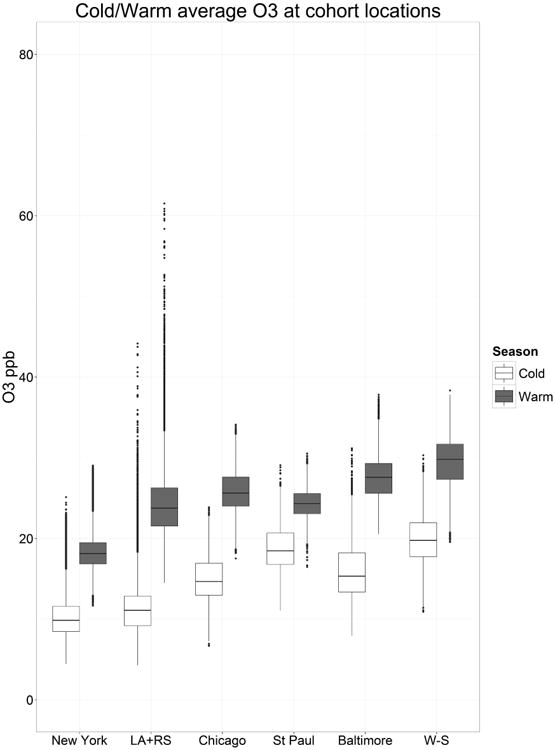
Boxplots of warm and cold season ozone predictions as long-term averages at all the participant addresses in the six MESA metropolitan regions. LA+RS: Los Angeles and Riverside in California. W-S: Winston-Salem in North Carolina. The upper, middle and lower lines in the box show the 75%, 50%(median) and 25% of the observations. The outliers are calculated as the observations higher or lower than 1.5 × IQR + median.

4. Discussion

We developed spatiotemporal models for ozone within a novel geo-statistical framework following a uniform set of procedures in six metropolitan regions. These models incorporated rich monitoring data, geographic information, and were capable of predicting spatial distributions of ozone over a long time period (1999-2013).

4.1 Model Structure

Although a uniform approach was used for modeling, we allowed flexible structures to best fit the final models. The ozone models included a second time trend in the Los Angeles (Los Angeles and Riverside), Baltimore, Winston-Salem and New York (New York and Rockland) regions. Despite a small contribution to ozone, the second time trend may reflect additional temporal variability due to different geographical features (e.g. downtown vs suburban, urban vs rural, elevation), emission sources (combustions and biogenic emissions), meteorological conditions (e.g. temperature and wind field) and long range transport of ozone in each of these regions. One challenge we encountered when developing the region-specific models for Winston-Salem and New York was the relatively low CV R² in PLS (data not shown) when GIS covariates were used to fit the coefficient (β_i) of the first time trend (main trend) at the monitoring locations. Because of the strong seasonality, the temporal variation patterns of ozone were largely the same across monitoring locations (i.e. small spatial contrast of β_i) in these two metropolitan regions, rendering this difficult to explain by GIS covariates. This suggests that changes in ozone exposure levels over time in these two regions will be less variable across the participant residences. In our study, spatial smoothing in the long-term mean was incorporated into the final model in four regions (Los Angeles, New York, Winston-Salem and Baltimore) with numerous monitors in larger buffers of study areas. This could be explained by large regional patterns of ozone compared with traffic-related pollutants. Overall, the spatial smoothing in long-term mean resulted in a 3-6% increase of CV_MSE R² compared to the R² of the PLS regression model alone.

4.2 Predictor Variables

The MESA Air study made a speical effort to collect detailed predictor variables for each study region. In our models, loadings of traffic indicators (e.g., road density), emission factors and population density were negative while loadings of urban green features and elevation were postive. This is consistent with the findings of previous studies on ozone modeling (Adam-Poupart et al., 2014; Beelen et al., 2009; Malmqvist et al., 2014) and is also in agreement with the known atmospheric processes of ozone formation (EPA, 2006). For instance, ozone is usually scavenged by primary NO emissions in locations where NOx/VOC ratios are high such as in urban core areas with dense traffic and is produced by biogenic VOCs from plants and NOx in rural areas or in locations downwind of major urban areas.

Although previous studies found a similar pattern in proximity to roadways, only two studies (Malmqvist et al., 2014; Kerckhoffs et al. 2015) selected sites to represent urban configurations as was done in the MESA Air measurement campaigns. Most prior studies have relied exclusively on the measurements from AQS monitors which were purposefully sited away from roads; therefore, the importance of traffic indicators as predictors of fine-scale variation (i.e., the magnitude of the loadings) may be underestimated in previous studies.

Predictor variables such as population density and impervious surface do not merely represent pollution from anthropogenic activities such as traffic, wood burning and house heating, but also reflect differences in urban-rural concentration distributions. In suburban and rural areas, the positive loadings of green space could be explained by both the absence of man-made ozone precursor emissions and the increasing biogenic VOCs by plants emissions. In Winston-Salem, green space contributed to higher ozone levels than in the other regions.

Elevation is an important factor in determining ozone concentrations, relating to the dispersion and transport of primary pollutants emitted in urban areas and to the accompanying production of ozone. In the Los Angeles basin, higher elevation level was one of the main predictors of the higher ozone levels in Riverside compared to metropolitan downtown Los Angeles. Overall, predictor variables with larger buffers were more important contributors to ozone concentrations, reflecting ozone's large regional distribution.

4.3 Model Perfomances

Our ozone models performed slightly worse in terms of the CV_MSE R² than the similar models we have reported recently for traffic-related pollutants such as NO₂, NOx and black carbon, but were more accurate in predicting spatial-only contrasts than the PM_2.5 models (Keller et al. 2015). This is likely because, compared with traffic-related pollutants, characteristics of secondary pollutants such as ozone are less well represented by important smaller scale GIS covariates such as road networks and population density. Moreover, the temporal and spatial variability of ozone concentration levels were smaller than those of the traffic-related pollutants and were larger than those of the PM_2.5 concentration levels indicative of the potential for ozone quenching by NO. Our models outperformed previously reported ozone LUR models in Quebec, Canada, partially because of better available predictor variables and better selection of sites (i.e. our study include large number of home sites) to represent spatial variability. In that study, Adam-poupart et al. (2014) estimated daily ozone concentrations using Bayesian Maximum Entropy (BME), incorporating ozone AQS data or AQS data together with LUR model outputs. The reported CV_REG R² ranged from 0.47 to 0.65. The CV_REG R² that represents the spatial correlation between annual average ozone predictions and observations at the AQS and the fixed locations in our study suggested good perfomances as the spatial models published by Beelen et al. (2009) (0.38 to 0.54, West Europe), Malmqvist et al. (2014) (0.40 to 0.67, Swiden cities) and Kerckhoffs et al. (0.71, the Netherlands).

We found much lower spatial CV_MSE R² (accuracy) than CV_REG R² (precision) at the AQS and fixed locations in the metropolitan regions with large buffer sizes (Los Angeles, New York, Winston-Salem and St Paul), even though the spatial CV_MSE R² was consistently high at the home locations. This could be attributed to the different geographical features of the AQS and home sites. In our study, the AQS sites were spread over a wide range of urban and rural areas while MESA Air monitoring sites that accounted for spatial variations, especially home sites, were mostly concentrated in urban areas. Hence model predictions may be more accurate in urban areas with intensive home monitoring sites but exhibit higher discrepancies (i.e., bias) when extrapolated to larger areas with sparse monitoring data.

Our models showed consistently higher predictive accuracy in cold seasons than in warm seasons. This is expected since the processes producing ozone are more active in warm seasons (EPA, 2006) producing more complex regional spatiotemporal distributions than in winter. Inclusion of a chemical transport model within the geospatial framework may help improve model performances by capturing more of this complexity than was possible with GIS covariates alone (Akita et al., 2014).

4.4 Model Predictions

A map of mean ozone levels in the Los Angeles basin (Figure 2a) demonstrates lower concentrations of ozone in the Los Angeles metropolitan region than in the neighboring more rural regions and in downwind cities such as Riverside. This same urban-rural gradient was apparent in all of the MESA Air study regions. Even though traffic emissions scavenge ozone by NO, other factors such as human behaviors (represented by population density and emission factors), land use (e.g., natural and urban green) and local meteorological environment (e.g. impervious cover as a surrogate for the urban heat island effects) also play important roles in ozone formation and destruction (EPA, 2006; ISA, 2013), leading to the substantial variability in ozone concentrations over time across space (Figure 2b).

We observed large between- and within-region contrasts of ozone predictions at the participant residences, which is important when considering these model predictions for use in epidemiological studies. It is also important to consider the added value of ozone models for application in epidemiologic studies beyond existing models for predicting concentrations of traffic related pollutants. The negative correlations between ozone and the other pollutants (NOx, PM_2.5 and black carbon) were attributed to the fact that NOx (in particular NO) and potentially other primary emissions titrate ozone directly and the predictions for PM_2.5 and black carbon variables are correlated to NOx. The variability in the correlations (very high in some communities and lower in others) suggests that health effects associated with ozone can be disentangled from those of other pollutants in cities such as Winston-Salem and St Paul where traffic and combustion sources were less dominant than in metropolitan cities such as New York and Baltimore with intensive anthropogenic emissions.

4.5 Limitations

A major limitation to our modeling efforts is the missing data in the cold seasons at several AQS sites, particularly in Winston-Salem and St Paul, which may constrain the power of the model to accurately predict ozone concentrations in that season. Nevertheless, our model still predicted ozone concentrations relatively well in cold seasons, possibly because of less secondary ozone formation in cold seasons. In addition, the two-week time frame of our sampling data limited the ability of our ozone model to predict 8-hour maximum values that are regulated by the U.S. EPA. However, correlations between daily average and daily 8-hour maximum ozone observations were generally high across the AQS sites (r=0.93 on average) (ISA, 2013), so this may not be a serious limitation.

5. Conclusion

Using rich temporal data from AQS montoring sites and a dedicated, study-specific spatial monitoring campaign, we were able to develop spatiotemporal models for ozone that perform well in terms of both prediction accuracy and precision in the six metropolitan regions of the MESA study in the United States. Most prior modeling of ozone concentrations has been based on chemical transport modeling, which incorporates meteorology and emissions information but typically is unable to provide the fine scale predictions of our approach (50 meters). The performance of the models described here suggests that approaches based on land-use regression and universal kriging are also useful in understanding spatial variation in ozone concentrations and thereby also improving exposure predictions. Since both spatiotemporal regression and chemical transport modeling approaches provide valuable information, the development of hybrid approaches may most accurately predict fine scale gradients in ozone concentrations.

Highlights.

• Few studies estimate long-term ozone exposure in large populations at fine scales

• Geo-statistical exposure models are developed for ozone in six US metropolitan regions

• The modeling framework incorporates land use regression with universal kriging

• The models accurately predict ozone concentrations in both spatial and temporal dimension

• Model predictions will be used for investigating long-term health effects.

Abbreviations

AQS

Air Quality System

CALINE

California Line-source model

CTM

chemical transport modeling

CO

carbon monoxide

CV

cross-validation

EM

Expectation-Maximization

LOD

limit of detection

LUR

land use regression

MESA Air

Multi-Ethnic Study of Atherosclerosis and Air Pollution

MSE

mean square error

NO

nitric oxide

NO₂

nitrogen dioxide

NOx

oxides of nitrogen

PLS

partial least squares

PM

particulate matter

SO₂

sulfur dioxide

SVD

singular value decomposition

VOCs

volatile organic compounds