Abstract
From the timing of amoeba development to the maintenance of stem cell pluripotency, many biological signaling pathways exhibit the ability to differentiate between pulsatile and sustained signals in the regulation of downstream gene expression. While the networks underlying this signal decoding are diverse, many are built around a common motif, the incoherent feedforward loop (IFFL), where an input simultaneously activates an output and an inhibitor of the output. With appropriate parameters, this motif can exhibit temporal adaptation, where the system is desensitized to a sustained input. This property serves as the foundation for distinguishing input signals with varying temporal profiles. Here, we use quantitative modeling to examine another property of IFFLs—the ability to process oscillatory signals. Our results indicate that the system’s ability to translate pulsatile dynamics is limited by two constraints. The kinetics of the IFFL components dictate the input range for which the network is able to decode pulsatile dynamics. In addition, a match between the network parameters and input signal characteristics is required for optimal “counting”. We elucidate one potential mechanism by which information processing occurs in natural networks, and our work has implications in the design of synthetic gene circuits for this purpose.
Author Summary
From circadian clocks to ultradian rhythms, oscillatory signals are found ubiquitously in nature. These oscillations are crucial in the regulation of cellular processes. While the fundamental design principles underlying the generation of these oscillations are extensively studied, the mechanisms for decoding these signals are underappreciated. With implications in both the basic understanding of how cells process temporal signals and the design of synthetic systems, we use quantitative modeling to probe one mechanism, the counting of pulses. We demonstrate the capability of an Incoherent Feedforward Loop motif for the differentiation between sustained and oscillatory input signals.
Introduction
From Ca+2 signaling to coordination of cell fates, oscillatory signals are essential to regulation of cellular processes [1–4]. The dynamic properties of such signals are crucial for controlling behaviors of single cells and cell populations [5]. As such, the mechanisms underlying the generation of these signals are well-established [2, 6, 7]. For instance, the network constraints governing the circadian clock elucidate design principles dictating the generation of both natural and synthetic pulses [8–10]. Some general requirements for the generation of oscillations include ‘nonlinear’ reaction rates and negative feedback [9]. A systems-level approach to oscillation characterization examines the topologies in natural systems that give rise to pulse generation [9]. This demonstrates the necessity of ‘nonlinear’ kinetic rate laws for the destabilization of the steady state in the generation of oscillations [9]. While this constraint allows the generation of pulses with a diverse set of network motifs, negative feedback (especially negative feedback with a time delay) is found in all these cases. This component is used to reset the network to its initial state [2, 9]. Engineered systems based on such design constraints demonstrate the capability to generate synthetic oscillators mimicking those found in nature [6]. Even in the absence of any apparent regulation, transient oscillations in gene expression can emerge from cell-size control [11].
Despite the ubiquity of oscillations in biology, much less is known about how cells process these signals. In particular, how do cells distinguish between oscillatory and sustained inputs? For a given oscillatory input, how do cells retrieve encoded information from the frequency and amplitude? For signal processing in the frequency domain, computational methods illustrate one potential mechanism, where a critical frequency defines the bandwidth for high fidelity signal propagation for each network [3]. This capacity can be changed with an increased oscillation amplitude or with increased kinetic rates. Regardless of the strategies that give rise to signal encoding, it is important to further understand how cells process oscillatory signals.
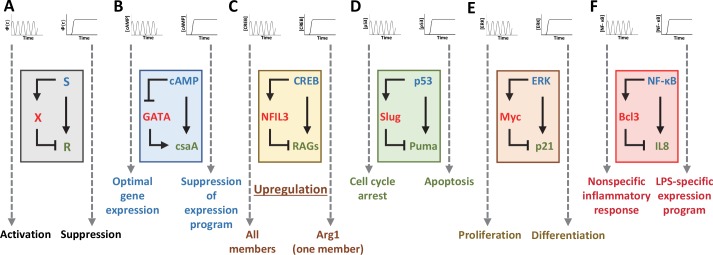
Many natural biological networks exhibit the ability to distinguish oscillatory and sustained signals. While several studies describe the contrasting downstream phenotypes, the architectures that give rise to such outcomes remain unclear. One common motif shared by such networks is the Incoherent Feed-Forward Loop (IFFL), in which an input both activates and represses a single output (Fig 1A) [4, 12, 13]. For example, oscillations in the transcription factor Ascl1 play a critical role in driving the proliferation of multipotent neural progenitor cells (NPCs) [14, 15]. In contrast, the sustained expression of Ascl1 promotes neuronal fate differentiation in NPCs [15, 16]. In social amoeba Dictyostelium discoideum, 3’ 5’-cyclic adenosine monophosphate (cAMP) oscillations result in the optimal gene expression for development while continuous stimulation inhibits transcription (Fig 1B) [17–19]. cAMP directly induces the expression of contact site A gene (csaA) while repressing the transcriptional activity of GtaC on csaA [17]. Additionally, the number of cAMP pulses regulates the coordination of development.
Fig 1. IFFL is a common motif underlying processing of transient or oscillatory signals.
(A) An IFFL often underlies signal decoding processes. In an IFFL, an input both activates and represses a single output. (B) GATA in development. Oscillating and sustained cAMP dynamics regulate the developmental program in social amoeba. (C) CREB in regeneration. CREB temporal dynamics control neural regeneration. (D) p53 in cell fate decisions. Pulsatile and sustained p53 stimulation results in either cell cycle arrest or apoptosis respectively. (E) ERK in cell fate decisions. Differentiating between pulsatile and sustained ERK stimulation is required for the regulation of stem cell differentiation and proliferation. (F) NF-κB in immune responses. Differentiating between pulsatile and sustained NF-κB stimulation is required for the induction of non-specific inflammatory responses and LPS-specific expression programs.
An IFFL also underlies the regulation of neuronal regeneration by cAMP response element binding protein (CREB). CREB activates regeneration-associated genes (RAGs) and nuclear factor interleukin-3-regulated protein (NFIL3), which negatively regulates RAGs (Fig 1C) [20]. In Drosophila, the constitutive activation of CREB upregulates a single RAG, Arg1, while CREB oscillations induced by neuronal injury increase the transcription of all members [20, 21].
The IFFL motif is also found downstream of p53 in the regulation of cell fate decisions. The tumor suppressor p53 oscillates in response to γ-radiation, and the number of oscillations increase the level of damage. In contrast, UV radiation induction results in a sustained pulse of p53 [22]. While p53 oscillations lead to cell cycle arrest, sustained p53 activation induces apoptosis [23, 24]. Here, p53 activates P53 upregulated modulator of apoptosis (PUMA), which plays a role in the induction of apoptosis, and Slug, a transcription factor which represses the activity of PUMA (Fig 1D) [25].
In mammalian cells, pulsatile dynamics of extracellular signal-regulated kinases (ERK) in response to epidermal growth factor (EGF) result in proliferation [26–28]. However, nerve growth factor (NGF) induces sustained ERK, driving differentiation [16]. Here, the transcription factor Myc and the cyclin-dependent kinase inhibitor p21 are both activated by ERK [29, 30]. Myc, an inducer of proliferation, represses the activity of p21, an inhibitor of cell cycle progression (Fig 1E) [31–35].
Tumor necrosis factor-α (TNFα) can stimulate oscillations in the transcription factor NF-κB, which in turn triggers nonspecific inflammatory response genes in immune cells [36]. In addition, persistence of the NF-κB oscillations dictates the resulting transcriptional profile [37, 38]. In contrast, bacterial liposaccharides (LPS) promote sustained NF-κB activation, which induces a LPS-specific expression program [39]. We identify a potential IFFL where NF-κB activates the expression of both IL8, a cytokine, and BCL3, a competitor for NF-κB target promoters including IL8 (Fig 1F) [40].
The common occurrence of IFFLs in these networks suggests a role in processing transient or oscillatory signals. This motif is ideal for decoding oscillatory signals due to its ability to react to fold-changes rather than the absolute concentration of an input [12, 13, 41, 42]. In addition, IFFLs are one of the major core topologies that can drive temporal adaptation, the generation of a pulse in response to a sustained input [43]. In essence, this network is able to desensitize a system to a sustained stimulus while maintaining the ability to respond to periodic stimulation. This property is the fundamental principle behind the ability to differentiate pulsatile and sustained signals.
Here, we examine a mechanism by which IFFLs process oscillations and the conditions that facilitate counting of pulses. This network exists in two states—one in which the system resets when the counting mechanism fails due to a conflict between the signal requirements and the actual input, and one where pulses result in a stepwise increase of the output. To differentiate between sustained and oscillatory signals, the network must display both states. The system must exhibit a stepwise increase of the output in response to oscillatory signals while having no response to sustained signals. Analogous to the use of radios to transform information from the frequency and amplitude domains of electromagnetic waves, the IFFL acts as a decoder, recognizing pulsatile signals.
Results
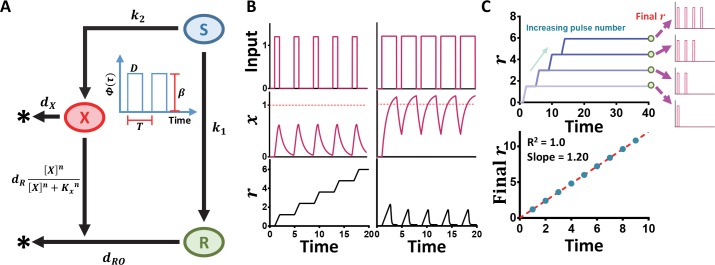
We model an IFFL consisting of three components (Fig 2A): an input node (S), an intermediate node (X), and an output node (R). S activates the production of both X and R, while X induces the degradation of R through Hill kinetics. The dynamics of the motif can be described with two dimensionless ordinary differential equations (ODE):
| (1) |
| (2) |
where Φ(τ) represents the input signal, which can be sustained, oscillatory, or transient. Unless noted otherwise, we define Φ(τ) as a periodic square wave function with k pulses: Φ(τ) = 1 when iT + τo ≤ τ < iT + D + τo and Φ(τ) = 0 otherwise. Here, i is the index of a pulse (0 ≤ i < k), τo is the start time of the first pulse, T is the cycle period, and D (< T) is the pulse duration. For all simulations we assume that τo = 1. x denotes the concentration of X, r denotes that of R, and τ denotes time. γo represents the basal degradation rate constant of R, γR is the maximal induced degradation rate of R by X, and β is the maximal synthesis rate of X and R. We require that the induced degradation of R have an ultrasensitive dependence on X, as indicated by a high Hill coefficient (n = 110). Such ultrasensitive dependence can be achieved with oligomerization, tandem binding sites, increased cascade lengths, covalent modification cycles, or titration by inhibitors [44–48]. For titration, competitive binding of the inhibitor sets an activation threshold to be overcome, thereby increasing the Hill coefficient.
Fig 2. Processing of oscillating signals by an IFFL.
(A) Signal processing by an IFFL. In this model, a pulsing input (Φ(τ)) simultaneously stimulates the production of an intermediate (X) and a reporter (R). X induces the degradation of R through a threshold response. The fundamental constraints for counting shown are based on the full model (Methods) while Eqs 1 and 2 are the non-dimensionalized form of the model. Here, the duration (D) represents the length of the pulse while the cycle period (T) represents the time between the start points of two adjacent pulses. The specific parameters of the IFFL limits the duration range for which counting can occur; only sufficiently short pulses are counted while pulses of a longer duration will shut down the system. (B) Time courses demonstrate counting mechanism. Using β = 1.2, γR = 10, γO = 0, and T = 4 (Left: D = 1 Right: D = 3). The top row contains time courses of the input pulses for two different pulse durations, either a pulsing input or a simulated sustained input. The second row shows time courses for X. The bottom row shows time courses for R. With identical parameters, an IFFL motif can generate two distinct outputs depending on the length of the duration of the input pulses. When x is below the threshold of induction, the circuit maintains the ability to produce a stepwise increase of r. However, when x overcomes the threshold, the circuit loses this ability. For a single parameter set, both outputs are desired to differentiate between oscillating and sustained signals. This ability is maintained in the case of an input pulse with the form of a sine function (S1 Fig). (C) Calibration curve for ideal counting. Using β = 1.2, γR = 10, γO = 0, and T = 4 (D = 1) The sample calibration curve is for a pulse duration within the optimal duration range, therefore it is able to demonstrate ideal counting. With an increasing number of input pulses from 1–4 in the top panel, R exhibits a stepwise increase. The linearity is demonstrated in the bottom panel by R2 ≥ 0.99.
We consider Φ(τ) with varying durations and cycle periods: a longer duration corresponds to a more sustained signal. We first consider the case where the degradation of R is solely induced by X (γo = 0). Fig 2B illustrates typical time courses of X and R in response to two different oscillatory signals. In either case, X peaks in response to each individual pulse and returns to a basal level before the subsequent pulse. When the duration is sufficiently small (Fig 2B: left column), r exhibits a linear stepwise increase with an increasing number of pulses (for a constant β and pulse duration). For a long duration (Fig 2B: right column), however, R exhibits transient pulses similar to that of X. That is, only an input with a sufficiently short duration generates a more sustained output. The critical determinant of these divergent outcomes is the dynamics of X, which triggers the effective degradation of R when it reaches its half-activation threshold (x = 1). For a sufficiently short duration, x never reaches 1, and thus is unable to trigger the degradation of R. As a result, r increases with each additional input pulse. In contrast, for a long duration, x exceeds 1 for each pulse, leading to the periodic resetting of R.
For an input signal with short pulses, R can count the number of pulses: the level of R at a fixed time point (r(τE)) is approximately proportional to the number of pulses for a fixed pulse duration and amplitude (Fig 2C). A least-squares linear regression on r(τE) versus the number of pulses provides a quantitative measure for the quality of counting. The slope of this line measures the strength of the response. For instance, the slope is near zero for the signal with long pulses (S2 Fig), indicating no response (Fig 2B). The quality of the fit, as measured by R2, quantifies the performance of counting. In all our simulations, we consider R2 = 0.99 as the cut-off for high-quality counting. With 0 < R2 < 0.99, low-quality counting emerges as r saturates (reaches a steady state) over time. This characteristic impairs the ability to predict r(τE) with an increasing number of pulses. In addition, the absolute failure of counting occurs when R2 = 0.
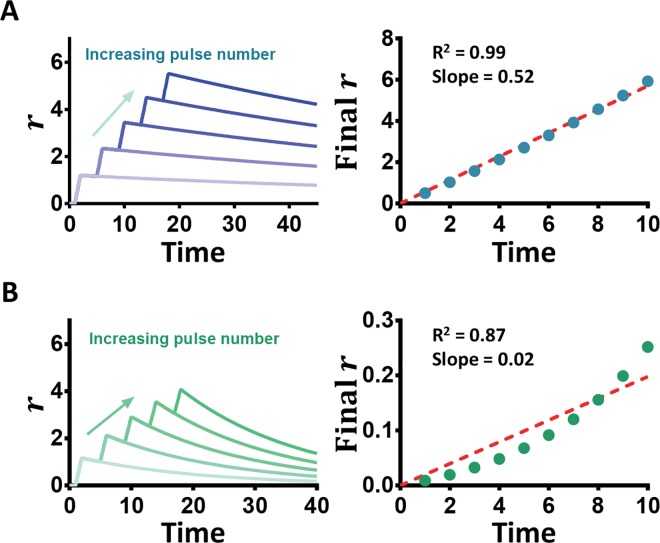
In the base model (Fig 2), we assume that R is degraded solely by X. In general, however, a basal level degradation of R can deteriorate the counting quality (Fig 3A). A highly unstable reporter (γo = 0.05; Fig 3B) decreases the counting quality such that R2 < 0.99. The decreased slope also indicates the weakened response to the oscillating input. This loss of counting is attributed to the decreased timespan for which r can be maintained in the absence of the input. Therefore, to reduce the impact of endogenous degradation of the reporter on the counting quality, γo can be minimized through the use of a highly stable reporter.
Fig 3. γo mediates counting quality.
Using β = 1.2, γR = 10, T = 4, and D = 1, time courses are shown to demonstrate cases of high quality counting and poor counting through the manipulation of γo. (A) High Quality counting (R2 ≥ 0.99) occurs in the case of a small γo (γo = 0.01), as characterized by the linearity of the calibration curve composed of the final r of between 1 and 10 pulses. (B) In the case of a large γo (γo = 0.05), the nonlinearity of the calibration curve and small slope demonstrate low quality counting (0 < R2 < 0.99).
Relaxing this assumption, we reach the same conclusions for reliable counting when γo is sufficiently small: our simulations demonstrate that the counting capability can be maintained in the general condition (γo > 0), like in the base case (Fig 4). IFFL kinetics constrains the ability to process oscillatory signals; therefore, we predict that both the production rate (β) and the induced degradation rate of the output (γR) are core parameters. In Fig 4A, we evaluate the range of the counting capability with respect to two parameters, β and D (sample time courses shown in Fig 4B). Even in the presence of basal degradation (γo = 0.01), counting can be maintained for appropriate combinations of β and D. We observe that as β increases, the range of durations for which counting occurs decreases while increasing the slope for different numbers of pulses (for R2 ≥ 0.99). On the other hand, increasing D increases the slope in cases when R2 ≥ 0.99 due to the increased time for R production.
Fig 4. Dynamic constraints underlying reliable counting.
Using γO = 0.01, γR = 10, T = 4, β = 0–4 (Panels A and B). (A) Effects of varying β and duration on R2 and slope. Simulation results for the R2 and slope of the calibration curve as both β and the pulse duration changes from 0–4 with a constant period of 4. From the graph of the R2 values, below the analytical border (solid line), counting is maintained (predominantly R2 ≥ 0.99), but is lost above this border (R2 = 0). From the graph of the slope, optimal counting (region with the highest slope) lies between the analytical border and the dashed line. In both plots, the region under the dotted line (at β = 1 in white) is where the IFFL cannot differentiate between pulsing and sustained inputs. (B) Effects of varying β and duration on time courses. Time courses with varying number of pulses demonstrate the range of counting for a changing β. As β increases, the ability to differentiate between different numbers of pulses increases while the range of counting decreases. Using γO = 0.01, β = 1.2, T = 4, γR = 0–3 (Panels C and D). (C) Effects of varying γR and duration on R2 and slope of calibration curves. Simulation results for the R2 value and the slope of the calibration curve as γR changes from 0–3 and the pulse duration changes from 0–4 with a constant period of 4. As γR decreases, the network loses the capability to distinguish between pulsing and sustained inputs. (D) Effects of varying γR and duration on time courses. Time courses with different number of pulses demonstrate the range in the counting capability for a changing γR. As γR increases, the range of the counting capability decreases.
To differentiate between pulsing and sustained inputs, X must overcome the activation threshold in the case of a sustained input. Therefore, the network cannot discern signals when β ≤ 1 because the threshold can never be reached. In this case, the network is unable to display the two necessary states to discern signals, illustrated by R2 ≥ 0.99 at all pulse durations (Fig 4A). However, when β > 1, the system has the potential to discriminate inputs (illustrated by a range of durations where R2 = 0 and a range where R2 ≥ 0.99) and the pulse duration restricts the counting capability. To count, the duration of input’s OFF state in each cycle (T − D) needs to be long enough to reset the basal level of the intermediate such that the subsequent pulse will not push x to 1. Generally, shorter pulse durations are more likely to exhibit this capability due to the longer duration of the OFF state (Fig 4B). The boundary between counting and no counting is determined by whether each pulse can drive X to the threshold, leading to complete degradation of R. The level of X at the end of the first pulse is (1 − e−D). Therefore, the boundary between the two regions is set by , which approximates the border observed in numerical simulations (Fig 4A).
For a small γo, another critical parameter for counting is the rate constant for induced degradation, γR. Fig 4C and 4D depicts the case when β > 1 with a varying γR and pulse duration for a constant cycle period. With a constant β, we expect the counting range to remain constant. Instead, numerical simulations demonstrate a monotonically decreasing trend of the counting range as γR increases. Above a point, increasing γR has no impact on counting because a higher γR provides no additional benefit on the ability to degrade R in the case of a sustained input. Below this point, however, the range of pulse durations that can count increases, but the ability to differentiate pulsing and more sustained inputs diminishes due to a higher range of low-quality counting (0 < R2 < 0.99). For a sufficiently low γR, the system cannot discriminate between the two types of inputs (Fig 4C). We attribute this characteristic to the decreased impact of the intermediate on the degradation of the reporter, which is required for maintaining temporal adaptation.
The kinetics of the system prevent the complete degradation of x to 0 after each pulse, leading to the progressive accumulation of X with each additional pulse. Starting from a basal level, X reaches the maximum concentration (peak) at the end of the pulse, and returns to a new basal level before the next pulse:
| (3) |
| (4) |
where xpeak, i is the peak concentration of X after the ith pulse, xbasal, i is the basal concentration of X before the ith pulse, and T = cycle period. To start, xpeak, 0 = 0 while both xbasal, i and xpeak, i increase alongside i. Counting fails at pulse nc, when xpeak, nc > 1. We term nc the counting capacity of an IFFL for a given input signal, which sets the maximum number of pulses the network can count. As nc approaches ∞, the network can maintain counting when the negligible accumulation of X allows for indefinite counting. This exists when the pulse duration satisfies . In addition, as T approaches ∞, the analytical border converges to 1 = β(1 − e−D) such that counting is maintained when 1 > β(1 − e−D).
Fig 5 shows that the duration at which counting exists decreases with increasing β. Consistent with the numerical analysis where slopes are generally higher at shorter pulse durations with an increasing β, higher synthesis rates of X shorten the duration range for which counting can occur (Fig 4). Thus, a higher β means that X will reach the threshold at shorter pulse durations, resulting in the loss of the counting capability beyond this duration. The curve of the boundary signifies that increasing the cycle period has little impact on the duration at which counting is lost (Fig 5). More specifically, at the analytical border, the duration at which is maintained relies on β. However, at low periods, the duration at which counting exists relies more heavily on the cycle period. As the pulse duration approaches the cycle period, there is less time for X to return to the basal value before subsequent pulses. This effect has a greater impact in the case of low cycle periods. Although the basal level of X will never return to the initial value, if x remains below the activation threshold, negligible increases can maintain the counting capability.
Fig 5. Dynamic constraint underlying counting capability.
The analytical border describes the effect of changing β (β = 12 or 2 or 1.2) on the relative duration (D/T) at which counting is lost. To the left of the solution for each β is the region with counting while the region to the right has no counting capability.
The analytical solution 1 > β(1 − e−D) defines the conditions under which indefinite counting occurs based on the peak concentration of the intermediate. When γo > 0, however, the number of pulses any particular system can count becomes finite due to the saturation of the reporter. This is described in S1 Text, which gives the final level of R at time τE (> (k − 1)T + D + τ0) after any arbitrary number of pulses (k > 0) when 1 > β(1 − e−D) as (1-). τ0, the time at which the pulses start, can impact the parameter range with the counting capability. Depending on γo, a series of pulses that start at the beginning of the simulation interval can have a different r(τE) than those that start near the end of the interval. To analyze the effect of the other parameters, we constrain our analysis by assuming a constant τ0 for all simulations. Here, r(τE) is a monotonically increasing function of the number of pulses, regardless of the other parameters (as long as X does not accumulate beyond its threshold to trigger the degradation of R). When γo = 0, r(τE) is proportional to k: r(τE) = kβ. However, the dependence of r(τE) on k deviates from the proportionality as γo increases. This is consistent with the numerical simulation results illustrated by Fig 3.
The key constraint for IFFLs to distinguish oscillatory signals resides in its ability for temporal adaptation where the network responds with a pulse to a sustained input. As long as an IFFL maintains this characteristic, the motif can respond to periodic stimulation and act as a pulse counter. Each time the input is removed, the intermediate is reset and the system can respond to subsequent pulses. We illustrate this principle by considering alternative implementations of the IFFL satisfying this constraint.
We examine the reliance of counting on the current architecture by shifting the ultrasensitive response to the production of X through a positive feedback loop (S1 Text). Like the initial model, this alternative model maintains the ability to count in the base case with no endogenous R degradation (S3 Fig). Here, when β is large, the linear dependence of the degradation of R on both X and R causes any X to induce the degradation of R, preventing counting. However, when β is small, R degrades slowly because of low concentrations of X, preventing the differentiation between sustained and pulsing inputs. Like in the initial model, γo dictates the length of time during which R remains constant and should be minimized to maximize the duration range in which counting can occur. For a large γR, the presence of a small concentration of R or X will lead to the efficient degradation of R, preventing the ability to count. Meanwhile, a small γR will be unable to induce the effective degradation of R even at high concentrations of X. To demonstrate the robustness of this counting mechanism, we develop additional models to take into account common properties of biological systems including time delay, modifications to the current architecture, and noise (S1 Text; S1, S3, S5, S8 and S9 Figs).
Discussion
Here, we analyze an underappreciated phenomenon in information processing by signaling networks: processing of oscillatory signals. In this context, we illustrate the unique ability of incoherent feedforward loops (IFFL) with proper network parameters to distinguish transient (or oscillatory) and sustained signals. For oscillatory signals, we analyze the extent to which the network is able to count the number of pulses. Additionally, we establish the dynamic constraints of the input signals and network parameters such that counting can occur. With the appropriate parameters, the ability of an IFFL motif to respond to transient signals but not to sustained signals relies upon the property of temporal adaptation in response to a sustained signal. Insights from our model can be used to identify natural information decoding systems and understand the effect of perturbations to such networks.
Our results can be applied to GtaC shuttling in social amoeba, which differentiates between pulsing and sustained cAMP and matches optimal signals to the ideal transcript accumulation. Cai et. al. show that when the network regulating CsaA is subjected to high frequency inputs, GtaC is unable to respond to each pulse, resulting in a decreased transcript accumulation. Similarly, a lower than optimal (natural) cAMP frequency results in a decrease in the overall transcript concentration. This phenomenon suggests the presence of a band-pass filter. As in Fig 5, this system illustrates the idea that a decreased frequency (higher period) corresponds to a reduced fraction of the period during which counting can occur. Here, the parameters of the endogenous circuit dictate the range of frequencies that can be decoded resulting in dynamics similar to those explained by our IFFL model.
In a similar manner, the frequency of ERK activation has been implicated in cell-fate determination. While previous studies have demonstrated the dependence of differential cell fates (differentiation or proliferation) on specific growth factors, Ryu et. al. illustrate that this decision relies more heavily on the frequency of ERK activity than on the growth-factor identity [49]. Unlike with the sustained application of growth factors, synthetic pulses provide control over the frequency of the ERK activity. This results in differentiation at intermediate frequencies and proliferation at high and low frequencies with a growth factor traditionally known to solely induce proliferation. While this shift in cell fates has been shown experimentally, the mechanisms underlying this frequency decoding are still unknown.
Evolution may have selected for an optimal pulse frequency for social amoeba and in mammalian cell differentiation for different purposes. However, despite differences in signaling dynamics, the IFFL is a general motif found downstream of divergent signals in both cases. Generally, IFFLs are known for acting as sign-sensitive accelerators by increasing the response time of gene expression, dictated by the specific combination of kinetic parameters [13]. While some parameter sets allow the IFFL to act as pulse generators or band-pass filters, others speed up an output response [13, 50]. In addition, the IFFL has been shown to generate both time-dependent and dose-dependent biphasic responses [51]. Our analysis defines the quantitative constraints of another property of IFFLs, the capability for counting.
In natural systems, motifs do not exist in isolation and the dynamics of a motif in isolation may not persist when placed in the context of a larger network. Despite this caveat, our analysis is valuable for two major reasons. First, we identify a new property of IFFLs—the potential for information processing. The importance of IFFLs in signal processing is implied with its presence in many natural networks that are able to respond differentially to oscillatory and sustained signals (Fig 1). Considering this caveat, we explore the extent by which the counting mechanism, can persist in the presence of different perturbations in S1 Text (e.g. introduction of time delay, alterations to the current architecture, and cellular noise). Second, our analysis is useful for guiding the design and implementation of synthetic gene circuits, which are often intended to operate in relative isolation from other regulatory networks in the host cell.
Understanding the constraints of this network for decoding mechanisms is important in the design of synthetic circuits with more complex functions [52, 53]. The conclusions from our study can be used in the design of a synthetic pulse counter [54, 55]. Many synthetic gene circuits respond to the characteristics of static signals. In contrast, circuits adapted from our model would respond to the temporal dynamics of input signals. This would provide a wider range of input attributes, giving rise to a larger spectrum of potential circuit responses. In addition, by matching IFFL characteristics to natural cellular oscillations, synthetic signal decoding circuits would have the capability to respond to natural as well as synthetic stimuli.
Natural systems including those involved in cell proliferation, cell death, and neural regeneration convert oscillatory and sustained signals into distinct biological outcomes. In the case of disease, these circuits become deregulated, altering the function of networks required for information encoding or decoding. Insights derived from our model for the pulse counting mechanism will be important for future work in understanding the ways in which these perturbations impact the way cells decode information.
Methods
We use the following system of ODEs to define the IFFL network:
| (5) |
| (6) |
where k1 and k2 are rate constants for the production of R and X respectively, and dx and dRo are rate constants for the endogenous degradation of X and R respectively. The term represents the threshold response through Hill kinetics for the induction of the degradation of R by X, with a maximal degradation rate of dR. Unless noted otherwise, we define Φ(t) as a periodic square wave function with k pulses: Φ(t) = 1 when iT′ + to ≤ t < iT′ + D′ + to and Φ(t) = 0 otherwise. Here i (0 ≤ i < k) is the pulse index, to is the start time, T′ is the cycle period, and D′ is the pulse duration.
We assume a square waveform input to simplify analysis. However, this assumption can be relaxed; numerical simulations indicate that other wave forms, such as sinusoidal input signals (S1 Fig), can also be counted. In our model, we assume first-order kinetics for the endogenous degradation of R and X. We assume that the induced degradation by X occurs through an ultrasensitive threshold response. In general, this arm can be found in other positions while maintaining the network structure. Our analysis can be generalized to other forms of the motif, as illustrated by the alternative models (S1 Text).
We non-dimensionalize the model by defining:
Supporting Information
(DOCX)
(A) Time courses for pulses defined by a sine function. This panel uses β = 1.2, γR = 10, γO = 0, and T = 4 (Left: D = 1 Right: D = 3). The top row contains the time courses of the input pulses for two different pulse durations, either a pulsing input or a simulated sustained input (with a sine waveform). The second row shows the time courses for X. The bottom row shows the time courses for R. With identical parameters, an IFFL motif can generate two distinct outputs depending on the length of the duration of the input pulses. When X is below the threshold of induction, the circuit maintains the ability to produce a stepwise increase of R. However, when X overcomes the threshold, the circuit loses this ability. For a single parameter set, both outputs are desired to quantify the system as being capable of counting. (B) Calibration curve for ideal counting. This panel uses β = 1.2, γR = 10, γO = 0, and T = 4 (D = 1). The sample calibration curve is for a pulse duration within the optimal duration range, therefore it is able to demonstrate ideal counting. With an increasing number of input pulses from 1–4 in the top panel, R exhibits a stepwise increase. The linearity is demonstrated in the bottom panel by R2 > 0.99.
(TIF)
Here, A and B both use β = 1.2, γR = 10, γO = 0, and T = 4 (D = 3), a parameter set which demonstrates the inability to count. (A) Time course for failed counting. With an increasing number of pulses, X overcomes the activation threshold and the ability to produce a stepwise increase of R is lost. (B) Calibration curve for failed counting. The sample calibration curve is for a pulse duration outside the optimal duration range, therefore it is able to demonstrate the case when counting fails. With an increasing number of input pulses from 1–10 r is suppressed and the non-linearity is demonstrated by R2 < 0.99.
(TIF)
(A) Alternative incoherent feedforward loop motif (Model in S1). In this model, a pulsing input simultaneously stimulates the production of X and R. Here, the threshold response is implemented with the additional production of X through a positive feedback loop. (B) Calibration curves for ideal or failed counting. The top panel uses β = 1.2, γR = 0.01, γO = 0, α = 100, and T = 10 (D = 1). The sample calibration curve is for a pulse duration within the optimal duration range, therefore it demonstrates counting. The bottom panel uses β = 1.2, γR = 0.01, γO = 0, α = 100, and T = 10 (D = 9). The sample calibration curve is for a pulse duration outside the optimal duration range, therefore it demonstrates the case when counting fails.
(TIF)
(A) Signal processing by an IFFL (Model in S2). In this model, a pulsing input (S) simultaneously stimulates the production of an intermediate (X1) and a reporter (R). The first intermediate (X1) then activates the production of the second intermediate (X) that induces the degradation of R through a threshold response. The fundamental constraints for counting shown are based on the full model (S1 Text). (B) Time courses demonstrate counting mechanism. Using β′ = 1, β″ = 1.2, γR = 10, δ = 1, γO = 0, and T = 4 (Left: D = 1 Right: D = 3). The top row contains time courses of the input pulses for two different pulse durations, either a pulsing input or a simulated sustained input. The second row shows time courses for X1. The third row shows time courses for X. The bottom row shows time courses for R. Despite the addition of time delay (of ~10% of the pulse duration) through an additional component, the IFFL motif maintains the ability to distinguish input signals with longer or shorter pulses.
(TIF)
(A) Signal processing by an IFFL (Model in S3). In this model, a pulsing input (S) simultaneously stimulates the production of an intermediate (X) and an intermediate reporter (R1). The intermediate reporter (R1) then activates the production of the reporter (R), which is degraded by the intermediate (X) through a threshold response. The fundamental constraints for counting shown are based on the full model (S1 Text). (B) Time courses demonstrate counting mechanism. Using β′ = 5, β″ = 1.2, γR = 10, γR1 = 5, γO = 0, and T = 4 (Left: D = 1 Right: D = 3). The top row contains time courses of the input pulses for two different pulse durations, either a pulsing input or a simulated sustained input. The second row shows time courses for X. The third row shows time courses for R1. The bottom row shows time courses for R. Despite the addition of time delay (of ~10% of the pulse duration) through an additional component, the IFFL motif maintains the ability to distinguish input signals with longer or shorter pulses.
(TIF)
(A) Time courses demonstrate counting mechanism. Using β = 1.2, γR = 10, γO = 0, and T = 4 (Left: D = 1 Right: D = 3). The top row contains time courses of the input pulses for two different pulse durations, either a pulsing input or a simulated sustained input. The second row shows time courses for X. The bottom row shows time courses for R. (B) Time courses demonstrate differentiation between a sustained and oscillatory input. Using β = 0.337, γR = 10, γO = 0. Here, the amplitude of the sustained input is equivalent to the mean of the oscillating input in panel A (D = 1).
(TIF)
Time courses of the reporter. Using β = 1.2, γR = 10, γO = 0, T = 4, D = 1. Here, we show time courses for R with varying values for the Hill coefficient (n = 5, 50, 110, or 1000) to demonstrate that the specific value for n is irrelevant. The hill coefficient must simply be high enough to induce a threshold response.
(TIF)
(A) Time courses demonstrate the effect of noise in the case of a small molecular number (Model S5). Using k1 = k2 = 5, dx = 1, dR = 10, n = 100, dRo = 0, Kx = 4, and T = 4 (D = 1) in equations 20–21. The top row shows time courses of the input pulses in the case of an oscillating input. The second row shows time courses for R in the absence of noise. The third row shows time courses for X in the presence of noise (ξ = 10). The fourth row shows time courses for R in the presence of noise. The bottom row shows the calibration curve for the system in the presence of noise. With an increasing number of input pulses from 1–10, R is unable to exhibit a stepwise increase due to the impact of noise on the low molecular number of the components; this poor linearity is demonstrated by R2 < 0.99. (B) Time courses demonstrate the effect of noise in the case of an increasing molecular number (Model S5). Using k1 = k2 = 50, dx = 1, dR = 10, n = 100, dRo = 0, Kx = 40, and T = 4 (D = 1) in equations 20–21. The top row contains time courses of the input pulses in the case of an oscillating input. The second row shows time courses for R in the absence of noise. The third row shows time courses for X in the presence of noise (ξ = 10). The fourth row shows time courses for R in the presence of noise. The bottom row shows the calibration curve for the system in the presence of noise. With an increasing number of input pulses from 1–10, R is unable to exhibit a stepwise increase due to the impact of noise on the low molecular number of the components; the poor linearity is demonstrated by R2 < 0.99. (C) Time courses demonstrate the effect of noise in the case of a sufficiently high molecular number (Model S5). Using k1 = k2 = 500, dx = 1, dR = 10, n = 100, dRo = 0, Kx = 400, and T = 4 (D = 1) in equations 20–21. The top row contains time courses of the input pulses in the case of an oscillating input. The second row shows time courses for R in the absence of noise. The third row shows time courses for X in the presence of noise (ξ = 10). The fourth row shows time courses for R in the presence of noise. The bottom row shows the calibration curve for the system in the presence of noise. With an increasing number of input pulses from 1–10, R is able to exhibit a stepwise increase despite the presence of noise due to the sufficiently high molecular number. Here, the linearity is demonstrated by R2 ≥ 0.99.
(TIF)
(A) Signal processing by an IFFL (Model S6). In this model, a pulsing input (S) simultaneously stimulates the production of an intermediate (X) and a reporter (R). The intermediate represses the production of R through a threshold response. The fundamental constraints for counting shown are based on the model described in S1 Text. (B) Time courses demonstrate counting mechanism. Using β = 12, γO = 0, and T = 4 (Left: D = 1 Right: D = 3). The top row contains time courses of the input pulses for two different pulse durations, either a pulsing input or a simulated sustained input. The second row shows time courses for X. The bottom row shows time courses for R. Here, an IFFL motif can generate two distinct outputs depending on the length of the duration of the input pulses.
(TIF)
Acknowledgments
We thank Yangxiaolu Cao and Igor Shats for critical reading of the draft manuscript.
Data Availability
All relevant data are within the paper and its Supporting Information files.
Funding Statement
This work was partially supported by the National Science Foundation (LY, MCB-1412459), the National Institutes of Health (LY, GM098642, GM110494, GM106107), the Army Research Office, a David and Lucile Packard Fellowship (LY), and the National Science Foundation Graduate Research Fellowship (CZ). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Dolmetsch R.E., Xu K., and Lewis R.S., Calcium oscillations increase the efficiency and specificity of gene expression. Nature, 1998. 392(6679): p. 933–6. [DOI] [PubMed] [Google Scholar]
- 2.Levine J.H., Lin Y., and Elowitz M.B., Functional roles of pulsing in genetic circuits. Science, 2013. 342(6163): p. 1193–200. 10.1126/science.1239999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Tan C., Reza F., and You L., Noise-limited frequency signal transmission in gene circuits. Biophys J, 2007. 93(11): p. 3753–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Davis D.M. and Purvis J.E., Computational analysis of signaling patterns in single cells. Semin Cell Dev Biol, 2015. 37: p. 35–43. 10.1016/j.semcdb.2014.09.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Micali G., et al. , Accurate encoding and decoding by single cells: amplitude versus frequency modulation. PLoS Comput Biol, 2015. 11(6): p. e1004222 10.1371/journal.pcbi.1004222 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Danino T., et al. , A synchronized quorum of genetic clocks. Nature, 2010. 463(7279): p. 326–30. 10.1038/nature08753 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Yosef N. and Regev A., Impulse control: temporal dynamics in gene transcription. Cell, 2011. 144(6): p. 886–96. 10.1016/j.cell.2011.02.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bell-Pedersen D., et al. , Circadian rhythms from multiple oscillators: lessons from diverse organisms. Nat Rev Genet, 2005. 6(7): p. 544–56. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Novak B. and Tyson J.J., Design principles of biochemical oscillators. Nat Rev Mol Cell Biol, 2008. 9(12): p. 981–91. 10.1038/nrm2530 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Stricker J., et al. , A fast, robust and tunable synthetic gene oscillator. Nature, 2008. 456(7221): p. 516–9. 10.1038/nature07389 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tanouchi Y., et al. , A noisy linear map underlies oscillations in cell size and gene expression in bacteria. Nature, 2015. 523(7560): p. 357–60. 10.1038/nature14562 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Adler M., Mayo A., and Alon U., Logarithmic and power law input-output relations in sensory systems with fold-change detection. PLoS Comput Biol, 2014. 10(8): p. e1003781 10.1371/journal.pcbi.1003781 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Mangan S. and Alon U., Structure and function of the feed-forward loop network motif. Proc Natl Acad Sci U S A, 2003. 100(21): p. 11980–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Imayoshi I., et al. , Oscillatory control of factors determining multipotency and fate in mouse neural progenitors. Science, 2013. 342(6163): p. 1203–8. 10.1126/science.1242366 [DOI] [PubMed] [Google Scholar]
- 15.Kageyama R., Shimojo H., and Imayoshi I., Dynamic expression and roles of Hes factors in neural development. Cell Tissue Res, 2015. 359(1): p. 125–33. 10.1007/s00441-014-1888-7 [DOI] [PubMed] [Google Scholar]
- 16.Isomura A. and Kageyama R., Ultradian oscillations and pulses: coordinating cellular responses and cell fate decisions. Development, 2014. 141(19): p. 3627–36. 10.1242/dev.104497 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Cai H., et al. , Nucleocytoplasmic shuttling of a GATA transcription factor functions as a development timer. Science, 2014. 343(6177): p. 1249531 10.1126/science.1249531 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gerisch G. and Hess B., Cyclic-AMP-controlled oscillations in suspended Dictyostelium cells: their relation to morphogenetic cell interactions. Proc Natl Acad Sci U S A, 1974. 71(5): p. 2118–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Maeda M., et al. , Periodic signaling controlled by an oscillatory circuit that includes protein kinases ERK2 and PKA. Science, 2004. 304(5672): p. 875–8. [DOI] [PubMed] [Google Scholar]
- 20.MacGillavry H.D., et al. , NFIL3 and cAMP response element-binding protein form a transcriptional feedforward loop that controls neuronal regeneration-associated gene expression. J Neurosci, 2009. 29(49): p. 15542–50. 10.1523/JNEUROSCI.3938-09.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ma T.C., et al. , cAMP-responsive element-binding protein (CREB) and cAMP co-regulate activator protein 1 (AP1)-dependent regeneration-associated gene expression and neurite growth. J Biol Chem, 2014. 289(47): p. 32914–25. 10.1074/jbc.M114.582460 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Batchelor E., et al. , Stimulus-dependent dynamics of p53 in single cells. Mol Syst Biol, 2011. 7: p. 488 10.1038/msb.2011.20 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Purvis J.E., et al. , p53 dynamics control cell fate. Science, 2012. 336(6087): p. 1440–4. 10.1126/science.1218351 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Purvis J.E. and Lahav G., Encoding and decoding cellular information through signaling dynamics. Cell, 2013. 152(5): p. 945–56. 10.1016/j.cell.2013.02.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Janicke R.U., Sohn D., and Schulze-Osthoff K., The dark side of a tumor suppressor: anti-apoptotic p53. Cell Death Differ, 2008. 15(6): p. 959–76. 10.1038/cdd.2008.33 [DOI] [PubMed] [Google Scholar]
- 26.Albeck J.G., Mills G.B., and Brugge J.S., Frequency-modulated pulses of ERK activity transmit quantitative proliferation signals. Mol Cell, 2013. 49(2): p. 249–61. 10.1016/j.molcel.2012.11.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Aoki K., et al. , Stochastic ERK activation induced by noise and cell-to-cell propagation regulates cell density-dependent proliferation. Mol Cell, 2013. 52(4): p. 529–40. 10.1016/j.molcel.2013.09.015 [DOI] [PubMed] [Google Scholar]
- 28.Shankaran H., et al. , Rapid and sustained nuclear-cytoplasmic ERK oscillations induced by epidermal growth factor. Mol Syst Biol, 2009. 5: p. 332 10.1038/msb.2009.90 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tsai W.B., et al. , Activation of Ras/PI3K/ERK pathway induces c-Myc stabilization to upregulate argininosuccinate synthetase, leading to arginine deiminase resistance in melanoma cells. Cancer Res, 2012. 72(10): p. 2622–33. 10.1158/0008-5472.CAN-11-3605 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lee T., et al. , Sensing and integration of Erk and PI3K signals by Myc. PLoS Comput Biol, 2008. 4(2): p. e1000013 10.1371/journal.pcbi.1000013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bretones G., Delgado M.D., and Leon J., Myc and cell cycle control. Biochim Biophys Acta, 2015. 1849(5): p. 506–516. 10.1016/j.bbagrm.2014.03.013 [DOI] [PubMed] [Google Scholar]
- 32.Gartel A.L., et al. , Myc represses the p21(WAF1/CIP1) promoter and interacts with Sp1/Sp3. Proc Natl Acad Sci U S A, 2001. 98(8): p. 4510–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Jung P. and Hermeking H., The c-MYC-AP4-p21 cascade. Cell Cycle, 2009. 8(7): p. 982–9. [DOI] [PubMed] [Google Scholar]
- 34.Seoane J., Le H.V., and Massague J., Myc suppression of the p21(Cip1) Cdk inhibitor influences the outcome of the p53 response to DNA damage. Nature, 2002. 419(6908): p. 729–34. [DOI] [PubMed] [Google Scholar]
- 35.Wong P.P., et al. , Histone demethylase KDM5B collaborates with TFAP2C and Myc to repress the cell cycle inhibitor p21(cip) (CDKN1A). Mol Cell Biol, 2012. 32(9): p. 1633–44. 10.1128/MCB.06373-11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ashall L., et al. , Pulsatile stimulation determines timing and specificity of NF-kappaB-dependent transcription. Science, 2009. 324(5924): p. 242–6. 10.1126/science.1164860 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Tay S., et al. , Single-cell NF-kappaB dynamics reveal digital activation and analogue information processing. Nature, 2010. 466(7303): p. 267–71. 10.1038/nature09145 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tian B., Nowak D.E., and Brasier A.R., A TNF-induced gene expression program under oscillatory NF-kappaB control. BMC Genomics, 2005. 6: p. 137 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Werner S.L., Barken D., and Hoffmann A., Stimulus specificity of gene expression programs determined by temporal control of IKK activity. Science, 2005. 309(5742): p. 1857–61. [DOI] [PubMed] [Google Scholar]
- 40.Lee R.E., et al. , Fold change of nuclear NF-kappaB determines TNF-induced transcription in single cells. Mol Cell, 2014. 53(6): p. 867–79. 10.1016/j.molcel.2014.01.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Goentoro L., et al. , The incoherent feedforward loop can provide fold-change detection in gene regulation. Mol Cell, 2009. 36(5): p. 894–9. 10.1016/j.molcel.2009.11.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Hart Y. and Alon U., The utility of paradoxical components in biological circuits. Mol Cell, 2013. 49(2): p. 213–21. 10.1016/j.molcel.2013.01.004 [DOI] [PubMed] [Google Scholar]
- 43.Ma W., et al. , Defining network topologies that can achieve biochemical adaptation. Cell, 2009. 138(4): p. 760–73. 10.1016/j.cell.2009.06.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Hooshangi S., Thiberge S., and Weiss R., Ultrasensitivity and noise propagation in a synthetic transcriptional cascade. Proc Natl Acad Sci U S A, 2005. 102(10): p. 3581–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Buchler N.E. and Cross F.R., Protein sequestration generates a flexible ultrasensitive response in a genetic network. Mol Syst Biol, 2009. 5: p. 272 10.1038/msb.2009.30 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Goldbeter A. and Koshland D.E. Jr., An amplified sensitivity arising from covalent modification in biological systems. Proc Natl Acad Sci U S A, 1981. 78(11): p. 6840–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Buchler N.E. and Louis M., Molecular titration and ultrasensitivity in regulatory networks. J Mol Biol, 2008. 384(5): p. 1106–19. 10.1016/j.jmb.2008.09.079 [DOI] [PubMed] [Google Scholar]
- 48.Kholodenko B.N., Cell-signalling dynamics in time and space. Nat Rev Mol Cell Biol, 2006. 7(3): p. 165–76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Ryu H., et al. , Frequency modulation of ERK activation dynamics rewires cell fate. Mol Syst Biol, 2015. 11(11): p. 838 10.15252/msb.20156458 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Cournac A. and Sepulchre J.A., Simple molecular networks that respond optimally to time-periodic stimulation. BMC Syst Biol, 2009. 3: p. 29 10.1186/1752-0509-3-29 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Kim D., Kwon Y.K., and Cho K.H., The biphasic behavior of incoherent feed-forward loops in biomolecular regulatory networks. Bioessays, 2008. 30(11–12): p. 1204–11. 10.1002/bies.20839 [DOI] [PubMed] [Google Scholar]
- 52.Hasty J., McMillen D., and Collins J.J., Engineered gene circuits. Nature, 2002. 420(6912): p. 224–30. [DOI] [PubMed] [Google Scholar]
- 53.Sohka T., et al. , An externally tunable bacterial band-pass filter. Proc Natl Acad Sci U S A, 2009. 106(25): p. 10135–40. 10.1073/pnas.0901246106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Friedland A.E., et al. , Synthetic gene networks that count. Science, 2009. 324(5931): p. 1199–202. 10.1126/science.1172005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Lehmann M. and Sneppen K., Genetic regulatory networks that count to 3. J Theor Biol, 2013. 329: p. 15–9. 10.1016/j.jtbi.2013.03.023 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(DOCX)
(A) Time courses for pulses defined by a sine function. This panel uses β = 1.2, γR = 10, γO = 0, and T = 4 (Left: D = 1 Right: D = 3). The top row contains the time courses of the input pulses for two different pulse durations, either a pulsing input or a simulated sustained input (with a sine waveform). The second row shows the time courses for X. The bottom row shows the time courses for R. With identical parameters, an IFFL motif can generate two distinct outputs depending on the length of the duration of the input pulses. When X is below the threshold of induction, the circuit maintains the ability to produce a stepwise increase of R. However, when X overcomes the threshold, the circuit loses this ability. For a single parameter set, both outputs are desired to quantify the system as being capable of counting. (B) Calibration curve for ideal counting. This panel uses β = 1.2, γR = 10, γO = 0, and T = 4 (D = 1). The sample calibration curve is for a pulse duration within the optimal duration range, therefore it is able to demonstrate ideal counting. With an increasing number of input pulses from 1–4 in the top panel, R exhibits a stepwise increase. The linearity is demonstrated in the bottom panel by R2 > 0.99.
(TIF)
Here, A and B both use β = 1.2, γR = 10, γO = 0, and T = 4 (D = 3), a parameter set which demonstrates the inability to count. (A) Time course for failed counting. With an increasing number of pulses, X overcomes the activation threshold and the ability to produce a stepwise increase of R is lost. (B) Calibration curve for failed counting. The sample calibration curve is for a pulse duration outside the optimal duration range, therefore it is able to demonstrate the case when counting fails. With an increasing number of input pulses from 1–10 r is suppressed and the non-linearity is demonstrated by R2 < 0.99.
(TIF)
(A) Alternative incoherent feedforward loop motif (Model in S1). In this model, a pulsing input simultaneously stimulates the production of X and R. Here, the threshold response is implemented with the additional production of X through a positive feedback loop. (B) Calibration curves for ideal or failed counting. The top panel uses β = 1.2, γR = 0.01, γO = 0, α = 100, and T = 10 (D = 1). The sample calibration curve is for a pulse duration within the optimal duration range, therefore it demonstrates counting. The bottom panel uses β = 1.2, γR = 0.01, γO = 0, α = 100, and T = 10 (D = 9). The sample calibration curve is for a pulse duration outside the optimal duration range, therefore it demonstrates the case when counting fails.
(TIF)
(A) Signal processing by an IFFL (Model in S2). In this model, a pulsing input (S) simultaneously stimulates the production of an intermediate (X1) and a reporter (R). The first intermediate (X1) then activates the production of the second intermediate (X) that induces the degradation of R through a threshold response. The fundamental constraints for counting shown are based on the full model (S1 Text). (B) Time courses demonstrate counting mechanism. Using β′ = 1, β″ = 1.2, γR = 10, δ = 1, γO = 0, and T = 4 (Left: D = 1 Right: D = 3). The top row contains time courses of the input pulses for two different pulse durations, either a pulsing input or a simulated sustained input. The second row shows time courses for X1. The third row shows time courses for X. The bottom row shows time courses for R. Despite the addition of time delay (of ~10% of the pulse duration) through an additional component, the IFFL motif maintains the ability to distinguish input signals with longer or shorter pulses.
(TIF)
(A) Signal processing by an IFFL (Model in S3). In this model, a pulsing input (S) simultaneously stimulates the production of an intermediate (X) and an intermediate reporter (R1). The intermediate reporter (R1) then activates the production of the reporter (R), which is degraded by the intermediate (X) through a threshold response. The fundamental constraints for counting shown are based on the full model (S1 Text). (B) Time courses demonstrate counting mechanism. Using β′ = 5, β″ = 1.2, γR = 10, γR1 = 5, γO = 0, and T = 4 (Left: D = 1 Right: D = 3). The top row contains time courses of the input pulses for two different pulse durations, either a pulsing input or a simulated sustained input. The second row shows time courses for X. The third row shows time courses for R1. The bottom row shows time courses for R. Despite the addition of time delay (of ~10% of the pulse duration) through an additional component, the IFFL motif maintains the ability to distinguish input signals with longer or shorter pulses.
(TIF)
(A) Time courses demonstrate counting mechanism. Using β = 1.2, γR = 10, γO = 0, and T = 4 (Left: D = 1 Right: D = 3). The top row contains time courses of the input pulses for two different pulse durations, either a pulsing input or a simulated sustained input. The second row shows time courses for X. The bottom row shows time courses for R. (B) Time courses demonstrate differentiation between a sustained and oscillatory input. Using β = 0.337, γR = 10, γO = 0. Here, the amplitude of the sustained input is equivalent to the mean of the oscillating input in panel A (D = 1).
(TIF)
Time courses of the reporter. Using β = 1.2, γR = 10, γO = 0, T = 4, D = 1. Here, we show time courses for R with varying values for the Hill coefficient (n = 5, 50, 110, or 1000) to demonstrate that the specific value for n is irrelevant. The hill coefficient must simply be high enough to induce a threshold response.
(TIF)
(A) Time courses demonstrate the effect of noise in the case of a small molecular number (Model S5). Using k1 = k2 = 5, dx = 1, dR = 10, n = 100, dRo = 0, Kx = 4, and T = 4 (D = 1) in equations 20–21. The top row shows time courses of the input pulses in the case of an oscillating input. The second row shows time courses for R in the absence of noise. The third row shows time courses for X in the presence of noise (ξ = 10). The fourth row shows time courses for R in the presence of noise. The bottom row shows the calibration curve for the system in the presence of noise. With an increasing number of input pulses from 1–10, R is unable to exhibit a stepwise increase due to the impact of noise on the low molecular number of the components; this poor linearity is demonstrated by R2 < 0.99. (B) Time courses demonstrate the effect of noise in the case of an increasing molecular number (Model S5). Using k1 = k2 = 50, dx = 1, dR = 10, n = 100, dRo = 0, Kx = 40, and T = 4 (D = 1) in equations 20–21. The top row contains time courses of the input pulses in the case of an oscillating input. The second row shows time courses for R in the absence of noise. The third row shows time courses for X in the presence of noise (ξ = 10). The fourth row shows time courses for R in the presence of noise. The bottom row shows the calibration curve for the system in the presence of noise. With an increasing number of input pulses from 1–10, R is unable to exhibit a stepwise increase due to the impact of noise on the low molecular number of the components; the poor linearity is demonstrated by R2 < 0.99. (C) Time courses demonstrate the effect of noise in the case of a sufficiently high molecular number (Model S5). Using k1 = k2 = 500, dx = 1, dR = 10, n = 100, dRo = 0, Kx = 400, and T = 4 (D = 1) in equations 20–21. The top row contains time courses of the input pulses in the case of an oscillating input. The second row shows time courses for R in the absence of noise. The third row shows time courses for X in the presence of noise (ξ = 10). The fourth row shows time courses for R in the presence of noise. The bottom row shows the calibration curve for the system in the presence of noise. With an increasing number of input pulses from 1–10, R is able to exhibit a stepwise increase despite the presence of noise due to the sufficiently high molecular number. Here, the linearity is demonstrated by R2 ≥ 0.99.
(TIF)
(A) Signal processing by an IFFL (Model S6). In this model, a pulsing input (S) simultaneously stimulates the production of an intermediate (X) and a reporter (R). The intermediate represses the production of R through a threshold response. The fundamental constraints for counting shown are based on the model described in S1 Text. (B) Time courses demonstrate counting mechanism. Using β = 12, γO = 0, and T = 4 (Left: D = 1 Right: D = 3). The top row contains time courses of the input pulses for two different pulse durations, either a pulsing input or a simulated sustained input. The second row shows time courses for X. The bottom row shows time courses for R. Here, an IFFL motif can generate two distinct outputs depending on the length of the duration of the input pulses.
(TIF)
Data Availability Statement
All relevant data are within the paper and its Supporting Information files.