Anomalous Diffusion Measured by a Twice-Refocused Spin Echo Pulse Sequence: Analysis Using Fractional Order Calculus

Abstract

Purpose

To theoretically develop and experimentally validate a formulism based on a fractional order calculus (FC) diffusion model to characterize anomalous diffusion in brain tissues measured with a twice-refocused spin-echo (TRSE) pulse sequence.

Materials and Methods

The FC diffusion model is the fractional order generalization of the Bloch-Torrey equation. Using this model, an analytical expression was derived to describe the diffusion-induced signal attenuation in a TRSE pulse sequence. To experimentally validate this expression, a set of diffusion-weighted (DW) images was acquired at 3 Tesla from healthy human brains using a TRSE sequence with twelve b-values ranging from 0 to 2,600 s/mm². For comparison, DW images were also acquired using a Stejskal-Tanner diffusion gradient in a single-shot spin-echo echo planar sequence. For both datasets, a Levenberg-Marquardt fitting algorithm was used to extract three parameters: diffusion coefficient D, fractional order derivative in space β, and a spatial parameter μ (in units of μm). Using adjusted R-squared values and standard deviations, D, β and μ values and the goodness-of-fit in three specific regions of interest (ROI) in white matter, gray matter, and cerebrospinal fluid were evaluated for each of the two datasets. In addition, spatially resolved parametric maps were assessed qualitatively.

Results

The analytical expression for the TRSE sequence, derived from the FC diffusion model, accurately characterized the diffusion-induced signal loss in brain tissues at high b-values. In the selected ROIs, the goodness-of-fit and standard deviations for the TRSE dataset were comparable with the results obtained from the Stejskal-Tanner dataset, demonstrating the robustness of the FC model across multiple data acquisition strategies. Qualitatively, the D, β, and μ maps from the TRSE dataset exhibited fewer artifacts, reflecting the improved immunity to eddy currents.

Conclusion

The diffusion-induced signal attenuation in a TRSE pulse sequence can be described by an FC diffusion model at high b-values. This model performs equally well for data acquired from the human brain tissues with a TRSE pulse sequence or a conventional Stejskal-Tanner sequence.

1. Introduction

It has been reported that water molecular diffusion in brain tissues is anomalous at high b-values (e.g., > 1,500 s/mm²) (1,2). This phenomenon is a consequence of the complex diffusion environment that is locally heterogeneous (1-4). Several models have been developed to characterize the anomalous diffusion behavior and thereby to infer tissue microstructures and the microenvironment (3-12). Recently, anomalous diffusion was described by applying fractional order differential operators in the Bloch-Torrey equation for the cases of a continuous diffusion gradient in a free induction decay (FID) sequence and the Stejskal-Tanner pulsed gradient in a spin-echo (SE) sequence (13-15). In either case, two new parameters, β and μ, have been introduced and for the Stejskal-Tanner gradient they exhibited remarkable contrast among human brain tissues (14,15). These studies suggest that the new parameters may provide an alternative way to characterize the tissue microenvironment through which water molecules diffuse.

The fractional order calculus (FC) diffusion model (13-15), as well as other anomalous diffusion models, is typically applied to a set of diffusion-weighted (DW) magnetic resonance (MR) images acquired at high b-values (e.g., up to ~4,000 s/mm²). Fast imaging sequences such as echo planar imaging (EPI) are commonly used to reduce scan time and to minimize the effects of motion (16-19). However, the strong diffusion-weighting gradients can induce excessive eddy currents (20-22), which are not adequately compensated for by using conventional eddy current compensation methods with pre-emphasis. The uncompensated eddy currents can cause image mis-registration as well as signal loss (20), leading to considerable errors in the parameters obtained from any anomalous diffusion model.

A number of approaches have been developed to address the eddy current issue in diffusion imaging (21-32). A commonly used method is based on a twice-refocused spin echo (TRSE) sequence first proposed by Reese et al. (21). This technique is designed to cancel the residual eddy-current magnetic fields by acquiring a spin echo signal after two radiofrequency (RF) refocusing pulses (21). Despite the wide-spread use of the TRSE technique for diffusion imaging on human subjects, the majority of the anomalous diffusion models still assume a Stejskal-Tanner gradient in a classical spin-echo sequence for acquiring high b-value DW images.

In the present work, we describe a formulism of the FC diffusion model for characterizing signal loss in diffusion images acquired using a TRSE pulse sequence. We also demonstrate that the formulism can accurately fit the diffusion data acquired from human brain tissues at high b-values.

2. Theory

2.1 The FC diffusion model

The FC diffusion model is the fractional order generalization of the Bloch-Torrey equation for the transverse magnetization. The Bloch-Torrey equation describes the spin dynamics of the magnetization $M(\stackrel{\rightharpoonup }{r},t)$ by

$$\frac{\partial M(\stackrel{\rightharpoonup }{r},t)}{\partial t}=\gamma M(\stackrel{\rightharpoonup }{r},t)\times B+D{\nabla }^{2}M(\stackrel{\rightharpoonup }{r},t)$$ [1]

where B is the effective magnetic field which includes contributions from the gradient G(t), $\stackrel{\rightharpoonup }{r}$ is a spatial variable ($\stackrel{\rightharpoonup }{r}=x\widehat{x}+y\widehat{y}+z\widehat{z}$), ${\nabla }^2={\partial }_{xx}^2+{\partial }_{yy}^2+{\partial }_{zz}^2$ is the Laplacian operator, γ is the gyromagnetic ratio (42.58 MHz/T for protons), and D is the diffusion coefficient. In Eq. [1], both T₁ and T₂ relaxations are neglected.

Eq. [1] can be generalized to fractional order dynamics in either spatial or temporal domain. In the present study, we limit our scope to fractional order dynamics in space:

$$\frac{\partial M_{xy}(\stackrel{\rightharpoonup }{r},t)}{\partial t}=\lambda M_{xy}(\stackrel{\rightharpoonup }{r},t)+D{\mu }^{2(\beta -1)}{\nabla }^{2\beta }{M}_{xy}(\stackrel{\rightharpoonup }{r},t)$$ [2]

where ${\nabla }^{2\beta }=D_x^{2\beta }+D_y^{2\beta }+D_z^{2\beta }$ is a sequential Riesz fractional order Laplacian operator in space (13-15,33,34), β is the fractional order (1 2 < β ≤ 1), and μ (in units of μm) is the fractional order space constant needed to preserve the nominal units (mm²/s) of diffusion coefficient D (13,15).

For a Stejskal-Tanner gradient pulse pair with amplitude G_d, pulse width δ, and pulse separation Δ, M_xy can be described by (13,15)

$$M_{xy}=M_0\exp [-D{\mu }^{2(\beta -1)}{\left(\gamma G_d\delta \right)}^{2\beta }(\Delta -\frac{2\beta -1}{2\beta +1}\delta \left)\right]$$ [3]

Eq. [3] reduces to the classic mono-exponential expression when β = 1 :

$$M_{xy}=M_0\exp [-D{\left(\gamma G_d\delta \right)}^2(\Delta -\frac{1}{3}\delta \left)\right]$$ [4]

2.2 The fractional order diffusion model for a TRSE pulse sequence

Eq. [3] is derived by integrating the Stejskal-Tanner gradient for the case of fractional order dynamics in space (13,15):

$$\ln \frac{M_{xy}}{M_0}=-D{\mu }^{2(\beta -1)}{\gamma }^{2\beta }{\int }_0^t{\left({\int }_0^{t^{\prime }}G\right(t^{″}\left)d{t}^{″}\right)}^{2\beta }d{t}^{\prime }$$ [5]

where G(t) is the time-varying magnetic field gradient. The solution for the case of TRSE can be derived by substituting for the Stejskal-Tanner gradient with the twice-refocused gradient waveform as shown in Fig. 1.

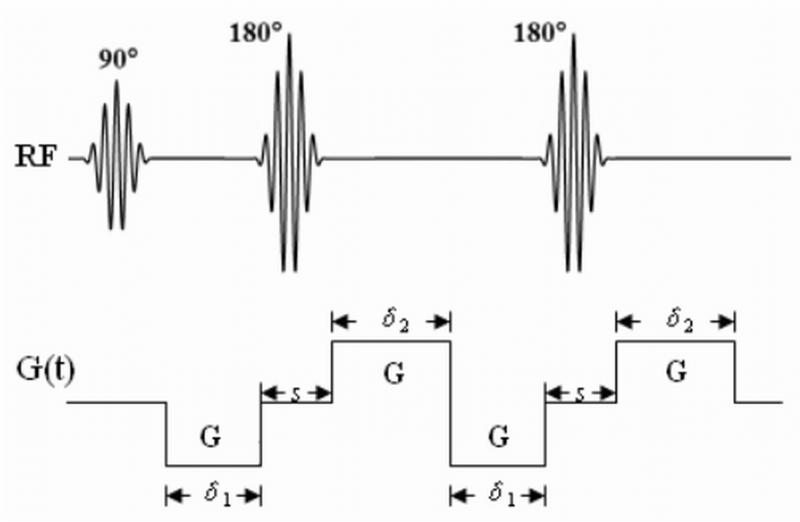
Figure 1.

A diagram of a TRSE pulse sequence with the diffusion gradient waveforms. The durations of the gradient pulses and their time separation are indicated in the figure.

In the TRSE pulse sequence, two pairs of bipolar diffusion gradient pulses, each with a pulse width of δ₁ and δ₂, respectively, are included (21). Assuming the inter-gradient separation is s (s must be longer than the width of the RF refocusing pulse) as shown in Fig. 1, we obtain the time integration of the diffusion gradient as follows:

$${\int }_0^{t}G\left(t^{\prime }\right)d{t}^{\prime }=\{\begin{array}{cc}-Gt\hfill & t\le {\delta }_1\hfill \\ -G{\delta }_1\hfill & {\delta }_1<t\le {\delta }_1+s\hfill \\ G(t-s)\hfill & {\delta }_1+s<t\le {\delta }_1+s+{\delta }_2\hfill \\ G(2{\delta }_1+2{\delta }_2+s-t)\hfill & {\delta }_1+s+{\delta }_2<t\le 2{\delta }_1+s+{\delta }_2\hfill \\ G{\delta }_2\hfill & 2{\delta }_1+s+{\delta }_2<t\le 2{\delta }_1+2s+{\delta }_2\hfill \\ G(t-2{\delta }_1-2s-2{\delta }_2)\hfill & 2{\delta }_1+2s+{\delta }_2<t\le 2({\delta }_1+{\delta }_2+s)\hfill \\ 0\hfill & 2({\delta }_1+{\delta }_2+s)<t\hfill \end{array}\phantom{\}}$$ [6]

Inserting Eq. [6] into Eq. [5] gives:

$$\ln \frac{M_{xy}}{M_0}=-D{\mu }^{2(\beta -1)}{\left(G\gamma \right)}^{2\beta }\left[\right({\delta }_1^{2\beta }+{\delta }_2^{2\beta })s+\frac{2}{2\beta +1}{({\delta }_1+{\delta }_2)}^{2\beta +1}]$$ [7]

Defining an effective inter-gradient pulse separation as _{δ’ = s +(δ1+,δ2)/2} Eq. [7] becomes

$$\ln \frac{M_{xy}}{M_0}=-D{\mu }^{2(\beta -1)}{\left(G\gamma \right)}^{2\beta }\left[\right({\delta }_1^{2\beta }+{\delta }_2^{2\beta }\left)\right({\Delta }^{\prime }-\frac{{\delta }_1+{\delta }_2}{2})+\frac{2}{2\beta +1}{({\delta }_1+{\delta }_2)}^{2\beta +1}]$$ [8]

In the limiting case of δ₁ = 0 or δ₂ = 0, it can be shown that Eq. [8] reduces to the expression for a Stejskal-Tanner gradient pulse pair described by Eq. [3]. (Note that s in Eq. [7] becomes Δ – δ for a Stejskal-Tanner gradient pair.)

3. Methods

3.1 Image Acquisition

To experimentally evaluate the model, diffusion-weighted imaging (DWI) experiments were carried out on a 3T GE Signa HDx (General Electric Health Care, Waukesha, Wisconsin) scanner with an 8-channel phased-array coil. DW images were acquired from healthy human brains using a customized single-shot TRSE pulse sequence with echo planar spatial encoding. Twelve b-values ranging from 0 to 2,600 s/mm² were used (b = 0, 194, 402, 596, 799, 986, 1,342, 1,500, 1,827, 2,219, 2,560, 2,600 s/mm²) with the diffusion gradient successively applied along the three orthogonal axes (i.e., x- y- and z-axes defined by the logical coordinates) to minimize the effect of diffusion anisotropy (35). (Note that the effect of diffusion anisotropy is discussed in the Discussion section.) For each non-zero b-value, a non-diffusion weighted image was acquired in the same series and used as a reference for motion correction (see the next sub-section). The timing parameters for the diffusion gradients were: δ₁ = 9.3 ms, δ₂ = 22.9 ms, and s = 5.7 ms (see Fig. 1). For comparison, DW images were also acquired using a Stejskal-Tanner diffusion gradient with δ = 32.2 ms and Δ = 38.8 ms in a single-shot spin-echo EPI pulse sequence using the same set of b-values. No parallel imaging method was used because of signal-to-noise (SNR) limitations at high b-values. For both sequences, the other key data acquisition parameters were: TR/TE = 4,000/115 ms, FOV = 22 cm, image matrix = 128 × 128 (Note that partial k-space sampling was used along the phase-encoding direction.), slice thickness = 4 mm with a slice gap of 3 mm, NEX = 4, and scan time = 24 min for the two sequences. A total of four healthy volunteer datasets were acquired to confirm consistency and reproducibility.

3.2 Image Analysis

Prior to diffusion image analysis, subject head motion was evaluated by subtracting a pair of non-diffusion weighted images, each acquired with adjacent b-values (and also adjacent data acquisition order), starting with the image of b = 0 s/mm². If the detected shift was more than a half of a pixel (the image with b = 0 was used as a reference), a motion correction was performed by applying a linear phase ramp in k-space in the direction along which the shift was detected (15). With multiple averages (NEX), image reconstruction was performed on each average prior to combining amplitude images from all averages. Motion correction among the averages was performed analogously to the method described above when needed. In this study, only in-plane motion was corrected, as further explained in the Discussion section.

After motion correction, the images acquired using either the Stejskal-Tanner gradient or the TRSE gradient were fitted voxel-by-voxel to Eq. [3] or Eq. [8], respectively. To perform the fitting, a mask with the intensity threshold of $\stackrel{‒}{n}+2\sigma$ was first applied to the images, where $\stackrel{‒}{n}$ represents the mean noise of the amplitude image in the background region of interest (ROI) and σ denotes the standard deviation of noise. Voxel intensities above this threshold were fitted to the equations using a Levenberg-Marquardt non-linear fitting algorithm. The initial D values were obtained from the data acquired with low b-values (b < 1,000 s/mm²) using the classical mono-exponential model. The initial values of β were empirically set to 0.7 (the fitting results were insensitive to the initial choice of β). With known initial values of D and β, the initial values of μ were determined from the models. After eleven iterations to ensure the convergence of the parameters, the final values of D, β, and μ were obtained on a voxel-by-voxel basis, yielding spatially resolved maps of D, β, and μ. In addition to voxel-based analysis, the fitting algorithm was also applied to specific ROIs in white matter (WM), gray matter (GM) and cerebrospinal fluid (CSF), respectively (indicated in Fig. 2), to evaluated the goodness-of-fit of the models in a relatively homogeneous region with an adequate signal-to-noise ratio (SNR), e.g., > 7 (see below).

Figure 2.

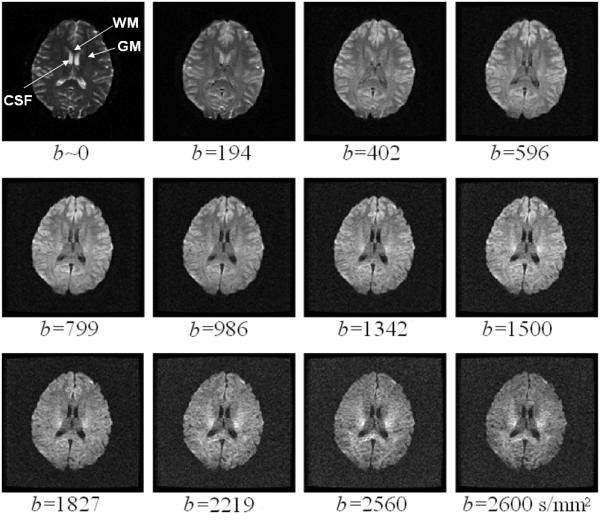
A set of 12 representative DW images acquired from a human volunteer using the TRSE pulse sequence with b-values ranging from 0 to 2,600 s/mm². The b-value is labeled underneath each image. The arrows in the first image indicate the ROIs in WM (genu of the corpus callosum), GM (putamen) and CSF (lateral cerebral ventricle) that were used in the analyses presented in Fig. 3 and Tables 1 and 2.

4. Results

Figure 2 displays a set of 12 representative DW images acquired from a human volunteer using the TRSE sequence with b-values ranging from 0 to 2,600 s/mm². With a NEX of 4 and a moderate TE (115 ms), an SNR greater than 7 was achieved in the brain tissues (except for CSF) even at the highest b-value. Although images with fewer averages were also attempted, it was found that 4 averages were needed to achieve an adequate SNR for reliable and stable fitting. Increasing the number of averages beyond 4 resulted in diminishing returns. The corresponding images acquired with the Stejskal-Tanner gradient exhibited similar SNR characteristics (images not shown). The problem with head motion during the long acquisition time (~ 24 minutes) was addressed effectively using the motion correction technique described in the Methods section for both the TRSE and the Stejskal-Tanner datasets.

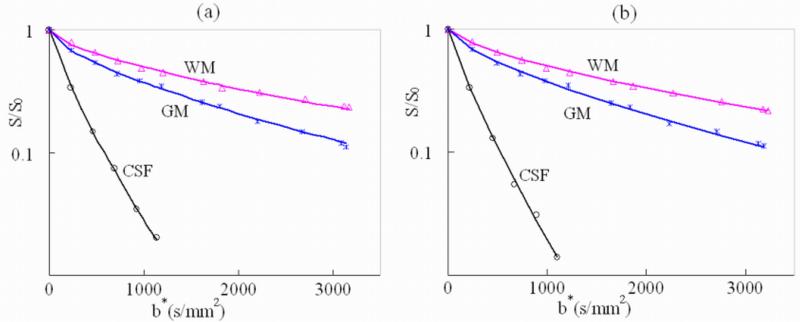
Figure 3 shows the signal attenuation and the fitting curves in the three representative ROIs chosen from the WM (genu of the corpus callosum), GM (putamen) and CSF (lateral cerebral ventricle) for the Stejskal-Tanner dataset (Fig. 3a) and the TRSE dataset (Fig. 3b), respectively. These ROIs are indicated in the non-diffusion-weighted image (b=0 s/mm²) shown in Fig. 2. The horizontal axis of Fig. 3 represents b*, which was defined as b* = (γG_dδ)²[Δ – (2β −1)δ/(2β +1)]for the Stejskal-Tanner dataset and $b^{\ast }={\left[\gamma G_d\right({\delta }_1+{\delta }_2\left)\right]}^2\left[\right({\delta }_1^{2\beta }+{\delta }_2^{2\beta })∕({\delta }_1+{\delta }_2){}^{2\beta }({\Delta }^{\prime }-({\delta }_1+{\delta }_2)∕2)+2({\delta }_1+{\delta }_2)∕(2\beta +1)]$ for the (TRSE dataset. The use of b* instead of b was to accommodate the FC diffusion model where the conventional definition of b-value does not hold (13,15). Fig. 3 demonstrates excellent agreement between the theoretical curves and the experimental data for both TRSE and Stejskal-Tanner datasets. The goodness-of-fit for each dataset was quantitatively evaluated by the adjusted R-squared values (36). The R-squared values for the TRSE and the Stejskal-Tanner datasets were evaluated on each of the four subjects and are summarized in Table 1. Both datasets exhibited excellent R-squared values, suggesting that the FC model works equally well for TRSE and Stejskal-Tanner sequences. The slightly superior performance in TRSE is likely a result of its improved robustness against eddy currents.

Figure 3.

Signal attenuation and the fitting curves as a function of b* for the three specific ROIs in white matter (WM), gray matter (GM), and the cerebrospinal fluid (CSF) indicated in Fig. 2. (a) Results from the Stejskal-Tanner pulse sequence where b* is defined as b* = (γG_dδ)²[Δ – (2β −1)δ/(2β +1)], and (b) results from the TRSE sequence in which b* is given by $b^{\ast }={\left[\gamma G_d\right({\delta }_1+{\delta }_2\left)\right]}^2\left[\right({\delta }_1^{2\beta }+{\delta }_2^{2\beta })∕({\delta }_1+{\delta }_2){}^{2\beta }({\Delta }^{\prime }-({\delta }_1+{\delta }_2)∕2)+2({\delta }_1+{\delta }_2)∕(2\beta +1)]$. In CSF, only images with b < 1,000 s/mm² were used in the fitting due to inadequate SNR in images with higher b-values.

Table 1.

The adjusted R-squared values of the fitting curves in three representative ROIs from images obtained with the Stejskal-Tanner and the TRSE pulse sequences for each of the four subjects.

		WM	GM	CSF
Sub1	Stejskal-Tanner	0.99	1.00	1.00
	TRSE	1.00	1.00	1.00
Sub2	Stejskal-Tanner	1.00	0.99	1.00
	TRSE	1.00	0.99	1.00
Sub3	Stejskal-Tanner	0.99	1.00	1.00
	TRSE	0.99	1.00	1.00
Sub4	Stejskal-Tanner	0.99	0.99	1.00
	TRSE	1.00	1.00	1.00

Abbreviations: CSF: cerebrospinal fluid; GM: gray matter; WM: white matter; TRSE: Twice-Refocused Spin Echo; Sub: subject.

Table 2 summarizes the mean and the standard deviation (STD) of the diffusion parameters in the three representative ROIs (WM, GM and CSF) for each of the four subjects. The results are shown for both the Stejskal-Tanner and the TRSE sequences. There was no significant difference in the mean values between the two cases. However, TRSE produced slightly lower STD in the parametric maps as compared with the results from the Stejskal-Tanner sequence, which again can be attributed to the robustness of TRSE against eddy currents.

Table 2.

Comparison of the mean and the standard deviation of the three diffusion parameters in the three representative ROIs selected from the Stejskal-Tanner (ST) and the TRSE datasets for each of the four subjects.

		Sub1		Sub2		Sub3		Sub4
		ST	TRSE	ST	TRSE	ST	TRSE	ST	TRSE
D (×10−3 mm2/s)	WM	0.61±0.01	0.61±0.01	0.60±0.01	0.61±0.01	0.60±0.02	0.59±0.02	0.62±0.02	0.61±0.01
	GM	0.71±0.02	0.71±0.01	0.70±0.01	0.70±0.01	0.70±0.02	0.71±0.01	0.70±0.01	0.71±0.01
	CSF	3.00±0.06	3.00±0.06	2.99±0.08	3.00±0.07	3.00±0.07	3.00±0.07	2.98±0.08	2.98±0.07
β	WM	0.72±0.02	0.72±0.01	0.73±0.01	0.72±0.01	0.72±0.01	0.71±0.01	0.73±0.02	0.73±0.02
	GM	0.85±0.01	0.85±0.01	0.85±0.02	0.84±0.01	0.84±0.01	0.84±0.01	0.84±0.02	0.85±0.02
	CSF	0.88±0.02	0.89±0.01	0.88±0.02	0.87±0.02	0.87±0.02	0.87±0.01	0.88±0.02	0.88±0.01
μ (μm)	WM	4.76±0.04	4.76±0.04	4.77±0.04	4.76±0.03	4.79±0.02	4.78±0.02	4.79±0.03	4.79±0.03
	GM	5.72±0.03	5.73±0.03	5.70±0.02	5.71±0.03	5.70±0.02	5.70±0.02	5.73±0.04	5.73±0.03
	CSF	7.67±0.16	7.64±0.12	7.68±0.14	7.68±0.14	7.66±0.16	7.67±0.15	7.65±0.14	7.68±0.13

Abbreviations: CSF: cerebrospinal fluid; GM: gray matter; WM: white matter; Sub: subject.

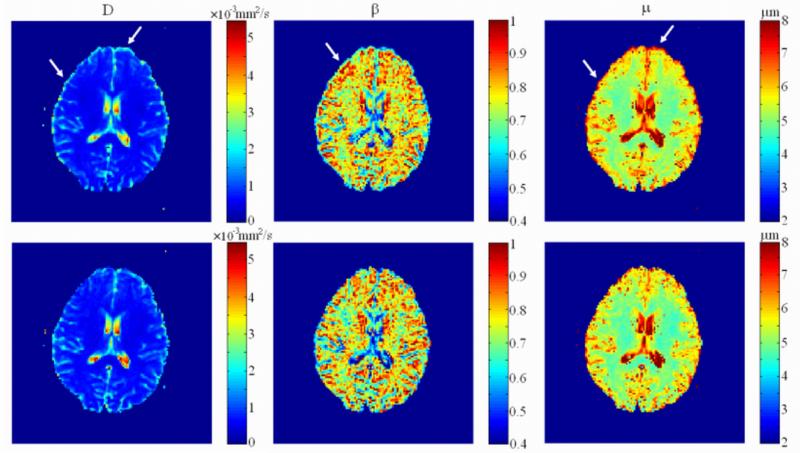
The spatially resolved maps of the diffusion parameters obtained from the FC diffusion model using voxel-by-voxel fitting are displayed in Fig. 4. The upper and lower rows show the results from the Stejskal-Tanner and the TRSE datasets, respectively. With the Stejskal-Tanner gradient, the eddy-current induced distortion manifested itself as edge artifacts (indicated by the arrows in the figure) resulting from mis-registration of the DW image series, as described in reference (20). These edge artifacts were effectively removed in the TRSE images (lower row). The most notable reduction in edge artifact was observed in the μ and D maps.

Figure 4.

Comparison of the parameter maps (D, β, and μ) obtained from the images acquired with the Stejskal-Tanner (upper row) and the TRSE pulse sequences (lower row). The arrows indicate the location of the edge artifacts due to residual eddy currents in the maps obtained using the Stejskal-Tanner gradient. These artifacts are noticeably reduced in the maps obtained with the TRSE pulse sequence.

5. Discussion

Following previous work on the FC diffusion model described by Magin et al. (13) and Zhou et al. (14,15), we have theoretically derived a new expression (Eq. [8]) to characterize the diffusion-induced signal loss in a TRSE pulse sequence. This theoretical expression can accurately characterize experimental diffusion data obtained from healthy human brain tissues at high b-values up to 2,600 s/mm². Additionally, the FC model produced a set of parameters that showed excellent consistency across multiple subjects (Tables 1 and 2).

Compared to the FC model for the Stejskal-Tanner gradient (13-15), the newly proposed FC formulism for TRSE produced at least equally good results. The slight improvements (i.e., better goodness-of-fit in Table 1, smaller standard deviations in Table 2, and fewer artifacts in Fig. 4) afforded by TRSE are likely the consequence of its improved robustness against eddy currents, not a reflection of the FC model itself. The strong diffusion gradient in a high b-value diffusion pulse sequence can induce excessive eddy currents, often beyond that which can be compensated for by using conventional compensation techniques, such as gradient pre-emphasis. The uncompensated eddy currents can cause image shear, shift, and compression/dilation (20), all of which contribute to the edge artifacts seen in the first row of Fig. 4. Such image mis-registration and the resulting edge artifacts and errors can be effectively reduced or even removed using the TRSE pulse sequence. In addition to the image mis-registration, specific types of eddy currents that interrupt the slice-selection gradient can also cause inconsistent image intensity change (20) depending on the diffusion gradient amplitude, and thus on the b-values. In quantitative diffusion analysis using the FC model, this effect was particularly detrimental and likely contributed to the errors shown in Tables 1 and 2. This argues that, when eddy currents are problematic, the TRSE sequence is preferred over the conventional diffusion pulse sequences that rely on the Stejskal-Tanner gradient. A shortcoming of the TRSE pulse sequence is the lower SNR due to the increased TE. But this can be mitigated by other means, such as employing more sensitive RF coils.

The TRSE sequence has been widely used in apparent diffusion coefficient (ADC) quantification using a mono-exponential or bi-exponential model where a new expression of b is needed to account for the altered gradient waveforms. A similar change is necessary in the case of the FC diffusion model, where the definition of b* (instead of b) differs from b* for the Stejskal-Tanner gradient (15). Unlike b-value, b* is a function of spatial fractional order β. Thus, b* cannot be pre-determined purely based on pulse sequence parameters without the knowledge of β.

The present study has several limitations. First, the effects of diffusion anisotropy were not investigated, primarily because of the scan time considerations. The analytical expression (Eq. [8]) of the FC model for TRSE, however, can be generalized to account for diffusion anisotropy effects not only in diffusion coefficient D but also in β and μ. As discussed in (15), such a generalization would result in a vector representation for β and μ, as well as a second-rank tensor for D. Theoretical analysis and experimental studies to investigate the anisotropy effects are expected to provide additional parameters, similar to fractional anisotropy, for quantifying the degree of anisotropy in D, β and μ. Second, when deriving the analytical expression given by Eq. [8], the cross-terms arising from the imaging gradients and the diffusion-gradients were not considered. Such cross-terms can adversely affect the accuracy of b*-values, and consequently the validity of Eq. [8] based on which analyses have been performed in this study. In the pulse sequence design, we have made effort to reduce the cross-term contributions by adjusting the gradient waveforms. A theoretical analysis based on the gradient waveforms revealed that the residual cross-tem contribution was approximately 4-5%. This effect will be considered in future studies. Lastly, our motion correction was limited to in-plane motion. Through-plane motion may not be negligible, especially considering the relatively long scan time of 24 minutes. Additionally, even for in-plane motion, the correction was limited to spatial shift among different b-values without considering the effect of image blurring that could occur within a single image acquisition at a fixed b-value using multiple averages. Clearly, a more comprehensive motion correction technique is needed to apply the FC diffusion analysis to clinical studies involving patients where through-plane motion and image blurring are more likely to occur compared to healthy volunteers.

In conclusion, we have theoretically developed and experimentally validated a signal expression of anomalous diffusion for a TRSE pulse sequence using the FC diffusion model. Despite the aforementioned limitations, this expression has accurately fitted to the experimental data acquired from multiple healthy human brain tissues with excellent consistency. Compared to a Stejskal-Tanner diffusion sequence whose FC model was described previously, the TRSE sequence offers improved robustness against eddy currents, allowing the FC diffusion model to be used more broadly for analyzing high b-value diffusion images.