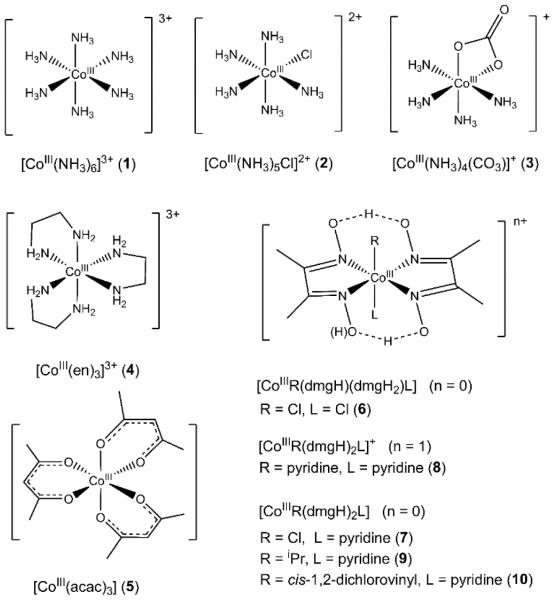
Abstract
Kβ valence-to-core (V2C) X-emission spectroscopy (XES) has gained prominence as a tool for molecular inorganic chemists to probe the occupied valence orbitals of coordination complexes, as illustrated by recent evaluation of Kβ V2C XES ranging from titanium to iron. However, cobalt Kβ V2C XES has not been studied in detail, limiting the application of this technique to probe cobalt coordination in molecular catalysts and bioinorganic systems. In addition, the community still lacks a complete understanding of all factors that dictate the V2C peak area. In this manuscript, we report experimental cobalt Kβ V2C XES spectra of low-spin octahedral Co(III) complexes with different ligand donors, in conjunction with DFT calculations. Cobalt Kβ V2C XES was demonstrated to be sensitive to cobalt-ligand coordination environments. Notably, we recognize here for the first time that there is a linear correlation between the V2C area and the spectrochemical series for low-spin octahedral cobalt(III) complexes, with strong field π acceptor ligands giving rise to the largest V2C area. This unprecedented correlation is explained by invoking different levels of π-interaction between cobalt p orbitals and ligand orbitals that modulate the percentage of cobalt p orbital character in donor MOs, in combination with changes in the average cobalt-ligand distance.
1. Introduction
Very recently, Kβ Valence-to-Core (V2C) X-ray emission spectroscopy (XES) has attracted much attention as a promising tool for investigating the coordination environment of transition metal centers.1–3 While the phenomenon of Kβ XES has been known for a long time by physicists, recent developments in hard X-ray spectrometer instrumentation,4–8 together with the high flux and brilliance provided by third-generation synchrotrons, have afforded the higher energy resolution and greater sensitivity needed to probe the chemically informative valence-to-core region of the Kβ X-ray emission spectrum. This greatly improved resolution and sensitivity have thus made the technique accessible and useful to the inorganic community. Traditionally, first row transition metal K-edge X-ray emission spectroscopy is carried out using a synchrotron radiation source to excite a 1s electron. The core hole is immediately filled by an electron from an orbital of higher energy, which is accompanied by the emission of an X-ray photon. Metal Kβ mainline emission is characterized by the transition from the metal np to 1s orbital, and is split into Kβ1,3 and Kβ’ features, with the spectral shape dominated by 3p-3d exchange.9,10 Previous studies of Fe Kβ XES suggest that these mainline features are sensitive to metal spin state,11 metal oxidation state, and metal-ligand covalency.12
Besides the Kβ mainline, it is possible to have the core hole filled by valence electrons from ligand np or ns orbitals. This pathway occurs at a much lower probability than the mainline transitions and gives rise to Kβ2,5 and Kβ’’ features located at energies higher than the mainline features. These Valence-to-Core (V2C) transitions directly probe filled, ligand-based valence orbitals, and have been shown to provide a wealth of information on ligand identity (including ionization potential, protonation state, and hybridization) and metal-ligand bond lengths for structurally well- characterized molecular complexes of iron,11,13–25 manganese,26–31 titanium,32 chromium33 and vanadium.34 Compared to traditional X- ray absorption spectroscopy (XAS), which probes unoccupied molecular orbitals (MOs), XES reveals information about occupied MOs and thus nicely complements XAS for providing electronic structure descriptions.11,12,22,26 While some of the early interpretations of Kβ V2C XES were largely empirical, more recently a good agreement between experimental and density functional theory (DFT) calculated V2C spectra has been achieved.11,26,35 This has facilitated in-depth and quantitative investigations of the composition of valence molecular orbitals, and their contributions to experimental spectra.
To better evaluate the benefits and limitations of this technique, researchers have attempted to correlate the intensity and peak areas of V2C features with molecular attributes of coordination complexes. Previous studies have demonstrated that Fe and Mn V2C XES features are dominated by electric dipole transitions, which follow the dipole selection rule.1–3 That is, mixing a higher percentage of metal p character into the donor MOs consisting primarily of ligand orbital character provides the mechanism for intensity. It was previously shown that high-oxidation state and low- spin complexes tend to produce bigger V2C areas compared to their low-oxidation state or high-spin counterparts, respectively.1 This has been attributed to the difference in metal-ligand average distance, a well-established factor to modulate V2C intensities, as shorter metal- ligand distances allow more effective overlap between ligand orbitals and metal p orbitals. In addition to the metal-ligand distance, the Fe–O–Fe bond angles of iron dimers were recently found to be an important factor that is correlated with V2C spectral intensity.22 In another study, the intensity of certain V2C features allows the counting of the number of CO ligands in model complexes of [FeFe]-hydrogenase.16 As V2C XES is still a relatively new technique, a complete understanding of all factors that dictate the spectral properties, including energy, shape, intensity, and peak areas, has not been achieved. This is therefore an area that has attracted considerable attention for the on-going development and application of Kβ V2C XES to probe molecular transition metal complexes.
These recent exciting results in experimental Kβ V2C XES for early first-row transition metal elements, ranging from Ti to Fe, prompted us to leverage V2C XES for late first-row transition metal elements. While cobalt X-ray emission spectra emphasizing the Kβ mainline features have been reported previously,9,36–39 the use of cobalt Kβ V2C XES to experimentally probe valence orbitals has not been deeply explored to the best of our knowledge. While elements like Cr and Mn are well suited for XES investigations with easily measurable Kβ satellite peaks as previously noted, there is a progressive decrease in the intensity of Kβ X-ray emission spectra with increasing Z values away from these elements across the first- row transition metal series, making the cobalt Kβ measurement intrinsically more challenging.9 On the other hand, cobalt is a critical element used in enzymes and in man-made catalysts. A thorough understanding of cobalt Kβ V2C XES characteristics will be of benefit for understanding structural factors contributing to the reactivities of these cobalt sites. In biology, cobalt is an essential trace element for life and is found in the cobalamin cofactor of vitamin B12 and other enzymes like nitrile hydratase.41 In catalysis, molecular cobalt catalysts have been successfully used for CO2 activation42 and H2 evolution43 by harnessing solar energy. Notably, cobalt(III) complexes of dimethylglyoxime ligands with different axial ligands, known as cobaloximes, were shown to function as a pre-catalyst for low over-potential hydrogen evolution.43 Cobaloximes were also developed as bioinorganic model compounds for vitamin B12.44 Finally, recent two-color Fe and Ni V2C XES studies of [NiFe]-hydrogenase suggested that signature features indicative of the presence of metal-hydrides are present in the iron Kβ V2C X-ray emission spectra but not in the Ni Kβ data.25 This suggests that conclusions drawn for a given metal element’s Kβ V2C X-ray emission spectra may or may not be readily applied to other metal elements. Therefore, we reason that it is necessary to carry out systematic cobalt Kβ XES studies to evaluate the benefits and limitations of this technique applied to this particular element.
In the current work, we carried out combined experimental and computational studies of a structurally diverse set of low-spin Co(III) complexes with octahedral coordination geometry. To the best of our knowledge, this is the first systematic study of cobalt Kβ V2C XES. The valence-to-core features were shown to be sensitive to cobalt-ligand coordination environments. Notably, we demonstrate through both experimental and theoretical approaches that V2C peak area is correlated with the spectrochemical series for low-spin cobalt(III) complexes, with strong field π-acceptor ligands producing the largest V2C area. This previously unrecognized correlation is explained by invoking the π-interaction between cobalt p orbitals and ligand orbitals, in combination with changes in the average cobalt-ligand distance.
2. Experimental Section
2.1 Sample Preparation and Characterization
All reagents, including [Co(NH3)6]Cl3 (1) and [Co(acac)3] (5), were purchased from commercial sources such as Sigma-Aldrich and used without further purification unless otherwise noted. Elemental analyses were performed at Atlantic Microlab, Inc. Abbreviations used: acac = acetylacetonate; dmgH = dimethylgloxime monoanion; dmgH2 = neutral dimethylgloxime; en = ethane-1,2-diamine. [CoIII(NH3)5Cl]Cl2 (2),45,46 [CoIII(NH3)4CO3]NO3 (3),45,47 [CoIII(en)3]Cl3 (4),45[CoIII(dmgH2)(dmgH)Cl2] (6),48 [CoIII(dmgH)2(py)Cl] (7),49[ CoIII(dmgH)2(iPr)(py)] (9),45 and [CoIII(dmgH)2(cis-1,2-dichlorovinyl)(py)] (10)50 were prepared following previously published procedures.
Synthesis of [CoIII(dmgH)2(py)2]NO3 (8). Cobalt nitrate hexahydrate (1.18 g, 4.05 mmol) and dimethylgloxime (0.99 g, 8.53 mmol) were placed in a large test tube with a stir bar, and then dissolved with a minimum volume of boiling absolute ethanol. Pyridine (0.80 mL, 9.93 mmol) dissolved in a minimum volume of absolute ethanol was added to the reaction mixture with vigorous stirring. Heating and stirring was continued for 30 minutes. After the heat was turned off, the solution was allowed to cool while a stream of air was bubbled into the solution for one hour. The air stream was then removed and the solution was allowed to sit at room temperature for an additional hour while the precipitate formed. The complex was collected using vacuum filtration and washed with absolute ethanol and diethyl ether. Yield: 0.78 g (38%). Anal calc. for [CoIII(dmgH)2(py)2]NO3 (CoC18H24N7O7): C: 42.44, H: 4.75, N: 19.25; found: C: 42.37, H: 4.78, N: 19.15. 1H NMR (300 MHz, d3-MeCN): δ ppm 2.24 (12H, s, CH3), 7.40 (4H, m, py), 7.88 (2H, m, py), 8.26 (4H, m, py).
2.2 X-ray Emission Data Collection and Analyses
Cobalt complexes as powders were mixed with boron nitride in a 1:4 ratio (wt:wt), ground to a fine powder, packed into 6×3×1.6 mm3 aluminum sample holders, and sealed with 0.0025 inch-thick Kapton tape. X-ray emission spectra were collected at the C1 station of the Cornell High Energy Synchrotron Source (5.3 GeV, 90-110 mA). The beamline was equipped with a multilayer monochromator (~90 eV bandpass), with the energy fixed at 9 keV for the measurements. Samples were mounted at 45° to the beam and measured at room temperature. Beam size on the sample was approximately 1mm x 4mm. Energy selection of emitted X-rays was achieved using five spherically-bent Si(533) analyzer crystals arranged in a Rowland circle. A PILATUS 100K pixel array detector was used to collect energy-selected photons. Data were measured in terms of the angular position of the analyzer and detector. A helium bag placed between the sample, analyzer crystals, and detector minimized attenuation of emitted photons. Energy calibration was provided by measurement of Co foil Kβ (7649.4 eV) and Dy foil Lβ2 (7635.7 eV) spectra, and spectra were normalized to the beam intensity measured with an ion chamber upstream of the sample. Individual scans for samples were overlaid and carefully examined for evidence of radiation damage during measurement, as judged by the Kβ main-line and V2C spectral features and energies. Only scans that show no signs of radiation damage are averaged using pyMCA,51 and the averaged scan was used for subsequent analysis. Typically, 8-12 scans were collected and averaged for each sample.
All subsequent data analysis was conducted with Fityk.52 Averaged scans for a given sample were converted to an energy scale using Bragg’s law and calibration factors derived from the Co and Dy reference spectra. Energy calibrated emission data were normalized to a total spectral intensity of 1000 units over the entire spectral range collected (7615.7 to 7726.7 eV). Energies for the most intense Kβ mainline feature were determined using a simple model consisting of two pseudo-Voigt functions where the fraction of Gaussian and Lorentzian character was allowed to float. The Kβ mainline energy was taken as the maximum of the more intense fit peak.
In order to isolate the valence-to-core features for quantitative peak-fitting analysis, the absorption tail from the Kβ mainline peak was removed following methods described previously, 2,33,53 in which the mainline absorption tail is fit with pseudo-Voigt functions over data points of the Kβ1,3 tail at energies lower and higher than the V2C features (7650.0–7680.0 eV and 7723.0–7726.7 eV), and then subtracted from normalized data to isolate the valence-to-core features for quantitative peak-fitting analysis. Briefly, the tail was fit to 4–5 pseudo-Voigt functions (fixed at 50:50 Gaussian:Lorentzian character), which were then subtracted from the normalized spectra. A good tail-removal fit was defined as one with a near-zero random residual in the 7650-7680 eV range with no rising or falling residual at the high end of this range. These baseline-subtracted spectra were then subjected to peak-fitting analysis over an energy range of 7680– 7725 eV. For energy-calibrated, baseline corrected, and normalized experimental spectra, the Kβ2,5 peaks were accurately modeled with two to four pseudo-Voigt functions with a fixed 50:50 mixture of Gaussian and Lorentzian character. Where appropriate, additional pseudo-Voigt functions (constrained to 50:50 Gaussian:Lorentzian) were added to model the Kβ″ peak and/or a small peak located at energies higher than the Kβ2,5 feature. Integrated peak areas, energies, and their errors are those reported by the Fityk program. The best fit to experimental V2C XES spectra was chosen by considering both the Weighted Sum of Squared Residuals (WSSR) and the errors in peak position and area. WSSR is defined as (σ is the standard deviation).
2.3 DFT Calculations
Unless otherwise specified, density functional theory (DFT) geometry optimizations of cobalt complexes investigated in this study were performed using the Gaussian 09 Revision D.01 software package54 as implemented on the Extreme Science and Engineering Discovery Environment (XSEDE).55 Optimized structures were obtained using the hybrid functional B3LYP56–59 and the 6-31g(d)60,61 basis set. Single-point DFT calculations to compute X-ray emission spectra based on geometry- optimized structure coordinates (tabulated in the SI) were performed using the BP86 functional and def2-TZVP basis set with the ORCA quantum chemical suite (v3.0.3).62 For complexes 1 and 5 where crystal structures are available, single-point DFT calculations to compute X-ray emission were also carried out. Quantitative analysis and deconvolution of calculated X-ray emission spectra using fragment analysis were aided by MOanalyzer (v1.2).63 To align with experimental data, calculated V2C X-ray emission spectra were calibrated by applying a scalar shift of +197.0 eV, and plotted with a 2.0 eV width (hwhm), i.e., every stick of the calculated V2C spectra is broadened with the specific width of 2.0 eV using a Pseudo-Voigt function that has a Gaussian weight of 0.5. Unless otherwise specified, molecular orbitals were visualized with contour levels of 0.050 using Chimera v1.10.1.64 The octahedral crystal field splitting parameter (Δoct) is determined from the DFT-calculated energy level difference between the average energy of eg-derived d orbitals and that of the t2g-derived d orbitals.
3. Results
3.1 General methodology remarks: experiment and theory
While much progress has been made in recent years, Kβ XES is still a developing tool for the inorganic community to probe metal-ligand interactions. In this vein, cobalt Kβ V2C XES has not been systematically studied.37,38 To develop the methodology for cobalt, we measured the Co Kβ X-ray emission spectra of a series of structurally well-characterized low-spin octahedral cobalt(III) complexes (Scheme 1) with a systematically varied donor set (6N, 2N/4O, 6O, 5N/1C, 5N/1Cl, 4N/2Cl). Ligand donors in our study include monodentate and polydentate amines (e.g., NH3, en), oxygen donors (acac and carbonate), halides, and a large family of N4 dmgH-based complexes that can bind a wide range of exogenous ligands in the trans-axial positions.
Scheme 1.
Cobalt complexes used in this study.
After carefully checking and overlaying scans for each sample,we concluded that we did not detect evidence for radiation damage for any of the 10 complexes described here during data collection, as both mainline and V2C features are superimposable for consecutive scans.65 The absence of radiation damage for these Co(III) complexes in the solid state is not surprising, as photo-reduction is generally caused by the production of hydrated electrons in solution from the solvent, e.g., water, that can react with the metal center. Recent XAS work has shown that freeze-dried biological materials exhibit greatly reduced sensitivity to X-ray induced photochemistry.66
To determine the peak area of the experimental V2C spectra, we employed a constrained fit model that consists of a limited number of pseudo-Voigt functions to accurately fit the V2C features (Table S1 and Figure S1). The areas of individual Pseudo-Voigt functions for each complex were summed up to produce the total area for the V2C region of the X-ray emission spectra. Table 1 summarizes the results of our analysis, with more detailed fitting summaries provided in the Supporting Information (Table S1).
Table 1.
Kβ1,3 energies, Kβ2,5 energies, background-subtracted V2C area of cobalt complexes studied in this work.
| Compounds | Exp. Energy of Kβ1,3 (eV)a |
Exp. Energy of Kβ2,5
(eV)b |
Exp. Area of V2Cc |
DFT-calculated Oscillator Strength (a.u.)d |
|---|---|---|---|---|
| [CoIII(NH3)6]Cl3 (1) | 7649.6 | 7705.7(1) | 12.5(4) | 7.12×10−3 |
| [CoIII(NH3)5Cl]Cl2 (2) | 7649.6 | 7706.1(1) | 12.0(5) | 6.00×10−3 |
| [CoIII(NH3)4(CO3)]NO3 (3) | 7649.6 | 7706.0(1) | 12.3(5) | 6.68×10−3 |
| [CoIII(en)3]Cl3 (4) | 7649.6 | 7706.4(1) | 12.5(10) | 7.14×10−3 |
| [CoIII(acac)3] (5) | 7649.8 | 7707.2(1)/7701.1(1) | 11.2(5) | 6.69×10−3 |
| [CoIII(dmgH)(dmgH2)(Cl)2] (6) | 7649.5 | 7706.5(1)/7701.6(1) | 13.4(10) | 6.81×10−3 |
| [CoIII(dmgH)2(Cl)(py)] (7) | 7649.4 | 7706.3(1)/7701.1(1) | 14.6(4) | 7.54×10−3 |
| [CoIII(dmgH)2(py)2](NO3) (8) | 7649.3 | 7706.5(1)/7701.4(1) | 14.0(9) | 7.29×10−3 |
| [CoIII(dmgH)2(iPr)(py)] (9) | 7649.3 | 7706.2(1)/7700.6(2) | 14.2(11) | 7.22×10−3 |
| [CoIII(dmgH)2(cis-1,2-diClvinyl)(py)] (10) | 7649.3 | 7706.6(1)/7701.2(1) | 13.8(9) | 7.40×10−3 |
Estimated error in the K±1,3 energy is ±0.1 eV;
The reported values for the Kβ2,5 energies and V2C areas are from the best curve-fitting results (see Table S1 for details). Standard deviations are provided in parentheses.
Energy calibrated emission data were normalized to a total spectral intensity of 1000.
The calculated oscillator strength in the V2C region encompass the electric dipole, magnetic dipole, and electric quadrupole contributions (see Figure S3 for a correlation plot of calculated oscillator strength with experimental V2C area).
To facilitate interpretation of our experimental Kβ V2C XES results, single-point DFT calculations using ORCA62 were performed on geometry-optimized and published crystal structures of cobalt complexes used in this study. A simple one-electron model was used to calculate X-ray emission spectra, with each donor MO providing a single transition comprising contributions from electric dipole, magnetic dipole, and electric quadrupole effects.11 The electric dipole accounts for 98 – 99% of total intensity for calculated V2C X-ray emission oscillator strength for this class of cobalt complexes, consistent with previous results for Fe11,14 and Mn.28
For all complexes, satisfactory agreement was achieved for the Kβ2,5 features between DFT-calculated spectra and experimental spectra, after an energy calibration and a set of width modulation parameters were applied to the calculated spectra (Figures 1B and 1C). The single-particle theoretical model, in correlation with experimental spectra, allows us to pinpoint V2C transitions to individual donor MOs, rather than multi-electron microstates. Therefore, both qualitative and quantitative insights into the transitions between molecular orbitals that produce spectral features can be gained, as presented in sections 3.2 and 3.3. Please note that for our discussion of the correlation of DFT-calculated V2C spectra with experimental spectra, we will focus more on the Kβ2,5 features, as the experimental Kβ’’ peaks are often obscured by the mainline Kβ1,3 tail.
Figure 1.
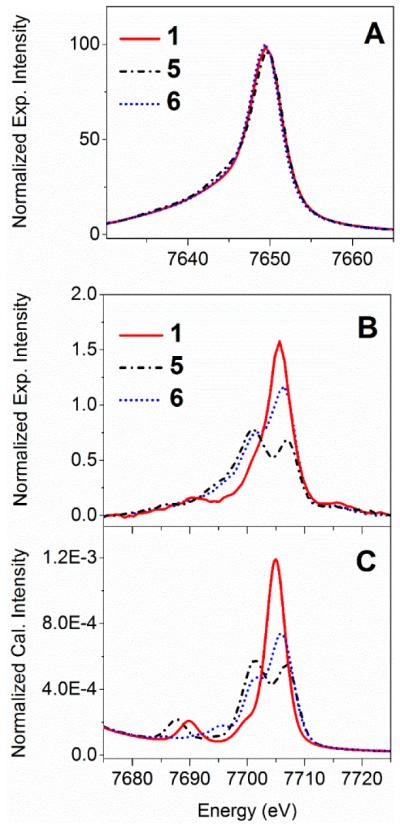
Energy-calibrated normalized background- subtracted experimental cobalt Kβ X-ray emission spectra of cobalt complexes [CoIII (NH3)6]Cl3 (1), [CoIII(acac)3] (5), and [CoIII(dmgH)(dmgH2)(Cl)2] (6), including the mainline region (Panel A), and the V2C region (Panel B). DFT-calculated cobalt Kβ V2C X-ray emission spectra of 1, 5, and 6 are shown in Panel C (plotting parameters: a scalar shift of 197.0 eV for energy calibration, a broadening of 2.0 eV for half-width-at-half-maximum, and Pseudo-Voigt functions with 50:50 Gaussian:Lorentzian). X-ray emission spectra were computed based on coordinates of crystal structures for complexes 1 and 5, and a DFT geometry-optimized structure for 6.
For computational methods utilized in this study, the energy calibration scalar shift was determined to be 197.0 ± 0.5 eV, and was used to align the calculated spectra with the experimental spectra. This is consistent with previous observations that DFT calculations using the BP86/def2-TZVP method underestimated the V2C X-ray emission energy, e.g., a scalar shift of 59.2 ± 0.6 eV for Mn28 and 182.5 ± 0.8 eV for Fe11 Kβ spectra. In addition to the scalar correction, a linear energy correction scheme following a published procedure33 was also attempted (Figure S2). Both energy calibration methods successfully correct for the systematic error introduced in DFT-calculated spectra, as judged by the average magnitude of the difference between energy-shifted calculated energies and experimental energies, |ΔE| (0.68 ± 0.55 eV for scalar correction, and 0.51 ± 0.48 eV for linear correction). The correlation plot of the calculated oscillator strength in the V2C region and experimental V2C area is shown in Figure S3. Similar correlation plots of experimental and theoretical V2C area were previously established for Fe11,14 and Mn28 Kβ spectra.
3.2 Low-spin octahedral cobalt(III) X-ray emission spectra
To compare the effects of different cobalt coordination environment on X-ray emission spectra, representative cobalt Kβ X-ray emission spectra of [CoIII(NH3)6]Cl3 (1), [CoIII(acac)3] (5), and [CoIII(dmgH)2(Cl)(py)] (6) with distinct ligand donor sets are shown in Figure 1. Their Kβ main-line features are characterized by a prominent Kβ1,3 peak at around 7649 eV, while a distinct Kβ’ peak is not present in spectra of any of the complexes. The absence of a sizable Kβ mainline splitting is consistent with previous predictions for a low-spin d6 system12 and experimental spectra.9 The Kβ mainline peak energies, spectral shape, and intensities for the family of low-spin cobalt(III) complexes studied here do not exhibit sizable sensitivity towards changes in the ligand donor sets (Figure 1A).
In contrast to the mainline peaks, the V2C regions of the Co Kβ X-ray emission spectra of complexes 1, 5, and 6 were very sensitive to changes in the cobalt-ligand coordination environment (Figure 1B). Notably, complex 1 with only pure σ-donor ligands exhibits a single Kβ2,5 peak at 7705.7 eV, while π-donor or acceptor-containing complexes 5 and 6 show split Kβ2,5 peaks, analogous to observations made previously for Fe Kβ V2C XES.14 The split Kβ2,5 peaks of 6 have one prominent peak at 7706.3 eV and a shoulder at 7701.1 eV, while two major peaks centered at 7707.2 and 7701.0 eV are observed for complex 5. The DFT calculations correctly replicate the Kβ2,5 spectral shapes for all these complexes (Figure 1C).
For experimental V2C features of cobalt complexes 1, we use two pseudo-Voigt functions to fit the Kβ2,5 V2C feature: one function models the majority of the peak centered at 7705.7 eV, and a second function accounts for the shoulder feature at 7701.1 eV. In addition, the Kβ” peak in the experimental spectrum is modeled by a single pseudo-Voigt function with a center at 7691.3 eV (Table S1). DFT calculations suggest that MOs of t1u symmetry (collectively labeled as MOs a) give rise to the Kβ2,5 peak at 7705.7 eV, with NH3-ligand-based p orbitals contributing significantly to these molecular orbitals (~77% nitrogen p-orbital character according to a Löwdin population analysis), as shown in Figure S4 and Table S2. For MOs a, a sizable cobalt p-orbital character of 9% is mixed into this donor MO, providing a mechanism for the intensity of the 7705.7 eV transition. In addition, DFT calculations predict that the Kβ2,5 shoulder at ~7701 eV is derived from donor MOs (labeled as MOs b) with ~62% nitrogen p-orbital and ~33% hydrogen s-orbital character. The Kβ” peak at 7691.3 eV is derived from MOs (labeled as MOs c) that have predominant contributions from ligand-based s orbitals (~47% nitrogen s-orbital and ~41% hydrogen s-orbital character). The relatively few MOs that contribute significantly to the predicted V2C XES allowed us to examine the theory-predicted transitions in correlation with the curve-fitting results of the experimental spectrum of complex 1. The calculated energies of Kβ” and Kβ2,5 peaks of complex 1 are in excellent alignment with component peaks in curve-fitted experimental spectra (Table S3).
For the double-humped Kβ2,5 features exhibited by the [Co(acac)]3+ (complex 5), two prominent pseudo-Voigt functions centered at 7707.2 and 7701.1 eV are required to fit the experimental spectrum; a third function is incorporated with a center at 7695.1 eV to account for the low-energy Kβ2,5 shoulder (Table S1). The Kβ” peak of 5 is modeled by a single peak centered at 7685.9 eV. The large energy shift of the Kβ” peak of 5 relative to that of complex 1 is reminiscent of that calculated for [Fe(III)X4]− where X = NH −, OH−, F−,11,17 and is ascribed to the difference in the ionization energies of oxygen vs. nitrogen 2s orbitals. DFT calculations indicate that the Kβ2,5 peaks of complex 5 centered at both 7707.2 eV and 7701.1 eV have contributions from multiple MOs, with these MOs having predominantly acac ligands’ p-orbital character (Figure S5, Table S4).
Labeled as d and e, two MOs contribute significantly to the intensity of the Kβ2,5 feature centered at 7707 eV of complex 5. A Löwdin population analysis reveals that these two MOs d and e consist primarily of acac-derived oxygen p orbitals (oxygen p-character in MO d and e is 63.2% and 57.5%, respectively). For MOs labeled as f, g, and h that play a sizable role in the observed intensity at 7701 eV, acac-derived carbon p-orbital character is significant (the carbon p-orbital character in MO f, g, and h is 50.3%, 53.1%, and 32.2%, respectively). The DFT-calculated spectrum suggests that the Kβ” region is derived from MOs with acac-ligand s-orbital character.
Generally we observe reasonable agreement between DFT- computed and experimental spectra, but there are some notable differences. First of all, the relative intensities of the Kβ” features for complexes 1 and 5 in the experimental spectra were considerably weaker than in calculated spectra. This discrepancy is attributed to the weak Kβ’’features being obscured by the mainline Kβ1,3 tail, and has been noted in V2C spectra of other elements.11,22,28 In addition, multi-electron features2 centered at ~7716 eV appear above the Kβ2,5 region of the experimental V2C spectra for complexes 1 to 6. These multi-electron features are not seen in the DFT-calculated V2C spectra, as the current level of theory represents a simple one- electron approximation.11
3.3 Cobaloximes
For V2C X-ray emission spectra of cobaloximes (complexes 6–10), two pseudo-Voigt functions are needed to fit the low and high energy features of the experimental Kβ2,5 peak centered at ~7701 eV and ~7707 eV, respectively; a third pseudo-Voigt function centered at ~7696 eV is used to model the Kβ2,5 shoulder on the low-energy side (Table S1). Kβ” features are not well-resolved in experimental spectra of complexes 6–10.
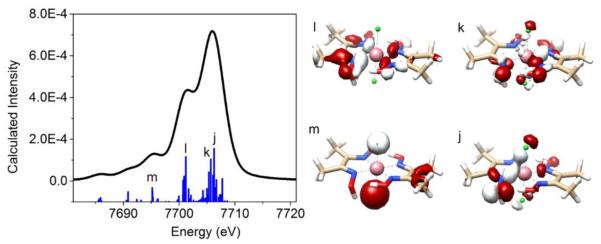
We will use complex [CoIII(dmgH)(dmgH2)Cl2] (6) as a representative example to discuss key MOs that contribute to the V2C X-ray emission spectra of cobaloximes. Two MOs, labeled as j and k, contribute considerably to the prominent Kβ2,5 feature centered at 7706.5 eV (Figure 2, Table S5). Based on a Löwdin population analysis, these two MOs have significant dimethylglyoxime-derived oxygen p-orbital character (46.7% for MO j, and 35.2% for MO k), while the sum of dimethylglyoxime- derived nitrogen p-orbital and axially coordinating chloride p-orbital character is also substantial (33.0% for MO j and 31.4% for MO k). For the Kβ2,5 shoulder centered at 7701.6 eV, the MO labeled as l immediately stands out as an important contributor. This MO has 95.2% dimethylglyoxime ligand character, including 34.8% N p, 19.8% O p, and 26.5% C p-orbital character. See Table S5 for detailed results of the Löwdin population analysis for MOs j – m.
Figure 2.
Calculated cobalt Kβ V2C X-ray Emission spectra of [CoIII(dmgH)(dmgH2)Cl2] (6) and molecular orbitals (labeled as MOs j to m) that contribute significantly to the calculated V2C X-ray emission spectrum (only transitions in the V2C region are plotted).
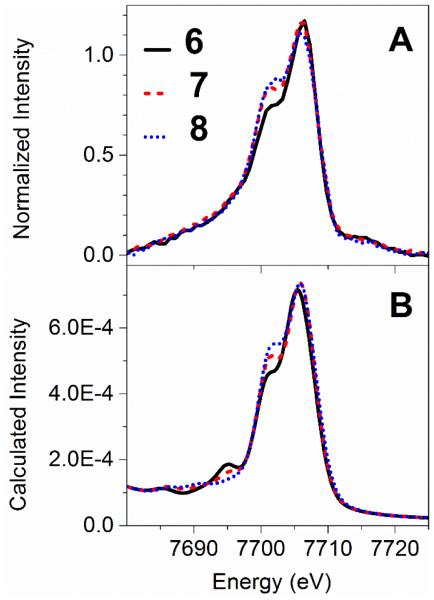
Next, we move on to compare V2C X-ray emission spectra of [CoIII(dmgH)(dmgH2)(Cl)2] (6), [CoIII(dmgH)2(Cl)(py)] (7), and [CoIII(dmgH)2(py)2](NO3) (8). Systematically varying the trans-axial ligands from two chloride ligands, to one chloride and one pyridine ligands, and finally to two pyridine ligands, results in a trend of increased intensity of the Kβ2,5 shoulder feature at 7701 eV relative to the 7706 eV peak in the experimental spectra (Figure 3A). DFT calculated spectra nicely replicate the experimental trend of increased intensity for the 7701 eV peak when going from the dichloro-, chloropyridine-, to dipyridine- bound cobaloxime complexes (Figure 3B).
Figure 3.
Comparison between experimental (panel A) and DFT-calculated (panel B) cobalt Kβ V2C X-ray emission spectra of [CoIII(dmgH)(dmgH2)(Cl)2] (6), [CoIII (dmgH)2(Cl) (py)] (7), and [CoIII (dmgH)2(py)2](NO3) (8).
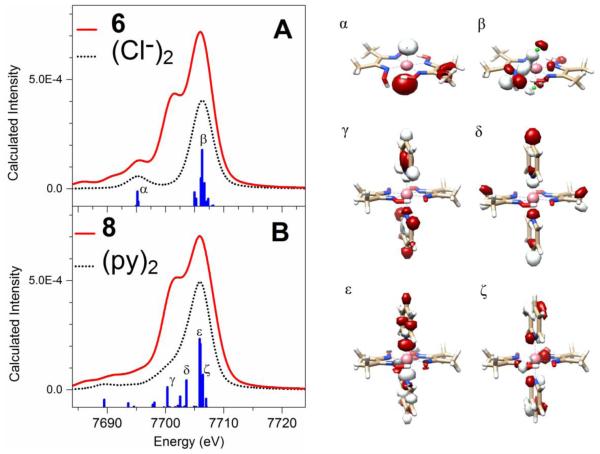
To provide more qualitative insights into the spectral changes that arise from substituting the trans-axial ligand, the cobaloxime theoretical spectra were investigated using fragment deconvolution analysis aided by MOAnalyzer.63 MOs with >20% Löwdin populations of atomic orbitals from the two chloride moieties in 6 or two pyridine ligands in 8 were grouped and examined, and XES transitions from these MOs are shown in Figure 4. See Tables S6–7 for detailed results of the Löwdin population analysis for MOs α – ζ. For complex 6, several MOs (labeled as MOs α and β) immediately stand out in the fragment deconvolution analysis. However, neither of MOs α or β contributes to the 7701 eV spectral feature. For complex 8, several orbitals with significant contributions from the pyridine ligands were singled out during our fragment deconvolution analysis, and are labeled as γ, δ, ε, and ζ, respectively. In particular, the two donor MOs γ and δ contribute to the intensity of the shoulder-like features at around 7701 eV, and are centered at 7700.3 eV and 7703.6 eV, respectively. Examination of the Löwdin population analysis and contour plot reveal that the MOs γ and δ have significant contributions from pyridine σ-bonding orbitals. This comparison of complexes 6 and 8 therefore reveals the molecular orbital origin for the spectral sensitivity of the py- vs. chloride- ligated cobaloximes.
Figure 4.
Deconvolution of calculated X-ray emission spectra (solid red line) of the complexes [CoIII(dmgH)(dmgH2)(Cl)2] (6) (Panel A) and [CoIII(dmgH)2(py)2](NO3) (8) (Panel B) showing contributions from MOs with significant character from the two chloride or two pyridine moieties (black dotted line), respectively; a threshold of >20% Löwdin population was applied to the fragment analysis.
3.4 Factors that contribute to V2C X-ray emission areas
The large set of low-spin octahedral cobalt(III) complexes investigated in this study allows us to evaluate factors that contribute to V2C X-ray emission spectra. Our experimental V2C data show that low-spin octahedral cobalt(III) complexes with stronger field ligands generally possess larger peak areas in the V2C region than those with weaker field ligands. For example, cobaloximes with the π-accepting dmgH ligands generally exhibit 10 – 25% bigger V2C areas compared to those of cobalt(III) complexes with amine and acac donors. Our results are reminiscent of a previous study reporting that the V2C area of [Fe(CN)6]3− with strong π-acceptor CN− ligands is ~5 units (i.e., ~30%) bigger than that of [Fe(tacn)2]3+ with pure σ-donor tacn ligands, while both complexes have a low-spin octahedral iron(III) center.11
This observation prompted us to examine whether the V2C X- ray emission areas correlate with the spectrochemical series. We therefore computed V2C X-ray emission spectra for over ten low- spin octahedral cobalt(III) complexes across the spectrochemical series, ranging from complexes with very strong field ligands like [Co(CN)6]3− to (hypothetical) complexes with very weak field ligands like [CoCl6]3−. As shown in Figure 5, the calculated V2C oscillator strength is linearly correlated with Δoct, with stronger field ligands in the spectrochemical series yielding bigger V2C areas. This trend is recognized for the first time here to the best of our knowledge.
Figure 5.
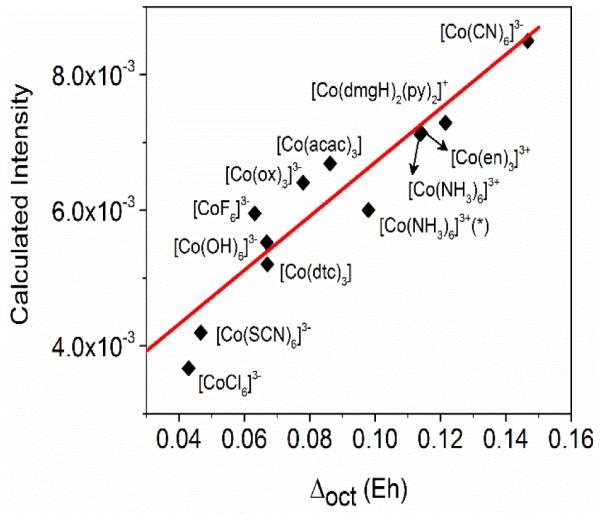
The correlation plot of calculated V2C XES oscillator strength vs. Δoct for low-spin octahedral cobalt(III) complexes. The octahedral crystal field splitting parameter (Δoct) is determined as the DFT-calculated energy level difference between the average energy of eg-derived d orbitals and that of the t2g-derived d orbitals. *[Co(NH3)6]3+ with Δoct = 0.114 is calculated from coordinates of a crystal structure, and [Co(NH3)6]3+ with Δoct = 0.0980 is based on coordinates of a DFT geometry-optimized structure (see SI for details of coordinates). Hypothetical low-spin cobalt(III) complexes with very weak field ligands, such as [CoF6]3−, are included in this correlation plot.
Why are the V2C areas correlated with the spectrochemical series, that is, the π-donor/acceptor/σ-donor properties of the ligands? Low-spin and high oxidation state metal complexes are known to give more intense V2C features,1 which was justified by invoking the presence of shorter metal-ligand bonds in these complexes.11,67 To examine whether the average metal- ligand bond distance is an important contributing factor here, we plotted the calculated V2C oscillator strength with the average metal-ligand bond length as shown in Figure 6. Low- spin octahedral cobalt(III) complexes with very weak field ligands that have heavy atom donors, such as [Co(dtc)3] (dtc = diethyldithiocarbamate), and hypothetical [CoCl6]3− complexes, have an average cobalt-ligand distance, r(Co-L), at around 2.3 – 2.4 Å. This is significantly longer compared to the rest of the complexes supported by stronger field ligands having lighter C/N/O/F donors, with r(Co-L) of 1.93±0.05 Å (e.g., 1.93 Å for [Co(CN)6]3− and 1.96 Å for [Co(NH3)6]3+, and 1.88 Å for the hypothetical low-spin [CoF6]3− complex). Therefore, there must be factors other than the average metal-ligand bond length that contribute to the higher V2C area for low-spin octahedral cobalt(III) complexes with relatively strong field ligands.
Figure 6.
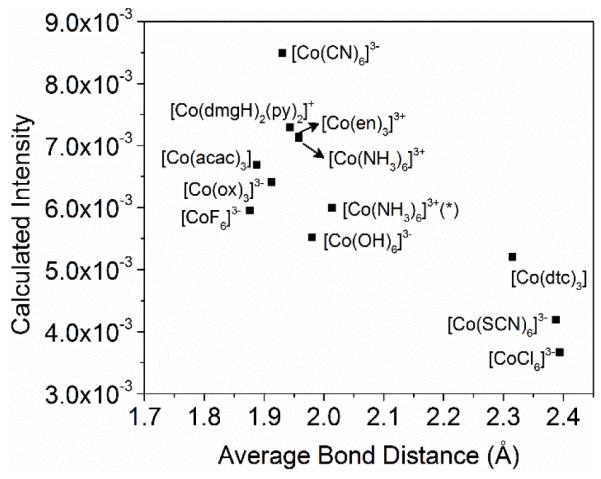
Calculated V2C XES oscillator strength vs. average Co-L bond distance for low-spin octahedral cobalt(III) complexes. * The two [Co(NH3)6]3+ complexes are based on coordinates of a crystal structure (average bond distance of 1.96 Å) and a DFT geometry-optimized structure (average bond distance 2.01 Å), respectively (see SI for details of coordinates).
In an effort to reveal additional factors, we tabulated the sum of cobalt p character (∑Co p%) in donor MOs in the V2C region for this series of low-spin octahedral cobalt(III) complexes with ligand strength across the spectrochemical series (Table 2). Notably, ∑Co p% decreases from 58.8% for [Co(CN)6]3− with strong π-acceptor ligands to 41.8% for [Co(NH3)6]3+ with purely σ-donating ligands. It was previously established that the V2C features gain intensity by mixing metal p character into the donor MOs,14 as the V2C features are derived primarily from electrical dipole contribution. It is the metal p character in these ligand-based MOs that provides a mechanism for electric dipole transition. Therefore, the higher metal p percentage for complexes with strong field π-acceptor ligands led to more intense V2C features.
Table 2.
Calculated Δoct, sum of cobalt p and d character in MOs contributing to the V2C region, and V2C XES oscillator strength for low-spin octahedral cobalt(III) complexes.
| Δoct (Eh) a | ΣCo p% b | ΣCo d% b | DFT-calculated Oscillator Strength (a.u.) c |
|
|---|---|---|---|---|
| [Co(CN)6]3− | 0.147 | 58.8 | 391.5 | 8.49×10−3 |
| [Co(dmgH)2(py)2]+ | 0.122 | 40.8 | 389.9 | 7.29×10−3 |
| [Co(en)3]3+ | 0.114 | 40.9 | 389.1 | 7.14×10−3 |
| [Co(NH3)6]3+ | 0.114 | 41.8 | 389.4 | 7.12×10−3 |
| [Co(NH3)6]3+ (*) | 0.0980 | 41.5 | 385.7 | 6.00×10−3 |
| [Co(acac)3] | 0.0862 | 35.7 | 385.9 | 6.69×10−3 |
| [Co(ox)3]3− | 0.0780 | 35.9 | 384.9 | 6.41×10−3 |
| [Co(OH)6]3− | 0.0669 | 35.1 | 383.6 | 5.52×10−3 |
| [CoF6]3− | 0.0632 | 36.1 | 378.6 | 5.95×10−3 |
| [Co(dtc)3] | 0.0680 | 50.3 | 398.9 | 5.20×10−3 |
| [Co(SCN)6]3− | 0.0467 | 48.6 | 396.7 | 4.19×10−3 |
| [CoCl6]3− | 0.0430 | 44.6 | 387.6 | 3.67×10−3 |
Δoct is determined as the energy level difference between the average energy of eg-derived d orbitals and that of t2g-derived d orbitals from DFT calculations.
ΣCo p% and ΣCo d% represent the sum of cobalt p and d character in donor MOs in the V2C region, respectively, based on the Löwdin population analysis.
The DFT-calculated oscillator strength in the V2C region encompass the electric dipole, magnetic dipole, and electric quadrupole contributions. * The two [Co(NH3)6]3+ are based on coordinates of crystal structure (Δoct = 0.114) and a DFT geometry-optimized structure (Δoct = 0.0980), respectively (see SI for details of coordinates).
The next question we try to shed light on is why the ∑Co p% in donor MOs in the V2C region is significantly higher for complexes with strong field π acceptor ligands. Towards this end, we examined the contour plots of key MOs (n, o, and p) as donor MOs that produce intense V2C features of [Co(CN)6]3− (Figure 7). Both ligand-based MOs n and p are well oriented to interact with the metal p orbital(s) via a σ interaction. This is consistent with previous results that suggest σ-interaction between metal p orbitals and ligand-based orbitals with t1u symmetry produce intense features in the V2C region. However, in addition to σ interaction, π-interaction between metal p orbitals and ligand-based orbitals are clearly invoked for MOs o and p. The ligand group orbitals constructed with CN− π2p-2p orbitals involved in the π-interaction indeed have the right symmetry to interact with metal p orbitals with t1u symmetry, as shown in the qualitative MO diagram of [M(CN)6] in Figure S8. As MOs o and p account for ~40% of total V2C intensity, the π- interaction is not negligible for intensity of V2C features of [Co(CN)6]3−.
Figure 7.
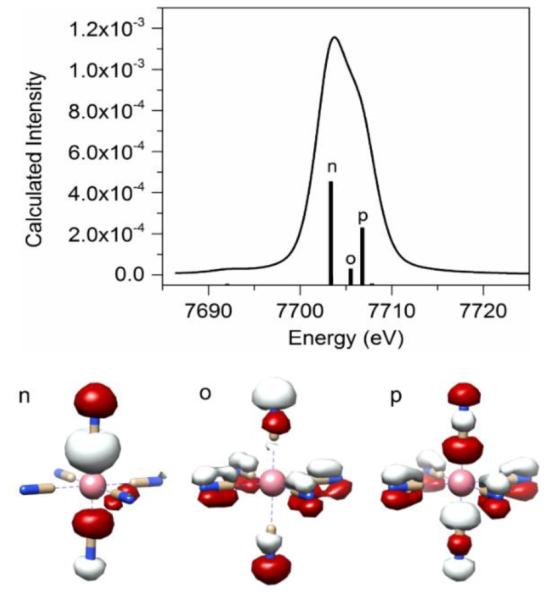
Calculated cobalt Kβ V2C X-ray Emission spectrum of [CoIII (CN)6]3− and key molecular orbitals (labeled as MOs o to p) that contribute significantly to the spectrum.
As a control experiment, we examined the key donor MOs that generate intense V2C features for complex 1 [Co(NH3)6]3+ (Figure S4), as NH3 is considered as a pure σ-donating ligand in ligand field theory. Among the donor MOs that contribute significantly to V2C features of complex 1, only MOs b invoke π-interaction between metal p orbitals and ligand-based atomic orbitals, while MOs a and c use σ-interactions; MOs b only contribute to ~7% of the V2C area for complex 1. For the low-spin [CoF6]3− complex as a second control experiment, the two donor MOs q and r that contribute to 92% of the V2C area only involve σ-interaction (Figure S9), suggesting that π-interaction is insignificant for this complex as well.68 Overall, these results suggest that there is a significant amount of π-interaction between cobalt p orbitals and ligand orbitals for low-spin octahedral cobalt(III) complexes with π- accepting ligands, leading to higher ∑Co p% in the V2C region and thus bigger V2C areas.
4. Discussion and Conclusions
4.1 General remarks
Valence-to-core (V2C) X-ray emission spectroscopy (XES) has attracted much recent interest within the inorganic community. Unlike iron, manganese and other lighter transition metal elements, the Kβ V2C XES of cobalt complexes has not been well explored. To this end, we have examined the application of cobalt Kβ V2C XES as a promising technique for probing cobalt-ligand interactions. In the current work, we develop a thorough understanding of cobalt Kβ V2C X-ray emission spectral features of a structurally diverse set of low-spin Co(III) complexes for the first time through combined experimental and computational studies. The experimental Co Kβ V2C features were found to be sensitive to valence orbital composition and cobalt-ligand environment, consistent with previous studies for iron,11,13–25 manganese,26–31 titanium,32 chromium33 and vanadium.34 The ORCA single particle model was used to compute the V2C features of the cobalt complexes in this study.
4.2 Kβ V2C XES of cobalt vs. other elements
Using Kβ V2C X-ray emission spectra of M(acac)3 complexes (M = Mn, Fe, or Co), we can gain some understanding into the benefits and limitations of the V2C XES applied to different elements. From Mn,28 Fe,11 to Co, the difference between the Kβ1,3 and Kβ2,5 energies increased significantly from 40.1 eV for Mn(acac)3, to 44.2 eV for Fe(acac)3, and then to 51.3 eV for Co(acac)3. Compared to Mn and Fe data, the greater energy separation between the Kβ1,3 and Kβ2,5 lines for Co facilitates the removal of the Kβ1,3 tail background. On the other hand, the area of the V2C region decreases sizably from 17.5 for Mn(acac)3, to 12.3 for Fe(acac)3, and finally to 11.2 for Co(acac)3 (Table 3). The reduced V2C area from Mn(acac)3 and Fe(acac)3 to Co(acac)3 does echo the trend previously observed in the normalized intensity of the X-ray emission Kβ’ mainline for trivalent Mn, Fe, and Co complexes.9 Also, it was previously demonstrated that the larger transition dipole moment for the Kβ2,5 region and the enhanced metal np character in the Kβ’’ region combine to give a larger V2C area for Mn compared to Fe.28 At last, we remind the readers that the most valuable comparisons are between compounds with the same spin state, which is not the case here for these three trivalent M(acac)3 complexes (M = Mn, Fe, or Co). Nevertheless, the comparison using M(acac)3 complexes provides useful insights for the application of this spectroscopic technique to cobalt in comparison with other 3d transition metals.
Table 3.
Comparison of X-ray emission data of M(acac)3 where M = Mn, Fe, or Co.
4.3 Sensitivity of V2C spectra to ligand environments
Complexes 6 – 8 have two trans-axial ligands that can be two chloride ligands, one chloride ligand and one pyridine ligand, or two pyridine ligands, respectively. For this series of complexes, we experimentally observed that the intensity of the 7701 eV shoulder relative to the 7706 eV peak is sensitive to the number of pyridine as the trans-axial ligands (i.e., 0, 1, or 2). Correlation with calculated V2C spectra and fragment analyses suggest that this sensitivity at 7701 eV is due to the pyridine σ bonding orbitals comprised of pyridine C and N p orbitals. The sensitivity of Co Kβ V2C XES to ligand environments (in this case the change of only one or two ligands) suggests that cobalt Kβ V2C XES could potentially be used to study spectra of mixtures of molecular transition metal complexes via methods like linear combination analysis of spectra of standard complexes,69,70 although current spectral resolution and signal-to-noise ratio might present challenges for the spectral analysis. Of course, complementary characterization techniques such as UV- visible and X-ray absorption spectroscopies should be utilized for future studies of mixtures in order to better gauge the sensitivity and limitation of V2C XES for this application.
4.4 Spectrochemical series
As Kβ V2C XES is an emerging technique for inorganic chemists, there has yet to be a complete understanding of all factors that modulate the energy, shape, intensity, and area of V2C features. We recognize here for the first time a linear correlation between V2C area and the spectrochemical series for low-spin octahedral cobalt(III) complexes, in which strong field π acceptor ligands give rise to the largest V2C areas. We suggest that the significant overlap between cobalt p orbitals and ligand-based orbitals via π-interaction, as seen in [Co(CN)6]3− with strong π acceptor ligands, increases cobalt p characters in donor MOs in the V2C region and thus provides the mechanism for increased V2C area. These π-interactions are absent or negligible for pure σ-donating ligands like NH3. Therefore, complexes with predominantly σ-donating ligands will have lower cobalt p characters in the donor MOs responsible for the V2C features. Furthermore, hypothetical low-spin octahedral cobalt(III) complexes with weak field π-donors, like Cl−, produce even smaller V2C areas than those with pure σ-donating ligands. This is attributed to significantly longer cobalt-ligand average bond lengths.
Pollock et al. showed previously that σ-donating ligands vs. π- donating/withdrawing ligands can be distinguished in Fe V2C XES by a single Kβ2,5 peak versus split Kβ2,5 features, respectively.14 Here, we further demonstrate using experimental and theoretical studies that the ability of ligands to participate in π-bonding with the metal center influences not only the spectral shape but also the V2C area of low-spin octahedral cobalt(III) complexes. Notably, while Pollock et al. showed that contributions from the metal-ligand π- interaction were negligible for the V2C intensities of iron complexes,14 we demonstrate in this study that the π-interaction for low-spin octahedral cobalt(III) plays a significant role in modulating the V2C area of complexes with π acceptor ligands relative to those with pure σ-donors.71
Overall, this study provides benchmark data to understand the benefits and utility of cobalt Kβ V2C XES. The results of this work will provide a firm basis for the use of Co Kβ V2C XES as a new spectroscopic tool to study the physical and electronic structures of a wide range of cobalt coordination centers in (bio)catalysts and for other applications. The observed correlation of Co V2C X-ray emission area with ligand spectrochemical series, coupled to the observed significance of π-interactions between ligand orbitals and metal p orbitals for this correlation, provides an impetus for future studies to better gauge the effects of different molecular attributes and other factors that modulate V2C X-ray emission spectral features.
Supplementary Material
Acknowledgements
This work reported here is supported by an institutional start-up grant to F. L. from New Mexico State University (NMSU), and a Mini-Grant to F. L. from the College of Arts and Sciences of NMSU. E.R.F. was supported by National Institutes of Health grant P30-EB-009998 (CWRU Center for Synchrotron Biosciences, PI: Mark R. Chance). K.V.H. acknowledges start-up funds from the Harvey Mudd College Chemistry Department. XES data was collected at the C1 station of Cornell High Energy Synchrotron Source (CHESS), which is supported by the National Science Foundation and the National Institutes of Health/National Institute of General Medical Sciences under NSF award DMR-1332208. We thank Dr. Ken Finkelstein for technical assistance at CHESS. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1053575.
Footnotes
Electronic Supplementary Information (ESI) available: Additional synthetic details, detailed table of V2C XES fits, Löwdin population analyses, and DFT-geometry optimized coordinates for all complexes. See DOI: 10.1039/x0xx00000x
Notes and references
- (1).Pollock CJ, DeBeer S. Acc. Chem. Res. 2015;48(11):2967–2975. doi: 10.1021/acs.accounts.5b00309. [DOI] [PubMed] [Google Scholar]
- (2).Gallo E, Glatzel P. Adv. Mater. 2014;26(46):7730–7746. doi: 10.1002/adma.201304994. [DOI] [PubMed] [Google Scholar]
- (3).Bauer M. Phys. Chem. Chem. Phys. 2014:13827–13837. doi: 10.1039/c4cp00904e. [DOI] [PubMed] [Google Scholar]
- (4).Alonso-Mori R, Kern J, Sokaras D, Weng T-C, Nordlund D, Tran R, Montanez P, Delor J, Yachandra VK, Yano J, Bergmann U. Rev. Sci. Instrum. 2012;83(7):073114. doi: 10.1063/1.4737630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Glatzel P, Sikora M, Smolentsev G, Fernàndez-Garcl̀a M. Catal. Today. 2009;145(3-4):294–299. [Google Scholar]
- (6).Finkelstein KD, Agyeman-Budu D, Lyndaker A, Pollock C, Krawczyk T. J. Phys. Conf. Ser. 2014;493:012033. [Google Scholar]
- (7).Gog T, Casa DM, Said AH, Upton MH, Kim J, Kuzmenko I, Huang X, Khachatryan R. J. Synchrotron Radiat. 2013;20:74–79. doi: 10.1107/S0909049512043154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Mattern BA, Seidler GT, Haave M, Pacold JI, Gordon RA, Planillo J, Quintana J, Rusthoven B. Rev. Sci. Instrum. 2012;83:023901. doi: 10.1063/1.3680598. [DOI] [PubMed] [Google Scholar]
- (9).Gamblin SD, Urch DS. J. Electron Spectros. Relat. Phenomena. 2001;113(2-3):179–192. [Google Scholar]
- (10).Glatzel P, Bergmann U. Coord. Chem. Rev. 2005;249(1-2):65–95. [Google Scholar]
- (11).Lee N, Petrenko T, Bergmann U, Neese F, Debeer S. J. Am. Chem. Soc. 2010;132(28):9715–9727. doi: 10.1021/ja101281e. [DOI] [PubMed] [Google Scholar]
- (12).Pollock C, Delgado-Jaime MU, Atanasov M, Neese F, Debeer S. J. Am. Chem. Soc. 2014;136(26):9453–9463. doi: 10.1021/ja504182n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Delgado-Jaime MU, Dible BR, Chiang KP, Brennessel WW, Bergmann U, Holland PL, DeBeer S. Inorg. Chem. 2011;50(21):10709–10717. doi: 10.1021/ic201173j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Pollock CJ, DeBeer S. J. Am. Chem. Soc. 2011;133(14):5594–5601. doi: 10.1021/ja200560z. [DOI] [PubMed] [Google Scholar]
- (15).Lancaster KM, Finkelstein KD, DeDeer S. Inorg. Chem. 2011;50(14):6767–6774. doi: 10.1021/ic200822b. [DOI] [PubMed] [Google Scholar]
- (16).Leidel N, Chernev P, Havelius KGV, Ezzaher S, Ott S, Haumann M. Inorg. Chem. 2012;51(8):4546–4559. doi: 10.1021/ic2024154. [DOI] [PubMed] [Google Scholar]
- (17).Lancaster KM, Roemelt M, Ettenhuber P, Hu Y, Ribbe MW, Neese F, Bergmann U, Debeer S. Science. 2012;334(6058):974–977. doi: 10.1126/science.1206445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Stieber SCE, Milsmann C, Hoyt JM, Turner ZR, Finkelstein KD, Wieghardt K, Debeer S, Chirik PJ. Inorg. Chem. 2012;51(6):3770–3785. doi: 10.1021/ic202750n. [DOI] [PubMed] [Google Scholar]
- (19).Delgado-Jaime MU, DeBeer S, Bauer M. Chem. A Eur. J. 2013;19(47):15888–15597. doi: 10.1002/chem.201301913. [DOI] [PubMed] [Google Scholar]
- (20).Pollock CJ, Grubel K, Holland PL, Debeer S. J. Am. Chem. Soc. 2013;135(32):11803–11808. doi: 10.1021/ja3116247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Chandrasekaran P, Chiang KP, Nordlund D, Bergmann U, Holland PL, Debeer S. Inorg. Chem. 2013;52(11):6286–6298. doi: 10.1021/ic3021723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (22).Pollock CJ, Lancaster KM, Finkelstein KD, DeBeer S. Inorg. Chem. 2014;53(19):10378–10385. doi: 10.1021/ic501462y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Te Lu, T., Weng TC, Liaw WF. Angew. Chem. Int. Ed. Engl. 2014;53(43):11562–11566. doi: 10.1002/anie.201407603. [DOI] [PubMed] [Google Scholar]
- (24).Kowalska JK, Hahn AW, Albers A, Schiewer CE, Bjornsson R, Lima F. a., Meyer F, DeBeer S. Inorg. Chem. 2016;55(9):4485–4497. doi: 10.1021/acs.inorgchem.6b00295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (25).Hugenbruch S, Shafaat HS, Krämer T, Delgado-Jaime MU, Weber K, Neese F, Lubitz W, DeBeer S. Phys. 2016;18(16):10688–10699. doi: 10.1039/c5cp07293j. [DOI] [PubMed] [Google Scholar]
- (26).Smolentsev G, Soldatov AV, Messinger J, Merz K, Weyhermu T, Bergmann U, Pushkar Y, Stanford POB, Biosciences P, Di V, Berkeley L. J. Am. Chem. Soc. 2009;131(9):13161–13167. doi: 10.1021/ja808526m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (27).Pushkar Y, Long X, Glatzel P, Brudvig GW, Dismukes GC, Collins TJ, Yachandra VK, Yano J, Bergmann U. Angew. Chem. Int. Ed. Engl. 2010;49(4):800–803. doi: 10.1002/anie.200905366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (28).Beckwith MA, Roemelt M, Collomb M-N, DuBoc C, Weng T-C, Bergmann U, Glatzel P, Neese F, DeBeer S. Inorg. Chem. 2011;50(17):8397–8409. doi: 10.1021/ic200970t. [DOI] [PubMed] [Google Scholar]
- (29).Taguchi T, Gupta R, Lassalle-kaiser B, Boyce DW, Yachandra VK, Tolman WB, Yano J, Hendrich MP, Borovik AS. J. Am. Chem. Soc. 2012;134(4):1996–1999. doi: 10.1021/ja210957u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (30).Lassalle-kaiser B, Boron TT, Krewald V, Kern J, Beckwith MA, Delgado-jaime MU, Schroeder H, Alonso-mori R, Nordlund D, Weng T, Sokaras D, Neese F, Bergmann U, Yachandra VK, Debeer S, Pecoraro VL, Yano J. Inorg. Chem. 2013;52(22):12915–12922. doi: 10.1021/ic400821g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (31).Rees JA, Martin-Diaconescu V, Kovacs JA, DeBeer S. Inorg. Chem. 2015;54(12):6410–6422. doi: 10.1021/acs.inorgchem.5b00699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (32).Swarbrick JC, Kvashnin Y, Schulte K, Seenivasan K, Lamberti C, Glatzel P. Inorg. Chem. 2010;49(18):8323–8332. doi: 10.1021/ic100755t. [DOI] [PubMed] [Google Scholar]
- (33).Macmillan SN, Walroth RC, Perry DM, Morsing TJ, Lancaster KM. Inorg. Chem. 2015;54(1):205–214. doi: 10.1021/ic502152r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (34).Rees JA, Bjornsson R, Schlesier J, Sippel D, Einsle O, DeBeer S. Angew. Chem. Int. Ed. 2015;54(45):13249–13252. doi: 10.1002/anie.201505930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Zhang Y, Mukamel S, Khalil M, Govind N. J. Chem. Theory Comput. 2015;11(12):5804–5809. doi: 10.1021/acs.jctc.5b00763. [DOI] [PubMed] [Google Scholar]
- (36).Vankó G, Neisius T, Molnár G, Renz F, Kárpáti S, Shukla A, De Groot FMF. J. Phys. Chem. B. 2006;110(24):11647–11653. doi: 10.1021/jp0615961. [DOI] [PubMed] [Google Scholar]
- (37).Wu L, Weng T, Hsu I, Liu Y, Lee G, Wang Y. Inorg. Chem. 2013;52(19):11023–11033. doi: 10.1021/ic401147b. [DOI] [PubMed] [Google Scholar]
- (38).Kuhn T-J, Hormes J. Inorg. Chem. 2014;53(16):8367–8375. doi: 10.1021/ic5000183. [DOI] [PubMed] [Google Scholar]
- (39).Corcos AR, Villanueva O, Walroth RC, Sharma SK, Bacsa J, Lancaster KM, MacBeth CE, Berry JF. J. Am. Chem. Soc. 2016;138(6):1796. doi: 10.1021/jacs.5b12643. [DOI] [PubMed] [Google Scholar]
- (40).Banerjee R, Ragsdale SW. Annu. Rev. Biochem. 2003;72(1):209–247. doi: 10.1146/annurev.biochem.72.121801.161828. [DOI] [PubMed] [Google Scholar]
- (41).Okamoto S, Eltis L. Metallomics. 2011;3(10):963–970. doi: 10.1039/c1mt00056j. [DOI] [PubMed] [Google Scholar]
- (42).Schneider J, Jia H, Muckerman JT, Fujita E. Chem. Soc. Rev. 2012;41(6):2036–2051. doi: 10.1039/c1cs15278e. [DOI] [PubMed] [Google Scholar]
- (43).Dempsey JL, Brunschwig BS, Winkler JR, Gray HB. Acc. Chem. Res. 2009;42(12):1995–2004. doi: 10.1021/ar900253e. [DOI] [PubMed] [Google Scholar]
- (44).Schrauzer G. Acc. Chem. Res. 1968;1(4):97–103. [Google Scholar]
- (45).Girolami G, Rauchfuss TB, Angelici RJ. Synthesis and Technique in Inorganic Chemistry: a laboratory manual. 3rd University Science Books; Sausa: 1999. [Google Scholar]
- (46).Schlesssinger GG. Inorg. Synth. 1967;9:160–163. [Google Scholar]
- (47).Schlesssinger GG, Simmons JW, Jabs G, Chamberlain MM. Inorg. Synth. 1960;6:173–175. [Google Scholar]
- (48).Wang K, Jordan RB. Can. J. Chem. 1996;665:658–665. [Google Scholar]
- (49).Trogler W, Stewart RC, Epps LA, Marzilli LG. Inorg. Chem. 1974;13(7):1564–1570. [Google Scholar]
- (50).Follett AD, McNeill K. Inorg. Chem. 2006;45(6):2727–2732. doi: 10.1021/ic052020d. [DOI] [PubMed] [Google Scholar]
- (51).Solé V. a., Papillon E, Cotte M, Walter P, Susini J. Spectrochim. Acta - Part B At. Spectrosc. 2007;62(1):63–68. [Google Scholar]
- (52).Wojdyr M. J. Appl. Crystallogr. 2010;43(5):1126–1128. [Google Scholar]
- (53).Pollock C. Development of Kβ X-ray Emission Spectroscopy as a Probe of Chemical and Biological Catalysis, PhD Dissertation. Max Planck Institute for Energy Conversion, 2011 [Google Scholar]
- (54).Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Scalmani G, Barone V, Mennucci B, Petersson GA, Nakatsuji H, Caricato M, Li X, Hratchian HP, Izmaylov AF, Bloino J, Zheng G, Sonnenberg JL, Had M, Fox DJ. Gaussian, Inc.; Wallingford CT: 2010. [Google Scholar]
- (55).Towns J, Cockerill T, Dahan M, Foster I, Gaither K, A. Grimshaw VH, Lathrop S, Lifka D, Peterson GD, Roskies R, Scott JR, Wilkins-Diehr N. Comput. Sci. Eng. 2014;16(5):62–74. [Google Scholar]
- (56).Becke AD. J. Chem. Phys. 1993;98(7):5648–5652. [Google Scholar]
- (57).Lee C, Yang W, Parr RG. Phys. Rev. B. 1988;37(2):785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- (58).Devlin FJ, Finley JW, Stephens PJ, Frisch MJ. J. Phys. Chem. 1995;99(46):16883–16902. [Google Scholar]
- (59).Becke AD. Phys. Rev. A. 1988;38(6):3098–3100. doi: 10.1103/physreva.38.3098. [DOI] [PubMed] [Google Scholar]
- (60).Petersson GA, Bennett A, Tensfeldt TG, Ai-laham MA, Shirley WA, Mantzaris J. J. Chem. Phys. 1988;89(4):2193–2218. [Google Scholar]
- (61).Petersson G. a. J. Chem. Phys. 1991;94(9):6081–6090. [Google Scholar]
- (62).Neese F. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012;2(1):73–78. doi: 10.1002/wcms.74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (63).Delgado-Jaime MU, Debeer S. J. Comput. Chem. 2012;33(27):2180–2185. doi: 10.1002/jcc.23028. [DOI] [PubMed] [Google Scholar]
- (64).Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, Meng EC, Ferrin TE. J Comput Chem. 2004;25(13):1605–1602. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- (65). We have collected parallel X-ray absorption spectroscopy data for these cobalt solid samples at room temperatures and we also did not observe any evidence for radiation damage (E. Farquhar, F. Li, unpublished observations)
- (66).George GN, Pickering IJ, Pushie MJ, Nienaber K, Hackett MJ, Ascone I, Hedman B, Hodgson KO, Aitken JB, Levina A, Glover C, Lay PA. J. Synchrotron Radiat. 2012;19:875–886. doi: 10.1107/S090904951203943X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (67).Bergmann U, Horne CR, Collins TJ, Workman JM, Cramer SP. Chem. Phys. Lett. 1999;302(1-2):119–124. [Google Scholar]
- (68). Compared to [CoCl6]3−, the low level of ΣCo p% in the hypothetical low-spin [CoF6]3− complex is correlated with a low level of π interaction in the MOs contributing to the V2C features of [CoF6]3− based on the contour plots of MOs, consistent with the notion that F− is not as good a π donating ligand as Cl−.
- (69).Safonov VA, Vykhodtseva LN, Polukarov YM, Safonova OV, Smolentsev G, Sikora M, Eeckhout SG, Glatzel P. J. Phys. Chem. B. 2006;110(46):23192–23196. doi: 10.1021/jp064569j. [DOI] [PubMed] [Google Scholar]
- (70).March AM, Assefa TA, Bressler C, Doumy G, Galler A, Gawelda W, Kanter EP, Németh Z, Pápai M, Southworth SH, Young L, Vankó G. J. Phys. Chem. C. 2015;119(26):14571–14578. doi: 10.1021/jp511838q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (71). Comparing [Co(CN)6]3− vs [Fe(CN)6]3−, we attribute this difference in π contributions to a change in the orbital overlap between the metal 4p orbitals and the t1u ligand group orbitals constructed using the CN− π2p-2p orbitals. The larger Zeff of Co(III) compared to Fe(III) lowers the energy of the cobalt 4p orbitals (Figure S8), leading to increased overlap with the CN− π2p-2p and thus increasing π character in the observed cobalt V2C XES features.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.