Testing the cranial evolutionary allometric ‘rule’ in Galliformes

Abstract

Recent comparative studies have indicated the existence of a common cranial evolutionary allometric (CREA) pattern in mammals and birds, in which smaller species have relatively smaller faces and bigger braincases than larger species. In these studies, cranial allometry was tested using a multivariate regression between shape (described using landmarks coordinates) and size (i.e. centroid size), after accounting for phylogenetic relatedness. Alternatively, cranial allometry can be determined by comparing the sizes of two anatomical parts using a bivariate regression analysis. In this analysis, a slope higher or lower than 1 indicates the existence of positive or negative allometry, respectively. Thus, in those species that support the CREA ‘rule’, positive allometry is expected for the association between face size and braincase size, which would indicate that larger species have disproportionally larger faces. In the present study, I applied these two approaches to explore cranial allometry in 83 Galliformes (Aves, Galloanserae), ranging in body weight from 30 g to 2.5 kg. The multivariate regression between shape and centroid size revealed the existence of a significant allometric pattern resembling CREA, whereas the second analysis revealed a negative allometry for beak size and braincase size (i.e. contrary to the CREA ‘rule’, larger galliform species have disproportionally shorter beaks than smaller galliform species). This study suggests that the presence of CREA may be overestimated when using cranium size as the standard measurement.

Introduction

It has been recently reported that there exists a common allometric pattern across mammalian taxa, in which small species possess proportionally shorter faces and wider braincases than large species. This trend has been called the cranial evolutionary allometric (CREA) ‘rule’ (Cardini & Polly 2013; Cardini et al. 2015). Previously described in four groups of placental mammals with divergent morphologies and lifestyles (antelopes, bats, mongooses, and squirrels) (Cardini & Polly 2013), this trend has also been found in marsupials (Cardini et al. 2015). Taking in to account both the long divergence time and the existence of relevant differences in craniofacial ossification between placentals mammals and marsupials (e.g. Smith 1997), the finding suggests the existence of a new ‘rule’ for cranial evolution.

Skull allometries have been generally interpreted as adjustments necessary to compensate the physical constraints predicted by the square-cube law (e.g. Emerson & Bramble 1993), originally formulated by Galileo Galilei in the Two New Sciences in 1638. In his book, Galilei already applied this law to explain the disproportionately thick bones of large animals. According to the square-cube law, when the length of an object is scaled up by a factor k, its area will be increased by k² and its volume by k³. In biological terms, this means that if organisms grow isometrically (i.e. maintaining their shape), both their length and area dimensions would gradually become smaller in proportion to their body mass (i.e. volume). Regarding the skull, maintenance of isometric growth would lead to large species with, for example, relatively small oral gapes, small tooth areas, thinner bones, small corneas or less muscle force, which could decrease their feeding performance and/or other organismal abilities. The physical constraints imposed by the square-cube law could be overcome by growing allometrically, i.e. by changing shape with size increase and growing, for example, disproportionately larger jaws or thicker muscles.

Slater and van Valkenburgh (2009) explicitly tested the effect of facial allometry on skull performance in felids. Using finite element analysis, the authors showed that the skulls of larger felids possess both a lower biting force and a decrease in work efficiency relative to the skull of small felids. This means that a disproportionally large face does not improve the feeding performance in felids, but it could still be advantageous for these ambush predators – felids capture their prey with a single bite – to have a disproportionally larger oral gape that facilitates the capture of large, energetically valuable preys (Slater & Van Valkenburgh 2009). The reduction in skull strength caused by a longer face seems to have been compensated by an allometry in bone thickness: large felids have relatively thicker skull bones than small felids (Slater & Van Valkenburgh 2009; Chamoli & Wroe 2011). These studies indicate that: 1) allometric growth does not necessarily increase performance, 2) the disadvantage due to one allometric trait can be compensated by other traits, 3) costs and benefits of growing allometrically would depend on the species' behaviour (Bock & Wahlert 1965), e.g. a disproportionately large mouth may be advantageous for an ambush predator, but not for species displaying other feeding behaviours (e.g. Slater et al. 2009).

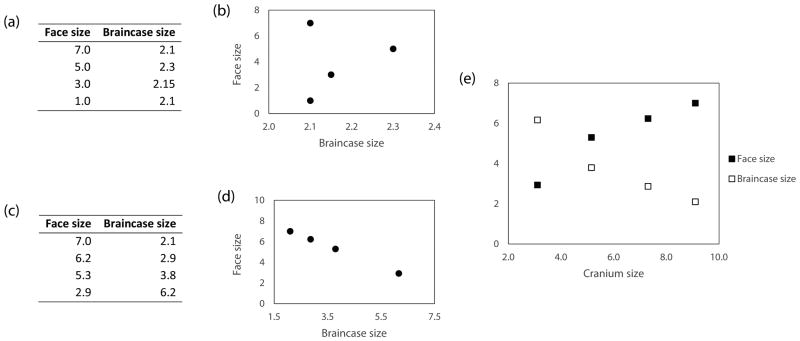
In contrast to mammals, geometric morphometric studies in birds are scarce. Nonetheless, available studies have shown that birds also display the CREA ‘rule’ (Bright et al 2016). In these CREA studies, cranium shape was quantified by geometric morphometric methods. Accordingly, species comparisons were conducted after the landmark configurations were set to the same orientation, position, and scale (i.e. after removing arbitrary shape differences). The scaling step was accomplished by using cranium size (i.e. centroid size) as the standard measurement. However, as stressed by Radinsky (1983; 1984), face and braincase proportion studies should be performed using a standard that is not a composite of these two regions, as scaling by cranium size induces covariation between the face and the braincase, even when they grow independently of each other. Thus, studies of cranial proportions based on cranium size as the standard measurement may lead to spurious results (see Fig. 1).

Figure 1.

(a) Face and braincase size measurements of four hypothetical species. The species have similar braincase sizes, but differ markedly in the size of their faces; that is, there is no relationship between face and braincase size (see b). (b) Plot of the variables in (a). (c) Standardization of face and braincase measurements shown in (a), using cranium size as the standard measurement. (d) Plot of the variables in (c). Note the strong relationship induced by the standardization method. (e) The induced pattern resembles the CREA ‘rule’, in which relatively shorter faces and larger braincases are noted for smaller species than for larger species.

Cranial allometry has traditionally been studied by computing the slope of a regression line in order to describe the relationship between the sizes of two anatomical parts (for a review see e.g. Klingenberg 1998; Warton et al. 2006). For the length-length relationship, a slope of 1 indicates isometry (i.e. the proportions of the two regions are similar in both small and large species). A slope higher or lower than 1 indicates the existence of positive or negative allometry, respectively. A positive allometry for face size relative to braincase size means that larger species have disproportionally larger faces (i.e. the CREA ‘rule’), whereas a negative allometry indicates that the face is relatively shorter in larger species. Thus, species displaying the CREA ‘rule’ should possess a positive allometry for face and braincase size. In this study, I tested this hypothesis in Galliformes by applying 3D geometric morphometric methods to quantify the cranium shape, and explored cranial allometry using two regressions: 1) a multivariate regression between shape and centroid size, and 2) a major axis regression of beak and braincase centroid size, after accounting for phylogenetic relatedness. These analyses led to contradictory results, suggesting that the presence of CREA in Galliformes might only be an artificial pattern induced when cranium size is used as the standard measurement.

Material and Methods

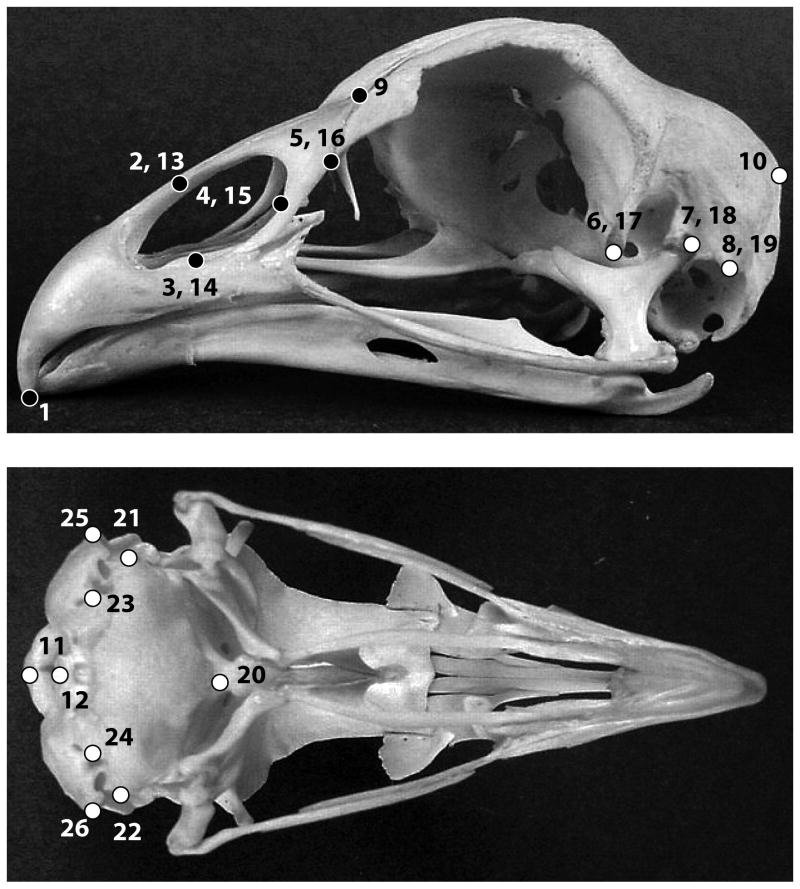
A total of 83 adult crania representing all living families of the order Galliformes were sampled. These crania are part of the osteological collection at the Natural History Museum at Tring (UK). A set of 26 landmark coordinates were obtained using a MicroScribe 3D digitizer (Fig. 2). Shape data was extracted from landmarks coordinates using Generalized Procrustes Analysis (GPA). Shape analyses were performed on the symmetric component derived from the GPA (Klingenberg et al. 2002).

Figure 2.

Localization of landmarks used to describe cranium shape in this study. Black and white dots represent beak and braincase landmarks, respectively (1: tip of the premaxilla; 2, 13: nasal bone – premaxilla juncture [dorsal]; 3, 14: nasal bone – premaxilla juncture [ventral]; 4, 15: posterior-most point of the nasal orifice; 5, 16: anterior-most point of the lacrimal; 6, 17: tip processus postorbitalis; 7, 18: quadrate – cranium joint; 8, 19: tip processus musculi depressor mandibulae; 9: tip processus frontalis premaxillare; 10: anterior-most middle point squamosal-parietal juncture; 11: anterior-most middle point foramen magnum; 12: incisura mediana condyli; 20: bassioccipital process; 21: lateralmost point bassioccipital [right]; 22: lateral-most point bassioccipital [left]; 23: foramen nervi vagi [right]; 24: foramen nervi vagi [left]; 25: tip processus paraoccipitalis [left]; 26: tip processus paraoccipitalis [right]) (Images downloaded from www.skullsite.com).

The www.birdtree.org platform was used for generating a subset of 1000 equally plausible phylogenetic trees for the 83 galliform species included in this study, using both Hackett and Ericson phylogenetic backbones (9993 OTUs) (Jetz et al. 2012). The phylogenetic information contained in each tree set was summarized by computing a single 50% majority-rule consensus tree (Rubolini et al. 2015). A set of phylogenetic independent contrasts (PICs) of shape and size (i.e. centroid size, CS) data was computed for each consensus tree (Klingenberg & Gidaszewski 2010). A Procrustes ANOVA using shape contrasts as the dependent variable, and the phylogenetic tree from which the contrasts were computed as an independent, discrete factor, was performed to test the effect of using different phylogenetic hypotheses to obtain the shape data.

Evolutionary allometry was studied using: 1) a multivariate regression of shape contrasts onto size contrasts (log-transformed centroid size, log-CS), 2) a major axis (MA) regression of upper beak size against braincase size (i.e. PICs centroid size). The statistical significance of the multivariate regression was assessed by a permutation approach (10,000 iterations). The allometric pattern was considered significant when the probability of randomly obtaining a regression vector that accounted for a higher percentage of shape variance was lower than 0.05 (Klingenberg & Marugán-Lobón 2013). The significance of the bivariate regression was tested against the null hypothesis (no correlation between the variables). The observed slope was considered equal to 1 (i.e. isometry) if the fitted and residual scores for the sample, computed from a regression with a slope of 1, were uncorrelated.

Generalized Procrustes Analysis, PICs and multivariate regressions were computed using MorphoJ v.1.06d (Klingenberg 2011). Procrustes ANOVA was performed in R (v. 3.2.3) (R Core Team 2016) using procD.lm in GEOMORPH (v. 3.0.1). Major axis analysis was performed in R using ma and slope test in SMATR (v. 3.4.3) (Warton et al. 2012. Consensus trees were obtained using Mesquite v.2.75 (Maddison & Maddison 2011) and three-dimensional visualizations of the results were generated in Landmark editor v.3.0.0.6 (Wiley et al. 2005).

Results

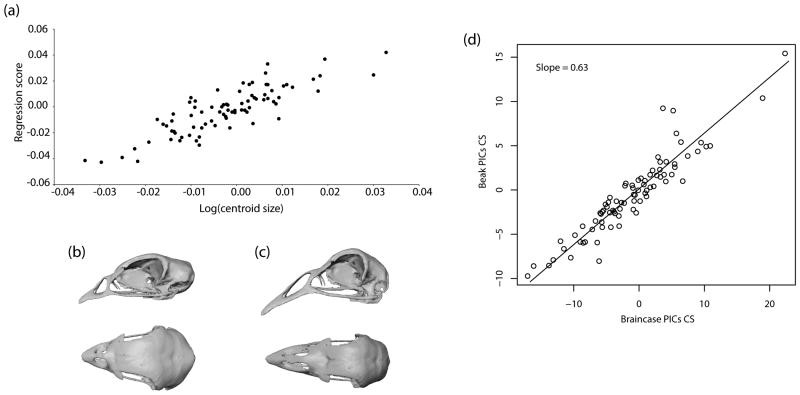
The Procrustes ANOVA showed non-significant differences between shape data obtained from Hackett or Ericson phylogenies (F = 0.0015; df = 163; P = 1); only the results obtained from the former will be discussed here. The multivariate regression of shape contrasts onto log-CS contrasts showed the existence of a significant allometric pattern that explained 12.3 % of the variation in shape (P < 0.001). This pattern coincided with the one described in mammals and other bird taxa where small species showed relatively shorter faces and wider braincases than larger species (Cardini & Polly 2013; Cardini et al. 2015 ref) (Fig. 3a-c).

Figure 3.

(a) Evolutionary allometry of the cranium in Galliformes obtained from the multivariate regression of shape contrasts onto size contrasts (i.e. log centroid size). (b, c) Expected shape of (b) a small and (c) a large cranium in lateral and top view (top and bottom, respectively). The observed pattern resembles the cranial evolutionary allometric (CREA) ‘rule’ described in mammals and birds where small species display relatively shorter faces and wider braincases than large species. (cranium scan downloaded from http://digimorph.org/). (d) Evolutionary allometry of the cranium in Galliformes obtained from a major axis analysis of beak and braincase size (i.e. centroid size contrasts). The regression slope deviated significantly from 1, indicating the presence of negative allometry (PICs: phylogenetic independent contrasts; CS: centroid size).

Contrary to expectations, the pattern depicted by CREA was not observed using a MA regression of beak size and braincase size (i.e. centroid size contrasts). The MA analysis showed that there was a significant linear relationship between beak and braincase size (r² = 0.87; P < 0.001). However, the observed slope (β = 0.63; C.I.: 0.58-0.68) deviated significantly from 1 (N = 82; F = 124.73; P = 0), indicating the existence of negative allometry between beak and braincase size (i.e. larger galliform species have disproportionally shorter beaks) (Fig. 3d).

Discussion

This study suggests that the common approaches for the study of cranial allometry may lead to conflicting results if cranium size is used as the standard measurement. Although the existence of a common developmental constraint between the face and the braincase, as suggested by the CREA ‘rule’, requires further empirical work, the existence of a strong negative allometry of brain mass—and therefore, braincase size—relative to body mass in amniotes is well documented (e.g. Martin, 1981; Armstrong, 1983). This observation led some researchers to suggest that brain size could be related primary to metabolism rather than to body mass (e.g. Martin 1981; Armstrong 1983; Bennett & Harvey 1985). It has been generally accepted that the material and energy exchange that takes place during metabolism would be physically constrained by the surface area of either the whole organism or its internal transport networks, in which case it is generally expected that the metabolism scales as an exponent of 2/3 or 3/4 relative to body mass, respectively (for a review see Glazier 2005). These scaling exponents corresponded to those estimated for brain mass and body mass (e.g. Martin, 1981; Armstrong, 1983), supporting the idea that the observed negative allometry between these two traits could be explained in terms of the square-cube law, as a consequence of the existence of a universal, physical constraint on metabolism.

Early studies focused on exploring the scaling relationships between brain mass and basal metabolic rate (BMR) reported a high and significant relationship, as would be expected if these two traits were causally related (Armstrong 1983; Hofman 1983; Bennett & Harvey 1985). However, these early analyses did not account for the confounding effects of either body mass or phylogenetic relationships. More recently, it has been shown that when these effects are corrected, BMR explains a very low amount of brain mass variation (Isler & Van Schaik 2006; Isler & van Schaik 2006). These results suggest that metabolism could not explain the strong negative allometry of brain mass – and therefore, braincase size – relative to body mass in amniotes.

However, the strong allometry of braincase size relative to body mass could still be explained in terms of the square-cube law if cranial proportions at early developmental stages are taken into account. It has been shown that juveniles of some amniote species display relatively larger braincases and shorter faces than adults (Mitteroecker et al. 2004; Bhullar et al. 2012). Probably a disproportionately large braincase is more accentuated in neonates. Taking this in to account, isometric growth during the postnatal stage – note that, according to the square-cube law, it is expected brain size grows with an exponent of 1 relative to body mass – would probably lead to a head too big to be supported by the neck at later developmental stages, i.e. head proportions at early developmental stages may be physically non-viable at adulthood in some amniote species. Therefore, the negative allometry of braincase size relative to body mass could be understood as an adjustment to the physical constraint (sensuMaynard Smith et al. 1985) imposed by the square-cube law not on metabolism, but on head size.