Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Sep 14;6:33301. doi: 10.1038/srep33301

Optical thermometry based on level anticrossing in silicon carbide

A N Anisimov 1, D Simin 2, V A Soltamov 1, S P Lebedev 1,3, P G Baranov 1, G V Astakhov 2,a, V Dyakonov 2,4,b
PMCID: PMC5022017  PMID: 27624819

Abstract

We report a giant thermal shift of 2.1 MHz/K related to the excited-state zero-field splitting in the silicon vacancy centers in 4H silicon carbide. It is obtained from the indirect observation of the optically detected magnetic resonance in the excited state using the ground state as an ancilla. Alternatively, relative variations of the zero-field splitting for small temperature differences can be detected without application of radiofrequency fields, by simply monitoring the photoluminescence intensity in the vicinity of the level anticrossing. This effect results in an all-optical thermometry technique with temperature sensitivity of 100 mK/Hz1/2 for a detection volume of approximately 10−6 mm3. In contrast, the zero-field splitting in the ground state does not reveal detectable temperature shift. Using these properties, an integrated magnetic field and temperature sensor can be implemented on the same center.

Temperature sensing with high spatial resolution may be helpful for mapping of biochemical processes inside living cells and monitoring of heat dissipation in electronic circuits1,2,3. Frequently used contact-less methods exploit temperature-dependent features either in Raman spectra of microfabricated chips4,5 or in photoluminescence (PL) spectra of nanoprobes such as quantum dots6, nanocrystals7,8 and fluorescent proteins9. Typical temperature resolution of these methods is several hundreds of mK or lower.

Using quantum-mechanical properties of the nitrogen-vacancy (NV) in diamond, the temperature sensitivity better than δT = 10 mK/Hz1/2 is achievable3,10,11,12. It is based on the moderate thermal shift dν0/dT = −74 kHz/K13,14 of the optically detected magnetic resonance (ODMR) frequency in the NV center (ν0 = 2.87 GHz at T = 300 K) and the use of the advanced readout protocols, particularly temperature-scanned ODMR15 or thermal spin echo10,11. However, this method is not universally usable, because the application of high-power radiofrequency (RF) fields in the pulsed ODMR technique may alter the temperature at the probe during the measurement. Therefore, the realization of highly-sensitive and RF-free optical thermometry is of broad interest.

Our approach is based on the silicon vacancy (VSi) centers in silicon carbide (SiC), demonstrating appealing properties for quantum sensing applications16,17,18. Particularly, the VSi excited state19,20 shows a giant thermal shift, exceeding 1 MHz/K18. Furthermore, these centers reveal an utterly long spin memory21 and possess favorable absorption and PL in the near infrared spectral range22, characterized by a deep tissue penetration. The concentration of the VSi centers can be precisely controlled over many orders of magnitude down to single defect level23,24 and they can be incorporated into SiC nanocrystals as well25.

We perform proof-of-concept thermometry measurements using 4H-SiC crystals. The 4H-SiC sample under study was grown by the physical vapour transport method. Silicon vacancies were created by irradiation of the crystal with 2 MeV electrons with a fluence of 1018 cm−2. The VSi centers possess a half-integer spin state S = 3/226, which is split without external magnetic field in two Kramers degenerate spin sublevels mS = ±3/2 and mS = ±1/2. Here, we address the VSi(V2) center27 with the zero-field splitting (ZFS) in the ground state (GS) 2DG = 70 MHz [Fig. 1(a)]. The spin states are split further when an external magnetic field B is applied. The spin Hamiltonian of the VSi center in the magnetic field has a complex form20 and five RF-induced transitions are allowed: ν1 (−1/2 ↔ −3/2), ν2 (+1/2 ↔ +3/2), ν3 (+1/2 ↔ −3/2), ν4 (−1/2 ↔ +3/2) and ν5 (+1/2 ↔ −1/2). In the ODMR experiments, we pump the VSi centers into the mS = ±1/2 state with a near infrared laser (785 nm or 808 nm with power in the range of several hundreds mW). To decrease the detection volume to approximately 10−6 mm3, we use a near-infrared optimized objective with N.A. = 0.3. The PL is recorded in the spectral range from 850 to 1000 nm, allowing optical readout of the VSi spin state: it is higher for mS = ±3/2. A detailed ODMR dependence on the magnetic field strength and orientation is presented elsewhere20,28.

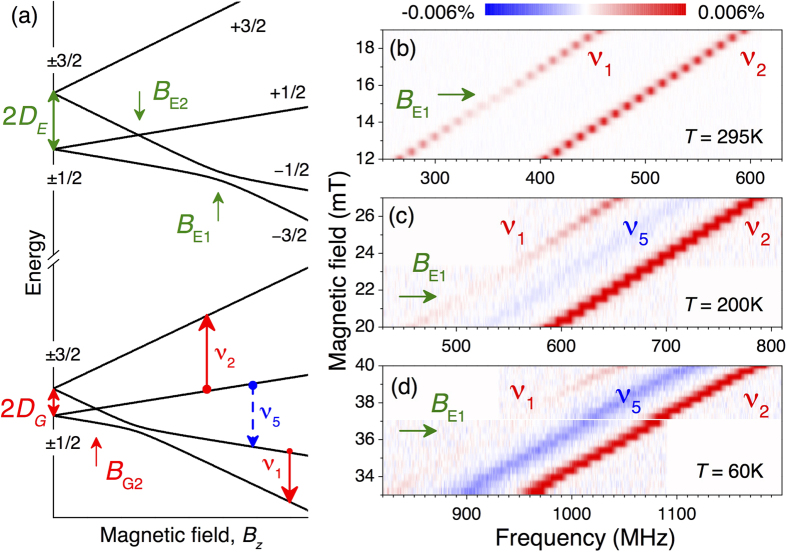
Figure 1. Indirect detection of the ES spin resonance in the VSi center of 4H-SiC.

Figure 1

Open in a new tab

(a) The GS and ES spin sublevels in the external magnetic field. The arrows labeled as ν1, ν2 and ν5 indicate the RF driven transitions in the GS, detected in the experiment. (b–d) Magnetic field dependence of the VSi ODMR spectra in the vicinity of the ESLAC-1, performed at different temperatures. The arrows indicate the magnetic field BE1, at which the minimum ODMR contrast of the ν1 transition is observed.

Due to the relatively short excited state (ES) lifetime of 6 ns in the VSi center22, the direct ODMR signal associated with the ES is weak. However, in the ES level anticrossing (LAC) between the mS = −1/2 and mS = −3/2 states (ESLAC-1) [magnetic field BE1 in Fig. 1(a)] the optical pumping cycle changes29,30,31,32. This results in a reduction of the ODMR contrast of the corresponding GS spin resonance19,20.

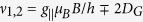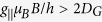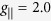Indeed, such a behavior is observed in our experiments. Figure 1(b) shows the magnetic field dependence of the ODMR spectrum in the vicinity of the ESLAC-1 at room temperature. The ν1 and ν2 lines shift linearly with magnetic field applied parallel to the symmetry axis (B||c) as Inline graphic for Inline graphic with Inline graphic denoting the g-factor. The transition with ΔmS = ±2 are also allowed, but corresponding ν3 and ν4 lines appear at different frequencies and have lower ODMR contrast20. The ν5 line is not resolved because of the same population of the mS = −1/2 and mS = +1/2 states under optical pumping at room temperature26. At BE1 = 15.7 mT, the ν1 contrast drops to nearly zero and according to Fig. 1(a) the ES ZFS can be determined as 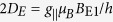Inline graphic. Simultaneously, the GS ZFS is directly measured as 2DG = (ν2 − ν1)/2.

We repeat the above experiment at lower temperature T = 200 K [Fig. 1(c)]. One can clearly see that the magnetic field associated with the ESLAC-1 is shifted towards higher values BE1 = 21.8 mT, while the splitting between the ν1 and ν2 ODMR lines remains the same. In addition, another spin resonance with negative contrast becomes visible 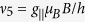Inline graphic. We ascribe the appearance of the ν5 line with lowering temperature with different transition rates to the mS = −1/2 and mS = +1/2 states. This may occur due to the either temperature-dependent interaction with phonons or some magnetic field misalignment, which in turn leads to the modification of the intersystem crossing as well as of the optical pumping cycle. The detailed analysis is beyond the scope of this work.

The tendency continues with lowering temperature down to T = 60 K [Fig. 1(d)]. Namely, we observe that the magnetic field associated with the ESLAC-1 is shifted to BE1 = 36.5 mT, indicating a further increase of DE. The splitting between the ν1 and ν2 ODMR lines remains unchanged, suggesting DG is nearly temperature independent. These findings are summarized in Fig. 2. The ES ZFS is well fitted to

Figure 2. The GS (2DG) and ES (2DE) ZFS in the VSi center of 4H-SiC as a function of temperature.

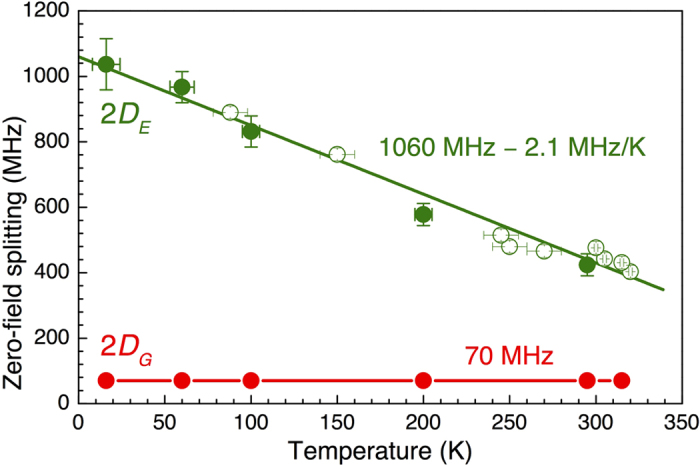
Figure 2

Open in a new tab

Solid symbols are observed from the ODMR experiments of Fig. 1 and open symbols from the LAC experiments of Fig. 3. The line for 2DE is a fit to Eq. (1). The line for 2DG is to guide the eye.

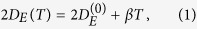graphic file with 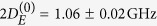name srep33301-m6.jpg

with Inline graphic denoting the ZFS in the limit T → 0 and β = −2.1 ± 0.1 MHz/K being the thermal shift. The latter is by more than one order of magnitude larger than that for the NV defect in diamond13 and by a factor of two larger than previously reported for 6H-SiC18. In following, we use this giant thermal shift for all-optical temperature sensing.

The idea is to exploit the variation of the PL intensity in the vicinity of LAC, occurring even without RF fields. This method has been initially implemented for all-optical magnetometry in SiC20, and later extended to the NV centers in diamond33. Figure 3 presents lock-in detection of the PL variation ΔPL/PL as a function of the dc magnetic field Bz, recorded at different temperatures. 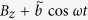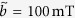The modulation of PL is caused by the application of an additional weak oscillating magnetic field B, i.e., Inline graphic with Inline graphic and ω/2π = 0.33 kHz. The sharp resonance at 1.25 mT corresponds to the LAC between the spin sublevels mS = −3/2 and mS = +1/2 (ΔmS = 2) in the GS, corresponding to GSLAC-2 in Fig. 1(a). A broader resonance at the double magnetic field of 2.5 mT relates to the LAC between the spin sublevels mS = −3/2 and mS = −1/2 (ΔmS = 1) , i.e., GSLAC-1. The magnetic fields corresponding to the LACs in the GS (BG1 and BG2) are temperature independent, which is in agreement with our ODMR experiments of Fig. 1.

Figure 3. Lock-in detection of the PL variation ΔPL/PL (in-phase voltage UX normalized to the dc photovoltage) as a function of the dc magnetic field B, recorded at different temperatures.

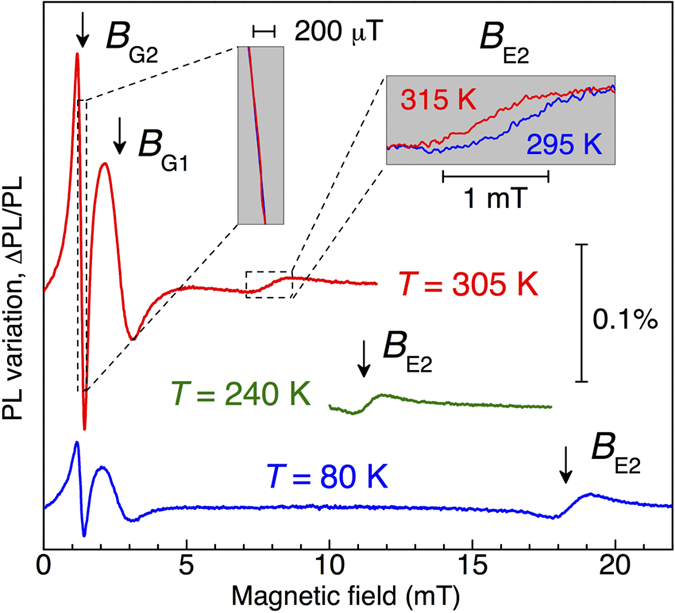
Figure 3

Open in a new tab

ΔPL is caused by the application of an additional weak oscillating magnetic field. The arrows indicate the characteristic magnetic fields of different LACs. RF is not applied.

In addition to that, the experimental data of Fig. 3 reveal another resonance at the magnetic field BE2. It corresponds to the LAC with ΔmS = 2 in the ES (ESLAC-2), as graphically explained in Fig. 1(a). Due to the strong reduction of the ES ZFS with growing temperature, this resonance shifts rapidly following Eq. (1) as 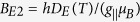Inline graphic. We recall that the lifetime in the ES is about 6 ns22. In order to observe ODMR signal associated with a spin state possessing such a short lifetime, one needs a RF field of about 2 mT. This alternating magnetic field, being in resonance with the spin transition, without strong impact on the temperature of the object under measurement is difficult to achieve.

We now discuss how small variations of the magnetic field ΔB and temperature ΔT can be measured. The in-phase lock-in voltage UX at the bias field BG2 can be written as (left inset of Fig. 3)

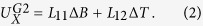graphic file with name srep33301-m11.jpg

Using calibration from our earlier experiments20, we obtain L11 = −39 mV/mT. Because BG2 is temperature independent and the variation of the signal amplitude for |ΔT| < 10 K is negligible, L12 ≈ 0 mV/K is a good approximation. The linear dependence of Eq. (2) holds for |ΔB| < 100 mT. The same can be written for UX at the bias field BE2 (right inset of Fig. 3)

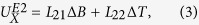graphic file with name srep33301-m12.jpg

and we find L21 = 1.8 mV/mT and L22 = 23 mV/K. From the factors Lij, it can be clearly seen that the magnetic field and temperature can be separately measured using GSLAC-2 and ESLAC-2. Particularly, the temperature sensing can be done in two steps. First, the bias field BG2 is applied and one measures 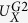Inline graphic to determine the actual magnetic field, accounting for ΔB in Eq. (3). Then, after applying BE2 and reading out 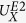Inline graphic, the magnetic noise can be excluded from the thermometry signal using

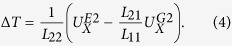graphic file with name srep33301-m15.jpg

The dynamic temperature range of such thermometry is |ΔT| < 10 K. A broad range thermometry can be realized (with lower sensitivity) by scanning the magnetic field from 5 mT to 20 mT and determining BE2, which can be then converted to temperature using 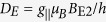Inline graphic in combination with Eq. (1).

We measure the in-phase and quadrature lock-in signals as a function of time to determine the upper limit of the noise level δU at a given modulation frequency (0.33 kHz). Then using the calibrated values for the L-matrix, we recalculate the noise level into the temperature sensitivity δT = δU/L22. It is estimated to be δT ≈ 100 mK/Hz1/2 within a detection volume of approximately 10−6 mm3. By improving the excitation/collection efficiency and increasing the PL intensity (the VSi concentration), the temperature sensitivity better than δT ≈ 1 mK/Hz1/2 is feasible with a sensor volume of 1 mm3. The suggested all-optical thermometry can be realized using various color centers in different SiC polytypes34,35. Furthermore, because color centers in SiC can be electrically driven36 even on single defect level37, an intriguing perspective is the implementation of a LAC-based thermometry with electrical readout using photoionization of the ES38.

Additional Information

How to cite this article: Anisimov, A. N. et al. Optical thermometry based on level anticrossing in silicon carbide. Sci. Rep. 6, 33301; doi: 10.1038/srep33301 (2016).

Acknowledgments

A.N.A., V.A.S. and P.G.B. acknowledge support by the RSF Nr. 14-12-00859; the RFBR Nr. 14-02-91344; 16-02-00877. D.S. and G.V.A. acknowledge support by the BMBF under the ERA. Net RUS Plus project “DIABASE”. V.D. acknowledges support by the DFG (DY 18/13-1). This publication was supported by the Open Access Publication Fund of the University of Wuerzburg.

Footnotes

Author Contributions P.G.B., V.A.S., G.V.A. and D.S. conceived different parts of the experiments; A.N.A. and D.S. performed the experiments; S.P.L. provided the samples; G.V.A. wrote the manuscript; V.D. and P.G.B. supervised the project; all authors discussed the results.

References

  1. Yang J.-M., Yang H. & Lin L. Quantum Dot Nano Thermometers Reveal Heterogeneous Local Thermogenesis in Living Cells. ACS Nano 5, 5067–5071 (2011). [DOI] [PubMed] [Google Scholar]
  2. Yue Y. & Wang X. Nanoscale thermal probing. Nano Reviews 3, 251 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Kucsko G. et al. Nanometre-scale thermometry in a living cell. Nature 500, 54–58 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Kim S. H. et al. Micro-Raman thermometry for measuring the temperature distribution inside the microchannel of a polymerase chain reaction chip. Journal of Micromechanics and Microengineering 16, 526–530 (2006). [Google Scholar]
  5. Beechem T., Graham S., Kearney S. P., Phinney L. M. & Serrano J. R. Invited Article: Simultaneous mapping of temperature and stress in microdevices using micro-Raman spectroscopy. Review of Scientific Instruments 78, 061301 (2007). [DOI] [PubMed] [Google Scholar]
  6. Walker G. W. et al. Quantum-dot optical temperature probes. Applied Physics Letters 83, 3555 (2003). [Google Scholar]
  7. Vetrone F. et al. Temperature Sensing Using Fluorescent Nanothermometers. ACS Nano 4, 3254–3258 (2010). [DOI] [PubMed] [Google Scholar]
  8. Plakhotnik T., Doherty M. W., Cole J. H., Chapman R. & Manson N. B. All-Optical Thermometry and Thermal Properties of the Optically Detected Spin Resonances of the NV –Center in Nanodiamond. Nano Letters 14, 4989–4996 (2014). [DOI] [PubMed] [Google Scholar]
  9. Donner J. S., Thompson S. A., Kreuzer M. P., Baffou G. & Quidant R. Mapping Intracellular Temperature Using Green Fluorescent Protein. Nano Letters 12, 2107–2111 (2012). [DOI] [PubMed] [Google Scholar]
  10. Toyli D. M., de las Casas C. F., Christle D. J., Dobrovitski V. V. & Awschalom D. D. Fluorescence thermometry enhanced by the quantum coherence of single spins in diamond. Proceedings of the National Academy of Sciences 110, 8417–8421 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Neumann P. et al. High-Precision Nanoscale Temperature Sensing Using Single Defects in Diamond. Nano Letters 13, 2738–2742 (2013). [DOI] [PubMed] [Google Scholar]
  12. Wang J. et al. High-sensitivity temperature sensing using an implanted single nitrogen-vacancy center array in diamond. Physical Review B 91, 155404 (2015). [Google Scholar]
  13. Acosta V. M. et al. Temperature Dependence of the Nitrogen-Vacancy Magnetic Resonance in Diamond. Physical Review Letters 104, 070801 (2010). [DOI] [PubMed] [Google Scholar]
  14. Toyli D. M. et al. Measurement and Control of Single Nitrogen-Vacancy Center Spins above 600 K. Physical Review X 2, 031001 (2012). [Google Scholar]
  15. Babunts R. A. et al. Temperature-scanned magnetic resonance and the evidence of two-way transfer of a nitrogen nuclear spin hyperfine interaction in coupled NV-N pairs in diamond. Journal of Experimental and Theoretical Physics Letters 95, 429–432 (2012). [Google Scholar]
  16. Baranov P. G. et al. Silicon vacancy in SiC as a promising quantum system for single-defect and single-photon spectroscopy. Physical Review B 83, 125203 (2011). [Google Scholar]
  17. Riedel D. et al. Resonant Addressing and Manipulation of Silicon Vacancy Qubits in Silicon Carbide. Physical Review Letters 109, 226402 (2012). [DOI] [PubMed] [Google Scholar]
  18. Kraus H. et al. Magnetic field and temperature sensing with atomic-scale spin defects in silicon carbide. Scientific Reports 4, 5303 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Carter S. G., Soykal Ö. O., Dev P., Economou S. E. & Glaser E. R. Spin coherence and echo modulation of the silicon vacancy in 4H-SiC at room temperature. Physical Review B 92, 161202 (2015). [Google Scholar]
  20. Simin D. et al. All-Optical dc Nanotesla Magnetometry Using Silicon Vacancy Fine Structure in Isotopically Purified Silicon Carbide. Physical Review X 6, 031014 (2016). [Google Scholar]
  21. Simin D. et al. Long-lived quantum memory in silicon carbide with natural isotope abundance. arXiv:1602.05775.
  22. Hain T. C. et al. Excitation and recombination dynamics of vacancy-related spin centers in silicon carbide. Journal of Applied Physics 115, 133508 (2014). [Google Scholar]
  23. Widmann M. et al. Coherent control of single spins in silicon carbide at room temperature. Nature Materials 14, 164–168 (2015). [DOI] [PubMed] [Google Scholar]
  24. Fuchs F. et al. Engineering near-infrared single-photon emitters with optically active spins in ultrapure silicon carbide. Nature Communications 6, 7578 (2015). [DOI] [PubMed] [Google Scholar]
  25. Muzha A. et al. Room-temperature near-infrared silicon carbide nanocrystalline emitters based on optically aligned spin defects. Applied Physics Letters 105, 243112 (2014). [Google Scholar]
  26. Kraus H. et al. Room-temperature quantum microwave emitters based on spin defects in silicon carbide. Nature Physics 10, 157–162 (2014). [Google Scholar]
  27. Sörman E. et al. Silicon vacancy related defect in 4H and 6H SiC. Physical Review B 61, 2613–2620 (2000). [Google Scholar]
  28. Simin D. et al. High-Precision Angle-Resolved Magnetometry with Uniaxial Quantum Centers in Silicon Carbide. Physical Review Applied 4, 014009 (2015). [Google Scholar]
  29. van Oort E. & Glasbeek M. Fluorescence detected level-anticrossing and spin coherence of a localized triplet state in diamond. Chemical Physics 152, 365–373 (1991). [Google Scholar]
  30. Martin J. P. D. et al. Spectral hole burning and Raman heterodyne signals associated with an avoided crossing in the NV centre in diamond. Journal of Luminescence 86, 355–362 (2000). [Google Scholar]
  31. Epstein R. J., Mendoza F. M., Kato Y. K. & Awschalom D. D. Anisotropic interactions of a single spin and dark-spin spectroscopy in diamond. Nature Physics 1, 94–98 (2005). [Google Scholar]
  32. Rogers L. J., McMurtrie R. L., Sellars M. J. & Manson N. B. Time-averaging within the excited state of the nitrogen-vacancy centre in diamond. New Journal of Physics 11, 063007 (2009). [Google Scholar]
  33. Wickenbrock A. et al. Microwave-free magnetometry with nitrogen-vacancy centers in diamond. arXiv:1606.03070.
  34. Falk A. L. et al. Polytype control of spin qubits in silicon carbide. Nature Communications 4, 1819 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Soltamov V. A. et al. Optically Addressable Silicon Vacancy-Related Spin Centers in Rhombic Silicon Carbide with High Breakdown Characteristics and ENDOR Evidence of Their Structure. Physical Review Letters 115, 247602 (2015). [DOI] [PubMed] [Google Scholar]
  36. Fuchs F. et al. Silicon carbide light-emitting diode as a prospective room temperature source for single photons. Scientific Reports 3, 1637 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Lohrmann A. et al. Single-photon emitting diode in silicon carbide. Nature Communications 6, 7783 (2015). [DOI] [PubMed] [Google Scholar]
  38. Bourgeois E. et al. Photoelectric detection of electron spin resonance of nitrogen-vacancy centres in diamond. Nature Communications 6, 8577 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES