Comparison of analytical and numerical approaches for CT-based aberration correction in transcranial passive acoustic imaging

Abstract

Computed tomography (CT)-based aberration corrections are employed in transcranial ultrasound both for therapy and imaging. In this study, analytical and numerical approaches for calculating aberration corrections based on CT data were compared, with a particular focus on their application to transcranial passive imaging. Two models were investigated: a three-dimensional full-wave numerical model [Connor and Hynynen, IEEE Trans. Biomed. Eng. 51, 1693–1706 (2004)] based on the Westervelt equation, and an analytical method [Clement and Hynynen, Ultrasound Med. Biol. 28, 617–624 (2002)] similar to that currently employed by commercial brain therapy systems. Trans-skull time delay corrections calculated from each model were applied to data acquired by a sparse hemispherical (30 cm diameter) receiver array (128 piezoceramic discs: 2.5 mm diameter, 612 kHz center frequency) passively listening through ex vivo human skullcaps (n = 4) to emissions from a narrow-band, fixed source emitter (1 mm diameter, 516 kHz center frequency). Measurements were taken at various locations within the cranial cavity by moving the source around the field using a three-axis positioning system. Images generated through passive beamforming using CT-based skull corrections were compared with those obtained through an invasive source-based approach, as well as images formed without skull corrections, using the main lobe volume, positional shift, peak sidelobe ratio, and image signal-to-noise ratio as metrics for image quality. For each CT-based model, corrections achieved by allowing for heterogeneous skull acoustical parameters in simulation outperformed the corresponding case where homogeneous parameters were assumed. Of the CT-based methods investigated, the full-wave model provided the best imaging results at the cost of computational complexity. These results highlight the importance of accurately modeling trans-skull propagation when calculating CT-based aberration corrections. Although presented in an imaging context, our results may also be applicable to the problem of transmit focusing through the skull.

1. INTRODUCTION

Aberration correction is of great importance in the field of biomedical acoustics, both for therapeutic applications of ultrasound where tight, accurate focusing is desired to reduce off-target effects, as well as for imaging purposes in order to improve spatial resolution and overall image quality. Transcranial applications demand particular attention in this regard, due to the large mismatch in acoustical properties (i.e. density, sound speed, attenuation) between skull bone and its surrounding tissues [1, 2, 3]. A number of techniques have been developed to counteract the effects of trans-skull propagation for both imaging and therapeutic applications of ultrasound in the brain. These include acoustic methods, which typically rely on the presence of a small hydrophone [4, 5, 6, 7] or source (e.g. transducer [8] or microbubble [9, 10, 11, 12, 13, 14]) near the desired focal point or involve analysis of the backscattered [15, 16] or transmitted [17, 18] signals, magnetic resonance (MR) acoustic radiation force imaging-based techniques [19, 20, 21, 22, 23], as well as approaches that use cranial morphology obtained from either MR imaging [24, 25, 26] or computed tomography (CT) [27, 28] scans of the head to calculate the required aberration corrections. The existing clinical devices used for focused ultrasound brain treatments apply CT-based focusing on transmit [29, 30, 31] using an analytic, ray-tracing approximation [32], which can rapidly (on the order of seconds) compute element corrections. Recently, our group [33, 34] and others [35, 36, 37], have demonstrated that CT-based corrections also have utility during beamforming on receive, and can enable passive acoustic imaging within the skull cavity for monitoring cavitation-mediated brain therapies [35, 36, 37, 38, 34]. The purpose of this study was to compare analytical and numerical methods for aberration correction based on CT image data, with a particular focus on their application to passive acoustic imaging in the brain.

2. METHODS

2.1. Experimental Setup

The experimental setup, which is similar to that which has been reported previously [34], is shown in figure 1. A 30 cm diameter, sparse hemispherical receiver array [12, 38, 34] was used to passively listen through ex vivo human skullcaps to emissions from a narrow-band, fixed source emitter (piezoceramic disc; 1 mm diameter, 516 kHz center frequency). The receiver array consisted of 128 piezoceramic discs sparsely distributed over the entire array aperture, each with an active diameter of 2.5 mm and a center frequency of 612 kHz, whose locations were optimized through computer simulations [33] to suppress grating lobe formation during imaging. Each skullcap had previously been imaged with a CT scanner (625 × 625 × 625 μm³ voxel size; LightSpeed VCT, GE Healthcare, Chalfont St Giles, UK), and was degassed in a vacuum chamber (Nalge, Rochester, NY, USA; Gast, Benton Harbor, MI, USA) for at least 3 h at −700 mmHg prior to experimentation. The hemispherical dome was filled with degassed/deionized water and a skullcap was placed between the array and the fixed source. A plastic bag was suspended within the skull cavity in order to raise the water level above the height provided by the dome. The fixed source was excited by a broadband impulse from a pulser/receiver (Panametrics, Olympus-NDT, Waltham, MA, USA) and the raw RF signals were captured by the receiver array using a 128-element data acquisition system (SonixDAQ, Ultrasonix, Richmond, BC, Canada) [39] at a sampling rate of 40 MS s⁻¹. The signal-to-noise ratio (SNR) was increased by averaging 16 consecutive traces during each acquisition. The resulting signals were band-pass filtered ([50,2000] kHz, fourth order Butterworth, MATLAB™) to remove noise, and passive beamforming was performed to generate spatial maps of source activity (see section 2.2). The source was mounted on a three-axis positioning system, allowing experiments to be conducted at various locations within the skull cavity. Measurements were taken with four different skullcaps (Skulls A–D, same specimens used in [34]) placed between the array and the source, for a total of 106 source locations spanning [−5,5] cm in X, [−7,6] cm in Y, and [0,4] cm in Z (see table 1).

Figure 1.

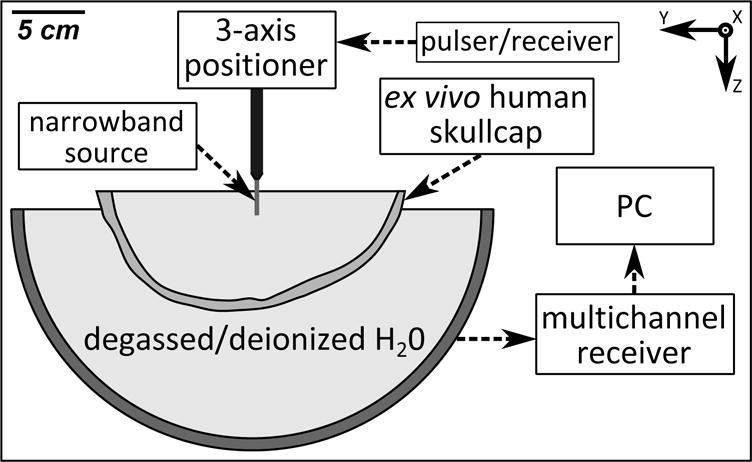
Experimental setup.

Table 1.

Dimensions of the inner and outer skull surfaces and the range of measurement locations (in mm) along the Cartesian axes of the receiver array’s reference frame. The spacing between measurement locations along each axis was 10 mm. The geometric focus of the array is [0,0,0], and the orientation of the X,Y, and Z axes can be found in figure 1.

Skull	Axis	Outer surface	Inner surface	Measurements
A	X Y Z	[−68.3,66.5] [−96.2,72.7] [N/A,52.2]	[−64.2,62.2] [−88.5,67.0] [N/A,45.8]	[−40,50] [−70,60] [0,40]
B	X Y Z	[−65.9,72.2] [−94.7,74.2] [N/A,58.0]	[−59.9,64.5] [−84.7,62.8] [N/A,48.7]	[−40,50] [−70,50] [0,40]
C	X Y Z	[−60.2,69.3] [−96.1,77.6] [N/A,58.1]	[−51.2,59.1] [−83.6,66.2] [N/A,48.0]	[−40,50] [−60,60] [0,40]
D	X Y Z	[−64.9,64.5] [−89.6,72.8] [N/A,42.9]	[−59.3,59.0] [−80.3,63.3] [N/A,36.5]	[−50,50] [−70,60] [0,30]

2.2. Aberration Correction and Image Formation

All data analysis was performed offline in MATLAB™ (R2013a, Mathworks, Natick, MA, USA). Images were formed using a modified version of the passive beamforming algorithm described in [40], which was augmented to include additional delay terms to account for the acoustic propagation through skull bone [33]. For each grid point r within a pre-defined imaging region of interest (20 × 20 × 20 mm³ volume centered about the source location, 0.25 × 0.25 × 0.25 mm³ voxel size), the received signals from the array are scaled and delayed as follows:

$$Q_n\left(\mathbf{r};t\right)={\widehat{p}}_n\left(t+\frac{\Vert {\mathbf{r}}_n-\mathbf{r}\Vert }{c_{\text{water}}}-s_n\right)\cdot \Vert {\mathbf{r}}_n-\mathbf{r}\Vert ,$$ (1)

where ${\widehat{p}}_n\left(t\right)$ represents the filtered, time-dependent pressure measured by receiver n located at position r_n, c_water is the speed of sound in water, s_n is the skull delay correction term for receiver n, and ‖r_n − r‖ represents the distance between receiver n and the grid point r. Multiplication by ‖r_n − r‖ accounts for the signal attenuation that would occur during acoustic propagation from a point source located at r to a receiver located at r_n due to geometric spreading. The speed of sound in water was estimated through measurement of the water temperature [41] using a digital thermometer (Extech Instruments, Waltham, MA, USA). An image is formed by combining the scaled and delayed signals as follows [40]:

$$I\left(\mathbf{r}\right)=\frac{1}{T}{\displaystyle {\int }_{t_0}^{t_0+T}\left[{\left|{\displaystyle \sum _{n=1}^N{Q}_n\left(\mathbf{r};t\right)}\right|}^2-{\displaystyle \sum _{n=1}^N{\left|Q_n\left(\mathbf{r};t\right)\right|}^2}\right]dt,}$$ (2)

where [t₀, t₀ + T] is the integration window (t₀ = 0, T = 10 μs), and N is the number of array elements (N = 128). It is worth pointing out that in general the skull correction terms ({s_n}) are spatially-dependent, and that in this study the source locations were known a priori. In practice, skull correction values corresponding to the intended target location can be used for imaging around the transmit focal region, since they have been shown not to vary substantially for small reconstruction volumes [34]. For monitoring cavitation events away from the transmit focus, voxel-specific skull corrections [33] could be employed.

Two different CT-based aberration correction approaches were investigated in this study. The first method employed numerical simulations using a three-dimensional full-wave model [42] based on the linearized Westervelt equation:

$${\nabla }^{2}p-\frac{1}{c^2}\frac{{\partial }^{2}p}{\partial t^2}+\frac{2\alpha }{c{\omega }^2}\frac{{\partial }^{3}p}{\partial t^3}-\nabla p\cdot \nabla \left(\text{ln}\rho \right)=0,$$ (3)

where p is the acoustic pressure field, c, α, and ρ represent the local sound speed, attenuation, and density, respectively, and ω = 2πf is the angular frequency. The model solves equation 3 in cylindrical coordinates for the pressure field within the simulation domain using a finite-difference time-domain (FDTD) approach. A super-absorbing layer [43] was placed along the domain boundary in order to truncate the simulation volume. As an initial condition, a point source was placed at the source location of interest and emitted a pulse (10 cycles, 40% cosine-tapered [44]) that propagated outward to the array and was recorded by the receive elements. Simulations were run with and without the skull in place and the respective signals for each receiver element were cross-correlated [45], using data from the first five cycles of each pulse, to determine the time delay between the two traces, and hence the skull delay correction terms ({s_n}).

For the results presented in this paper, the simulation domain consisted of a cylinder with a 2.5 cm radius and a height of ‖r_rcv − r_src‖ + 3 cm (1.5 cm on either end), where r_rcv and r_src denote the receiver element and source locations, respectively. The simulations were run long enough for each transducer to receive the entire 10 cycle pulse after propagation through water. The spatial discretization of the simulations was set to Δh = λ/10 along the longitudinal and radial axes, where λ is the acoustic wavelength in water, while the angular discretization was Δθ = 7.5°. The temporal “gearing” approach described in [46] was employed (gearRadius = 11, gearRatio = 16), which led to a temporal discretization of Δt_inner = 1.3 ns and Δt_outer = 20.7 ns for voxels within and beyond the gearRadius, respectively. A custom-built CPU (2.0 GHz processor, 32 GB memory, 6 cores) containing a single NVIDIA (GeForce GTX Titan, 6 GB memory, 2688 cores) graphics processing unit (GPU) was used to run the full-wave ultrasound propagation model, which was implemented in C++ and the compute unified device architecture (CUDA) GPU platform.

The second method was an analytical method [47] similar to that currently employed by commercial focused ultrasound brain systems (ExAblate^® 4000, InSightec, Haifa, Israel) for transmit focusing through the skull bone [32]. For a given source location, the delay term for each receiver was determined by analyzing the longitudinal sound speed profile (Δh = λ/10) within the skull along the ray cast between the source location and the center of the receiver element [47], similar to the method employed in [37] for transcranial imaging. The skull delay term for receiver element n was calculated as the difference between the trans-skull time-of-flight estimated using this approach, which ignores both reflection and refraction effects, and the corresponding water-path case:

$$s_n=\left[\frac{L_n}{c_{\text{water}}}-{\displaystyle {\int }_0^{L_n}\frac{dr}{c_{\text{skull}}\left(\rho \left(r\right)\right)}}\right],$$ (4)

where c_skull is the longitudinal skull sound speed, and the integration is carried out over the portion of the ray within the skull bone, whose length is denoted by L_n.

Both CT-based techniques were evaluated assuming either homogeneous or heterogeneous acoustical properties. Spatial maps of the material properties of skull bone were extracted from the CT data [33, 34] based on the empirical relations between apparent density and longitudinal sound speed/attenuation for skull bone presented in [48]. For the homogeneous cases, the mean values of the acoustical parameters for each skull specimen were used (see table 2). Multiple landmarks (5–8, depending on the skull specimen [34]) on the inner and outer skull surfaces that were easily identifiable in the CT image data of the same specimen were measured in order to register the skullcaps to the receiver array for the simulations, which led to a mean landmark error of less than 1 mm for all experiments performed [34]. Images generated using the various CT-based approaches were compared with those obtained through an invasive source-based method [38], as well as images formed without skull corrections. The invasive source method is the experimental analogue of the full-wave CT-based technique; a fixed source emitter is placed at the source location of interest, excited with an impulse from the pulser/receiver, and the signals received by the array with and without the presence of the skull are compared to determine the correction term for each receiver element. This technique has been used as the gold standard method in many studies investigating aberration correction in transcranial ultrasound [24, 27, 10, 19]. Figure 2 illustrates phase aberration calculation for one skull near the array’s geometric focus using both the invasive source- and noninvasive CT-based approaches.

Table 2.

Mean (± standard deviation) density and longitudinal sound speed/attenuation values for the skull specimens used in this study. The acoustical parameters are based on interpolating the data presented in Pichardo et al. [48] for a frequency of 516 kHz. The values are calculated based on rays from the array’s geometric focus to each of the 128 receiver elements.

Skull	Density [kg m−3]	Sound Speed [m s−1]	Attenuation [Np m−1]
A	1797 ± 85	2282 ± 250	121 ± 16
B	1951 ± 196	2466 ± 315	129 ± 19
C	1946 ± 86	2433 ± 289	126 ± 18
D	1687 ± 91	2190 ± 267	121 ± 16

Figure 2.

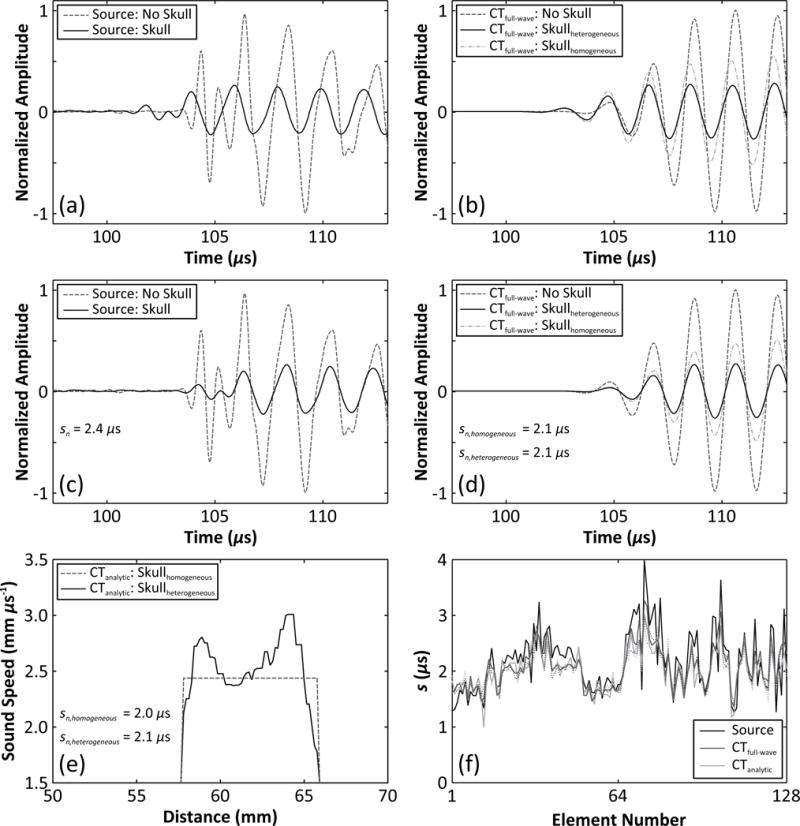
Representative example of skull aberration calculations at the array’s geometric focus for Skull B. (a) Measured and (b) simulated (full-wave model; heterogeneous and homogeneous cases) signals captured with and without the skull in place are shown for a single receiver (element 45), along with the aligned signals (c,d) after cross-correlation to determine the delay value. (e) Longitudinal sound speed profile along the ray cast between the receiver element and the source location, illustrating skull delay calculation with the analytical model (heterogeneous and homogeneous cases). (f) Skull delay terms for the entire 128-element array. The dotted lines in (f) represent results for the homogeneous skull case for each CT-based method.

3. RESULTS

Figure 3 shows representative examples of images generated from the fixed source emitter placed at the array’s geometric focus. In general, the inclusion of skull corrections (source- or CT-based) into the beamforming algorithm resulted in improved image quality (i.e. increased peak intensity, decreased sidelobe levels and general background signal, and reduced positional shift) compared to the case without corrections [Fig. 3]. Considering each CT-based model separately, the corrections obtained from simulations with heterogeneous skull properties provided improvements (e.g. larger peak intensity, smaller signal volume) over the corresponding homogeneous case [Fig. 3]. Finally, comparing the two CT-based methods, the numerical full-wave approach led to image reconstructions with a smaller main lobe volume, lower sidelobe levels, and a higher peak intensity than those obtained using the relatively simple analytic approach [Fig. 3].

Figure 3.

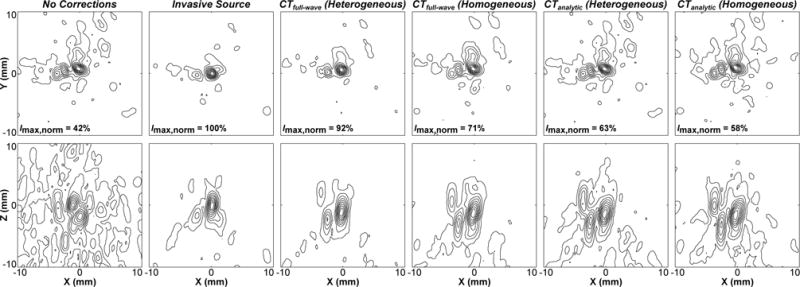
Contour images of the fixed source emitter located at the array’s geometric focus, reconstructed through a human skullcap (Skull B) without corrections, with source- and various CT-based skull delay corrections. Lateral (top row) and axial (bottom row) maximum intensity projection images (2 cm stack) are shown. The peak intensity for each image is given normalized to the gold standard source-based correction case (I_max,norm). Linear contours are displayed at 10% intervals.

Figure 4 demonstrates the dependence of image signal-to-noise ratio (SNR) on source location within the skull cavity for each aberration correction approach, using data from a single skullcap. In general, image SNR decreased as the source location was moved away from the geometric focus of the array [33, 34] [Fig. 4]. Both CT-based techniques (homogeneous and heterogeneous) provided improvements in image SNR compared to the no correction case, however, both were outperformed by the invasive source-based approach [Fig. 4]. For each CT-based approach, calculations made with heterogeneous skull properties yielded a higher image SNR than the corresponding homogeneous case [Fig. 4]. Finally, of the two CT-based techniques the full-wave simulation approach restored the image SNR closer to the values obtained from the gold standard method than did the ray approximation [Fig. 4].

Figure 4.

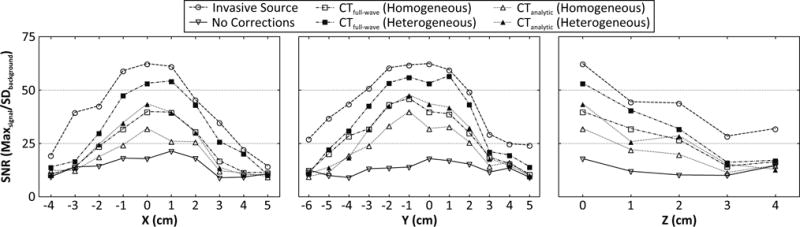
Image signal-to-noise ratio (SNR, defined as the the ratio of the maximum intensity to the standard deviation of the background signal [34]) as a function of source location. Results from transcranial (Skull C) reconstructions without skull corrections, with source-based and various CT-based skull delay corrections are shown.

Figure 5 and table 3 quantify the performance of each trans-skull aberration correction technique. The plots show the percentage of data points greater than a particular error margin, defined as the deviation from the gold standard source-based correction technique, for four different image quality metrics [Fig. 5]. The sharper the decay of the curve the better the correlation between the particular method and the gold standard approach. The plots were generated by considering source locations at least 2.5 cm from the inner skull surface, since more superficial locations can result in multiple foci when CT-based corrections are employed [34]. For each image quality metric, the area under the curves plotted in figure 5 were calculated to quantitatively compare the different techniques [Table 3], with a smaller area corresponding to better performance. Similar trends to those apparent in figures 3 and 4 are present; namely each of the CT-based techniques provided improvements in all four metrics compared to the no correction case, secondly, corrections calculated with heterogeneous skull properties led to improvements in each metric when compared to the corresponding homogeneous case for both the analytical and numerical models, and finally, the full-wave model outperformed the ray-based approach in terms of all four metrics considered [Table 3].

Figure 5.

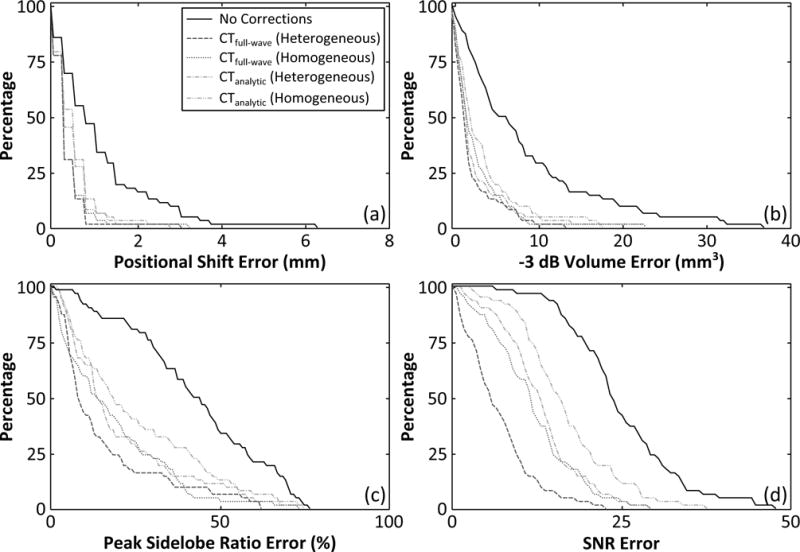
Comparison of different aberration correction techniques for transcranial passive imaging. The percentage of data points with a given error value (deviation from the gold standard, source-based correction method) or greater are plotted for four different metrics: (a) positional shift, (b) −3 dB volume, (c) peak sidelobe ratio, and (d) image SNR. The plots were generated from data points corresponding to source locations at least 2.5 cm from the inner skull surface [62/106].

Table 3.

Area under the curve of the histograms plotted in figure 5, normalized to the “no corrections” case.

Correction Technique	Positional Shift	−3 dB Volume	Peak Sidelobe Ratio	Image SNR
No Corrections	1.00	1.00	1.00	1.00
CTfull–wave (Heterogeneous)	0.34	0.26	0.52	0.39
CTfull–wave (Homogeneous)	0.36	0.33	0.58	0.58
CTanalytic (Heterogeneous)	0.46	0.32	0.62	0.62
CTanalytic (Homogeneous)	0.47	0.41	0.69	0.74

The improvements in image quality obtained from the full-wave ultrasound propagation model came at the cost of increased computational complexity. The computational times for the two CT-based models are compared in figure 6. On average, the full-wave simulations took approximately three orders of magnitude longer (7.8±0.4 h vs. 27±2 s) to compute than calculations using the analytic, ray-based approximation for our 128-element array (p < 10⁻⁴; two-tailed paired t-test).

Figure 6.

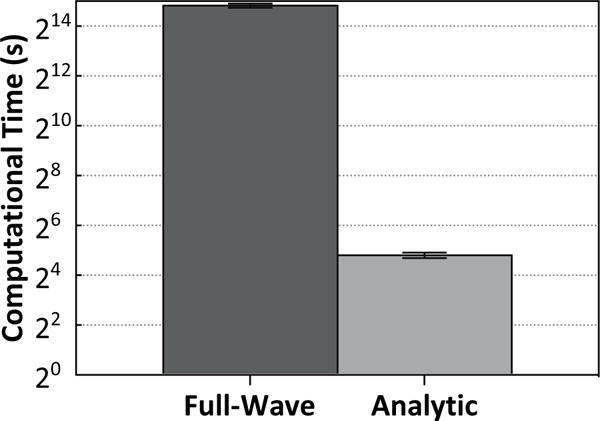
Computational time (mean ± standard deviation) for the two different CT-based aberration correction techniques, plotted on a logarithmic scale. The values quoted are for the full 128-element array, and are averaged over all skulls and locations.

4. DISCUSSION

Two non-invasive, CT-based methods for aberration correction in transcranial ultrasound imaging were compared in terms of their resulting improvements in image quality, as well as computational efficiency. A trade-off was demonstrated between image quality and calculation time; corrections calculated via three-dimensional full-wave ultrasound propagation simulations provided better image quality than those obtained from a ray-based approximation, however, they took considerably longer to calculate. Such long computation times (on the order of hours) are currently prohibitive from a treatment planning standpoint, however, as the performance capabilities of affordable hardware increases, it is expected that numerical simulations will replace their analytic counterparts in this domain. In particular, the use of hybrid numerical methods where acoustic propagation in weakly heterogeneous, fluid-like media such as water or brain tissue is treated using efficient, approximate models (e.g. ray acoustics, angular spectrum method) whilst more sophisticated (e.g. finite-element, finite-difference) methods are employed in strongly heterogeneous bone regions [49, 50] is an attractive option for reducing computational complexity without sacrificing model performance. Although this study was concerned with aberration correction for trans-skull imaging, our results are expected to hold for the case of transmit focusing through the skull, due to the principle of spatial reciprocity.

It is well known that the skull’s acoustical parameters vary as a function of location within the bone [2, 47, 51, 48]. As a result, the waves emitted/received by each transducer element will experience different aberrations based on the specific path traversed by the beam through the skull. It is therefore not surprising that calculations accounting for intra-skull heterogeneity outperform those that assume homogeneous properties, and this in direct agreement with the previous work of Clement and Hynynen [47]. In that study, it was demonstrated that CT-based models accounting for cranial heterogeneity were capable of better predicting the phase lags induced by the skull bone compared to both single- and three-layer models that employed bulk acoustical properties based on values found in the literature [47].

The propagation of acoustic waves through the cranial bone is a complex process involving many different physical phenomena (e.g. reflection, refraction, attenuation, mode-conversion, etc.). The approximate ray-based model considered in this study assumes normal incidence conditions throughout trans-skull propagation [47], and therefore fails to account for any refraction occurring at the inner and outer skull surfaces or within the bone itself. Refraction is a major source of de-focusing in transcranial ultrasound [2, 3] and indeed, taking refraction into account using numerical full-wave simulations resulted in improved image quality with our experimental setup. This finding is consistent with a recent simulation study [52], which showed that the use of a full-wave model to calculate the driving signals for a clinical brain therapy device (ExAblate^® 4000, 650 kHz system; InSightec, Haifa, Israel) led to improved focusing and, as a result, a 45% increase in the peak focal temperature achieved compared to the case where the driving signals were determined by the device’s treatment planning software (Fig. 7 of that study). A similar finding was subsequently obtained in a simulation study of transcranial sonications with InSightec’s low-frequency (230 kHz) device [53].

Neither model investigated in this study incorporated shear waves, which are supported by the human cranium [2] and in certain configurations can be the dominant mode of propagation through the skull bone [54, 55]. If the shear acoustical properties of skull bone could be accurately determined, the use of more complex models [49, 56, 52] might further improve simulation-based aberration correction, particularly in the case of transmit focusing or imaging at locations close to the inner skull surface where the angles of incidence are such that significant mode conversion is present [57]. Similarly, models based on Biot’s theory of acoustic propagation in elastic porous media [58] may create more physically realistic predictions, hence improving transcranial aberration correction calculations, though this would require the measurement of new material parameters for human skull bone.

5. CONCLUSION

Analytical and numerical approaches for CT-based aberration correction during transcranial passive acoustic imaging (at f ≈ 0.5 MHz) were compared. For both models, corrections achieved by allowing for heterogeneous skull acoustical parameters in simulation outperformed the corresponding case where homogeneous parameters were assumed. Of the two methods, the full-wave numerical model provided the best image quality (e.g. higher image SNR, lower peak sidelobe ratio), at the cost of having a significantly larger computational burden (increased calculation time by over three orders of magnitude). As the power of computational resources increases, the feasibility of more sophisticated numerical approaches for CT-based aberration correction in transcranial ultrasound increases. Although presented in an imaging context, our results may be applicable to the problem of transmit focusing through the skull.