Abstract
Recent model development of the Zodiacal Dust Cloud (ZDC) model (Nesvorný et al. 2010, 2011b) argue that the incoming flux of meteoric material into the Earth’s upper atmosphere is mostly undetected by radars because they cannot detect small extraterrestrial particles entering the atmosphere at low velocities due to the relatively small production of electrons. In this paper we present a new methodology utilizing meteor head echo radar observations that aims to constrain the ZDC physical model by ground-based measurements. In particular, for this work, we focus on Arecibo 430 MHz observations since this is the most sensitive radar utilized for this type of observations to date. For this, we integrate and employ existing comprehensive models of meteoroid ablation, ionization and radar detection to enable accurate interpretation of radar observations and show that reasonable agreement in the hourly rates is found between model predictions and Arecibo observations when: 1) we invoke the lower limit of the model predicted flux (~16 t/d) and 2) we estimate the ionization probability of ablating metal atoms using laboratory measurements of the ionization cross sections of high speed metal atom beams, resulting in values up to two orders of magnitude lower than the extensively utilized figure reported by Jones (1997) for low speeds meteors. However, even at this lower limit the model over predicts the slow portion of the Arecibo radial velocity distributions by a factor of 3, suggesting the model requires some revision.
Subject headings: Zodiacal Dust Cloud, Meteors, Head-Echo, Radars
1. Introduction
The global meteoric input to the upper atmosphere is a hotly debated quantity, with estimates varying by 2 orders of magnitude, depending on measuring techniques (Plane 2012). The majority of the input is in the form of microgram size particles which, in most cases, completely ablate injecting metals to planetary atmospheres. Accurate constraint of this quantity is crucial for a variety of research areas. The meteoric mass input is transported into the middle atmosphere, where the coupling between the lower and upper atmosphere takes place. If the meteoric mass input is closer to the upper limits of current estimates, then the vertical transport in the middle atmosphere must be considerably faster than generally believed; while the opposite case would require the revision of our understanding of dust evolution in the solar system. There is thus a need for better understanding of this quantity in a comprehensive manner, that is by combining models of dust release from celestial bodies, orbital evolution, ablation and ionization processes when dust particles encounter planetary atmospheres and ultimately by constraining these models simultaneously by all available observing techniques.
A new Zodiacal Dust Cloud (ZDC) model, hereafter referred as ZoDy, recently developed by Nesvorný et al. (2010) represents a fundamental approach to understanding the origins of Interplanetary Dust Particles (IDPs). The model follows the dynamical evolution of dust particles after ejection utilizing the orbital properties of comets and asteroids. One of the main results is that it predicts that 85–95% of the dust in the inner solar system comes from Jupiter Family Comets (JFCs), with the remainder from the asteroid belt, Halley type comets and Oort Cloud comets (OCCs). Furthermore, the modeled results show that most of the dust, which drifts down towards the inner solar system under the influence of Poynting-Robertson drag, has a mass in the range 1 – 10 μg and provides a continuous input of extra terrestrial material into Earth that has dynamical characteristics that are in disagreement with various type of measurement results. Specifically, the model predicts that most of the IDPs enter the terrestrial atmosphere from a near-prograde orbit with a mean speed with respect to Earth of about 14 km/s and a peak at 12 km/sec (solid line in Figure 1). The low average speed and the absence of significant orbital eccentricities, also a prediction of the model, do not accord with various types of meteor radar observations, which record average speeds closer to 30 km/s (dash line in Figure 1). Furthermore, these low speeds are in disagreement with results from the impact experiments on board of the five Lunar Orbiters and Explorers XVI and XXIII (the latter the same detectors flown near the Earth, P. Brown, Personal Communication, 2014). The impact rate at the moon was ~1/2 that of the Earth to a limiting mass of >10−9 g. The factor of roughly two indicates that the speed needs to be approximately (at the top of Earth’s atmosphere) ~15 km/s. For ZoDy-like values (just ~1 km/s from escape speed, so just 12–13 km/s) the enhancement between the Earth and Moon would be many times larger (Zook 1975). More recently, Cremonese et al. (2013) showed that in order to model the Na production on the Moon by micrometeoroid impacts with masses in the similar range than those considered by ZoDy, the mean velocity of the impactors was required to be 15.3 km/s and 18.6 km/s at the Moon and Earth respectively, which is closer to that assumed in the interpretation of the Long Duration Exposure Facility (LDEF) results (Love & Brownlee 1993).
Fig. 1.
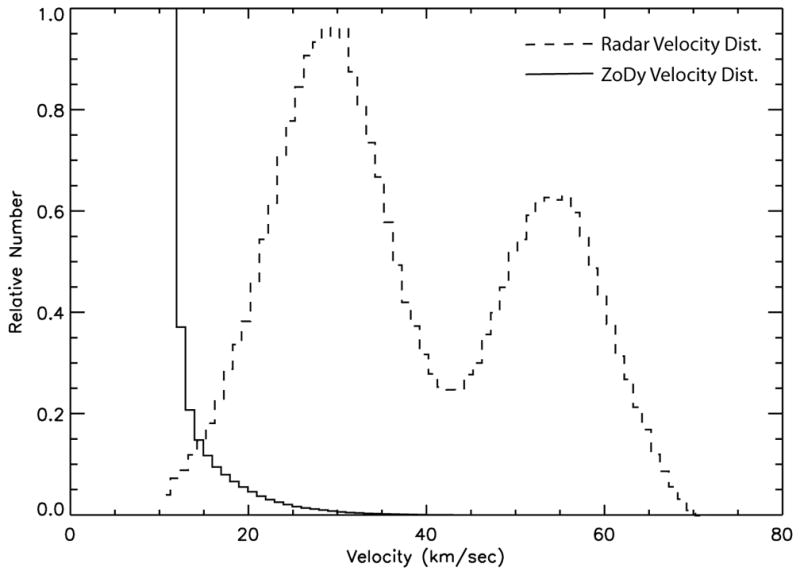
Solid line shows the velocity distribution resulting from ZoDy (Nesvorný et al. 2010). Dash line represents the velocity distribution at the top of the atmosphere generally measured by radars (Fentzke & Janches 2008).
ZoDy is currently quantitatively only constrained by Infrared Astronomical Satellite (IRAS) observations of the ZDC and originally predicted a total global meteoric mass input onto the Earth’s atmosphere equal to 270 t.d−1 (metric tons). However, Nesvorný et al. (2011a) later improved ZoDy by including a perihelion distance (q) dependent meteoroid production rate taking into account orbits with q<1.5 AU, a continuous Size Frequency Distributions (SFD) of particles instead of the original delta functions, and the proper inclusion of collisional lifetimes of JFC particles which resulted in a more precise parameterization of their collisional disruption in space. These improvements resulted in a revised total mass input on Earth of 32 t.d−1. Because the IRAS observations primarily constrains the modeled ZDC cross section and not the mass, then different assumptions regarding the particle mass distribution or distributions of q results in the uncertainties on the total flux being as large as 50% (Nesvorný et al. 2011a), where the cross-section is given by
| (1) |
where πr2 is the cross-section of a particle with radius r and N(r) is the total number of particles with radius r contributing to the IR emission. This total cross-section determines the ability of ZoDy to emit in infrared, and thus to be constrained from observations.
In addition to a revision to the model, Nesvorný et al. (2011a) attempted to loosely constrain the model with terrestrial observations using results from the Canadian Meteor Orbit Radar (CMOR; Webster et al. 2004) and the Advanced Meteor Orbit Radar (AMOR; Baggaley et al. 1994). The authors concluded that this flux, and consequently most of the incoming meteoric mass flux into the Earth’s atmosphere, is mostly undetected by CMOR while the more sensitive AMOR should detect between 10 to 50% of the incoming flux predicted by ZoDy, depending on model assumptions. The large difference in detections by specular trail meteor radars, as compared to those from satellite dust impact detector measurements, has been noted in the past by Hughes (1978) who concluded that, similarly to Nesvorný et al. (2011a), meteor radars cannot be used to retrieve the mass flux reliably. The radar measurements used by Nesvorný et al. (2011a), however, do not have the sensitivity to observe the particle masses dominant in ZoDy when the particles travel at low speeds (because of a low production of electrons through ablating elements making hyperthermal collisions with air molecules). AMOR is the most sensitive of the two meteor radars with reported limiting masses for particles traveling at 30 km/sec of the order of 1 μg, while CMOR’s limiting mass at this speed is 2 orders of magnitude larger (Galligan & Baggaley 2005; Brown et al. 2008). Therefore, the conclusions reported by Nesvorný et al. (2010) and Nesvorný et al. (2011a) that these radars cannot detect most of the ZoDy meteors is consistent with expectations. However, one of ZoDy’s main implications that most of this flux comes into the atmosphere largely undetected by ground-based instrumentation could not be unequivocally tested.
It is crucial to constrain the ZDC model with radar observations not only to obtain a unique value of the total incoming mass flux, which must be independent of the observing technique but also to precisely characterize the orbital distribution of dust in the Near-Earth space. The ZDC is the source of meteoroids originating from the so-called Sporadic Meteor Complex (SMC). Ground-based meteor observations with radars detect thousand of sporadic events every day providing data sets with great statistics optimal to study the ZDC. The SMC is composed of six main directional enhancements of the meteor radiants (i.e. orbital families). These are referred to as apparent sources since they are not linked to their original parent body. These apparent sources are known as the North and South Apex, composed mainly of dust from long period comets and initially studied by Sekanina (1976); the Helion and Anti-Helion, composed of dust from short period comets originally reported by Hawkins (1956)1 and Weiss & Smith (1960); and the North and South Toroidal composed of dust from Halley-family comets (Jones & Brown 1993; Taylor 1997; Taylor & Elford 1998; Campbell-Brown & Wiegert 2009; Pokorný et al. 2014). Each of these sources produce specific signatures in the radar detected distributions that depend on geographical location of the observer, seasonality and radar system characteristics (Janches & Chau 2005; Janches et al. 2006; Fentzke & Janches 2008; Fentzke et al. 2009; Sparks et al. 2009; Sparks & Janches 2009b,a; Pifko et al. 2013). Because of the wide variety of radar systems utilized for meteor observations (Janches et al. 2008, 2014) and their different locations, these observations are key to constrain not only the total amount of meteoric material coming into the atmosphere, but also the directionality and seasonality of the flux which is directly related to the orbital characteristics.
The most sensitive radar in the world currently used for meteor studies is the Arecibo 430 MHz radar. While traditional VHF meteor radars (often called all-sky radars) such as CMOR and AMOR primarily detect the specular reflection of meteor trails traveling perpendicular to the line of sight of the scattering trail, high-power and large-aperture (HPLA) radars, such as Arecibo, efficiently detect meteor head echoes (Janches et al. 2003; Janches et al. 2014). Trails are generally semistationary echoes that originate from the ionization left behind by the meteoroid (Baggaley 2002) and are confined to one altitude. Head echoes, on the other hand, are reflections from the plasma immediately surrounding the meteoroid itself traveling at, or near, its speed (Janches et al. 2000a, 2003). HPLA radars are also very sensitive instruments with generally very narrow beam width and much higher transmitted power densities (Janches et al. 2008, 2014) and thus sensitive to the detection of meteors produced by smaller particles because they require a lower amount of electrons than systems like AMOR and CMOR. In this manuscript we utilize a combination of several models as well as Arecibo meteor observations to determine if the sensitivity of this system is sufficient to constrain ZoDy with ground-based observations. To accomplish this task we: 1) determine if Arecibo can detect 1–10 μg particles traveling at 11–20 km/sec; and 2) if that is the case, then estimate what portion of the Arecibo meteor observations can be modeled with the flux predicted by ZoDy in order to further constrain the model with ground – based observations.
2. Radar Detection Sensitivity Modeling
2.1. Meteor Head-Echo Signal-to-Noise Ratio
The first task we address is to assess the ability of the Arecibo 430 MHz radar to detect small particles (m < 10 μg) traveling at slow velocities (V < 20 km/s). Although similar attempts have been made in the past (e.g. Janches et al. 2008, 2014), in the work presented here we introduce several improvements to our methodology that include our latest understanding of meteor ablation processes and the determination of the meteor head-echo Signal-to-Noise Ratio (SNR) that will be detected by the Arecibo 430 MHz, given a set of meteor dynamical parameters (i.e. mass, velocity and entry angle). For this we utilize the radar equation given by
| (2) |
where in particular for the observational results we utilize here, Pt is the transmitted power (1 MW), λR is the radar wavelength (69 cm), G is one-way antenna gain pattern, R is the meteor range, σ is the meteor Radar Cross Section (RCS) and Pn is the system noise power given by
| (3) |
where k is the Boltzmann constant, B is the noise bandwidth (1 MHz) and Tsys is the system temperature (~120 K).
In previous works we have utilized σ as a proxy of the sensitivity of the radar to the detection of meteor head echoes (Janches et al. 2008; Fentzke & Janches 2008; Fentzke et al. 2009; Pifko et al. 2013), which requires the assumption that the antenna radiation pattern is uniform and thus for a particle with a given σ, the resulting SNR will be independent of where the meteor is detected within the radar beam. In the present study we improve our previous treatment by modeling the meteor SNR, a task that requires understanding the relation between equation 2 and the meteor entry parameters. In other words, we need to calculate how the SNR varies as a function of particle mass, velocity and entry angle while considering all possible paths that the meteoroid trajectory can take while crossing the radar beam. For this we need to model both the Arecibo antenna gain and σ.
2.2. Arecibo Radar Gain
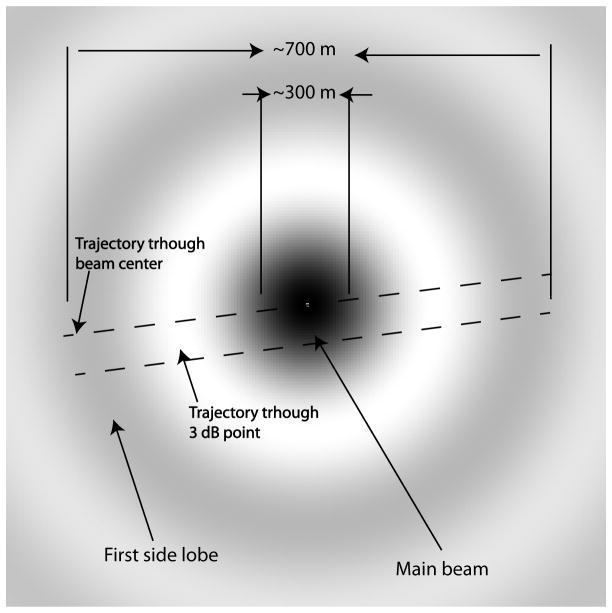
In order to model the gain (G) of the Arecibo antenna we adopt the same approach reported by Dyrud & Janches (2008), which characterizes the pattern of the radar main beam as a Gaussian with a 3 dB point at approximately 150 m from the center. The peak of the main lobe is given by
| (4) |
where the Aeff is the approximate aperture given by
| (5) |
where η is the approximate aperture efficiency of 0.7 and 150 m is the Arecibo dish radius, resulting in G ~ 61 dB. This is 2 dB lower than considered previously in Janches et al. (2014) because in that work we considered η to be equal to 1. However this difference is within the expected uncertainty. We also consider the Arecibo first side lobe in which detection occurs frequently (Janches et al. 2004), assuming it to be also a Gaussian centered about 500 m from the center of the main beam and a 3 dB width of 50 m. Although the description of the Arecibo beam as two Gaussians is somewhat simplistic, it is in good agreement with more robust modeling of the antenna pattern described in the past (Breakall & Mathews 1982; Mathews et al. 1997). The peak of the side lobe is considered to be 17 dB lower than the peak of the main beam. This description resulted in good agreements with observations in previous modeling work of head echoes (Dyrud & Janches 2008). It is worth noting that the expected error in the SNR values resulting from Equation 2 introduced by errors in the measured variables of Equations 3 and 4 is approximately 3 dB (factor of 2).
2.3. Meteor Radar Cross Section (RCS) derived from the Chemical Ablation Model (CABMOD)
The meteoroid RCS depends on the production of electrons as the meteoroid ablates while entering the Earth’s atmosphere. In this work, we adopt the description of the RCS reported by Mathews et al. (1997), which assumes that the radar return originates from coherent electron-scatter from the free electrons in the small volume surrounding the meteor and that the backscatter cross-section of an ensemble of Ne electrons is given by
| (6) |
where re is the classical electron radius (2.8179402894 × 10−15m) and V, α and m are the meteoroid entry velocity, zenith angle and mass respectively. In this scenario all electrons (single) scatter in-phase and thus the scattered electric fields add so that scattered power is a function of . This is valid because the characteristic size of the ensemble is small compared with the radar wavelength (Mathews et al. 1997). We assume also that, at a given time, the diameter of the cloud of electrons producing the head-echo is of the order of the atmospheric mean free path (MFP), which is in agreement to various head echo models (Close et al. 2002; Close et al. 2004), given by
| (7) |
where R is the Gas Law constant (8.314510 J/(K mol)), Ta(h) is the atmospheric temperature at a given altitude, da is the air molecule collisional cross section (3.57×10−10m), and Pa(h) is the air pressure at a given altitude.
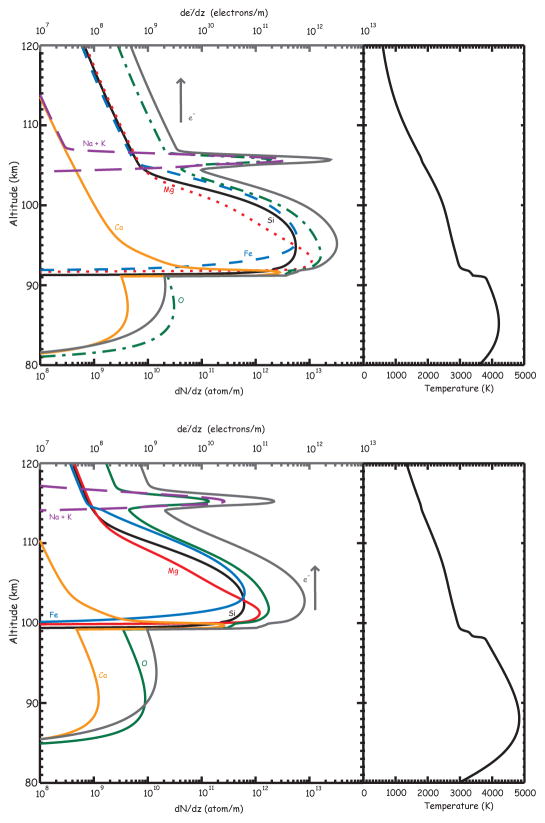
The production rate of electrons depends on the ionization probability βip (Jones 1997), which in turns depends only on meteoroid mass, composition and velocity. Radar detectability of meteors has typically been estimated by using a crude average of this parameter (Close et al. 2002; Close et al. 2005), which in reality it can vary up to 2 orders of magnitude depending on the constituent under consideration (Vondrak et al. 2008). Thus, in order to overcome this limitation we further improve our radar detection sensitivity treatment by including results from the Chemical Ablation Model (CABMOD) developed by Vondrak et al. (2008). CABMOD predicts differential ablation, i.e. the most volatile elements – Na and K – ablate first, followed by the main constituents Fe, Mg and Si, and finally the most refractory elements such as Ca. The model considers the full treatment of the ablation and ionization of the individual chemical elements by including the following processes: sputtering by inelastic collisions with air molecules before the meteoroids melt; evaporation of atoms and oxides from the molten particle; diffusion-controlled migration of the volatile constituents (Na and K) through the molten particle; and impact ionization of the ablated fragments by hyperthermal collisions with the air molecules. Evaporation is based on thermodynamic equilibrium in the molten meteoroid (treated as a melt of metal oxides), and between the particle and surrounding vapour phase. The loss rate of each element is then estimated by applying Langmuir evaporation. Figure 2 illustrates the elemental injection profiles calculated by CABMOD for two different meteoroid speeds assuming the initial composition of the meteoroids is chondritic (Plane 1991). The two cases shown in this figure in particular have been validated against meteor head-echo observations using the Arecibo radar in which the predicted small scale, temporal and spatial, features have been observed (Janches et al. 2009).
Fig. 2.
Ablation profiles of the individual elements, electron production and the meteoroid temperature, for particles moving at 35 (top) and 50 km/sec (bottom) produced by CABMOD. The arrows point at the upper abscissa for the units of the electron profile curve (grey line).
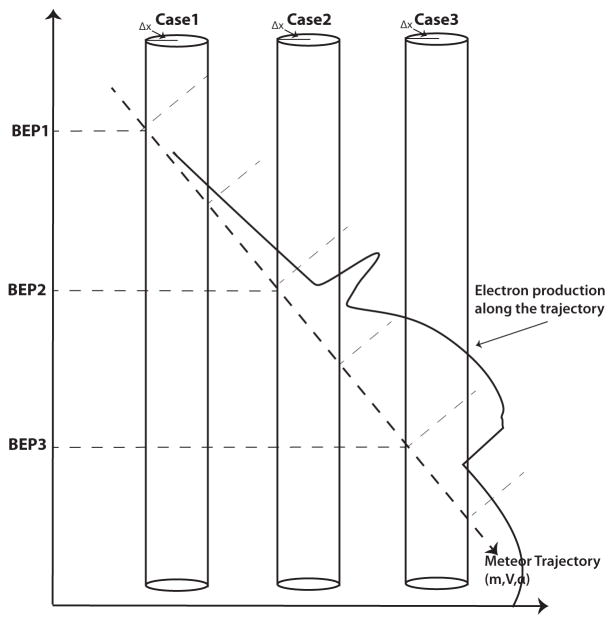
As shown in Figure 2 the entire ablation profile, and thus electron production, of a meteoroid with a given mass, entry angle and velocity will occur over a prolonged altitude range (> 60 km). However, only a relatively small part of the ablation curve of the meteoroid will occur within the same region of space that is being illuminated by a given radar. If we define the Beam Entry Point (BEP) as the meteoroid altitude when the particle is at a predefined horizontal distance Δx from the beam center, then for meteoroid BEPs higher than a certain value, the particle will cross the radar beam at the beginning of the ablation process when Ne is small and the detected SNR will be below the radar detection threshold. On the other hand, if the BEP is in the range of typical meteor observed altitudes (~80–120 km; Janches & ReVelle 2005; Sparks & Janches 2009b,a), then the meteoroid will cross the beam during the time when most of the ablation occurs and result in an SNR well above the noise threshold and the event will be detected. Finally, if the BEP is lower than a certain value, most of the ablation of the particle would have occurred before it entered the radar beam and thus the electron production will be low resulting in an undetected event. This is shown in Figure 3 where three examples of beam entry cases of a given meteor trajectory are displayed. In fact, within this altitude range, there are two different ablation regimes that can produce the detected signal as shown in Janches et al. (2009). The first one occurs at higher altitudes over a narrow altitude range producing very strong signals due to the rapid ablation of the meteoroid alkalis (Na and K), while the second regime produces lower signal intensity at lower altitudes and over a wider range and is produced by the ablation of the main elements. This effect will be discussed in more detail later in this section.
Fig. 3.
Three possible entry points to the Arecibo radar beam by a given meteor
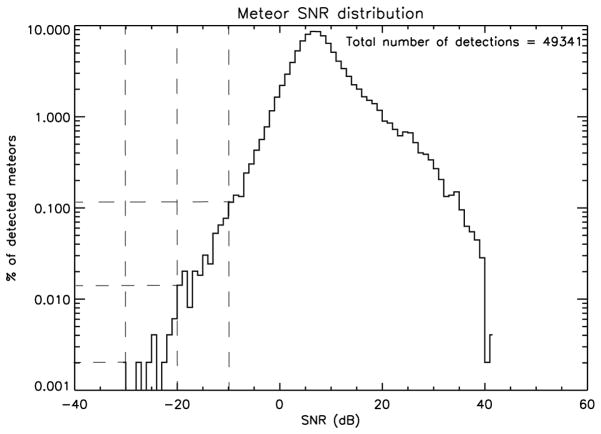
For the purpose of this work, we use CABMOD to produce look-up tables (LUTs) of elemental injection profiles as well as the number of electrons per unit length along the meteor trajectory as a function of altitude (grey line in Figure 2) for meteoroids of specified mass, speed and entry angle. The electron density is then multiplied by the MFP at the given altitude in order to obtain Ne. These results are then used in equation 6, which together with G, is then used in equation 2 to determine the SNR as a function of (V, α, m) for all possible BEPs. Given the results of ZoDy mentioned in Section 1, we first focused on determining Arecibo’s ability to detect 10 μg particles traveling at 11 km/sec. For this purpose we calculate the SNR along the trajectory of the meteor as it crosses the radar beam for BEPs ranging from 80 to 150 km, calculated every 100 m. If at some point along the trajectory the calculated SNR reaches a value above a predefined threshold we assume that the meteor was detected. The threshold value is determined from Figure 4 where the distribution of detected SNR is shown for nearly fifty thousands particles detected during a year long observing campaign carried out in 2002 utilizing the Arecibo radar. The meteor head-echo arises from the radar return scattered back from a plasma region that moves at the speed of the meteoroid. From the measurements the SNR is calculated as
Fig. 4.
Distribution of measured meteor head-echo SNR (in percent of total) for all the meteors detected by the Arecibo Observatory during the 2002 campaign. The dash lines indicate that over 0.1 % of the detected meteors will have SNR above −10 dB and approximately 1 and 2 orders of magnitude lower percentages for SNR values of −20 and −30 respectively.
| (8) |
where the Signal is the intensity of the radar return when the meteor is present and the Noise is the intensity of the radar return from the background noise. Typical meteor head echo observations transmit radar pulses approximately every millisecond and since a meteor will take longer time to travel through the radar beam, this technique enables to measure the instantaneous meteor SNR along its trajectory, as long as enough electrons are produced. The details of these measurements have been reported in several investigations employing various radars. Some examples can be found in Janches et al. (2003); Chau & Woodman (2004); Sparks et al. (2009); Pifko et al. (2013) and Janches et al. (2014).
Figure 4 demonstrates the large dynamic range in SNR of the Arecibo detections with a clear peak in the distribution located approximately at 5–6 dB. However, targets with an SNR as low as −30 dB are detected by the radar. In particular, 0.1% of the detections have recorded SNR of −10 dB and approximately 1 order of magnitude less for SNR values equal to −20 dB. These are significant percentages considering that only 10% of the detected meteors have SNRs equal to the peak value. Note that although an SNR value of −10 or −20 dB may appear to be low, this value refers to an SNR measurement for a single pulse, in which not only the object is detected but the instantaneous Doppler shift due to its radial velocity can be obtained.
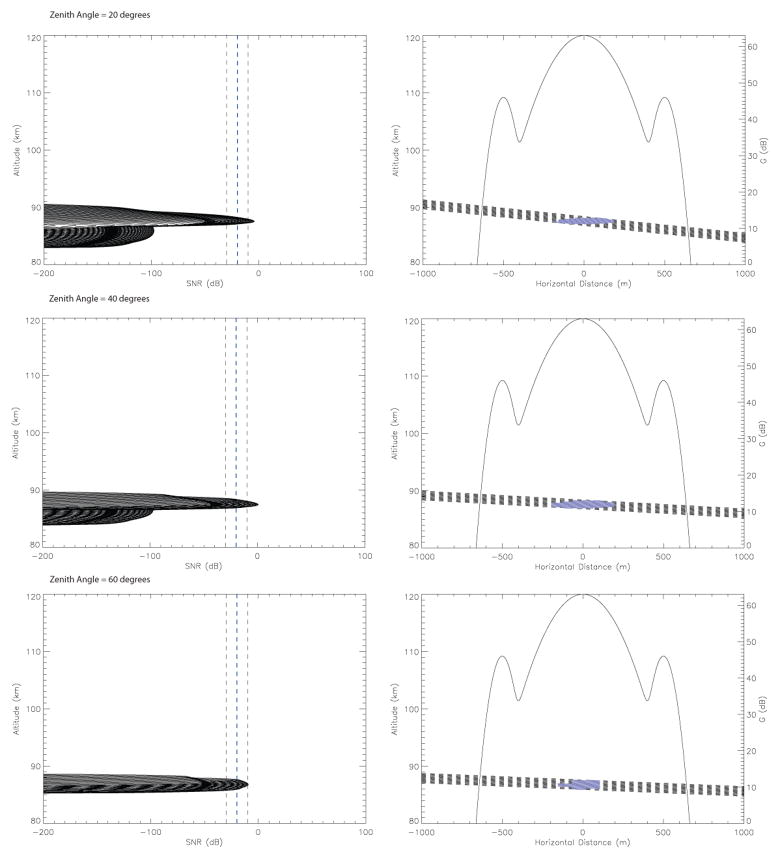
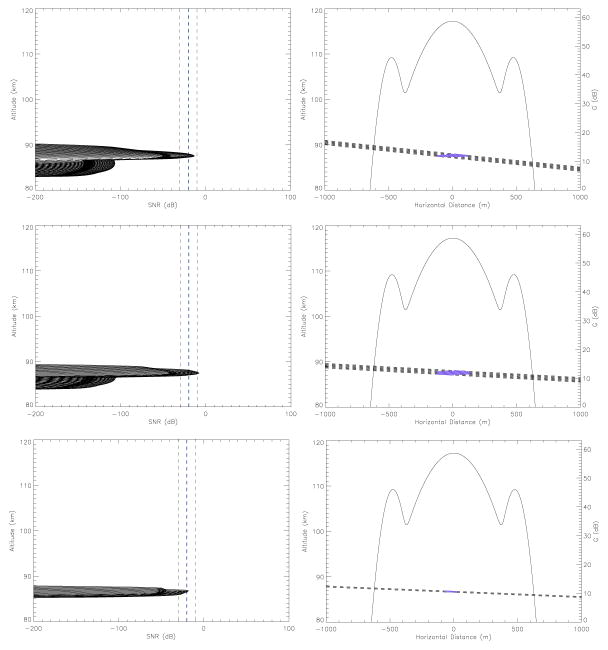
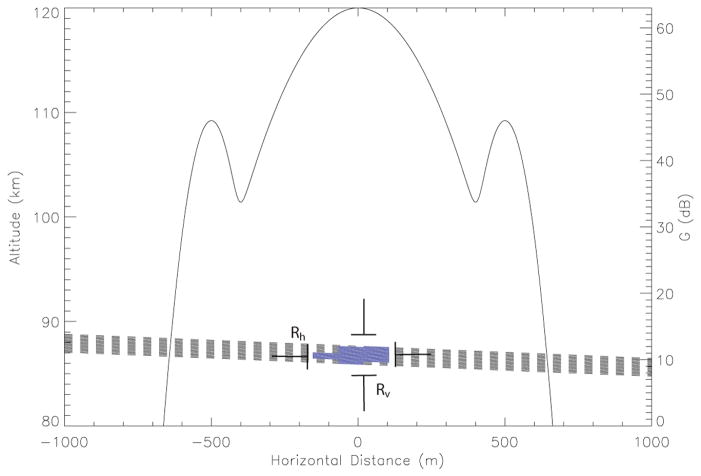
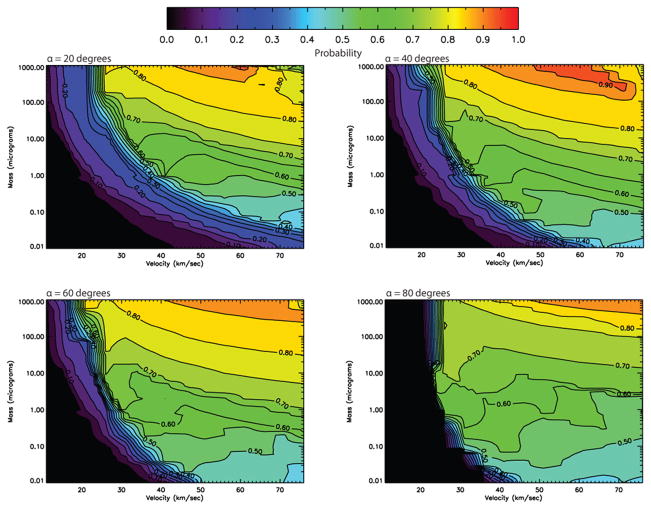
Results from our new methodology are shown in Figure 5 where the three rows represent particles entering at three different zenith angles (20°, 40° and 60°). If we define Δx to be equal to 700 m from the radar beam center, which represents the outer edge of the first radar side lobe (Mathews et al. 1997; Janches et al. 2004; Dyrud & Janches 2008), the three panels on the left of Figure 5 show the meteoroid SNR as a function of altitude for those meteors for which the BEP was such that their SNR exceeded the threshold value at some point during the ablation of the particle while entering the atmosphere (−20 dB for the examples shown in this figure). That is, particles with higher or lower BEPs would have resulted in meteors with undetected SNR’s because significant ablation would have occurred before or after crossing the radar beam. For reference purposes we also show in these panels vertical lines representing Arecibo detection threshold of −30, −20 and −10 dB. The three panels on the right of Figure 5 show the meteoroid trajectories (traveled altitude vs traveled horizontal distance; dash lines). The solid blue portion of the trajectories, showed the section during which the meteor was detectable (i.e. the SNR value was above the detectable threshold). Plotted on these panels is also G in dB (left vertical axis) to provide an indication of where in the radar beam, these meteors become detectable.
Fig. 5.
Results for the case of a 10 μg object with a speed of 11 km/sec for three different entry angles. Left panels: Meteor SNR as a function of altitude for all BEP for which the meteor calculated SNR was above −20 dB at some point during its trajectory. The vertical lines in these panels represent −30, −20 and −10 dB SNR. Right Panels: Trajectories (traveled altitude vs traveled horizontal distance; dash lines) of those meteors for which their SNR exceeded −20 dB at some point during their ablation profile. The solid blue dark portion of the trajectories, represents the section during which the SNR was greater than −20 dB. Also plotted on these panels is G in dB (right vertical axis) to provide an indication of where in the radar beam, these meteors become detectable. Each row represent a particular zenith entry angle and the trajectories are assume to cross the radar beam center.
The results shown in Figure 5 assumes that all these trajectories will cross the radar beam at the center (maximum gain). This is represented in Figure 6 where a horizontal cross-section of the radar main beam and first side lobe is shown. The dash lines represent the cases considered int his work, that is meteors crossing the center and traveling through the 3 dB point (150 m off center). Figure 7 shows the same cases but assuming that the trajectory crosses the beam at the 3 dB point (Figure 6). Examining Figures 5 and 7 we can conclude that, according to our model, a 10 μg particle traveling at 11 km/sec will produce enough electrons and thus an echo radar return signal to be detectable by the Arecibo radar. However, this is true as long as the value of the meteor BEP falls within a certain range of altitudes, which for this case is very narrow as can be seen in these figures. In addition, it is observed that the range of BEPs for which detectable SNR will be produced will depend on the entry angle and for the cases displayed in these panel the range is greatest for an entry angle around 40°, and decreases at both larger and smaller angles. Furthermore, results not shown here indicate that for this particle mass and velocity the head echo SNR will be below the detectable level for entry zenith angles higher than 60°. This is due to the fact that particles entering at very large zenith angle never heat up enough to melt because the effective scale height experienced by the meteoroid upon entry is inversely proportional to the cosine of the entry zenith angle. This means that the rate of pressure increase encountered by the particle is relatively slow, allowing the particle to radiate heat and stay cool enough to avoid melting. This is in agreement with previous modeling efforts reported by Janches & Chau (2005); Janches et al. (2006) and Fentzke & Janches (2008) who required the assumption of an empirical atmospheric filtering effect, introduced to take into account how the meteor detection rate from a source region varies with elevation above the radar site local horizon. The authors assumed that on average meteors with radiant elevations below 20° (i.e. entry Zenith angles greater than 70°) should be completely neglected.2 Our modeling results show that the effective angle at which this filtering effect will occur will depend on the physical properties of the meteoroids (i.e. velocity, composition and mass) and will be discussed in more detail in the next section.
Fig. 6.
Schematics of two tested meteor trajectories through the radar beam.
Fig. 7.
Same as Figure 5 but for trajectories crossing the 3 dB point of the radar beam (i.e. 150 m off center).
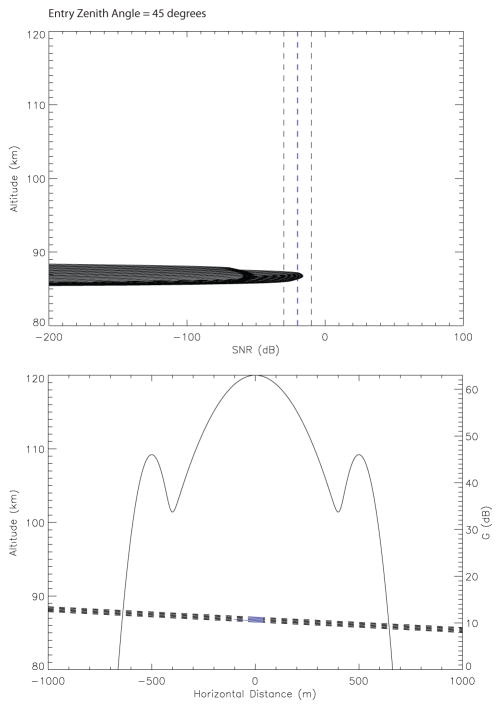
Figures 8 and 9 show the importance of considering an accurate description of the ablation process that includes the dependence of the ionization efficiency as a function, not only of meteor entry parameters, but also its constituents rather than a crude mean value. Specifically at low velocities, the entry conditions become more limited as the particle mass decreases. For example, Figure 8 shows that a 5 μg traveling at 11 km/sec and with a zenith entry angle of 45°, will also be detectable by Arecibo as long as the BEP is within a ~0.5 km altitude range. Note that the electron production is completely due to the ablation of alkalis. The transition from becoming undetectable occurs very rapidly as a particle of mass equal to 4 μg entering at the same angle results in an SNR value below the −20 dB Arecibo threshold. Interestingly, this more comprehensive detection treatment that includes the Arecibo radar gain, the meteor SNR and CABMOD shows good agreement with previously modeled results by our more simplistic approach that considered only the meteor RCS (Fentzke & Janches 2008; Pifko et al. 2013; Janches et al. 2014), which predicted that particles traveling at 15 km/sec would be detected only for masses equal or larger than 1 μg.
Fig. 8.
SNR and trajectory plots for a particle with mass equal to 5 μg, zenith entry angle equal to 45° and velocity equal to 11 km/sec travelling through the center of the radar beam.
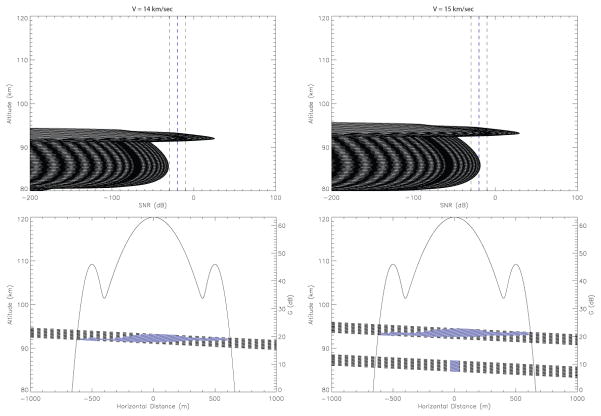
Fig. 9.
SNR and trajectory plots for 10 μg particles entering at V=14 km/sec (left panels) and 15 km/sec (right panels) and an α=45° travelling through the center of the radar beam.
On the other hand, Figure 9 shows that with a change of 1 km/sec in the incoming particle velocity the portion of the ablation profile produced by the main elements becomes detectable, increasing significantly the beam entry conditions required for the resulting meteor to be detected. Because the evaporation rates depend exponentially on the temperature (according to the Herz-Knudsen treatment utilized in CABMOD), the effect will be an apparently sudden change. This is shown in the four panels in Figure 9 where the SNR and trajectories for a 10 μg particle with speeds of 14 and 15 km/sec are displayed for a particle crossing the beam center. Comparing the top two panels of Figure 9 we can observed that the peak of the portion of the ablation curve which is produced by the evaporation of the main elements increases over 10 dB (i.e. an order of magnitude) in signal strength with only 1 km/sec increase in velocity. The alkalis, on the other hand, ablated efficiently at both speeds and produced enough electrons to enable detection even at the much–lower–gain side lobes. Furthermore, the figure suggests that if the particle’s composition would lack of alkali elements at the moment it encounters the atmosphere, then it would have been completely undetected for velocities lower than 14 km/sec. It is important to note that the meteoroid speeds and masses used in these examples are the typical values of the majority of meteoroids predicted by ZoDy, suggesting that Arecibo should detect at least a portion of the flux predicted by ZoDy. It is also worth noticing that if we take instead a more conservative detection threshold of −10 dB, some of the cases discussed would be undetected by the Arecibo radar. For example, this is the case for the a 10 μg particle traveling at a speed of 11 km/sec entering the beam at 60° off zenith and passing through the center of the beam (Figure 5; bottom panels) or entering at angles greater than 40° for the case of particles traveling off center (Figure 7; middle and bottom panels).
The results presented in Figures 5, 7, 8 and 9 show once again that, in fact, the Arecibo 430 MHz radar is sensitive to the detection of small/slow meteors and thus the optimal radar to constrain ZoDy with ground-based observations. However, these results also imply that, in order to accurately model the ability of a system to detect a certain population of particles, it is not only crucial to understand if the population posses the physical characteristics required to produce enough electrons, but also the probability that a particle from this population with those characteristics will enter the radar beam within the adequate BEP in order for those electrons to produce a detectable signal. In the next section we develop a scheme to estimate this probability as well as to determine the amount of detected particles given an incoming flux.
3. Probabilistic Approach to Estimate the Radar Detection Efficiency
In the previous section we have shown that, given the βip values reported by Jones (1997), the Arecibo Observatory can detect meteoroids with mass equal to 10 μg particles (and smaller) traveling at 11 km/sec. At these low velocities, CABMOD predicts that the particle temperature will not reach values high enough to ablate the main meteoroids elements, suchs as Fe, Mg or Si, and thus only the ablation of alkalis (Na and K) will produce electrons (Vondrak et al. 2008). This will occur very rapidly and in a very limited altitude range (see Figures 5, 7, 8 and 9; Janches et al. 2009). Since the detection of the particles depends on where in the radar beam these electrons are produced, and given the fact that this detection region will become more constrained as the amount of electrons decreases (i.e. with decreasing mass and/or velocity), this implies that the probability of detection will also decrease. On the other hand, we have also shown that only a relatively small increase in the particle’s entry velocity is sufficient to “turn on” the ablation of the main elements and “relax” the radar entry constraint. As such this will add a bias to the observations and the resulting velocity distributions that needs to be corrected for. In the past this bias was estimated using methods developed for specular trail echo observations using crude averages of the ionization efficiency and other effects typical of a semi-stationary relatively large region of ions and electrons which resulted in underestimation of the detectability (Hunt et al. 2004; Close et al. 2007; Janches et al. 2008). In this section we introduce a probabilistic approach to estimate this bias utilizing for the first time a comprehensive model of the meteoroid ablation and by quantifying the spatial limits in which the electron production is optimal for detection.
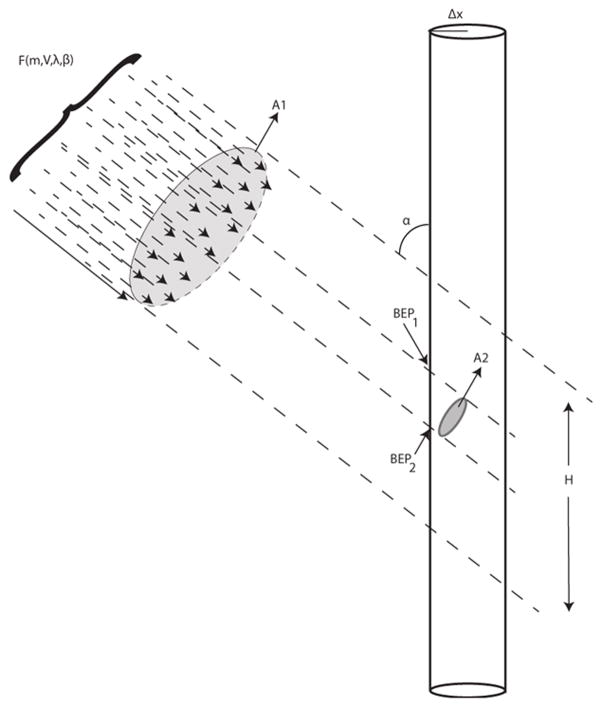
Our approach is summarized in Figure 10 where a sketch of a flux of particles (F) with a given m and V, and originating from a particular radiant characterized by the ecliptic longitude (λ) and ecliptic latitude (β) is impinging the radar illuminated volume in the atmosphere. At a given instantaneous time during the day and season, the ecliptic pair (λ,β) will be located at an angle α(t) with respect to the local zenith, where t denotes the dependance of this quantity at the instantaneous time that it is measured. Furthermore, if we denote as H the altitude range where the atmosphere is dense enough to produce ablation and hence meteors, independently of their detection, then the projection of the radar volume within this altitude range onto the direction of the flux is represented by the area A1, and given by
Fig. 10.
Schematic of our probabilistic approach.
| (9) |
As shown in Section 2.3, for a given m, V and α, out of all the particles that travel through A1, only those entering the beam between BEP1 and BEP2 will produce enough signal for detection, setting a condition that constrains the portion of the incoming flux that will be detected by the radar under consideration. That is, only those meteoroids traveling through the elliptical area identified as A2 in Figure 10 will be detected by the radar. In order to calculate this area we define two distances, displayed in Figure 11: 1) the vertical range (Rv(m, V, α)) of BEPs for which a detectable signal will be produced; and 2) the combined total horizontal distance (Rh(m, V, α)) during which a detectable signal is produced. Once they are obtained we define A2 as
Fig. 11.
Definition of horizontal and vertical distances chose to calculate A2 displayed in Figure 10. This example corresponds to a particle with m = 10 μg, V = 11 km/sec and α = 60°.
| (10) |
Note that A1 is only dependent on the zenith angle while A2 depends on the particle’s characteristics. Given these two areas we can define the probability of detection of a particle with a given mass, velocity and entry angle as:
| (11) |
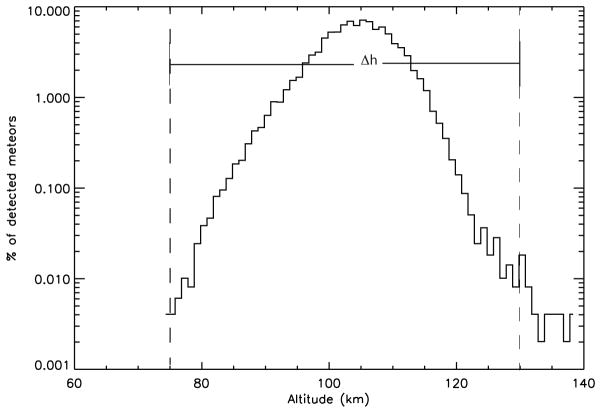
In this work we define H as the total range of altitudes in which meteors are observed at Arecibo. This value is obtained from the observed altitude distribution at Arecibo displayed in Figure 12, where it can be seen that meteors are detected between 75 and almost 140 km of altitude (i.e. H ~65 km/sec). However, the very high altitude meteors (h >130 km) seem to be outliers suggesting to be rare events and thus we adopt a more conservative value of 55 km. Δx was defined in Section 2.3 as the horizontal distance from the center of the beam to the outer edge of the first side lobe (700 m).
Fig. 12.
Observed altitude distribution with the Arecibo radar during the 2002 observing campaign. Observations are clearly present in the 75–130 km altitude range which results in a Δh = 55 km.
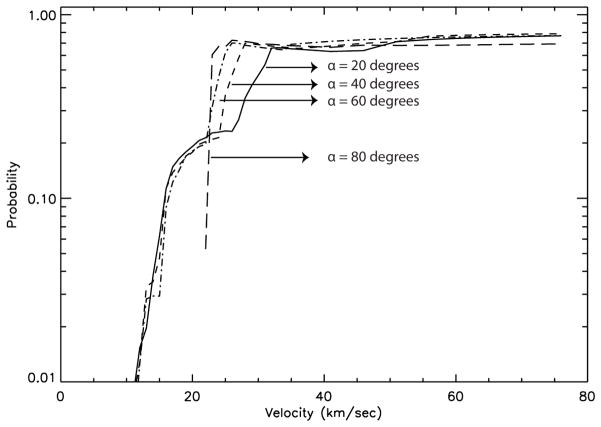
Figure 13 shows P(m, V, α) as a function of meteor velocity for a particle mass equal to 10 μg and for four entry zenith angles. It is evident from this figure that for the particles traveling at zenith angles of 20°, 40° and 60° the probability varies similarly while the meteoroid velocity is lower than 27 km/sec. For instance, for these angles at V=11 km/sec the probability of detection is about 1 %, rapidly increasing to 10 % with only a ~4 km/sec increase in velocity, and reaching ~25% for velocities equal to 27 km/sec. For these angles, the highest probability is 80%. However, the steeper the entry angle is, the less velocity is needed to achieve the maximum value. For the case of particles with entry angle equal to 80°, the atmospheric filtering effect is evident, with particles having zero probability if their velocity is lower than 20 km/sec. In fact this is true for entry angles equal or greater than 65°. At these large entry zenith angles, the particles are detected only when the velocities are high enough to ablate the main elements, at which point they have a high chance of detection (~70%). A more general view of these results is presented in Figure 14 where contour plots of the probability as a function of meteoroid mass and velocity are shown. Each of the panels represent a different entry angle specified at the top of the panel. It can be seen from this figure that for a chosen Arecibo detection threshold of −20 dB, meteors will have 50% or higher probability of detection for masses greater than 10 μg and velocities greater than 25 km/sec and for the case of large entry angles, particles will never be detected if their velocity is lower than 25 km/sec.
Fig. 13.
Detection probability as a function of meteor velocity for a particle with m=10 μg for four different entry angles.
Fig. 14.
Contour plot of probability of detection for all masses and velocities considered in this work for a SNR threshold of −20 dB and four different entry angles. The atmospheric filtering effect is evident at α=80°.
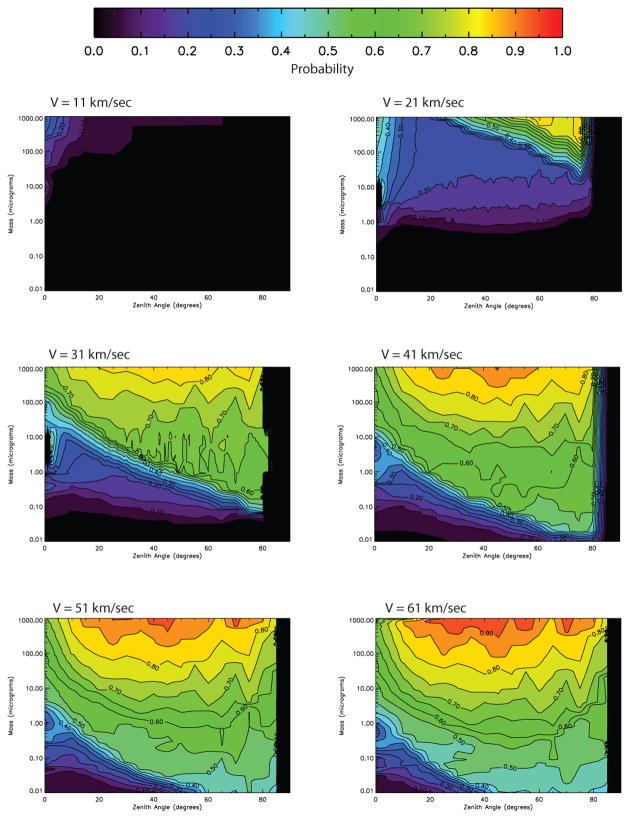
The atmospheric filtering effect due to the meteor entry angle is clearly shown in Figure 15 where contour plots of the probability as a function of meteoroid mass and entry angle are displayed for six entry velocities. It can be first observed from the panels in this figure that for Zenith angles greater than 80° the probability is zero for almost all velocities, except when the entry speed is very high which extends the allowed entry angle up to 85 degrees. At 11 km/sec, particles are practically unobserved unless the masses are greater than 50 μg, in which case the probability is 10–20 % only when particles travel practically vertical with respect to the local zenith. And only when the velocity is greater than 14–15 km/sec does the probability increase for larger entry angles, although it remains low in particular for those masses that represent the majority of ZoDy’s predicted particle flux.
Fig. 15.
Contour plot of the probability of detection for all masses and angles considered in this work, for an SNR threshold of −20 dB and 6 different entry velocities.
4. Implementation to the Zodiacal Dust Model
As discussed earlier, the work presented here is motivated by the findings reported in Nesvorný et al. (2010) that predicts that low speed (11–20 km/sec) particles with masses of the order of 1–10 μg represent 90% of the total meteoroid mass flux into the Earth’s atmosphere, and which are largely undetected by meteor radars, in particular AMOR and CMOR (Nesvorný et al. 2011a). In this section we will use the results derived in Sections 2 and 3 to: 1) determine if this flux can be detected by the much more sensitive Arecibo radar and its head echo observing technique; and 2) if that is the case, then to estimate what portion of the Arecibo meteor observations can be modeled with this flux in order to further quantitatively constrain ZoDy with ground–based observations.
To perform this validation we must first consider the fact that Arecibo lacks interferometry capabilities, and thus the observations do not have information regarding direction. This implies that they only provide line–of–sight (vertical for the Arecibo case, Janches et al. 2003) velocity information (VR in Figure 16). Furthermore, although we have reported in the past mass information from these observations (Janches et al. 2000b), those results are not optimal for the level of accuracy required in this work. This is due to the fact that the mass is calculated using the meteor momentum equation (Bronshten 1983) using the measured meteoroid deceleration. Because Arecibo does not have interferometric capabilities, it was assumed that the measured radial deceleration was the absolute deceleration, which can introduce large uncertainties. Also this “dynamical” mass determination technique can have up to an order of magnitude differences with those determined using more sophisticated methods (Close et al. 2005). Thus, instead of correcting the Arecibo observations with the detection bias resulting from the probability calculated in Section 3 and compare them with ZoDy’s predictions, we do the reverse: see what portion of the ZoDy particle flux should be detected by Arecibo and compare these predictions with the actual observations.
Fig. 16.
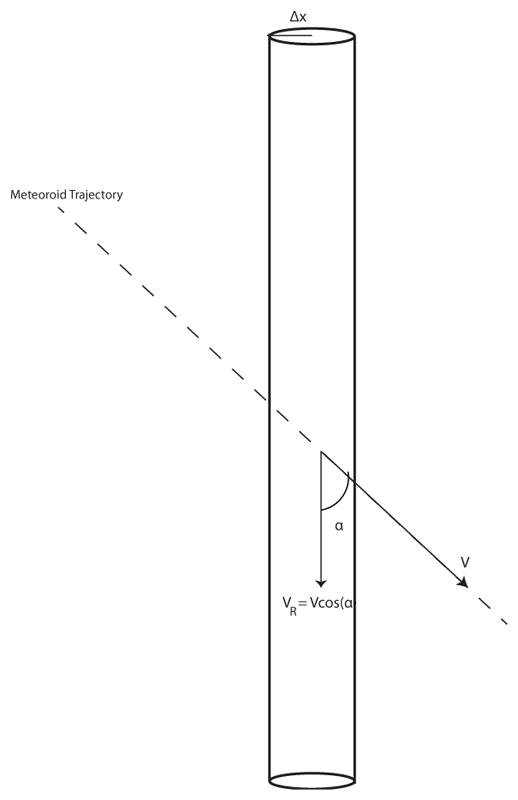
Definition line-of-sight (i.e. radial) and absolute meteor velocity.
Currently ZoDy provides the total number of meteors that cross the Earth’s cross section during the entire year as a function of particle mass, entry velocity and radiant (in ecliptic coordinates). We will refer to this number as N(m, V, λ, β) and thus ZoDy’s flux (i.e. particles per unit area and per day) is given by
| (12) |
where REarth is the Earth’s radius, m is the particle mass provided in 28 bins ranging from 10−5 to 30 mg, V is the particle absolute geocentric velocity ranging from 11.5 to 71.5 km/sec every 1 km/sec, and λ and β are the ecliptic longitude and latitude, respectively, of the meteoroid’s radiant provided every 2 degrees in both directions. Although, the input velocity distribution includes the full spectrum of possible meteor speeds for particles with Sun-bound orbits, it is heavily weighted towards the slow speeds (Figure 1). For the purpose of this work we will focus on comparing ZoDy’s results with two quantities observed by Arecibo: the daily rates and the meteor line-of-sight velocity distributions. Both quantities are strongly dependent on the time-of-day and day-of-year (Janches et al. 2006; Fentzke & Janches 2008). To perform these tasks we first calculate what portion of F(m, V, λ, β) occurs over Arecibo during a relatively short (Δt ~1 – 5 minutes) period of time. In addition we calculate the instantaneous local zenith angle of λ and β during this short period, in order to estimate the meteoroid entry angle and thus obtain the radial velocity. Once these variables are calculated they need to be “biased” by their probability-of-observation using the methodology derived in the previous sections. For this we assume that the the portion of the incoming flux that will be detected is given by
| (13) |
Replacing Equation 11 in 13 results in
| (14) |
becoming independent on assumptions regarding the beam size.
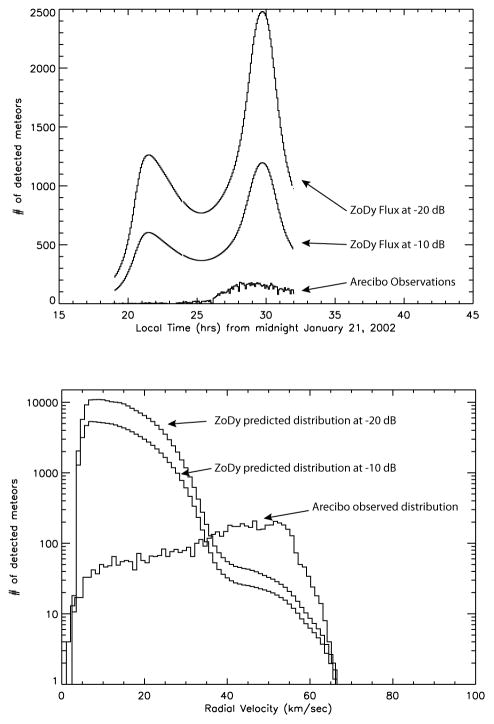
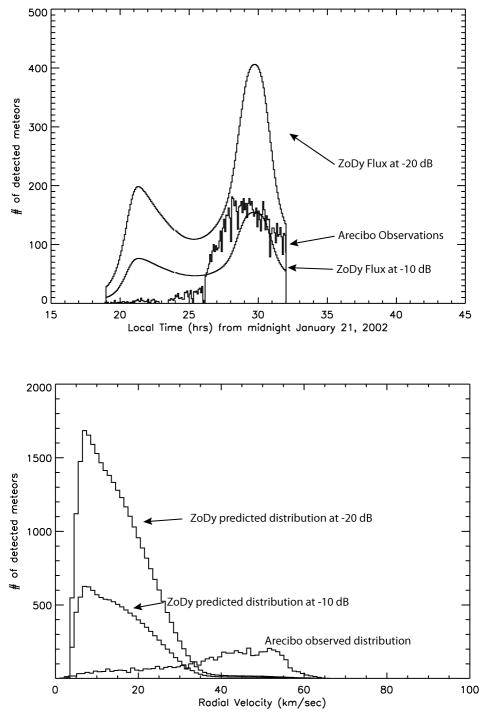
The comparison between Arecibo Observations and ZoDy are shown in Figure 17. In the top panel of this figure the detected meteor rates between approximately 6 pm on January 21st, 2002, and 8 am local time of the next day are shown. This represents the diurnal behavior typically measured by HPLA radars although seasonal difference are also present and their magnitude strongly depends on geographical location (Janches et al. 2006; Fentzke et al. 2009; Sparks et al. 2009; Pifko et al. 2013). The predicted detected rates utilizing the methodology described in this paper are also presented in the same panel. To obtain these predictions we utilize two different radar SNR thresholds (−10 and −20 dB) to estimate what portion of the flux provided by ZoDy will be detected by Arecibo. It can be seen from these panels that the predicted fluxes are much larger than those observed. The results show that at a detection threshold of −20 dB, the detection rate should be 19 times larger than what Arecibo actually observes, while at a more conservative threshold of −10 dB it should be 9 times larger than the observed rates. The bottom panel of Figure 17 shows a comparison between the predicted line-of-sight velocity distributions for the chosen detection thresholds and the actual Arecibo observations. That is, the predicted radial distribution includes only those meteors from ZoDy which are predicted to be detected by Arecibo and not all the meteors originating from ZoDy’s flux. In this panel the vertical axis is presented in logarithmic scale due to the large difference between prediction and observations. As can be seen in this panel, if the incoming flux is that described by ZoDy then the Arecibo observed distributions should be heavily dominated by low velocity particles, with a clear peak between 11 and 15 km/sec. At these velocities ZoDy predicts 240 times more detections than what Arecibo observes at the lower detection threshold, and 100 times more detections at −10 dB.
Fig. 17.
Top Panel: Comparison between predicted detected meteor rates assuming ZoDy to be the incoming flux and those observed by Arecibo. Bottom Panel: Comparison between predicted radial velocities of detected meteors assuming ZoDy to be the incoming flux and those observed by Arecibo.
It is important to note that, besides the lack of agreement at low velocities, the total lack of agreement in the high velocity end of the distributions is due to the fact that currently ZoDy does not include most of the populations that provide the faster (V>30 km/sec) particles. What is currently included in the model is only JFC particles, because those provide a good fit to the zodiacal cloud thermal emission and Helion/Anti-Helion meteors (Nesvorný et al. 2010, 2011a,b). Future efforts will require the inclusion of particles from asteroid belt, Halley type comets, and Oort cloud comets (OCCs). The latter two sources will be the most relevant to the high-velocity portion of the radar observations. In particular, preliminary studies reported by Nesvorný et al. (2011b) explored small debris particles produced by OCC disruptions to determine whether the imprints of a hypothetical population of OCC meteoroids can be found in the existing meteor radar data. It was determined by those authors that about 1% of these particles orbitally evolve by Poynting-Robertson drag to reach orbits with a semi major axis of 1 AU. This lead to a hypothesis regarding the long-standing problem in meteor science related to the relative strength of apex and H/AH sources: that the reason why apex meteors are more prominent in observations of highly sensitive radars, can be related to orbital dynamics of particles released on the long-period orbits. However, even when these sources are included, the lower velocities should still be dominant according to Nesvorný et al. (2010), and the disagreement between ZoDy and the Arecibo observations will remain.
5. Discussion
5.1. Potential sources for disagreements: The need for a revised βip
In the previous sections we have described a new method for estimating the sensitivity of the 430 MHz radar to detect meteor head-echoes produced by small and slow extraterrestrial particles and used those results to asses the probability of detection as a function of particle mass, velocity and entry angle. We then weighted the meteor flux predicted by ZoDy in order to examine what potion of the Arecibo observed distribution should be attributed to the ZoDy flux. With our current knowledge of meteor ablation and ionization we have estimated that the Arecibo detections should be heavily dominated by the ZoDy flux, at least an order of magnitude higher than the actual observations. In principle one could argue that such results suggest that ZoDy’s description of the ZDC needs revision. However, besides the strong constraint by IRAS observations reported by Nesvorný et al. (2010), the meteoric mass input rate of 30–40 t.d−1 of slow particles predicted by ZoDy is able to explain several atmospheric phenomena related to the meteoric flux. For example, Marsh et al. (2013); Feng et al. (2013) and Langowski et al. (2014) recently described global modeling of the mesospheric Na, Fe and Mg/Mg+ layers, respectively, using the Meteor Input Function (MIF) developed by Fentzke & Janches (2008). The authors showed that in order to find agreement between the model and observations for these three metals, the MIF had to be artificially scaled because the larger average speed predicted by the MIF (~25–30 km/sec) does not produce the degree of differential ablation observed in these layers (Plane 2003). A larger and slower MIF, as predicted by ZoDy, would in principle produce the degree of differential ablation required to model the Fe, Mg and Ca mesospheric layers at the same time as the Na layer, without artificially reducing their injection rates. In addition, the ZoDy flux produces a sensible input rate of cosmic spherules and the correct optical extinction of meteoric smoke in the mesosphere (these topics will be treated in a forthcoming publication). Thus, these arguments, together with the strong agreement found with IRAS spectral measurements, motivates a deeper exploration of possible reasons for the disagreement between ZoDy and Arecibo’s observations.
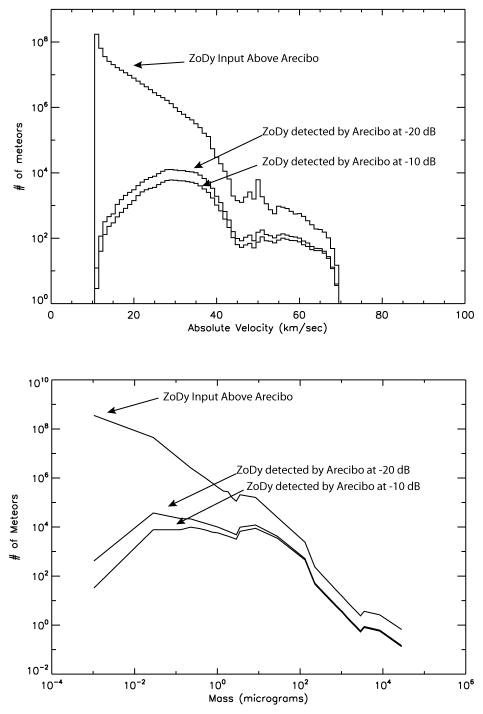
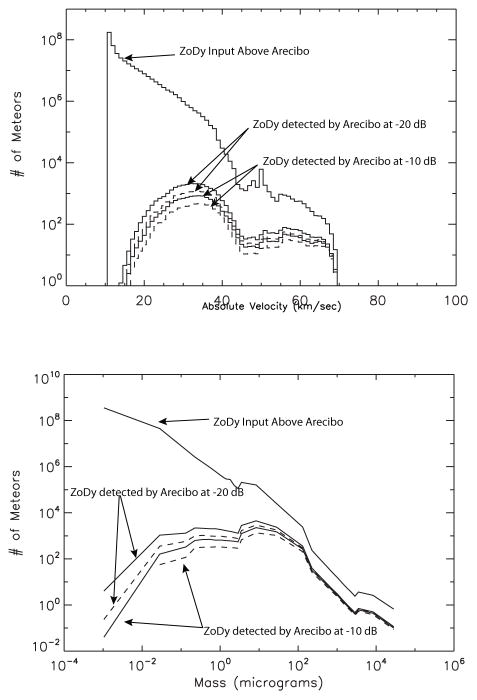
In order to first understand these results we show in Figure 18 a comparison between the characteristics of the ZoDy flux that travels through the Arecibo beam, which we refer here as the input distributions, and the portion that is predicted to be detected by Arecibo. The top panel shows the absolute velocity distributions while the bottom panel shows the mass distribution. As expected, the input distributions reflect ZoDy’s main characteristics with a velocity distribution heavily weighted toward meteors with absolute speeds of 12–14 km/sec. As can be seen in the top panel, less than 1 in 105 of these particles are detected by Arecibo. In fact the slow line-of-sight velocity distribution predicted to be detected by Arecibo (Figure 17 bottom panel) is comprised of particles with an absolute velocity distribution peak of ~30 km/sec, even though particles are detected with velocities as low as 11 km/sec, which are the typical radar detected velocities of meteors originating from the Helion and Antihelion Sporadic Sources (Fentzke & Janches 2008). Furthermore, although ZoDy’s input includes masses as low as 10−3μg, the IRAS measurements effectively constrained by particles with masses between 1 and 10 μg. Thus the distribution below about 1 μg is essentially unconstrained, except that it is known that these small particles do not contribute to the ZDC IR emission due to the featureless nature of its spectrum. The manner in which ZoDy mimic the continuos distribution of particles as a function of size, N(D), is by parameterizing this quantity as a power law given by
Fig. 18.
Top panel: Comparison between the distribution of absolute velocities of meteors traveling through the radar beam predicted by ZoDy and those predicted to be detected by the radar using our approach. Bottom panel: Comparison between the distribution of meteors masses input by ZoDy and those predicted to be detected by the radar using our approach.
| (15) |
where N0 is a normalization constant and a is the mass index of the distribution. ZoDy assumes a=2.9. Because of Arecibo’s sensitivity it could be argued that the excess in predicted detections is at least in part due to the large amount of small unconstrained particles in the model. This is explored in the bottom panel of Figure 18 where the number of meteors as a function of their mass is displayed for the input and detected distributions. While particles greater than 1 μg suffer a decrease of about an order of magnitude between input and detection, the difference increases significantly for lower masses. In fact, while the number of particles with masses lower than 1 μg represent 99% of the input distribution, their contribution is reduced to 67 and 54% in the detected distributions for the −20 and −10 dB thresholds. In terms of the mass input these numerous particles provide 50% of the input and only 4 and 7% of the detected mass for both thresholds (Table 1). Thus, a potential solution to reach better agreement would involve reducing the exponential in the size distributions of small particles. Although not shown here, we have performed this sensitivity study introducing a shallower distribution (a = 2) for particles with diameter lower than 100 μm. Because the whole population had to be re-calibrated to match IRAS fluxes, this change results in an accretion rate slightly larger than in the original distribution and the overall result is an increase in the discrepancy between Arecibo observations and ZoDy. A simpler approach is to invoke the stated 50% uncertainty on ZoDy’s prediction (Nesvorný et al. 2010, 2011a). However, it is evident from the results presented in Section 4 that reducing the influx by a factor of 2 would not suffice to obtain agreement and most likely the solution must be found in our treatment of the detectability.
Table 1.
Percentage of number and mass input contributed by particles with masses smaller than 1 μg
| β | Threshold (dB) |
|
|
||
|---|---|---|---|---|---|
| Jones (1997) | −10 | 0.54 | 0.04 | ||
| −20 | 0.67 | 0.07 | |||
|
| |||||
| Revision 1 | −10 | 0.27 | 0.01 | ||
| −20 | 0.38 | 0.02 | |||
|
| |||||
| Revision 1 | −10 | 0.3 | 0.02 | ||
| −20 | 0.67 | 0.07 | |||
5.2. Revision of βip
In particular in this section we will explore the origins of the extensively used βip value derived by Jones (1997)3, which is based on experiments involving the firing of high velocity Fe particles into a chamber of air at low pressure, and measuring electron production along the particle track. These experiments reported in Friichtenicht & Becker (1973) are a rather indirect way of measuring ionization efficiency, because the rate of ablation of Fe from the particles has to be inferred from the deceleration of the particles. Nevertheless, Jones (1997) used these experiments combined with data on meteor luminosity and radar scattering to derive expressions for the ionization efficiency of the major elements. As stated by the author, however, the expressions reported in that work overpredicted the ionization efficiency by an order of magnitude4 (Jones 1997).
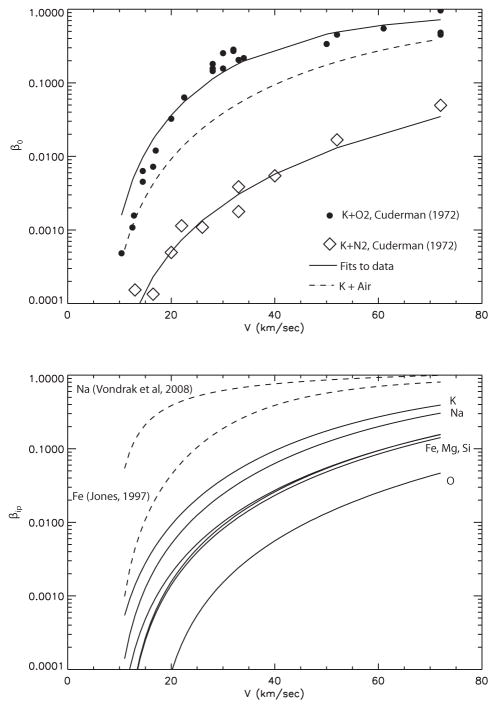
In this work we re-estimate βip as a function of collision energy by utilizing measurements of the ionization cross section of K atoms in collision with O2 and N2 over the full range of collision energies reported by Cuderman (1972). This is the only metal atom for which there is experimental data with both collision partners over a wide collision energy, and a detailed description of how the absolute cross sections were measured. The results show that charge transfer with O2 is much more important than with N2: the K + N2 cross section is at least 1 order of magnitude less than that for O2, so in air N2 collisions cause a 5% contribution to the total ionization at a collision velocity of 11 km/s, increasing to a 16% contribution at 72 km/s. Although about 70% of the product is rather than free electrons at the relatively low maximum impact velocities employed in a study by Moutinho et al. (1971), the will be produced with sufficient translational speed (and internal vibrational excitation) to auto-detach the electron since the electron affinity of O2 is only 0.45 eV. Thus we assume that the final products of these collisions are K+ and e−.
In order to compute βip, the ionization cross section is first divided by the cross section for momentum-changing collisions to produce a single collision ionization probability β0; β0 is then increased to allow for ionization through subsequent collisions of the metal atom as it loses momentum (Jones 1997). In order to estimate the momentum-changing collision cross section, we employed quantum chemistry trajectory calculations. The hybrid density functional / Hartree-Fock B3LYP method was employed from within the Gaussian 09 suite of programs (Frisch et al. 2009), combined with the 6–311+G(2d) triple zeta basis set. This is a large, flexible basis set which has both polarization and diffuse functions added to the atoms. Classical trajectories were performed using the Atom Centered Density Matrix Propagation (ADMP) molecular dynamics model (Schlegel et al. 2002). Trajectories were initiated at relative velocities of 11 to 72 km/s. One definition of a momentum-changing collision is that it is inelastic i.e. there is a transfer of collisional kinetic energy into internal vibrational energy of the O2. The maximum impact parameter bmax was then determined for collisions in which the O2 after the collision possessed just 1 vibrational quantum. On the doublet surface for K + O2, the average over the range of collision velocities is bmax = 2.9 Å(bmax increases by only 20% when V increases from 11 to 72 km/s). For the less reactive quartet surface, bmax = 2.0 Å. Statistically, reaction on the quartet surface is twice as likely as on the doublet surface, so overall for K + O2, bmax = 1/3×2.9 + 2/3×2.0 = 2.3 Å. For K + N2, bmax = 1.8 Å. These impact parameters are treated as independent of collision velocity. The momentum-changing cross section is then given by . Figure 19 (top panel) illustrates β0 for O2 and N2 as a function of collision velocity, calculated from the ionization cross sections of Cuderman (1972). Also shown in this figure are fits to the experimental data points using the analytic expression of Jones (1997):
| (16) |
where V0 is the threshold velocity, given by
Fig. 19.
Top Panel: β measured by Cuderman (1972) for K + O2 and K + N2. The solid lines through the experimental points are fits of the expression from Jones (1997). The dash line is the estimate β for K + air collisions, which includes the correction for multiple high energy collisions. Bottom Panel: Variation of β for all the meteoric atoms colliding with air, as a function of particle velocity.
| (17) |
where Me and ψ are the mass and ionization potential of the atom (K, in this case), respectively, e is the electronic charge, and Ma is the molecular mass of O2 or N2. c is a fitted parameter.
In the atmosphere, K has a 20% chance of collision with an O2. β0 for air is then obtained as 0.2 β0(O2) + 0.8 β0(N2). The composite fit of eqn. 16 for K in air is then achieved with c = 5×106 (km/s)−2.8, V0 = 7 km/s (an average between 6.9 km/s for K + O2 and 7.1 km/s for K + N2). βip is then given by Jones (1997):
| (18) |
The resulting curve of βip versus V0 for K + air collisions is also shown in Fig. 19.
There is some experimental data available for Na + O2 and N2 collisions (Bydin & Bukteev 1960; Moutinho et al. 1971; Kleyn et al. 1978), but the absolute cross sections are not consistent, although the Na ionization cross sections are clearly smaller than the corresponding K cross sections. Therefore, in order to determine βip for Na and other meteoric metals, we adopt the following approach. The maximum interaction distance between a metal atom and a collision partner is given by the curve-crossing (or harpoon) distance (Smith 1980):
| (19) |
where γ, the vertical electron affinity of O2 and N2, is close to zero. The ionization cross section is likely to scale as , particularly at high V where threshold effects are small. We therefore estimate c for Na, Mg, Fe, Si and O by dividing c = 5×10−6(km/s)−2.8 for K by factors of 1.4, 3.1, 3.3, 3.5, 9.8, respectively. V0 for each element from its respective ψ (eqn. 17). The values of c and V0 for calculating βip(V) using equations 16 and 17 are listed in Table 2.
Table 2.
Fitted parameters for calculating βip as a function of V
| Atom | c/(km/s) −2.8 | V0/(km/s) |
|---|---|---|
| K | 5 × 10 −6 | 7.0 |
| Na | 3.6 × 10 −6 | 8.6 |
| Mg | 1.6 × 10 −6 | 10.6 |
| Fe | 1.5 × 10 −6 | 9.0 |
| Si | 1.4 × 10 −6 | 10.5 |
| O | 5.1 × 10 −7 | 16.0 |
The resulting βip for the six elements are plotted against V in Fig. 19 (bottom panel). This shows that, compared to previous estimates (Jones 1997; Vondrak et al. 2008), the ionization efficiencies are about 2 orders of magnitude lower for Na and K at speeds below 20 km/s, and slightly less than 1 order of magnitude lower for the main elements (Fe, Mg, Si and O) at higher speeds.
5.3. Modeled Results utilizing the Revised βip
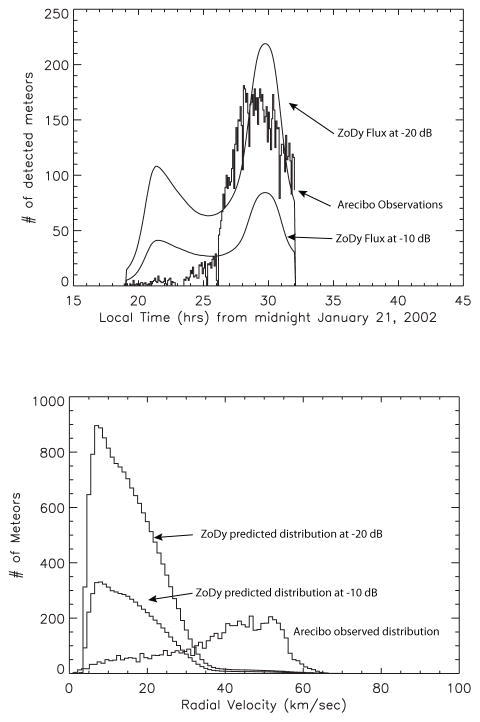
Figure 20 shows the same results as Figure 17 but utilizing the revised values of βip shown in the bottom panel of Figure 19, to which we refer as Revision 1 in Table 1. As can be seen in these figures, although improvement is achieved, ZoDy still predicts a flux that should dominate the Arecibo meteor rate and velocity distributions. In particular, at a detection threshold of −20 dB, ZoDy predicts that Arecibo should detect 3 times more particles that is actually observed, while at −10 dB they would represent 1.3 times the detected rates. Once again we emphasize that the final disagreement will be even greater because ZoDy does not include the populations that would produce most of the detected particles by Arecibo (high speed). In terms of the radial velocity distributions, the ZoDy flux should provide a peak at ~7 km/s that is 10 to 80 times larger than those currently detected.
Fig. 20.
Same as Figure 17 using the β estimates resulted from Revision 1.
As discussed above, βip is calculated by dividing the ionization cross section by the cross section for momentum-changing collisions between the metal atom and the air molecule (O2 or N2). The requirement that a momentum-changing collision has to be inelastic (i.e. arising from translational-vibrational energy transfer) may be too restrictive, since elastic collisions at large impact parameters will makes small changes to the momentum of the metal atom. The upper limit to the cross section for interaction between a metal atom and O2 or N2 molecules is given by (see eqn. 19 for the definition of Rc). For K + O2/ N2, Rc is about 48% larger than the distance required to impart vibrational excitation (bmax), which would correspond to a decrease of βip by a factor of 1.482 ~ 2.2 for K (and the other metal atoms which are scaled to it). We refer to this lower limit of βip as Revision 2 in Table 1. The comparison between ZoDy predictions and Arecibo observations utilizing this second revision are displayed in Figure 21 where it can be seen that a much better agreement is found, in particular for a detected threshold of −10 dB. According to these results, if ZoDy provides most of the incoming flux, it would represent about 60 % of the actual detected rates at the lower higher threshold. However, if we invoke the higher sensitivity (i.e. detection threshold of −20 dB) ZoDy should provide 1.6 times more meteors than actually detected. Note that even at the −10 dB results, ZoDy predicts a rate of particles in the evening before midnight which is significantly larger (a factor of 4) than those detected by the radar. If we take the lower limit to the ZoDy flux (50% uncertainty), then a reasonable agreement is obtained between model prediction and observations, in particular for the −10 dB detection threshold where they would represent about 30% of the observed rates and agree well with the diurnal distributions. Interestingly, ZoDy’s particles originating from JFC’s will have radiants mostly concentrated around the Helion and Antihelion Sporadic Meteor sources (Nesvorný et al. 2010) and thus the 30% rate in the detections of particles coming from these sources is in good agreement with predictions of our earlier Meteor Input Function (MIF) model reported by Fentzke & Janches (2008). In terms of the radial velocity distribution, however the disagreement is still significant.
Fig. 21.
Same as Figure 17 using the β estimates resulted from Revision 2.
To explore potential sources of improvement we display in Figure 22 a comparison between the input and detected distributions predicted by ZoDy, similar to Figure 18, but for both revised estimates of βip. The solid lines in Figure 22 represent the results derived with Revision 1, while the dash lines represent Revision 2. These panels show, as expected, that the revised estimates of βip contribute even more to filter out particles with masses lower than ~1 μg. However, for higher masses the reduction of detected particles is not significant when compared to the results utilizing the original values of βip. Looking at the top panel of Figure 22, particles with velocities lower than 15 km/sec were completely removed from the detected distributions. As discussed in Section 2.3, once the “larger” particles have speeds higher than 15 km/sec, the SNR is much higher than the detection threshold, so that even if the ionization efficiency is close to its lower limit, these particles will be detected. So while these results do support ZoDy’s main hypothesis that most of the 12–14 km/sec particles with mass equal to 1–10 μg could remain undetected, even by the most sensitive radar utilized for meteor observations, the number of particles with higher velocities entering the beam at larger zenith angles is too high and thus continues to dominate the predicted distributions. One potential solution is perhaps to explore the possibility to revised ZoDy such that then IRAS constrain is still met, but with a reduced contribution from particles with velocities larger than 15 km/sec.
Fig. 22.
Same as Figure 18 using the β estimates resulted from Revision 1 and 2.
6. Conclusions
In this manuscript we presented a new approach that aims at addressing the meteoric mass flux into planetary atmospheres in a comprehensive manner by combining models of dust release from celestial bodies, orbital evolution, ablation and ionization processes when dust particles encounter planetary atmospheres and ultimately by constraining these models simultaneously by all available observing techniques. We started with a recently developed physical model of the Zodiacal Dust Cloud (ZDC) reported by Nesvorný et al. (2010) constrained with spectral observations of the ZDC provided by the InfraRed Astronomical Satellite (IRAS) in order to predict the daily rates and radial velocity distributions that should be detected by a ground-based radar. In particular, we have compared these model results with head echo meteor observations obtained with the most sensitive radar in the world utilized to date for meteor studies – the Arecibo Observatory 430 MHz Radar located in Puerto Rico (Janches et al. 2008, 2014). We have also combined ZoDy with a new approach based on the Chemical Ablation Model developed by (Vondrak et al. 2008) to determine: 1) the sensitivity of the radar to detect meteors produced by particles with a certain mass, velocity and entry angle, and 2) the probability of detection based on the traveling conditions through the radar beam that such particles are required to have in order to be detected. We have found that using the meteor ionization probability, βip, derived by Jones (1997) which is universally utilized in radar meteor research (Close et al. 2002; Vondrak et al. 2008; Janches et al. 2009; Nesvorný et al. 2011a; Weryk & Brown 2013, among some assorted type of invesitgations), ZoDy overpredicts the Arecibo observed rates by 10 to 20 times and the peak of the slow portion of the line-of-sight velocity distribution by 2 to 3 orders of magnitude. This strong disagreement, however is due, at least in part, to the accuracy of the determination of βp which, as argued by Jones (1997), is likely overpredicted by at least an order of magnitude. Further exploration on this issue lead to a re-estimation of βip as a function of collision energy, utilizing earlier measurements of the ionization cross section of K atoms over the full range of collision energies reported by Cuderman (1972) and demonstrated that most likely βip is about 2 orders of magnitude lower than the values reproduced by Jones (1997) for the case of Na and K at speeds below 20 km/s, and slightly less than 1 order of magnitude lower for the main elements (Fe, Mg, Si and O) at higher speeds. This revision lead to finding better agreement between ZoDy predictions and Arecibo observations. In particular at a chosen SNR detection threshold of −10 dB and invoking the lower value of ZoDy’s flux estimate (16 t/d) particles originating from JFC’s, with radiants mostly concentrated around the Helion and Antihelion Sporadic Meteor sources, would represent about 30% of the observed rates and agree well with the diurnal distributions. This percentage in the detections is in good agreement with predictions of our earlier Meteor Input Function (MIF) model reported by Fentzke & Janches (2008). One must be cautious with this agreement though, since an SNR threshold of −10 db may be too conservative as Arecibo can detect meteors with up to 20 dB (2 orders of magnitude) lower signal strength. However, even at this lower limit of the flux ZoDy over predicts the slow portion of the Arecibo radial velocity distributions by a factor of 3. A detail investigations of the results by our new approach shows that particles with velocities lower than 15 km/sec for most of the particle masses considered are mostly undetected as hypothesized by Nesvorný et al. (2010). The decrease in βip however does not produce significant differences for particles with masses greater than 1 μg and larger velocities. This produces a detected absolute velocity distribution with a peak at ~30 km/sec in agreement with those measured by radars from particles originating from the Helion and Antihelion sources (Jones & Brown 1993; Galligan & Baggaley 2004; Fentzke & Janches 2008). However, the combination of the high number of these particles predicted by ZoDy together with the fact that they will mostly enter the Arecibo beam at some angle greater than 0 produces a peak at slow radial velocities that is at best greater by a factor of 3 with respect to the observations. This implies that ZoDy requires some revision. In order to maintain the flux, a potential solution perhaps is a scenario with a steeper distribution where the number of particles with speeds lower than 15 km/sec is increased while those with higher velocities are decreased.
In a second paper we will apply our new approach to observations performed during other seasons, geographical locations and additional HPLA radars with less sensitivity than Arecibo and explore how the current ZoDy predicts the observed seasonal and geographical distributions (Fentzke et al. 2009; Pifko et al. 2013) and compare what portion of the predicted flux contributes to the the detections of the various systems utilized (Janches et al. 2008, 2014).
Acknowledgments
DJ work is supported by NASA awards 12-PAST12-0007 and 12-PATM12-0006; DN work has been supported through NASA’s Solar System Works; JMCP and WF work is supported by the European Research Council (project number 291332 - CODITA) and the work of DV was partly supported by the Czech Grant Agency (grant P209-13-013085). The Arecibo Observatory is is operated by SRI International under a cooperative agreement with the National Science Foundation.
Footnotes
In ZoDy the main contributions are meteors from those sources (Nesvorný et al. 2010).
Observationally, the effect is evident in the interferometric observations of meteor head echoes result using the MU radar in Japan reported by Pifko et al. (2013) and the Southern Argentina Agile Meteor Radar (SAAMER) reported by Janches et al. (2014). However, Kero et al. (2012) using similar observations with the MU radar argues that such an effect is not evident in their results.
For the case of CABMOD, Vondrak et al. (2008) used the analytic expression for how this parameter varies with collision energy, but determined it for individual elements.
Jones (1997) abstract concludes “The observational ionization coefficients are much lower than predicted by the present theory and we provisionally explain this as a consequence of transfer of charge from the meteoric ion to a molecule of the air.”
Contributor Information
D. Janches, Email: diego.janches@nasa.gov, Space Weather Lab., Mail Code 674, GSFC/NASA, Greenbelt, MD 20771
J.M.C. Plane, Email: j.m.c.plane@leeds.ac.uk, School of Chemistry, University of Leeds, Leeds, U.K
D. Nesvorný, Email: davidn@boulder.swri.edu, SouthWest Research Institute, Boulder, CO, USA
W. Feng, Email: w.feng@leeds.ac.uk, School of Chemistry, University of Leeds, Leeds, U.K
D. Vokrouhlický, Email: vokrouhl@cesnet.cz, Institute of Astronomy, Charles University, Prague, Czech Republic
M.J. Nicolls, Email: Michael.Nicolls@sri.com, SRI International, Menlo Park, CA, USA
References
- Baggaley W. In: Meteors in the Earth’s Atmosphere. Murad E, Williams I, editors. Cambridge University Press; 2002. pp. 123–148. [Google Scholar]
- Baggaley W, Bennett R, Steel D, Taylor A. Q J R Astr Soc. 1994:293. [Google Scholar]
- Breakall JK, Mathews JD. J Atmos Terr Phys. 1982;44:449. [Google Scholar]
- Bronshten V. Physics of meteoric phenomena. d. Reidel Publishing Co; 1983. [Google Scholar]
- Brown P, Weryk RJ, Wong DK, Jones J. Earth Moon and Planets. 2008;102:209. [Google Scholar]
- Bydin JF, Bukteev AM. In: Ionization Phenomena in Gases. Nilsson NR, editor. I. 1960. p. 65. [Google Scholar]
- Campbell-Brown M, Wiegert P. Meteoritics and Planetary Science. 2009;44:1837. [Google Scholar]
- Chau JL, Woodman R. Atmos Chem Phys. 2004;3:6063. [Google Scholar]
- Close S, Brown P, Campbell-Brown M, Oppenheim M, Colestock P. Icarus. 2007;186:547. [Google Scholar]
- Close S, Oppenheim M, Durand D, Dyrud L. Journal of Geophysical Research (Space Physics) 2005;110:9308. [Google Scholar]
- Close S, Oppenheim M, Hunt S, Coster A. Icarus. 2004;168:43. [Google Scholar]
- Close S, Oppenheim M, Hunt S, Dyrud L. jgr. 2002;107:1295. doi: 10.1029/2002JA009253. [DOI] [Google Scholar]
- Cremonese G, Borin P, Lucchetti A, Marzari F, Bruno M. A&A. 2013;551:A27. [Google Scholar]
- Cuderman JF. Physical Review A. 1972;5:1687. [Google Scholar]
- Dyrud LP, Janches D. J Atmos Sollar Terr Phys. 2008;70:1621. [Google Scholar]
- Feng W, Marsh DR, Chipperfield MP, et al. Journal of Geophysical Research (Atmospheres) 2013;118:9456. [Google Scholar]
- Fentzke JT, Janches D. Journal of Geophysical Research (Space Physics) 2008:113. doi: 10.1029/2007JA012531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fentzke JT, Janches D, Sparks JJ. J Atmos Solar Terr Phys. 2009;71:653. [Google Scholar]
- Friichtenicht JF, Becker DG. NASA Special Publication. 1973;319:53. [Google Scholar]
- Frisch MJ, Trucks GW, Schlegel HB, et al. Gaussian–09 Revision D.01. gaussian Inc; Wallingford CT: 2009. [Google Scholar]
- Galligan DP, Baggaley WJ. Month Not R Astron Soc. 2004;353:422. [Google Scholar]
- Galligan DP, Baggaley WJ. Month Not R Astron Soc. 2005;359:551. [Google Scholar]
- Hawkins GS. Astron J. 1956;61:386. [Google Scholar]
- Hughes DW. In: Cosmic Dust. McDonnell JAM, editor. Chichester: John Willey; 1978. pp. 123–186. [Google Scholar]
- Hunt S, Oppenheim M, Close S, et al. Icarus. 2004:168. [Google Scholar]
- Janches D, Chau J. J Atmos Solar Terr Phys. 2005:67. [Google Scholar]
- Janches D, Close S, Fentzke JT. Icarus. 2008;193:105. [Google Scholar]
- Janches D, Dyrud LP, Broadley SL, Plane JMC. Geoph Res Lett. 2009;36:6101. [Google Scholar]
- Janches D, Heinselman C, Chau J, Chandran A, Woodman R. J Geophys Res. 2006:111. [Google Scholar]
- Janches D, Hocking W, Pifko S, et al. J Geophys Res Space Physics. 2014:119. doi: 10.1002/2013JA019241. [DOI] [Google Scholar]
- Janches D, Mathews J, Meisel D, Getman V, Zhou Q. Icarus. 2000a;143:347. [Google Scholar]
- Janches D, Mathews J, Meisel D, Zhou Q. Icarus. 2000b;145:53. [Google Scholar]
- Janches D, Nolan M, Meisel D, et al. J Geophys Res. 2003;108:1222. doi: 10.1029/2002JA009789. [DOI] [Google Scholar]
- Janches D, Nolan M, Sulzer M. Atmos Chem Phys. 2004;4:621. [Google Scholar]
- Janches D, ReVelle D. J Geophys Res. 2005:110. [Google Scholar]
- Jones J, Brown P. Mon Not R Astron Soc. 1993;265:524. [Google Scholar]
- Jones W. Month Not R Astron Soc. 1997;288:995. [Google Scholar]
- Kero J, Szasz C, Nakamura T, et al. Month Not R Astr Soc. 2012;425:135. [Google Scholar]
- Kleyn AW, Hubers MM, Los J. Chemical Physics. 1978;34:55. [Google Scholar]
- Langowski M, von Savigny C, Burrows JP, et al. Atmospheric Chemistry & Physics Discussions. 2014;14:1971. [Google Scholar]
- Love S, Brownlee DE. Science. 1993;262:550. doi: 10.1126/science.262.5133.550. [DOI] [PubMed] [Google Scholar]
- Marsh D, Janches D, Plane J, Feng W. J Geophys Res (Atmospheres) 2013;118:11442. [Google Scholar]
- Mathews JD, Meisel DD, Hunter KP, Getman VS, Zhou Q. Icarus. 1997;126:157. [Google Scholar]
- Moutinho AMC, Baede APM, Los J. Physica. 1971;51:432. [Google Scholar]
- Nesvorný D, Janches D, Vokrouhlický D, et al. Ap J. 2011a;743:129. [Google Scholar]
- Nesvorný D, Jenniskens P, Levison HF, et al. Ap J. 2010;713:816. [Google Scholar]
- Nesvorný D, Vokrouhlický D, Pokorný P, Janches D. Ap J. 2011b;743:37. [Google Scholar]
- Pifko S, Janches D, Close S, et al. 2013;223:444. [Google Scholar]
- Plane J. Chem Rev. 2003;103:4963. doi: 10.1021/cr0205309. [DOI] [PubMed] [Google Scholar]
- Plane JMC. International Reviews of Physical Chemistry. 1991;10:55. [Google Scholar]
- Plane JMC. Chemical Society Reviews. 2012;41:6507–6518. doi: 10.1039/c2cs35132c. [DOI] [PubMed] [Google Scholar]
- Pokorný P, Vokrouhlický D, Nesvorný D, Campbell-Brown M, Brown P. Ap J. 2014;789:25. [Google Scholar]
- Schlegel HB, Iyengar SS, Li X, et al. J Chem Phys. 2002;117:8694. [Google Scholar]
- Sekanina Z. Icarus. 1976;27:265. [Google Scholar]
- Smith I. Kinetics and Dynamics of Elementary Gas Reactions. Butterworths; 1980. [Google Scholar]
- Sparks JJ, Janches D. Geophys Res Lett. 2009a;36:17101. [Google Scholar]
- Sparks JJ, Janches D. Geophys Res Lett. 2009b;36:12105. [Google Scholar]
- Sparks JJ, Janches D, Nicolls MJ, Heinselman CJ. J Atm Solar Terr Phys. 2009;71:644. [Google Scholar]
- Taylor A. Adv Space Sci. 1997;20:1505. [Google Scholar]
- Taylor A, Elford W. Earth Planets Space. 1998;50:569. [Google Scholar]
- Vondrak T, Plane JMC, Broadley S, Janches D. Atmospheric Chemistry & Physics. 2008;8:7015. [Google Scholar]
- Webster AR, Brown PG, Jones J, Ellis KJ, Campbell-Brown M. Atmospheric Chemistry & Physics Discussions. 2004;4:1181. [Google Scholar]
- Weiss AA, Smith JW. Month Not R Astron Soc. 1960;121:5. [Google Scholar]
- Weryk RJ, Brown PG. Planetary and Space Science. 2013;81:32. [Google Scholar]
- Zook HA. Lunar and Planetary Science Conference, Vol. 6, Lunar and Planetary Science Conference. 1975:898. [Google Scholar]