Accurate determination of rates from non-uniformly sampled relaxation data

Abstract

The application of non-uniform sampling (NUS) to relaxation experiments traditionally used to characterize the fast internal motion of proteins is quantitatively examined. Experimentally acquired Poisson-gap sampled data reconstructed with iterative soft thresholding (IST) are compared to regular sequentially sampled (RSS) data. Using ubiquitin as a model system, it is shown that 25% sampling is sufficient for the determination of quantitatively accurate relaxation rates. When the sampling density is fixed at 25%, the accuracy of rates is shown to increase sharply with the total number of sampled points until eventually converging near the inherent reproducibility of the experiment. Perhaps contrary to some expectations, it is found that accurate peak height reconstruction is not required for the determination of accurate rates. Instead, inaccuracies in rates arise from inconsistencies in reconstruction across the relaxation series that primarily manifest as a non-linearity in the recovered peak height. This indicates that the performance of an NUS relaxation experiment cannot be predicted from comparison of peak heights using a single RSS reference spectrum. The generality of these findings was assessed using three alternative reconstruction algorithms, eight different relaxation measurements, and three additional proteins that exhibit varying degrees of spectral complexity. From these data, it is revealed that non-linearity in peak height reconstruction across the relaxation series is strongly correlated with errors in NUS-derived relaxation rates. Importantly, it is shown that this correlation can be exploited to reliably predict the performance of an NUS-relaxation experiment by using three or more RSS reference planes from the relaxation series. The RSS reference time points can also serve to provide estimates of the uncertainty of the sampled intensity, which for a typical relaxation times series incurs no penalty in total acquisition time.

Introduction

Classical NMR spin relaxation can provide site-resolved, quantitative measures of the amplitudes and timescales of protein motions (Igumenova et al. 2006; Jarymowycz and Stone 2006). These experiments are sensitive to equilibrium fluctuations of interaction (bond) vectors that occur on the ps-ns timescale. The characterization of motions on this timescale can potentially reveal critical aspects of the thermodynamics and kinetics of molecular recognition and other aspects of protein function (Frederick et al. 2007; Henzler-Wildman et al. 2007; Kay et al. 1996; Li et al. 1996; Marlow et al. 2010; Stevens et al. 2001; Tzeng and Kalodimos 2009; Tzeng and Kalodimos 2012; Wand 2001; Wand et al. 2013; Zidek et al. 1999) In structured proteins, relaxation rates are dominated by the molecular tumbling and complete interpretation requires separation of the overall correlation time from internal motions. This is commonly done using the ‘model-free’ formalism (Lipari and Szabo 1982a; Lipari and Szabo 1982b) and variations thereof (Clore et al. 1990; Ryabov et al. 2012) wherein internal motion is described with a local correlation time and an amplitude metric called the square of the generalized order parameter. This type of analysis requires collecting multiple relaxation experiments often at more than one static field strength. Traditionally, relaxation phenomena are resolved using two dimensional experiments where cross peak intensity or volume is quantified as a function of an incremented delay period creating a pseudo-three dimensional (pseudo-3D) spectrum. High S/N and high spectral resolution are therefore required to ensure reliable cross peak quantification. As a result, data collection is usually very instrument time intensive and often prohibitively so for unstable or dilute protein preparations. The need to accelerate NMR relaxation experiments has promoted several approaches over the years including reducing the number of relaxation delays (Jones 1997), reducing the number of NMR observables used for downstream analysis (Lee and Wand 1999), and the recent revival of ‘accordion’ spectroscopy (Bodenhausen and Ernst 1982; Harden and Frueh 2014).

A potentially more general method for accelerating multidimensional NMR experiments is the use of non-uniform sampling (NUS) strategies in one or more indirectly sampled time domains. Regular sequential sampling (RSS) with uniform increments, which is required for the successful application of the discrete Fourier transform (DFT), has been the dominant approach for decades. However, application of this strategy to multidimensional data acquisition is inherently time intensive. So-called ‘on-grid’ NUS schemes capture only a subset of the uniform-grid and omitted data points are typically reconstructed in processing prior to application of the DFT. NUS methods have existed for quite some time in the context of biomolecular NMR (Barna et al. 1987) and many different implementations of data sampling and reconstruction exist (Mobli and Hoch 2015). To date, these methods have found the widest applicability in contexts where only the resonance frequency is of interest or where peak heights are treated in a semi-quantitative manner. This is largely due to uncertainty regarding the fidelity of reconstructed peak heights and the relationship between sampling density, spectral sparseness, and spectral complexity. The later issues are particularly important for experiments of lower dimensionality such as those typically collected for NMR relaxation. Indeed, among the recent quantitative applications of NUS to date, many have involved the serial collection of higher dimensional 3D (pseudo-4D) experiments (Gledhill et al. 2009; Long et al. 2015; Mayzel et al. 2014).

To our knowledge, only a few studies have applied NUS to a quantitative pseudo-3D experiment. In the earliest study, ¹⁵N R₁ rates were obtained using a variation of maximum entropy (Max-Ent) reconstruction (Hoch 1985; Laue et al. 1985; Sibisi et al. 1984) where in situ calibration was employed to correct for the inherent non-linearity of Max-Ent (Schmieder et al. 1997). Though spectra reconstructed using calibrated Max-Ent were of high quality and largely devoid of artifacts, the resulting relaxation rates were inaccurate relative to reference data. A more recent study demonstrated that the Spectroscopy by Integration of Frequency and Time domain information (SIFT) method (Matsuki et al. 2010; Matsuki et al. 2009) is capable of determining accurate ¹⁵N relaxation dispersion parameters using 40% random sampling (Matsuki et al. 2011). However, the generality and limitations of this method were not quantitatively explored. A third study has analyzed the relationship between sampling density, accuracy in peak height, and accuracy in NUS-derived ¹⁵N relaxation dispersion parameters for exponentially biased sampling (Linnet and Teilum 2016). Various implementations of multi-dimensional decomposition (MDD) (Hiller et al. 2009; Jaravine et al. 2008; Mayzel et al. 2014; Orekhov and Jaravine 2011) and iterative re-weighted least squares (IRLS) reconstruction (Kazimierczuk and Orekhov 2011a) were evaluated and it was shown that incorporation of a single uniformly sampled spectrum in a series of NUS spectra can facilitate the accurate determination of relaxation dispersion parameters from data sampled at impressively low densities (12.5–20%). However, high quality data at such low sampling densities were only obtained for highly resolved spectra of modest complexity and only using recursive MDD reconstruction with co-processing. An additional NUS ¹⁵N relaxation dispersion study utilizing MDD reconstruction has also been recently presented, but the fidelity of the NUS-derived relaxation parameters was not discussed (Oyen et al. 2015).

To provide a quantitative evaluation of classical spin relaxation rates derived from pseudo-3D data, a large-scale experimental study comprised of over 60 relaxation experiments (over 30 RSS & NUS pairs) has been undertaken here. The sinusoidally-weighted Poisson-gap sampling method was used for NUS (Hyberts et al. 2010) and iterative soft thresholding (IST) (Donoho 1995; Drori 2007; Hyberts et al. 2012b; Hyberts et al. 2010; Stern et al. 2007) was used as the primary reconstruction method. Poisson-gap sampling has the advantage of being relatively insensitive to the seed of the random number generator used during schedule generation; though schedule-specific performance has been shown to vary (Aoto et al. 2014). IST-reconstructed frequency domain data has been shown to exhibit highly linear peak heights with respect to RSS references, even in 2D at lower sampling densities (25–32%) (Hyberts et al. 2012b). Finally, these methods are widely used within the NMR community. Here, these approaches are evaluated with respect to their performance in a quantitative context. First, ubiquitin is used as a model system to examine the relationship between the total number of NUS points collected at a fixed sampling density and the accuracy of NUS-derived relaxation rates. Then a comprehensive error analysis is performed to characterize the nature of the inaccuracy of NUS-derived relaxation rates. Finally, the generality of the error analysis is assessed using three alternative reconstruction methods: IRLS as implemented in the MddNMR software package (Kazimierczuk and Orekhov 2011a; Orekhov and Jaravine 2011), ℓ₁-norm regularization using the NESTA algorithm (NESTA-L1) (Becker et al. 2011; Nesterov 2005) as implemented in the NESTA-NMR software package (Sun et al. 2015), and iterative re-weighted ℓ₁-norm regularization using the NESTA algorithm (NESTA-IRL1) (Candes et al. 2008) as implemented in the NESTA-NMR software package (Sun et al. 2015), three additional proteins, and eight different relaxation experiments. The protein samples and experiments were chosen to span a wide range of concentrations, feature different numbers of observable cross peaks, and exhibit varying degrees of spectral complexity.

Materials and Methods

Protein expression and purification

Four different proteins were recombinantly expressed from T7 promoters in the E. coli strain BL21(DE3) or derivatives thereof. ¹⁵N human ubiquitin was expressed in H₂O-M9 minimal medium and purified as described (Wand et al. 1996). Random fractionally deuterated ²H, U-[¹⁵N,¹³C]-ubiquitin was prepared similarly using 55% v/v D₂O-M9 minimal medium. Ubiquitin NMR samples were ~1 mM in protein in 50 mM d₃-acetate, pH 5.0, and 0.02% w/v NaN₃. An additional U-[²H,¹⁵N] ubiquitin sample was prepared in the same way using 99.9% v/v D₂O-M9 minimal medium. The NMR buffer was the same except with 30% glycerol v/v added to simulate the effect of slow tumbling. ¹⁵N vertebrate calmodulin (CaM) was prepared as described using H₂O-M9 minimal medium (Kranz et al. 2002). The NMR sample was ~1 mM in protein in 20 mM imidazole, pH 6.5, 100 mM KCl, 6 mM CaCl₂, and 0.02% w/v NaN₃. U-[²H,¹⁵N], ILV-¹³CHD₂ crab arginine kinase (AK) was prepared as described (Dodevski et al. 2014) using 99.9% v/v D₂O-M9 minimal medium. Isoleucine, leucine, and valine methyl groups were specifically labeled as [U-²H, Ile-δ₁-¹³CHD₂], [U-²H, Val -¹³CHD₂/¹²CHD₂], and [U-²H, Leu-¹³CHD₂/¹²CHD₂] using the precursors and protocol previously described (Tugarinov et al. 2006). The NMR sample was ~75 μM in protein in 10 mM sodium citrate, 50 mM sodium chloride, pH 6.0. U-[²H,¹⁵N] maltose binding protein (MBP) was prepared as described using 99.9% v/v D₂O-M9 minimal medium (Nucci et al. 2011). The NMR sample was ~700 μM in protein in 20 mM sodium phosphate, pH 7.5, and 5 mM EDTA.

NMR spectroscopy

All data were recorded on Bruker AVANCE III spectrometers equipped with TXI cryoprobes and z-axis pulse field gradients. TopSpin 2.1 or 3.0 software was used for data collection. The temperature was calibrated prior to data collection using a sample of 99.8% d₄-methanol (Findeisen et al. 2007). All relaxation experiments were collected as interleaved, pseudo-3D datasets where 1/3 of the total number of planes was duplicated for estimating uncertainties in peak height. NUS pulse programs were hardcoded to utilize a non-uniform dwell in TopSpin 2.1 syntax but were otherwise identical to the RSS versions with the exception of ²H relaxation experiments which required a receiver phase flip in the NUS versions for proper quadrature selection. NUS sampling schedules were generated using the PoissonGap2 program (Hyberts et al. 2012b). The sinusoidal weight was set to 2. The seed value for generating all schedules was 12321. Sampling schedules were not optimized or ranked prior to use. Experiment-specific parameters and delays for the RSS experiments are shown below. NUS experiments were setup identically to the RSS experiments but utilized 25% sampling in the indirect dimension.

¹⁵N T₁ experiments (Farrow et al. 1994) collected on ubiquitin were performed at 11.7 T at 25°C. The spectral widths were 10504.20 Hz (F2, ¹H) and 1417.64 Hz (F1, ¹⁵N), corresponding to 21 ppm and 28 ppm, respectively. The acquisition time in F2 was 97.5 ms while the acquisition time in F1 was varied between 33.9 ms and 141.0 ms. The delay durations were: 0.030 s (twice), 0.800 s, 0.084 s, 0.670 s (twice), 0.154 s, 0.549 s, 0.237 s, 0.435 s, 0.331 s (twice). 8 transients/FID were collected and the recycle delay was 2.0 s. ¹⁵N T₁ experiments collected on CaM were performed at 14.1 T at 35°C. The spectral widths were 13157.90 Hz (F2, ¹H) and 1700.91 (F1, ¹⁵N), corresponding to 22 ppm and 28 ppm, respectively. The acquisition time was 77.9 ms in F2 and 75.3 ms or 108.2 ms in F1. The delay durations were: 0.026 s (twice), 0.700 s, 0.073 s (twice), 0.587 s, 0.135 s, 0.480 s, 0.207 s, 0.381 s, 0.290 s (twice). 8 transients/FID were collected and the recycle delay was 2.0 s.

¹⁵N T₂ experiments (Farrow et al. 1994) collected on ubiquitin were performed at 11.7 T at 25°C. The spectral widths were 10504.20 Hz (F2, ¹H) and 1417.64 Hz (F1, ¹⁵N), corresponding to 21 ppm and 28 ppm, respectively. The acquisition time in F2 was kept constant at 97.5 ms while the acquisition time in F1 was either 33.9 ms or 84.7 ms. The delay durations were: 0.016 s (twice), 0.164 s, 0.033 s, 0.145 s (twice), 0.049 s, 0.131 s, 0.066 s, 0.099 s, 0.082 s (twice). 8 transients/FID were collected and the recycle delay was 2.0 s. The effective CPMG field was 4.0 kHz.

²H I_ZC_Z compensated R^Q(D_z) and R^Q(D₊) experiments (Millet et al. 2002) collected on ubiquitin were performed at 17.6 T at 25°C. The spectral widths were 15756.303 Hz (F2, ¹H) and 3713.302 (F1, ¹³C), corresponding to 21 ppm and 19.7 ppm, respectively. The acquisition time was 65.0 ms in F2 and 17.2 ms in F1. R^Q(D_z) delay durations were: 0.2 ms (twice), 20.0 ms, 2.1 ms, 16.8 ms (twice), 3.9 ms, 13.7 ms, 5.9 ms, 10.9 ms, 8.3 ms (twice). R^Q(D₊) delay durations were: 3.0 ms (twice), 75.0 ms, 8.0 ms, 63.0 ms (twice), 14.0 ms, 51.0 ms, 22.0 ms, 41.0 ms, 31.0 ms (twice). 48 transients/FID were collected and the recycle delay was 2.0 s. The R^Q(D₊) spin lock strength was 1.0 kHz.

¹³C T₁ and T_1ρ experiments (Tugarinov and Kay 2005) collected on AK were performed at 17.6T at 25°C. The spectral widths were 15756.303 Hz (F2, ¹H) and 3015.885 (F1, ¹³C), corresponding to 21 ppm and 16 ppm, respectively. The acquisition time was 65.0 ms in F2 and 33.1 ms in F1. ¹³C T₁ delay durations were 0.044 s, 1.200 s, 0.126 s (twice), 1.000 s (twice), 0.231 s, 0.823 s, 0.356 s, 0.653 s, 0.497 s (twice). ¹³C T_1ρ delay durations were 2.00 ms, 100.00 ms, 10.48 ms (twice), 83.81 ms (twice), 19.25 ms, 68.59 ms, 29.63 ms, 54.43 ms, 41.41 ms (twice). For the ¹³C T₁ experiment, 48 transients/FID were collected and the recycle delay was 2.5 s. For the ¹³C T_1ρ experiment, 64 transients/FID were collected and the recycle delay was 2.5 s. The ¹³C T_1ρ spin lock strength was 3.7 kHz.

TROSY-detected ¹⁵N T₁ and T_1ρ experiments (Lakomek et al. 2012) collected on AK were performed at 17.6T at 25°C. The spectral widths were 15756.303 Hz (F2, ¹H) and 2316.975 (F1, ¹⁵N), corresponding to 21 ppm and 30.5 ppm, respectively. The acquisition time was 65.0 ms in F2 and 27.6 ms in F1. ¹⁵N T₁ delay durations were 0.00 s, 2.00 s, 0.32 s (twice), 1.44 s (twice), 0.64 s, 0.96 s. ¹⁵N T_1ρ delay durations were 1.0 ms, 40.0 ms, 7.7 ms (twice), 30.5 ms (twice), 14.1 ms, 22.0 ms. For the ¹⁵N T₁ experiment, 128 transients/FID were collected and the recycle delay was 2.3 s. For the ¹⁵N T_1ρ experiment, 160 transients/FID were collected and the recycle delay was 2.3s. The ¹⁵N T_1ρ spin lock strength was 1.5 kHz. TROSY-detected ¹⁵N T₁ and T_1ρ experiments collected on ubiquitin in 30% glycerol were performed at 11.7T at 25°C. The spectral widths were 11961.72 Hz (F2, ¹H) and 1414.358 (F1, ¹⁵N), corresponding to 24 ppm and 28 ppm, respectively. The acquisition time was 85.7 ms in F2 and 90.5 ms in F1. ¹⁵N T₁ delay durations were 0.00 s, 0.88 s, 0.16 s (twice), 0.64 s (twice), 0.32 s, 0.48 s. ¹⁵N T_1ρ delay durations were 1.0 ms, 65.0 ms, 12.5 ms (twice), 49.5 ms (twice), 23.0 ms, 35.0 ms. 40 transients/FID were collected and the recycle delay was 2.5 s. The ¹⁵N spinlock field strength was 1.5 kHz. TROSY-detected ¹⁵N T₁ and T_1ρ experiments collected on MBP were performed at 17.6T at 35°C. The spectral widths were 15756.303 Hz (F2, ¹H) and 2354.952 Hz (F1, ¹⁵N), corresponding to 21 ppm and 31 ppm, respectively. The acquisition time was 65.0 ms in F2 and 84.9 ms in F1. ¹⁵N T₁ delay durations were 0.00 s, 2.00 s, 0.32 s (twice), 1.44 s (twice), 0.64 s, 0.96 s. ¹⁵N T_1ρ delay durations were 1.0 ms, 40.0 ms, 7.7 ms (twice), 30.5 ms (twice), 14.1 ms, 22.0 ms. 8 transients/FID were collected and the recycle delay was 3.0 s. The ¹⁵N spinlock field strength was 2.0 kHz.

All data were processed using NMRPipe/NMRDraw (Delaglio et al. 1995). All RSS and NUS data used for comparison were processed identically with the exception of the ²H relaxation experiments which required a sign alternating Fourier transform in the NUS dimension. NUS data were reconstructed using the hmsIST software (v. 211) (Hyberts et al. 2012b). A threshold of 98% and 400 iterations of IST were used for all data sets. Increasing the threshold value and number of iterations did not change the results described significantly (data not shown).

A subset of the data was also reconstructed with IRLS (Kazimierczuk and Orekhov 2011a) as implemented in the MddNMR software package (Orekhov and Jaravine 2011). All IRLS reconstructed data utilized 50 iterations.

A subset of the data was also reconstructed with the NESTA algorithm (Becker et al. 2011; Nesterov 2005) using L1 or IRL1 regularization (Candes et al. 2008) as implemented in the NESTA-NMR program (Sun et al. 2015). For L1 regularization, 50 iterations were used. For IRL1 regularization 30 iterations were used and the number of re-weighted iterations was set to 5. Increasing the number of iterations and number of re-weighted iterations did not change the results described significantly (data not shown).

The final matrix size for each RSS and NUS data set used in an individual comparison was identical.

Fitting of relaxation data

Relaxation rates were determined by quantification of the maximum cross peak height as a function of relaxation delay period using the built-in peak picking functionality and seriesTab program of NMRPipe/NMRDraw. Rates were fitted using in-house software written in Python to a two-parameter single exponential decay:

$$I(t)=I_{0}exp(-Rt)$$ (1)

Where I(t) is the cross peak height at relaxation delay time, t, and I₀ is the initial cross peak height. Best-fit parameters for rates, R, were determined using a Levenberg-Marquardt weighted non-linear least squares algorithm which minimizes χ², the sum of the square of the residuals:

$${\chi }^2=\sum _{n=1}^N\frac{{(I_{\mathit{calc}}(t)-I_{exp}(t))}^2}{{\sigma }^2}$$ (2)

Where I_calc(t) is the peak height at time t calculated from the fit, I_exp(t) is the experimentally measured peak height at time t, σ is the uncertainty in the peak height and N is the number of planes comprising the relaxation series. The uncertainty was taken to be the standard deviation of the differences in peak height based on replicate measurements scaled by $\sqrt{2}$ (Skelton et al. 1993). In cases where the data were collected with exceptional S/N, σ was increased by a factor of 2. Errors in the fitted parameters were obtained from the covariance matrix of the fitting routine or from 250–500 Monte Carlo simulations (Kamath and Shriver 1989) where the sampling bounds were defined by the uncertainty in peak height. Errors obtained from both methods were generally in good agreement.

Statistical analysis

Relaxation rates and peak heights derived from RSS and NUS were compared using the square of the Pearson correlation coefficient (R²) and the RMSD. R² values were calculated as:

$$R^2={\left[\frac{{\displaystyle \sum _k^n}(y_k^{\mathit{RSS}}-{\overline{y}}^{\mathit{RSS}})(y_k^{\mathit{NUS}}-{\overline{y}}^{\mathit{NUS}})}{\sqrt{{\displaystyle \sum _k^n}{(y_k^{\mathit{RSS}}-{\overline{y}}^{\mathit{RSS}})}^2{(y_k^{\mathit{NUS}}-{\overline{y}}^{\mathit{NUS}})}^2}}\right]}^2$$ (3)

RMSD was calculated as:

$$\mathit{RMSD}=\sqrt{\frac{{\displaystyle \sum _k^n}{(y_k^{\mathit{RSS}}-y_k^{\mathit{NUS}})}^2}{n}}$$ (4)

Where y is any NMR observable (e.g. peak height, relaxation rate) for a given cross peak, k, and n is the total number of cross peaks. The overbar denotes the mean value. In cases where RMSD is reported as a percentage, it has been normalized by the mean value of the NUS-derived observables.

Percent error was calculated as:

$$\mathit{Error}=\frac{|y_k^{\mathit{NUS}}-y_k^{\mathit{RSS}}|}{y_k^{\mathit{RSS}}}\times 100$$ (5)

where y is any NMR observable (e.g. peak height, relaxation rate) for a given cross peak, k. In cases where error distributions are shown, the absolute value is not calculated. Comparison of RSS and NUS data was performed only for sites where the quality of fit was sufficiently high in the RSS reference as judged by the reduced chi-squared value.

The interquartile range (IQR) method was used to identify outliers using in-house software as previously described (Fu et al. 2012). Briefly, any metric exhibiting > 1.5 times the IQR above the third quartile or below the first quartile was considered an outlier.

In some cases, linear regression was performed where both dependent and independent variables had associated uncertainties. Under these conditions, regression was performed using the orthogonal distance regression method (Boggs and Rogers 1990). This was accomplished using the ODRPACK FORTRAN-77 library implemented in SciPy (Oliphant et al. 2001 http://www.scipy.org/) and employs a Levenberg-Marquardt minimization for parameter estimation. Initial guesses for the fitted parameters were the best-fit parameters from a standard un-weighted linear regression.

Results

Choice of sampling density

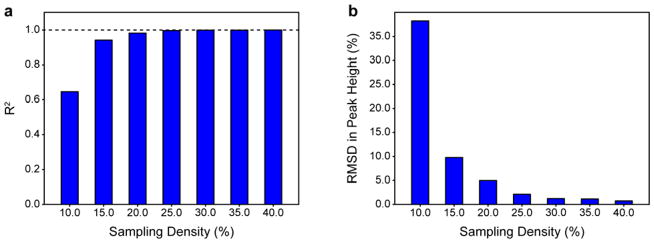
IST belongs to a larger family of compressed sensing (CS) techniques that seek to reconstruct data objects from an incomplete number of data samples. Theory indicates that this can be done by minimizing a regularization term, such as the ℓ_p -norm (for p ∈ [0,1]), of the preferred solution provided that the object is sufficiently sparse (Candes et al. 2006; Candes and Wakin 2008; Donoho and Stark 1989; Kazimierczuk and Orekhov 2012; Logan 1965; Stern et al. 2007). In general, frequency-domain NMR data and noise do not meet this requirement so the predictive value of CS theory in this context is limited (Kazimierczuk and Orekhov 2011b). In qualitative terms, it is well known that the sampling density (percentage of total points collected in the NUS dimension) must increase with decreasing dimensionality and increasing cross peak number and spectral complexity. Formally, the number of cross peaks must be considered independently for each vector. Previous work has recommended that ~20% sampling be used per NUS dimension (Hyberts et al. 2014) based on the number and distribution of cross peaks for proteins typically studied using NMR, though it was noted that this recommendation may not be applicable in all contexts. Therefore, the optimal sampling density for an HSQC-type correlation experiment that would typically be employed in a classical pseudo-3D relaxation experiment was determined first. Of interest is the fidelity of the NUS-reconstructed peak height relative to the same peak height derived using RSS. Fig. 1 shows the dependence of the R² and the RMSD in peak height between RSS sampled and NUS ¹⁵N HSQC experiments collected on ubiquitin with a moderate number of sampled points in the indirect dimension (120* RSS points, 28 ppm spectral width). The number of transients was kept constant and only sampling density was allowed to vary. The total number of points after reconstruction was the same for all data. Consistent with previous work, IST reconstruction is shown to yield highly linear peak heights with respect to RSS-derived references and 20% sampling yields quantitatively accurate peak heights with a R² of 0.982 and a RMSD of 4.97%. The fidelity of NUS-derived peak heights begins to plateau at 25% sampling with a R² of 0.996 and a RMSD of 1.15%. Therefore, all subsequent studies employed 25% sampling.

Fig. 1.

The accuracy of NUS-derived peak heights depends strongly on sampling density. Regular sequentially sampled (RSS)-derived and NUS-derived peak heights for a ¹H-¹⁵N HSQC of ubiquitin are compared quantitatively as a function of sampling density. (a) Dependence of the R² for the correlation between RSS-derived and NUS-derived peak heights as a function of sampling density. (b) Dependence of the RMSD of the same correlation as a function of sampling density. The number of transients and spectral width of the NUS dimension were kept constant and the final size of all reconstructed data was identical to that of the RSS data.

Evaluation of NUS-derived relaxation rates

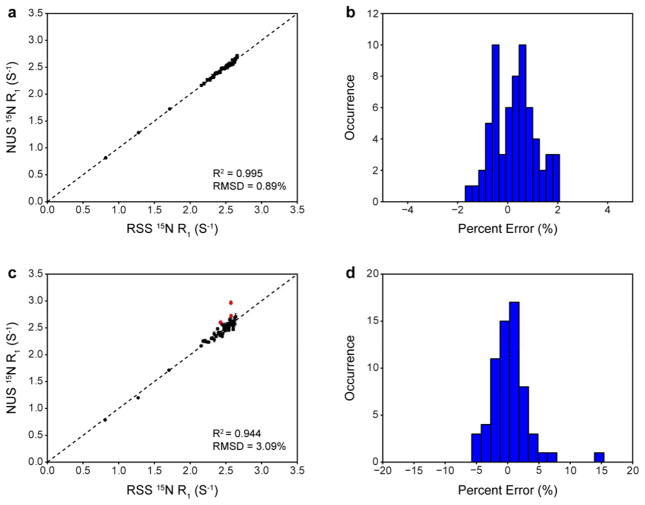
In order to assess the reliability of NUS-derived relaxation rates, RSS and NUS ¹⁵N T₁ relaxation experiments (Farrow et al. 1994) were performed on ubiquitin. The NUS data was collected experimentally rather than derived from re-sampling of the RSS reference data set because small but sometimes significant differences between experimentally-determined rates and re-sampled rates were observed (Fig. S1). The origin of these differences is not clear but it does not seem to be due to spectrometer stability as the data were collected in an interleaved manner and replicates of the entire RSS and NUS time series yield highly similar results (vide infra). The data were collected with the same moderate number of points in the indirect dimension (120* RSS points, 30* NUS points, 28 ppm spectral width). In the analysis that follows, the accuracy of an NUS-derived relaxation rate is judged with respect to the same rate derived from a RSS reference data set. Fig. 2a shows the correlation between R₁ rates derived from RSS and 25% NUS. Relaxation decays obtained from NUS data were nearly identical to those obtained from RSS data (Fig. S2). Uncertainties in peak heights (estimated from duplicate spectra) and errors in fitted rates were slightly larger for NUS-derived data (Fig. S3), which indicates that NUS-derived peak heights are less reproducible than RSS-derived peak heights. The correlation between relaxation rates derived from RSS and NUS is excellent, with a R² of 0.995 and a RMSD of 0.89%. A histogram of the errors between RSS-derived and NUS-derived rates indicates that they are normally distributed around a mean value near zero (0.29%) with a standard deviation of 0.82% (Fig. 2b). It should be noted that the largest error observed (~2.0%) is comparable to the typical reproducibility of RSS data for this particular experiment (Ferrage et al. 2008; Skelton et al. 1993). This finding is in contrast to a previous report that relaxation rates derived from Poisson-gap sampling and IST reconstruction are systematically offset by ~5% (Hyberts et al. 2014). This suggests that 25% sampling comprised of 30* NUS points is sufficient to obtain quantitatively accurate relaxation rates from reconstructed spectra of ubiquitin.

Fig. 2.

Quantitative evaluation of NUS-derived relaxation rates as a function of number of sampled NUS points for a ¹⁵N T₁ experiment on ubiquitin. (a) Correlation between RSS-derived and NUS-derived rates for data collected with 30* NUS points. The dotted line is y = x. (b) Distribution of errors in NUS-derived relaxation rates calculated relative to RSS-derived rates for data collected with 30* NUS points. (c) Correlation between RSS-derived and NUS-derived rates for data collected with 12* NUS points. The dotted line is y = x. Outliers identified using the IQR method are shown in red. (d) Distribution of errors in NUS-derived relaxation rates calculated relative to RSS-derived rates for data collected with 12* NUS points.

While sampling densities of 20–25% have been previously reported in the literature to yield quantitatively accurate peak heights (Hyberts et al. 2012b) and relaxation dispersion parameters (Linnet and Teilum 2016) for 2D spectra of other proteins, the choice of the total number of points used in such studies is often not fully explained. Indeed, there is no general consensus for how far an indirect dimension should be sampled (Hyberts et al. 2013) though the signal-to-noise ratio (S/N) is maximized when the indirect dimension is sampled to 1.26*T₂ (Rovnyak et al. 2004) and resolution is maximized when the indirect dimension is sampled to 3.14*T₂. However, recent work has shown that weighted NUS can lead to simultaneous improvements in S/N and resolution beyond 1.26*T₂ (Palmer et al. 2015). Sampling to maximize the resolution or sometimes even the S/N can lead to prohibitively long experiment times for serially collected data. It is also difficult to define a minimum number of sampled NUS points required for faithful reconstruction a priori since many confounding issues contribute to the quality of NUS reconstruction. Moreover, it has been noted that the probability of finding a “good” Poisson-gap sampling schedule decreases as the number of desired points decreases, presumably due to the stochastic nature of small sets (Hyberts et al. 2012a). The extent to which the total number of points could be decreased was thus explored empirically while maintaining a fixed sampling density. Fig. 2c shows the correlation between R₁ rates derived from RSS and NUS where the total number of points had been reduced by a factor of 2.5 but a 25% sampling density was maintained (48* RSS points, 12* NUS points, 28 ppm spectral width). Perhaps surprisingly, as few as 12* NUS points yielded interpretable spectra albeit with noticeable artifacts. All resolved cross peaks exhibited typical relaxation decays that still could be fit. It is clear, however, that the accuracy of the rates has been compromised significantly by such drastic undersampling. The correlation has a R² of 0.944 and a RMSD of 3.09%. Three statistically significant outliers were identified using the interquartile range (IQR) method and these outliers are shown in red. Fig. 2d shows the distribution of errors between RSS-derived and NUS-derived rates. Though the errors are still normally distributed around a mean value near zero (0.39%), the spread is much larger, with a standard deviation of 3.06%. The three statistically significant outliers exhibit errors over 5.0%, with a maximum error of 15.4%. Though it is difficult to attribute a single source to the degradation in accuracy, it may arise due to consequences associated with violation of the sparseness condition for CS and/or the increased difficulty associated with generating a proper sine-weighted Poisson distribution of gaps for 12* points.

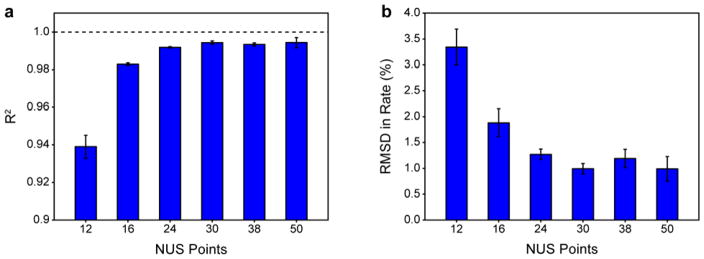
Based on the stark differences in performance between the data collected with 30* NUS points and 12* NUS points, additional RSS- and NUS-derived ¹⁵N T₁ comparisons were collected to gauge the relationship between the number of NUS points and the accuracy in rates empirically. Each experiment utilized a different number of total points but with a constant sampling density of 25%. In order to estimate contributions from experimental variance, each full RSS/NUS comparison was collected in triplicate—with replicate measurements often occurring several months apart. The statistics for each RSS/NUS comparison were determined individually and then averaged. In general, comparisons were highly reproducible. Fig. 3 shows the relationship between R² (Fig. 3a) and RMSD (Fig. 3b) in relaxation rate and total number of sampled points. The accuracy of NUS-derived relaxation rates exhibits a rather steep dependence on the total number of sampled points. The dependence appears to plateau at 30* points where the number of measurements is sufficiently high to accurately reconstruct the spectrum of ubiquitin. Increasing the total number of sampled points beyond this does not lead to improvement.

Fig. 3.

The accuracy of NUS-derived relaxation rates depends strongly on the number of sampled NUS points at a fixed sampling density of 25%. RSS-derived and NUS-derived ¹⁵N R₁ rates for ubiquitin are compared quantitatively for spectra collected with a variable number of points at a constant spectral width. (a) Dependence of the R² on the number of NUS points. (b) Dependence of the RMSD on the number of NUS points. Error bars are one standard deviation from the mean of three independent replicate data sets.

Since the data shown in Fig. 3 consisted of variable numbers of NUS points, each bar represents a different sized matrix. To explore if this affected peak height reconstruction, all of the RSS and NUS data were re-processed to a uniform size of 512* points in the indirect dimension via zero-filling. The observed dependencies did not change significantly (Fig. S4).

The nature of inaccuracies in NUS-derived relaxation rates

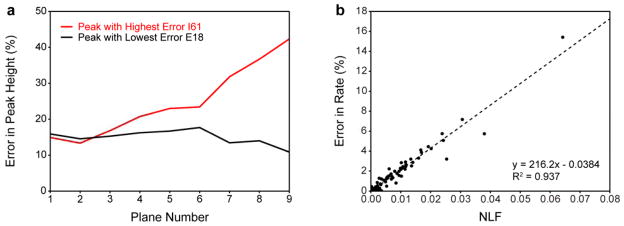
To understand the nature of inaccurate NUS-derived relaxation rates, the fidelity of peak height reconstruction was further characterized for the data set collected with 12* NUS points, which exhibited the largest deviations from the reference RSS-derived rates. Errors in NUS-derived relaxation rates did not correlate with errors in NUS-derived peak heights from any plane in the relaxation series (Fig. S5). Instead, the largest errors in relaxation rate tended to originate from cross peaks with inconsistent errors in peak height across the relaxation series. Fig. 4a illustrates this point by showing the error in reconstructed peak height as a function of relaxation plane number. Data is shown for the cross peak with the highest error in NUS-derived relaxation rate and the cross peak with lowest error in NUS-derived relaxation rate. Both cross peaks exhibited inaccurate peak height reconstruction in the first plane of the relaxation series (~15% error). However, their respective errors in relaxation rate ultimately differed by over 15 fold. The cross peak with the lowest error in relaxation rate maintained nearly the same ~15% peak height error across the entire relaxation series (standard deviation in peak height error ~2%). The cross peak with the highest error in NUS-derived relaxation rate exhibited a peak height error which increased dramatically and in a non-linear fashion across the relaxation series (standard deviation in peak height error ~10%). This demonstrates that changes in the consistency of peak height reconstruction can manifest as large changes in relaxation rate. It is important to note that these data were collected in an interleaved manner so the observed non-linearity is unlikely to arise due to spectrometer stability. Importantly, similar trends were also observed for data that were not as significantly undersampled.

Fig. 4.

Inaccuracy in NUS-derived relaxation rates stem from a lack of peak height reconstruction consistency. Errors in NUS-derived peak heights and relaxation rates calculated relative to RSS-derived references were quantitatively analyzed for ¹⁵N R₁ rates of ubiquitin for data collected with 12* NUS points (a) Error in NUS-derived peak height as a function of relaxation plane number (relaxation delay) for the cross peak with the largest error in NUS-derived relaxation rate (red) and the cross peak with the smallest error in NUS-derived relaxation rate (black). (b) The error in NUS-derived relaxation rate as a function of the non-linearity factor (NLF) (see full text and Fig. S6 for a more complete explanation). The NLF is a cross peak specific metric that is correlated with the error in NUS-derived relaxation rate. The dotted line is the best-fit line determined by linear regression: y = 216.2x − 0.0384, R² = 0.937.

The consistency of peak height reconstruction was then quantitatively evaluated. For each cross peak, the RSS-derived peak height was plotted against the NUS-derived peak height for each plane in the relaxation series and the result was fitted to a straight line. The deviation of the fitted intercept from zero is used an estimate of the non-linearity in peak height across all planes in the relaxation series (the reasoning behind this approach is illustrated in more detail in Fig. S6). We define the absolute value of the fitted intercept as the “non-linearity factor.” The nonlinearity factor is a cross peak specific quantification of how non-linear peak height reconstruction is across a relaxation series. Fig. 4b shows that the non-linearity factor of each cross peak is strongly correlated with the error in its NUS-derived relaxation rate. This indicates that the consistency of peak height reconstruction across the relaxation series is a strong determinant of the accuracy of NUS-derived relaxation rates. Such behavior could not be detected by just comparing peak heights to a single RSS reference plane as has been done in the optimization of sampling schedule generators (Aoto et al. 2014) or determination of minimum sampling density (Linnet and Teilum 2016).

The average of all non-linearity factors reports on the overall accuracy of an entire NUS relaxation series and is useful for comparing the performance of different relaxation series. Fig. 5 shows that the average non-linearity factor scales with the total number of sampled points and converges once the number of sampled points is sufficiently high to accurately reconstruct the spectrum of ubiquitin. The average non-linearity factor decreases substantially as a function of sampled points, though it never reaches zero, even when as many as 50* NUS points are used.

Fig. 5.

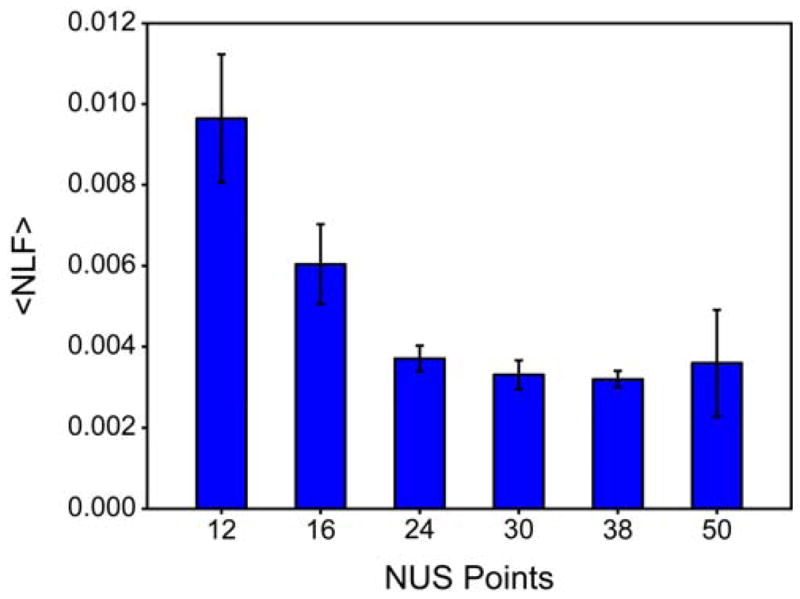
Peak height reconstruction linearity improves as a function of the number of NUS points at a fixed sampling density of 25%. The average non-linearity factor (NLF) decreases with increasing number of NUS points.

Generalization to other reconstruction algorithms

In order to assess if the non-linearity in peak height reconstruction was specific to the IST implementation in hmsIST, the ubiquitin ¹⁵N T₁ data sets collected with 12* and 30* NUS points were re-processed with IRLS, NESTA-L1, and NESTA-IRL1. While all three algorithms could reconstruct the 30* NUS points data, only IRLS yielded quantifiable reconstructions for the 12* points data. The accuracy of the rates relative to the RSS reference data is shown in Table S1. In general, IRLS yielded rates with accuracies comparable to those obtained using hmsIST whereas NESTA-L1 and NESTA-IRL1 yielded slightly less accurate rates.

Fig. S7a–d shows the error in reconstructed peak height as a function of relaxation plane number for the cross peak which exhibited the highest error in relaxation rate and the cross peak which exhibited the lowest error in relaxation rate. Again, high errors in relaxation rate are shown to arise from non-linearities in peak height across the relaxation series as was demonstrated for data reconstructed with hmsIST, though the nature of the non-linearity seems to be variable. Importantly, errors in NUS-derived relaxation rates are found to be strongly correlated with non-linearity factors as shown Fig. S7e–h. All correlations yielded R² values greater than 0.8, indicating that peak height non-linearity may be a general origin of errors in NUS-derived relaxation rates and not just specific to reconstructions performed using hmsIST.

Generalization to other proteins

Additional RSS/NUS comparisons using the proteins calcium-saturated calmodulin (CaM), arginine kinase (AK), and maltose binding protein (MBP) were collected to assess the generality of these findings. Table S2 shows the relevant protein details and statistics for each of these experiments. In each experiment, the minimum number of scans to obtain reliable RSS data was used and then the remaining time was invested toward sampling of the indirect dimension. Most experiments yielded high correlations (R² > 0.95) with reasonable RMSDs (< 4%). Additionally, poorer correlations and RMSDs were again shown to improve dramatically with an increase in NUS points as evidenced by the CaM data which exhibits twice as many cross peaks as ubiquitin and limited spectral dispersion. Notably, all data shown in Table S2 exhibit a correlation between errors in NUS-derived relaxation rate and nonlinearity factors (<R²> = 0.769 ± 0.141; n = 14). These data confirm that the conclusions drawn from the ubiquitin data are general to many types of relaxation measurements and to proteins with different properties. Perhaps the most impressive example of this is the ¹³C relaxation data collected on a very dilute (~75 μM) solution of the 40 kDa monomer arginine kinase (AK). Though ¹³C relaxation experiments are quite sensitive, the rather dilute sample and room temperature data collection make their execution challenging. In this sample, only ILV methyl groups are labeled so the total number of peaks of low. However, the narrow chemical shift dispersion for ILV methyl groups results in a high density of peaks for each directly detected frequency. Despite this, the R² values were ~0.98 – 0.99 and the RMSDs were only ~4 – 5.5% using 26* NUS points.

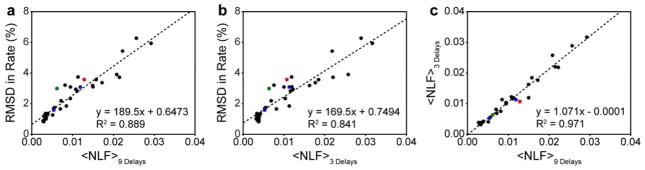
Since all of the proteins used in this study exhibit different degrees of spectral complexity and data were collected at different static field strengths, utilized different spectral widths, and consist of different numbers of total NUS points, it is extremely difficult to present a truly complete comparison across all data sets. However, a reasonably fair comparison can be made with respect to non-linearity factors. Fig. 6a shows that for all data presented here, the average non-linearity factor is approximately linearly related to the accuracy of NUS-derived relaxation rates. The relationship in Fig. 6a is essentially a calibration curve that allows one to identify a required average non-linearity factor necessary to obtain a desired accuracy in relaxation rate. For example, if one desired NUS-derived relaxation rates with less than a 5% RMSD relative to RSS-derived reference rates, then the average non-linearity factor should be ~0.02, or for 2% RMSD then it should be 0.007 or better, and so on.

Fig. 6.

Calibration curve relating RMSD in relaxation rate to the normalized sum of non-linearity factors where normalization is done by the number of cross peaks used to calculate the sum of the non-linearity factors. Points in black were obtained by IST reconstruction using hmsIST. Points in blue were obtained by IRLS reconstruction using MddNMR. The point in red was obtained by NESTA-IRL1 reconstruction using NESTA-NMR and the point in green was obtained by NESTA-L1 reconstruction using NESTA-NMR. (a) Correlation between RMSD in relaxation rate and average non-linearity factor (<NLF>) determined from all nine delay times. (b) Correlation between RMSD in relaxation rate and <NLF> determined from only three delay times. The goodness of fit indicates that using the three time point duplicates routinely used to estimate intensity uncertainty and in RSS mode are sufficient to confirm the accuracy of obtained relaxation rates. (c) Correlation between <NLF> values determined from nine and three delay times.

Predicting non-linearity factors from reference data

The calibration curve shown in Fig. 6a is only useful if non-linearity factors can be determined prior to full data collection. Ideally, it is most desirable to determine the reliability of a given NUS scheme with little or no penalty in spectrometer time. We therefore explored whether it is possible to estimate non-linearity factors from a smaller set of data that could be collected prior to starting a suite of relaxation experiments. It is apparent that multiple RSS reference planes from the relaxation series must be collected. However, it is unclear how many are required and which planes should be used. Fig. S8a shows the correlation between non-linearity factors derived from a minimal set of data and those derived from a full relaxation series for an example ubiquitin ¹⁵N T₁ relaxation series. Fig. S8a. shows that non-linearity factors determined from just two planes are only modestly accurate. However, Fig. S8b. shows that non-linearity factors determined from three planes are quite accurate. This is perhaps unsurprising considering the non-linearity factor is derived by linear regression. It should be noted that the three planes that were chosen were the shortest delay time and the two longest delay times. This was determined empirically but is consistent with the typical nature of peak height non-linearity observed in this study. In order to test the generality of this method, all remaining data sets were subject to the same analysis. Fig. S8c–d shows that excellent estimations of non-linearity factors can be obtained for the less than ideal AK ¹³C T₁ relaxation data. Fig. 6b–c shows that average non-linearity factors estimated from three reference planes are indeed in superb agreement with non-linearity factors determined from entire time series for all data presented in this study.

Conclusions

Despite the recent renaissance in NUS methodology, quantitative experiments are still largely collected using RSS. This is primarily due to uncertainty regarding the fidelity of reconstructed peak heights. The purpose of this work was to investigate the practical aspects of applying NUS to classical spin relaxation experiments. Sampling density is often emphasized when setting up NUS experiments, however, it is often unclear how sensitive reconstructions are to the total number of NUS points. This coupled with the lack of a general consensus for how far indirect dimensions need to be sampled for a given spectrum and the need to align sampling with spectral complexity complicate the design of NUS experiments. As such, the relationship between the total number of NUS points collected with a fixed sampling density of 25% and the accuracy of relaxation rates was explored. For ubiquitin, it was found that accuracy in NUS-derived ¹⁵N R₁ rates improved sharply with the total number of points and plateaued near the inherent reproducibility of the experiment once the spectral sparseness and complexity were met.

Comprehensive error analysis shows that inaccurate rates arise from inconsistencies in peak height reconstruction across the relaxation series. These inconsistencies become more prevalent when the number of NUS points is not chosen appropriately and data are undersampled. This was demonstrated to be true for three other reconstruction algorithms, three different proteins with very different spectral properties, and eight types of relaxation measurements. Accordingly, the accuracy of reconstructed peak heights is of less importance for relaxation experiments. Since NUS reconstruction methodologies and sampling schedules are commonly evaluated on the basis of how accurately peak heights are reproduced relative to a single RSS reference spectrum only, additional evaluative measures must be included when assessing relaxation experiments. We have presented an empirically-derived calibration curve which relates the non-linearity in peak height reconstruction to errors in relaxation rate. By using three reference planes from the relaxation series (the shortest delay and two longest delays), nonlinearity factors can be estimated which report directly on the accuracy of NUS-derived relaxation rates. These three RSS reference planes can substitute for the duplicates normally collected to estimate uncertainty in peak height intensities for weighting in subsequent fitting of the relaxation profiles as long as the reconstruction algorithm used faithfully reproduces peak heights such as the ones used in this study. For example, our laboratory typically collects 9 relaxation time points with three duplicates. Thus, in this scenario, no time penalty in total acquisition time is incurred to obtained definitive assessment of the inherent accuracy of NUS-derived relaxation rate constants. Based on the available data, accurate rates (< 2% RMSD relative to RSS-derived reference data) can be obtained if the average non-linearity factors is < 0.007. We recommend estimating non-linearity factors from three reference planes prior to data collection in order to ensure that the obtained relaxation rates are reliable.